Effects of Applied Magnetic Field on the Optical Properties and Binding Energies Spherical GaAs Quantum Dot with Donor Impurity
Abstract
:1. Introduction
2. Theoretical Framework
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jia, C.-S.; Jia, Y. Relativistic rotation-vibrational energies for the Cs2 molecule. Eur. Phys. J. D 2017, 71, 3. [Google Scholar] [CrossRef]
- Edet, C.O.; Ikot, A.N. Effects of Topological Defect on the Energy Spectra and Thermo-magnetic Properties of CO Diatomic Molecule. J. Low Temp. Phys. 2021, 203, 84. [Google Scholar] [CrossRef]
- Jia, C.-S.; Zhang, L.-H.; Wang, C.-W. Thermodynamic properties for the lithium dimer. Chem. Phys. Lett. 2017, 667, 211. [Google Scholar] [CrossRef]
- Edet, C.O.; Ikot, A.N.; Onyeaju, M.C.; Okorie, U.S.; Rampho, G.J.; Lekala, M.L.; Kaya, S. Thermo-magnetic properties of the screened Kratzer potential with spatially varying mass under the influence of Aharanov-Bohm (AB) and position-dependent magnetic fields. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 131, 114710. [Google Scholar] [CrossRef]
- Edet, C.O.; Mahmoud, S.; Inyang, E.P.; Ali, N.; Aljunid, S.A.; Endut, R.; Ikot, A.N.; Asjad, M. Non-Relativistic Treatment of the 2D Electron System Interacting via Varshni–Shukla Potential Using the Asymptotic Iteration Method. Mathematics 2022, 10, 2824. [Google Scholar] [CrossRef]
- Edet, C.O.; Osang, J.E.; Ali, N.; Agbo, E.P.; Aljunid, S.A.; Endut, R.; Ettah, E.B.; Khordad, R.; Ikot, A.N.; Asjad, M. Non-Relativistic Energy Spectra of the Modified Hylleraas Potential and Its Thermodynamic Properties in Arbitrary Dimensions. Quantum Rep. 2022, 4, 238–250. [Google Scholar] [CrossRef]
- Edet, C.O.; Ettah, E.B.; Aljunid, S.A.; Endut, R.; Ali, N.; Ikot, A.N.; Asjad, M. Global Quantum Information-Theoretic Measures in the Presence of Magnetic and Aharanov-Bohm (AB) Fields. Symmetry 2022, 14, 976. [Google Scholar] [CrossRef]
- Edet, C.O.; Nwbabuzor, P.O.; Ettah, E.B.; Duque, C.A.; Ali, N.; Ikot, A.N.; Mahmoud, S.; Asjad, M. Magneto-transport and thermal properties of the Yukawa potential in cosmic string space-time. Results Phys. 2022, 39, 105749. [Google Scholar] [CrossRef]
- Edet, C.O.; Amadi, P.O.; Ettah, E.B.; Ali, N.; Asjad, M.; Ikot, A.N. The magnetocaloric effect, thermo-magnetic and transport properties of LiH diatomic molecule. Mol. Phys. 2022, 120, e2059025. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Edet, C.O.; Ikot, A.N. Non-relativistic quark model under external magnetic and Aharanov–Bohm (AB) fields in the presence of temperature-dependent confined Cornell potential. Can. J. Phys. 2021, 99, 1024. [Google Scholar] [CrossRef]
- Hall, R.L.; Saad, N. Schrödinger spectrum generated by the Cornell potential. Open Phys. 2015, 13, 83–89. [Google Scholar] [CrossRef]
- Fulcher, L.P.; Chen, Z.; Yeong, K.C. Energies of quark-antiquark systems, the Cornell potential, and the spinless Salpeter equation. Phys. Rev. D 1993, 47, 4122. [Google Scholar] [CrossRef]
- Yukawa, H. On the interaction of elementary particles. I. Proc. Phys.-Math. Soc. Jpn. 1935, 17, 48. [Google Scholar]
- Yukawa, T. Exchange potential between “nearly” identical nuclei. Phys. Rev. C 1974, 9, 864. [Google Scholar] [CrossRef]
- Edet, C.O.; Lima, F.C.E.; Almeida, C.A.S.; Ali, N.; Asjad, M. Quantum Information of the Aharanov–Bohm Ring with Yukawa Interaction in the Presence of Disclination. Entropy 2022, 24, 1059. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Khokha, E.M. Bound state solutions of the Dirac equation for the generalized Cornell potential model. Int. J. Mod. Phys. A 2021, 36, 2150195. [Google Scholar] [CrossRef]
- Morse, P.M. Diatomic molecules according to the wave mechanics. II. Vibrational levels. Phys. Rev. 1929, 34, 57. [Google Scholar] [CrossRef]
- Morse, P.M.; Stueckelberg, E.C.G. Diatomic molecules according to the wave mechanics I: Electronic levels of the hydrogen molecular ion. Phys. Rev. 1929, 33, 932. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Weizer, V.G. Application of the Morse potential function to cubic metals. Phys. Rev. 1959, 114, 687. [Google Scholar] [CrossRef]
- Gomez, I.S.; Santos, E.S.; Abla, O. Morse potential in relativistic contexts from generalized momentum operator: Schottky anomalies, Pekeris approximation and mapping. Mod. Phys. Lett. A 2021, 36, 2150140. [Google Scholar] [CrossRef]
- Okoi, P.O.; Edet, C.O.; Magu, T.O. Relativistic treatment of the Hellmann-generalized Morse potential. Rev. Mex. Fis. 2019, 66, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Jia, C.-S.; Wang, C.-W.; Zhang, L.-H.; Peng, X.-L.; Zeng, R.; You, X.-T. Partition function of improved Tietz oscillators. Chem. Phys. Lett. 2017, 676, 150. [Google Scholar] [CrossRef]
- Deng, Z.H.; Fan, Y.P. A Potential Function of Diatomic Molecules. J. Shandong Univ. (Nat. Sci.) 1957, 1, 11. [Google Scholar]
- Dong, S.-H. Relativistic treatment of spinless particles subject to a rotating Deng—Fan oscillator. Commun. Theor. Phys. 2011, 55, 969. [Google Scholar] [CrossRef]
- Edet, C.O.; Okorie, U.S.; Osobonye, G.; Ikot, A.N.; Rampho, G.J.; Sever, R. Thermal properties of Deng–Fan–Eckart potential model using Poisson summation approach. J. Math. Chem. 2020, 58, 989. [Google Scholar] [CrossRef]
- McChesney, M. Debye-Huckel Plasma Corrections. AIAA J. 1963, 1, 1666. [Google Scholar] [CrossRef]
- Kar, S. Dynamic dipole polarizability of the helium atom with Debye-Hückel potentials. Phys. Rev. A 2012, 86, 062516. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Bray, I. Electron scattering in a helium Debye plasma. Chem. Phys. 2012, 398, 214. [Google Scholar] [CrossRef]
- Mahdavi, M.; Akbarian, H. Calculation of effective potential of Hulthen interaction for a nonideal dense plasma using dielectric response method. Chin. J. Phys. 2021, 77, 1381–1386. [Google Scholar] [CrossRef]
- Yoon, J.H.; Yun, Y.S. Hulthen potential for the plasma-screening effect on the continuum electron capture rate in the solar core. J. Korean Phys. Soc. 2000, 37, 73. [Google Scholar]
- Bahar, M.K.; Soylu, A.; Poszwa, A. The hulthén potential model for hydrogen atoms in debye plasma. IEEE Trans. Plasma Sci. 2016, 44, 2297. [Google Scholar] [CrossRef]
- Sedehi, H.R.; Khordad, R. Magnetocaloric effect, magnetic susceptibility and specific heat of tuned quantum dot/ring systems. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 134, 114886. [Google Scholar] [CrossRef]
- Ikot, A.N.; Okorie, U.; Ngiangia, A.T.; Onate, C.A.; Edet, C.O.; Akpan, I.O.; Amadi, P.O. Bound state solutions of the Schrödinger equation with energy-dependent molecular Kratzer potential via asymptotic iteration method. Eclet. Quim. J. 2020, 45, 65. [Google Scholar] [CrossRef] [Green Version]
- Boyacioglu, B.; Chatterjee, A. Dia-and paramagnetism and total susceptibility of GaAs quantum dots with Gaussian confinement. Phys. E Low-Dimens. Syst. Nanostruct. 2012, 44, 1826. [Google Scholar] [CrossRef]
- Khordad, R. Pressure effect on optical properties of modified Gaussian quantum dots. Phys. B Condens. Matter 2012, 407, 1128. [Google Scholar] [CrossRef]
- Gharaati, A.; Khordad, R. A new confinement potential in spherical quantum dots: Modified Gaussian potential. Superlattices Microstruct. 2010, 48, 276. [Google Scholar] [CrossRef]
- Khordad, R.; Mirhosseini, B. Linear and nonlinear optical properties in spherical quantum dots: Rosen-Morse potential. Opt. Spectrosc. 2014, 117, 434. [Google Scholar] [CrossRef]
- Ebeling, W.; Sokolov, I. Statistical Thermodynamics and Stochastic Theory of Nonequilibrium Systems; World Scientific Publishing Company: Singapore, 2005; Volume 8. [Google Scholar]
- Oyewumi, K.J.; Falaye, B.J.; Onate, C.A.; Oluwadare, O.J.; Yahya, W.A. Thermodynamic properties and the approximate solutions of the Schrödinger equation with the shifted Deng–Fan potential model. Mol. Phys. 2014, 112, 127. [Google Scholar] [CrossRef]
- Jia, C.-S.; Zhang, L.-H.; Peng, X.-L.; Luo, J.-X.; Zhao, Y.-L.; Liu, J.-Y.; Guo, J.-J.; Tang, L.-D. Prediction of entropy and Gibbs free energy for nitrogen. Chem. Eng. Sci. 2019, 202, 70. [Google Scholar] [CrossRef]
- Jia, C.-S.; Wang, C.-W.; Zhang, L.-H.; Peng, X.-L.; Tang, H.-M.; Zeng, R. Enthalpy of gaseous phosphorus dimer. Chem. Eng. Sci. 2018, 183, 26. [Google Scholar] [CrossRef]
- Jia, C.-S.; Diao, Y.-F.; Liu, X.-J.; Wang, P.-Q.; Liu, J.-Y.; Zhang, G.-D. Equivalence of the Wei potential model and Tietz potential model for diatomic molecules. J. Chem. Phys. 2012, 137, 014101. [Google Scholar] [CrossRef]
- Hamzavi, M.; Ikhdair, S.M.; Thylwe, K.-E. Equivalence of the empirical shifted Deng–Fan oscillator potential for diatomic molecules. J. Math. Chem. 2013, 51, 227. [Google Scholar] [CrossRef]
- Edet, C.O.; Ikot, A.N.; Okorie, U.S.; Ramantswana, M.; Rampho, G.J.; Horchani, R.; Abdullah, H.Y.; Zahran, H.Y.; Obagboye, L.F.; Abdel-Aty, A.-H. Eigenfunctions, uncertainties and thermal properties of diatomic molecules under screened modified Kratzer potential. Indian J. Phys. 2022, 1, 1–20. [Google Scholar] [CrossRef]
- Donfack, B.; Mbognou, F.C.; Tedondje, G.T.; Cedric, T.M.; Fotue, A.J. Cumulative Effects of Laser and Spin–Orbit Interaction (SOI) on the Thermal Properties of Quantum Pseudo-dot. J. Low Temp. Phys. 2021, 206, 63–79. [Google Scholar] [CrossRef]
- Al, E.B.; Kasapoglu, E.; Sari, H.; Sokmen, I. Zeeman splitting, Zeeman transitions and optical absorption of an electron confined in spherical quantum dots under the magnetic field. Philos. Mag. 2021, 101, 117. [Google Scholar] [CrossRef]
- Acosta, R.E.; Morales, A.L.; Duque, C.M.; Mora-Ramos, M.E.; Duque, C.A. Optical absorption and refractive index changes in a semiconductor quantum ring: Electric field and donor impurity effects. Phys. Status Solidi (B) 2016, 253, 744. [Google Scholar] [CrossRef]
- Al, E.B. Effect of size modulation and donor position on intersubbands refractive index changes of a donor within a spherical core/shell/shell semiconductor quantum dot. Cumhur. Sci. J. 2021, 42, 694. [Google Scholar] [CrossRef]
- M’zerd, S.; Haouari, M.E.; Talbi, A.; Feddi, E.; Mora-Ramos, M.E. Impact of electron-LO-phonon correction and donor impurity localization on the linear and nonlinear optical properties in spherical core/shell semiconductor quantum dots. J. Alloys Compd. 2018, 753, 68. [Google Scholar] [CrossRef]
- Duque, C.M.; Mora-Ramos, M.E.; Duque, C.A. On-center donor impurity-related nonlinear corrections to optical absorption and refractive index in a two-dimensional quantum ring. Opt. Commun. 2012, 285, 5456. [Google Scholar] [CrossRef]
- Rastegar-Sedehi, H.R. Magnetocaloric effect in Rashba spin-orbit coupling and Zeeman splitting of a narrow nanowire quantum dot. Eur. Phys. J. Plus 2021, 136, 514. [Google Scholar] [CrossRef]
- Baghramyan, H.M.; Barseghyan, M.G.; Kirakosyan, A.A.; Laroze, D.; Duque, C.A. Donor-impurity related photoionization cross section in GaAs/Ga1- xAlxAs concentric double quantum rings: Effects of geometry and hydrostatic pressure. Phys. B Condens. Matter 2014, 449, 193. [Google Scholar] [CrossRef]
- Al, E.B.; Kasapoglu, E.; Sakiroglu, S.; Sari, H.; Sokmen, I.; Duque, C.A. Binding energies and optical absorption of donor impurities in spherical quantum dot under applied magnetic field. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 119, 114011. [Google Scholar] [CrossRef]
- Ozmen, A.; Yakar, Y.; Çakır, B.; Atav, U. Computation of the oscillator strength and absorption coefficients for the intersubband transitions of the spherical quantum dot. Opt. Commun. 2009, 282, 3999. [Google Scholar] [CrossRef]
- Al, E.B.; Kasapoglu, E.; Sari, H.; Sokmen, I. Optical properties of spherical quantum dot in the presence of donor impurity under the magnetic field. Phys. B Condens. Matter 2021, 613, 412874. [Google Scholar] [CrossRef]
- Wu, S.; Wan, L. Electronic structures in a CdSe spherical quantum dot in a magnetic field: Diagonalization method and variational method. J. Appl. Phys. 2012, 111, 063711. [Google Scholar] [CrossRef]
- Mathe, L.; Onyenegecha, C.P.; Farcas, A.-A.; Pioras-Ţimbolmas, L.-M.; Solaimani, M.; Hassanabadi, H. Linear and nonlinear optical properties in spherical quantum dots: Inversely quadratic Hellmann potential. Phys. Lett. A 2021, 397, 127262. [Google Scholar] [CrossRef]
- Khordad, R.B. Application of Tietz potential to study optical properties of spherical quantum dots. Mirhosseini Pramana 2015, 85, 723. [Google Scholar] [CrossRef]
- Berkdemir, C. Application of the Nikiforov-Uvarov method in quantum mechanics. In Theoretical Concepts of Quantum Mechanics; BoD—Books on Demand: Norderstedt, Germany, 2012; p. 225. [Google Scholar]
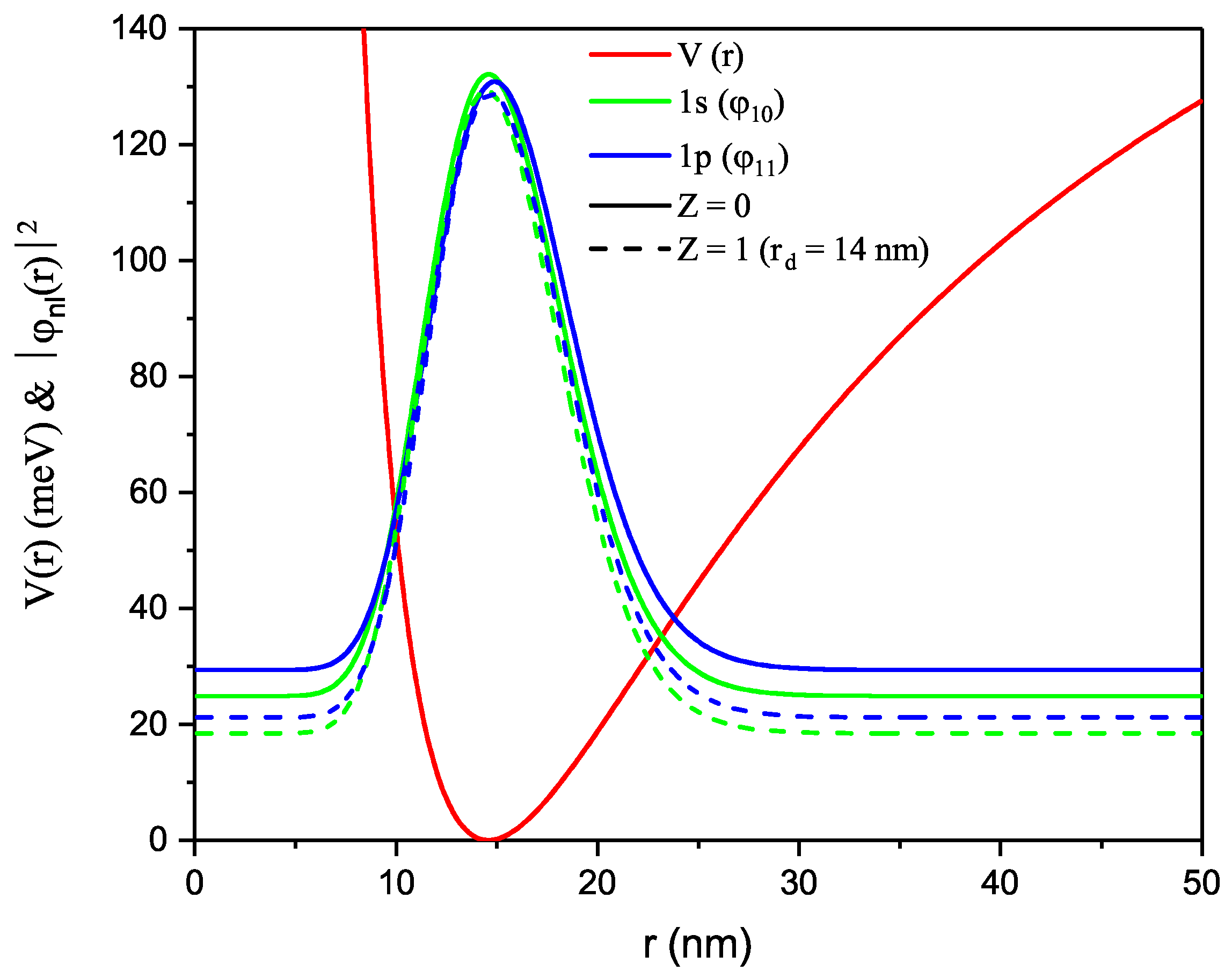
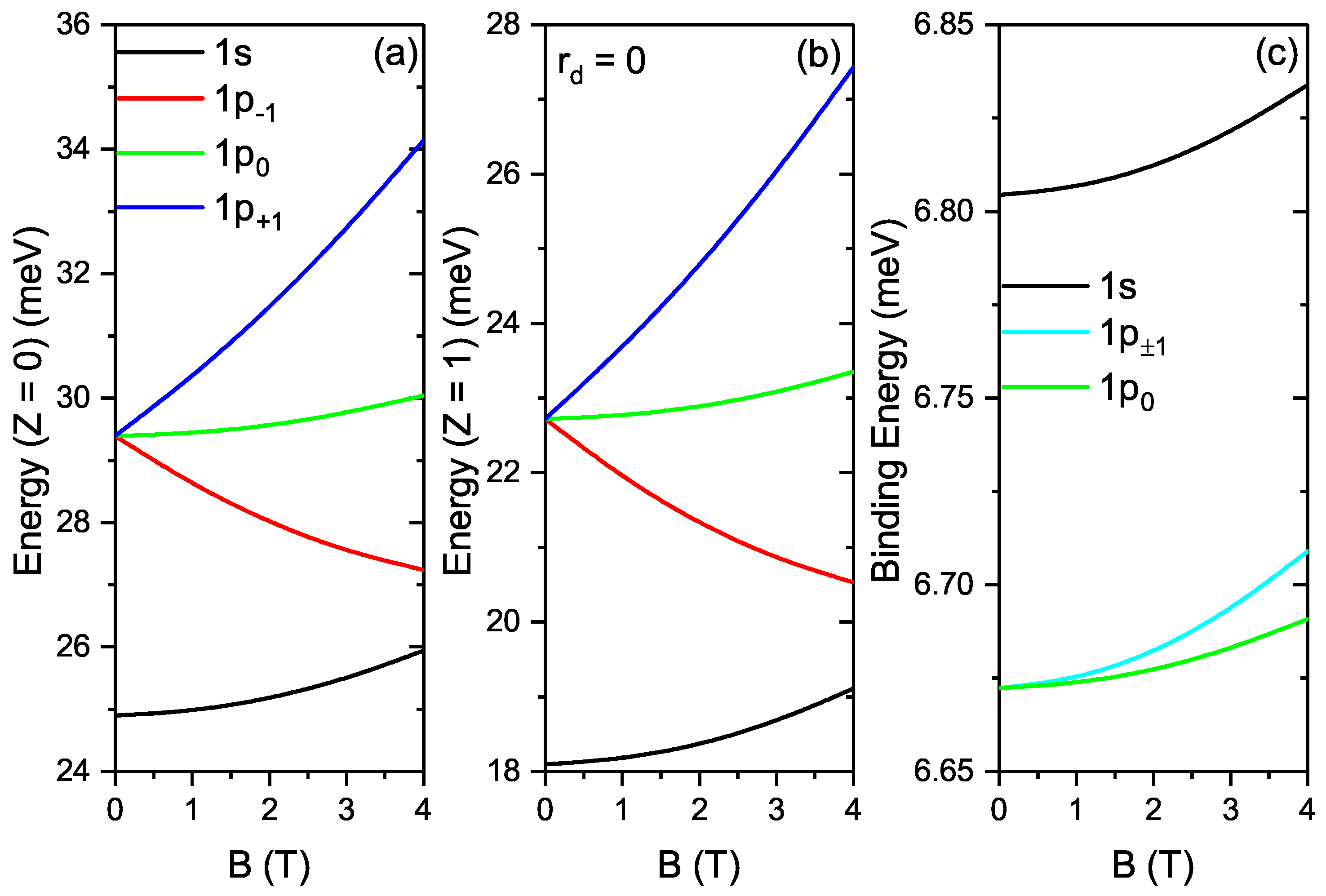
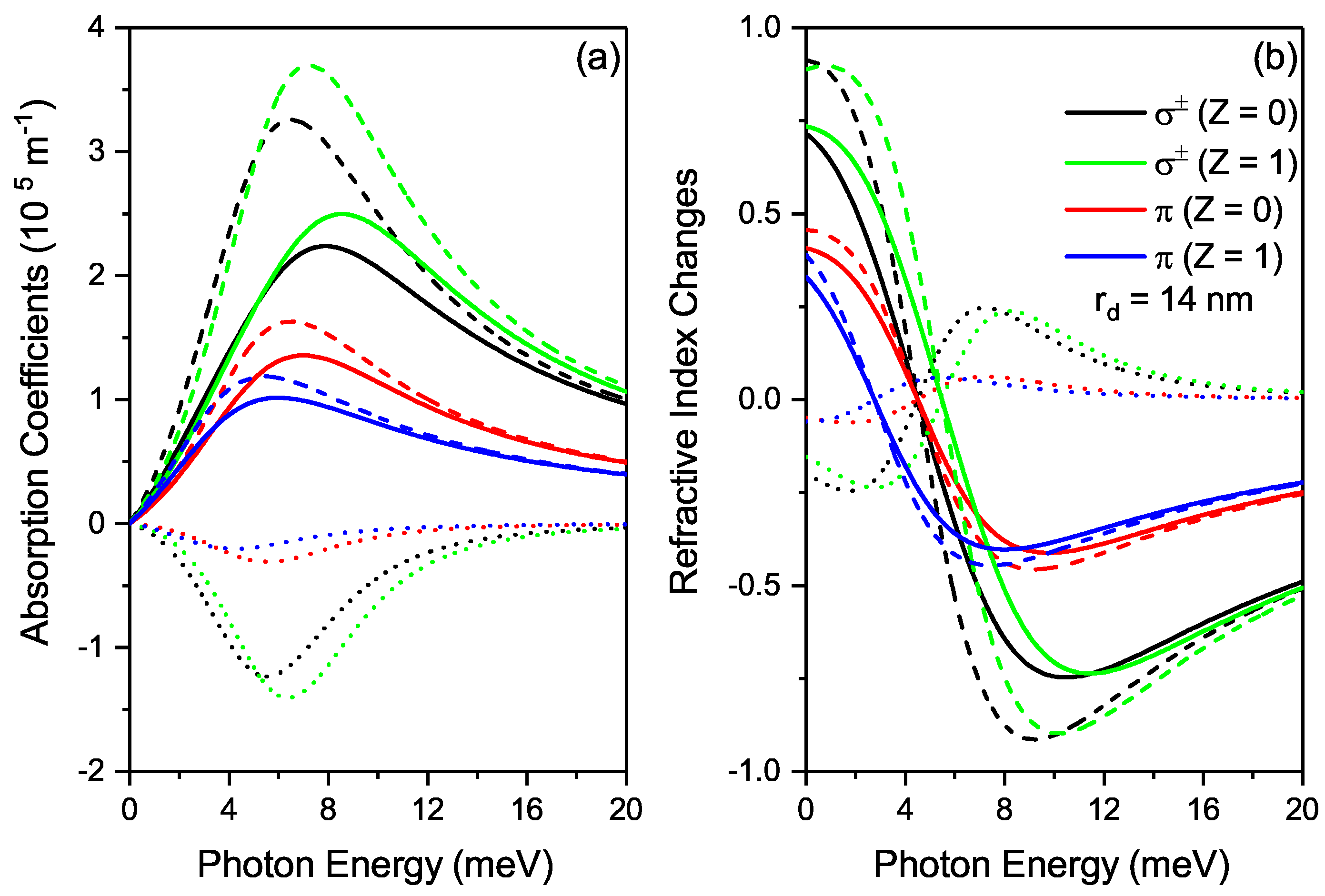

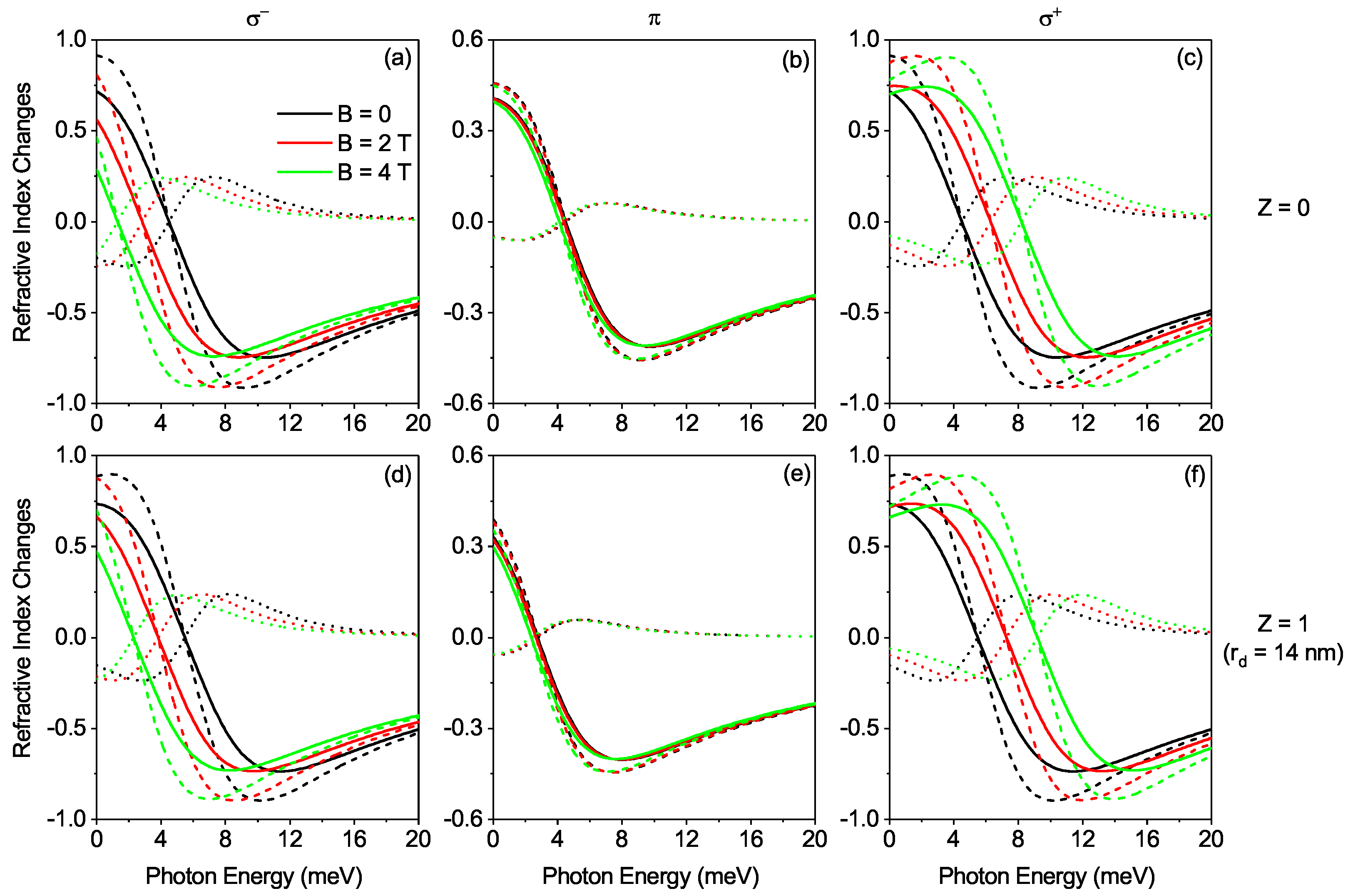
| B | 0 | 2T | 4T |
|---|---|---|---|
| 4.49174 | 2.83055 | 1.29578 | |
| 13.9468 | 13.9282 | 13.8737 | |
| 4.49174 | 4.39326 | 4.10013 | |
| 9.86191 | 9.85168 | 9.82146 | |
| 4.49174 | 6.28157 | 8.19782 | |
| 13.9468 | 13.9282 | 13.8737 | |
| 5.4793 | 3.81847 | 2.28483 | |
| 13.824 | 13.8066 | 13.7554 | |
| 2.75256 | 2.65404 | 2.36068 | |
| 9.74208 | 9.73287 | 9.70561 | |
| 5.4793 | 7.26949 | 9.18687 | |
| 13.824 | 13.8066 | 13.7554 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edet, C.O.; Al, E.B.; Ungan, F.; Ali, N.; Rusli, N.; Aljunid, S.A.; Endut, R.; Asjad, M. Effects of Applied Magnetic Field on the Optical Properties and Binding Energies Spherical GaAs Quantum Dot with Donor Impurity. Nanomaterials 2022, 12, 2741. https://doi.org/10.3390/nano12162741
Edet CO, Al EB, Ungan F, Ali N, Rusli N, Aljunid SA, Endut R, Asjad M. Effects of Applied Magnetic Field on the Optical Properties and Binding Energies Spherical GaAs Quantum Dot with Donor Impurity. Nanomaterials. 2022; 12(16):2741. https://doi.org/10.3390/nano12162741
Chicago/Turabian StyleEdet, Collins Okon, Emre Bahadir Al, Fatih Ungan, Norshamsuri Ali, Nursalasawati Rusli, Syed Alwee Aljunid, Rosdisham Endut, and Muhammad Asjad. 2022. "Effects of Applied Magnetic Field on the Optical Properties and Binding Energies Spherical GaAs Quantum Dot with Donor Impurity" Nanomaterials 12, no. 16: 2741. https://doi.org/10.3390/nano12162741
APA StyleEdet, C. O., Al, E. B., Ungan, F., Ali, N., Rusli, N., Aljunid, S. A., Endut, R., & Asjad, M. (2022). Effects of Applied Magnetic Field on the Optical Properties and Binding Energies Spherical GaAs Quantum Dot with Donor Impurity. Nanomaterials, 12(16), 2741. https://doi.org/10.3390/nano12162741










