Nanoparticle Sphericity Investigation of Cu-Al2O3-H2O Hybrid Nanofluid Flows between Inclined Channels Filled with a Porous Medium
Abstract
:1. Introduction
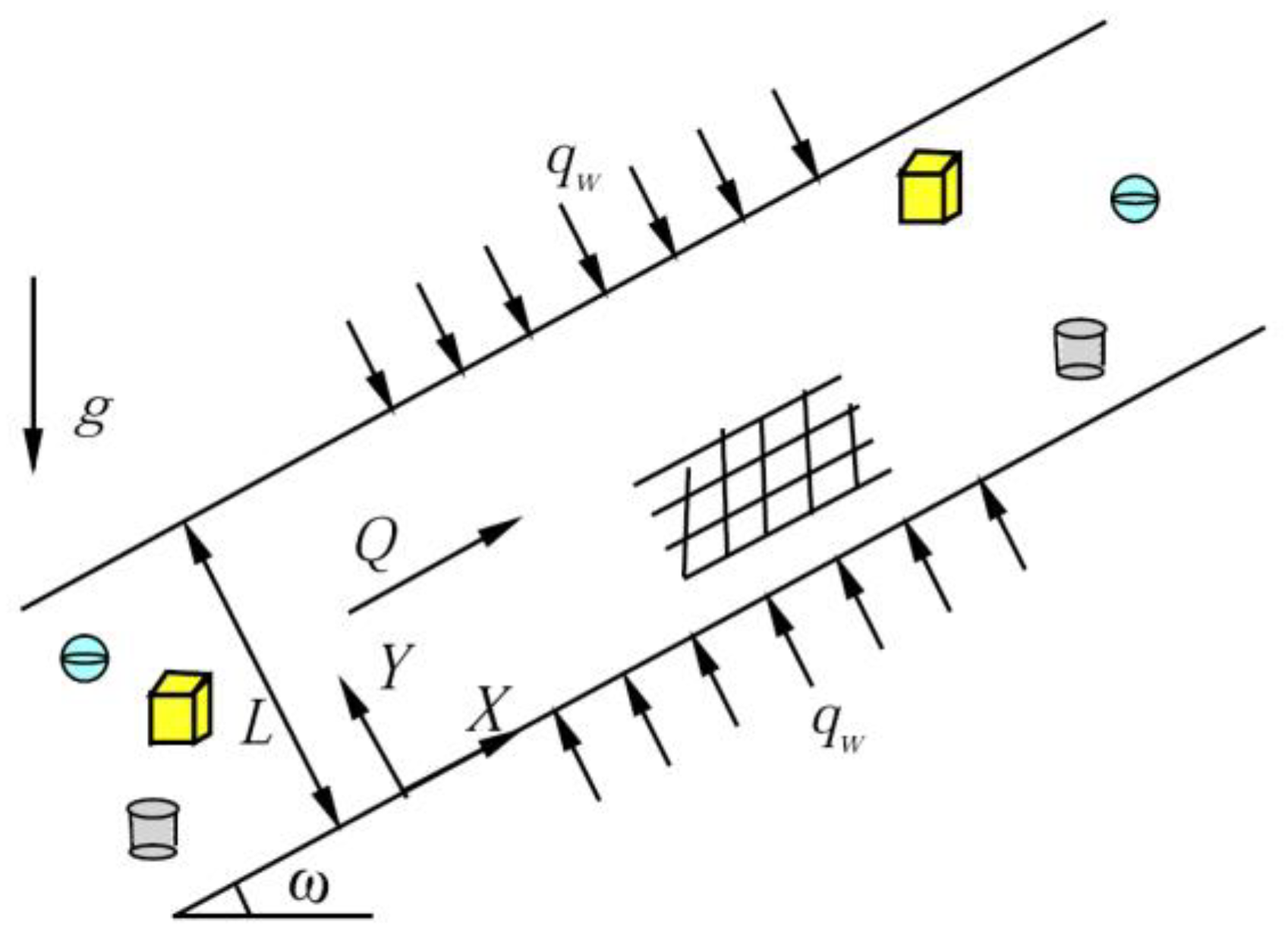
2. Model of Mathematics
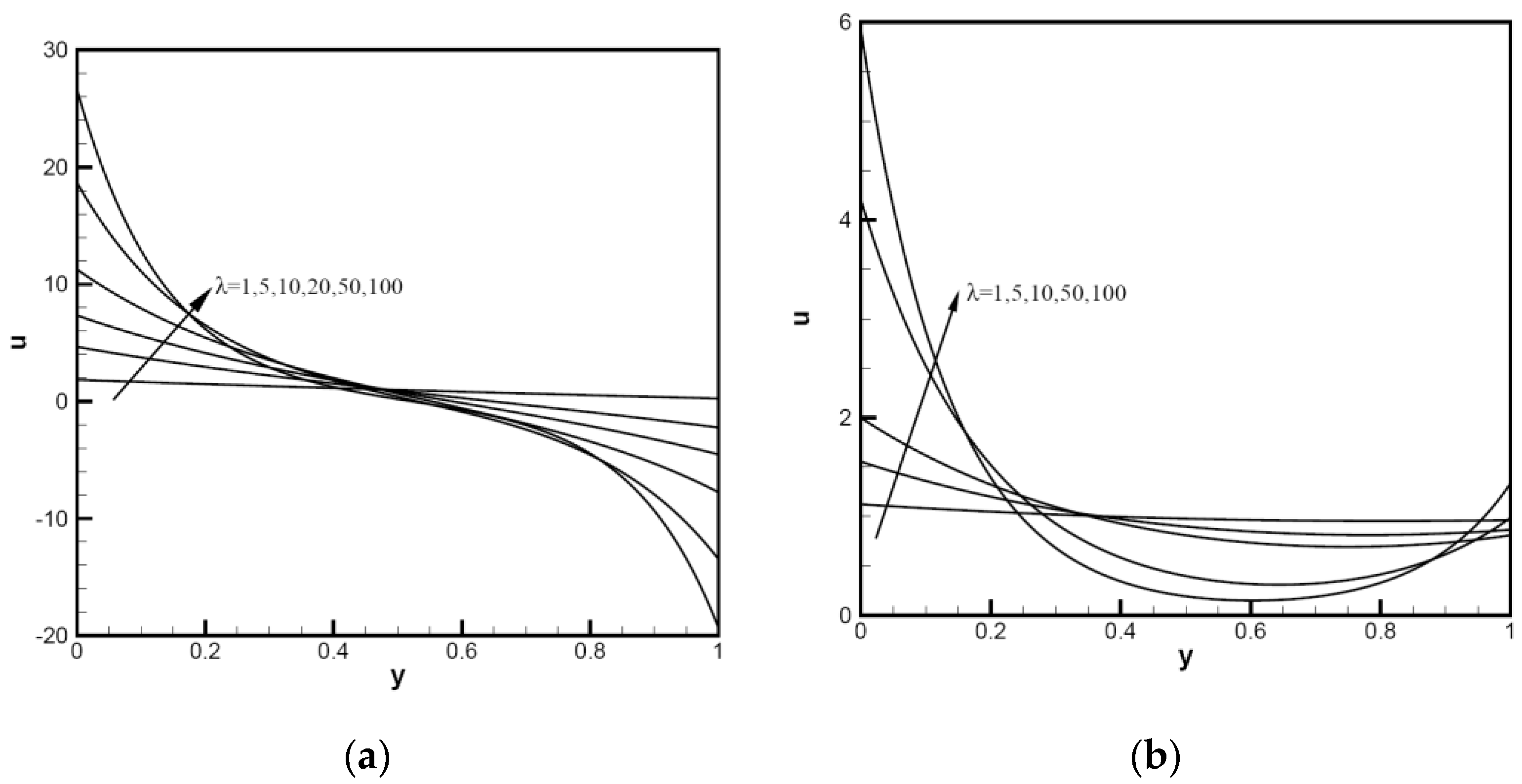
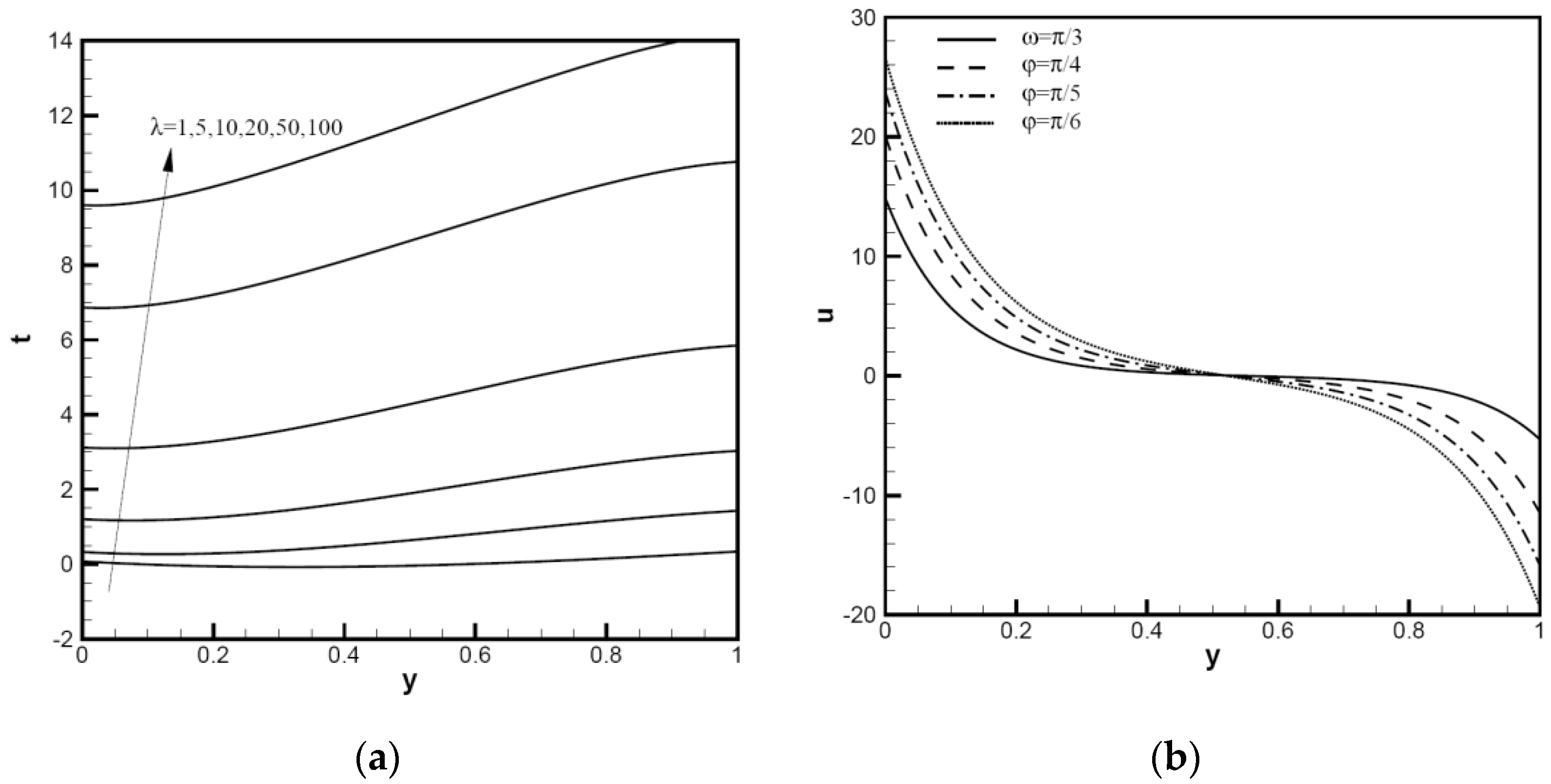
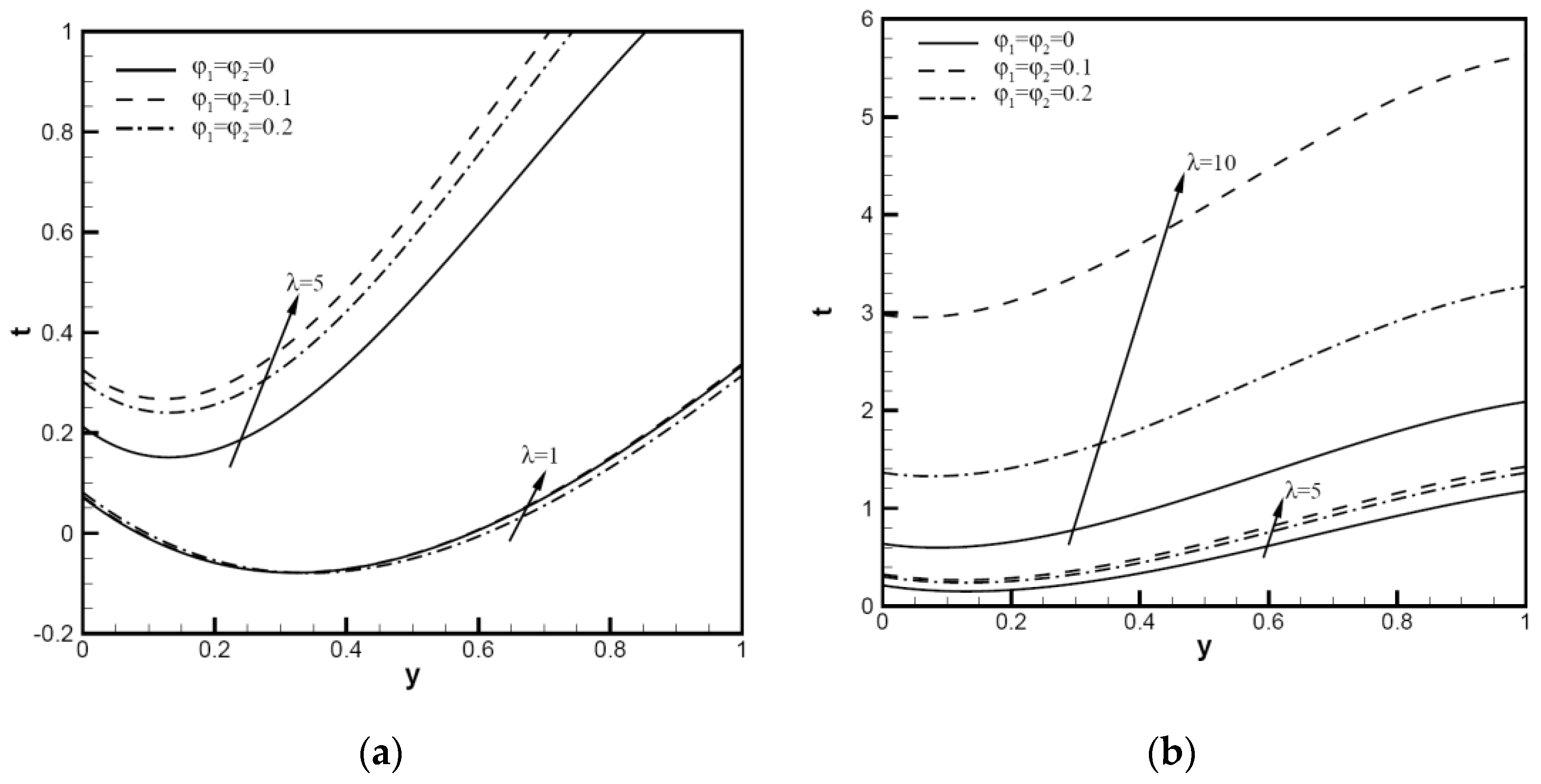
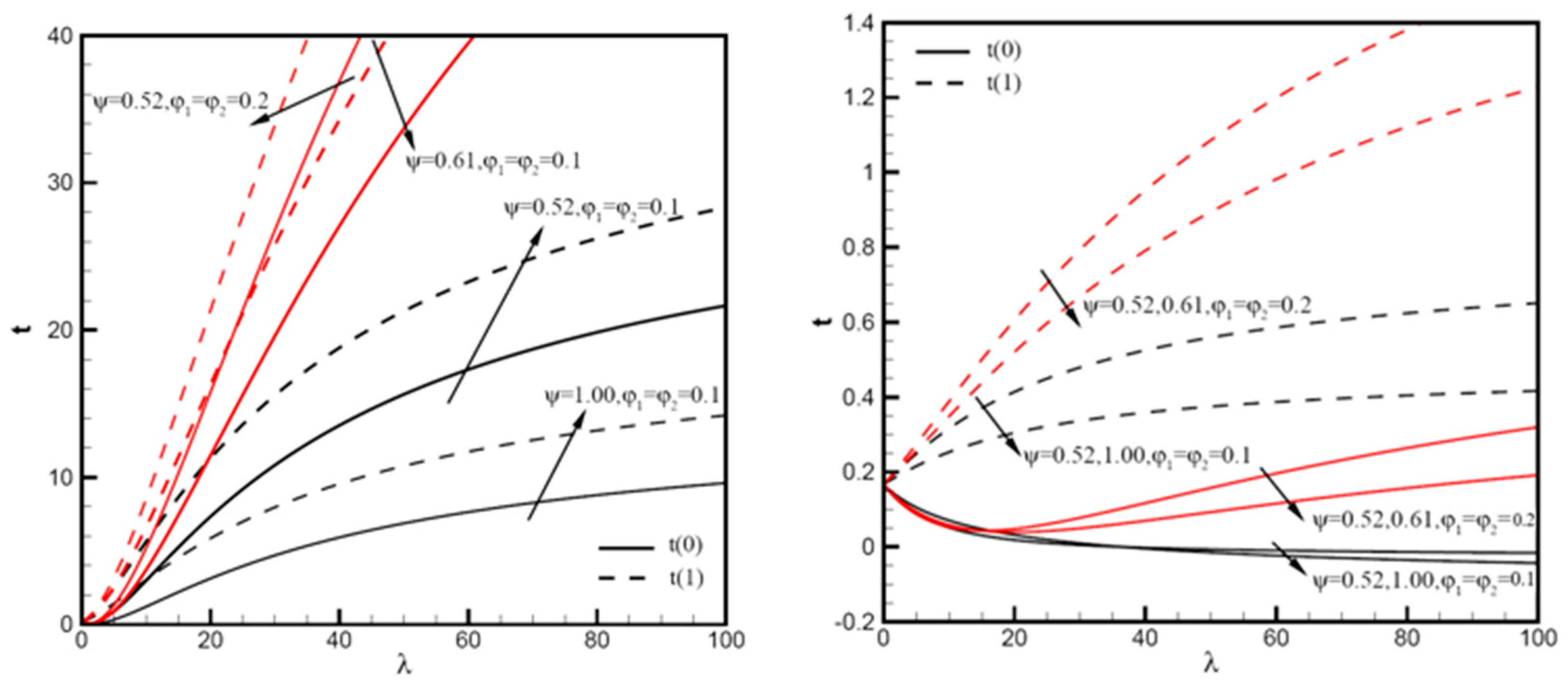
3. Discussion of Results
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME Fluids Eng. Div. 1995, 231, 99–105. [Google Scholar]
- Eltoum, H.; Yang, Y.; Hou, J. The efect of nanoparticles on reservoir wettability alteration: A critical Review. Pet. Sci. 2021, 18, 136–153. [Google Scholar] [CrossRef]
- Rostami, P.; Sharif, M.; Aminshahidy, B.; Fahimpour, J. The effect of nanoparticles on wettability alteration for enhanced oil recovery: Micromodel experimental studies and CFD simulation. Pet. Sci. 2019, 16, 859–873. [Google Scholar] [CrossRef] [Green Version]
- Jiang, A.; Song, Z.; Cheng, T.; Hou, J.; Zhai, H.; Shang, D.; Li, Y.; Zhao, C. Adsorption and desorption behavior of nanoparticles on rock surfaces. Pet. Sci. Bull. 2020, 1, 93–100. [Google Scholar]
- Zhai, Y.; Wang, J.; Li, L.; Ma, M.; Yao, P. Evaluation and effect of mixture ratio on heat transfer performance of Al2O3/water nanofluids. Chem. Ind. Eng. Prog. 2019, 38, 4865–4872. [Google Scholar]
- Devi, S.P.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu-Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Maskeen, M.M.; Zeeshan, A.; Mehmood, O.U.; Hassan, M. Heat transfer enhancement in hydromagnetic alumina-copper/water hybrid nanofluid flow over a stretching cylinder. J. Therm. Anal. Calorim. 2019, 138, 1127–1136. [Google Scholar] [CrossRef]
- Wainia, I.; Ishakb, A.; Pop, I. Flow and heat transfer of a hybrid nanofluid past a permeable moving surface. Chin. J. Phys. 2020, 66, 606–619. [Google Scholar] [CrossRef]
- Elsaid, E.M.; Abdel-wahed, M.S. Mixed convection hybrid-nanofluid in a vertical channel under the effect of thermal radiative flux. Appl. Therm. Eng. 2021, 25, 100913. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Abu-Hamdeh, N.H.; Goodarzi, M. Entropy optimization of first-grade viscoelastic nanofluid flow over a stretching sheet by using classical Keller-Box scheme. Mathematics 2021, 9, 2563. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Alshehri, H.M.; Goodarzi, M. Marangoni-bioconvectional flow of Reiner-Philippoff nanofluid with melting phenomenon and nonuniform heat source/sink in the presence of a swimming microorganisms. Math. Methods Appl. Sci. 2021, 5, 1–19. [Google Scholar] [CrossRef]
- Jamshed, W.; Devi, S.S.U.; Goodarzi, M.; Prakash, K.; Nisar, S.; Zakarya, M.; Abdel-Aty, A. Evaluating the unsteady Casson nanofluid over a stretching sheet with solar thermal radiation: An optimal case study. Case Stud. Therm. Eng. 2021, 26, 101160. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Nazari, M.A.; Mahariq, I.; Assad, M.E.H.; Ali, M.E.; Almuzaiqer, R.; Nuhait, A.; Murshid, N. Thermophysical properties of hybrid nanofluids and the proposed models: An updated comprehensive study. Nanomaterials 2021, 11, 3084. [Google Scholar] [CrossRef] [PubMed]
- Nonlaopon, K.; Khan, N.A.; Sulaiman, M.; Alshammari, F.S.; Laouini, G. Heat transfer analysis of nanofluid flow in a rotating system with magnetic field using an intelligent strength stochastic-driven approach. Nanomaterials 2022, 12, 2273. [Google Scholar] [CrossRef] [PubMed]
- Dero, S.; Lund, L.A.; Shaikh, A.W.; Alhadri, M.; Said, L.B.; Khan, S.U.; Kolsi, L. Stability aspect of magnetized hybrid nanofluid with suction and injection phenomenon: Modified thermal model. J. Indian Chem. Soc. 2022, 99, 100608. [Google Scholar] [CrossRef]
- Mannu, R.; Karthikeyan, V.; Velu, N.; Arumugam, C.; Roy, V.A.L.; Gopalan, A.; Saianand, G.; Sonar, P.; Lee, K.; Kim, W.; et al. Polyethylene glycol coated magnetic nanoparticles: Hybrid nanofluid formulation, properties and drug delivery prospects. Nanomaterials 2021, 11, 440. [Google Scholar] [CrossRef]
- Al-Weheibi, S.M.; Rahman, M.M.; Alam, M.S.; Vajravelu, K. Numerical simulation of natural convection heat transfer in a trapezoidal enclosure filled with nanoparticles. Int. J. Mech. Sci. 2017, 131–132, 599–612. [Google Scholar] [CrossRef]
- Ho, C.J.; Chang, C.Y.; Yan, W.; Amani, P. A combined numerical and experimental study on the forced convection of Al2O3-water nanofluid in a circular tube. Int. Commun. Heat Mass Transf. 2018, 120, 66–75. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Q.; Ma, B.S. Effect of sphericity of nanoparticles on forced convection heat transfer of Al2O3-water nanofluid in parallel-plate channel. J. Lanzhou Univ. Technol. 2021, 47, 62–65. [Google Scholar]
- Chang, T.S.; Lin, T.F. Steady and oscillatory opposing mixed convection in a symmetrically heated vertical channel with a low-Prandtl number fluid. Int. Commun. Heat Mass Transf. 1993, 36, 3783–3795. [Google Scholar]
- Barletta, A. Dual mixed convection flows in a vertical channel. Int. Commun. Heat Mass Transf. 2005, 48, 4835–4845. [Google Scholar] [CrossRef]
- Chang, T.S. Effects of a finite section with linearly varying wall temperature on mixed convection in a vertical channel. Int. Commun. Heat Mass Transf. 2007, 50, 2346–2354. [Google Scholar] [CrossRef]
- Xu, H.; Pop, I. Fully developed mixed convection flow in a vertical channel filled with nanofluids. Int. Commun. Heat Mass Transf. 2012, 39, 1086–1092. [Google Scholar] [CrossRef]
- Jamaludin, A.; Naganthran, K.; Nazar, R.; Pop, I. MHD mixed convection stagnation-point flow of Cu-Al2O3/water hybrid nanofluid over a permeable stretching/shrinking surface with heat source/sink. Eur. J. Mech. B/Fluids 2020, 84, 71–80. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Yassari, M.; Sadeghi, H.; Hosseinzadeh, K.; Ganji, D.D. Investigation on thermophysical properties of TiO2-Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Powder Technol. 2017, 322, 428–438. [Google Scholar] [CrossRef]
- Dinarvand, S.; Rostami, M.N.; Pop, I. A novel hybridity model for TiO2-CuO/water hybrid nanofuid fow over a static/moving wedge or corner. Sci. Rep. 2019, 9, 16290. [Google Scholar] [CrossRef]
- Benkhedda, M.; Boufendi, T.; Tayebi, T.; Chamkha, A.J. Convective heat transfer performance of hybrid nanofluid in a horizontal pipe considering nanoparticles shapes effect. J. Therm. Anal. Calorim. 2020, 140, 411–425. [Google Scholar] [CrossRef]
- Puneeth, V.; Manjunatha, S.; Makinde, O.D.; Gireesha, B.J. Bioconvection of a radiating hybrid nanofluid past a thin needle in the presence of heterogeneous-homogeneous chemical reaction. ASME J. Heat Transf. 2021, 143, 042502. [Google Scholar] [CrossRef]
- Iftikhar, N.; Rehman, A.; Sadaf, H. Theoretical investigation for convective heat transfer on Cu/water nanofluid and (SiO2-copper)/water hybrid nanofluid with MHD and nanoparticle shape effects comprising relaxation and contraction phenomenon. Int. Commun. Heat Mass Transf. 2021, 120, 105012. [Google Scholar] [CrossRef]
- Rashid, U.; Liang, H.; Ahmad, H.; Abbas, M.; Iqbal, A.; Hamed, Y.S. Study of (Ag and TiO2)/water nanoparticles shape effect on heat transfer and hybrid nanofluid flow toward stretching shrinking horizontal cylinder. Results Phys. 2021, 21, 103812. [Google Scholar] [CrossRef]
- Lavine, A.S. Analysis of fully developed opposing mixed convection between inclined parallel plates. Heat Mass Transf. 1988, 23, 249–257. [Google Scholar] [CrossRef]
- Barletta, A.; Zanchini, E. Mixed convection with viscous dissipation in an inclined channel with prescribed wall temperatures. Int. Commun. Heat Mass Transf. 2001, 44, 4267–4275. [Google Scholar] [CrossRef]
- Aydin, O.; Kaya, A. MHD mixed convective heat transfer flow about an inclined plate. Heat Mass Transf. 2009, 46, 129–136. [Google Scholar] [CrossRef]
- Cimpean, D.S.; Pop, I. Fully developed mixed convection flow of a nanofluid through an inclined channel filled with a porous medium. Int. J. Heat Mass Transf. 2012, 55, 907–914. [Google Scholar] [CrossRef]
- Goyal, M.; Bhargava, R. Simulation of natural convective boundary layer flow of a nanofluid past a convectively heated inclined plate in the presence of magnetic field. Int. J. Appl. Comput. 2018, 4, 63. [Google Scholar] [CrossRef] [Green Version]
- Khademi, R.; Razminia, A.; Shiryaev, V.I. Conjugate-mixed convection of nanofluid flow over an inclined flat plate in porous media. Appl. Math. Comput. 2020, 366, 124761. [Google Scholar] [CrossRef]
- You, X.C.; Li, S.Y. Fully developed opposing mixed convection flow in the inclined channel filled with a hybrid nanofluid. Nanomaterials 2021, 11, 1107. [Google Scholar] [CrossRef]
- You, X.C.; Li, S.Y. Effect of nanoparticle sphericity on mixed convective flow of nanofluids in an inclined channel. Pet. Sci. Bull. 2021, 6, 604–613. [Google Scholar]
- Anuar, N.S.; Bachok, N.; Pop, I. Influence of buoyancy force on Ag-MgO/water hybrid nanofluid flow in an inclined permeable stretching/shrinking sheet. Int. Commun. Heat Mass Transf. 2021, 123, 105236. [Google Scholar] [CrossRef]
- Cimpean, D.S.; Pop, I.; Ingham, D.B.; Merkin, J.H. Fully developed mixed convection flow between inclined parallel plates filled with a porous medium. Transp. Porous Media 2009, 77, 87–102. [Google Scholar] [CrossRef]
- Qi, C.; He, G.; Li, Y.; He, Y. Numerical simulation of natural convection of square enclosure filled with Cu/Al2O3-water mixed nanofluid based on lattice Boltzmann method. Acta Phys. Sin. 2015, 64, 024703. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: New York, NY, USA, 2017; pp. 24–36. [Google Scholar]
- Bear, J. Modeling Phenomena of Flow and Transport in Porous Media, 1st ed.; Springer: Cham, Switzerland, 2018; pp. 54–96. [Google Scholar]
- Pop, I.; Ingham, D.B. Convective Heat Transfer: Mathematical and Computational Modeling of Viscous Fluids and Porous Media, 1st ed.; Pergamon: Oxford, UK, 2001; pp. 134–156. [Google Scholar]
- Iqbal, Z.; Akbar, N.S.; Azhar, E.; Maraj, E.N. Performance of hybrid nanofluid (Cu-CuO/water) on MHD rotating transport in oscillating vertical channel inspired by Hall current and thermal radiation. Alex. Eng. J. 2018, 57, 1943–1954. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, X. Nanoparticle Sphericity Investigation of Cu-Al2O3-H2O Hybrid Nanofluid Flows between Inclined Channels Filled with a Porous Medium. Nanomaterials 2022, 12, 2552. https://doi.org/10.3390/nano12152552
You X. Nanoparticle Sphericity Investigation of Cu-Al2O3-H2O Hybrid Nanofluid Flows between Inclined Channels Filled with a Porous Medium. Nanomaterials. 2022; 12(15):2552. https://doi.org/10.3390/nano12152552
Chicago/Turabian StyleYou, Xiangcheng. 2022. "Nanoparticle Sphericity Investigation of Cu-Al2O3-H2O Hybrid Nanofluid Flows between Inclined Channels Filled with a Porous Medium" Nanomaterials 12, no. 15: 2552. https://doi.org/10.3390/nano12152552
APA StyleYou, X. (2022). Nanoparticle Sphericity Investigation of Cu-Al2O3-H2O Hybrid Nanofluid Flows between Inclined Channels Filled with a Porous Medium. Nanomaterials, 12(15), 2552. https://doi.org/10.3390/nano12152552






