DFT Analysis of Hole Qubits Spin State in Germanium Thin Layer
Abstract
1. Introduction
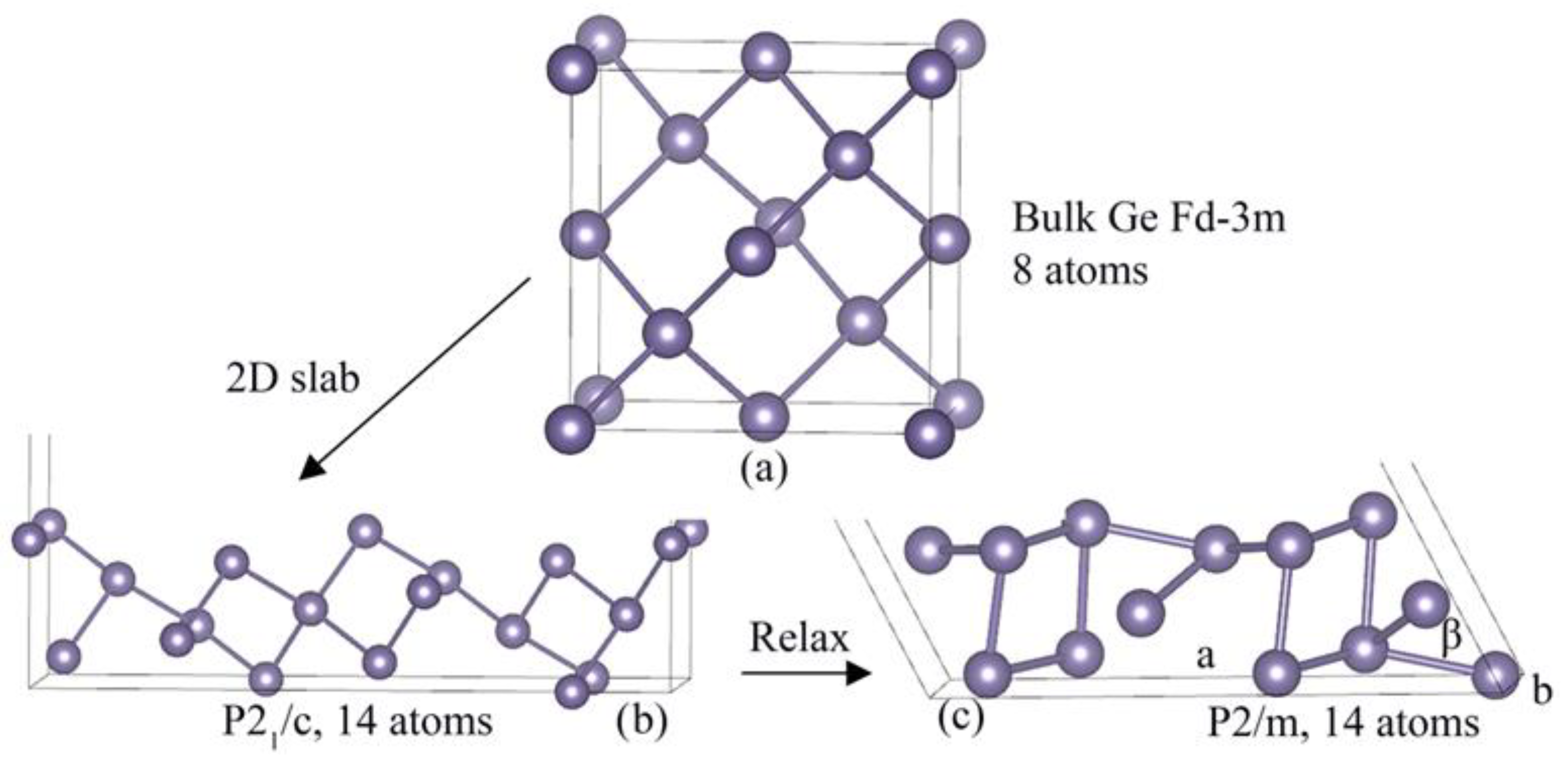
2. Computational Details
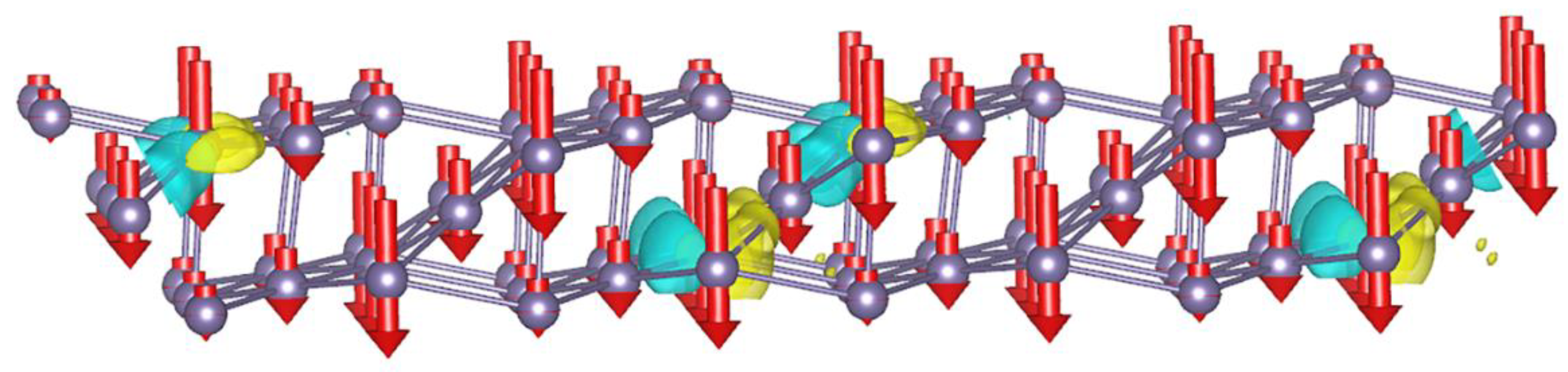
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Loss, D.; DiVincenzo, D.P. Quantum Computation with Quantum Dots. Phys. Rev. A 1998, 57, 120–126. [Google Scholar] [CrossRef]
- DiVincenzo, D.P. The Physical Implementation of Quantum Computation. Fortschr. Phys. 2000, 48, 771–783. [Google Scholar] [CrossRef]
- Koppens, F.H.L.; Buizert, C.; Tielrooij, K.J.; Vink, I.T.; Nowack, K.C.; Meunier, T.; Kouwenhoven, L.P.; Vandersypen, L.M.K. Driven Coherent Oscillations of a Single Electron Spin in a Quantum Dot. Nature 2006, 442, 766–771. [Google Scholar] [CrossRef] [PubMed]
- Muhonen, J.T.; Dehollain, J.P.; Laucht, A.; Hudson, F.E.; Kalra, R.; Sekiguchi, T.; Itoh, K.M.; Jamieson, D.N.; McCallum, J.C.; Dzurak, A.S.; et al. Storing Quantum Information for 30 Seconds in a Nanoelectronic Device. Nat. Nanotech. 2014, 9, 986–991. [Google Scholar] [CrossRef] [PubMed]
- Maurand, R.; Jehl, X.; Kotekar-Patil, D.; Corna, A.; Bohuslavskyi, H.; Laviéville, R.; Hutin, L.; Barraud, S.; Vinet, M.; Sanquer, M.; et al. A CMOS Silicon Spin Qubit. Nat. Commun. 2016, 7, 13575. [Google Scholar] [CrossRef]
- Kloeffel, C.; Loss, D. Prospects for Spin-Based Quantum Computing in Quantum Dots. Annu. Rev. Condens. Matter Phys. 2013, 4, 51–81. [Google Scholar] [CrossRef]
- Higginbotham, A.P.; Larsen, T.W.; Yao, J.; Yan, H.; Lieber, C.M.; Marcus, C.M.; Kuemmeth, F. Hole Spin Coherence in a Ge/Si Heterostructure Nanowire. Nano Lett. 2014, 14, 3582–3586. [Google Scholar] [CrossRef][Green Version]
- Marcellina, E.; Hamilton, A.R.; Winkler, R.; Culcer, D. Spin-Orbit Interactions in Inversion-Asymmetric Two-Dimensional Hole Systems: A Variational Analysis. Phys. Rev. B 2017, 95, 075305. [Google Scholar] [CrossRef]
- Watzinger, H. Ge Hut Wires—From Growth to Hole Spin Resonance. Ph.D. Thesis, Faculty of the Graduate School of the Institute of Science and Technology Austria, Klosterneuburg, Austria, 2018. [Google Scholar] [CrossRef]
- Scappucci, G.; Kloeffel, C.; Zwanenburg, F.A.; Loss, D.; Myronov, M.; Zhang, J.-J.; De Franceschi, S.; Katsaros, G.; Veldhorst, M. The Germanium Quantum Information Route. Nat. Rev. Mater. 2021, 6, 926–943. [Google Scholar] [CrossRef]
- Luttinger, J.M.; Kohn, W. Motion of Electrons and Holes in Perturbed Periodic Fields. Phys. Rev. 1955, 97, 869–883. [Google Scholar] [CrossRef]
- Winkler, R.; Culcer, D.; Papadakis, S.J.; Habib, B.; Shayegan, M. Spin Orientation of Holes in Quantum Wells. Semicond. Sci. Technol. 2008, 23, 114017. [Google Scholar] [CrossRef][Green Version]
- Aggarwal, K.; Hofmann, A.; Jirovec, D.; Prieto, I.; Sammak, A.; Botifoll, M.; Martí-Sánchez, S.; Veldhorst, M.; Arbiol, J.; Scappucci, G.; et al. Enhancement of Proximity-Induced Superconductivity in a Planar Ge Hole Gas. Phys. Rev. Res. 2021, 3, L022005. [Google Scholar] [CrossRef]
- Jirovec, D.; Hofmann, A.; Ballabio, A.; Mutter, P.M.; Tavani, G.; Botifoll, M.; Crippa, A.; Kukucka, J.; Sagi, O.; Martins, F.; et al. A Singlet-Triplet Hole Spin Qubit in Planar Ge. Nat. Mater. 2021, 20, 1106–1112. [Google Scholar] [CrossRef] [PubMed]
- Vukusic, L. Charge Sensing and Spin Relaxation Times of Holes in Ge Hut Wires. Ph.D. Thesis, Faculty of the Graduate School of the Institute of Science and Technology Austria, Klosterneuburg, Austria, 2018. [Google Scholar] [CrossRef]
- Gao, F.; Wang, J.; Watzinger, H.; Hu, H.; Rančić, M.J.; Zhang, J.; Wang, T.; Yao, Y.; Wang, G.; Kukučka, J.; et al. Site-Controlled Uniform Ge/Si Hut Wires with Electrically Tunable Spin–Orbit Coupling. Adv. Mater. 2020, 32, 1906523. [Google Scholar] [CrossRef]
- Lauhon, L.J.; Gudiksen, M.S.; Wang, D.; Lieber, C.M. Epitaxial Core–Shell and Core–Multishell Nanowire Heterostructures. Nature 2002, 420, 57–61. [Google Scholar] [CrossRef]
- Kodambaka, S.; Tersoff, J.; Reuter, M.C.; Ross, F.M. Germanium Nanowire Growth Below the Eutectic Temperature. Science 2007, 316, 729–732. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.J.; Katsaros, G.; Montalenti, F.; Scopece, D.; Rezaev, R.O.; Mickel, C.; Rellinghaus, B.; Miglio, L.; De Franceschi, S.; Rastelli, A.; et al. Monolithic Growth of Ultrathin Ge Nanowires on Si(001). Phys. Rev. Lett. 2012, 109, 085502. [Google Scholar] [CrossRef]
- Katsaros, G.; Kukučka, J.; Vukušić, L.; Watzinger, H.; Gao, F.; Wang, T.; Zhang, J.-J.; Held, K. Zero Field Splitting of Heavy-Hole States in Quantum Dots. Nano Lett. 2020, 20, 5201–5206. [Google Scholar] [CrossRef]
- Kukucka, J. Implementation of a Hole Spin Qubit in Ge Hut Wires and Dispersive Spin Sensing. Ph.D. Thesis, Faculty of the Graduate School of the Institute of Science and Technology Austria, Klosterneuburg, Austria, 2020. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter. 2017, 29, 465901. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Aroyo, M.I. (Ed.) International Tables for Crystallography: Space-Group Symmetry, 2nd ed.; International Union of Crystallography: Chester, UK, 2016; Volume A, ISBN 978-0-470-97423-0. [Google Scholar]
- Hom, T.; Kiszenik, W.; Post, B. Accurate Lattice Constants from Multiple Reflection Measurements. II. Lattice Constants of Germanium Silicon, and Diamond. J. Appl. Crystallogr. 1975, 8, 457–458. [Google Scholar] [CrossRef]
- Fan, Q.; Peng, H.; Zhang, W.; Yu, X.; Yun, S. Physical Properties of Group 14 Elements in P2/m Phase. J. Solid State Chem. 2022, 305, 122641. [Google Scholar] [CrossRef]
- Gallego, S.V.; Tasci, E.S.; de la Flor, G.; Perez-Mato, J.M.; Aroyo, M.I. Magnetic Symmetry in the Bilbao Crystallographic Server: A Computer Program to Provide Systematic Absences of Magnetic Neutron Diffraction. J. Appl. Crystallogr. 2012, 45, 1236–1247. [Google Scholar] [CrossRef]
- Perez-Mato, J.M.; Gallego, S.V.; Tasci, E.S.; Elcoro, L.; de la Flor, G.; Aroyo, M.I. Symmetry-Based Computational Tools for Magnetic Crystallography. Annu. Rev. Mater. Res. 2015, 45, 217–248. [Google Scholar] [CrossRef]
- Hanson, R.; Kouwenhoven, L.P.; Petta, J.R.; Tarucha, S.; Vandersypen, L.M.K. Spins in Few-Electron Quantum Dots. Rev. Mod. Phys. 2007, 79, 1217–1265. [Google Scholar] [CrossRef]
- Kouwenhoven, L.P.; Austing, D.G.; Tarucha, S. Few-Electron Quantum Dots. Rep. Prog. Phys. 2001, 64, 701–736. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chibisov, A.; Aleshin, M.; Chibisova, M. DFT Analysis of Hole Qubits Spin State in Germanium Thin Layer. Nanomaterials 2022, 12, 2244. https://doi.org/10.3390/nano12132244
Chibisov A, Aleshin M, Chibisova M. DFT Analysis of Hole Qubits Spin State in Germanium Thin Layer. Nanomaterials. 2022; 12(13):2244. https://doi.org/10.3390/nano12132244
Chicago/Turabian StyleChibisov, Andrey, Maxim Aleshin, and Mary Chibisova. 2022. "DFT Analysis of Hole Qubits Spin State in Germanium Thin Layer" Nanomaterials 12, no. 13: 2244. https://doi.org/10.3390/nano12132244
APA StyleChibisov, A., Aleshin, M., & Chibisova, M. (2022). DFT Analysis of Hole Qubits Spin State in Germanium Thin Layer. Nanomaterials, 12(13), 2244. https://doi.org/10.3390/nano12132244





