Ab Initio Study of Graphene/hBN Van der Waals Heterostructures: Effect of Electric Field, Twist Angles and p-n Doping on the Electronic Properties
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Structural Properties and Stacking Energies
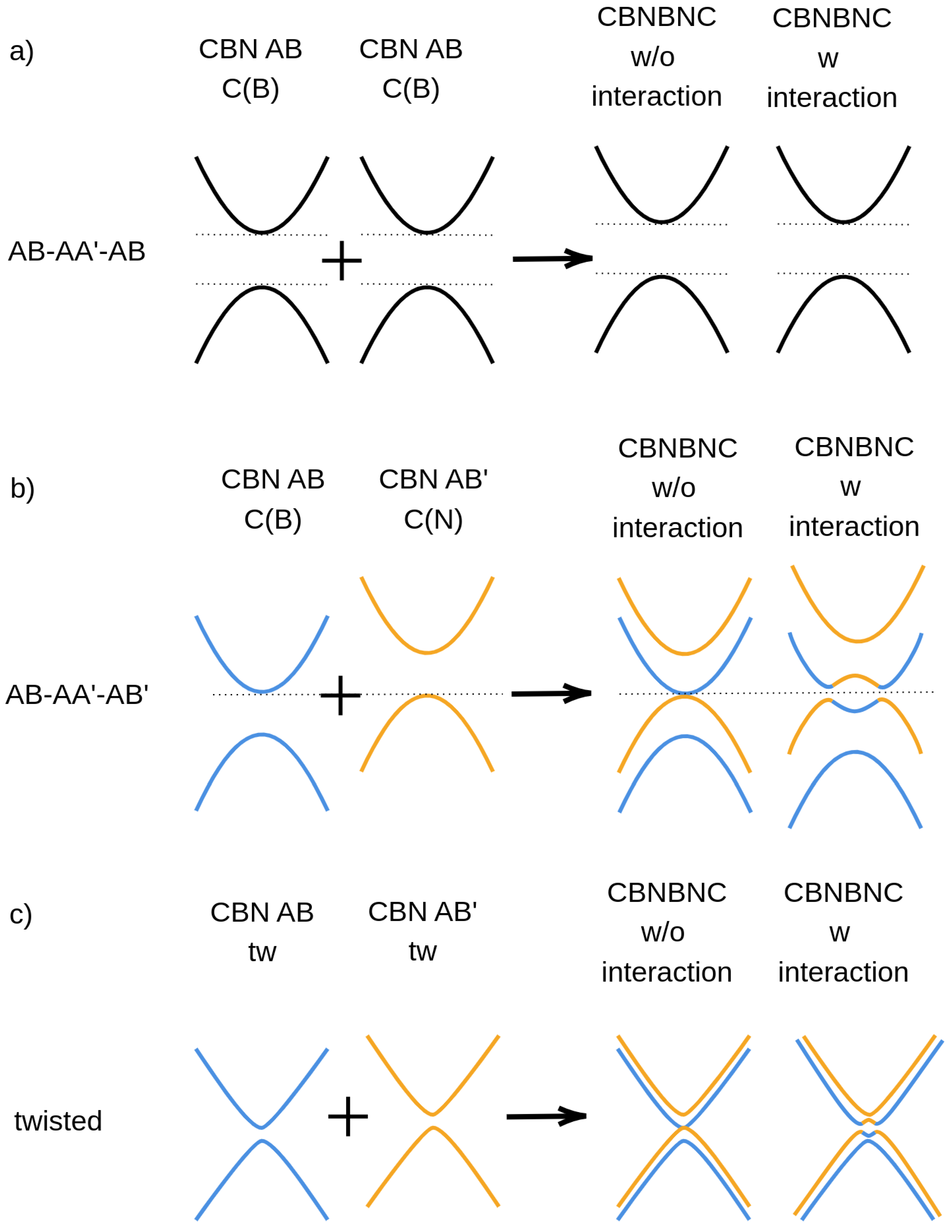
3.2. Electronic Properties
Doping and Electric Field
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Neto, A.H.C. Two-dimensional crystals-based heterostructures: Materials with tailored properties. Phys. Scr. 2012, T146, 014006. [Google Scholar] [CrossRef]
- Bhimanapati, G.R.; Lin, Z.; Meunier, V.; Jung, Y.; Cha, J.; Das, S.; Xiao, D.; Son, Y.; Strano, M.S.; Cooper, V.R.; et al. Recent Advances in Two-Dimensional Materials beyond Graphene. ACS Nano 2015, 9, 11509–11539. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, M.; Ataca, C.; Palummo, M.; Grossman, J. Electronic Properties of Two-Dimensional Layered Materials. Nanophotonics 2016, 6, 479–493. [Google Scholar] [CrossRef]
- Das, S.; Robinson, J.A.; Dubey, M.; Terrones, H.; Terrones, M. Beyond Graphene: Progress in Novel Two-Dimensional Materials and Van der Waals Solids. Annu. Rev. Mater. Res. 2015, 45, 1–27. [Google Scholar] [CrossRef]
- Chiodo, L. Two-dimensional innovative materials for photovoltaics. Curr. Opin. Green Sustain. Chem. 2019, 17, 49–56. [Google Scholar] [CrossRef]
- Bartolomei, M.; Carmona-Novillo, E.; Hernández, M.I.; Campos-Martínez, J.; Pirani, F.; Giorgi, G. Graphdiyne pores: “Ad Hoc” openings for helium separation applications. J. Phys. Chem. 2014, 118, 29966–29972. [Google Scholar] [CrossRef] [Green Version]
- Bartolomei, M.; Carmona-Novillo, E.; Hernández, M.I.; Campos-Martínez, J.; Pirani, F.; Giorgi, G.; Yamashita, K. Penetration barrier of water through graphynes’ pores: First-principles predictions and force field optimization. J. Phys. Chem. Lett. 2014, 5, 751–755. [Google Scholar] [CrossRef] [Green Version]
- Bartolomei, M.; Carmona-Novillo, E.; Giorgi, G. First principles investigation of hydrogen physical adsorption on graphynes’ layers. Carbon 2015, 95, 1076–1081. [Google Scholar] [CrossRef] [Green Version]
- Bartolomei, M.; Giorgi, G. A novel nanoporous graphite based on graphynes: First-principles structure and carbon dioxide preferential physisorption. ACS Appl. Mater. Interfaces 2016, 8, 27996–28003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palummo, M.; Yamashita, K.; Giorgi, G. Advances in two-dimensional green materials for organic electronics applications. In Sustainable Strategies in Organic Electronics; Elsevier: Amsterdam, The Netherlands, 2022; pp. 391–422. [Google Scholar]
- Bechstedt, F.; Gori, P.; Pulci, O. Beyond graphene: Clean, hydrogenated and halogenated silicene, germanene, stanene, and plumbene. Prog. Surf. Sci. 2021, 96, 100615. [Google Scholar] [CrossRef]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.; Khotkevich, V.; Morozov, S.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, G.; Gao, W.; Cannuccia, E.; Taha-Tijerina, J.; Balicas, L.; Mathkar, A.; Narayanan, T.; Liu, Z.; Gupta, B.K.; Peng, J.; et al. Artificially stacked atomic layers: Toward new Van der Waals solids. Nano Lett. 2012, 12, 3518–3525. [Google Scholar] [CrossRef] [Green Version]
- Morozov, S.; Novoselov, K.; Katsnelson, M.; Schedin, F.; Elias, D.; Jaszczak, J.A.; Geim, A. Giant intrinsic carrier mobilities in graphene and its bilayer. Phys. Rev. Lett. 2008, 100, 016602. [Google Scholar] [CrossRef] [Green Version]
- Jian-Hao, C.; Jang, C.; Xiao, S.; Masa, I.; Fuhrer, M. Intrinsic and extrinsic performance limits of graphene devices on SiO2. Nat. Nanotechnol. 2008, 3, 206–209. [Google Scholar]
- Dean, C.R.; Young, A.F.; Meric, I.; Lee, C.; Wang, L.; Sorgenfrei, S.; Watanabe, K.; Taniguchi, T.; Kim, P.; Shepard, K.L.; et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 2010, 5, 722–726. [Google Scholar] [CrossRef]
- N’Diaye, A.T.; Coraux, J.; Plasa, T.N.; Busse, C.; Michely, T. Structure of epitaxial graphene on Ir (111). New J. Phys. 2008, 10, 043033. [Google Scholar] [CrossRef]
- Levinshtein, M.E.; Rumyantsev, S.L.; Shur, M.S. Properties of Advanced Semiconductor Materials: GaN, AIN, InN, BN, SiC, SiGe; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Ju, L.; Velasco, J.; Huang, E.; Kahn, S.; Nosiglia, C.; Tsai, H.Z.; Yang, W.; Taniguchi, T.; Watanabe, K.; Zhang, Y.; et al. Photoinduced doping in heterostructures of graphene and boron nitride. Nat. Nanotechnol. 2014, 9, 348–352. [Google Scholar] [CrossRef] [PubMed]
- Zomer, P.; Guimarães, M.; Brant, J.; Tombros, N.; Van Wees, B. Fast pick up technique for high quality heterostructures of bilayer graphene and hexagonal boron nitride. Appl. Phys. Lett. 2014, 105, 013101. [Google Scholar] [CrossRef] [Green Version]
- Mishchenko, A.; Tu, J.; Cao, Y.; Gorbachev, R.V.; Wallbank, J.; Greenaway, M.; Morozov, V.; Morozov, S.; Zhu, M.; Wong, S.; et al. Twist-controlled resonant tunnelling in graphene/boron nitride/graphene heterostructures. Nat. Nanotechnol. 2014, 9, 808–813. [Google Scholar] [CrossRef] [PubMed]
- Ni, G.; Wang, H.; Wu, J.; Fei, Z.; Goldflam, M.; Keilmann, F.; Özyilmaz, B.; Castro Neto, A.; Xie, X.; Fogler, M.; et al. Plasmons in graphene moiré superlattices. Nat. Mater. 2015, 14, 1217–1222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Woessner, A.; Lundeberg, M.B.; Gao, Y.; Principi, A.; Alonso-González, P.; Carrega, M.; Watanabe, K.; Taniguchi, T.; Vignale, G.; Polini, M.; et al. Highly confined low-loss plasmons in graphene–boron nitride heterostructures. Nat. Mater. 2015, 14, 421–425. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Liu, M.; Zhang, Y.; Liu, Z. Hexagonal boron nitride–graphene heterostructures: Synthesis and interfacial properties. Small 2016, 12, 32–50. [Google Scholar] [CrossRef]
- Pan, W.; Xiao, J.; Zhu, J.; Yu, C.; Zhang, G.; Ni, Z.; Watanabe, K.; Taniguchi, T.; Shi, Y.; Wang, X. Biaxial compressive strain engineering in graphene/boron nitride heterostructures. Sci. Rep. 2012, 2, 893. [Google Scholar] [CrossRef] [Green Version]
- Wickramaratne, D.; Weston, L.; Van de Walle, C.G. Monolayer to bulk properties of hexagonal boron nitride. J. Phys. Chem. 2018, 122, 25524–25529. [Google Scholar] [CrossRef]
- Arnaud, B.; Lebègue, S.; Rabiller, P.; Alouani, M. Huge excitonic effects in layered hexagonal boron nitride. Phys. Rev. Lett. 2006, 96, 026402. [Google Scholar] [CrossRef] [Green Version]
- Schué, L.; Sponza, L.; Plaud, A.; Bensalah, H.; Watanabe, K.; Taniguchi, T.; Ducastelle, F.M.C.; Loiseau, A.; Barjon, J. Bright Luminescence from Indirect and Strongly Bound Excitons in h-BN. Phys. Rev. Lett. 2019, 122, 067401. [Google Scholar] [CrossRef] [Green Version]
- Pikalov, A.A.; Fil, D.V. Graphene bilayer structures with superfluid magnetoexcitons. Nanoscale Res. Lett. 2012, 7, 145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ponomarenko, L.A.; Geim, A.K.; Zhukov, A.A.; Jalil, R.; Morozov, S.V.; Novoselov, K.S.; Grigorieva, I.V.; Hill, E.H.; Cheianov, V.V.; Fal’ko, V.I.; et al. Tunable metal—Insulator transition in double-layer graphene heterostructures. Nat. Phys. 2011, 7, 958–961. [Google Scholar] [CrossRef]
- Profumo, R.E.V.; Asgari, R.; Polini, M.; MacDonald, A.H. Double-layer graphene and topological insulator thin-film plasmons. Phys. Rev. B 2012, 85, 085443. [Google Scholar] [CrossRef] [Green Version]
- Farmani, A.; Yavarian, M.; Alighanbari, A.; Miri, M.; Sheikhi, M.H. Tunable graphene plasmonic Y-branch switch in the terahertz region using hexagonal boron nitride with electric and magnetic biasing. Appl. Opt. 2017, 56, 8931–8940. [Google Scholar] [CrossRef]
- Yadav, D.; Tombet, S.B.; Watanabe, T.; Arnold, S.; Ryzhii, V.; Otsuji, T. Terahertz wave generation and detection in double-graphene layered Van der Waals heterostructures. 2D Mater. 2016, 3, 045009. [Google Scholar] [CrossRef] [Green Version]
- Viti, L.; Purdie, D.G.; Lombardo, A.; Ferrari, A.C.; Vitiello, M.S. HBN-encapsulated, graphene-based, room-temperature terahertz receivers, with high speed and low noise. Nano Lett. 2020, 20, 3169–3177. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum Espresso: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
- Giannozzi, P.; Baseggio, O.; Bonfà, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; De Gironcoli, S.; Delugas, P.; Ferrari Ruffino, F.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef] [Green Version]
- Fuchs, M.; Scheffler, M. Ab initio pseudopotentials for electronic structure calculations of poly-atomic systems using density-functional theory. Comput. Phys. Commun. 1999, 119, 67–98. [Google Scholar] [CrossRef] [Green Version]
- Hamann, D. Generalized norm-conserving pseudopotentials. Phys. Rev. B 1989, 40, 2980. [Google Scholar] [CrossRef] [PubMed]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Hamada, I. Van der Waals density functional made accurate. Phys. Rev. B 2014, 89, 121103. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liao, J.; Sa, B.; Zhou, J.; Ahuja, R.; Sun, Z. Design of high-efficiency visible-light photocatalysts for water splitting: MoS2/AlN (GaN) heterostructures. J. Phys. Chem. 2014, 118, 17594–17599. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, B.; Qian, Q.; Gao, Z.; Tang, X.; Li, B. Strain-tunable III-nitride/ZnO heterostructures for photocatalytic water-splitting: A hybrid functional calculation. APL Mater. 2020, 8, 041114. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Zhang, Z.; Huang, B.; Wang, X.; Niu, H.; Guo, Y.; Li, B.; Zheng, R.; Wu, H. Theoretical study on the photocatalytic properties of 2D InX ( X= S, Se)/transition metal disulfide (MoS2 and WS2) Van der Waals heterostructures. Nanoscale 2020, 12, 20025–20032. [Google Scholar] [CrossRef]
- Guo, H.; Yin, Y.; Niu, H.; Robertson, J.; Zhang, Z.; Guo, Y. Tunable contacts and device performances in graphene/group-III monochalcogenides MX (M= In, Ga; X= S, Se) Van der Waals heterostructures. J. Appl. Phys. 2021, 130, 144303. [Google Scholar] [CrossRef]
- Jiang, H.L.; Pan, J.; Zhou, W.; Li, H.M.; Liu, S. Fabrication and application of arrays related to two-dimensional materials. Rare Met. 2021, 41, 262–286. [Google Scholar] [CrossRef]
- Giovannetti, G.; Khomyakov, P.A.; Brocks, G.; Kelly, P.J.; Van Den Brink, J. Substrate-induced band gap in graphene on hexagonal boron nitride: Ab initio density functional calculations. Phys. Rev. B 2007, 76, 073103. [Google Scholar] [CrossRef] [Green Version]
- Siegel, D.A.; Zhou, S.Y.; El Gabaly, F.; Fedorov, A.V.; Schmid, A.K.; Lanzara, A. Self-doping effects in epitaxially grown graphene. Appl. Phys. Lett. 2008, 93, 243119. [Google Scholar] [CrossRef] [Green Version]
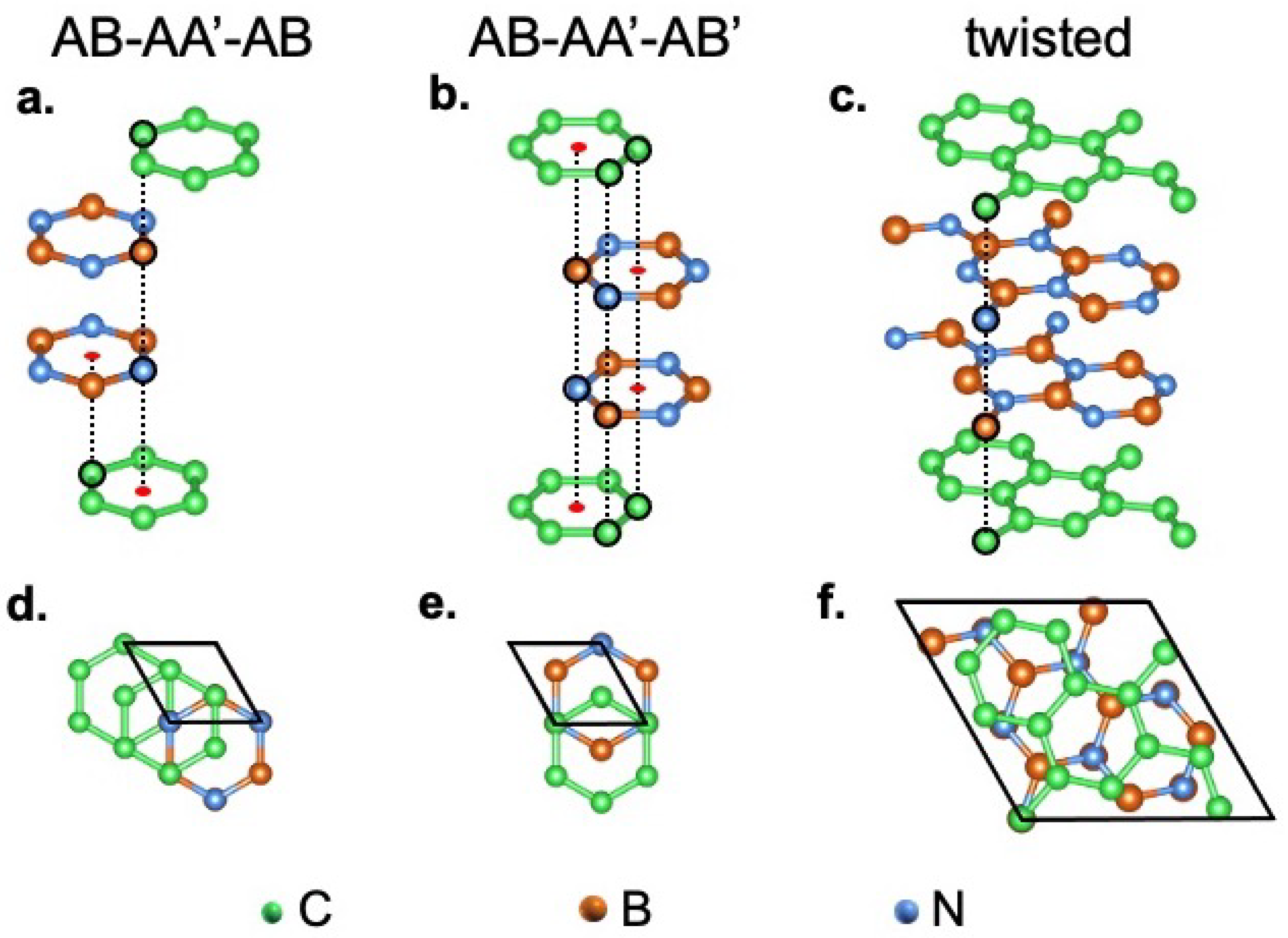
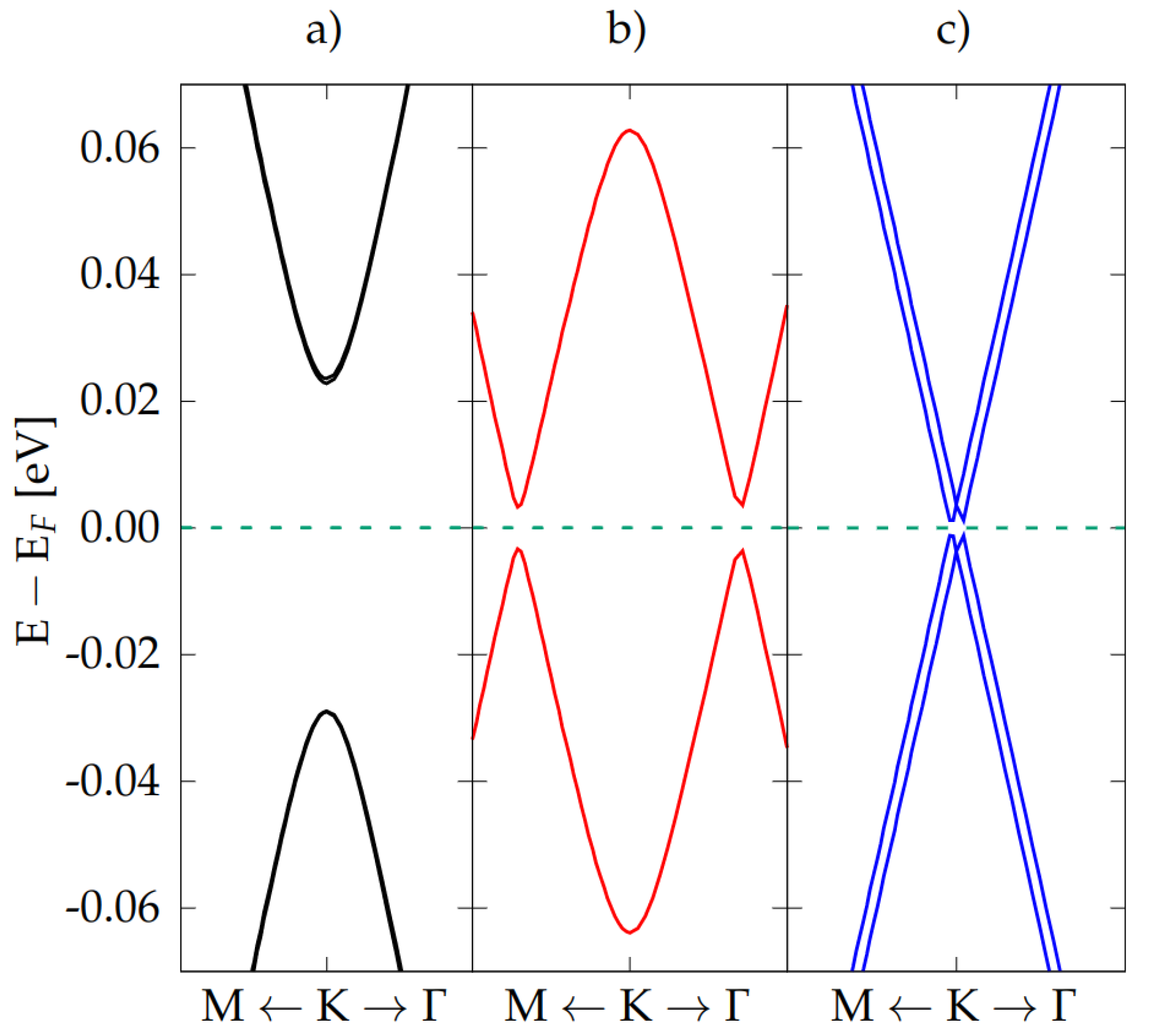
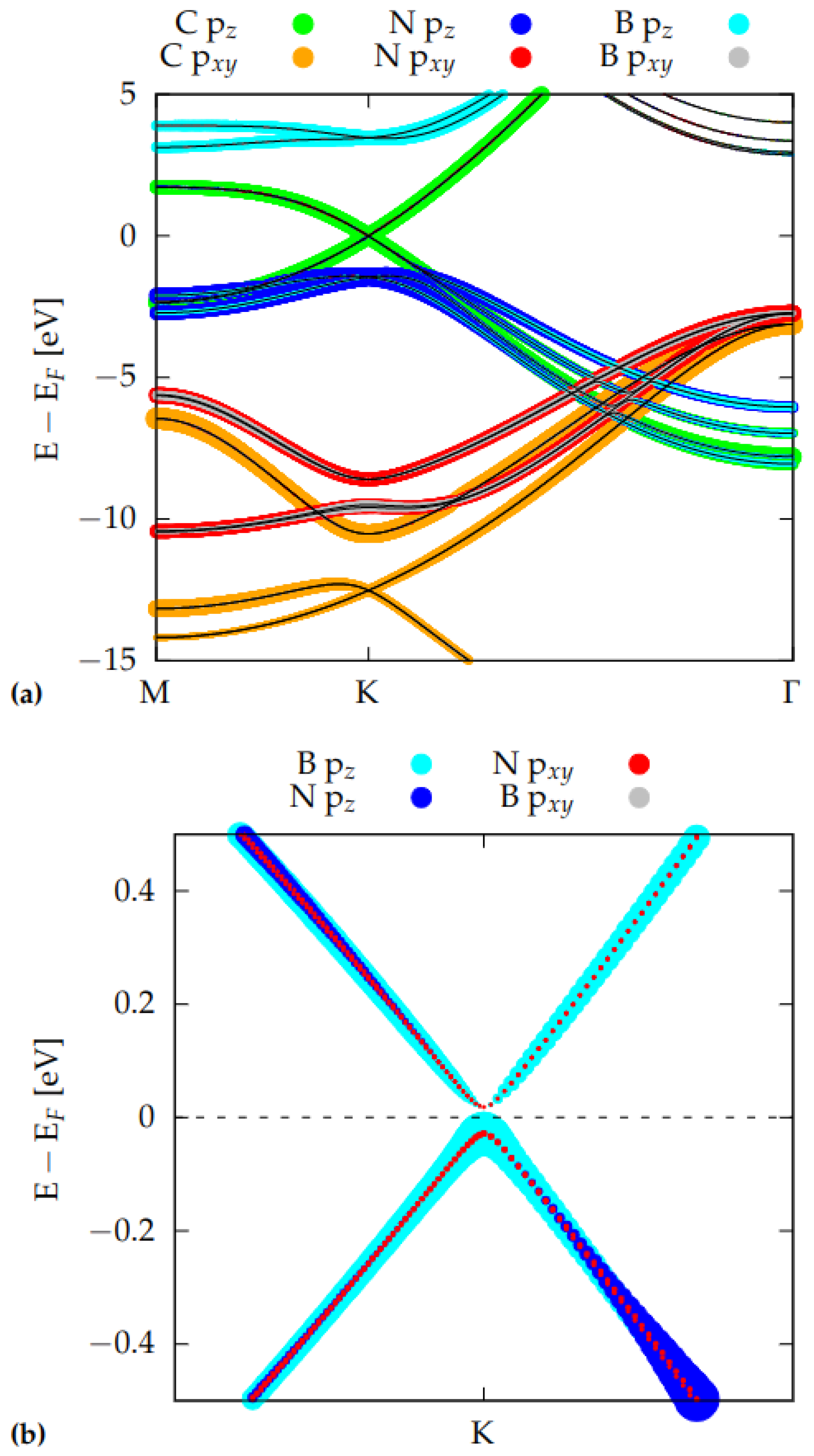
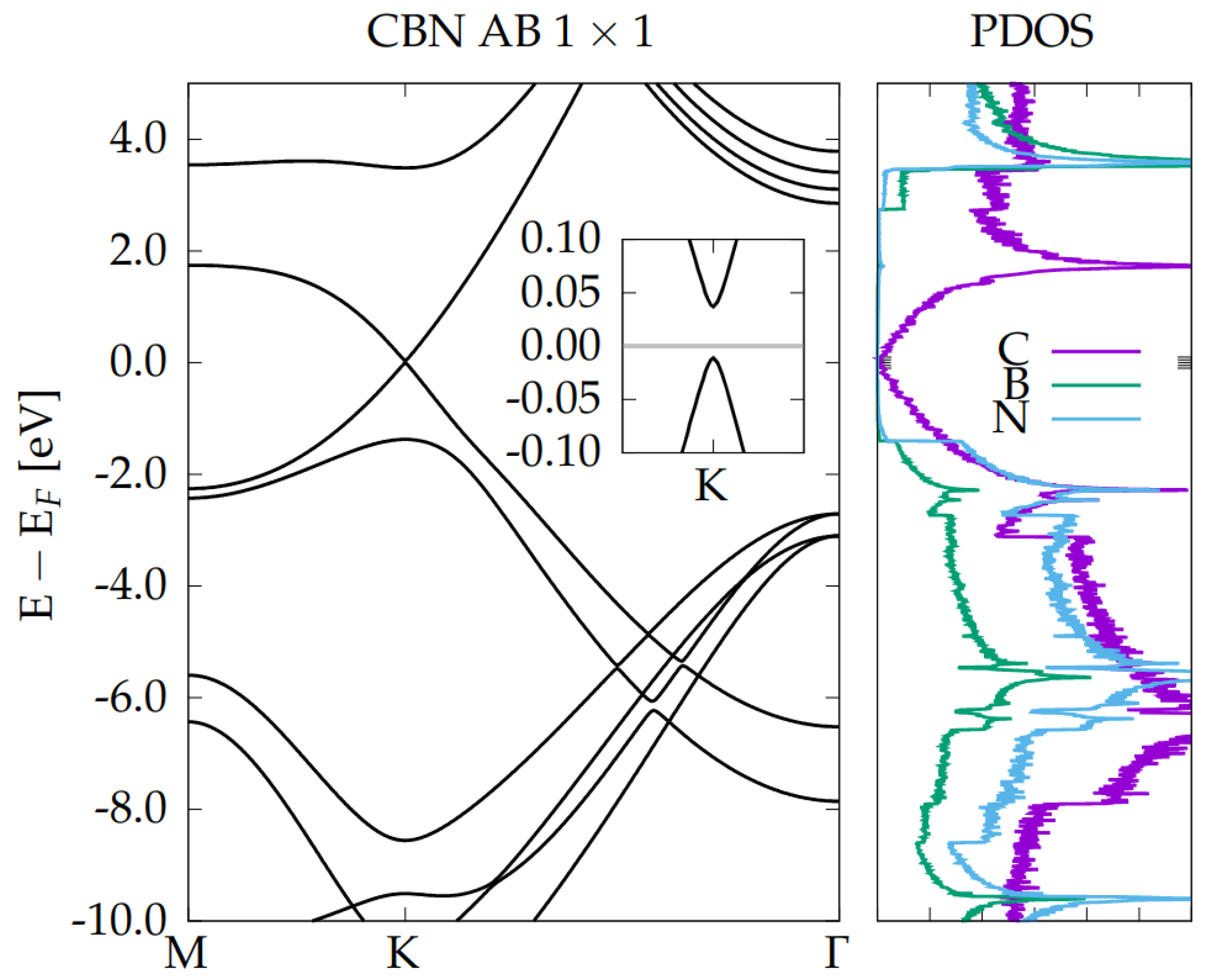
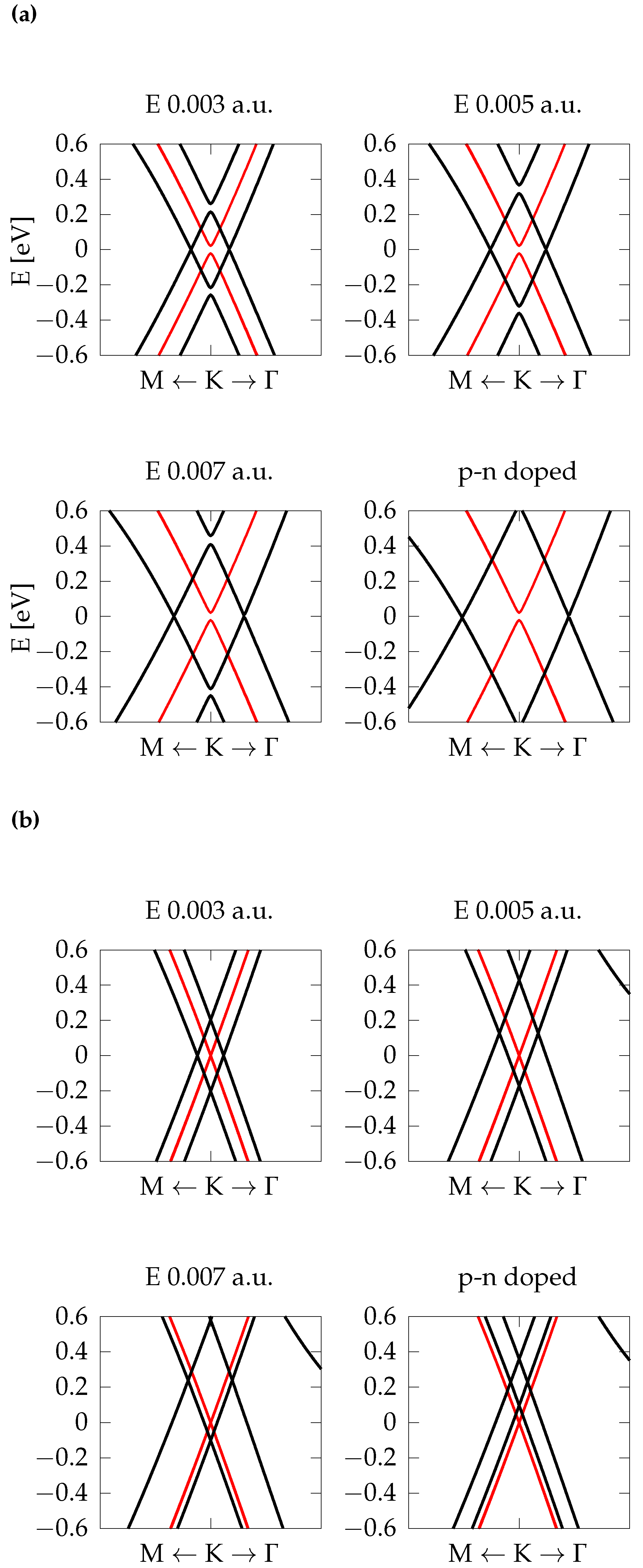
| System | Stacking | |
|---|---|---|
| AB-AA-AB | −57.8 | |
| C-BN-BN-C | AB-AA-AB | −34.7 |
| T-AA-T | −34.3 | |
| C-BN | AB | −42.6 |
| C-BN | AB | −18.7 |
| BN-BN | AA | −22.7 |
| System | Stacking | a [Å] | dC-BN(bottom) [Å] | dBN-BN [Å] | dC-BN-C(top) [Å] | |
|---|---|---|---|---|---|---|
| 4L | C-BN-BN-C | AB-AA-AB | 2.49 | 3.23 | 3.24 | 3.23 |
| AB-AA-AB | 2.48 | 3.29 | 3.26 | 3.42 | ||
| T-AA-T | 6.55 | 3.40 | 3.23 | 3.40 | ||
| 2L | C-BN | AB | 2.49 | 3.28 | ||
| C-BN | AB | 2.48 | 3.44 | |||
| BN-BN | AA | 2.52 | 3.30 | |||
| 1L | Graphene | AB | 2.46 | |||
| hBN | AA | 2.50 |
| System | m | ||
|---|---|---|---|
| m/s] | [10 m] | ||
| M → K | K → | ||
| AB-AA-AB | 7.71 | 8.01 | 7.3 |
| AB-AA-AB | 7.82 | 8.40 | 0.9 |
| T-AA-T | 8.20 | 8.14 | 0.05 |
| Graphene | 8.30 | 8.40 | 0 |
| C-BN-BN-C | E | E |
|---|---|---|
| Stacking | [eV] | [meV] |
| AB-AA-AB | ||
| Pristine | 0.051 | – |
| 0.003 | 0.430 | 8.0 |
| 0.005 | 0.639 | 3.8 |
| 0.007 | 0.819 | 5.8 |
| doped | 1.245 | 7.3 |
| T-AA-T | ||
| pristine | 0.0073 | 0.4 |
| 0.003 | 0.406 | 0.1 |
| 0.005 | 0.599 | 2.0 |
| 0.007 | 0.681 | 1.8 |
| doped | 0.261 | 3.1 |
| AB-AA-AB | 0.126 | 6.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brozzesi, S.; Attaccalite, C.; Buonocore, F.; Giorgi, G.; Palummo, M.; Pulci, O. Ab Initio Study of Graphene/hBN Van der Waals Heterostructures: Effect of Electric Field, Twist Angles and p-n Doping on the Electronic Properties. Nanomaterials 2022, 12, 2118. https://doi.org/10.3390/nano12122118
Brozzesi S, Attaccalite C, Buonocore F, Giorgi G, Palummo M, Pulci O. Ab Initio Study of Graphene/hBN Van der Waals Heterostructures: Effect of Electric Field, Twist Angles and p-n Doping on the Electronic Properties. Nanomaterials. 2022; 12(12):2118. https://doi.org/10.3390/nano12122118
Chicago/Turabian StyleBrozzesi, Simone, Claudio Attaccalite, Francesco Buonocore, Giacomo Giorgi, Maurizia Palummo, and Olivia Pulci. 2022. "Ab Initio Study of Graphene/hBN Van der Waals Heterostructures: Effect of Electric Field, Twist Angles and p-n Doping on the Electronic Properties" Nanomaterials 12, no. 12: 2118. https://doi.org/10.3390/nano12122118
APA StyleBrozzesi, S., Attaccalite, C., Buonocore, F., Giorgi, G., Palummo, M., & Pulci, O. (2022). Ab Initio Study of Graphene/hBN Van der Waals Heterostructures: Effect of Electric Field, Twist Angles and p-n Doping on the Electronic Properties. Nanomaterials, 12(12), 2118. https://doi.org/10.3390/nano12122118









