Integrated Multifunctional Graphene Discs 2D Plasmonic Optical Tweezers for Manipulating Nanoparticles
Abstract
:1. Introduction
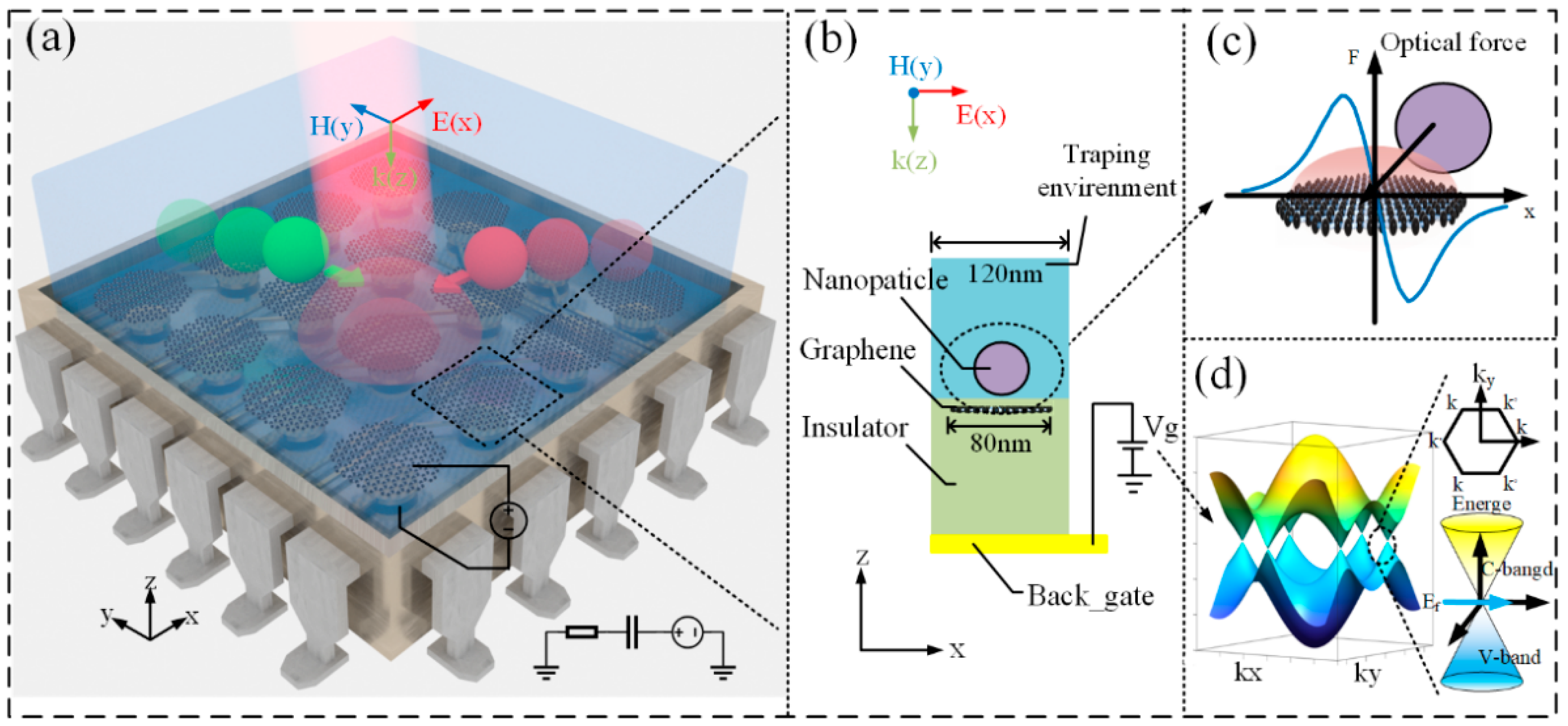
2. Structure Design and Modeling
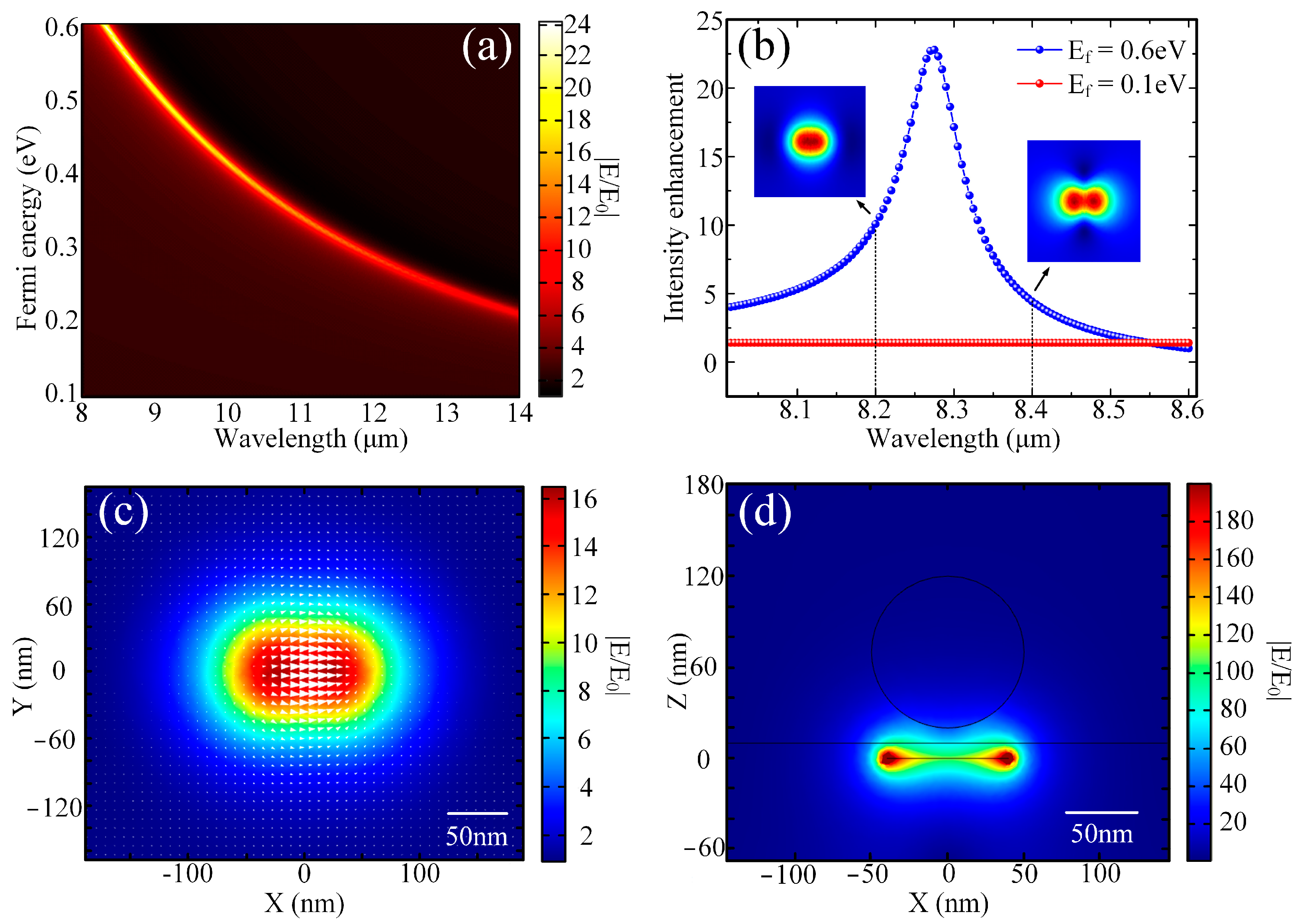
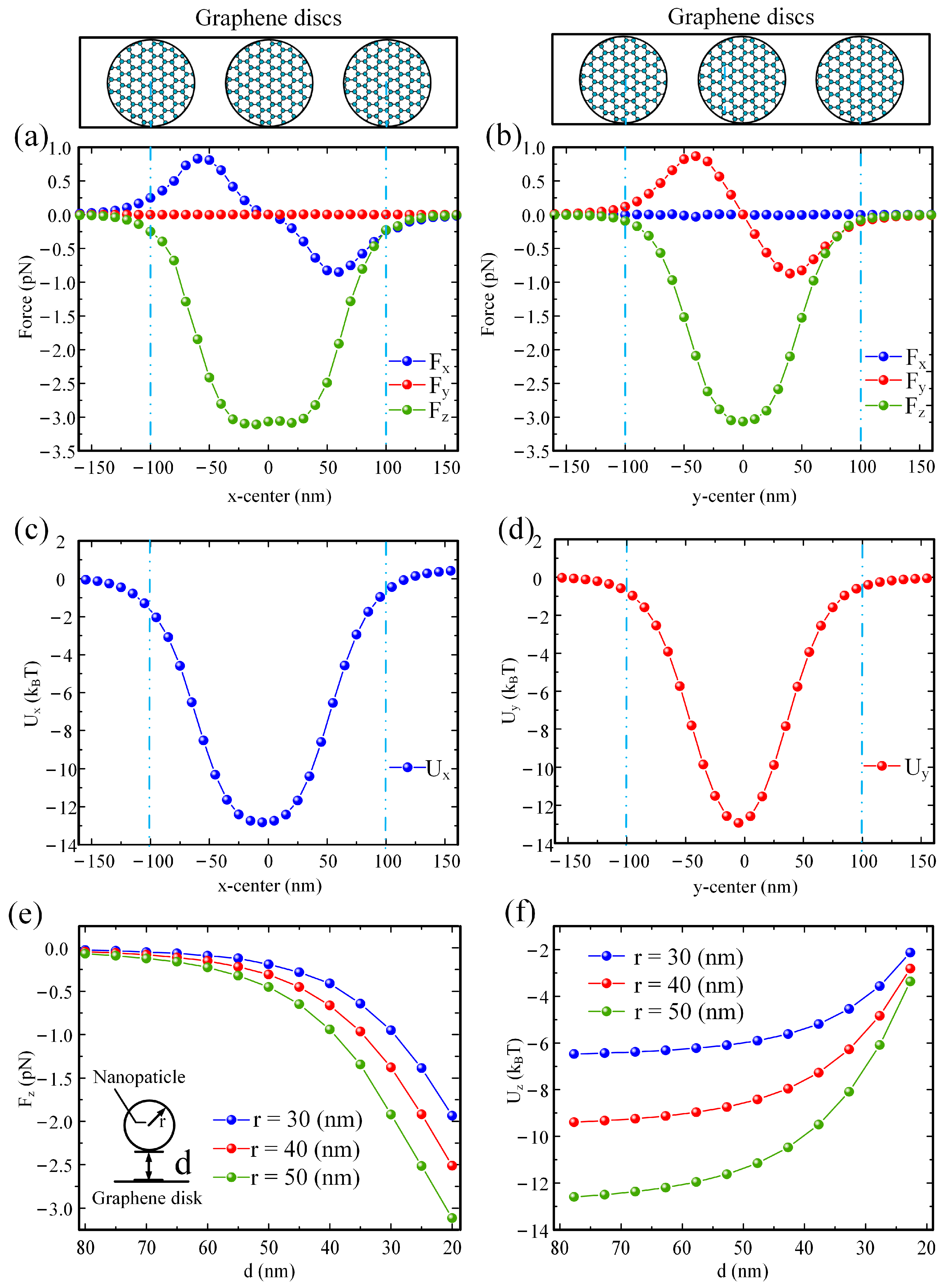
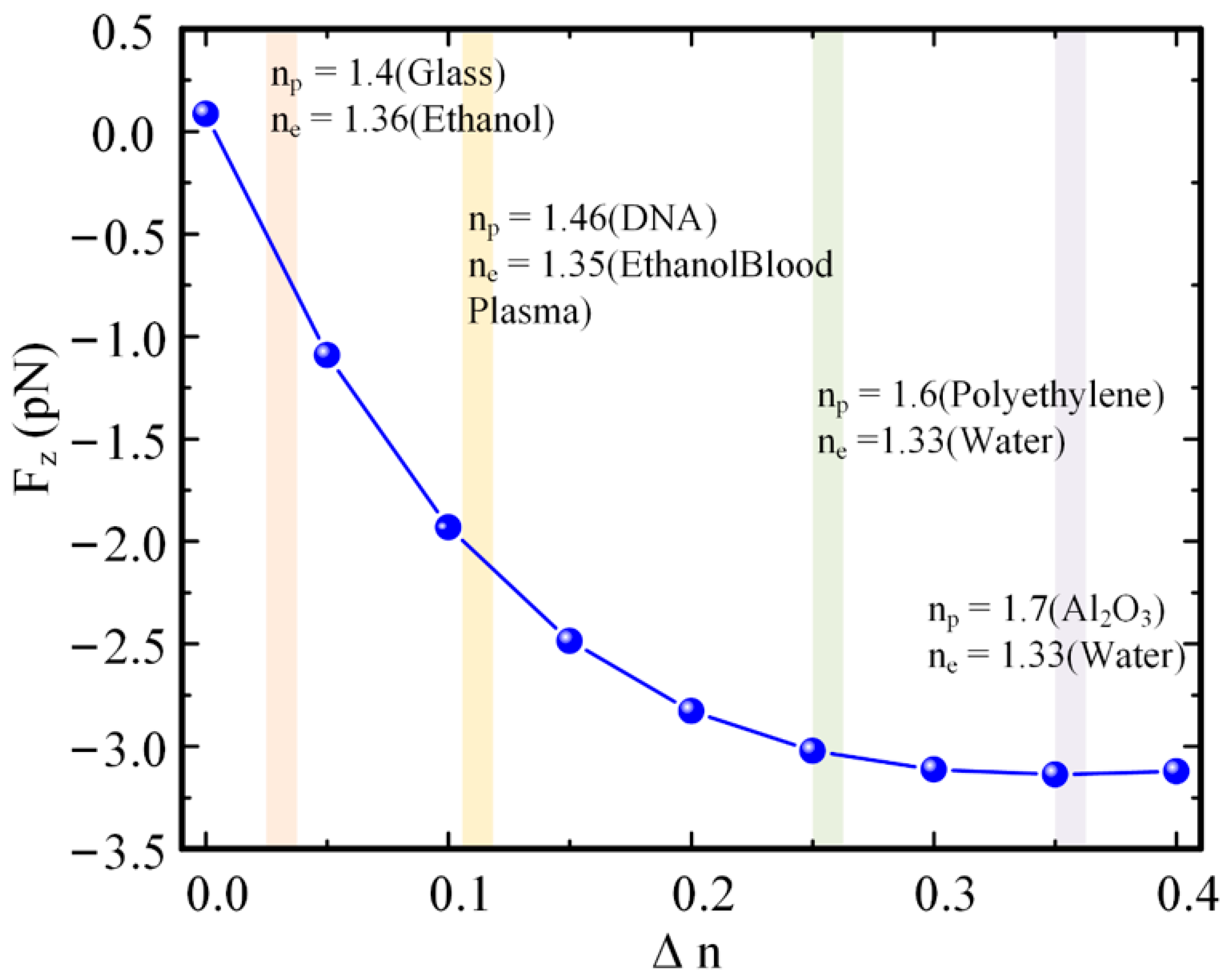
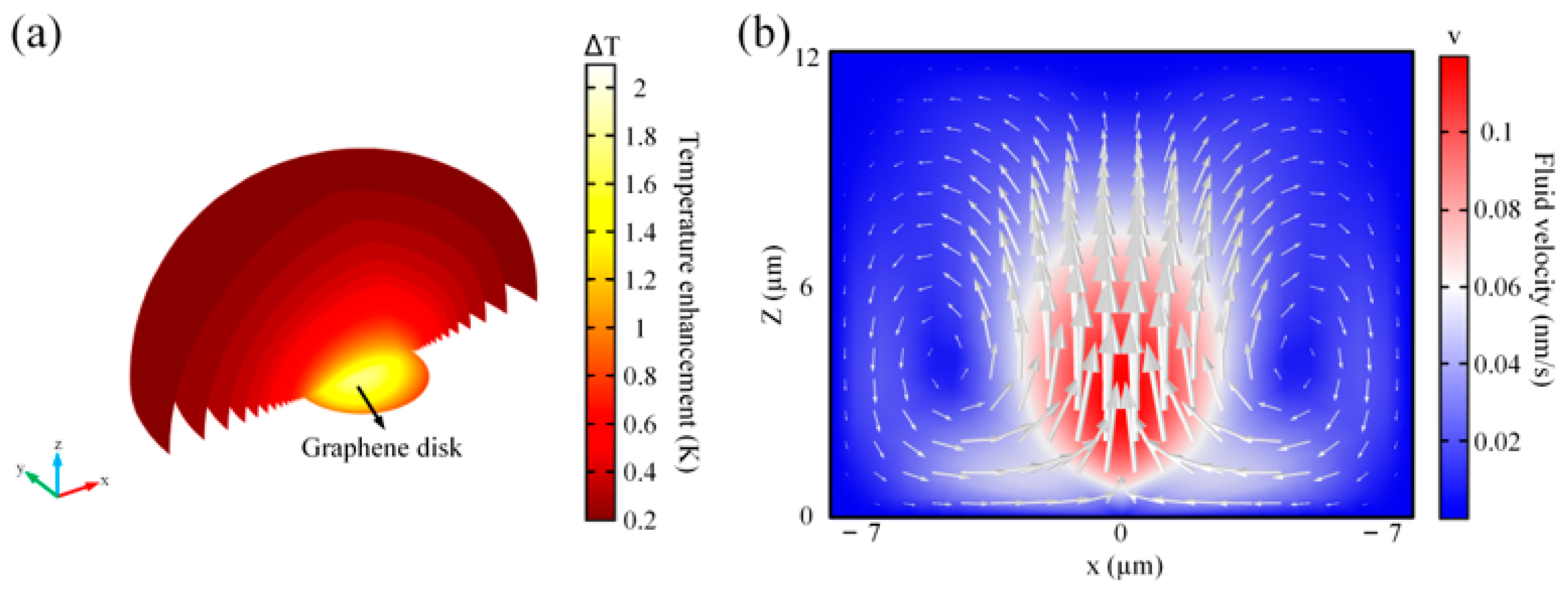
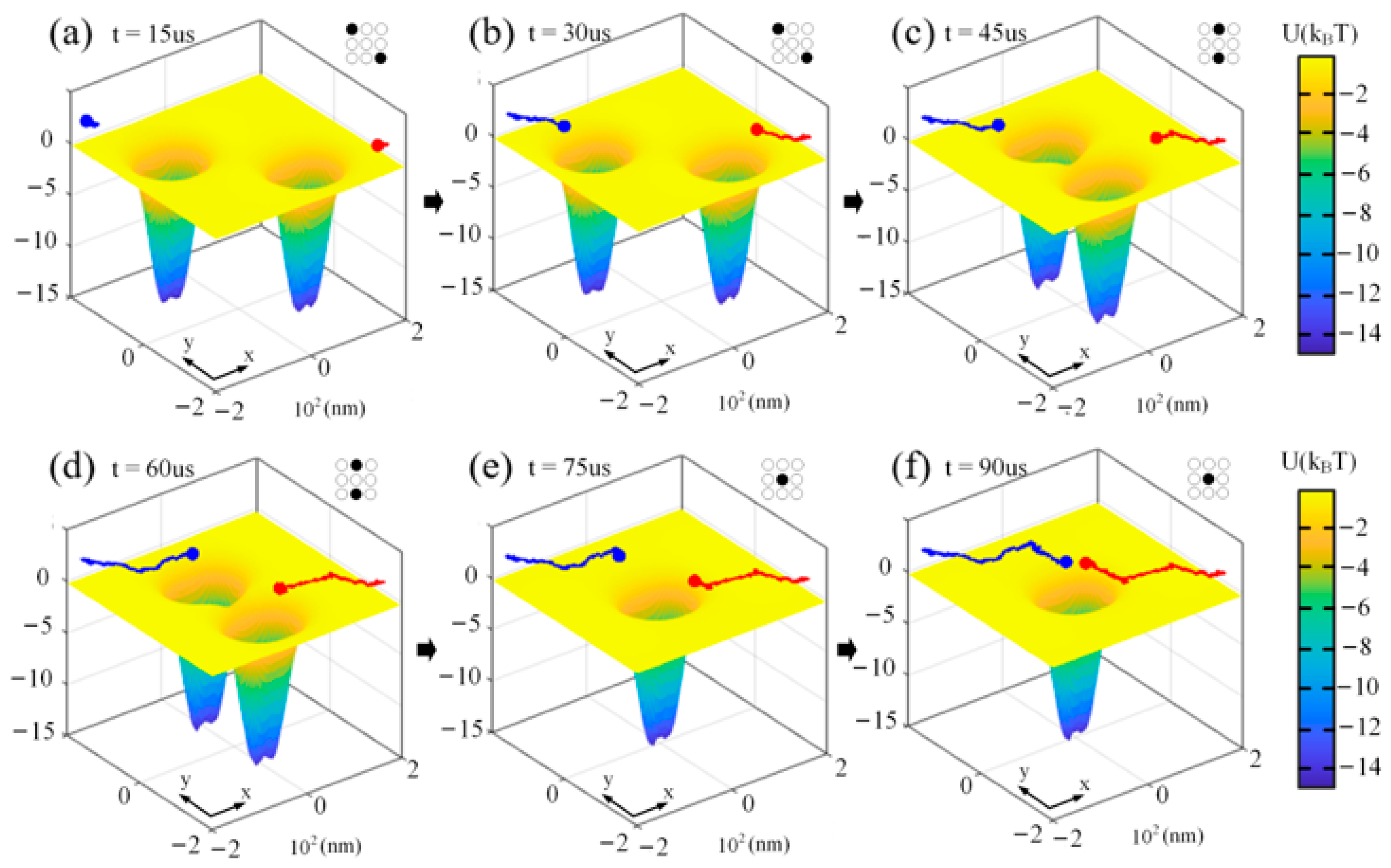
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ashkin, A. Acceleration and Trapping of Particles by Radiation Pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef] [Green Version]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S.J.O.L. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashkin, A.; Dziedzic, J.M. Optical Trapping and Manipulation of Viruses and Bacteria. Science 1987, 235, 1517–1520. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Marago, O.M.; Jones, P.; Gucciardi, P.G.; Volpe, G.; Ferrari, A.C. Optical trapping and manipulation of nanostructures. Nat. Nanotechnol. 2013, 8, 807–819. [Google Scholar] [CrossRef] [Green Version]
- Neuman, K.C.; Nagy, A. Single-molecule force spectroscopy: Optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods 2008, 5, 491–505. [Google Scholar] [CrossRef]
- Jamshidi, A.; Pauzauskie, P.J.; Schuck, P.J.; Ohta, A.T.; Chiou, P.-Y.; Chou, J.; Yang, P.; Wu, M.C.J.N.P. Dynamic manipulation and separation of individual semiconducting and metallic nanowires. Nat. Photonics 2008, 2, 86–89. [Google Scholar] [CrossRef]
- Heller, I.; Hoekstra, T.P.; King, G.A.; Peterman, E.; Wuite, G.J.C.R. Optical Tweezers Analysis of DNA–Protein Complexes. Chem. Rev. 2014, 114, 3087–3119. [Google Scholar] [CrossRef]
- Bustamante, C.; Bryant, Z.; Smith, S.B.J.N. Ten years of tension: Single-molecule DNA mechanics. Nature 2003, 421, 423–427. [Google Scholar] [CrossRef]
- Chiou, P.Y.; Ohta, A.T.; Wu, M.C.J.N. Massively parallel manipulation of single cells and microparticles using optical images. Nature 2005, 436, 370–372. [Google Scholar] [CrossRef]
- Grigorenko, A.N.; Roberts, N.W.; Dickinson, M.R.; Photonics, Z.J.N. Nanometric optical tweezers based on nanostructured substrates. Nat. Photonics 2008, 2, 365–370. [Google Scholar] [CrossRef] [Green Version]
- Schön, A.; Clarkson, B.R.; Jaime, M.; Freire, E. Temperature stability of proteins: Analysis of irreversible denaturation using isothermal calorimetry. Proteins Struct. Funct. Bioinform. 2017, 85, 2009–2016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blázquez-Castro, A.J.M. Optical tweezers: Phototoxicity and thermal stress in cells and biomolecules. Micromachines 2019, 10, 507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novotny, L.; Bian, R.X.; Xie, X.S. Theory of Nanometric Optical Tweezers. Phys. Rev. Lett. 1997, 79, 645–648. [Google Scholar] [CrossRef] [Green Version]
- Righini, M.; Volpe, G.; Girard, C.; Petrov, D.; Quidant, R.J.P.R.L. Surface Plasmon Optical Tweezers: Tunable Optical Manipulation in the Femtonewton Range. Phys. Rev. Lett. 2008, 100, 186804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Juan, M.L.; Righini, M.; Quidant, R.J.N.P. Plasmon nano-optical tweezers. Nat. Photonics 2011, 5, 349. [Google Scholar] [CrossRef]
- Balushi, A.A.A.; Kotnala, A.; Wheaton, S.; Gelfand, R.M.; Rajashekara, Y.; Gordon, R.J.A. Label-free free-solution nanoaperture optical tweezers for single molecule protein studies. Analyst 2015, 140, 4760–4778. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, L.; Santschi, C.; Martin, O.J.F. Trapping and sensing 10 nm metal nanoparticles using plasmonic dipole antennas. Nano Lett. 2010, 10, 1006–1011. [Google Scholar] [CrossRef] [Green Version]
- Juan, M.L.; Gordon, R.; Pang, Y.; Eftekhari, F.; Quidant, R.J.N.P. Self-induced back-action optical trapping of dielectric nanoparticles. Nat. Phys. 2009, 5, 915–919. [Google Scholar] [CrossRef]
- Willets, K.A.; Van Duyne, R.P. Localized Surface Plasmon Resonance Spectroscopy and Sensing. Annu. Rev. Phys. Chem. 2007, 58, 267–297. [Google Scholar] [CrossRef] [Green Version]
- Hutter, E.; Fendler, J.H. Exploitation of Localized Surface Plasmon Resonance. Adv. Mater. 2010, 16, 1685–1706. [Google Scholar] [CrossRef]
- Hou, W.; Cronin, S.B. A Review of Surface Plasmon Resonance-Enhanced Photocatalysis. Adv. Funct. Mater. 2012, 23, 1612–1619. [Google Scholar] [CrossRef]
- Liu, P.Q.; Paul, P. Graphene Nanoribbon Plasmonic Conveyor Belt Network for Optical Trapping and Transportation of Nanoparticles. ACS Photonics 2020, 7, 3456–3466. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Y.; Zhang, S.; Wang, Y.; Yang, W.; Min, C.; Yuan, X. Nonlinear modulation on optical trapping in a plasmonic bowtie structure. Opt. Express 2021, 29, 11664–11673. [Google Scholar] [CrossRef] [PubMed]
- Chun-Fu, K.; Chu, S.C. Dynamic control of the interference pattern of surface plasmon polaritons and its application to particle manipulation. Opt. Express 2018, 26, 19123. [Google Scholar]
- Hansen, P.; Zheng, Y.; Ryan, J.; Hesselink, L. Nano-Optical Conveyor Belt, Part I: Theory. Nano Lett. 2014, 14, 2965–2970. [Google Scholar] [CrossRef]
- Zheng, Y.; Ryan, J.; Hansen, P.; Cheng, Y.T.; Lu, T.J.; Hesselink, L. Nano-Optical Conveyor Belt, Part II: Demonstration of Handoff Between Near-Field Optical Traps. Nano Lett. 2014, 14, 2971–2976. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Wang, G.; Xu, W.; Ji, W.; Zou, N.; Ho, H.-P.; Zhang, X. Two-dimensional arbitrary nano-manipulation on a plasmonic metasurface. Opt. Lett. 2018, 43, 1602–1605. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Y.; Shi, B.; Li, H.; Ding, W. Subwavelength optical trapping and transporting using Bloch mode. Opt. Lett. 2020, 45, 1886–1889. [Google Scholar] [CrossRef]
- Wu, M.C. Optoelectronic tweezers. Nat. Photonics 2011, 5, 322–324. [Google Scholar] [CrossRef]
- Zaman, M.A.; Padhy, P.; Cheng, Y.-T.; Galambos, L.; Hesselink, L. Optoelectronic tweezers with a non-uniform background field. Appl. Phys. Lett. 2020, 117, 171102. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koppens, F.H.L.; Chang, D.E.; de Abajo, F.J.G. Graphene Plasmonics: A Platform for Strong Light–Matter Interactions. Nano Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef] [Green Version]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photonics 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Oliveira, M.I.A.; Rivelino, R.; Mota, F.D.B.; Gueorguiev, G.K. Optical Properties and Quasiparticle Band Gaps of Transition-Metal Atoms Encapsulated by Silicon Cages. J. Phys. Chem. C 2014, 118, 5501–5509. [Google Scholar] [CrossRef] [Green Version]
- Freitas, R.R.; de Brito Mota, F.; Rivelino, R.; De Castilho, C.M.C.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. Spin-orbit-induced gap modification in buckled honeycomb XBi and XBi3 (X=B, Al, Ga, and In) sheets. J. Phys. Condens. Matter 2015, 27, 485306. [Google Scholar] [CrossRef] [Green Version]
- Fei, Z.; Rodin, A.; Andreev, G.O.; Bao, W.; McLeod, A.S.; Wagner, M.; Zhang, L.M.; Zhao, Z.; Thiemens, M.; Dominguez, G.; et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 2012, 487, 82–85. [Google Scholar] [CrossRef]
- Chen, J.; Badioli, M.; Alonso-González, P.; Thongrattanasiri, S.; Huth, F.; Osmond, J.; Spasenović, M.; Centeno, A.; Pesquera, A.; Godignon, P.; et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 2012, 487, 77–81. [Google Scholar] [CrossRef] [Green Version]
- Han, M.Y.; Oezyilmaz, B.; Zhang, Y.; Kim, P. Energy Band-Gap Engineering of Graphene Nanoribbons. Phys. Rev. Lett. 2007, 98, 206805. [Google Scholar] [CrossRef] [Green Version]
- Brar, V.W.; Jang, M.S.; Sherrott, M.; Lopez, J.J.; Atwater, H.A. Highly Confined Tunable Mid-Infrared Plasmonics in Graphene Nanoresonators. Nano Lett. 2013, 13, 2541–2547. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Li, X.; Chandra, B.; Tulevski, G.S.; Wu, Y.; Freitag, M.; Zhu, W.; Avouris, P.; Xia, F. Tunable infrared plasmonic devices using graphene/insulator stacks. Nat. Nanotechnol. 2012, 7, 330–334. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fang, Z.; Wang, Y.; Schlather, A.E.; Liu, Z.; Ajayan, P.M.; García de Abajo, F.J.; Nordlander, P.; Zhu, X.; Halas, N.J. Active Tunable Absorption Enhancement with Graphene Nanodisk Arrays. Nano Lett. 2013, 14, 299–304. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, T.G.; Flindt, C.; Pedersen, J.; Jauho, A.-P.; Mortensen, N.A.; Pedersen, K. Optical properties of graphene antidot lattices. Phys. Rev. B 2008, 77, 245431. [Google Scholar] [CrossRef] [Green Version]
- Eroms, J.; Weiss, D. Weak localization and transport gap in graphene antidot lattices. New J. Phys. 2009, 11, 095021. [Google Scholar] [CrossRef]
- Zhu, B.; Ren, G.; Gao, Y.; Yang, Y.; Cryan, M.J.; Jian, S. Giant Gradient Force for Nanoparticle Trapping in Coupled Graphene Strips Waveguides. IEEE Photonics- Technol. Lett. 2015, 27, 891–894. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, W.; Zhu, Z.; Yuan, X.; Qin, S. Towards nano-optical tweezers with graphene plasmons: Numerical investigation of trapping 10-nm particles with mid-infrared light. Sci. Rep. 2016, 6, 38086. [Google Scholar] [CrossRef]
- Samadi, M.; Darbari, S.; Moravvej-Farshi, M.K. Numerical Investigation of Tunable Plasmonic Tweezers based on Graphene Stripes. Sci. Rep. 2017, 7, 14533. [Google Scholar] [CrossRef]
- Koya, A.N.; Cunha, J.; Guo, T.; Toma, A.; Garoli, D.; Wang, T.; Juodkazis, S.; Cojoc, D.; Zaccaria, R.P. Novel Plasmonic Nanocavities for Optical Trapping-Assisted Biosensing Applications. Adv. Opt. Mater. 2020, 8, 1901481. [Google Scholar] [CrossRef]
- Banszerus, L.; Schmitz, M.; Engels, S.; Dauber, J.; Oellers, M.; Haupt, F.; Watanabe, K.; Taniguchi, T.; Beschoten, B.; Stampfer, C. Ultrahigh-mobility graphene devices from chemical vapor deposition on reusable copper. Sci. Adv. 2015, 1, e1500222. [Google Scholar] [CrossRef] [Green Version]
- Fang, Z.; Thongrattanasiri, S.; Schlather, A.; Liu, Z.; Ma, L.; Wang, Y.; Ajayan, P.M.; Nordlander, P.; Halas, N.J.; García de Abajo, F.J. Gated Tunability and Hybridization of Localized Plasmons in Nanostructured Graphene. ACS Nano 2013, 7, 2388–2395. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation Optics Using Graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Falkovsky, L.A.; Varlamov, A.A. Space-time dispersion of graphene conductivity. Eur. Phys. J. B 2007, 56, 281–284. [Google Scholar] [CrossRef] [Green Version]
- Gosciniak, J.; Tan, D.T. Theoretical investigation of graphene-based photonic modulators. Sci. Rep. 2013, 3, 1897. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Wang, X.B.; Gascoyne, P. General expressions for dielectrophoretic force and electrorotational torque derived using the Maxwell stress tensor method—ScienceDirect. J. Electrost. 1997, 39, 277–295. [Google Scholar] [CrossRef]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Zaman, M.A.; Padhy, P.; Hansen, P.C.; Hesselink, L. Extracting the potential-well of a near-field optical trap using the Helmholtz-Hodge decomposition. Appl. Phys. Lett. 2018, 112, 091103. [Google Scholar] [CrossRef]
- Zaman, M.A.; Padhy, P.; Hesselink, L. Near-field optical trapping in a non-conservative force field. Sci. Rep. 2019, 9, 649. [Google Scholar] [CrossRef]
- Xu, H.; Käll, M. Surface-Plasmon-Enhanced Optical Forces in Silver Nanoaggregates. ChemPhysChem 2003, 89, 246802. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.; Liu, G.; Khan, J.M.; Balandin, A.A. Graphene-Graphite Quilts for Thermal Management of High-Power GaN Transistors. Nat. Commun. 2012, 3, 827. [Google Scholar]
- Donner, J.S.; Baffou, G.; McCloskey, D.; Quidant, R. Plasmon-Assisted Optofluidics. ACS Nano 2011, 5, 5457–5462. [Google Scholar] [CrossRef]
- Zhan, W.; Gao, K.; Zhu, C.; Song, W. Optical trapping using all silicon nanoantennas with ultra-high electric field enhancement. Appl. Phys. Lett. 2020, 117, 241102. [Google Scholar] [CrossRef]
- Cuche, A.; Canaguier-Durand, A.; Devaux, E.; Hutchison, J.A.; Genet, C.; Ebbesen, T.W. Sorting Nanoparticles with Intertwined Plasmonic and Thermo-Hydrodynamical Forces. Nano Lett. 2013, 13, 4230–4235. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.-H.; Li, S.-F.; Xu, H.-T.; Xiang, Z.-X.; Long, Y.-B.; Deng, H.-D. Tunable optical forces enhanced by plasmonic modes hybridization in optical trapping of gold nanorods with plasmonic nanocavity. Opt. Express 2018, 26, 6202–6213. [Google Scholar] [CrossRef] [PubMed]
- Volpe, G.; Volpe, G. Simulation of a Brownian particle in an optical trap. Am. J. Phys. 2013, 81, 224–230. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Narushima, T.; Okamoto, H. Nonlinear optical effects in trapping nanoparticles with femtosecond pulses. Nat. Phys. 2010, 6, 1005–1009. [Google Scholar] [CrossRef]
| Force | Method | Maximum (pN) |
|---|---|---|
| Optical force | MST | 3.25 |
| Brown motion force | 2.6126 × 103 | |
| Drag force | 8.378 × 103 | |
| Thermophoretic force | 7.221 × 102 | |
| Gravity force | 4.974 × 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Mei, Z.; Li, Z.; Liu, H.; Deng, H.; Xiao, G.; Li, J.; Luo, Y.; Yuan, L. Integrated Multifunctional Graphene Discs 2D Plasmonic Optical Tweezers for Manipulating Nanoparticles. Nanomaterials 2022, 12, 1769. https://doi.org/10.3390/nano12101769
Yang H, Mei Z, Li Z, Liu H, Deng H, Xiao G, Li J, Luo Y, Yuan L. Integrated Multifunctional Graphene Discs 2D Plasmonic Optical Tweezers for Manipulating Nanoparticles. Nanomaterials. 2022; 12(10):1769. https://doi.org/10.3390/nano12101769
Chicago/Turabian StyleYang, Hongyan, Ziyang Mei, Zhenkai Li, Houquan Liu, Hongchang Deng, Gongli Xiao, Jianqing Li, Yunhan Luo, and Libo Yuan. 2022. "Integrated Multifunctional Graphene Discs 2D Plasmonic Optical Tweezers for Manipulating Nanoparticles" Nanomaterials 12, no. 10: 1769. https://doi.org/10.3390/nano12101769
APA StyleYang, H., Mei, Z., Li, Z., Liu, H., Deng, H., Xiao, G., Li, J., Luo, Y., & Yuan, L. (2022). Integrated Multifunctional Graphene Discs 2D Plasmonic Optical Tweezers for Manipulating Nanoparticles. Nanomaterials, 12(10), 1769. https://doi.org/10.3390/nano12101769








