Real-Time Analysis of Laser-Induced Plasmon Tuning in Nanoporous Glass Composite
Abstract
1. Introduction
2. Materials, Laser Procedure and Modelling
2.1. Materials
2.2. Laser Irradiation
2.3. Real-Time Control: Background
- (i)
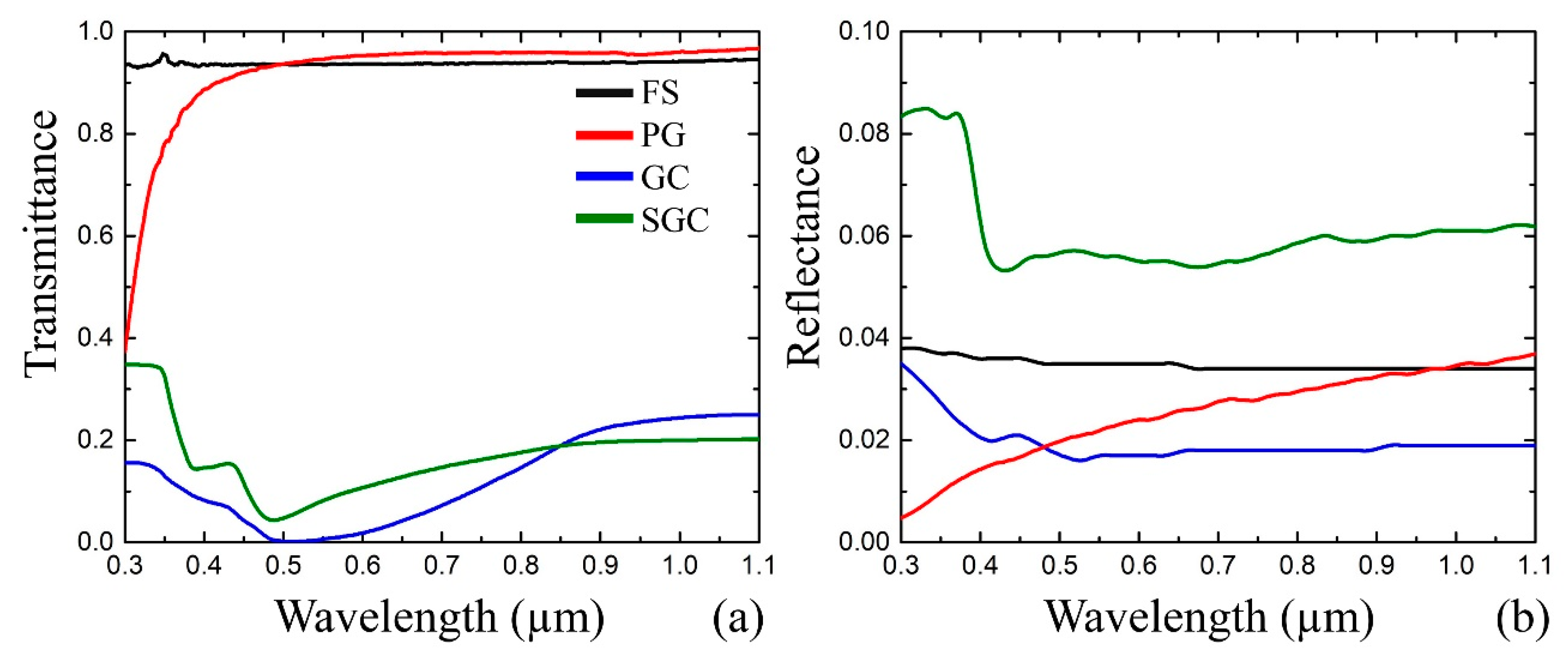
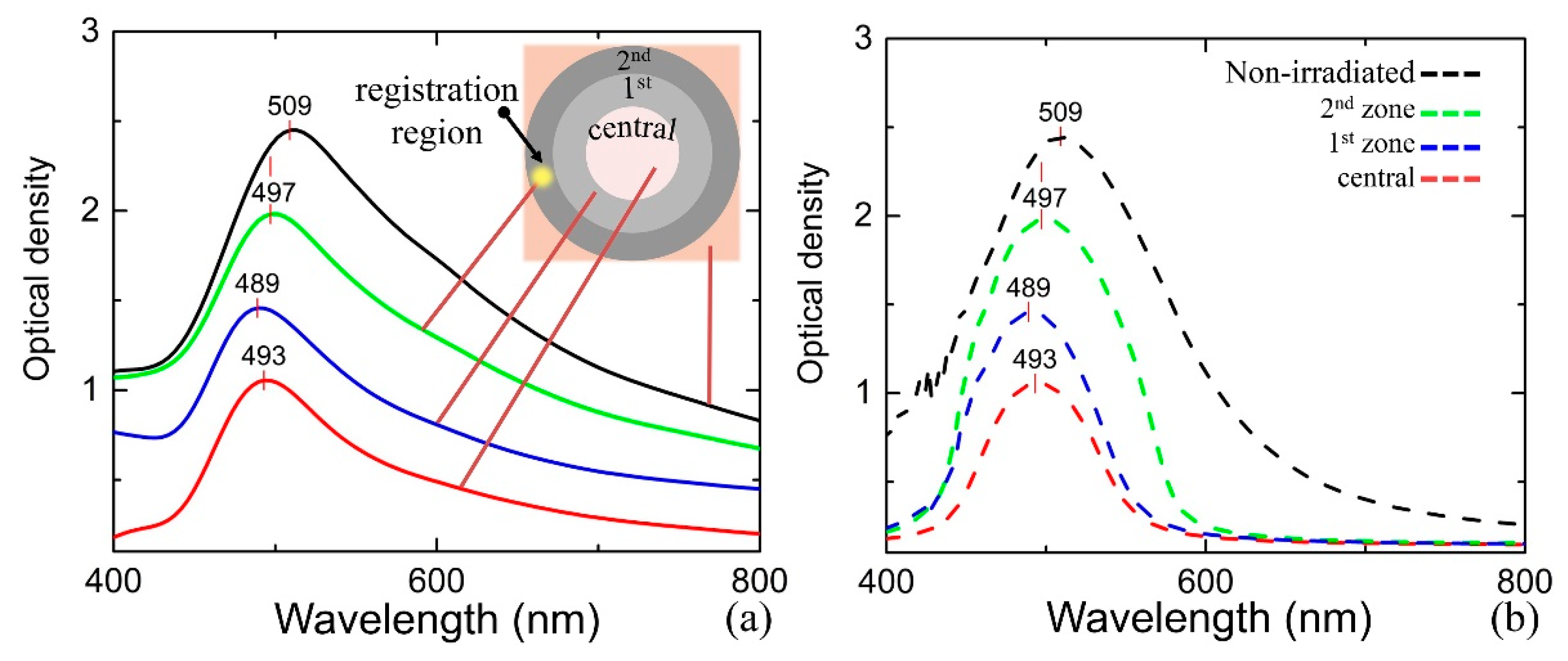
- First, we set input data: the material to irradiate – GC, and the reference sample, which possesses the desired optical properties of the structure to fabricate, in our case it is SGC (Figure 3a).
- (ii)
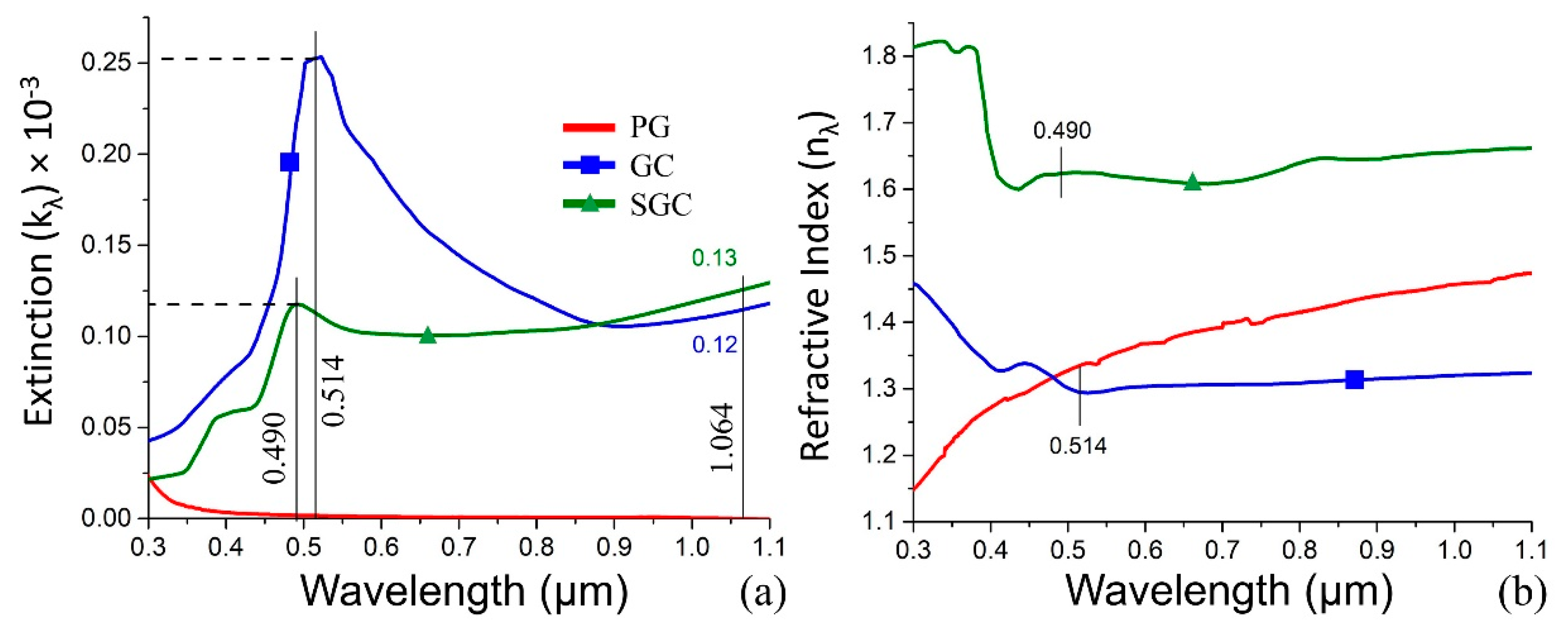
- Subsequently, the transmittance and reflectance of the samples are measured (Figure 3b). The registration range covers possible plasmonic peaks and applied laser wavelength. Simultaneously, the main optical constants, namely, the absorption (αλ), extinction (kλ), and refractive index (nλ) are estimated by the mathematical simulation. The optical properties of the structure to fabricate are homologated with the reference sample.
- (iii)
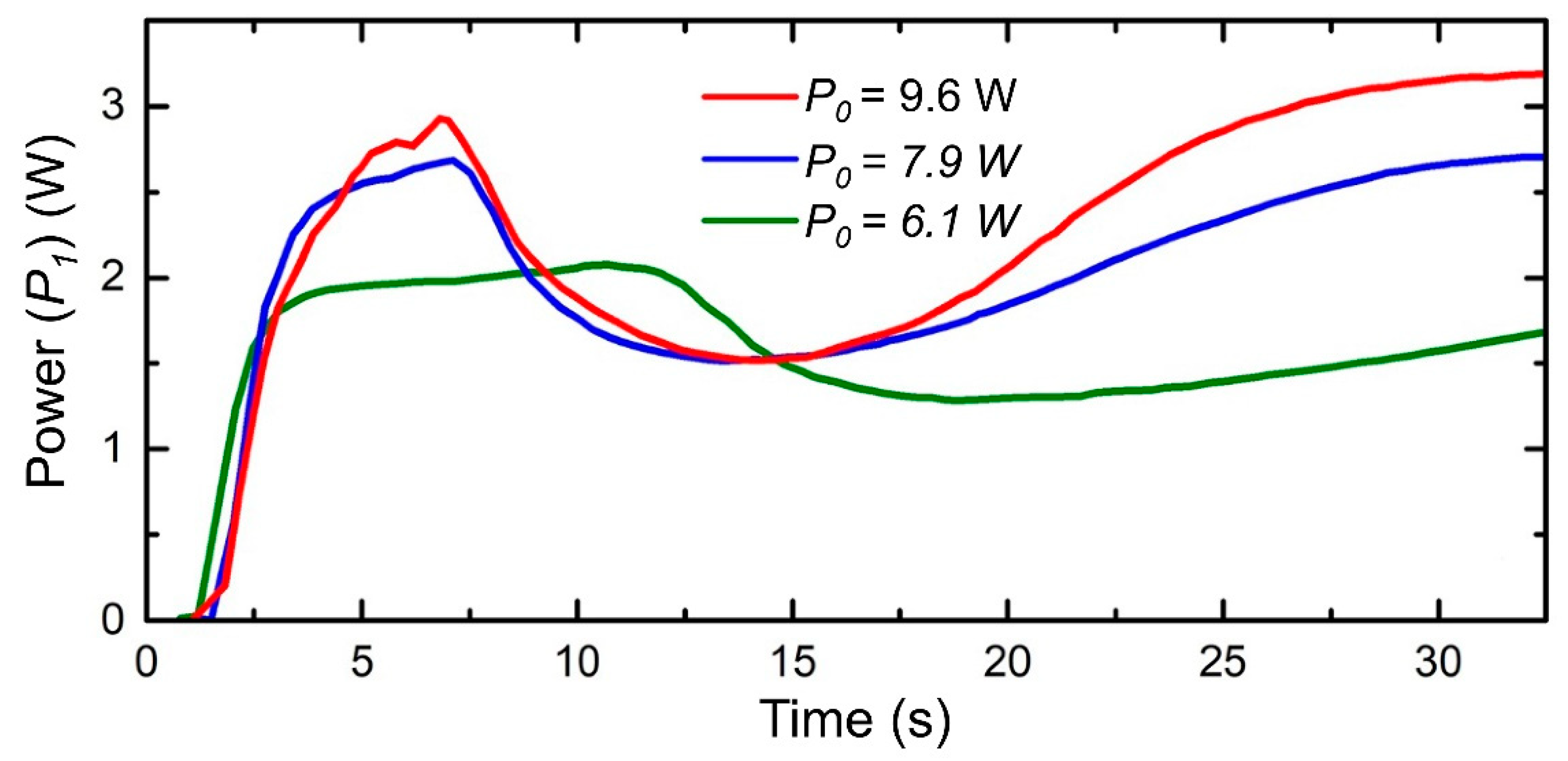
- Next, GC laser irradiation is accompanied by the incident and transmitted laser power monitoring (Figure 3c).
- (iv)
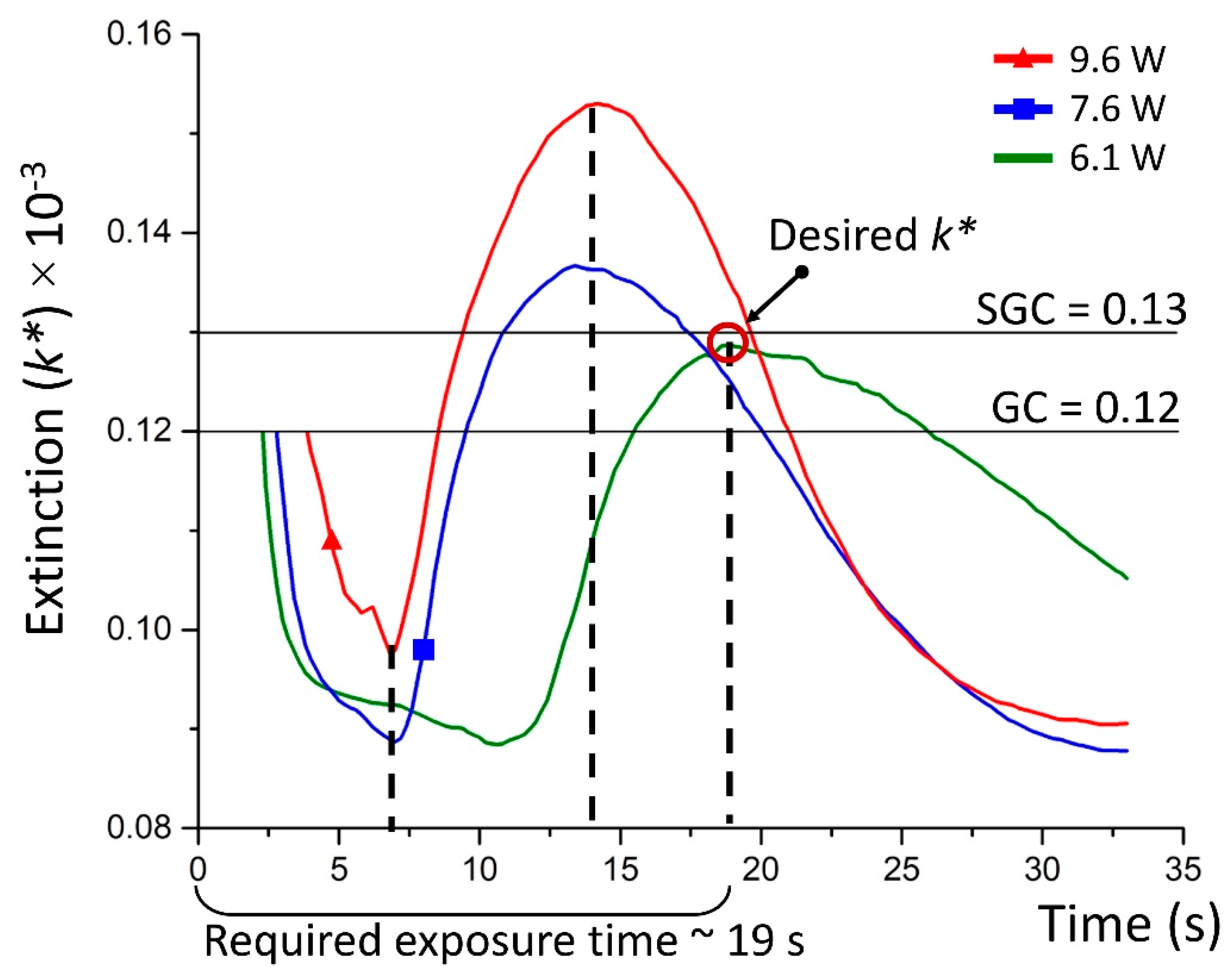
- Since the structure is fabricated inside GC, the transmitted laser power brings the key optical parameter, such as an extinction (k*). This enables us to leap ahead to convert the transmitted power signal into k* behaviour at a specific period of the irradiation time through the mathematical simulation (Figure 3d). Laser irradiation activates photo-thermo-chemical mechanisms that dramatically deviate the extinction curve and confuses the exposure time. Hence, it is also important to describe the mechanisms that are involved for any new glass composite to irradiate.
- (v)
- Afterwards, the user sets the desired extinction for the structure to fabricate. For example, in the experiment, we associate the desired extinction with one of SGC (kλ) estimated in the second step. The convergence of both extinction values—the initial and reference one—shows the required exposure time and laser power to fabricate a plasmonic structure.
3. Results and Discussion
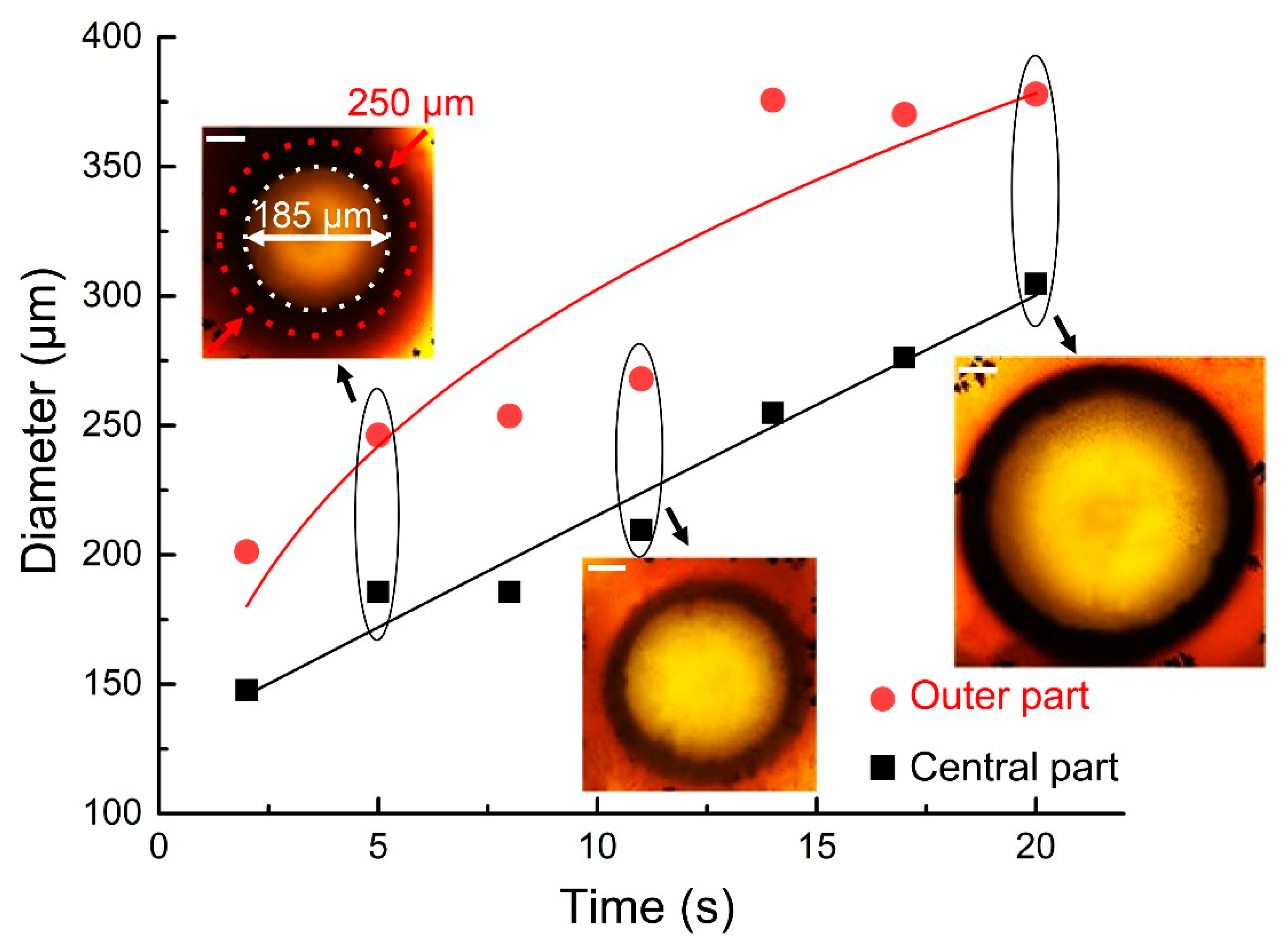
3.1. Results of Glass Composite Laser Processing
3.2. Laser Power Monitoring and Mechanism Description
3.3. Simulation of Optical Properties
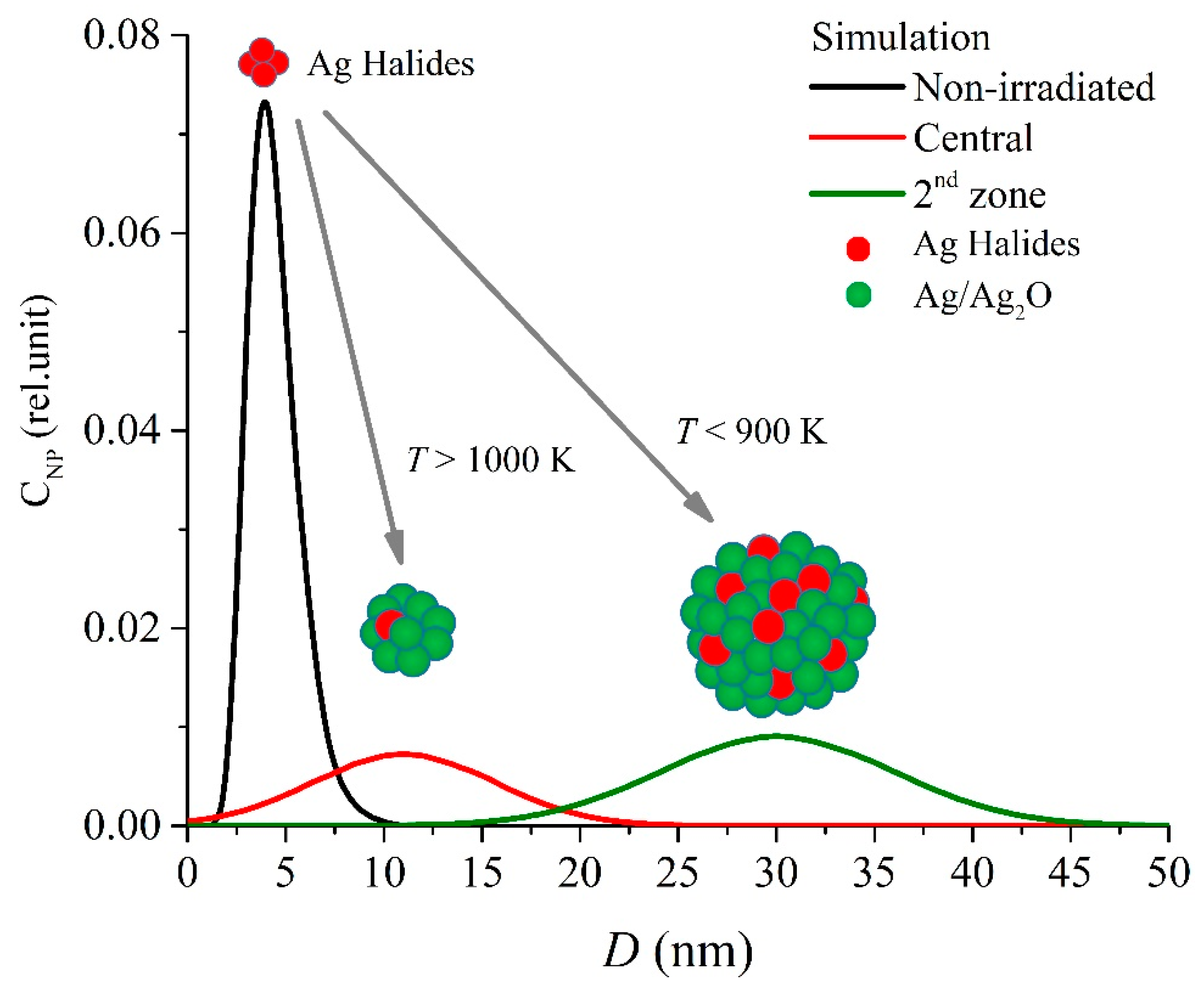
3.4. Plasmonic Properties and Nanoparticles Properties Simulation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Singh, S.P.; Karmakar, B. Controlled oxidative synthesis of Bi nanoparticles and emission centers in bismuth glass nanocomposites for photonic application. Opt. Mater. 2011, 33, 1760–1765. [Google Scholar] [CrossRef]
- Schneider, R.; Schneider, R.; de Campos, E.A.; Mendes, J.B.S.; Felix, J.F.; Santa-Cruz, P.A. Lead–germanate glasses: An easy growth process for silver nanoparticles and their promising applications in photonics and catalysis. RSC Adv. 2017, 7, 41479–41485. [Google Scholar] [CrossRef]
- Abou Khalil, A.; Bérubé, J.-P.; Danto, S.; Desmoulin, J.-C.; Cardinal, T.; Petit, Y.; Vallée, R.; Canioni, L. Direct laser writing of a new type of waveguides in silver containing glasses. Sci. Rep. 2017, 7, 11124. [Google Scholar] [CrossRef] [PubMed]
- Nedyalkov, N.; Dikovska, A.; Koleva, M.; Stankova, N.; Nikov, R.; Borisova, E.; Genova, T.; Aleksandrov, L.; Iordanova, R.; Terakawa, M. Luminescence properties of laser-induced silver clusters in borosilicate glass. Opt. Mater. 2020, 100, 109618. [Google Scholar] [CrossRef]
- de Castro, T.; Fares, H.; Khalil, A.A.; Laberdesque, R.; Petit, Y.; Strutinski, C.; Danto, S.; Jubera, V.; Ribeiro, S.J.L.; Nalin, M.; et al. Femtosecond laser micro-patterning of optical properties and functionalities in novel photosensitive silver-containing fluorophosphate glasses. J. Non-Cryst. Solids 2019, 517, 51–56. [Google Scholar] [CrossRef]
- Heinz, M.; Srabionyan, V.V.; Avakyan, L.A.; Bugaev, A.L.; Skidanenko, A.V.; Kaptelinin, S.Y.; Ihlemann, J.; Meinertz, J.; Patzig, C.; Dubiel, M.; et al. Formation of bimetallic gold-silver nanoparticles in glass by UV laser irradiation. J. Alloys Compd. 2018, 767, 1253–1263. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Ouyang, X.; Lei, D.Y.; Zhang, A.P.; Tam, H.-Y. Ultrafast light-controlled growth of silver nanoparticles for direct plasmonic color printing. ACS Nano 2018, 12, 9913–9921. [Google Scholar] [CrossRef]
- Capoen, B.; Chahadih, A.; El Hamzaoui, H.; Cristini, O.; Bouazaoui, M. Laser-induced growth of nanocrystals embedded in porous materials. Nanoscale Res. Lett. 2013, 8, 1–10. [Google Scholar] [CrossRef]
- Antropova, T.; Girsova, M.; Anfimova, I.; Drozdova, I.; Polyakova, I.; Vedishcheva, N. Structure and spectral properties of the photochromic quartz-like glasses activated by silver halides. J. Non-Cryst. Solids 2014, 401, 139–141. [Google Scholar] [CrossRef]
- Iskhakova, L.D.; Mashinsky, V.M.; Milovich, F.O.; Velmiskin, V.V.; Plastinin, E.A.; Firstov, S.V.; Lukashova, M.V.; Somov, P.A.; Dianov, E.M. Microstructure, composition, and luminescent properties of bismuth-doped porous glass and optical fiber preforms. J. Non-Cryst. Solids 2019, 503, 28–35. [Google Scholar] [CrossRef]
- Santos, E.d.B.; Sigoli, F.A.; Mazali, I.O. Metallic Cu nanoparticles dispersed into porous glass: A simple green chemistry approach to prepare SERS substrates. Mater. Lett. 2013, 108, 172–175. [Google Scholar] [CrossRef]
- Teng, Y.; Zhou, J.; Lin, G.; Hua, J.; Zeng, H.; Zhou, S.; Qiu, J. Ultrafast modification of elements distribution and local luminescence properties in glass. J. Non-Cryst. Solids 2012, 358, 1185–1189. [Google Scholar] [CrossRef]
- Sergeev, M.M.; Kostyuk, G.K.; Zakoldaev, R.A.; Girsova, M.A.; Anfimova, I.N.; Antropova, T.V. Organization of silver nanoclusters in porous glass bulk by laser irradiation. Glass Phys. Chem. 2017, 43, 395–398. [Google Scholar] [CrossRef]
- Goutaland, F.; Sow, M.; Ollier, N.; Vocanson, F. Growth of highly concentrated silver nanoparticles and nanoholes in silver-exchanged glass by ultraviolet continuous wave laser exposure. Opt. Mater. Express 2012, 2, 350–357. [Google Scholar] [CrossRef]
- Seifert, G.; Stalmashonak, A.; Hofmeister, H.; Haug, J.; Dubiel, M. Laser-Induced, Polarization Dependent Shape Transformation of Au/Ag Nanoparticles in Glass. Nanoscale Res. Lett. 2009, 4, 1380. [Google Scholar] [CrossRef] [PubMed]
- Garnett, J.M., XII. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. London. Ser. Acontaining Pap. A Math. Or Phys. Character 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Bergman, D.J. The dielectric constant of a composite material—A problem in classical physics. Phys. Rep. 1978, 43, 377–407. [Google Scholar] [CrossRef]
- Pinchuk, A.; Kreibig, U.; Hilger, A. Optical properties of metallic nanoparticles: Influence of interface effects and interband transitions. Surf. Sci. 2004, 557, 269–280. [Google Scholar] [CrossRef]
- Sturm, J.; Grosse, P.; Theiss, W. Effective dielectric functions of alkali halide composites and their spectral representation. Zeitschrift für Physik B Condens. Matter 1991, 83, 361–365. [Google Scholar] [CrossRef]
- Drozdova, I.A.; Antropova, T.V.; Tolkachev, M.D. Application of electron microscopy methods to the study of porous and quartz-like glasses. Opt. Appl. 2005, 35, 709–715. [Google Scholar]
- Kreisberg, V.; Antropova, T.; Kalinina, S. Formation of micro-and mesoporous substructures in the course of the leaching process of two-phase alkali borosilicate glass. Glass Phys. Chem. 2014, 40, 384–387. [Google Scholar] [CrossRef]
- Kreisberg, V.; Antropova, T.; Kalinina, S. Effect of the composition and conditions of the synthesis of porous glass on their micro-and mesoporous structures. Glass Phys. Chem. 2014, 40, 501–512. [Google Scholar] [CrossRef]
- Antropova, T.; Girsova, M.; Anfimova, I.; Drozdova, I. Spectral properties of the high-silica porous glasses doped by silver halides. J. Lumin. 2018, 193, 29–33. [Google Scholar] [CrossRef]
- Girsova, M.; Drozdova, I.; Antropova, T. Structure and optical properties of photochromic quartz-like glass doped with silver halides. Glass Phys. Chem. 2014, 40, 162–166. [Google Scholar] [CrossRef]
- Malasi, A.; Kalyanaraman, R.; Garcia, H. From Mie to Fresnel through effective medium approximation with multipole contributions. J. Opt. 2014, 16, 065001. [Google Scholar] [CrossRef]
- Kriegel, I.; Scotognella, F.; Manna, L. Plasmonic doped semiconductor nanocrystals: Properties, fabrication, applications and perspectives. Phys. Rep. 2017, 674, 1–52. [Google Scholar] [CrossRef]
- Nikonorov, N.; Sidorov, A.; Tsekhomskii, V. Silver Nanoparticles in Oxide Glasses: Technologies and Properties; IntechOpen: London, UK, 2010; Volume 177. [Google Scholar] [CrossRef]
- Malerba, C.; Biccari, F.; Ricardo, C.L.A.; D’Incau, M.; Scardi, P.; Mittiga, A. Absorption coefficient of bulk and thin film Cu2O. Sol. Energy Mater. Sol. Cells 2011, 95, 2848–2854. [Google Scholar] [CrossRef]
- Kasap, S.; Capper, P. Springer Handbook of Electronic and Photonic Materials; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Tite, T.; Ollier, N.; Sow, M.C.; Vocanson, F.; Goutaland, F. Ag nanoparticles in soda-lime glass grown by continuous wave laser irradiation as an efficient SERS platform for pesticides detection. Sens. Actuators B Chem. 2017, 242, 127–131. [Google Scholar] [CrossRef]
- Siozios, A.; Koutsogeorgis, D.; Lidorikis, E.; Dimitrakopulos, G.; Pliatsikas, N.; Vourlias, G.; Kehagias, T.; Komninou, P.; Cranton, W.; Kosmidis, C. Laser-matter interactions, phase changes and diffusion phenomena during laser annealing of plasmonic AlN: Ag templates and their applications in optical encoding. J. Phys. D Appl. Phys. 2015, 48, 285306. [Google Scholar] [CrossRef][Green Version]
- Chiasera, A.; Macchi, C.; Mariazzi, S.; Valligatla, S.; Lunelli, L.; Pederzolli, C.; Rao, D.N.; Somoza, A.; Brusa, R.S.; Ferrari, M. CO2 laser irradiation of GeO2 planar waveguide fabricated by rf-sputtering. Opt. Mater. Express 2013, 3, 1561–1570. [Google Scholar] [CrossRef]
- Kreisberg, V.A.; Antropova, T.V. Changing the relation between micro- and mesoporosity in porous glasses: The effect of different factors. Microporous Mesoporous Mater. 2014, 190, 128–138. [Google Scholar] [CrossRef]
- Petrov, D.V.; Dyukareva, A.S.; Antropova, T.V.; Veiko, V.P.; Kostyuk, G.K.; Yakovlev, E.B. Surface sintering of porous glass plates under laser radiation. Glass Phys. Chem. 2003, 29, 456–460. [Google Scholar] [CrossRef]
- Grigoriev, I.S.; Meæilikhov, E.Z. Handbook of Physical Quantities; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Varkey, A.; Fort, A. Some optical properties of silver peroxide (AgO) and silver oxide (Ag2O) films produced by chemical-bath deposition. Sol. Energy Mater. Sol. Cells 1993, 29, 253–259. [Google Scholar] [CrossRef]
- Sancho-Parramon, J. Surface plasmon resonance broadening of metallic particles in the quasi-static approximation: A numerical study of size confinement and interparticle interaction effects. Nanotechnology 2009, 20, 235706. [Google Scholar] [CrossRef]
- Cavaliere, E.; Benetti, G.; Van Bael, M.; Winckelmans, N.; Bals, S.; Gavioli, L. Exploring the optical and morphological properties of ag and Ag/TiO2 nanocomposites grown by supersonic cluster beam deposition. Nanomaterials 2017, 7, 442. [Google Scholar] [CrossRef]
- Smith, D.; Shiles, E.; Inokuti, M.; Palik, E. Handbook of optical constants of solids. Handb. Opt. Constants Solids 1985, 1, 369–406. [Google Scholar]



| Zone | Cu | Cu2O | Ag | Ag2O | AgCl | AgBr | AgI | N2 | O2 | Ar | H2O |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial GC | |||||||||||
| Non-irradiated | 1 | 2 | 1 | 0 | 32 | 32 | 32 | 64 | 17.2 | 0.8 | 18 |
| Fabricated structure | |||||||||||
| Center | 1 | 2 | 83 | 14 | 0 | 0 | 0 | 78.1 | 21 | 0.9 | 0 |
| 1st | 32 | 20 | 25 | 15 | 5 | ||||||
| 2nd | 16 | 6 | 30 | 30 | 15 | ||||||
| Cu | Cu2O | Ag | Ag2O | AgCl | AgBr | AgI | |
|---|---|---|---|---|---|---|---|
| N (cm−3) m τ (s) υF (m/s) | 8.47 × 1022 1.49 8.52 × 10−15 1.287 × 106 | 5.47 × 1022 0.98 1.18 × 10−14 1.466 × 106 | 5.86 × 1022 0.55 9.20 × 10−15 1.876 × 106 | 2.86 × 1022 0.7 1.10 × 10−14 1.568 × 106 | 2.59 × 1019 0.25 1.0 × 10−4 2.685 × 106 | 1.85 × 1018 0.177 5.0 × 10−8 2.924 × 106 | 1.4 × 1020 0.147 1.0 × 10−7 3.312 × 106 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sergeev, M.M.; Zakoldaev, R.A.; Itina, T.E.; Varlamov, P.V.; Kostyuk, G.K. Real-Time Analysis of Laser-Induced Plasmon Tuning in Nanoporous Glass Composite. Nanomaterials 2020, 10, 1131. https://doi.org/10.3390/nano10061131
Sergeev MM, Zakoldaev RA, Itina TE, Varlamov PV, Kostyuk GK. Real-Time Analysis of Laser-Induced Plasmon Tuning in Nanoporous Glass Composite. Nanomaterials. 2020; 10(6):1131. https://doi.org/10.3390/nano10061131
Chicago/Turabian StyleSergeev, Maksim M., Roman A. Zakoldaev, Tatiana E. Itina, Pavel V. Varlamov, and Galina K. Kostyuk. 2020. "Real-Time Analysis of Laser-Induced Plasmon Tuning in Nanoporous Glass Composite" Nanomaterials 10, no. 6: 1131. https://doi.org/10.3390/nano10061131
APA StyleSergeev, M. M., Zakoldaev, R. A., Itina, T. E., Varlamov, P. V., & Kostyuk, G. K. (2020). Real-Time Analysis of Laser-Induced Plasmon Tuning in Nanoporous Glass Composite. Nanomaterials, 10(6), 1131. https://doi.org/10.3390/nano10061131







