Unraveling Origins of EPR Spectrum in Graphene Oxide Quantum Dots
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis of GOQDs
2.2. UV–Vis Spectroscopy
2.3. Fluorescence Spectroscopy
2.4. Magnetization Measurements
2.5. Scanning Electron Microscopy (SEM) and Energy Dispersive X-ray Spectroscopy (EDX)
2.6. Electron Paramagnetic Resonance (EPR)
3. Results and Discussion
3.1. GOQDs Fabrication
3.2. Optical Measurements Confirm GOQDs
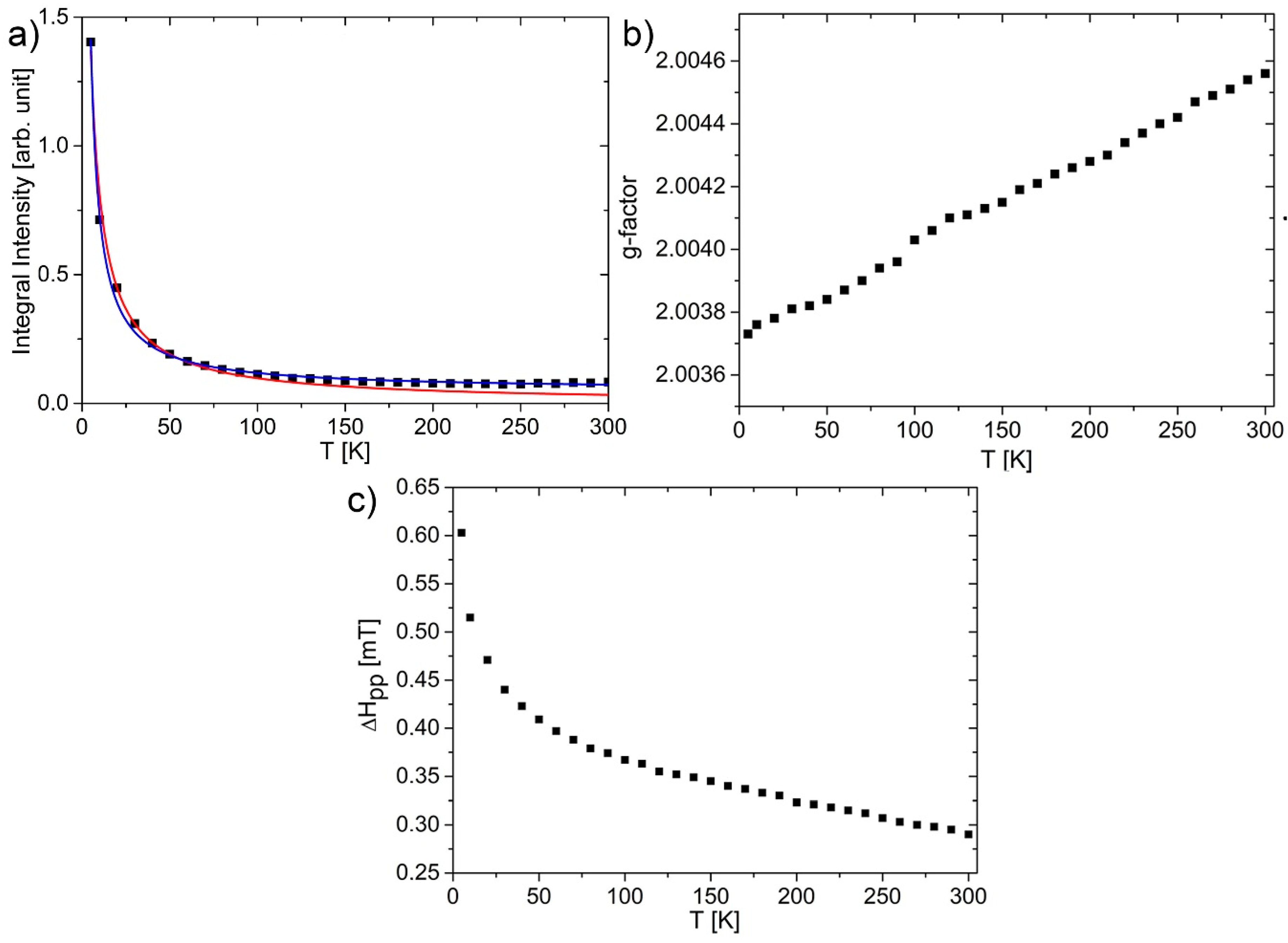
3.3. Magnetic Properties of GOQDs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yang, J.; Ling, T.; Wu, W.-T.; Liu, H.; Gao, M.-R.; Ling, C.; Li, L.; Du, X.-W. A top–down strategy towards monodisperse colloidal lead sulphide quantum dots. Nat. Commun. 2013, 4, 1695. [Google Scholar] [CrossRef] [PubMed]
- Efros, A.L.; Nesbitt, D.J. Origin and control of blinking in quantum dots. Nat. Nanotechnol. 2016, 11, 661–671. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, Y.; Xu, T.; Liao, H.; Yao, C.; Liu, Y.; Li, Z.; Chen, Z.; Pan, D.; Sun, L.; et al. Gram-scale synthesis of single-crystalline graphene quantum dots with superior optical properties. Nat. Commun. 2014, 5, 5357. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Ji, R.; Li, X.; Teng, K.S.; Lau, S.P. Size-Dependent Structural and Optical Characteristics of Glucose-Derived Graphene Quantum Dots. Part. Part. Syst. Charact. 2013, 30, 523–531. [Google Scholar] [CrossRef]
- Cayuela, A.; Soriano, M.L.; Carrillo-Carrión, C.; Valcárcel, M. Semiconductor and carbon-based fluorescent nanodots: The need for consistency. Chem. Commun. 2016, 52, 1311–1326. [Google Scholar] [CrossRef] [PubMed]
- Stuttgen, V.; Giffney, H.E.; Anandan, A.; Alabdali, A.; Twarog, C.; Belhout, S.A.; O′Loughlin, M.; Podhorska, L.; Delaney, C.; Geoghegan, N.; et al. The UCD nanosafety workshop (03 December 2018): Towards developing a consensus on safe handling of nanomaterials within the Irish university labs and beyond—A report. Nanotoxicology 2019, 13, 717–732. [Google Scholar] [CrossRef]
- Liu, F.; Jang, M.-H.; Ha, H.D.; Kim, J.-H.; Cho, Y.-H.; Seo, T.S. Facile Synthetic Method for Pristine Graphene Quantum Dots and Graphene Oxide Quantum Dots: Origin of Blue and Green Luminescence. Adv. Mater. 2013, 25, 3657–3662. [Google Scholar] [CrossRef]
- Tadyszak, K.; Wychowaniec, J.K.; Litowczenko, J. Biomedical Applications of Graphene-Based Structures. Nanomaterials 2018, 8, 944. [Google Scholar] [CrossRef]
- Štengl, V.; Bakardjieva, S.; Henych, J.; Lang, K.; Kormunda, M. Blue and green luminescence of reduced graphene oxide quantum dots. Carbon 2013, 63, 537–546. [Google Scholar] [CrossRef]
- Li, K.; Liu, W.; Ni, Y.; Li, D.; Lin, D.; Su, Z.; Wei, G. Technical synthesis and biomedical applications of graphene quantum dots. J. Mater. Chem. B 2017, 5, 4811–4826. [Google Scholar] [CrossRef]
- Benítez-Martínez, S.; Valcárcel, M. Graphene quantum dots in analytical science. TrAC Trends Anal. Chem. 2015, 72, 93–113. [Google Scholar] [CrossRef]
- Chen, Q.; Shi, C.; Zhang, C.; Pu, S.; Wang, R.; Wu, X.; Wang, X.; Xue, F.; Pan, D.; Xiao, M. Magnetic enhancement of photoluminescence from blue-luminescent graphene quantum dots. Appl. Phys. Lett. 2016, 108, 061904. [Google Scholar] [CrossRef]
- Pei, H.; Zhu, S.; Yang, M.; Kong, R.; Zheng, Y.; Qu, F. Graphene oxide quantum dots@silver core-shell nanocrystals as turn-on fluorescent nanoprobe for ultrasensitive detection of prostate specific antigen. Biosens. Bioelectron. 2015, 74, 909–914. [Google Scholar] [CrossRef] [PubMed]
- Benítez-Martínez, S.; Caballero-Díaz, E.; Valcárcel, M. Development of a biosensing system for tacrine based on nitrogen-doped graphene quantum dots and acetylcholinesterase. Analyst 2016, 141, 2688–2695. [Google Scholar] [CrossRef] [PubMed]
- De, S.; Patra, K.; Ghosh, D.; Dutta, K.; Dey, A.; Sarkar, G.; Maiti, J.; Basu, A.; Rana, D.; Chattopadhyay, D. Tailoring the Efficacy of Multifunctional Biopolymeric Graphene Oxide Quantum Dot-Based Nanomaterial as Nanocargo in Cancer Therapeutic Application. ACS Biomater. Sci. Eng. 2018, 4, 514–531. [Google Scholar] [CrossRef]
- Cao, J.; An, H.; Huang, X.; Fu, G.; Zhuang, R.; Zhu, L.; Xie, J.; Zhang, F. Monitoring of the tumor response to nano-graphene oxide-mediated photothermal/photodynamic therapy by diffusion-weighted and BOLD MRI. Nanoscale 2016, 8, 10152–10159. [Google Scholar] [CrossRef] [PubMed]
- Wychowaniec, J.K.; Litowczenko, J.; Tadyszak, K. Fabricating versatile cell supports from nano- and micro-sized graphene oxide flakes. J. Mech. Behav. Biomed. Mater. 2020, 103, 103594. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zheng, Y.; Chen, J.; Zhang, W.; Tang, N.; Du, Y. Intrinsic magnetism of monolayer graphene oxide quantum dots. Appl. Phys. Lett. 2016, 108, 033105. [Google Scholar] [CrossRef]
- Colburn, A.; Wanninayake, N.; Kim, D.Y.; Bhattacharyya, D. Cellulose-graphene quantum dot composite membranes using ionic liquid. J. Membr. Sci. 2018, 556, 293–302. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, S.; Hou, X.; Sun, Z.; Jiang, Y.; Dong, Z.; Tao, Q.; Man, J.; Cao, Y. Coal-derived nitrogen, phosphorus and sulfur co-doped graphene quantum dots: A promising ion fluorescent probe. Appl. Surf. Sci. 2018, 445, 519–526. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, H.; Wu, Y.; Wang, T.; Sun, L.; Gao, P.; Sun, Y.; Huang, H.; Zhou, G.; Hu, J. Bottom-up synthesis and structural design strategy for graphene quantum dots with tunable emission to the near infrared region. Carbon 2019, 142, 673–684. [Google Scholar] [CrossRef]
- More, M.P.; Lohar, P.H.; Patil, A.G.; Patil, P.O.; Deshmukh, P.K. Controlled synthesis of blue luminescent graphene quantum dots from carbonized citric acid: Assessment of methodology, stability, and fluorescence in an aqueous environment. Mater. Chem. Phys. 2018, 220, 11–22. [Google Scholar] [CrossRef]
- Wang, H.; Tian, H.; Wang, S.; Zheng, W.; Liu, Y. Simple and eco-friendly solvothermal synthesis of luminescent reduced graphene oxide small sheets. Mater. Lett. 2012, 78, 170–173. [Google Scholar] [CrossRef]
- Shen, J.; Zhu, Y.; Chen, C.; Yang, X.; Li, C. Facile preparation and upconversion luminescence of graphene quantum dots. Chem. Commun. 2011, 47, 2580–2582. [Google Scholar] [CrossRef]
- Zhao, S.; Lavie, J.; Rondin, L.; Orcin-Chaix, L.; Diederichs, C.; Roussignol, P.; Chassagneux, Y.; Voisin, C.; Müllen, K.; Narita, A.; et al. Single photon emission from graphene quantum dots at room temperature. Nat. Commun. 2018, 9, 3470. [Google Scholar] [CrossRef]
- Tian, P.; Tang, L.; Teng, K.S.; Lau, S.P. Graphene quantum dots from chemistry to applications. Mater. Today Chem. 2018, 10, 221–258. [Google Scholar] [CrossRef]
- Yazyev, O.V.; Helm, L. Defect-induced magnetism in graphene. Phys. Rev. B 2007, 75, 125408. [Google Scholar] [CrossRef]
- López-Sancho, M.P.; de Juan, F.; Vozmediano, M.A.H. Magnetic moments in the presence of topological defects in graphene. Phys. Rev. B 2009, 79, 075413. [Google Scholar] [CrossRef]
- Nair, R.R.; Sepioni, M.; Tsai, I.L.; Lehtinen, O.; Keinonen, J.; Krasheninnikov, A.V.; Thomson, T.; Geim, A.K.; Grigorieva, I.V. Spin-half paramagnetism in graphene induced by point defects. Nat. Phys. 2012, 8, 199–202. [Google Scholar] [CrossRef]
- Eng, A.Y.S.; Poh, H.L.; Šaněk, F.; Maryško, M.; Matějková, S.; Sofer, Z.; Pumera, M. Searching for Magnetism in Hydrogenated Graphene: Using Highly Hydrogenated Graphene Prepared via Birch Reduction of Graphite Oxides. ACS Nano 2013, 7, 5930–5939. [Google Scholar] [CrossRef]
- Boukhvalov, D.W.; Katsnelson, M.I. sp-Electron Magnetic Clusters with a Large Spin in Graphene. ACS Nano 2011, 5, 2440–2446. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sepioni, M.; Nair, R.R.; Rablen, S.; Narayanan, J.; Tuna, F.; Winpenny, R.; Geim, A.K.; Grigorieva, I.V. Limits on Intrinsic Magnetism in Graphene. Phys. Rev. Lett. 2010, 105, 207205. [Google Scholar] [CrossRef] [PubMed]
- Lehtinen, P.O.; Foster, A.S.; Ayuela, A.; Krasheninnikov, A.; Nordlund, K.; Nieminen, R.M. Magnetic Properties and Diffusion of Adatoms on a Graphene Sheet. Phys. Rev. Lett. 2003, 91, 017202. [Google Scholar] [CrossRef] [PubMed]
- Boukhvalov, D.W. Modeling of hydrogen and hydroxyl group migration on graphene. Phys. Chem. Chem. Phys. 2010, 12, 15367–15371. [Google Scholar] [CrossRef]
- Tadyszak, K.; Chybczyńska, K.; Ławniczak, P.; Zalewska, A.; Cieniek, B.; Gonet, M.; Murias, M. Magnetic and electric properties of partially reduced graphene oxide aerogels. J. Magn. Magn. Mater. 2019, 492, 165656. [Google Scholar] [CrossRef]
- Augustyniak-Jabłokow, M.A.; Tadyszak, K.; Strzelczyk, R.; Fedaruk, R.; Carmieli, R. Slow spin relaxation of paramagnetic centers in graphene oxide. Carbon 2019, 152, 98–105. [Google Scholar] [CrossRef]
- Augustyniak-Jabłokow, M.A.; Tadyszak, K.; MaćKowiak, M.; Lijewski, S. ESR study of spin relaxation in graphene. Chem. Phys. Lett. 2013, 557, 118–122. [Google Scholar] [CrossRef]
- Tadyszak, K.; Strzelczyk, R.; Coy, E.; Mac’Kowiak, M.; Augustyniak-Jabłokow, M.A. Size effects in the conduction electron spin resonance of anthracite and higher anthraxolite. Magn. Reson. Chem. 2016, 54, 239–245. [Google Scholar] [CrossRef]
- Tadyszak, K.; Litowczenko, J.; Majchrzycki, Ł.; Jeżowski, P.; Załęski, K.; Scheibe, B. Sucrose based cellular glassy carbon for biological applications. Mater. Chem. Phys. 2019, 239, 122033. [Google Scholar] [CrossRef]
- Fedaruk, R.; Strzelczyk, R.; Tadyszak, K.; Markevich, S.A.; Augustyniak-Jabłokow, M.A. Effect of Rabi splitting on the low-temperature electron paramagnetic resonance signal of anthracite. J. Magn. Reson. 2017, 274, 73–79. [Google Scholar] [CrossRef]
- Tadyszak, K.; Augustyniak-Jabłokow, M.A.; Więckowski, A.B.; Najder-Kozdrowska, L.; Strzelczyk, R.; Andrzejewski, B. Origin of electron paramagnetic resonance signal in anthracite. Carbon 2015, 94, 53–59. [Google Scholar] [CrossRef]
- Tadyszak, K.; Majchrzycki, Ł.; Szyller, Ł.; Scheibe, B. Preparation and characterization of partially reduced graphene oxide aerogels doped with transition metal ions. J. Mater. Sci. 2018, 53, 16086–16098. [Google Scholar] [CrossRef]
- Hummers, W.S.; Offeman, R.E. Preparation of Graphitic Oxide. J. Am. Chem. Soc. 1958, 80, 1339. [Google Scholar] [CrossRef]
- Chien, C.-T.; Li, S.-S.; Lai, W.-J.; Yeh, Y.-C.; Chen, H.-A.; Chen, I.-S.; Chen, L.-C.; Chen, K.-H.; Nemoto, T.; Isoda, S.; et al. Tunable Photoluminescence from Graphene Oxide. Angew. Chem. Int. Ed. 2012, 51, 6662–6666. [Google Scholar] [CrossRef] [PubMed]
- Chuang, C.H.; Wang, Y.F.; Shao, Y.C.; Yeh, Y.C.; Wang, D.Y.; Chen, C.W.; Chiou, J.W.; Ray, S.C.; Pong, W.F.; Zhang, L.; et al. The Effect of Thermal Reduction on the Photoluminescence and Electronic Structures of Graphene Oxides. Sci. Rep. 2014, 4, 4525. [Google Scholar] [CrossRef]
- Wang, Y.F.; Singh, S.B.; Limaye, M.V.; Shao, Y.C.; Hsieh, S.H.; Chen, L.Y.; Hsueh, H.C.; Wang, H.T.; Chiou, J.W.; Yeh, Y.C.; et al. Visualizing chemical states and defects induced magnetism of graphene oxide by spatially-resolved-X-ray microscopy and spectroscopy. Sci. Rep. 2015, 5, 15439. [Google Scholar] [CrossRef]
- Augustyniak-Jabłokow, M.A.; Maćkowiak, M.; Tadyszak, K.; Strzelczyk, R. FMR evidence of stable ferromagnetic correlations at zigzag edge states in graphene. Acta Phys. Pol. A 2015, 127, 537–539. [Google Scholar] [CrossRef]
- Augustyniak-Jabłokow, M.A.; Tadyszak, K.; Maćkowiak, M.; Yablokov, Y.V. EPR evidence of antiferromagnetic ordering in single-layer graphene. Phys. Status Solidi Rapid Res. Lett. 2011, 5, 271–273. [Google Scholar] [CrossRef]
- Panich, A.M.; Shames, A.I.; Tsindlekht, M.I.; Osipov, V.Y.; Patel, M.; Savaram, K.; He, H. Structure and Magnetic Properties of Pristine and Fe-Doped Micro- and Nanographenes. J. Phys. Chem. C 2016, 120, 3042–3053. [Google Scholar] [CrossRef]
- Yordanov, N.D. Quantitative EPR spectrometry—“State of the art”. Appl. Magn. Reson. 1994, 6, 241–257. [Google Scholar] [CrossRef]
- Dyson, F.J. Electron Spin Resonance Absorption in Metals. II. Theory of Electron Diffusion and the Skin Effect. Phys. Rev. 1955, 98, 349–359. [Google Scholar] [CrossRef]
- Augustyniak-Jabłokow, M.A.; Yablokov, Y.V.; Andrzejewski, B.; Kempiński, W.; Łoś, S.; Tadyszak, K.; Yablokov, M.Y.; Zhikharev, V.A. EPR and magnetism of the nanostructured natural carbonaceous material shungite. Phys. Chem. Miner. 2010, 37, 237–247. [Google Scholar] [CrossRef]
- Shames, A.I.; Katz, E.A.; Panich, A.M.; Mogilyansky, D.; Mogilko, E.; Grinblat, J.; Belousov, V.P.; Belousova, I.M.; Ponomarev, A.N. Closed pi-electron Network in Large Polyhedral Multi-shell Carbon Nanoparticles. Nanosci. Nanotechnol. Lett. 2011, 3, 41–43. [Google Scholar] [CrossRef]
- Nicklin, R.C.; Farach, H.A.; Poole, C.P., Jr. EPR of Mn2+, Fe3+, and Cu2+ in glasses of the systems BaO–B2O3–Al2O3 and CaO–B2O3–Al2O3. J. Chem. Phys. 1976, 65, 2998–3005. [Google Scholar] [CrossRef]
- Griscom, D.L.; Griscom, R.E. Paramagnetic Resonance of Mn2+ in Glasses and Compounds of the Lithium Borate System. J. Chem. Phys. 1967, 47, 2711–2722. [Google Scholar] [CrossRef]
- Tadyszak, K.; Rudowicz, C.; Ohta, H.; Sakurai, T. Electron magnetic resonance data on high-spin Mn (III; S = 2) ions in porphyrinic and salen complexes modeled by microscopic spin Hamiltonian approach. J. Inorg. Biochem. 2017, 175, 36–46. [Google Scholar] [CrossRef]
- Tadyszak, K.; Rudowicz, C. EMR data on Mn(III; S = 2) ions in MnTPPCl complex modelled by microscopic spin hamiltonian approach. Acta Phys. Pol. A 2017, 132, 15–18. [Google Scholar] [CrossRef]
- Rudowicz, C.; Tadyszak, K. Single magnetic 3dNadatoms on surfaces—Proper outlook on compatibility of orthorhombic zero-field splitting parameters and their relationships with magnetic anisotropy quantities. Polyhedron 2017, 127, 126–134. [Google Scholar] [CrossRef]
- Panich, A.M.; Shames, A.I.; Aleksenskii, A.E.; Dideikin, A. Magnetic resonance evidence of manganese–graphene complexes in reduced graphene oxide. Solid State Commun. 2012, 152, 466–468. [Google Scholar] [CrossRef]
- Panich, A.M.; Shames, A.I.; Sergeev, N.A. Paramagnetic Impurities in Graphene Oxide. Appl. Magn. Reson. 2013, 44, 107–116. [Google Scholar] [CrossRef]
- Tadyszak, K.; Maćkowiak, M.; Augustyniak-Jabłokow, M.A.; Roman, S. FMR evidence of ferromagnetic correlations at zigzag edge states in single-layer graphene. J. Mol. Struct. 2014, 1076, 31–34. [Google Scholar] [CrossRef]
- Rao, S.S.; Stesmans, A.; van Tol, J.; Kosynkin, D.V.; Higginbotham-Duque, A.; Lu, W.; Sinitskii, A.; Tour, J.M. Spin Dynamics and Relaxation in Graphene Nanoribbons: Electron Spin Resonance Probing. ACS Nano 2012, 6, 7615–7623. [Google Scholar] [CrossRef] [PubMed]
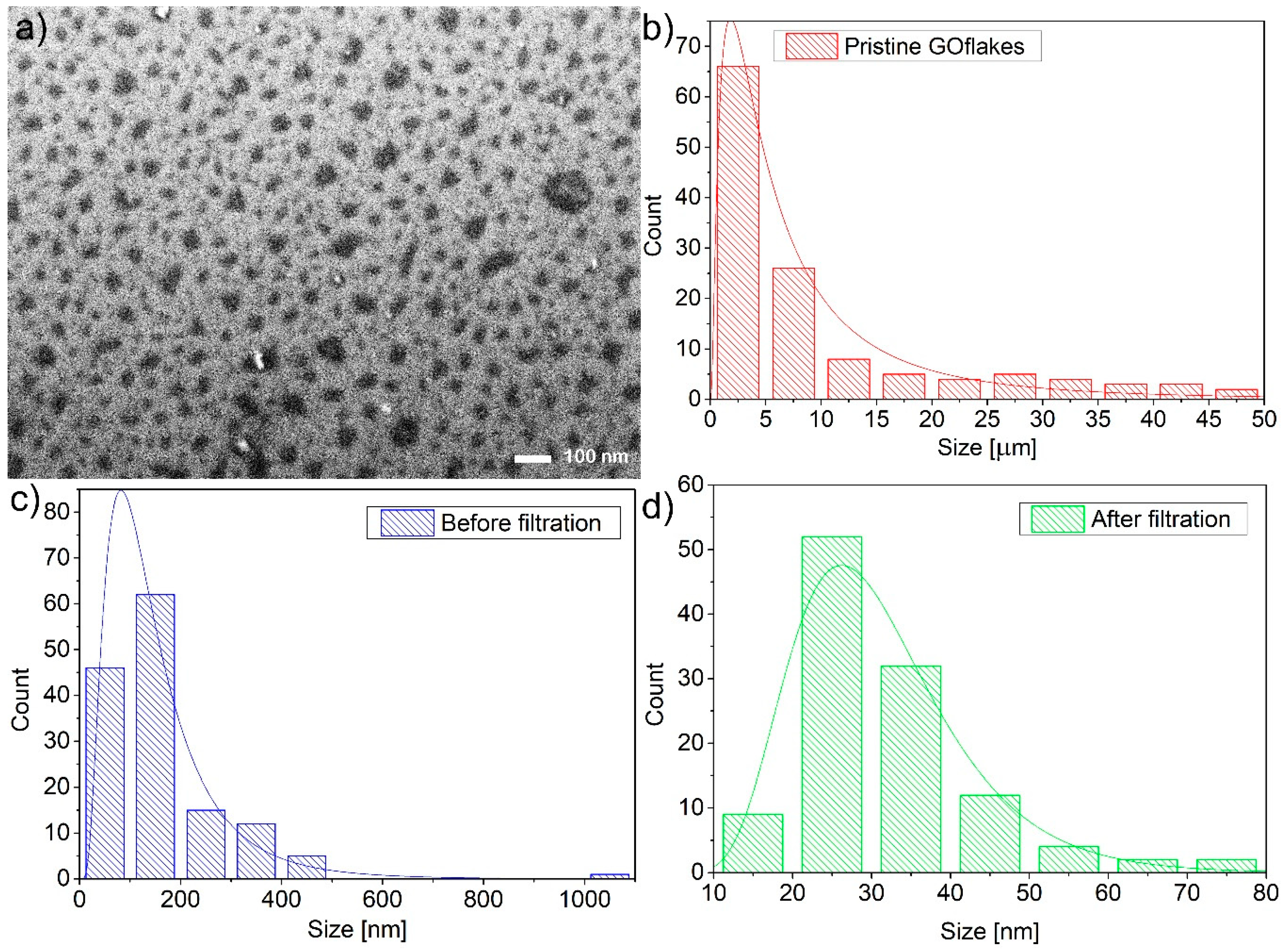
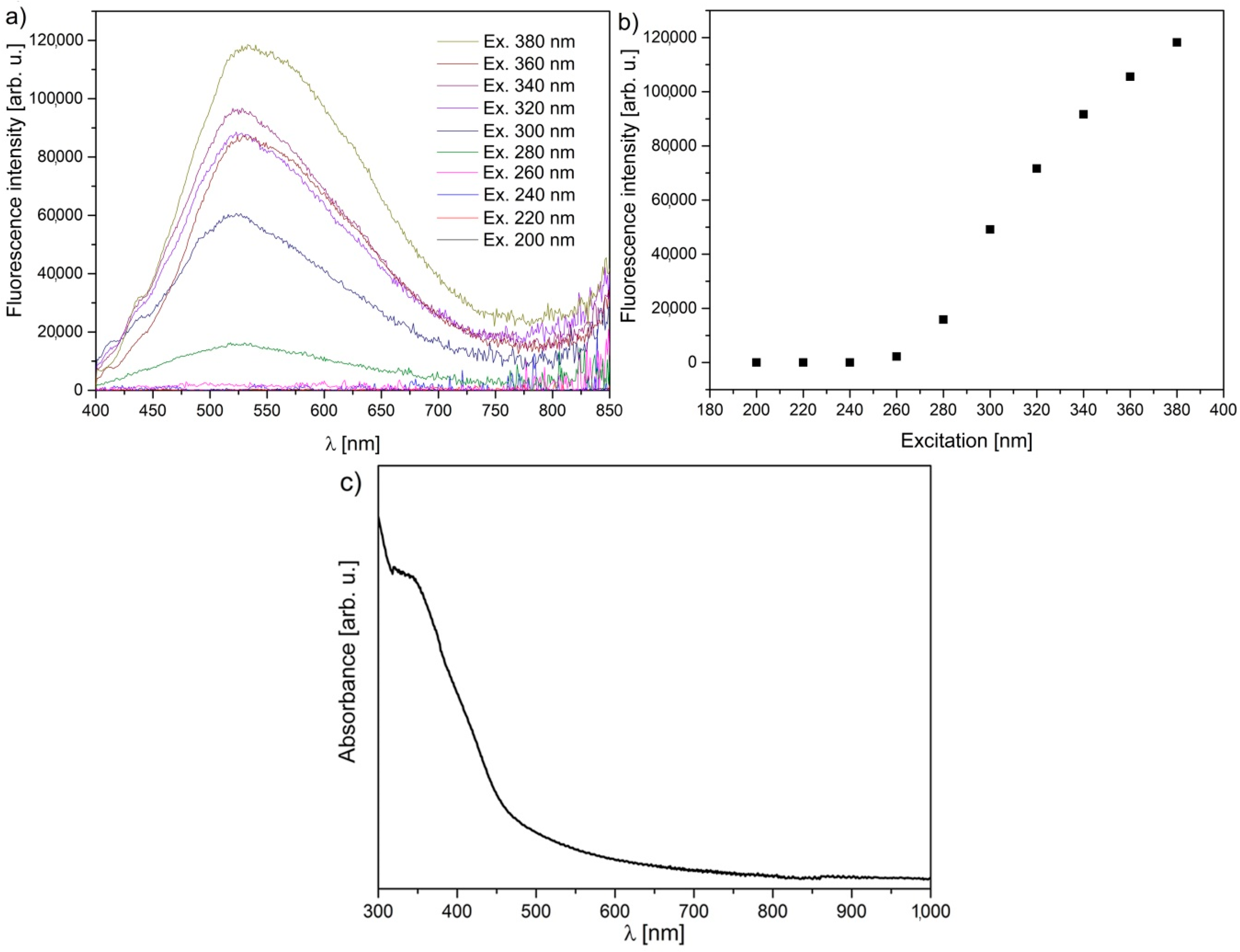
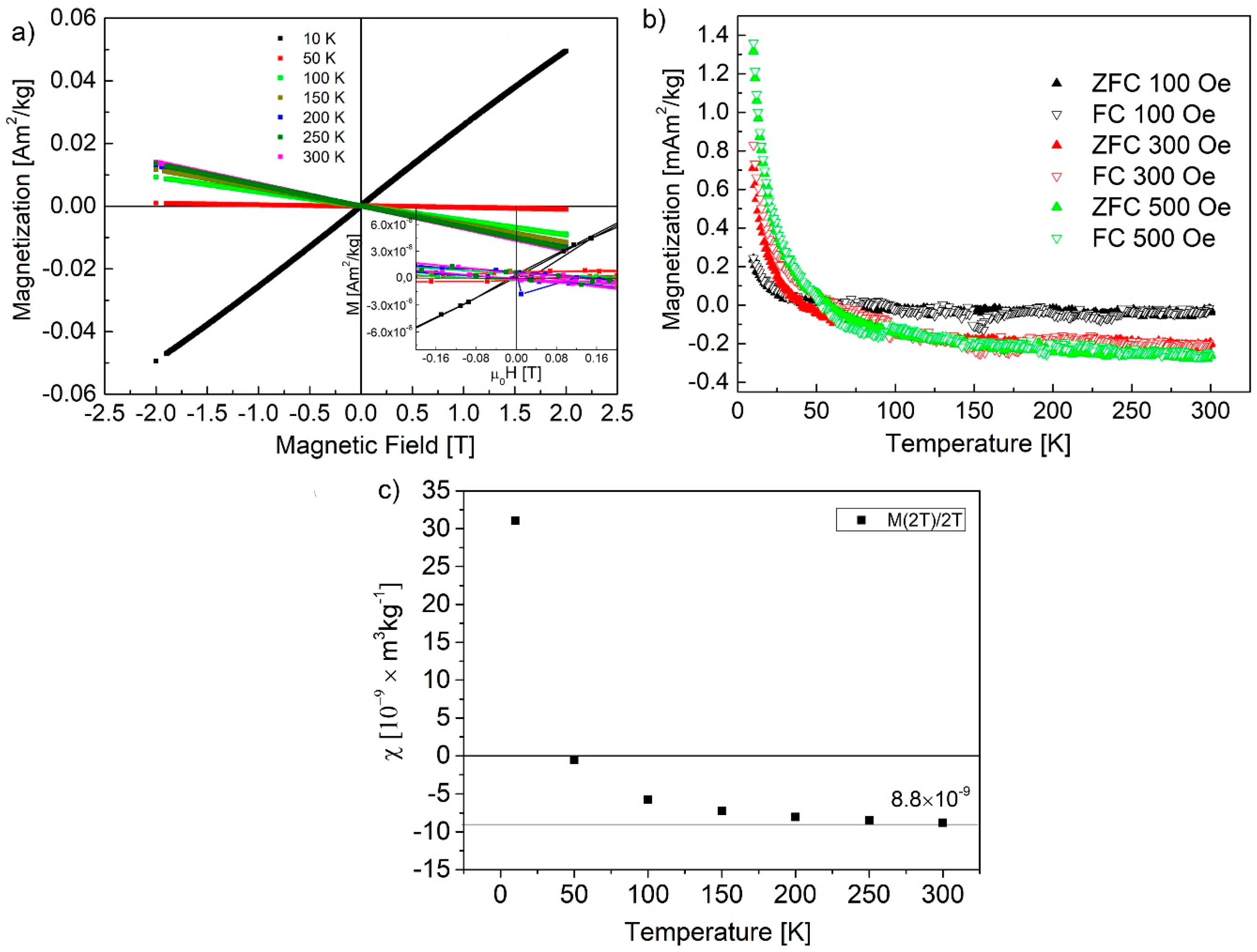

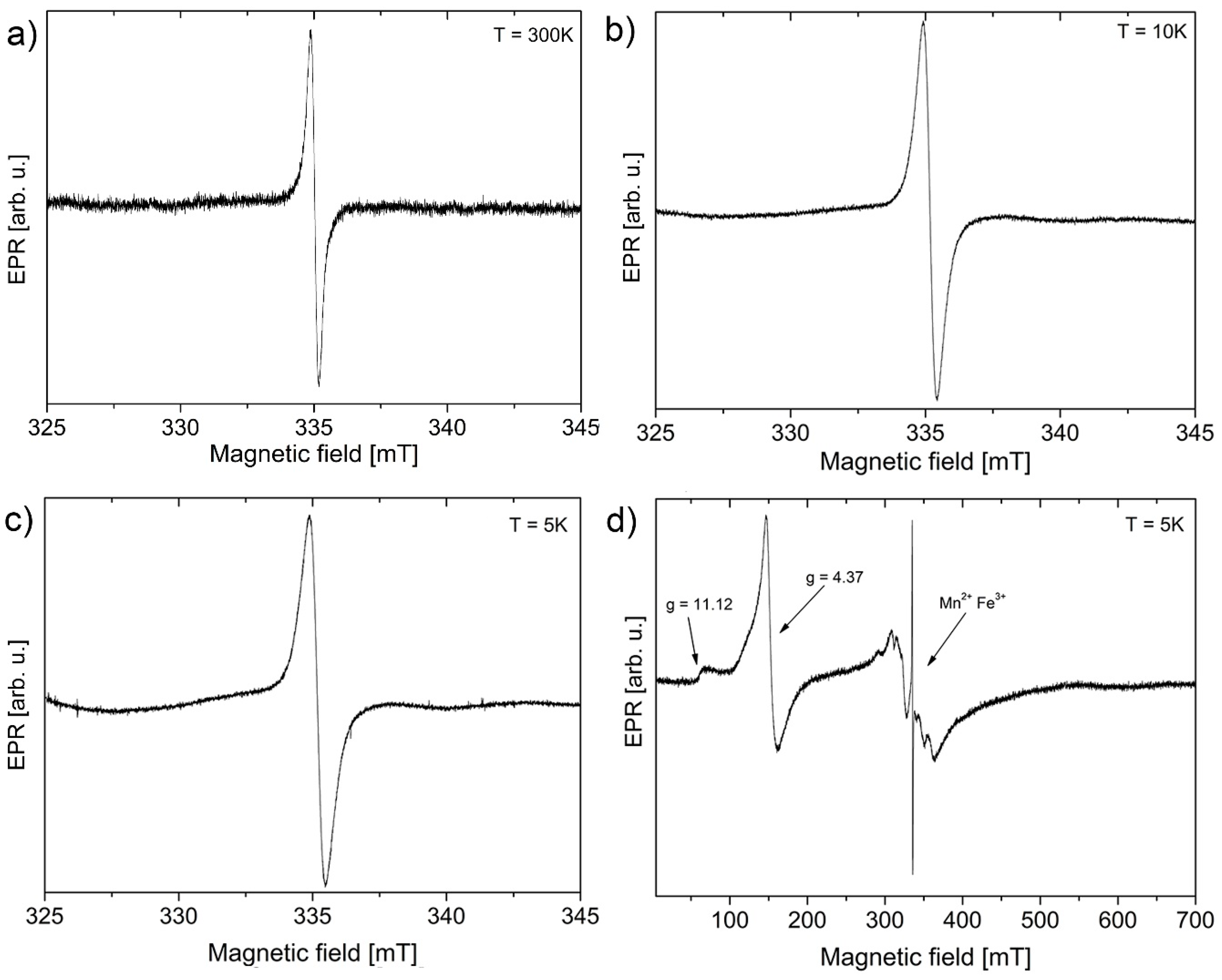
| Sample | Maximum of Lognormal Distribution [nm] | Mean [nm] | SD [nm] | SD/Mean [%] | Minimum [nm] | Median [nm] | Maximum [nm] |
|---|---|---|---|---|---|---|---|
| Pristine GO | 1822 | 9771 | 11,363 | 116 | 709 | 4613 | 46,366 |
| GO after boiling in acid, ultracentrifugation, and decantation | 82 | 157 | 125 | 79 | 33 | 128 | 1047 |
| GOQDs | 26 | 31 | 12 | 38 | 13 | 29 | 77 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tadyszak, K.; Musiał, A.; Ostrowski, A.; Wychowaniec, J.K. Unraveling Origins of EPR Spectrum in Graphene Oxide Quantum Dots. Nanomaterials 2020, 10, 798. https://doi.org/10.3390/nano10040798
Tadyszak K, Musiał A, Ostrowski A, Wychowaniec JK. Unraveling Origins of EPR Spectrum in Graphene Oxide Quantum Dots. Nanomaterials. 2020; 10(4):798. https://doi.org/10.3390/nano10040798
Chicago/Turabian StyleTadyszak, Krzysztof, Andrzej Musiał, Adam Ostrowski, and Jacek K. Wychowaniec. 2020. "Unraveling Origins of EPR Spectrum in Graphene Oxide Quantum Dots" Nanomaterials 10, no. 4: 798. https://doi.org/10.3390/nano10040798
APA StyleTadyszak, K., Musiał, A., Ostrowski, A., & Wychowaniec, J. K. (2020). Unraveling Origins of EPR Spectrum in Graphene Oxide Quantum Dots. Nanomaterials, 10(4), 798. https://doi.org/10.3390/nano10040798






