Computational Study of pH-sensitive Hydrogel-based Microfluidic Flow Controllers
Abstract
:1. Introduction

2. Mathematical Formulation
2.1. Governing Equations
2.2. Constitutive Relations
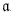 i,
and
i,
and
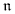 are constants summarized in Table 1.
are constants summarized in Table 1.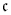 1 is a constant presented in Table 1.
1 is a constant presented in Table 1.2.3. Boundary and Initial Conditions
- At the inlet of the channel, we prescribe
- At the outlet of the channel, we prescribe
- At the walls of the channel, we prescribe
- In the centre of hydrogel, we prescribe
- At the hydrogels/fluid interface, the fluid velocity and fluid pressure are prescribed as
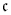 2 is a constant presented in Table 1. The boundary condition in the centre of hydrogel is necessary in order to prevent translational movement of the hydrogel and corresponds to the way the hydrogel is attached to the flow channel; see e.g., [14,15].
2 is a constant presented in Table 1. The boundary condition in the centre of hydrogel is necessary in order to prevent translational movement of the hydrogel and corresponds to the way the hydrogel is attached to the flow channel; see e.g., [14,15].| Parameter | Value | Unit | Reference |
|---|---|---|---|
| E0 | MPa | [31] | |
| ν | 0.409 | - | [31] |
| kB | 1 38054 × 10−23 | JK−1 | [35] |
| Vm | 3.3 × 10−28 | m3 | [35] |
| F | 9.648 × 104 | C mol−1 | [32] |
| ℜ | 8.314 | JK−1 mol−1 | [32] |
| κ0 | 2 8 × 10−21 | m2 | calibrated |
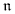 | −2.5 | - | - |
| Ka | 10−2 | mol m−3 | [31] |
| 1800 | mol m−3 | [31] | |
| 300 | mol m−3 | [31] | |
| ψ* | 0 | V | prescribed |
| DH+ | 9.311 × 10−9 | m2 s−1 | [47] |
| DNa+ | 1.334 × 10−9 | m2 s−1 | [47] |
| DCl− | 2.032 × 10−9 | m2 s−1 | [47] |
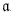 1 1 | 0.6612 | kg m−1 s−1 K1.562 | [48] |
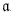 2 2 | −229 | K | [48] |
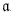 3 3 | −1.562 | - | [48] |
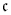 1 1 | 10−3 | m3 mol−1 | - |
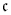 2 2 | - | equilibrium model | |
| 103 | kg m−3 | [49] | |
| Δh | −1 38 ×10−20 | J | calibrated |
| Δs | −4.8 × 10−23 | J K−1 | calibrated |
| χ2 | 1.34 | - | calibrated |
| pin | 0.02 | Pa | - |
| pout | 0.00 | Pa | - |
| T | 298 | K | - |
| L | 1.5 × 10−3 | m | - |
| W | 6.0 × 10−4 | m | - |
| H | 1.8 × 10−4 | m | - |
3. Numerical Methodology
4. Results and Discussions
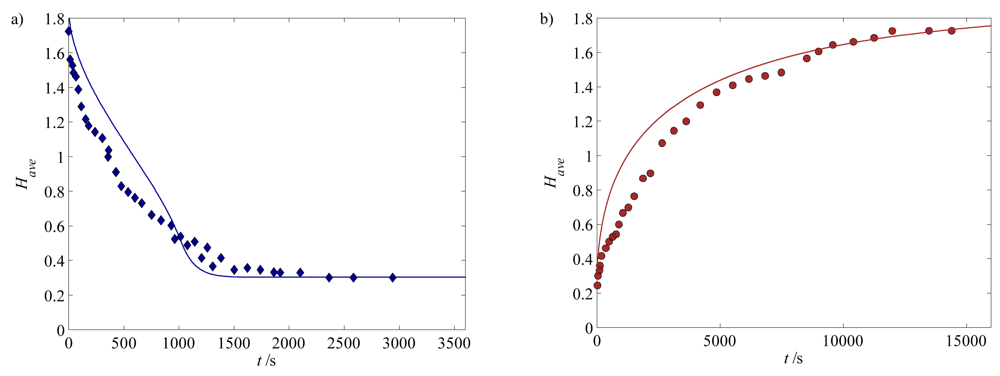
4.1. Calibration and Validation of the Hydrogel Model
 ) 300 μm, (
) 300 μm, (
 ) 500 μm, and (
) 500 μm, and (
 ) 700 μm. The solids lines are the corresponding model predictions.
) 700 μm. The solids lines are the corresponding model predictions.
 ) 300 μm, (
) 300 μm, (
 ) 500 μm, and (
) 500 μm, and (
 ) 700 μm. The solids lines are the corresponding model predictions.
) 700 μm. The solids lines are the corresponding model predictions.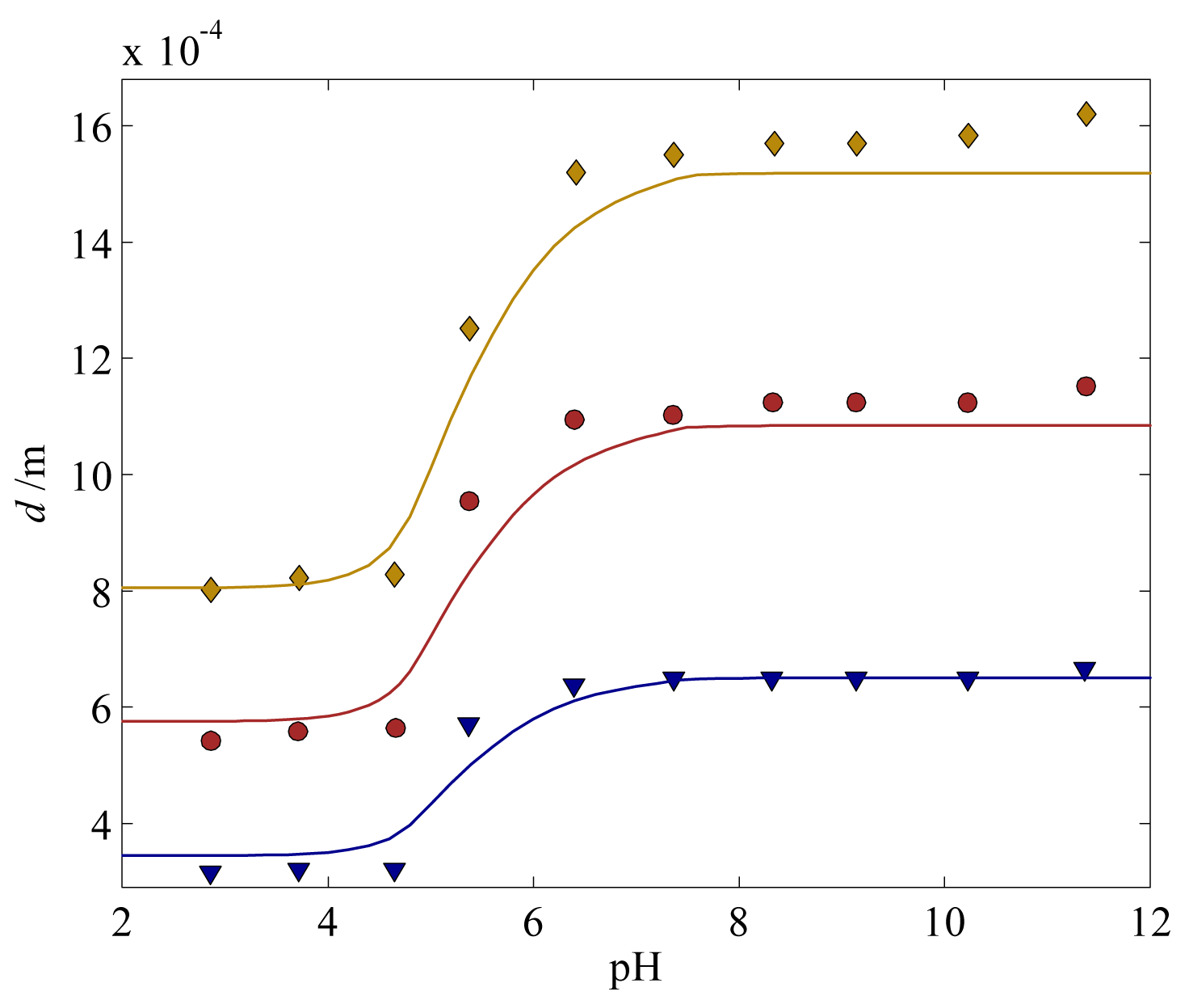
4.2. Flow Behavior inside a T-Junction with one or Several Hydrogels in One Branch
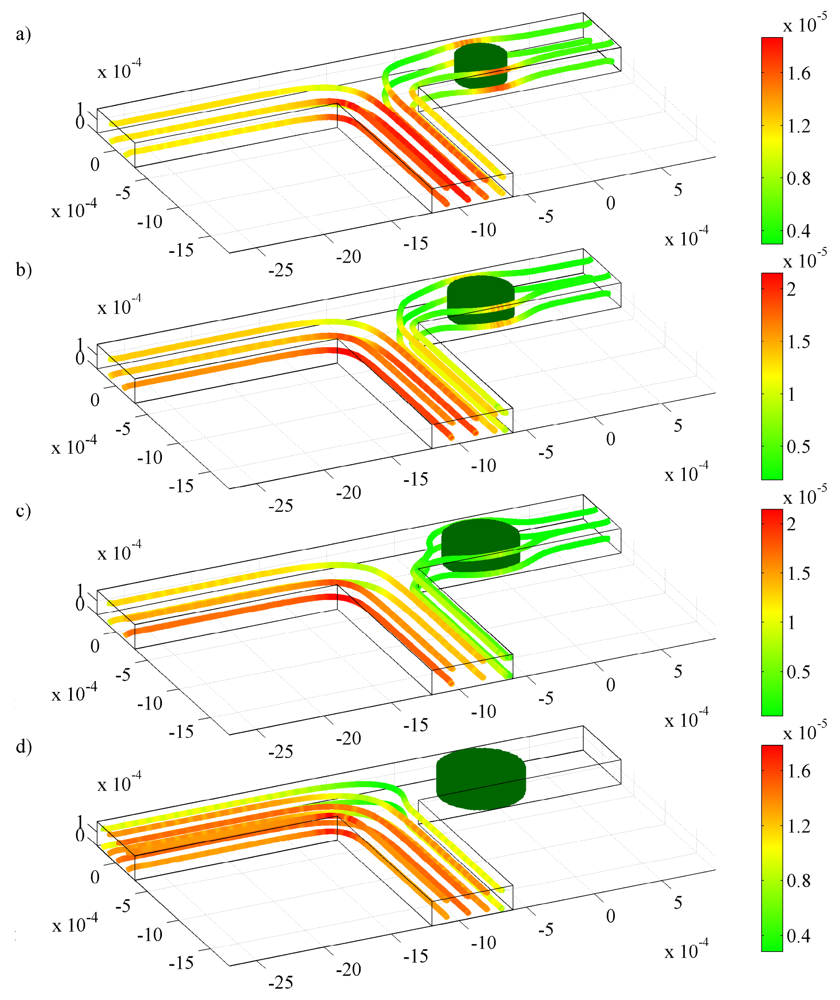
 ) one 300 μm hydrogel, (
) one 300 μm hydrogel, (
 ) two 150 μm hydrogels, and (
) two 150 μm hydrogels, and (
 ) three 100 μm hydrogels. Mass flow rates of the fluid are for pH changes between 3 and 7 at (a) the inlet; (b) the left outlet; and (c) the right outlet.
) three 100 μm hydrogels. Mass flow rates of the fluid are for pH changes between 3 and 7 at (a) the inlet; (b) the left outlet; and (c) the right outlet.
 ) one 300 μm hydrogel, (
) one 300 μm hydrogel, (
 ) two 150 μm hydrogels, and (
) two 150 μm hydrogels, and (
 ) three 100 μm hydrogels. Mass flow rates of the fluid are for pH changes between 3 and 7 at (a) the inlet; (b) the left outlet; and (c) the right outlet.
) three 100 μm hydrogels. Mass flow rates of the fluid are for pH changes between 3 and 7 at (a) the inlet; (b) the left outlet; and (c) the right outlet.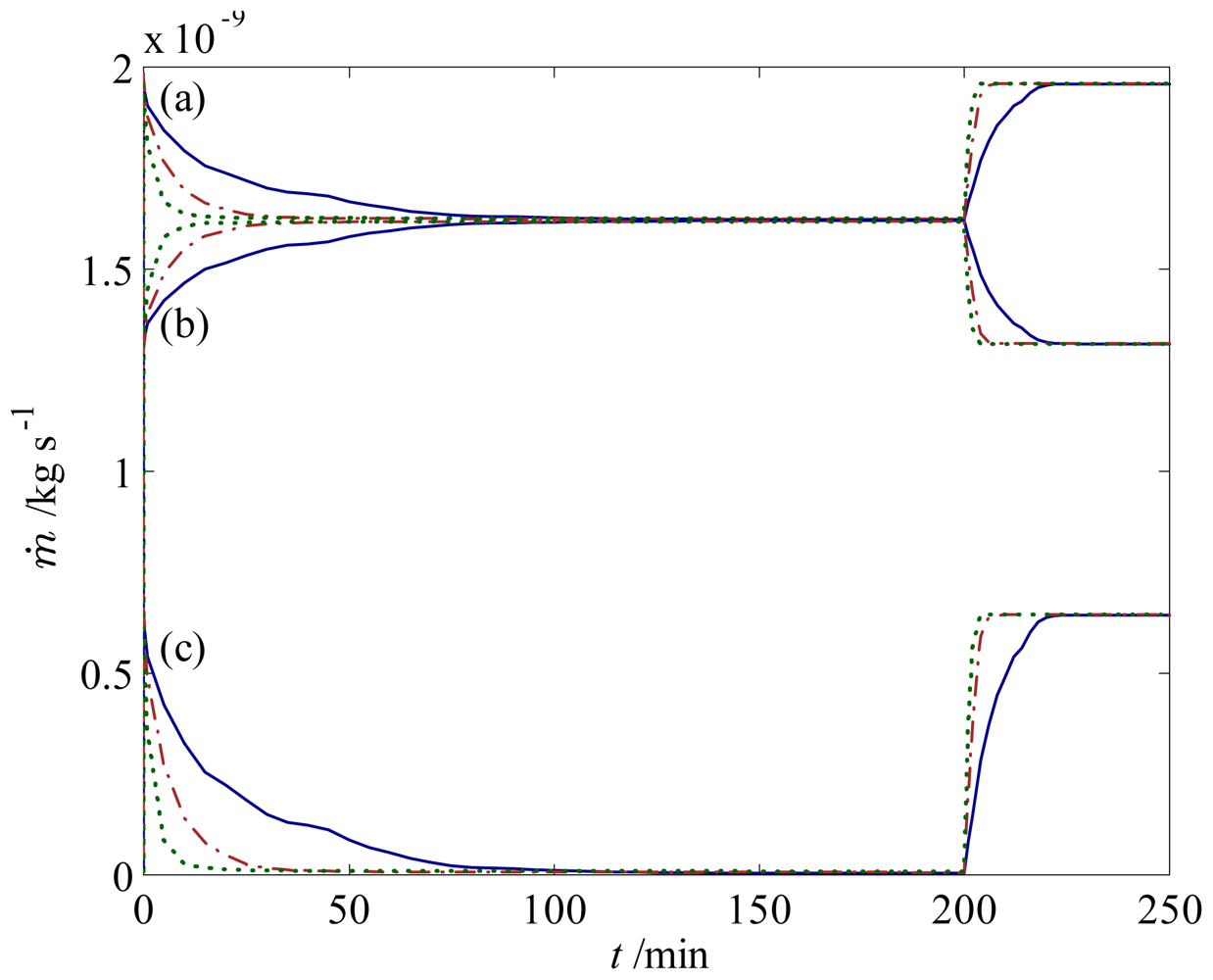
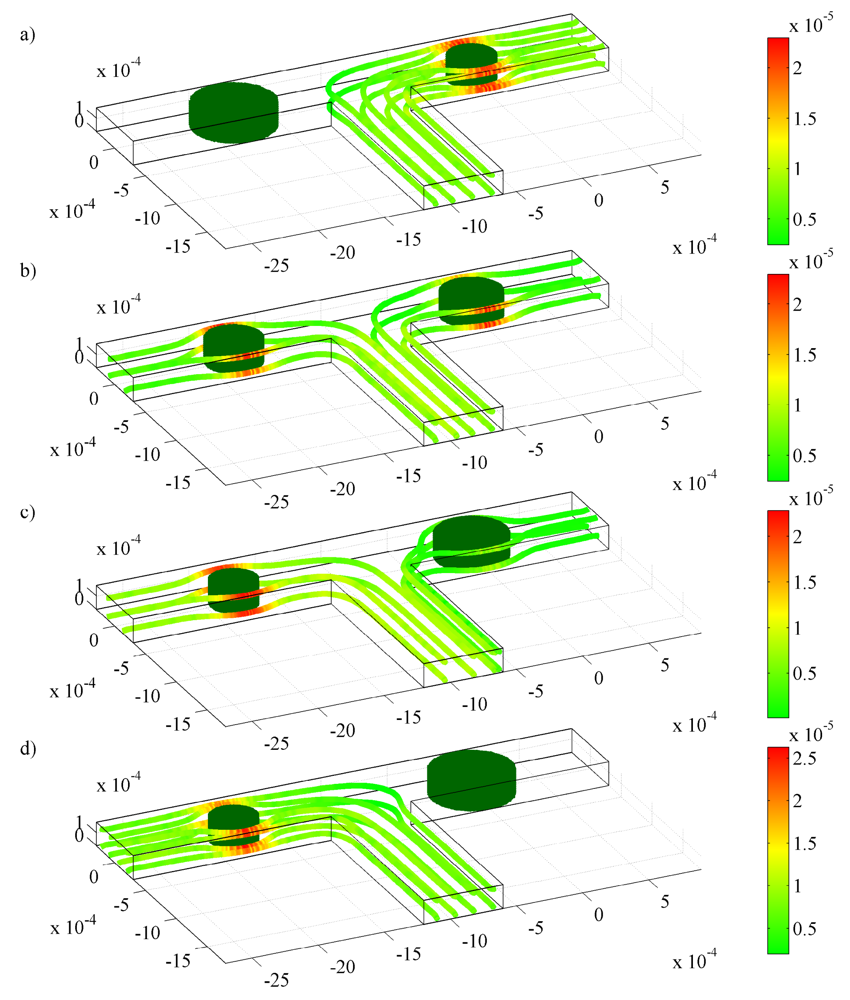
4.3. Flow Behavior Inside a T-Junction with a Hydrogel in Each Branch
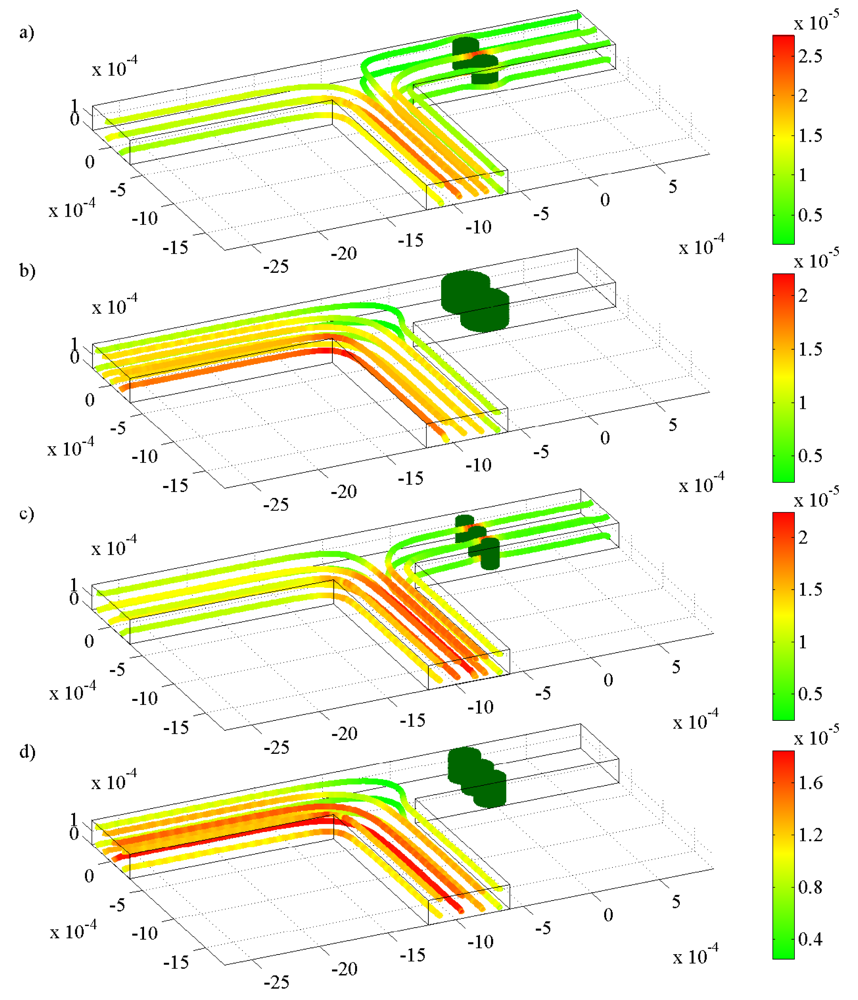
 ) a base-case permeability; (
) a base-case permeability; (
 ), 10 times higher permeability, and (
), 10 times higher permeability, and (
 ) 100 times higher permeability. Mass flow rates of the fluid are for pH changes between 3 and 7 at (a) the inlet; (b) the left outlet; and (c) the right outlet.
) 100 times higher permeability. Mass flow rates of the fluid are for pH changes between 3 and 7 at (a) the inlet; (b) the left outlet; and (c) the right outlet.
 ) a base-case permeability; (
) a base-case permeability; (
 ), 10 times higher permeability, and (
), 10 times higher permeability, and (
 ) 100 times higher permeability. Mass flow rates of the fluid are for pH changes between 3 and 7 at (a) the inlet; (b) the left outlet; and (c) the right outlet.
) 100 times higher permeability. Mass flow rates of the fluid are for pH changes between 3 and 7 at (a) the inlet; (b) the left outlet; and (c) the right outlet.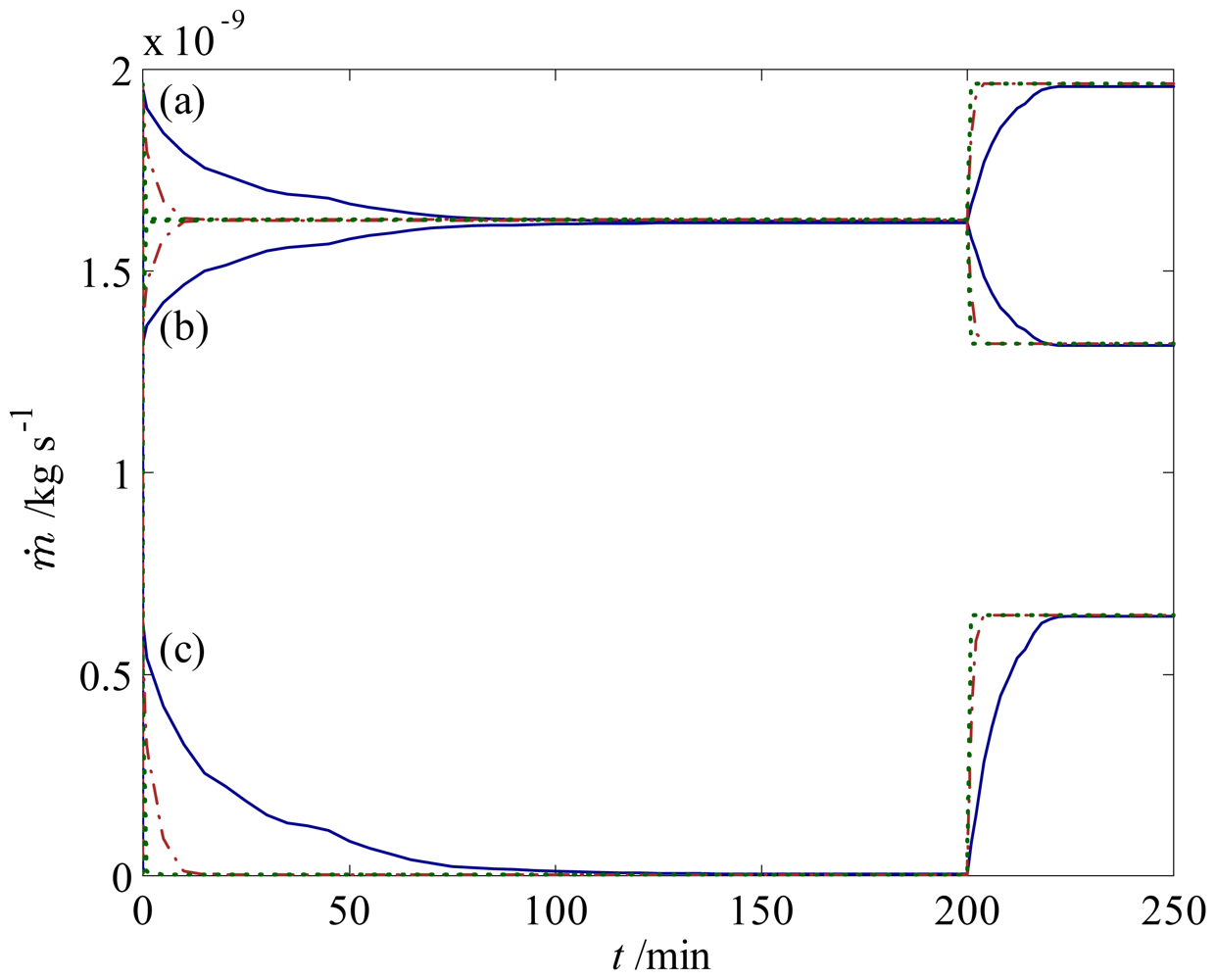
5. Conclusions
 ) the inlet, (
) the inlet, (
 ) the left outlet, and (
) the left outlet, and (
 ) the right outlet.
) the right outlet.
 ) the inlet, (
) the inlet, (
 ) the left outlet, and (
) the left outlet, and (
 ) the right outlet.
) the right outlet.
Acknowledgments
References
- Nguyen, N.T.; Wereley, S.T. Fundamentals and Applications of Microfluidics, 2nd ed.; Artech House, Inc.: Boston, MA, USA, 2006. [Google Scholar]
- Jong, J.D.; Lammertink, R.G.H.; Wessling, M. Membranes and microfluidics: A review. Lab Chip 2006, 6, 1125–1139. [Google Scholar]
- Erickson, D.; Li, D. Review: Integrated microfluidic devices. Anal. Chim. Acta 2004, 507, 11–26. [Google Scholar]
- Koch, M.; Evans, A.; Brunnschweiler, A. Microfluidic Technology and Applications; Research Studies Press: Philadelphia, PA, USA, 2000. [Google Scholar]
- Delamarche, E.; Juncker, D.; Schmid, H. Microfluidics for processing surfaces and miniaturizing biological assays. Adv. Mater. 2005, 17, 2911–2933. [Google Scholar]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977–1026. [Google Scholar]
- Hossain, S.; Ansari, M.A.; Kim, K.Y. Evaluation of the mixing performance of three passive micromixers. Chem. Eng. J. 2009, 150, 492–501. [Google Scholar]
- Ottino, J.M.; Wiggins, S. Introduction: Mixing in microfluidics. Philos. Trans. R. Soc. London 2004, 362, 923–935. [Google Scholar]
- Yi, C.; Li, C.W.; Ji, S.; Yang, M. Microfluidics technology for manipulation and analysis of biological cells. Anal. Chim. Acta 2006, 560, 1–23. [Google Scholar]
- Ohno, K.; Tachikawa, K.; Manz, A. Microfluidics: Applications for analytical purposes in chemistry and biochemistry. Electrophoresis 2008, 29, 4443–4453. [Google Scholar]
- Huh, D.; Gu, W.; Kamotani, Y.; Grotberg, J.B.; Takayama, S. Microfluidics for flow cytometric analysis of cells and particles. Physiol. Meas. 2005, 26, R73–R98. [Google Scholar]
- Beebe, D.J.; Mensing, G.A.; Walker, G.M. Physics and applications of microfluidics in biology. Annu. Rev. Biomed. Eng. 2002, 4, 261–286. [Google Scholar]
- Chen, Z.; Wang, J.; Qian, S.; Bau, H.H. Thermally-actuated, phase change flow control for microfluidic sytem. Lab Chip 2005, 5, 1277–1285. [Google Scholar]
- Beebe, D.J.; Moore, J.S.; Bauer, J.M.; Yu, Q.; Liu, R.H.; Devados, C.; Jo, B. Functional hydrogel structures for autonomous flow control inside microfluidic channels. Nature 2000, 404, 588–590. [Google Scholar]
- Eddington, D.T.; Beebe, D.J. Flow control with hydrogels. Adv. Drug Deliv. Rev. 2004, 56, 199–210. [Google Scholar]
- Qiu, Y.; Park, K. Environment sensitive hydrogels for drug delivery. Adv. Drug Deliv. Rev. 2001, 53, 321–339. [Google Scholar]
- Roy, I.; Gupta, N. Smart polymeric materials: Emerging biochemical applications. Chem. Biol. 2003, 10, 1161–1171. [Google Scholar]
- Liu, Z.S.; Swaddiwudhipong, S.; Cui, F.S.; Hong, W.; Suo, Z.; Zhang, Y.W. Analytical solutions of polymer gel structures under buckling and wrinkle. Int. J. Appl. Mech. 2011, 3, 235–257. [Google Scholar]
- Marcombe, R.; Cai, S.; Hong, W.; Zhao, X.; Lapusta, Y.; Suo, Z. A theory of constrained swelling of a pH-sensitive hydrogel. Soft Matter. 2010, 6, 784–793. [Google Scholar]
- Hong, W.; Liu, Z.S.; Suo, S. Inhomogeneous swelling of a gel in equilibrium with a solvent mechanical load. Int. J. Solids Struct. 2009, 46, 3282–3289. [Google Scholar]
- Eddington, D.T.; Liu, R.H.; Moore, J.S.; Beebe, D.J. An organic self-regulating microfluidic system. Lab Chip 2001, 1, 96–99. [Google Scholar]
- Liu, C.; Park, J.Y.; Xu, Y.; Lee, S.H. Arrayed pH-responsive microvalves controlled by multiphase laminar flow. J. Micromech. Microeng. 2007, 17, 1985–1991. [Google Scholar]
- Dong, L.; Jiang, H. Autonomous microfluidics with stimuli-responsive hydrogels. Soft Mater. 2007, 3, 1223–1230. [Google Scholar]
- Park, J.Y.; Oh, H.J.; Kim, D.J.; Baek, J.Y.; Lee, S.H. A polymeric microfluidic valve employing a pH-responsive hydrogel microspheres as an actuating source. J. Micromech. Microeng. 2006, 16, 656–663. [Google Scholar]
- Stoeber, B.; Yang, Z.; Liepmann, D.; Muller, S.J. Flow control in microfluidic using thermally responsive triblock copolymers. J. Microelectromech. Syst. 2005, 14, 207–213. [Google Scholar]
- Wang, J.; Chen, Z.; Mauk, M.; Hong, K.S.; Li, M.; Yang, S.; Bau, H.H. Self-actuated, thermo-responsive hydrogels valves for lab on chip. Biomed. Microdevices 2005, 7, 313–322. [Google Scholar]
- Baldi, A.; Gu, Y.; Loftness, P.E.; Siegel, R.A.; Ziaie, B. A hydrogel-actuated environmentally sensitive microvalve for active flow control. J. Microelectromech. Syst. 2003, 12, 613–621. [Google Scholar]
- Kurnia, J.C.; Birgersson, E.; Mujumdar, A.S.; Quah, L.C. Mathematical modeling of hydrogels for microfluidic flow control. Adv. Mater. Res. 2009, 74, 33–36. [Google Scholar]
- Tehranirokh, M.; Majlis, B.Y.; Bais, B. Design and simulation of a normally closed glucose sensitive hydrogel based microvalve. Microsyst. Technol. 2009, 15, 753–762. [Google Scholar]
- Ibrahim, M.W.A.; Saunders, J.R.; Wallied, M. Hydrogel Microvalve Device Modeling and Simulation. Proceeding of the International Conference on MEMS, NANO and Smart Systems, Banff, Alberta, Canada, July 2005; pp. 221–222.
- De, S.K.; Aluru, N.R.; Jhonson, B.; Crone, W.C.; Beebe, D.J.; Moore, J. Equilibrium swelling and kinetics of pH-responsive hydrogels: Models, experiments and simulations. J. Microelectromech. Syst. 2002, 11, 544–555. [Google Scholar]
- Li, H.; Yew, Y.K.; Ng, T.Y.; Lam, K.Y. Meshless steady-state analysis of chemo-electro-mechanical coupling behavior of pH sensitive hydrogel in buffered solution. J. Electroanal. Chem. 2005, 580, 161–172. [Google Scholar]
- Li, H.; Yuan, Z.; Lam, K.Y.; Lee, H.P.; Chen, J.; Hanes, J.; Fu, J. Model development and numerical simulation of electric-stimulus-responsive hydrogels subject to an externally applied electric field. Biosens. Bioelectron. 2004, 19, 1097–1107. [Google Scholar]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3 ed.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Birgersson, E.; Li, H.; Wu, S. Transient analysis of temperature-sensitive neutral hydrogels. J. Mech. Phys. Solids. 2008, 56, 444–466. [Google Scholar]
- Barry, S.I.; Holmes, M. Asymptotic behavior of thin poroelastic layer. IMA. J. Appl. Math. 2001, 66, 175–194. [Google Scholar]
- Barry, S.I.; Mercer, G.N. Flow and deformation in poroelasticity-I Unusual exact solutions. Math. Comput. Model 1999, 30, 23–29. [Google Scholar]
- Sun, D.N.; Gu, W.Y.; Guo, X.E.; Lai, W.M.; Mow, V.C. A mixed finite element formulation of triphasic mechano-electrochemical theory for charged, hydrated biological soft tissues. Int. J. Numer. Meth. Eng. 1999, 45, 1375–1402. [Google Scholar]
- Reddy, J.N. An Introduction to Continuum Mechanics with Applications; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Shirota, H.; Endo, N.; Horie, K. Volume phase transition of polymer in water and heavy water. Chem. Phys. 1998, 238, 487–494. [Google Scholar]
- Hirotsu, S. Softening of bulk modulus and negative Poisson's ratio near the volume phase transition of polymer gels. J. Chem. Phys. 1991, 94, 3949–3957. [Google Scholar]
- Oh, K.S.; Bae, Y.C. Swelling behavior of submicron gel particles. J. Appl. Polym. Sci. 1998, 69, 109–114. [Google Scholar]
- Popov, E.P. Engineering Mechanics of Solids, 2nd ed.; Prentice Hall Inc.: Upper Saddle Rvr, NJ, USA, 1998. [Google Scholar]
- Solecki, R.; Conant, R.J. Advanced Mechanics of Materials; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Gu, W.Y.; Yao, H.; Huang, C.Y.; Cheung, H.S. New insight into deformation-dependent hydraulic permeability of gels and cartilage, and dynamic behavior of agarose gels in confined compression. J. Biomech. 2003, 36, 593–598. [Google Scholar]
- Agarwal, A.S.; Landau, U.; Payer, J.H. Modeling particulates effects on the cathode current capacity in crevice corrosion. J. Electrochem. Soc. 2008, 155, C269–C278. [Google Scholar]
- Marcus, Y. Ion Properties; Marcel Dekker Inc.: New York, NY, USA, 1997. [Google Scholar]
- Gawin, D.; Majorana, C.E.; Schrefter, B.A. Numerical analysis of hygro-thermal behavior and damage of concrete at high temperature. Mech. Cohesive-Frict. Mater. 1999, 4, 37–74. [Google Scholar]
- Kaviany, M. Principle of Heat Transfer; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Gunasekaran, S.; Wang, T.; Chai, C.X. Swelling of pH sensitive chitosan-poly(vinyl alcohol) hydrogels. J. Appl. Polym. Sci. 2006, 102, 4665–4671. [Google Scholar]
- Yew, Y.K.; Ng, T.Y.; Li, H.; Lam, K.Y. Analysis of pH and electically controlled swelling of hydrogel-based micro-sensors/actuators. Biomed. Microdevices 2007, 9, 487–499. [Google Scholar]
- De, S.K.; Aluru, N.R. A chemo-electro-mechanical mathematical model for simulation of pH sensitive hydrogels. Mech. Mater. 2004, 36, 395–410. [Google Scholar]
- Zhao, Q.; Sun, J.; Zhou, Q. Synthesis of macroporous poly(N-isopropylacrylamide) hydrogel with ultrarapid swelling-deswelling properties. J. Appl. Polym Sci. 2007, 104, 4080–4087. [Google Scholar]
- Zhang, X.Z.; Zhuo, R.X. Novel synthesis of temperature sensitive poly(N-isopropylacrylamide) hydrogel with fast deswelling rate. Eur. Polym. J. 2000, 36, 643–645. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kurnia, J.C.; Birgersson, E.; Mujumdar, A.S. Computational Study of pH-sensitive Hydrogel-based Microfluidic Flow Controllers. J. Funct. Biomater. 2011, 2, 195-212. https://doi.org/10.3390/jfb2030195
Kurnia JC, Birgersson E, Mujumdar AS. Computational Study of pH-sensitive Hydrogel-based Microfluidic Flow Controllers. Journal of Functional Biomaterials. 2011; 2(3):195-212. https://doi.org/10.3390/jfb2030195
Chicago/Turabian StyleKurnia, Jundika C., Erik Birgersson, and Arun S. Mujumdar. 2011. "Computational Study of pH-sensitive Hydrogel-based Microfluidic Flow Controllers" Journal of Functional Biomaterials 2, no. 3: 195-212. https://doi.org/10.3390/jfb2030195
APA StyleKurnia, J. C., Birgersson, E., & Mujumdar, A. S. (2011). Computational Study of pH-sensitive Hydrogel-based Microfluidic Flow Controllers. Journal of Functional Biomaterials, 2(3), 195-212. https://doi.org/10.3390/jfb2030195