Is the Correlation between Storage Capacity and Matrix Reasoning Driven by the Storage of Partial Solutions? A Pilot Study of an Experimental Approach
Abstract
:1. Introduction
2. Figural Matrices and Storage Demands
2.1. Processes in Figural Matrices
2.2. The Role of WM in Figural Matrices
3. The Present Study
4. Method
4.1. Participants and Design
4.2. Test Methods
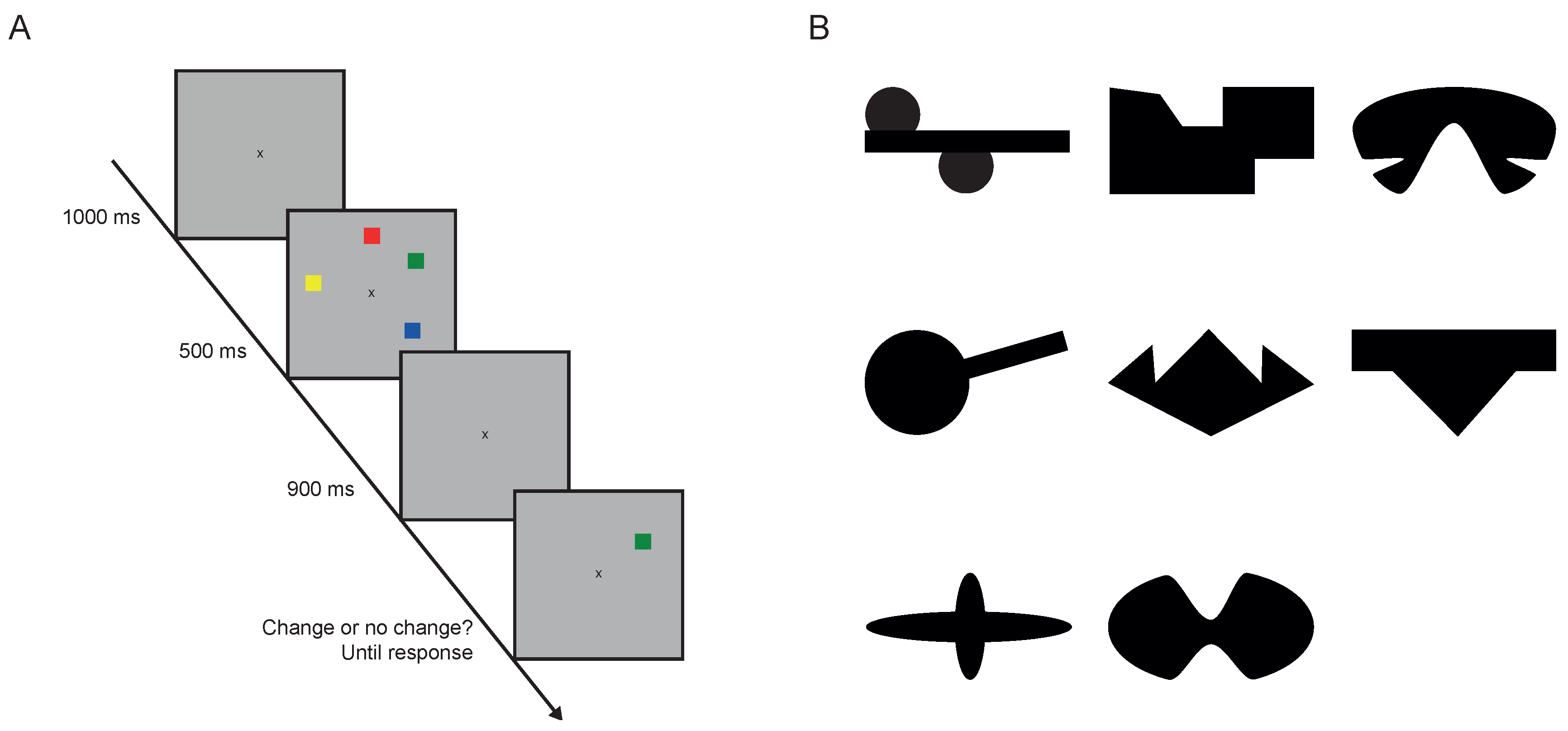
4.2.1. Change Detection
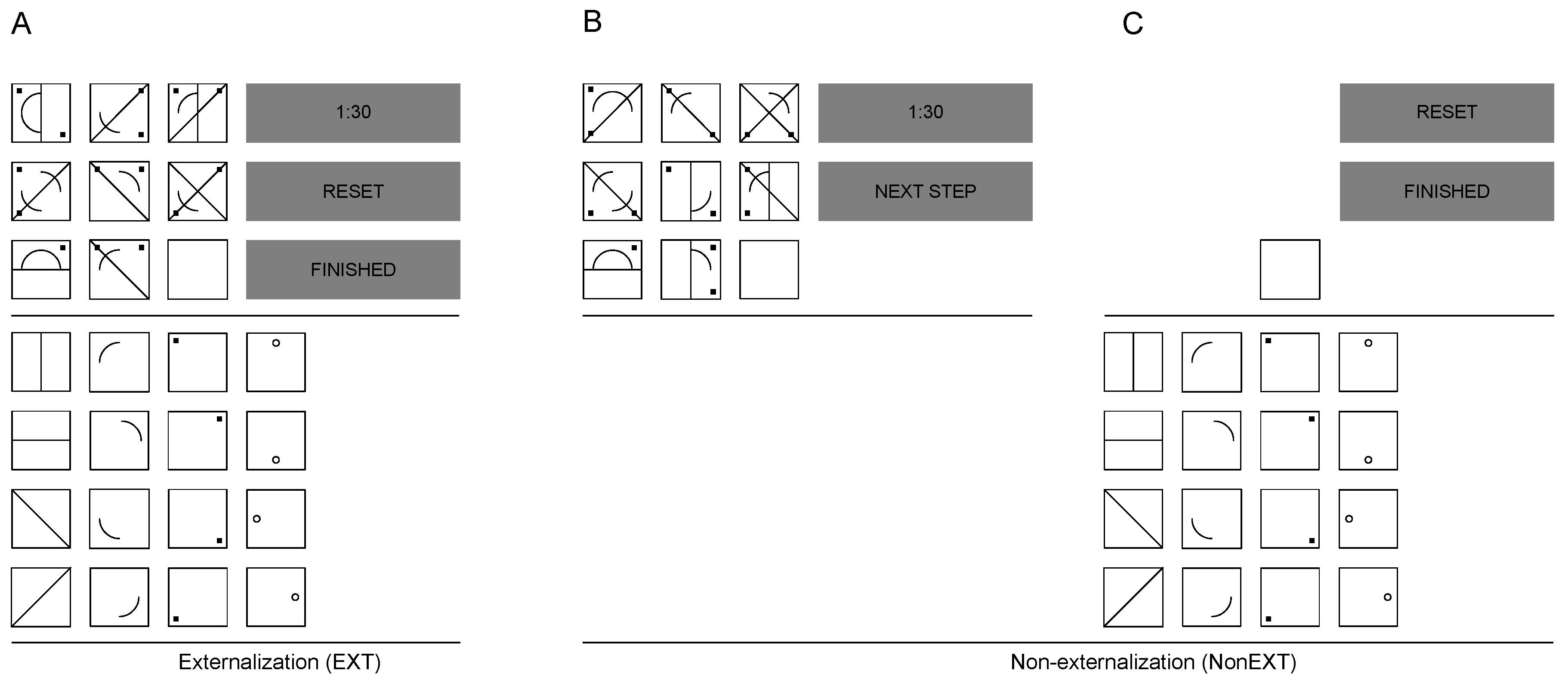
4.2.2. Matrices Tests
4.3. Data Analysis
4.3.1. Change Detection
4.3.2. Matrices Tests
4.3.3. Statistical Analyses
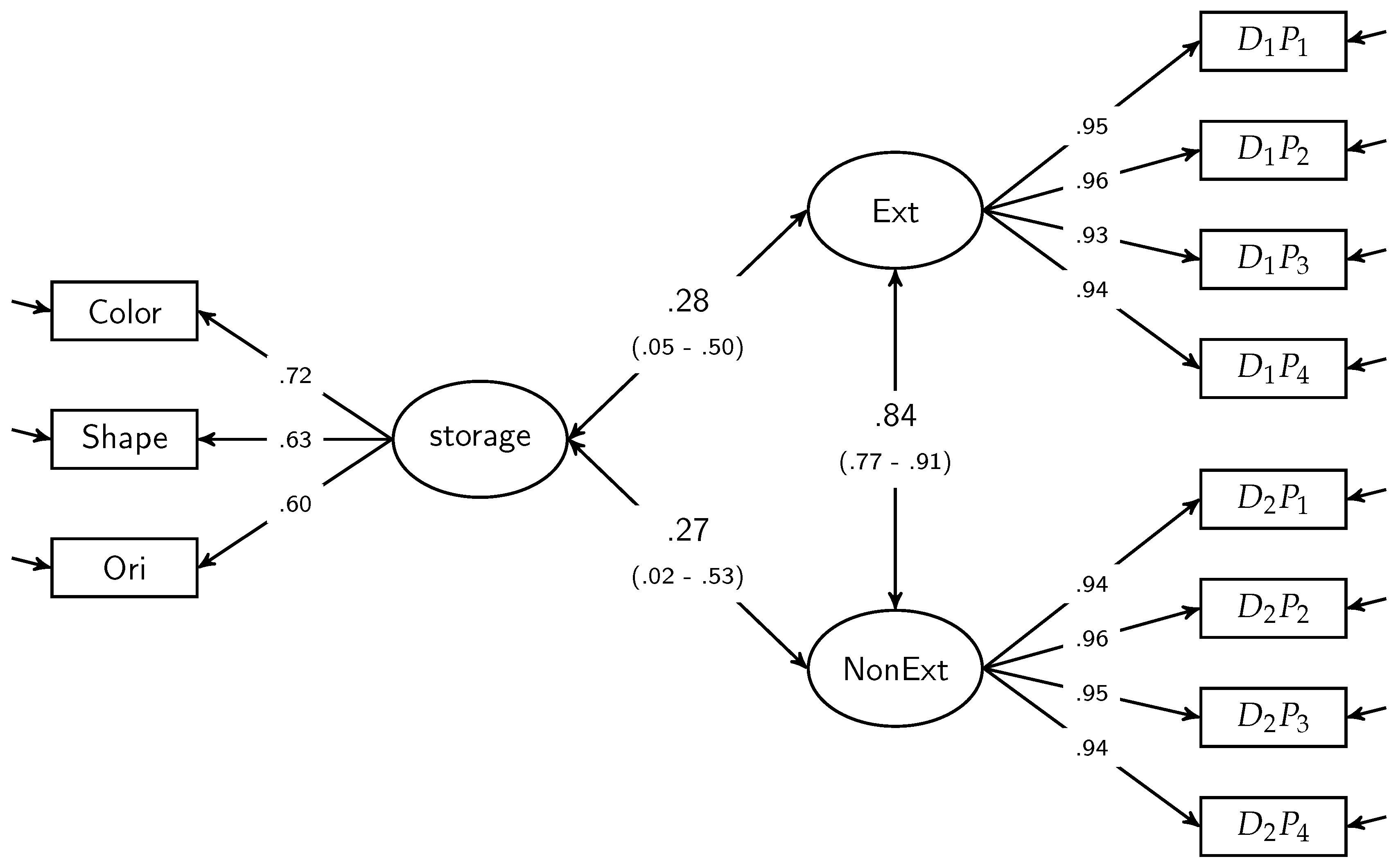
5. Results
6. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Engle, R.W.; Tuholski, S.W.; Laughlin, J.E.; Conway, A. Working Memory, Short-Term Memory, and General Fluid Intelligence: A Latent-Variable Approach. J. Exp. Psychol. Gen. 1999, 12, 309–331. [Google Scholar] [CrossRef]
- Conway, A.R.; Cowan, N.; Bunting, M.F.; Therriault, D.J.; Minkoff, S.R. A latent variable analysis of working memory capacity, short-term memory capacity, processing speed, and general fluid intelligence. Intelligence 2002, 30, 163–183. [Google Scholar] [CrossRef]
- Süß, H.M.; Oberauer, K.; Wittmann, W.W.; Wilhelm, O.; Schulze, R. Working-memory capacity explains reasoning ability—And a little bit more. Intelligence 2002, 30, 261–288. [Google Scholar] [CrossRef]
- Conway, A.R.; Kane, M.J.; Engle, R.W. Working memory capacity and its relation to general intelligence. Trends Cogn. Sci. 2003, 7, 547–552. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, P.L.; Beier, M.E.; Boyle, M.D. Individual differences in working memory within a nomological network of cognitive and perceptual speed abilities. J. Exp. Psychol. Gen. 2002, 131, 567–589. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, P.L.; Beier, M.E.; Boyle, M.O. Working memory and intelligence: The same or different constructs? Psychol. Bull. 2005, 131, 30–60. [Google Scholar] [CrossRef] [PubMed]
- Colom, R.; Flores-Mendoza, C.; Quiroga, M.Á.; Privado, J. Working memory and general intelligence: The role of short-term storage. Person. Individ. Differ. 2005, 39, 1005–1014. [Google Scholar] [CrossRef]
- Kane, M.J.; Hambrick, D.Z.; Tuholski, S.W.; Wilhelm, O.; Payne, T.W.; Engle, R.W. The generality of working memory capacity: A latent-variable approach to verbal and visuospatial memory span and reasoning. J. Exp. Psychol. Gen. 2004, 133, 189–217. [Google Scholar] [CrossRef] [PubMed]
- Engle, R.W. Working Memory Capacity as Executive Attention. Curr. Dir. Psychol. Sci. 2002, 11, 19–23. [Google Scholar] [CrossRef]
- Cowan, N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behav. Brain Sci. 2001, 24, 87–185. [Google Scholar] [CrossRef] [PubMed]
- Vogel, E.K.; Woodman, G.F.; Luck, S.J. Storage of features, conjunctions, and objects in visual working memory. J. Exp. Psychol. Hum. Percept. Perform. 2001, 27, 92–114. [Google Scholar] [CrossRef] [PubMed]
- Chuderski, A.; Taraday, M.; Nęcka, E.; Smoleń, T. Storage capacity explains fluid intelligence but executive control does not. Intelligence 2012, 40, 278–295. [Google Scholar] [CrossRef]
- Luck, S.J.; Vogel, E.K. The capacity of visual working memory for features and conjunctions. Nature 1997, 390, 279–281. [Google Scholar] [CrossRef] [PubMed]
- Cowan, N.; Elliott, E.M.; Scott Saults, J.; Morey, C.C.; Mattox, S.; Hismjatullina, A.; Conway, A.R. On the capacity of attention: Its estimation and its role in working memory and cognitive aptitudes. Cogn. Psychol. 2005, 51, 42–100. [Google Scholar] [CrossRef] [PubMed]
- Fukuda, K.; Vogel, E.; Mayr, U.; Awh, E. Quantity, not quality: The relationship between fluid intelligence and working memory capacity. Psychon. Bull. Rev. 2010, 17, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Jarosz, A.F.; Wiley, J. Why does working memory capacity predict RAPM performance? A possible role of distraction. Intelligence 2012, 40, 427–438. [Google Scholar] [CrossRef]
- Loesche, P.; Wiley, J.; Hasselhorn, M. How knowing the rules affects solving the Raven Advanced Progressive Matrices Test. Intelligence 2015, 48, 58–75. [Google Scholar] [CrossRef]
- Verguts, T.; De Boeck, P. On the correlation between working memory capacity and performance on intelligence tests. Learn. Individ. Differ. 2002, 13, 37–55. [Google Scholar] [CrossRef]
- Unsworth, N.; Engle, R. Working memory capacity and fluid abilities: Examining the correlation between Operation Span and Raven. Intelligence 2005, 33, 67–81. [Google Scholar] [CrossRef]
- Marshalek, B.; Lohman, D.F.; Snow, R.E. The complexity continuum in the radex and hierarchical models of intelligence. Intelligence 1983, 7, 107–127. [Google Scholar] [CrossRef]
- Harrison, T.L.; Shipstead, Z.; Engle, R.W. Why is working memory capacity related to matrix reasoning tasks? Mem. Cogn. 2015, 43, 389–396. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, P.A.; Just, M.A.; Shell, P. What one intelligence test measures: A theoretical account of the processing in the Raven Progressive Matrices Test. Psychol. Rev. 1990, 97, 404–431. [Google Scholar] [CrossRef] [PubMed]
- Raven, J.C.; Raven, J.E.; Court, J.H. (Eds.) Advanced Progressive Matrices; Oxford Psychologists Press: Oxford, UK, 1998. [Google Scholar]
- Wiley, J.; Jarosz, A.F.; Cushen, P.J.; Colflesh, G.J.H. New rule use drives the relation between working memory capacity and Raven’s Advanced Progressive Matrices. J. Exp. Psychol. Learn. Mem. Cogn. 2011, 37, 256–263. [Google Scholar] [CrossRef] [PubMed]
- Unsworth, N.; Fukuda, K.; Awh, E.; Vogel, E. Working memory and fluid intelligence: Capacity, attention control, and secondary memory retrieval. Cogn. Psychol. 2014, 71, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Shipstead, Z.; Redick, T.S.; Hicks, K.L.; Engle, R.W. The scope and control of attention as separate aspects of working memory. Memory (Hove, England) 2012, 20, 608–628. [Google Scholar] [CrossRef] [PubMed]
- Shipstead, Z.; Lindsey, D.R.; Marshall, R.L.; Engle, R.W. The mechanisms of working memory capacity: Primary memory, secondary memory, and attention control. J. Mem. Lang. 2014, 72, 116–141. [Google Scholar] [CrossRef]
- Chow, M.; Conway, A.R.A. The scope and control of attention: Sources of variance in working memory capacity. Mem. Cogn. 2015, 43, 325–339. [Google Scholar] [CrossRef] [PubMed]
- Vogel, E.K.; Awh, E. How to Exploit Diversity for Scientific Gain: Using Individual Differences to Constrain Cognitive Theory. Curr. Dir. Psychol. Sci. 2008, 17, 171–176. [Google Scholar] [CrossRef]
- Hitch, G.J. The role of short-term working memory in mental arithmetic. Cogn. Psychol. 1978, 10, 302–323. [Google Scholar] [CrossRef]
- Just, M.A.; Carpenter, P.A. A capacity theory of comprehension: Individual differences in working memory. Psychol. Rev. 1992, 99, 122–149. [Google Scholar] [CrossRef] [PubMed]
- Green, K.E.; Kluever, R.C. Components of item difficulty of Raven’s matrices. J. Gen. Psychol. 1992, 119, 189–199. [Google Scholar] [CrossRef]
- Primi, R. Complexity of geometric inductive reasoning tasks: Contribution to the understanding of fluid intelligence. Intelligence 2002, 30, 41–70. [Google Scholar] [CrossRef]
- Becker, N.; Schmitz, F.; Göritz, A.; Spinath, F. Sometimes More Is Better, and Sometimes Less Is Better: Task Complexity Moderates the Response Time Accuracy Correlation. J. Intell. 2016, 4, 11. [Google Scholar] [CrossRef]
- Meo, M.; Roberts, M.J.; Marucci, F.S. Element salience as a predictor of item difficulty for Raven’s Progressive Matrices. Intelligence 2007, 35, 359–368. [Google Scholar] [CrossRef]
- Vigneau, F.; Caissie, A.F.; Bors, D.A. Eye-movement analysis demonstrates strategic influences on intelligence. Intelligence 2006, 34, 261–272. [Google Scholar] [CrossRef]
- Vodegel Matzen, L.B.; van der Molen, M.W.; Dudink, A.C. Error analysis of raven test performance. Person. Individ. Differ. 1994, 16, 433–445. [Google Scholar] [CrossRef]
- Becker, N.; Preckel, F.; Karbach, J.; Raffel, N.; Spinath, F.M. Die Matrizenkonstruktionsaufgabe. Diagnostica 2015, 61, 22–33. [Google Scholar] [CrossRef]
- Becker, N.; Schmitz, F.; Falk, A.; Feldbrügge, J.; Recktenwald, D.; Wilhelm, O.; Preckel, F.; Spinath, F. Preventing Response Elimination Strategies Improves the Convergent Validity of Figural Matrices. J. Intell. 2016, 4, 2. [Google Scholar] [CrossRef]
- Peirce, J.W. PsychoPy—Psychophysics software in Python. J. Neurosci. Methods 2007, 162, 8–13. [Google Scholar] [CrossRef] [PubMed]
- Rosseel, Y. lavaan: An R Package for Structural Equation Modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Hu, L.; Bentler, P.M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Model. 1999, 6, 1–55. [Google Scholar] [CrossRef]
- Oberauer, K.; Süß, H.M.; Wilhelm, O.; Sander, N. Individual differences in working memory capacity and reasoning ability. In Variation in Working Memory; Oxford University Press: Oxford, UK, 2007; pp. 49–75. [Google Scholar]
- Oberauer, K.; Süß, H.M.; Wilhelm, O.; Wittmann, W.W. Which working memory functions predict intelligence? Intelligence 2008, 36, 641–652. [Google Scholar] [CrossRef]
- Oberauer, K.; Farrell, S.; Jarrold, C.; Lewandowsky, S. What limits working memory capacity? Psychol. Bull. 2016, 142, 758–799. [Google Scholar] [CrossRef] [PubMed]
- Cattell, R.B. Theory of fluid and crystallized intelligence: A critical experiment. J. Educ. Psychol. 1963, 54, 1–22. [Google Scholar] [CrossRef]
- Donders, F. Over de snelheid van psychische processen. Onderzoekingen gedaan in het Physiologisch Laboratorium der Utrechtsche Hoogeschool, 1868–1869, Tweede reeks, II: 92–120. Reprinted as Donders, Franciscus C. (1969). On the speed of mental processes. Acta Psychol. 1868, 30, 412–431. [Google Scholar] [CrossRef]
- Sternberg, S. Memory-scanning: Mental processes revealed by reaction-time experiments. Am. Sci. 1969, 57, 421–457. [Google Scholar] [PubMed]
| Rule Type | Description |
|---|---|
| Addition | Elements of first two cells are summed up in third cell |
| Subtraction | Elements of second cell are subtracted from elements in first cell and the result is shown in third cell |
| Overlap | Elements that are shown in first and second cell are presented in third cell |
| Addition of unique elements | Elements that are shown in first or second cell are presented in third cell |
| M | SD | Min | Max | Color k | Shapes k | Ori k | Mean k | Ext | NonExt | |
|---|---|---|---|---|---|---|---|---|---|---|
| Color k | 3.27 | 0.70 | 1.30 | 4.45 | 0.73 | |||||
| Shapes k | 1.96 | 0.70 | 0.40 | 3.20 | 0.48 *** | .72 | ||||
| Ori k | 1.88 | 0.86 | 0.05 | 3.70 | 0.42 *** | .37 *** | .70 | |||
| Mean k | 0.00 | 0.78 | –2.07 | 1.36 | 0.81 *** | .78 *** | .76 *** | - | ||
| Ext | 28.94 | 16.17 | 0 | 48 | 0.18 | .13 | .25 * | .24 * | .97 | |
| NonExt | 26.21 | 15.79 | 0 | 48 | 0.16 | .11 | .29 * | .24 * | .81 *** | .97 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domnick, F.; Zimmer, H.D.; Becker, N.; Spinath, F.M. Is the Correlation between Storage Capacity and Matrix Reasoning Driven by the Storage of Partial Solutions? A Pilot Study of an Experimental Approach. J. Intell. 2017, 5, 21. https://doi.org/10.3390/jintelligence5020021
Domnick F, Zimmer HD, Becker N, Spinath FM. Is the Correlation between Storage Capacity and Matrix Reasoning Driven by the Storage of Partial Solutions? A Pilot Study of an Experimental Approach. Journal of Intelligence. 2017; 5(2):21. https://doi.org/10.3390/jintelligence5020021
Chicago/Turabian StyleDomnick, Florian, Hubert D. Zimmer, Nicolas Becker, and Frank M. Spinath. 2017. "Is the Correlation between Storage Capacity and Matrix Reasoning Driven by the Storage of Partial Solutions? A Pilot Study of an Experimental Approach" Journal of Intelligence 5, no. 2: 21. https://doi.org/10.3390/jintelligence5020021
APA StyleDomnick, F., Zimmer, H. D., Becker, N., & Spinath, F. M. (2017). Is the Correlation between Storage Capacity and Matrix Reasoning Driven by the Storage of Partial Solutions? A Pilot Study of an Experimental Approach. Journal of Intelligence, 5(2), 21. https://doi.org/10.3390/jintelligence5020021





