Network Models for Cognitive Development and Intelligence
Abstract
:1. Introduction
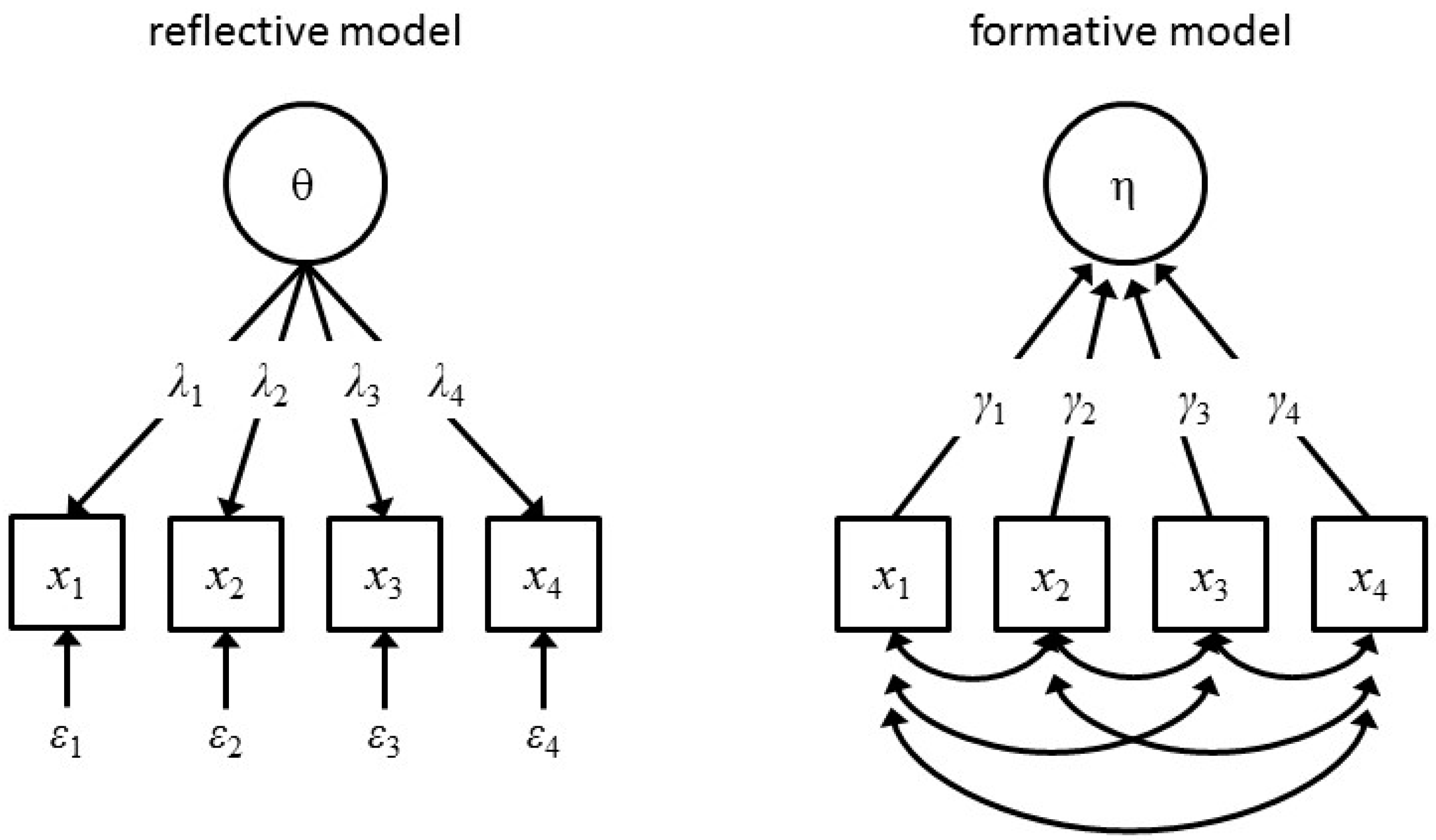
2. The Factor Model Dominance
3. Alternative Explanations for the Positive Manifold of Cognitive Abilities
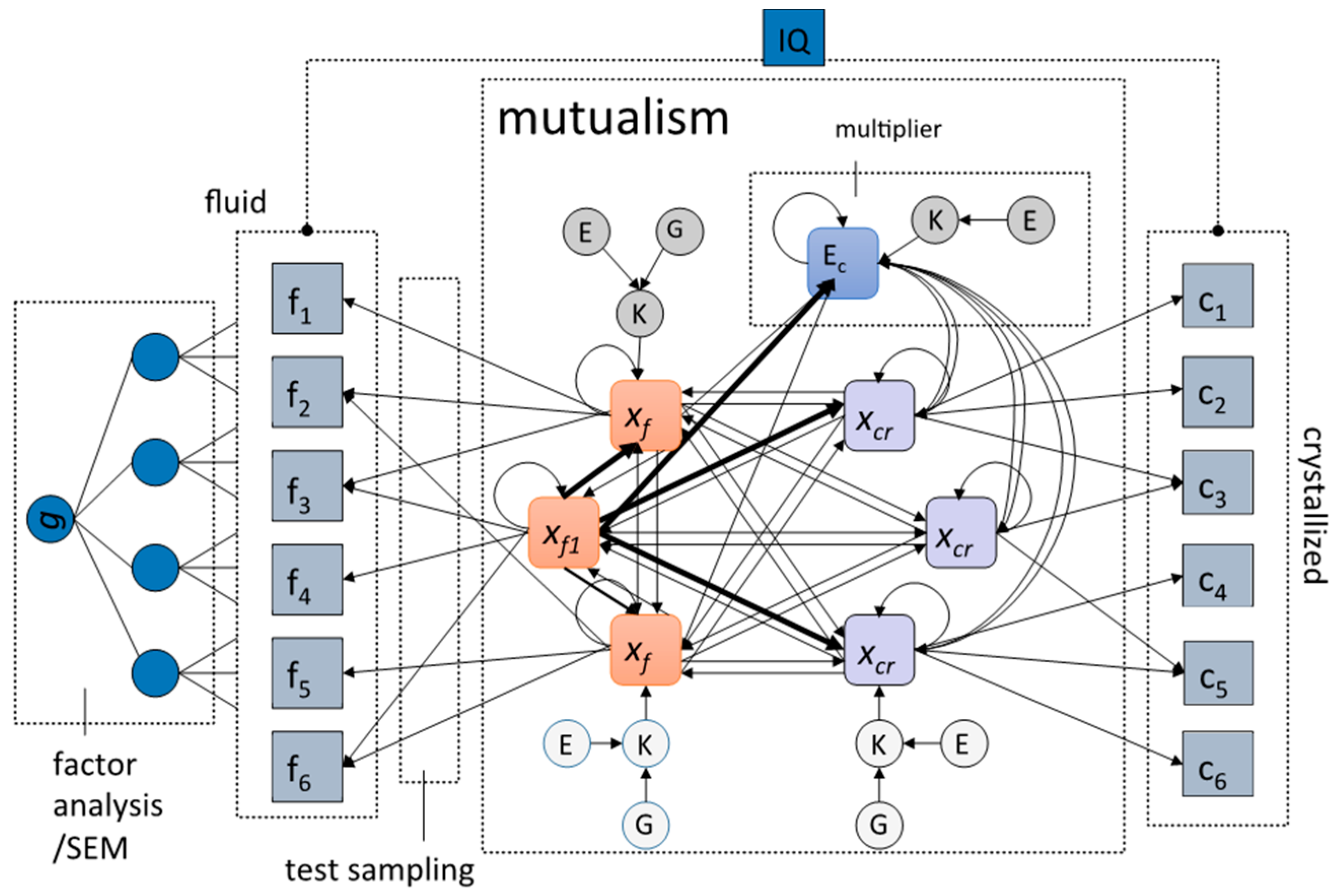
3.1. The Sampling Model
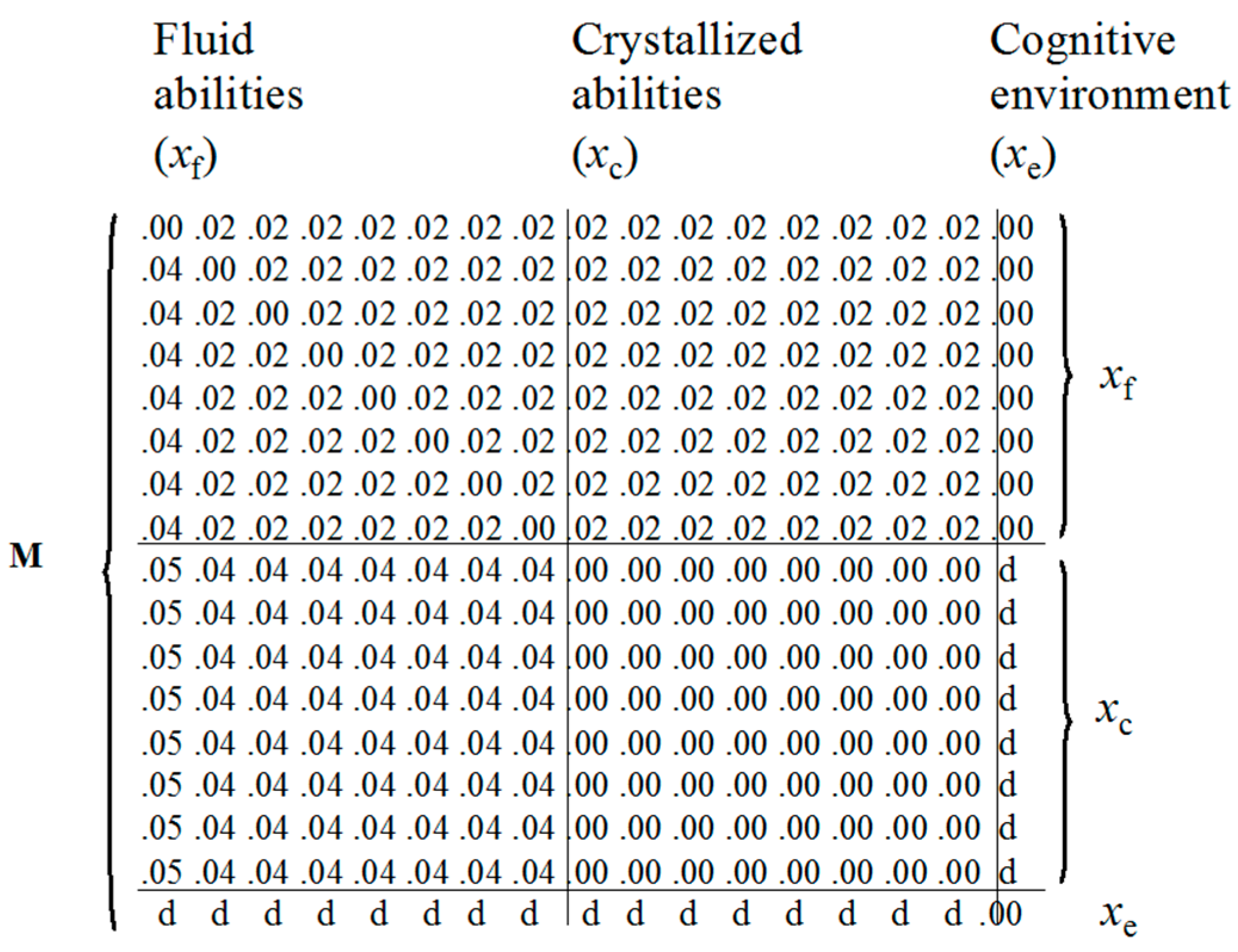
3.2. Network Models
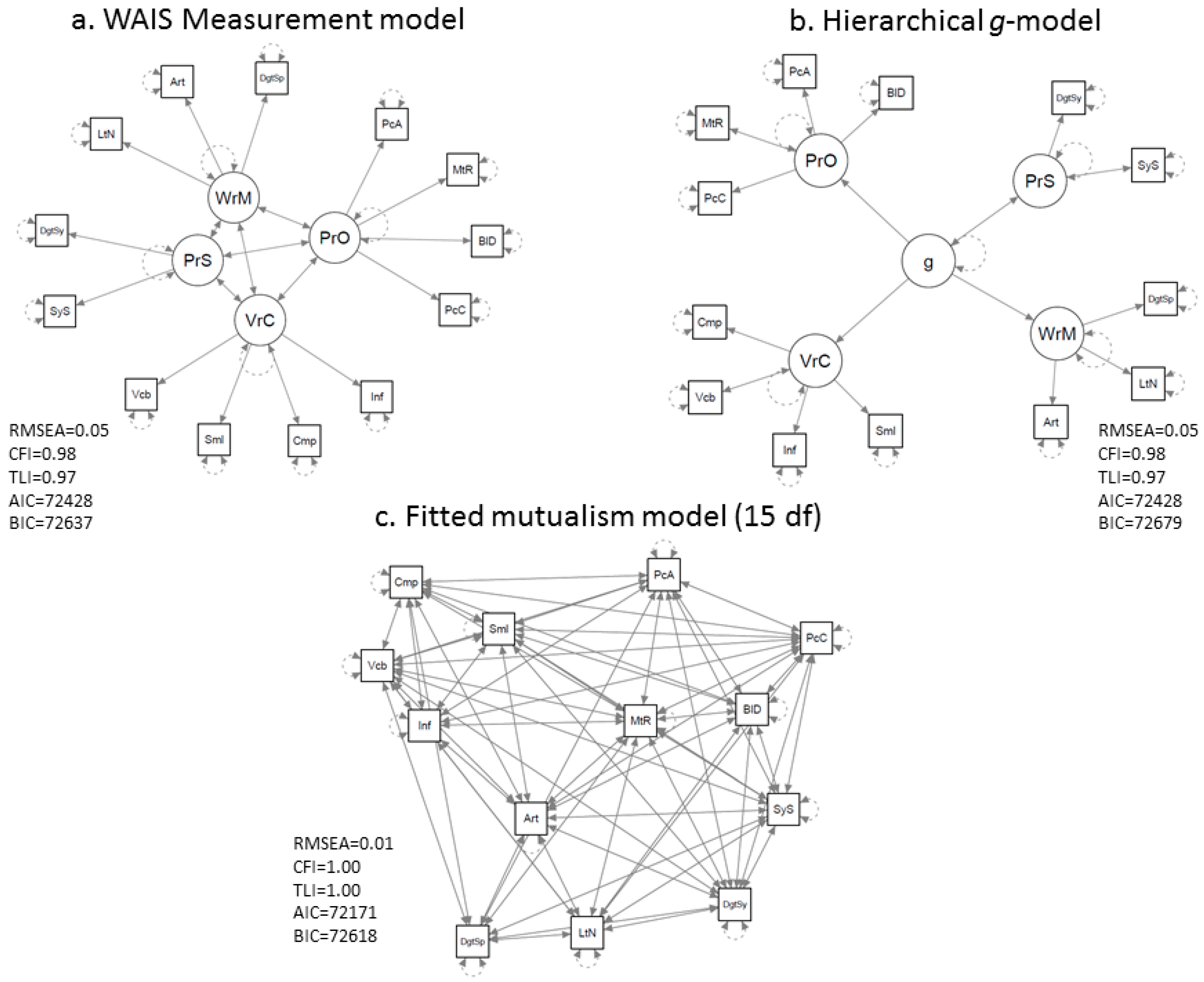
3.3. g, Sampling, and/or Mutualism
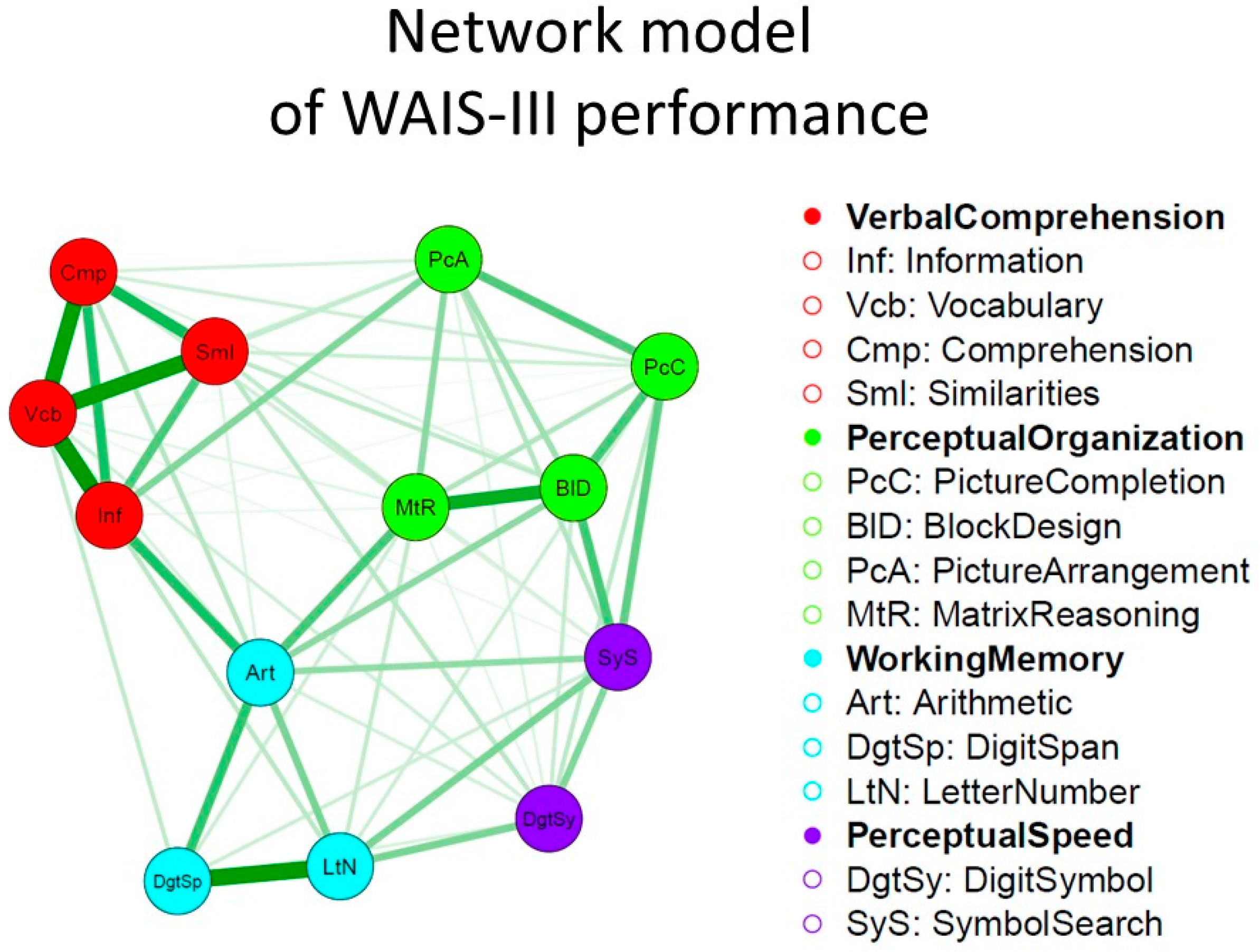
4. Network Psychometrics
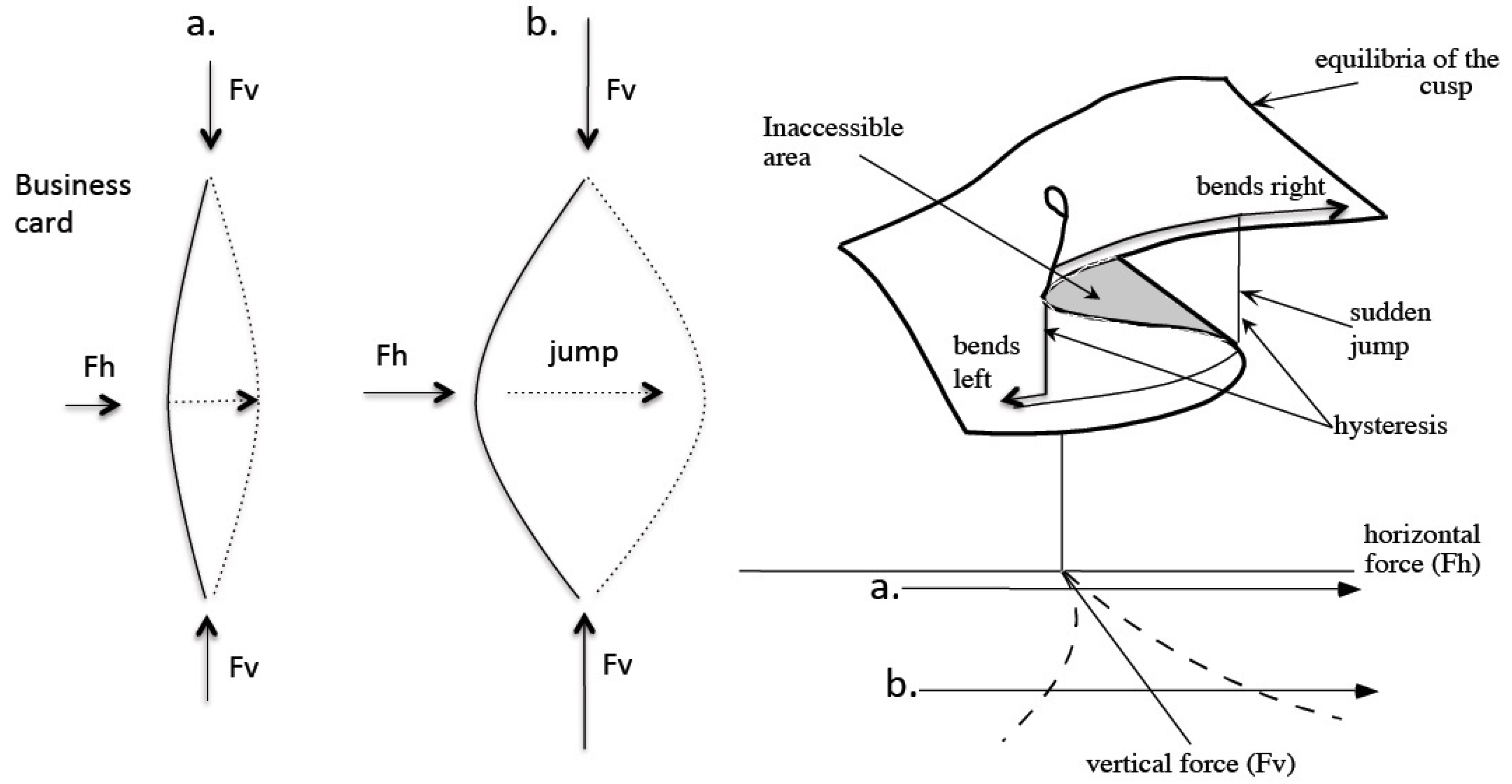
Complex Behavior in Networks
5. Discussion
Author Contributions
Conflicts of Interest
References
- Cronbach, L.J. The two disciplines of scientific psychology. Am. Psychol. 1957, 12, 671–684. [Google Scholar] [CrossRef]
- Kanazawa, S. General Intelligence as a Domain-Specific Adaptation. Psychol. Rev. 2004, 111, 512–523. [Google Scholar] [CrossRef] [PubMed]
- Borsboom, D.; Dolan, C.V. Why g is not an adaptation: A comment on Kanazawa (2004). Psychol. Rev. 2006, 113, 433–437. [Google Scholar] [CrossRef] [PubMed]
- Baer, J. The Case for Domain Specificity of Creativity. Creat. Res. J. 1998, 11, 173–177. [Google Scholar] [CrossRef]
- Spearman, C. ‘General Intelligence’, Objectively Determined and Measured. Am. J. Psychol. 1904, 15, 201–292. [Google Scholar] [CrossRef]
- Cattell, R.B. Theory of fluid and crystallized intelligence: A critical experiment. J. Educ. Psychol. 1963, 54, 1–22. [Google Scholar] [CrossRef]
- Bartholomew, D.J. Measuring Intelligence: Facts and Fallacies; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Borsboom, D.; Mellenbergh, G.J.; van Heerden, J. The Concept of Validity. Psychol. Rev. 2004, 111, 1061–1071. [Google Scholar] [CrossRef] [PubMed]
- Arendasy, M.E.; Sommer, M.; Gutiérrez-Lobos, K.; Punter, J.F. Do individual differences in test preparation compromise the measurement fairness of admission tests? Intelligence 2016, 55, 44–56. [Google Scholar] [CrossRef]
- Jensen, A.R. The g Factor: The Science of Mental Ability; Praeger Publishers/Greenwood Publishing Group Inc.: Westport, CT, USA, 1998. [Google Scholar]
- Gottfredson, L.S. The General Intelligence Factor. Sci. Am. Present. 1998, 9, 24–29. [Google Scholar]
- Jonas, K.G.; Markon, K.E. A descriptivist approach to trait conceptualization and inference. Psychol. Rev. 2016, 123, 90–96. [Google Scholar] [CrossRef] [PubMed]
- Van der Maas, H.L.J.; Dolan, C.V.; Grasman, R.P.P.P.; Wicherts, J.M.; Huizenga, H.M.; Raijmakers, M.E.J. A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Intelligence 2006, 113, 842–861. [Google Scholar] [CrossRef] [PubMed]
- Bartholomew, D.J.; Deary, I.J.; Lawn, M. A new lease of life for Thomson’s bonds model of intelligence. Psychol. Rev. 2009, 116, 567–579. [Google Scholar] [CrossRef] [PubMed]
- Kovacs, K.; Conway, A.R.A. Process Overlap Theory: A Unified Account of the General Factor of Intelligence. Psychol. Inq. 2016, 27, 151–177. [Google Scholar] [CrossRef]
- Thorndike, R.L. The Measurement of Intelligence; Teachers College: New York, NY, USA, 1927. [Google Scholar]
- Thomson, G. The Factorial Analysis of Human Ability, 5th ed.; University of London Press: London, UK, 1951. [Google Scholar]
- Lumsden, J. Test Theory. Annu. Rev. Psychol. 1976, 27, 251–280. [Google Scholar] [CrossRef]
- Anderson, M. Annotation: Conceptions of Intelligence. J. Child Psychol. Psychiatry 2001, 42, 287–298. [Google Scholar] [CrossRef] [PubMed]
- Cannon, T.D.; Keller, M.C. Endophenotypes in the Genetic Analyses of Mental Disorders. Annu. Rev. Clin. Psychol. 2006, 2, 267–290. [Google Scholar] [CrossRef] [PubMed]
- Kievit, R.A.; Davis, S.W.; Griffiths, J.; Correia, M.M.; Henson, R.N. A watershed model of individual differences in fluid intelligence. Neuropsychologia 2016, 91, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Fisher, C.; Hall, D.G.; Rakowitz, S.; Gleitman, L. When it is better to receive than to give: Syntactic and conceptual constraints on vocabulary growth. Lingua 1994, 92, 333–375. [Google Scholar] [CrossRef]
- Pinker, S. How could a child use verb syntax to learn verb semantics? Lingua 1994, 92, 377–410. [Google Scholar] [CrossRef]
- Sternberg, R.J. Metacognition, abilities, and developing expertise: What makes an expert student? Instr. Sci. 1998, 26, 127–140. [Google Scholar] [CrossRef]
- Gibson, J.J. The Ecological Approach to Visual Perception; Lawrence Erlbaum Associates, Inc.: Hillsdale, NJ, USA, 1986. [Google Scholar]
- Dweck, C.S. Motivational processes affecting learning. Am. Psychol. 1986, 41, 1040–1048. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology. I: An Introduction, 3rd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Van der Maas, H.L.J.; Kan, K.J. Comment on ‘Residual group-level factor associations: Possibly negative implications for the mutualism theory of general intelligence’ by G.E. Gignac (2016). Intelligence 2016, 57, 81–83. [Google Scholar] [CrossRef]
- Barnett, S.M.; Ceci, S.J. When and where do we apply what we learn?: A taxonomy for far transfer. Psychol. Bull. 2002, 128, 612–637. [Google Scholar] [CrossRef] [PubMed]
- Eysenck, H.J. Thomson’s “Bonds” or Spearman’s “Energy”: Sixty years on. Mankind Q. 1987, 27, 259–274. [Google Scholar]
- Gignac, G.E. Fluid intelligence shares closer to 60% of its variance with working memory capacity and is a better indicator of general intelligence. Intelligence 2014, 47, 122–133. [Google Scholar] [CrossRef]
- Gignac, G.E. Residual group-level factor associations: Possibly negative implications for the mutualism theory of general intelligence. Intelligence 2016, 55, 69–78. [Google Scholar] [CrossRef]
- Nisbett, R.E.; Aronson, J.B.; Dickens, C.; Flynn, W.; Halpern, D.F.; Al, E. Intelligence: New findings and theoretical developments. Am. Psychol. 2012, 67, 130–159. [Google Scholar] [CrossRef] [PubMed]
- Dickens, W.T.; Flynn, J.R. Heritability estimates versus large environmental effects: The IQ paradox resolved. Psychol. Rev. 2001, 108, 346–369. [Google Scholar] [CrossRef] [PubMed]
- Dickens, W.T. What is g? Available online: https://www.brookings.edu/wp-content/uploads/2016/06/20070503.pdf (accessed on 3 May 2007).
- Kan, K.-J.; Wicherts, J.M.; Dolan, C.V.; van der Maas, H.L.J. On the Nature and Nurture of Intelligence and Specific Cognitive Abilities: The More Heritable, the More Culture Dependent. Psychol. Sci. 2013, 24, 2420–2428. [Google Scholar] [CrossRef] [PubMed]
- Van der Maas, H.L.J.; Kan, K.J.; Hofman, A.; Raijmakers, M.E.J. Dynamics of Development: A complex systems approach. In Handbook of Developmental Systems Theory and Methodology; Molenaar, P.C.M., Lerner, R.M., Newell, K.M., Eds.; Guilford Press: New York, NY, USA, 2014; pp. 270–286. [Google Scholar]
- Cattell, R.B. Intelligence: Its Structure, Growth, and Action; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Kan, K.-J. The Nature of Nurture: The Role of Gene-Environment Interplay in the Development of Intelligence. Ph.D. Thesis, University of Amsterdam, Amsterdam, The Netherlands, 2012. [Google Scholar]
- Borsboom, D. A network theory of mental disorders. World Psychiatry 2017, 16, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Dalege, J.; Borsboom, D.; van Harreveld, F.; van den Berg, H.; Conner, M.; van der Maas, H.L.J. Toward a formalized account of attitudes: The Causal Attitude Network (CAN) model. Psychol. Rev. 2016, 123, 2–22. [Google Scholar] [CrossRef] [PubMed]
- Cramer, A.O.J.; Waldorp, L.J.; van der Maas, H.L.J.; Borsboom, D. Comorbidity: A network perspective. Behav. Brain Sci. 2010, 33, 137–150. [Google Scholar] [CrossRef] [PubMed]
- Van de Leemput, I.A.; Wichers, M.; Cramer, A.O.J.; Borsboom, D.; Tuerlinckx, F.; Kuppens, P.; van Nes, E.H.; Viechtbauer, W.; Giltay, E.J.; Aggen, S.H.; et al. Critical slowing down as early warning for the onset and termination of depression. Proc. Natl. Acad. Sci. USA 2014, 111, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Wichers, M.; Groot, P.C.; Psychosystems, E.S.M.; EWS Group. Critical Slowing Down as a Personalized Early Warning Signal for Depression. Psychother. Psychosom. 2016, 85, 114–116. [Google Scholar] [CrossRef] [PubMed]
- Van der Maas, H.L.J.; Kolstein, R.; van der Pligt, J. Sudden Transitions in Attitudes. Sociol. Methods Res. 2003, 32, 125–152. [Google Scholar] [CrossRef]
- Haslbeck, J.M.B.; Waldorp, L.J. Structure estimation for mixed graphical models in high-dimensional data. arXiv, 2015; arXiv:1510.05677. [Google Scholar]
- Van Borkulo, C.D.; Borsboom, D.; Epskamp, S.; Blanken, T.F.; Boschloo, L.; Schoevers, R.A.; Waldorp, L.J. A new method for constructing networks from binary data. Sci. Rep. 2014, 4, srep05918. [Google Scholar] [CrossRef] [PubMed]
- Epskamp, S.; Cramer, A.O.J.; Waldorp, L.J.; Schmittmann, V.D.; Borsboom, D. qgraph: Network Visualizations of Relationships in Psychometric Data. J. Stat. Softw. 2012, 48, 1–18. [Google Scholar] [CrossRef]
- Lauritzen, S.L. Graphical Models; Clarendon Press: Oxford, UK, 1996. [Google Scholar]
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Lauritzen, S.L.; Wermuth, N. Graphical Models for Associations between Variables, some of which are Qualitative and some Quantitative. Ann. Stat. 1989, 17, 31–57. [Google Scholar] [CrossRef]
- Bringmann, L.F.; Vissers, N.; Wichers, M.; Geschwind, N.; Kuppens, P.; Peeters, F.; Borsboom, D.; Tuerlinckx, F. A Network Approach to Psychopathology: New Insights into Clinical Longitudinal Data. PLoS ONE 2013, 8, e96588. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. A Fused Latent and Graphical Model for Multivariate Binary Data. arXiv, 2016; arXiv:1606.08925. [Google Scholar]
- Epskamp, S.; Rhemtulla, M.; Borsboom, D. Generalized Network Psychometrics: Combining Network and Latent Variable Models. arXiv, 2016; arXiv:1605.09288. [Google Scholar] [CrossRef] [PubMed]
- Epskamp, S. Network Psychometrics. Ph.D. Thesis, University of Amsterdam, Amsterdam, The Netherlands, 2017. [Google Scholar]
- Mackintosh, N.J. IQ and Human Intelligence, 2nd ed.; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 2008, 9, 432–441. [Google Scholar] [CrossRef] [PubMed]
- Foygel, R.; Drton, M. Extended Bayesian Information Criteria for Gaussian Graphical Models. Proceedings of 24th Annual Conference on Neural Information Processing Systems 2010, NIPS 2010, Vancouver, BC, Canada, 6–9 December 2010; pp. 604–612. [Google Scholar]
- Wirth, R.J.; Edwards, M.C. Item factor analysis: Current approaches and future directions. Psychol. Methods 2007, 12, 58–79. [Google Scholar] [CrossRef] [PubMed]
- Lenz, W. Beiträge zum verständnis der magnetischen eigenschaften in festen körpern. Phys. Z. 1920, 21, 613–615. [Google Scholar]
- Niss, M. History of the Lenz-Ising Model 1920–1950: From Ferromagnetic to Cooperative Phenomena. Arch. Hist. Exact Sci. 2005, 59, 267–318. [Google Scholar] [CrossRef]
- Borsboom, D.; Cramer, A.O.J.; Schmittmann, V.D.; Epskamp, S.; Waldorp, L.J. The Small World of Psychopathology. PLoS ONE 2011, 6, e27407. [Google Scholar] [CrossRef] [PubMed]
- Epskamp, S.; Maris, G.K.J.; Waldorp, L.J.; Borsboom, D. Network Psychometrics. arXiv, 2016; arXiv:1609.02818. [Google Scholar]
- Kruis, J.; Maris, G. Three representations of the Ising model. Sci. Rep. 2016, 6, srep34175. [Google Scholar] [CrossRef] [PubMed]
- Marsman, M.; Maris, G.; Bechger, T.; Glas, C. Bayesian inference for low-rank Ising networks. Sci. Rep. 2015, 5, srep9050. [Google Scholar] [CrossRef] [PubMed]
- Marsman, M.; Borsboom, D.; Kruis, J.; Epskamp, S.; Waldorp, L.J.; Maris, G.K.J. An introduction to network psychometrics: Relating Ising network models to item response theory models. 2017; Submitted. [Google Scholar]
- Kac, M. Mathematical mechanisms of phase transitions. In Statistical Physics: Phase Transitions and Superfluidity; Chrétien, M., Gross, E., Deser, S., Eds.; Gordon and Breach Science Publishers: New York, NY, USA, 1968; Volume I, pp. 241–305. [Google Scholar]
- Demetriou, A.; Spanoudis, G.; Mouyi, A. Educating the Developing Mind: Towards an Overarching Paradigm. Educ. Psychol. Rev. 2011, 23, 601–663. [Google Scholar] [CrossRef]
- Waddington, C.H. Principles of Development and Differentiation; MacMillan Company: London, UK, 1966. [Google Scholar]
- Jansen, B.R.J.; van der Maas, H.L.J. Evidence for the Phase Transition from Rule I to Rule II on the Balance Scale Task. Dev. Rev. 2001, 21, 450–494. [Google Scholar] [CrossRef]
- Van der Maas, H.L.; Molenaar, P.C. Stagewise cognitive development: An application of catastrophe theory. Psychol. Rev. 1992, 99, 395–417. [Google Scholar] [CrossRef] [PubMed]
- Cramer, A.O.J.; van Borkulo, C.D.; Giltay, E.J.; van der Maas, H.L.J.; Kendler, K.S.; Scheffer, M.; Borsboom, D. Major Depression as a Complex Dynamic System. PLoS ONE 2016, 11, e0167490. [Google Scholar]
- De Boeck, P.A.L.; Wilson, M.; Acton, G.S. A conceptual and psychometric framework for distinguishing categories and dimensions. Psychol. Rev. 2005, 112, 129–158. [Google Scholar] [CrossRef] [PubMed]
- Hofman, A.D.; Visser, I.; Jansen, B.R.J.; van der Maas, H.L.J. The Balance-Scale Task Revisited: A Comparison of Statistical Models for Rule-Based and Information-Integration Theories of Proportional Reasoning. PLoS ONE 2015, 10, e0136449. [Google Scholar] [CrossRef] [PubMed]
- Van der Maas, H.L.J.; Molenaar, D.; Maris, G.; Kievit, R.A.; Borsboom, D. Cognitive psychology meets psychometric theory: On the relation between process models for decision making and latent variable models for individual differences. Psychol. Rev. 2011, 118, 339–356. [Google Scholar] [CrossRef] [PubMed]
- Roger, R. A theory of memory retrieval. Psychol. Rev. 1978, 85, 59–108. [Google Scholar]
| 1 | Though factor analysis on sum scores of subtests is most common, it is not a necessity. An alternative is item factor analysis [59], for instance. The positive manifold and “statistical” g can be investigated with both continuous and dichotomous scores. We focus here on the Ising model since it is very simple and the formal relation with a psychometric model has been established. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Der Maas, H.L.J.; Kan, K.-J.; Marsman, M.; Stevenson, C.E. Network Models for Cognitive Development and Intelligence. J. Intell. 2017, 5, 16. https://doi.org/10.3390/jintelligence5020016
Van Der Maas HLJ, Kan K-J, Marsman M, Stevenson CE. Network Models for Cognitive Development and Intelligence. Journal of Intelligence. 2017; 5(2):16. https://doi.org/10.3390/jintelligence5020016
Chicago/Turabian StyleVan Der Maas, Han L. J., Kees-Jan Kan, Maarten Marsman, and Claire E. Stevenson. 2017. "Network Models for Cognitive Development and Intelligence" Journal of Intelligence 5, no. 2: 16. https://doi.org/10.3390/jintelligence5020016
APA StyleVan Der Maas, H. L. J., Kan, K.-J., Marsman, M., & Stevenson, C. E. (2017). Network Models for Cognitive Development and Intelligence. Journal of Intelligence, 5(2), 16. https://doi.org/10.3390/jintelligence5020016