Next Article in Journal
Methodological Issues Associated with Studying the Flynn Effect: Exploratory and Confirmatory Efforts in the Past, Present, and Future
Previous Article in Journal
Differences in Judgments of Creativity: How Do Academic Domain, Personality, and Self-Reported Creativity Influence Novice Judges’ Evaluations of Creative Productions?
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
J. Intell.
Volume 3
Issue 3
10.3390/jintelligence3030091
jintelligence-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Interaction Effects between Openness and Fluid Intelligence Predicting Scholastic Performance

by
Jing Zhang
* and
Matthias Ziegler
Institut für Psychologie, Humboldt-Universität zu Berlin, Rudower Chaussee 18, 12489 Berlin, Germany
*
Author to whom correspondence should be addressed.
J. Intell. 2015, 3(3), 91-110; https://doi.org/10.3390/jintelligence3030091
Submission received: 23 April 2015 / Revised: 10 September 2015 / Accepted: 14 September 2015 / Published: 18 September 2015
Browse Figure
Versions Notes

Abstract

:
Figural reasoning as an indicator of fluid intelligence and the domains of the Five Factor Model were explored as predictors of scholastic performance. A total of 836 Chinese secondary school students (406 girls) from grades 7 to 11 participated. Figural reasoning, as measured by Raven’s Standard Progressive Matrices, predicted performance in Math, Chinese, and English, and also for a composite score. Among the personality domains, Openness had a positive effect on performance for all subjects after controlling for all the other variables. For Conscientiousness, the effects were smaller and only significant for Math. Neuroticism had a negative effect on Math grades. The effects of Extraversion on all grades were very small and not significant. Most importantly, hierarchical latent regression analyses indicated that all interaction effects between Openness and figural reasoning were significant, revealing a compensatory interaction. Our results further suggest that scholastic performance basically relies on the same traits through the secondary school years. However, importance is given to interaction effects between ability and personality. Implications along with limitations and suggestions for future research are discussed.

1. Interaction Effects between Openness and Fluid Intelligence Predicting Scholastic Performance

Educational success plays an important role in students’ future opportunities and success in later life [1]. Although general intelligence is known to be the strongest predictor of educational and scholastic performance [2,3,4], other research has identified several non-cognitive factors that are of importance as well, e.g., motivation, school anxiety, and interests, but especially the Five Factor Model (FFM) of personality [5,6,7,8,9,10,11]. Across different levels of education, the domains of the FFM have been shown to contribute to the prediction of performance independent of intelligence [12,13]. Moreover, small-sized correlations between intelligence and personality traits have consistently been reported [12,14]. Therefore, it is reasonable to look at intelligence and the domains of the FFM simultaneously in order to control for their shared variance and to identify specific contributions to performance.
Most previous studies addressing the prediction of scholastic performance have been conducted in Western cultures, and little is known about effects in other cultures (e.g., Asian cultures). This is especially important because previous intercultural research has reported systematic differences between Asian and Western students from preschool to college. For example, Chinese people are reported to put more emphasis on hard work compared to innate ability, and believe that knowledge depends on accumulation. Moreover, Chinese students are also reported to believe that success comes from hard work, and show higher achievement motivation than their Western peers [15,16,17]. Considering these differences, it can be assumed that the effects regarding scholastic performance reported in Western cultures do not necessarily replicate in Chinese samples. Consequently, the present study aimed at examining the explanatory power of intelligence and the domains of the FFM on scholastic performance in a Chinese sample, and further exploring their potential interactions [18,19,20].

1.1. Fluid Intelligence and Scholastic Performance

In order to understand the influence of intelligence on scholastic performance, it is important to clarify the distinction between fluid intelligence (Gf) and crystallized intelligence (Gc) [21,22,23]. Fluid intelligence (Gf) is defined as “the use of deliberate mental operations to solve novel problems that cannot be performed as a function of simple memorization or routine behavior” [24]. Also, Gf is considered as a very good proxy for general intelligence (g) [25,26], and is often measured with tests such as the Progressive Matrices or Cattell’s Culture Fair test [27,28]. Many prior studies mainly focused on the prediction of mathematics performance and showed that broad cognitive abilities (i.e., fluid reasoning, Gc, and processing speed) were important predictors, speaking to the cognitive complexity of mathematics [29,30]. However, there is also evidence that the effect of intelligence on scholastic performance varies across different subjects. For example, Spinath et al. [10] used a sample of German primary school students and reported that g was the strongest predictor in three subjects (i.e., Mathematics, Science, and English), and even the only significant predictor in Science when compared to non-cognitive factors (i.e., domain-specific self-perceived ability and intrinsic values). Lu et al. [8] measured working memory as another cognitive predictor and found that it explained more variance in Math, while figural reasoning, as an indicator of Gf, explained more variance in Chinese in a sample of Chinese primary school students. Those authors also showed that the total amount of variance explained in Math was substantially larger than for Chinese. Consequently, the present study will include grades from different subjects as an indicator of Gf.

1.2. Personality and Scholastic Performance

Across different levels of education, personality has been shown to contribute independently to the prediction of academic performance above and beyond intelligence [7,9,11,18,31,32,33,34,35,36], which was summarized in recent meta-analyses [12,13,37,38]. Among the FFM domains, Conscientiousness is consistently identified as an important predictor of performance [5,7,12,13,38]. Conscientiousness reflects a tendency to be purposeful, organized, reliable, determined, and ambitious [39], all of which are believed to be important for performance in work and academic settings [40,41]. After Conscientiousness, meta-analyses have shown that Openness also significantly predicted performance at the secondary and tertiary level (ρ = 0.12 and ρ = 0.09) [12], which was often interpreted in terms of the positive correlation between Openness and intelligence. By contrast, the results of the relations between academic performance and the other three FFM domains are relatively weak or inconsistent. Agreeableness is characterized by altruism, cooperation, and trust [39]. Meta-analyses indicate that Agreeableness had slightly lower correlations with performance at the secondary and tertiary level (ρ = 0.05 and ρ = 0.06) [12], which was interpreted in terms of cooperation within learning processes [38]. Neuroticism was reported to have a weak negative relation to scholastic performance [5,7,41], as neurotic students are thought to experience more negative affect and anxiety, reducing learning motivation [42] and impairing scholastic performance. However, other studies reported no or even positive effects [43,44,45,46]. For Extraversion, a positive correlation with performance was reported in elementary school but became negative when kids grew older [47,48,49]. This might be due to the two components of Extraversion: Ambition (referring to the need for dominance) and Sociability (referring to the need for affiliation). Especially the latter aspect of Extraversion may bring students to devoting time to socializing rather than studying.
Similar to what has been found for intelligence, relations between the FFM and scholastic performance were also subject-specific [9,18]. For instance, Neuroticism was found to predict grades in Math, Science, and foreign languages, but not in students’ native language [18]. Furthermore, Spinath, Freudenthaler, and Neubauer [9] found that Conscientiousness and Neuroticism were important for Math achievement, but Extraversion was important for language achievement. It is important to note that these subject-specific effects might also explain some of the mixed results reported before.

1.3. Intelligence and the Domains of the FFM

A substantial body of literature has demonstrated complex relations between intelligence and personality [12,14,50]. Ackerman and Heggestad [14] reported small-to-moderate correlations between intelligence and Openness to Experience (ρ = 0.33), Neuroticism (ρ = −0.15), and Extraversion (ρ = 0.08). Weaker correlations were reported with Conscientiousness (ρ = 0.02) and Agreeableness (ρ = 0.01). Another meta-analysis by Poropat [12], only using student samples, found small correlations between the FFM and intelligence (i.e., Agreeableness, ρ = 0.01; Conscientiousness, ρ = 0.03; Emotional Stability, ρ = 0.06; Extraversion, ρ = −0.01; Openness, ρ = 0.15). Because of these overlaps, it seems important to control for shared variance between the traits in order to identify specific effects. Surprisingly, very few studies have included both intelligence and personality measures to predict scholastic performance [5,7,18,33,35]. Besides focusing on the additive effects of intelligence and the FFM, other researchers proposed the idea of interaction effects between ability and personality.

1.4. Interaction Hypotheses

Very early [51] on, it was already proposed that performance might be determined by factors relating to the capacity to perform (i.e., knowledge, skills, and intelligence), the opportunity to perform, which is affected by environmental constraints such as socioeconomic resources, and the willingness to perform (i.e., motivation, cultural norms, and personality) [12,52,53]. In other words, the willingness to perform does not automatically follow from the ability to perform. Thus, intelligence and personality variables might enhance or buffer their respective impact on scholastic performance. Zeidner [54] contended that Conscientiousness might increase while Neuroticism might decrease the correlation between intelligence and performance. As mentioned, this general idea of an interaction between ability and personality can be traced back to early work performance models [51,55,56,57,58], which state that job performance is an interactive function of motivation and ability. Denissen and Penke [59] suggested that motivational reaction norms underlie the FFM. For Conscientiousness they hypothesized differences in the tenacity to pursue goals under difficult circumstances as the motivational root. This clearly reflects the notions by Zeidner [54]. Thus, based on the ideas by work psychologists and the theoretical assumptions by Denissen and Penke, it could be assumed that Conscientiousness enhances the impact of intelligence when predicting scholastic performance. This idea was supported in a study by Ziegler, Knogler, and Bühner [60]. Prior research also points to a specific interaction between Openness and intelligence. Ziegler, Danay, Heene, Asendorpf, and Bühner [20] developed an integrative model of Openness, Gf, and Gc describing the complex interplay between those three traits. Those authors also found that Openness decreased the impact of fluid ability on grades that was used as a proxy for Gc. Unfortunately, no subject-specific analyses were conducted in either study. Moreover, the studies were conducted in a Western culture. Thus, the current study aimed at replicating the effects in a Chinese setting while also differentiating school subjects.

1.5. Aims of the Study

The aim of this study was to document the influences of Gf and the domains of the FFM on scholastic performance in a sample of Chinese secondary school students. Moreover, we extended previous research by focusing on interactive effects. Due to the practical and logistical limitations of a field study, we chose to measure figural reasoning as an indicator of Gf.
On the basis of the literature overview, we will test the following hypotheses:
Hypothesis 1: Effect of figural reasoning as an indicator of Gf on scholastic performance.
Controlling for other variables (FFM, possible interaction with FFM, age, gender), figural reasoning (as an indicator of Gf) is positively related to the performance in all three subjects (Chinese, Math, and English).
Hypothesis 2: Effect of the domains of the FFM.
Controlling for other variables (figural reasoning, possible interaction with figural reasoning, age, gender), the domains of the FFM are related to the performance in the three subjects. We expect a positive effect of Conscientiousness and Openness for all three subjects, of Extraversion for Chinese and English, and a negative effect of Neuroticism for Math and English.
Hypothesis 3: Moderation effects (interaction between figural reasoning and the domains of the FFM).
We expect that Conscientiousness has an enhancing effect and that Openness and Neuroticism have a buffering effect. Conscientiousness will make the effect of figural reasoning on performance stronger. If Openness is high, figural reasoning will not add much, and neither is figural reasoning expected to help when Neuroticism is high.

2. Method

2.1. Sample and Procedure

Students were surveyed at the beginning of their new semester (February 2013). A total of 836 Chinese secondary school students (girls = 406, M = 15.35, SD = 1.31 years) from grades 7 to 11 from five middle and high schools in the Fujian province took part in the study. Participants were offered detailed feedback as an incentive. All the assessments took place during regular class hours. Participants first had to provide some demographic information and then completed a figural reasoning test and a FFM questionnaire within two weeks. Midterm school grades in Math, Chinese, and English were collected from the teachers following the end of the courses three months later.

2.2. Measures

2.2.1. Scholastic Performance

Students’ scholastic performance was based on the test scores from their midterm examinations in Math, Chinese, and English. Grades range from 0, the worst grade, to 150, the very best, with grades lower than 90 indicating insufficient performance. In the Chinese education system, midterm examinations are an important test for school students. All teachers teaching the same subject in the same grade of secondary school (usually three to four teachers) prepare test items according to what their students were supposed to have learned during the first half of the semester. The same teachers later correct and mark the tests. Importantly, the whole process is anonymous, i.e., teachers do not know which student they are grading. The contents that were tested differ across subjects: In Math, greater emphasis is placed on the processing of number information, application of arithmetic rules, and problem solving using arithmetic facts. In China, school textbooks in English are designed to teach grammar, vocabulary, and reading with less emphasis on listening, speaking, and writing. In addition, oral components are not manifested in the examinations at all, but are only part of regular class. In Chinese, teachers emphasize the mastering of grammar and sentence rules, as well as reading comprehension and writing.

2.2.2. Figural Reasoning

Raven’s Standard Progressive Matrices (SPM) [61] were used to assess students’ figural reasoning as an indicator of Gf. This test is a measure of pure nonverbal reasoning ability, which is relatively independent of specific learning acquired in particular cultural or educational contexts [62]. The SPM comprises five sets (A to E) of 12 items each (i.e., A1 to A12) with increasing difficulty across the items within a set. For each item, participants are asked to identify the missing element that completes a matrix from a number of options printed below [59]. The test can be used across a wide age range. In the current study, the reliability estimate for the specified latent variable was McDonald’s Ωw = 0.97 [63,64].

2.2.3. Domains of the FFM

The Chinese version of the NEO-Five-Factor-Inventory (NEO-FFI) is a measure of 60 items assessing Neuroticism, Extraversion, Openness, Agreeableness, and Conscientiousness (12 items per domain). Participants indicate the extent to which they agree or disagree with each item on a five-point scale ranging from 1 (totally disagree) to 5 (totally agree). In the current study, reliability estimates for the specified latent variables (Ωw) were: 0.83 (Neuroticism), 0.81 (Extraversion), 0.67 (Openness), 0.63 (Agreeableness), and 0.82 (Conscientiousness), which is in line with other Chinese studies using the same scales [65,66].

2.3. Statistical Analyses

First, we computed zero-order correlations between all sum scores of the variables involved in this study using R [67]. Second, to test Hypotheses 1 to 3 for each of the three school subjects and for the composite of the three (Grade Composite), structural equation modeling was used. For the interaction hypotheses, an interaction effect was added based on latent moderated structural equations (LMS) as outlined by Klein and Moosbrugger [68], which is more robust compared to ordinary least squares regressions. The latent variables corresponding to the five personality domains and to the three subjects are defined on the basis of item parcels, as will be explained. For the Grade Composite, the grades for Math, English, and Chinese were used as indicators. Third, we have also performed a regression analysis with ordinary least squares with the observed grade scores of the three subjects as dependent variables to double-check the results from the structural equation modeling (SEM) approach. Because the ordinary least squares results are very similar to the SEM results, only the latter will be reported (see Table A in Appendix).
All analyses were conducted in two steps. In step 1, figural reasoning, the FFM domains, age and gender were entered in the model. For the SEM analyses, figural reasoning and the FFM domains were latent variables, and for the ordinary least squares analyses, they were sum scores. In step 2, the interaction terms were added, following the latent moderator approach in case SEM was used. Because this SEM procedure has two steps, we use the term “hierarchical latent regression”. For the ordinary least squares procedure, it is a regular hierarchical regression. This second step was repeated five times, for the interaction of each of the five personality domains with figural reasoning. It has to be noted that there are no regular fit indices available for the models containing latent interaction terms. Thus, these models were compared with the respective preceding model (i.e., the one without the latent interaction term) using a Chi-square difference test (χ2) based on log-likelihood values and scaling correction factors obtained with a robust maximum likelihood estimator (MLR) [69]. In addition, the Bayesian Information Criterion (BIC) was used to compare nested models. All other models were evaluated based on the Comparative Fit Index (CFI), the Standardized Root Mean Square Residual (SRMR), and the Root Mean Square Error of Approximation (RMSEA) with a 90% confidence interval [70,71,72,73,74]. We deemed the fit to be acceptable with cut-offs of CFI ≥ 0.90, RMSEA ≤ 0.08, and SRMR ≤ 0.06 [75]. Models with lower BIC values are expected to be more parsimonious and better-fitting when compared with other nested models [76]. We applied full information maximum likelihood estimation (FIML) to deal with missing values [77]. In addition, a robust estimator was used to deal with violations of the multivariate normal distribution (MLR), along with academic level as a stratification variable to correct for the nested data structure due to different academic levels. Standardized regression coefficients are not provided by Mplus [78] for LMS models. Following the suggestion by Klein and Moosbrugger [68], standardized beta coefficients were obtained by standardizing the data prior to analyses. Finally, for the latent moderation models from step 2, a procedure outlined by Preacher, Curran, and Bauer [79] was used to obtain interaction plots if the moderation effect was significant. Thus, specific values for the (centered) moderator were entered into a regression equation to assess the effect of figural reasoning on school grades at specific conditional values of the moderator (i.e., the mean, 1 SD above and 1 SD below the mean; see [80]).
In order to define latent variables for figural reasoning and the FFM, we first tested measurement models. Each of the latent variables was represented by three parcels [81]. In order to construct the parcels, we conducted a series of single factor analyses for each latent construct except for figural reasoning. When parceling the items for the FFM domains, we allocated each of the three items with the highest loadings to one parcel. The next three highest-loading items were allocated likewise but in a reverse order starting with parcel 3 and so on. Using these three parcels as indicators of a latent variable yields a just-identified model. Such models have zero degrees of freedom and thus, by definition, a perfect model fit: CFI = 1.00, RMSEA = 0.00, SRMR = 0.00. According to Brown [82], such models can still be evaluated in terms of the interpretability and strength of their parameter estimates. As for figural reasoning, three parcels were built representing the three factors underlying the SPM suggested by Lynn, Allik, and Irwing [83]. Our results showed that factor loadings in all measurement models were significant (p < 0.001), ranging from 0.23 to 0.59 1.

3. Results

3.1. Missing Data Analysis

A significant Little’s Missing Completely at Random test, χ2 (144) = 252.60, p < 0. 05, indicated our missing data were not missing completely at random [84]. However, as recommend by Schafer and Graham [85], multiple imputation or FIML are preferable to deal with missing data compared to casewise or listwise deletion with less than 5% missing data, which was the case here. It is also important to note that participants who had missing data did not differ significantly from those who had no missing data along any of the variables under study. Therefore, we decided to use FIML to deal with missing data.

3.2. Correlational Analyses

Descriptive statistics, reliability estimates, and zero-order correlations between all sum scores are reported in Table 1. As can be seen, figural reasoning was most strongly associated with Math and English grades but only had a small correlation with Chinese grades. Regarding the FFM domains, Conscientiousness and Openness displayed significant and small-to-moderate correlations with Math, Chinese, and English grades. Neuroticism was negatively associated with Math grades only, whereas Extraversion was positively associated with Chinese grades only. Gender and age displayed small-to-medium correlations with figural reasoning, personality, and school grades in Math, Chinese, and English.

3.3. Latent Moderated Structural Equation Modeling

Table 2 shows acceptable model fits for all models, and Table 3 shows the estimates for the analyses without and with the moderator effect. Because the moderation was only significant for Openness, only the estimates for the models with a moderator effect of Openness are shown.
Hypothesis 1 was supported in all models. Thus, figural reasoning predicted performance for all grades and for the composite. Hypothesis 2 was confirmed for Openness. Openness had a positive effect on performance for all subjects. For Conscientiousness, the effects were clearly smaller and, at the .05 level, only significant for Math in both steps. For Extraversion, the results do not support the research hypothesis. All estimated effects for this domain are very small and not significant. Finally, Neuroticism had a negative effect on Math performance but not on English performance.
Finally, Hypothesis 3 was confirmed for Openness but not for Conscientiousness and Neuroticism. All interactions with Openness were significant and Figure 1 shows that, as expected, figural reasoning had positive effects if Openness was low but not if it was high. A high degree of Openness is a buffer against lower fluid intelligence as far as was measured through figural reasoning.
Table
Table 1. Descriptive statistics and zero-order correlations between sum scores of all variables studied.
Table 1. Descriptive statistics and zero-order correlations between sum scores of all variables studied.
VariableBivariate CorrelationsDescriptive Statistics
123456789MSD
1. Gender---1.520.50
2. Age0.01---15.351.51
3. Figural reasoning< 0.010.14 **(0.97)46.8512.15
4. Neuroticism0.14 **0.17 **< 0.01(0.83)35.287.76
5. Extraversion0.03−0.12 **0.01−0.37 ***(0.81)42.496.60
6. Openness0.020.10 *0.09 *−0.030.14 **(0.67)41.785.70
7. Agreeableness0.010.10 *−0.010.38 ***−0.16 **−0.07(0.63)29.035.16
8. Conscientiousness0.07 *−0.08 *−0.03−0.41 ***0.16 **0.20 ***−0.30 ***(0.82)38.346.30
9. Math grades−0.060.070.31 ***−0.12 **0.050.21 ***−0.040.13 **---96.4733.10
10. Chinese grades0.23 **−0.13 **0.11 **−0.070.13 **0.18 ***−0.09 *0.14 **0.54 ***---97.5219.19
11. English grades0.13 **0.14 **0.31 ***−0.030.060.28 ***−0.010.11 *0.67 ***0.61 ***---98.0732.56
Note: N = 686 to 836. Reliability estimates for each variable (Ωw) are in parentheses on the diagonal. Gender: 1 = men and 2 = women. * p < 0.05. ** p < 0.01. *** p < 0.001. All p-values are two-tailed.
Table
Table 2. Model fits.
Table 2. Model fits.
School SubjectModelχ2 (df)RMSEA [90% CI]CFISRMRBICChi-square Difference Test (TRd)
Grade CompositeStep 1817.32 (208)0.059 [0.055,0 .063]0.9200.05740731.53
Step 2------------40706.37∆ χ2 (df) = 9.69 (1), p < 0.001
ChineseStep 1614.72 (168)0.056 [0.052, 0.061]0.9330.05427303.51
Step 2------------27289.58∆ χ2 (df) = 6.27 (1), p < 0.05
MathStep 1632.28 (168)0.057 [0.053, 0.062]0.9310.05528100.34
Step 2------------28085.67∆ χ2 (df) = 11.87 (1), p < 0.001
EnglishStep 1638.98 (168)0.058 [0.053, 0.063]0.9300.05528055.25
Step 2------------28041.59∆ χ2 (df) = 11.03 (1), p < 0.001
Note: N = 836. The model showing the best fit in each school subject is in bold. Because traditional model fit indices are not developed for latent moderation structural (LMS) models, we used a Chi-square difference test based on log-likelihood values and scaling correction factors obtained by a robust maximum likelihood estimator (MLR) to compare the relative fit of Step 1 and Step 2: Satorra-Bentler scaled chi-square difference test (TRd) = −2 * (L0–L1)/[(p0 * c0–p1 * c1)/(p0–p1)] where L0 and L1 are the log-likelihood values for Step 1 and Step 2, respectively, as well as scaling correction factors c0 and c1 for Step 1 and Step 2, respectively. p0 and p1 are the number of parameters in Step 1 and Step 2, respectively.
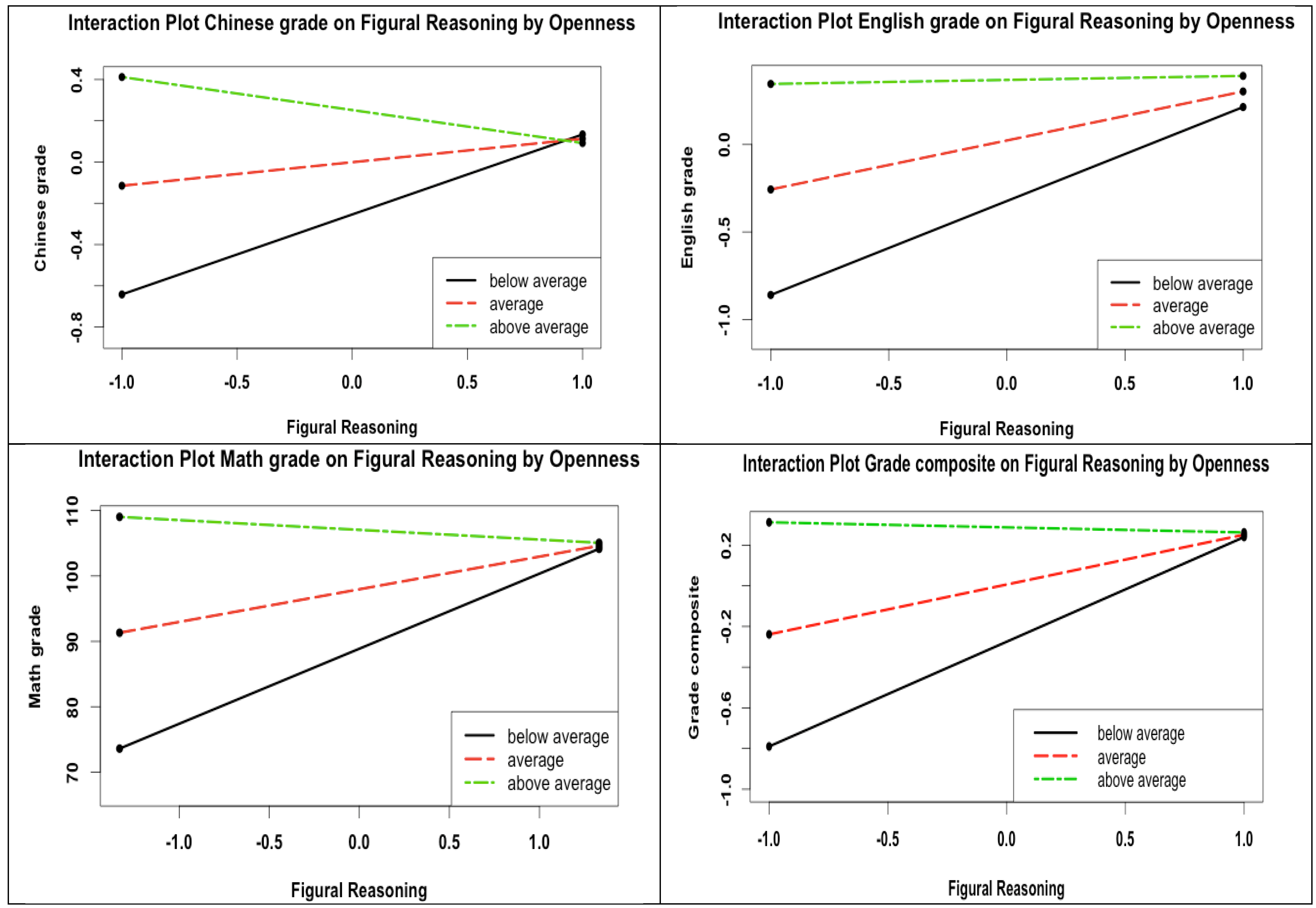
Jintelligence 03 00091 g001 1024
Figure 1. Interaction plots for the moderating effect of Openness on the correlation between figural reasoning and school grades in Chinese, Math, English, and a grade composite.
Figure 1. Interaction plots for the moderating effect of Openness on the correlation between figural reasoning and school grades in Chinese, Math, English, and a grade composite.
Jintelligence 03 00091 g001
Table
Table 3. Prediction of scholastic performance in Chinese, Math, and English: results from hierarchical latent regression models.
Table 3. Prediction of scholastic performance in Chinese, Math, and English: results from hierarchical latent regression models.
Enter VariablesChinese GradeMath GradeEnglish GradeGrade Composite
ßR2ΔR2ßR2ΔR2ßR2ΔR2ßR2ΔR2
Step 10.15 ***0.05 *0.17 ***0.08 **0.21 ***0.10 ***0.25 ***0.12 ***
Gender0.23 ***−0.050.13 ***0.13 **
Age−0.14 **0.040.10 **0.06
Figural reasoning0.12 **0.29 ***0.26 ***0.29 ***
Neuroticism−0.03−0.12 *−0.08−0.09
Extraversion0.04−0.02−0.02−0.01
Openness0.19 ***0.23 ***0.31 ***0.33 ***
Agreeableness−0.020.110.090.09
Conscientiousness0.050.12 *0.070.09 *
Step 20.22 ***0.07 **0.24 ***0.07 **0.25 ***0.04 *0.36 ***0.11 ***
Gender0.22 ***−0.050.13 ***0.09 **
Age−0.15 ***0.010.09 *0.02
Figural reasoning0.12 **0.31 ***0.28 ***0.25 ***
Neuroticism−0.04−0.13 *−0.08−0.08 #
Extraversion0.03−0.03−0.03−0.02
Openness0.25 ***0.28 ***0.35 ***0.28 ***
Agreeableness0.010.14 *0.11 #0.09 #
Conscientiousness0.060.13 *0.08 #0.08 #
Figural reasoning *Openness−0.27 ***−0.28 ***−0.26 ***−0.27 ***
* p < 0.05; ** p < 0.01; *** p < 0.001; # p < 0.10. All p-values are two-tailed.

4. Discussion

This study aimed at evaluating the specific contributions of figural reasoning as an indicator of Gf, the domains of the FFM, and their interaction in predicting scholastic performance in Chinese secondary school students. Generally speaking, our findings replicated the specific effects for Gf and some of the personality domains on scholastic performance found in Western cultures in an Eastern culture. In addition, our findings further supported the idea that Gf and Openness interacted with each other in predicting scholastic performance across three subjects.

4.1. Fluid Intelligence

Although the positive relationship with all grades turned out to be clearly positive for all subjects, the effect was smaller for Chinese. This smaller effect is in line with earlier results [29,30] and may be due to how students learn Chinese in comparison with other subjects. Because the other subjects are new (Math, English) they may require more Gf than is the case for the native language. Mathematics requires the students to solve new and difficult problems, and English places heavy demands on learning a new grammar and a new vocabulary. In contrast, people learn their native language through everyday interactions and what they have to learn has a higher degree of familiarity. This may explain why there is less variation in proficiency for Chinese than for Math and English (see Table 1). On the whole, the total amount of variance explained by figural reasoning as an indicator of Gf in school grades, especially in Chinese (native language), was smaller than reported in Western cultures [10,35]. We attribute this difference mainly to Chinese culture. Adopting Confucian doctrines, Chinese parents and teachers might encourage their children and students to compensate for limitations in abilities with Conscientiousness and hard work [17]. Thus, such cultural differences might produce mean level differences and also influence the relative importance of variables in predicting scholastic performance [8]. Another explanation could be that within the field of intelligence research, very elaborate models have been developed, including different intelligence facets: verbal, numerical, and figural reasoning abilities [87]. According to Brunswik’s lens model [88], symmetry between predictor and criterion could increase correlations (see also [49,89]). Future studies should therefore strive to apply broad measures of Gf in Chinese contexts. In fact, another study conducted in China found stronger test criterion correlations for Gf [8] using a broader cognitive test battery in a sample of elementary school students.

4.2. Domains of the FFM

In line with prior research [12], Openness was found to be a significant and positive predictor for performance in all three subjects. Further, Conscientiousness was a positive predictor and Neuroticism a negative predictor of performance in Math. Conscientious students are more likely to perform well academically because they are more likely to be achievement-oriented, organized, responsible, and willing to work hard. Our findings that Neuroticism is a negative predictor are consistent with Spinath, Freudenthaler, and Neubauer [9], who suggested that the negative effect of Neuroticism on Math grades might be due to anxiety. Mathematics is associated with challenges, exam stress, and problem solving, all of which might spark anxiety, leading to a decrease in performance.

4.3. Moderation

The results support the interaction hypothesis for Openness and Gf. Specifically, the effect each of the traits is smaller the higher the score of the other is. Though the moderation found here was reported before [20], no conclusive explanation was provided. Now that the moderation has been replicated in an independent sample and a different culture, concrete hypotheses regarding the nature of the mechanism at work are justified. Formally speaking, the negative interaction between Openness and figural reasoning can be interpreted as a disjunctive or compensatory relationship: one of both traits is sufficient to perform well, so the fact that the other trait does not add to the variance explained when one trait is already high. This means that students high in Gf are able to handle school tasks even when they are not curious or seeking new knowledge. Similarly, students high in Openness may not need strong fluid intelligence because they are curious about different fields, actively grasping new ideas and seeking novel experiences. Another possible explanation is that a high intelligence combined with a high openness is not necessarily beneficial in a school context. A high intelligence combined with lots of imagination and curiosity might lead to distraction and low interest in the contents taught in schools. For a student with lower intelligence and a high openness the contents may satisfy the high level of curiosity, and for a student with a high intelligence and a low level of openness the school contents would be sufficient as a challenge. Future research could apply experimental methods or experience sampling to gather more data to help test these different ideas.
However, our results failed to support the enhancing effect of Conscientiousness, so the results of Ziegler, Knogler, and Bühner [60] could not be confirmed. Whereas the present study only employed short tests, Ziegler, Knogler, and Bühner [60] used a faceted intelligence measure and a broad personality questionnaire. Thus, future studies trying to replicate this specific interaction in a Chinese context should also employ such broad measures. The same argument holds regarding the other interaction effects which were insignificant in this study.

4.4. Limitations of the Current Study

The use of a short personality inventory and a figural reasoning test as an indicator of Gf limits the findings to the tests used. Broader and, most importantly, faceted measures are needed to provide a more comprehensive answer to the research questions posed above. Second, our findings rely on self-reported data. Prior research has shown that other reports are incremental predictors of academic performance above and beyond intelligence [49] and self-reports [90]. The sole reliance on self-reports should be opened up in future studies by using other reports as well. Finally, using grades as dependent variables might be considered a limitation. Despite the importance of grades in students’ lives, aspects other than actual performance differences affect grades, which therefore can be considered contaminated [91,92]. Using more objective criteria like standardized assessments will most likely increase the predictive power of ability.

5. Conclusions

The current study confirmed the influences of Gf-type test performance and the FFM domains on scholastic performance within the Chinese culture. In general, a higher Gf leads to better scholastic performance. However, it does not follow that intelligence is the only determinant of scholastic performance. Clearly, personality traits, particularly Openness, can be used along with Gf to better predict scholastic performance. Moreover, this study also emphasizes the importance of considering specific subjects when predicting scholastic performance (i.e., Chinese, English, and Math). More importantly, this study further indicated that Openness moderated the effects of Gf on scholastic performance in three subjects. Chinese teachers and parents may want to stimulate the students’ Openness because of its positive contribution to scholastic achievement, especially when fluid intelligence is not so high.

Acknowledgments

We acknowledge the financial support of Humboldt-Universität zu Berlin and China Scholarship Council (Study Number: 201206140015). We also thank the school principals, teachers and students whose support made this study possible.

Author Contributions

Jing Zhang collected the data, conducted the analyses and wrote most of the manuscript. Matthias Ziegler contributed to the analysis framework, revised and reworked the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix

Table
Table A. Prediction of scholastic performance in Chinese, Math, and English: results from hierarchical regression analyses.
Table A. Prediction of scholastic performance in Chinese, Math, and English: results from hierarchical regression analyses.
Enter VariablesChinese GradeMath GradeEnglish Grade
ßR2ΔR2ßR2ΔR2ßR2ΔR2
Step 10.15 ***0.16 ***0.18 ***
Gender0.20 ***−0.050.14 ***
Age−0.21 ***−0.020.06 #
Figural reasoning0.14 **0.31 ***0.28 ***
Neuroticism−0.01−0.06−0.02
Extraversion0.050.01−0.01
Openness0.15 ***0.16 ***0.23 ***
Agreeableness−0.050.030.03
Conscientiousness0.07 #0.11 **0.08 *
Step 20.17 ***0.02 *0.18 ***0.02 *0.20 ***0.02 *
Gender0.20 ***−0.050.14 ***
Age−0.22 ***−0.020.05
Figural reasoning0.12 **0.29 ***0.27 ***
Neuroticism−0.01−0.06−0.03
Extraversion0.050.01−0.01
Openness0.16 ***0.17 ***0.23 ***
Agreeableness−0.050.030.03
Conscientiousness0.08 #0.12 **0.09 *
Figural reasoning * Openness−.016 ***−0.17 ***−0.16 ***
* p < 0.05; ** p < 0.01; *** p < 0.001; # p < 0.10. All p-values are two-tailed.

References

  1. Ceci, S.J.; Williams, W.M. Schooling, intelligence, and income. Am. Psychol. 1997, 52, 1051–1058. [Google Scholar] [CrossRef]
  2. Deary, I.J.; Strand, S.; Smith, P.; Fernandes, C. Intelligence and educational achievement. Intelligence 2007, 35, 13–21. [Google Scholar] [CrossRef]
  3. Gottfredson, L.S. g: Highly general and highly practical. In The General Factor of Intelligence: How General is it; Erlbaum: Mahwah, NJ, USA, 2002; pp. 331–380. [Google Scholar]
  4. Kuncel, N.R.; Hezlett, S.A.; Ones, D.S. Academic performance, career potential, creativity, and job performance: Can one construct predict them all? J. Personal. Soc. Psychol. 2004, 86, 148–161. [Google Scholar] [CrossRef] [PubMed]
  5. Bratko, D.; Chamorro-Premuzic, T.; Saks, Z. Personality and school performance: Incremental validity of self-and peer-ratings over intelligence. Personal. Individ. Differ. 2006, 41, 131–142. [Google Scholar] [CrossRef]
  6. Greene, B.A.; Miller, R.B.; Crowson, H.M.; Duke, B.L.; Akey, K.L. Predicting high school students’ cognitive engagement and achievement: Contributions of classroom perceptions and motivation. Contemp. Educ. Psychol. 2004, 29, 462–482. [Google Scholar] [CrossRef]
  7. Laidra, K.; Pullmann, H.; Allik, J. Personality and intelligence as predictors of academic achievement: A cross-sectional study from elementary to secondary school. Personal. Individ. Differ. 2007, 42, 441–451. [Google Scholar] [CrossRef]
  8. Lu, L.; Weber, H.S.; Spinath, F.M.; Shi, J. Predicting school achievement from cognitive and non-cognitive variables in a Chinese sample of elementary school children. Intelligence 2011, 39, 130–140. [Google Scholar] [CrossRef]
  9. Spinath, B.; Harald Freudenthaler, H.; Neubauer, A.C. Domain-specific school achievement in boys and girls as predicted by intelligence, personality and motivation. Personal. Individ. Differ. 2010, 48, 481–486. [Google Scholar] [CrossRef]
  10. Spinath, B.; Spinath, F.M.; Harlaar, N.; Plomin, R. Predicting school achievement from general cognitive ability, self-perceived ability, and intrinsic value. Intelligence 2006, 34, 363–374. [Google Scholar] [CrossRef]
  11. Steinmayr, R.; Bipp, T.; Spinath, B. Goal orientations predict academic performance beyond intelligence and personality. Learn. Individ. Differ. 2011, 21, 196–200. [Google Scholar] [CrossRef]
  12. Poropat, A.E. A meta-analysis of the five-factor model of personality and academic performance. Psychol. Bull. 2009, 135, 322–328. [Google Scholar] [CrossRef] [PubMed]
  13. Richardson, M.; Abraham, C.; Bond, R. Psychological correlates of university students’ academic performance: A systematic review and meta-analysis. Psychol. Bull. 2012, 138, 363–387. [Google Scholar] [CrossRef] [PubMed]
  14. Ackerman, P.L.; Heggestad, E.D. Intelligence, personality, and interests: Evidence for overlapping traits. Psychol. Bull. 1997, 121, 219–245. [Google Scholar] [CrossRef] [PubMed]
  15. Dweck, C.; Molden, D.C. Self-Theories. In Handbook of Competence and Motivation; The Guilford Press: New York, NY, USA, 2005; pp. 122–140. [Google Scholar]
  16. Tong, N.; Zhao, R.; Yang, X. An investigation into the current ideology of middle school students. Chin. Educ. 1985, 17, 6–21. [Google Scholar]
  17. Tweed, R.G.; Lehman, D.R. Learning considered within a cultural context: Confucian and Socratic approaches. Am. Psychol. 2002, 57, 89–99. [Google Scholar] [CrossRef] [PubMed]
  18. Furnham, A.; Monsen, J. Personality traits and intelligence predict academic school grades. Learn. Individ. Differ. 2009, 19, 28–33. [Google Scholar] [CrossRef]
  19. Ziegler, M.; Cengia, A.; Mussel, P.; Gerstorf, D. Openness as a Buffer Against Cognitive Decline: The Openness-Fluid-Crystallized-Intelligence (OFCI) Model Applied to Late Adulthood. Psychol. Aging 2015, 30, 573–588. [Google Scholar] [CrossRef] [PubMed]
  20. Ziegler, M.; Danay, E.; Heene, M.; Asendorpf, J.; Bühner, M. Openness, fluid intelligence, and crystallized intelligence: Toward an integrative model. J. Res. Personal. 2012, 46, 173–183. [Google Scholar] [CrossRef]
  21. Cattell, R.B. Theory of fluid and crystallized intelligence: A critical experiment. J. Educ. Psychol. 1963, 54, 1–22. [Google Scholar] [CrossRef]
  22. Cattell, R.B. Intelligence: Its Structure, Growth and Action; North-Holland: Oxford, UK, 1987. [Google Scholar]
  23. McGrew, K.S. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 2009, 37, 1–10. [Google Scholar] [CrossRef]
  24. Primi, R.; Ferrão, M.E.; Almeida, L.S. Fluid intelligence as a predictor of learning: A longitudinal multilevel approach applied to math. Learn. Individ. Differ. 2010, 20, 446–451. [Google Scholar] [CrossRef]
  25. Ackerman, P.L.; Beier, M.E.; Boyle, M.D. Individual differences in working memory within a nomological network of cognitive and perceptual speed abilities. J. Exp. Psychol. Gen. 2002, 131, 567–589. [Google Scholar] [CrossRef] [PubMed]
  26. Blair, C. How similar are fluid cognition and general intelligence? A developmental neuroscience perspective on fluid cognition as an aspect of human cognitive ability. Behav. Brain Sci. 2006, 29, 109–160. [Google Scholar] [CrossRef] [PubMed]
  27. Colom, R.; Garcıa-López, O. Sex differences in fluid intelligence among high school graduates. Personal. Individ. Differ. 2002, 32, 445–451. [Google Scholar] [CrossRef]
  28. Furnham, A.; Forde, L.; Cotter, T. Personality and intelligence. Personal. Individ. Differ. 1998, 24, 187–192. [Google Scholar] [CrossRef]
  29. McGrew, K.S. CHC COG-ACH Correlates Meta-Analysis; Institute for Applied Psychometrics: Minneapolis, MN, USA, 2008. [Google Scholar]
  30. Taub, G.E.; Floyd, R.G.; Keith, T.Z.; McGrew, T.Z. Effects of general and broad cognitive abilities on mathematics achievement. Sch. Psychol. Quart. 2008, 23, 187–198. [Google Scholar] [CrossRef]
  31. Chamorro-Premuzic, T.; Furnham, A. Intellectual competence and the intelligent personality: A third way in differential psychology. Rev. Gen. Psychol. 2006, 10, 251–267. [Google Scholar] [CrossRef]
  32. Chamorro-Premuzic, T.; Furnham, A. Personality, intelligence and approaches to learning as predictors of academic performance. Personal. Individ. Differ. 2008, 44, 1596–1603. [Google Scholar] [CrossRef]
  33. Di Fabio, A.; Busoni, L. Fluid intelligence, personality traits and scholastic success: Empirical evidence in a sample of Italian high school students. Personal. Individ. Differ. 2007, 43, 2095–2104. [Google Scholar] [CrossRef]
  34. Furnham, A.; Chamorro-Premuzic, T. Personality and intelligence as predictors of statistics examination grades. Personal. Individ. Differ. 2004, 37, 943–955. [Google Scholar] [CrossRef]
  35. Heaven, P.C.; Ciarrochi, J. When IQ is not everything: Intelligence, personality and academic performance at school. Personal. Individ. Differ. 2012, 53, 518–522. [Google Scholar] [CrossRef]
  36. Noftle, E.E.; Robins, R.W. Personality predictors of academic outcomes: Big five correlates of GPA and SAT scores. J. Personal. Soc. Psychol. 2007, 93, 116–130. [Google Scholar] [CrossRef] [PubMed]
  37. De Raad, B.; Schouwenburg, H.C. Personality in learning and education: A review. Eur. J. Personal. 1996, 10, 303–336. [Google Scholar] [CrossRef]
  38. O’Connor, M.C.; Paunonen, S.V. Big Five personality predictors of post-secondary academic performance. Personal. Individ. Differ. 2007, 43, 971–990. [Google Scholar] [CrossRef]
  39. Digman, J.M. Personality structure: Emergence of the five-factor model. Annu. Rev. Psychol. 1990, 41, 417–440. [Google Scholar] [CrossRef]
  40. Barrick, M.R.; Mount, M.K. FFM personality dimensions and job performance: A meta-analysis. Pers. Psychol. 1991, 44, 1–26. [Google Scholar] [CrossRef]
  41. Steinmayr, R.; Spinath, B. Sex differences in school achievement: What are the roles of personality and achievement motivation? Eur. J. Personal. 2008, 22, 185–209. [Google Scholar] [CrossRef]
  42. Major, D.A.; Turner, J.E.; Fletcher, T.D. Linking proactive personality and FFM to motivation to learn and development activity. J. Appl. Psychol. 2006, 91, 927–935. [Google Scholar] [CrossRef] [PubMed]
  43. De Feyter, T.; Caers, R.; Vigna, C.; Berings, D. Unraveling the impact of FFM personality traits on academic performance: The moderating and mediating effects of self-efficacy and academic motivation. Learn. Individ. Differ. 2012, 22, 439–448. [Google Scholar] [CrossRef]
  44. Komarraju, M.; Karau, S.J.; Schmeck, R.R. Role of FFM personality traits in predicting college students’ academic motivation and achievement. Learn. Individ. Differ. 2009, 19, 47–52. [Google Scholar] [CrossRef]
  45. Martin, J.H.; Montgomery, R.L.; Saphian, D. Personality, achievement test scores, and high school percentile as predictors of academic performance across four years of coursework. J. Res. Personal. 2006, 40, 424–431. [Google Scholar] [CrossRef]
  46. Nguyen, N.T.; Allen, L.C.; Fraccastoro, K. Personality predicts academic performance: Exploring the moderating role of gender. J. High. Educ. Policy Manag. 2005, 27, 105–117. [Google Scholar] [CrossRef]
  47. Hogan, R.; Hogan, J. Hogan Personality Inventory Manual, 2nd ed.; Hogan Assessment Systems: Tulsa, OK, USA, 1995. [Google Scholar]
  48. Ziegler, M.; Bensch, D.; Maaß, U.; Schult, V.; Vogel, M.; Bühner, M. Big Five facets as predictor of job training performance: The role of specific job demands. Learn. Individ. Differ. 2014, 29, 1–7. [Google Scholar] [CrossRef]
  49. Ziegler, M.; Danay, E.; Schölmerich, F.; Bühner, M. Predicting academic success with the Big 5 rated from different points of view: Self-rated, other rated and faked. Eur. J. Personal. 2010, 24, 341–355. [Google Scholar] [CrossRef]
  50. Chamorro-Premuzic, T.; Von Stumm, S.; Furnham, A. (Eds.) The Wiley-Blackwell Handbook of Individual Differences; John Wiley & Sons: Hoboken, NJ, USA, 2015; Volume 3.
  51. Heider, F. The Psychology of Interpersonal Relations; Wiley: New York, NY, USA, 1958. [Google Scholar]
  52. Blumberg, M.; Pringle, C.D. The missing opportunity in organizational research: Some implications for a theory of work performance. Acad. Manag. Rev. 1982, 7, 560–569. [Google Scholar]
  53. Traag, T.; van der Valk, J.; van der Velden, R.; de Vries, R.; Wolbers, M.H.J. Why does education matter? Explaining the effect of the highest level of education attained by school leavers on their labor market position. Pedagog. Stud. 2005, 82, 453–469. [Google Scholar]
  54. Zeidner, M. Personality trait correlates of intelligence. In International Handbook of Personality and Intelligence; Saklofske, D.H., Zeidner, M., Eds.; Plenum Press: New York, NY, USA, 1995. [Google Scholar]
  55. Campbell, J.P. Psychometric theory. In Handbook of Industrial and Organizational Psychology; Dunnette, M.D., Ed.; Rand McNally: Chicago, IL, USA, 1976. [Google Scholar]
  56. Maier, N.R.F. Psychology in Industry; Houghton-Mifflin: Boston, MA, USA, 1958. [Google Scholar]
  57. Mount, M.K.; Barrick, M.R.; Strauss, J.P. The joint relationship of conscientiousness and ability with performance: Test of the interaction hypothesis. J. Manag. 1999, 25, 707–721. [Google Scholar] [CrossRef]
  58. Sackett, P.R.; Gruys, M.L.; Ellingson, J.E. Ability-personality interactions when predicting job performance. J. Appl. Psychol. 1998, 83, 545–556. [Google Scholar] [CrossRef]
  59. Denissen, J.J.A.; Penke, L. Motivational individual reaction norms underlying the Five-Factor model of personality: First steps towards a theory-based conceptual framework. J. Res. Personal. 2008, 42, 1285–1302. [Google Scholar] [CrossRef]
  60. Ziegler, M.; Knogler, M.; Bühner, M. Conscientiousness, Achievement Striving, and Intelligence as Performance Predictors in a Sample of German Psychology Students: Always a Linear Relationship? Learn. Individ. Differ. 2009, 19, 288–292. [Google Scholar] [CrossRef]
  61. Raven, J. Manual for Raven’s Progressive Matrices and Mill Hill Vocabulary Scales; Oxford Psychologists Press: Oxford, UK, 1981. [Google Scholar]
  62. Jensen, A.R. The g Factor: The Science of Mental Ability; Praeger: New York, NY, USA, 1998. [Google Scholar]
  63. Revelle, W.; Zinbarg, R.E. Coefficients alpha, beta, omega, and the glb: Comments on Sijtsma. Psychometrika 2009, 74, 145–154. [Google Scholar] [CrossRef]
  64. Zinbarg, R.E.; Revelle, W.; Yovel, I.; Li, W. Cronbach’s α, Revelle’s β, and McDonald’s ω H: Their relations with each other and two alternative conceptualizations of reliability. Psychometrika 2005, 70, 123–133. [Google Scholar] [CrossRef]
  65. Yao, R.S.; Liang, L.Y. Analysis of the application of simplified NEO-FFI to undergraduates. Chin. J. Clin. Psychol. 2010, 18, 457–459. [Google Scholar]
  66. Yangang, N.; Boxing, L.; Junqian, L. A Study on the Relationship of Adolescents’ Big Five Personality and Coping Style With Traits of Mental Crises. Psychol. Sci. 2010, 3, 055. [Google Scholar]
  67. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012. [Google Scholar]
  68. Klein, A.; Moosbrugger, H. Maximum likelihood estimation of latent interaction effects with the LMS method. Psychometrika 2000, 65, 457–474. [Google Scholar] [CrossRef]
  69. Satorra, A.; Bentler, P.M. A scaled difference chi-square test statistic for moment structure analysis. Psychometrika 2001, 66, 507–514. [Google Scholar] [CrossRef]
  70. Beauducel, A.; Wittmann, W.W. Simulation study on fit indexes in CFA based on data with slightly distorted simple structure. Struct. Equ. Model. 2005, 12, 41–75. [Google Scholar] [CrossRef]
  71. Hu, L.T.; Bentler, P.M. Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychol. Methods 1998, 3, 424–453. [Google Scholar] [CrossRef]
  72. Hu, L.T.; Bentler, P.M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Model. Multidiscip. J. 1999, 6, 1–55. [Google Scholar] [CrossRef]
  73. Marsh, H.W.; Hau, K.T.; Grayson, D. Goodness of fit in structural equation models. In Contemporary Psychometrics: A Festschrift for Roderick P. McDonald; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2005. [Google Scholar]
  74. Maydeu-Olivares, A.; McArdle, J.J. (Eds.) Contemporary Psychometrics; Psychology Press: East Sussex, UK, 2005.
  75. Heene, M.; Hilbert, S.; Draxler, C.; Ziegler, M.; Bühner, M. Masking misfit in confirmatory factor analysis by increasing unique variances: A cautionary note on the usefulness of cutoff values of fit indices. Psychol. Methods 2011, 16, 319–336. [Google Scholar] [CrossRef] [PubMed]
  76. Kline, R.B. Principles and Practice of Structural Equation Modelingc, 3rd ed.; The Guilford Press: New York, NY, USA, 2011. [Google Scholar]
  77. Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Values; Wiley: New York, NY, USA, 2002. [Google Scholar]
  78. Muthén, L.K.; Muthén, B.O. Mplus User’s Guide, 7th ed.; Muthen & Muthen: Los Angeles, CA, USA, 1998–2012. [Google Scholar]
  79. Preacher, K.J.; Curran, P.J.; Bauer, D.J. Computational tools for probing interactions in multiple linear regression, multilevel modeling, and latent curve analysis. J. Educ. Behav. Stat. 2006, 31, 437–448. [Google Scholar] [CrossRef]
  80. Preacher, K.J.; Curran, P.J.; Bauer, D.J. Simple Intercepts, Simple Slopes, and Regions of Significance in MLR 2-Way Interactions. Available online: http://quantpsy.org/interact/mlr2.htm (accessed on 2 July 2015).
  81. Little, T.D.; Rhemtulla, M.; Gibson, K.; Schoemann, A.M. Why the items versus parcels controversy needn’t be one. Psychol. Methods 2013, 18, 285–300. [Google Scholar] [CrossRef] [PubMed]
  82. Brown, T.A. Confirmatory Factor Analysis for Applied Research; The Guilford Press: New York, NY, USA, 2006. [Google Scholar]
  83. Lynn, R.; Allik, J.; Irwing, P. Sex differences on three factors identified in Raven’s Standard Progressive Matrices. Intelligence 2004, 32, 411–424. [Google Scholar] [CrossRef]
  84. Schafer, J.L.; Graham, J.W. Missing data: Our view of the state of the art. Psychol. Methods 2002, 7, 147–177. [Google Scholar] [CrossRef] [PubMed]
  85. Schafer, J.L.; Graham, J.W. Missing data: Our view of the state of the art. Psychol. Methods 2002, 7, 147–177. [Google Scholar] [CrossRef] [PubMed]
  86. Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics; Allyn and Bacon: Needham Heights, MA, USA, 2001. [Google Scholar]
  87. Beauducel, A.; Brocke, B.; Liepmann, D. Perspectives on fluid and crystallized intelligence: Facets for verbal, numerical, and figural intelligence. Personal. Individ. Differ. 2001, 30, 977–994. [Google Scholar] [CrossRef]
  88. Wittmann, W.W.; Süß, H.M. Investigating the Paths between Working Memory, Intelligence, Knowledge, and Complex Problem-Solving Performances via Brunswik Symmetry; American Psychological Association: Washington, DC, USA, 1999. [Google Scholar]
  89. Ziegler, M.; Dietl, E.; Danay, E.; Vogel, M.; Bühner, M. Predicting Training Success with General Mental Ability, Specific Ability Tests, and (Un) Structured Interviews: A meta analysis with unique samples. Int. J. Sel. Assess. 2011, 19, 170–182. [Google Scholar] [CrossRef]
  90. Poropat, A.E. Other-rated personality and academic performance: Evidence and implications. Learn. Individ. Differ. 2014, 34, 24–32. [Google Scholar] [CrossRef]
  91. Brogden, H.E.; Taylor, E.K. The theory and classification of criterion bias. Educ. Psychol. Meas. 1950, 10, 159–183. [Google Scholar] [CrossRef]
  92. Ziegler, M.; Brunner, M. Test Standards and Psychometric Modeling. In Psychosocial Skills and School Systems in the Twenty-First Century: Theory, Research, and Applications; Lipnevich, A.A., Preckel, F., Roberts, R., Eds.; Springer: Göttingen, Germany, in press.
  • 1In order to decide whether an item parcel loaded appropriately on its respective factor, we used a cut-off of 0.40 for standardized factor loadings [86]. In our study, most of the standardized factor loadings were close to or larger than 0.40, except for some indicators of Openness and Agreeableness that were slightly lower than 0.40.

Share and Cite

MDPI and ACS Style

Zhang, J.; Ziegler, M. Interaction Effects between Openness and Fluid Intelligence Predicting Scholastic Performance. J. Intell. 2015, 3, 91-110. https://doi.org/10.3390/jintelligence3030091

AMA Style

Zhang J, Ziegler M. Interaction Effects between Openness and Fluid Intelligence Predicting Scholastic Performance. Journal of Intelligence. 2015; 3(3):91-110. https://doi.org/10.3390/jintelligence3030091

Chicago/Turabian Style

Zhang, Jing, and Matthias Ziegler. 2015. "Interaction Effects between Openness and Fluid Intelligence Predicting Scholastic Performance" Journal of Intelligence 3, no. 3: 91-110. https://doi.org/10.3390/jintelligence3030091

Article Metrics

Back to TopTop