Large-Scale Item-Level Analysis of the Figural Matrices Test in the Norwegian Armed Forces: Examining Measurement Precision and Sex Bias
Abstract
1. Introduction
1.1. General Mental Ability Testing
1.2. Sex Differences in Non-Verbal Fluid Intelligence
1.3. The Present Study
2. Materials and Methods
2.1. Sample
2.2. Test Administration Procedure
2.3. Measures and Data Management
2.4. Statistical Analysis
- Step 1:
- (a)
- We estimate the constrained baseline model (all item parameters set equal between groups, but the mean and variance of the latent variable were freely estimated in one group).
- (b)
- For each item, we removed the equality restriction for the item parameters between the groups and estimated the model. If there was a statistically significant difference to the constrained baseline model, we flagged that item as an item with a potential violation of measurement invariance.
- (c)
- For the items that did not show statistically significant differences, we ranked the items from the item with the highest estimated discrimination parameter to the item with the lowest estimated discrimination parameter, based on the results from the constrained baseline model. The five items with the highest estimated factor loadings were selected as anchor items.
- Step 2:
- (d)
- We estimated the free baseline model, in which the five items from Step 1 (c) were constrained to be equal between the groups, while the remaining items were allowed to vary.
- (e)
- For each item, we removed the equality restriction for the item parameters between the groups and estimated the model. If there was a statistically significant difference to the constrained baseline model, we flagged that item as an item with potential violation of measurement invariance.
- (f)
- We obtained a model with items that were considered invariant, where j is the number of items identified in Step 2 (e).
3. Results
3.1. Item Response Modeling
3.1.1. Configural Invariance
3.1.2. Partial Invariance
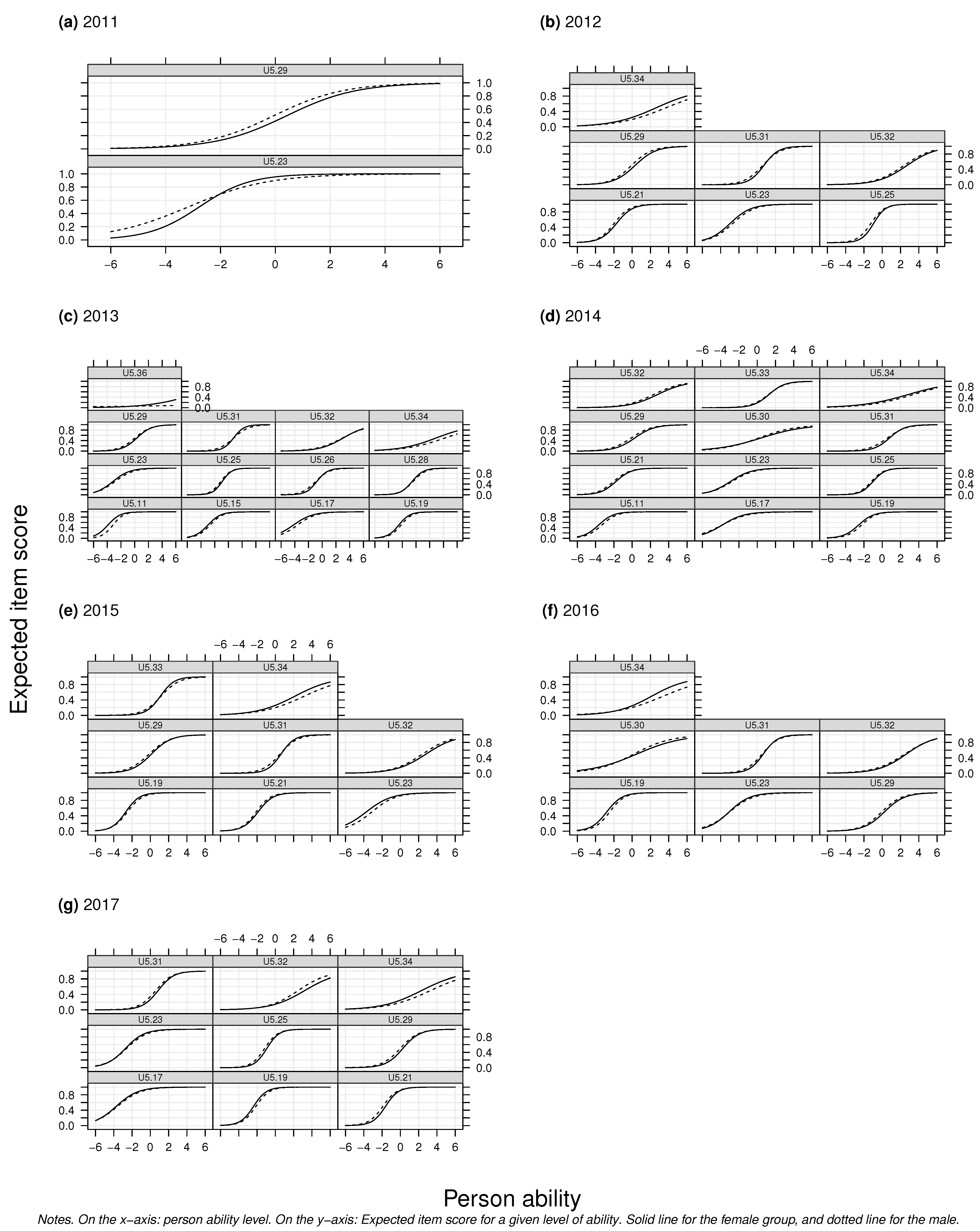
3.1.3. Information Curves and Expected Score Functions
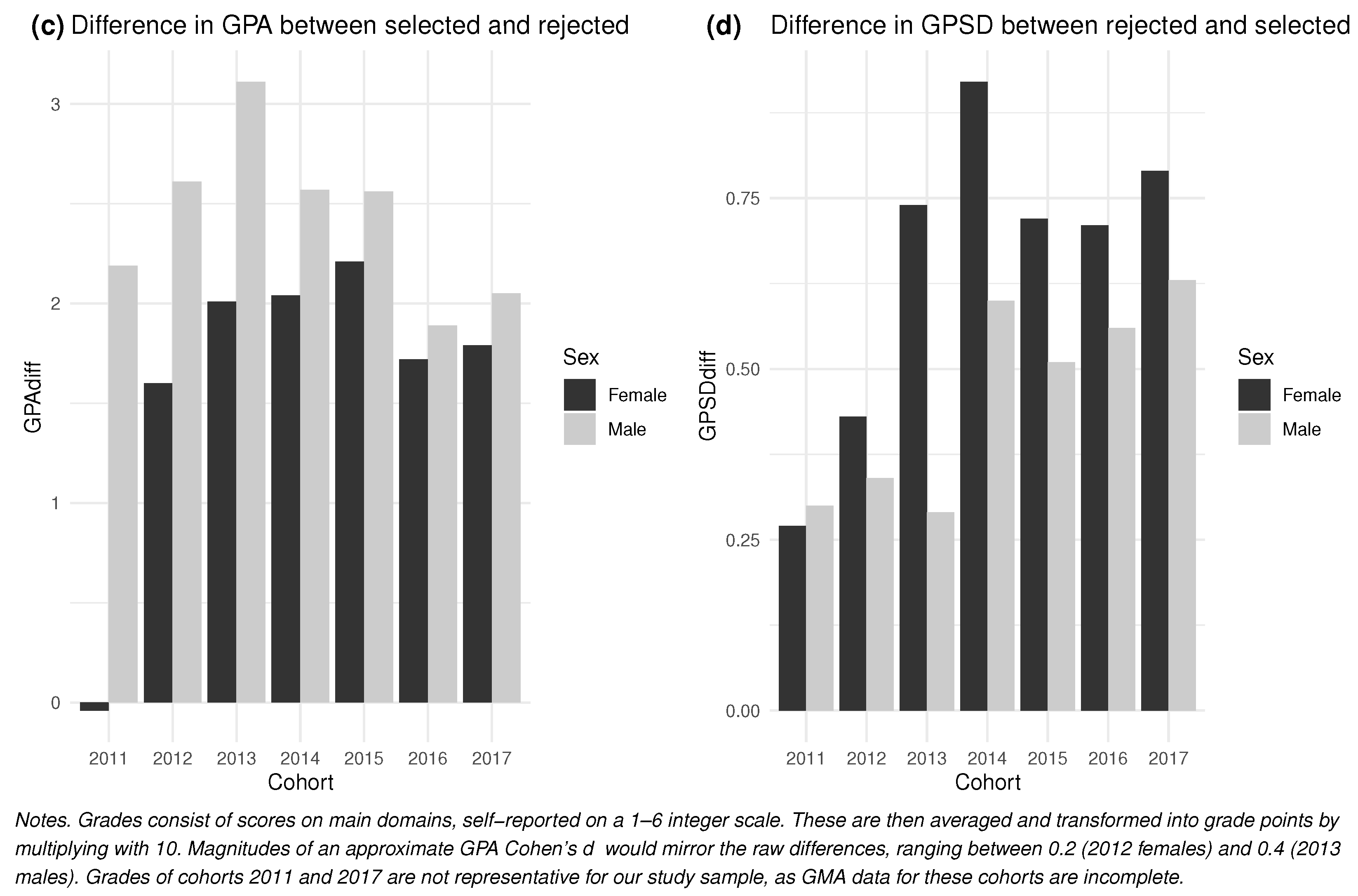
3.2. Consequences of Invariance
4. Discussion
4.1. General Measurement Properties of the Figural Matrices
4.1.1. Test Reliability
4.1.2. Test Validity and Scaling
4.2. Sex Differences on Non-Verbal Fluid Intelligence Measures
4.3. Limitations of the Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GMA | General mental ability |
| NAFs | Norwegian Armed Forces |
| IRT | Item response theory |
| DIF | Differential item functioning |
| CHC | Cattell–Horn–Carroll |
| SIKT | Norwegian Agency for Shared Services in Education and Research |
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
| CI | Confidence interval |
| GPA | Grade point averages |
| GPSD | Grade point standard deviations |
Appendix A
Appendix A.1. Invariance Tests
| Item | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | DIF |
|---|---|---|---|---|---|---|---|---|
| 11 | o | o | o | 3 | ||||
| 12 | 0 | |||||||
| 13 | 0 | |||||||
| 14 | 0 | |||||||
| 15 | o | o | 2 | |||||
| 16 | 0 | |||||||
| 17 | o | o | o | o | 4 | |||
| 18 | 0 | |||||||
| 19 | o | o | o | o | o | o | 6 | |
| 20 | 0 | |||||||
| 21 | o | o | o | o | o | 5 | ||
| 22 | o | 1 | ||||||
| 23 | o | o | o | o | o | o | o | 7 |
| 24 | 0 | |||||||
| 25 | o | o | o | o | 4 | |||
| 26 | o | 1 | ||||||
| 27 | o | 1 | ||||||
| 28 | o | o | o | o | o | 5 | ||
| 29 | o | o | o | o | o | o | o | 7 |
| 30 | o | 1 | ||||||
| 31 | o | o | o | o | o | o | 6 | |
| 32 | o | o | o | o | o | o | 6 | |
| 33 | o | o | 2 | |||||
| 34 | o | o | o | o | o | o | 6 | |
| 35 | 0 | |||||||
| 36 | o | 1 | ||||||
| DIF | 2 | 12 | 14 | 11 | 8 | 10 | 11 |
| Item | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | DIF | Anchors |
|---|---|---|---|---|---|---|---|---|---|
| 11 | A | A | o | o | A | 2 | 3 | ||
| 12 | A | A | A | A | A | A | A | 0 | 7 |
| 13 | A | 0 | 1 | ||||||
| 14 | 0 | 0 | |||||||
| 15 | o | 1 | 0 | ||||||
| 16 | 0 | 0 | |||||||
| 17 | o | o | o | 3 | 0 | ||||
| 18 | A | A | A | A | A | 0 | 5 | ||
| 19 | o | o | o | o | o | 5 | 0 | ||
| 20 | A | A | A | A | 0 | 4 | |||
| 21 | o | A | o | o | o | 4 | 1 | ||
| 22 | 0 | 0 | |||||||
| 23 | o | o | o | o | o | o | o | 7 | 0 |
| 24 | A | A | A | 0 | 3 | ||||
| 25 | A | o | o | o | A | A | o | 4 | 3 |
| 26 | o | A | A | 1 | 2 | ||||
| 27 | A | A | A | A | A | A | 0 | 6 | |
| 28 | o | 1 | 0 | ||||||
| 29 | o | o | o | o | o | o | o | 7 | 0 |
| 30 | o | o | 2 | 0 | |||||
| 31 | o | o | o | o | o | o | 6 | 0 | |
| 32 | o | o | o | o | o | o | 6 | 0 | |
| 33 | o | o | 2 | 0 | |||||
| 34 | o | o | o | o | o | o | 6 | 0 | |
| 35 | 0 | 0 | |||||||
| 36 | o | 1 | 0 | ||||||
| DIF | 2 | 7 | 13 | 12 | 8 | 7 | 9 |


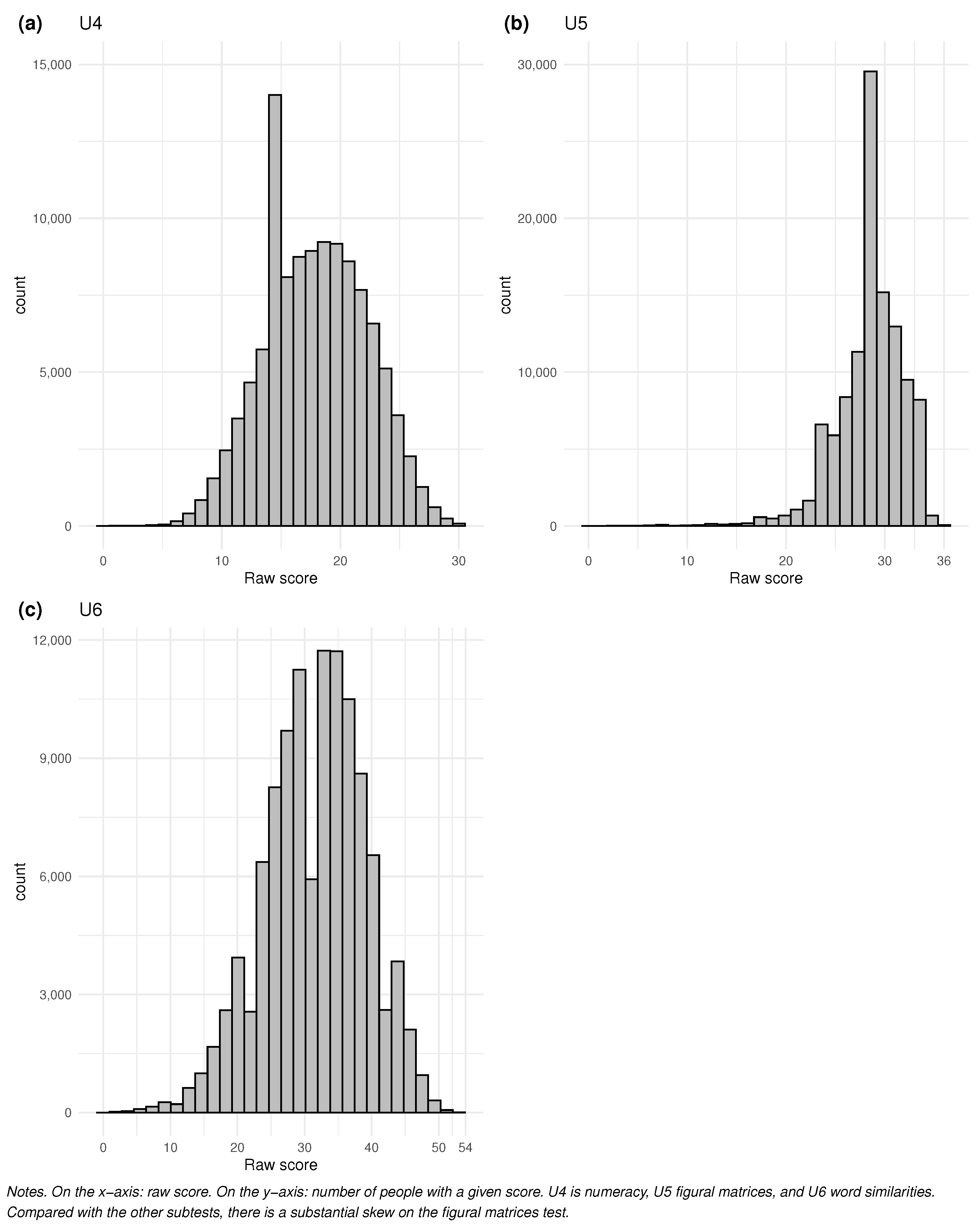
Appendix A.2. Descriptive Statistics, Score Distributions, and Sample Characteristics

| Item | M | SD | Item–Total |
|---|---|---|---|
| 11 | .97–.97 | .16–.18 | .27–.34 |
| 12 | .98–.98 | .13–.15 | .24–.32 |
| 13 | .96–.97 | .17–.19 | .23–.32 |
| 14 | .93–.95 | .22–.26 | .31–.35 |
| 15 | .92–.94 | .24–.27 | .32–.38 |
| 16 | .93–.94 | .24–.26 | .22–.29 |
| 17 | .93–.94 | .23–.25 | .22–.32 |
| 18 | .91–.93 | .25–.28 | .36–.41 |
| 19 | .90–.94 | .25–.29 | .37–.45 |
| 20 | .94–.95 | .22–.24 | .30–.38 |
| 21 | .86–.89 | .31–.35 | .43–.46 |
| 22 | .88–.90 | .30–.33 | .24–.29 |
| 23 | .89–.91 | .28–.31 | .31–.36 |
| 24 | .91–.93 | .26–.29 | .35–.40 |
| 25 | .77–.81 | .39–.42 | .51–.54 |
| 26 | .71–.75 | .44–.45 | .49–.51 |
| 27 | .91–.93 | .25–.29 | .42–.49 |
| 28 | .63–.67 | .47–.48 | .50–.53 |
| 29 | .51–.53 | .50–.50 | .45–.49 |
| 30 | .47–.52 | .50–.50 | .35–.37 |
| 31 | .38–.41 | .49–.49 | .47–.50 |
| 32 | .19–.21 | .40–.41 | .30–.33 |
| 33 | .26–.30 | .44–.46 | .43–.46 |
| 34 | .22–.24 | .42–.43 | .25–.29 |
| 35 | .23–.25 | .42–.43 | .31–.34 |
| 36 | .06–.07 | .24–.25 | .09–.13 |
| Cohort | M | SD | Skewness | Kurtosis | Q05 | Q95 | Min | Max | n |
|---|---|---|---|---|---|---|---|---|---|
| 2011 | 28.55 | 3.60 | −1.61 | 8.88 | 23 | 33 | 5 | 36 | 2820 |
| 2012 | 28.57 | 3.63 | −1.66 | 9.04 | 22 | 33 | 0 | 36 | 13,251 |
| 2013 | 28.35 | 3.66 | −1.58 | 8.51 | 22 | 33 | 0 | 36 | 13,953 |
| 2014 | 28.45 | 3.55 | −1.54 | 8.77 | 22 | 33 | 1 | 36 | 12,621 |
| 2015 | 28.89 | 3.25 | −1.44 | 8.80 | 23 | 33 | 0 | 36 | 12,854 |
| 2016 | 28.83 | 3.35 | −1.48 | 8.95 | 23 | 33 | 1 | 36 | 11,437 |
| 2017 | 28.42 | 3.61 | −1.62 | 9.13 | 22 | 33 | 1 | 36 | 10,065 |
| All | 28.58 | 3.53 | −1.59 | 9.04 | 23 | 33 | 0 | 36 | 77,335 |
| Range | 0.54 | 0.41 | 0.22 | 0.62 |
| Cohort | M | SD | Skewness | Kurtosis | Q05 | Q95 | Min | Max | n |
|---|---|---|---|---|---|---|---|---|---|
| 2011 | 28.10 | 3.10 | −1.13 | 7.14 | 23 | 32 | 5 | 35 | 1105 |
| 2012 | 28.03 | 3.23 | −1.22 | 7.66 | 23 | 32 | 2 | 36 | 4992 |
| 2013 | 27.94 | 3.11 | −1.05 | 6.86 | 23 | 32 | 3 | 36 | 6101 |
| 2014 | 28.08 | 3.11 | −1.09 | 7.16 | 23 | 33 | 3 | 36 | 5677 |
| 2015 | 28.44 | 3.01 | −1.01 | 6.48 | 23 | 33 | 5 | 36 | 6710 |
| 2016 | 28.27 | 3.01 | −0.97 | 6.66 | 23 | 33 | 0 | 35 | 6757 |
| 2017 | 27.97 | 3.29 | −1.19 | 7.28 | 22 | 33 | 3 | 35 | 4886 |
| All | 28.14 | 3.12 | −1.09 | 7.05 | 23 | 33 | 0 | 36 | 36,336 |
| Range | 0.50 | 0.28 | 0.25 | 1.18 |
Appendix B. Other Studies Using the GMA Measures of the Norwegian Armed Forces
| 1 | If we multiply by 15 and add 100 to get IQ equivalents, males have estimates of 109–113.5 with standard errors of 10.65–12.30 IQ points; and females have estimates of 109–112 with standard errors of 10.35–11.70 IQ points. |
References
- Abad, Francisco J., Roberto Colom, Irene Rebollo, and Sergio Escorial. 2004. Sex differential item functioning in the Raven’s Advanced Progressive Matrices: Evidence for bias. Personality and Individual Differences 36: 1459–70. [Google Scholar] [CrossRef]
- Andersson, Björn, and Tao Xin. 2018. Large Sample Confidence Intervals for Item Response Theory Reliability Coefficients. Educational and Psychological Measurement 78: 32–45. [Google Scholar] [CrossRef] [PubMed]
- Arden, Rosalind, and Robert Plomin. 2006. Sex differences in variance of intelligence across childhood. Personality and Individual Differences 41: 39–48. [Google Scholar] [CrossRef]
- Arendasy, Martin, and Markus Sommer. 2005. The effect of different types of perceptual manipulations on the dimensionality of automatically generated figural matrices. Intelligence 33: 307–24. [Google Scholar] [CrossRef]
- Arendasy, Martin E., and Markus Sommer. 2012. Gender differences in figural matrices: The moderating role of item design features. Intelligence 40: 584–97. [Google Scholar] [CrossRef]
- Bjerkedal, Tor, Petter Kristensen, Geir A. Skjeret, and John I. Brevik. 2007. Intelligence test scores and birth order among young Norwegian men (conscripts) analyzed within and between families. Intelligence 35: 503–14. [Google Scholar] [CrossRef]
- Black, Sandra E., Paul J. Devereux, and Kjell G. Salvanes. 2007. Small family, smart family? Family size and the IQ scores of young men. Journal of Human Resources 45: 33–58. [Google Scholar] [CrossRef]
- Black, Sandra E., Paul J. Devereux, and Kjell G. Salvanes. 2009. Like father, like son? A note on the intergenerational transmission of IQ scores. Economics Letters 105: 138–40. [Google Scholar] [CrossRef]
- Black, Sandra E., Paul J. Devereux, and Kjell G. Salvanes. 2011. Older and wiser? Birth order and IQ of young men. CESifo Economic Studies 57: 103–20. [Google Scholar] [CrossRef]
- Bock, R. Darrell, and Murray Aitkin. 1981. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika 46: 443–59. [Google Scholar] [CrossRef]
- Bratsberg, Bernt, and Ole Rogeberg. 2017. Childhood socioeconomic status does not explain the IQ-mortality gradient. Intelligence 62: 148–54. [Google Scholar] [CrossRef]
- Bratsberg, Bernt, and Ole Rogeberg. 2018. Flynn effect and its reversal are both environmentally caused. Proceedings of the National Academy of Sciences of the United States of America 115: 6674–78. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, Patricia A., Marcel A. Just, and Peter Shell. 1990. What one intelligence test measures: A theoretical account of the processing in the Raven Progressive Matrices Test. Psychological Review 97: 404–31. [Google Scholar] [CrossRef]
- Cattell, Raymond B. 1940. A culture-free intelligence test. I. Journal of Educational Psychology 31: 161–79. [Google Scholar] [CrossRef]
- Chalmers, R. Philip. 2012. mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software 48: 1–29. [Google Scholar] [CrossRef]
- Colom, Roberto, and Oscar García-López. 2002. Sex differences in fluid intelligence among high school graduates. Personality and Individual Differences 32: 445–51. [Google Scholar] [CrossRef]
- Dahl, Gordon B, Andreas Kotsadam, and Dan-Olof Rooth. 2021. Does Integration Change Gender Attitudes? The Effect of Randomly Assigning Women to Traditionally Male Teams. The Quarterly Journal of Economics 136: 987–1030. [Google Scholar] [CrossRef]
- Deary, Ian J., Graham Thorpe, Valerie Wilson, John M. Starr, and Lawrence J. Whalley. 2003. Population sex differences in IQ at age 11: The Scottish mental survey 1932. Intelligence 31: 533–42. [Google Scholar] [CrossRef]
- de Ayala, Rafael Jaime. 2022. The Theory and Practice of Item Response Theory, 2nd ed. New York: Guilford Press. [Google Scholar]
- Embretson, Susan E., and Steven P. Reise. 2000. Item Response Theory for Psychologists. Mawah: Lawrence Erlbaum. [Google Scholar]
- Endringslov til vernepliktsloven og heimevernloven. 2014. Lov om endringer i vernepliktsloven og heimevernloven (allmenn verneplikt—Verneplikt for kvinner). § 50 a. [Enactment of Changes in the Conscription Law and the Territorial Defence Law (General Conscription—Conscription for Women)]. Oslo: Forsvarsdepartementet. [Google Scholar]
- Feingold, Alan. 1992. Sex Differences in Variability in Intellectual Abilities: A New Look at an Old Controversy. Review of Educational Research 62: 61–84. [Google Scholar] [CrossRef]
- Feng, Jing, Ian Spence, and Jay Pratt. 2007. Playing an action video game reduces gender differences in spatial cognition. Psychological Science 18: 850–55. [Google Scholar] [CrossRef] [PubMed]
- Fischer, Felix, Chris Gibbons, Joël Coste, Jose M. Valderas, Matthias Rose, and Alain Leplège. 2018. Measurement invariance and general population reference values of the PROMIS Profile 29 in the UK, France, and Germany. Quality of Life Research 27: 999–1014. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, Dawn P., and Erin M. McDonough, eds. 2018. Contemporary Intellectual Assessment, Fourth Edition: Theories, Tests, and Issues. New York: Guilford Publications. [Google Scholar]
- Flynn, James R. 1987. Massive IQ Gains in 14 Nations: What IQ Tests Really Measure. Psychological Bulletin 101: 171–91. [Google Scholar] [CrossRef]
- Flynn, James R., and Michael Shayer. 2018. IQ decline and Piaget: Does the rot start at the top? Intelligence 66: 112–21. [Google Scholar] [CrossRef]
- Galloway, Taryn Ann, and Stephen Pudney. 2011. Initiation into Crime: An Analysis of Norwegian Register Data on Five Cohorts. ISER Working Paper Series, No. 2011-11. Oslo: Statistics Norway, pp. 1–44. [Google Scholar]
- Gustafsson, Jan-Eric. 1984. A unifying model for the structure of intellectual abilities. Intelligence 8: 179–203. [Google Scholar] [CrossRef]
- Gustafsson, Jan-Eric, Berner Lindström, and Eva Björck-Åkesson. 1981. A General Model for the Organization of Cognitive Abilities. Götborg: Department of Education, University of Götborg. [Google Scholar]
- Halpern, Diane F., and Mary L. LaMay. 2000. The Smarter Sex: A Critical Review of Sex Differences in Intelligence. Educational Psychology Review 12: 229–46. [Google Scholar] [CrossRef]
- Hansen, Ivar. 2006. Bidrag til Psykologitjenestens historie i Forsvaret fra 1946–2006 [Contributions to the History of the Psychological Services of the Norwegian Armed Forces from 1946–2006]. Militærpsykologiske meddelelser nr. 25 (ISSN 0801-8960). Oslo: Forsvarets Institutt for Ledelse. [Google Scholar]
- Helland-Riise, Fredrik, and Monica Martinussen. 2017. Måleegenskaper ved de norske versjonene av Ravens matriser [Standard Progressive Matrices (SPM)/Coloured Progressive Matrices (CPM)] [Measurement properties of the Norwegian versions of Raven’s Matrices]. PsykTestBarn 7: 1–20. [Google Scholar] [CrossRef]
- Hyde, Janet S. 2016. Sex and cognition: Gender and cognitive functions. Current Opinion in Neurobiology 38: 53–56. [Google Scholar] [CrossRef]
- Isaksen, Nina Margrethe. 2014. Felles opptak og seleksjon til Luftforsvarets befalskole—En analyse av seleksjonsmetodenes prediktive validitet [Joint Admission and Selection to the Air Force Leadership Training School—An Analysis of the Predictive Validity of the SELECTION methods]. Oslo: Forsvarets Høgskole. [Google Scholar]
- Janssen, Rianne, Jan Schepers, and Deborah Peres. 2004. Models with item and item group predictors. In Explanatory Item Response Models: A Generalized Linear and Nonlinear Approach. Edited by Paul Boeck and Mark Wilson. New York: Springer, chp. 6. pp. 189–212. [Google Scholar]
- Jensen, Arthur R. 1998. The g Factor: The Science of Mental Ability. Westport: Praeger publishers. [Google Scholar]
- Jensen, Arthur R., and Li-Jen Weng. 1994. What is a good g? Intelligence 18: 231–58. [Google Scholar] [CrossRef]
- Keith, Timothy Z., Matthew R. Reynolds, Lisa G. Roberts, Amanda L. Winter, and Cynthia A. Austin. 2011. Sex differences in latent cognitive abilities ages 5 to 17: Evidence from the Differential Ability Scales-Second Edition. Intelligence 39: 389–404. [Google Scholar] [CrossRef]
- Keith, Timothy Z., Matthew R. Reynolds, Puja G. Patel, and Kristen P. Ridley. 2008. Sex differences in latent cognitive abilities ages 6 to 59: Evidence from the Woodcock-Johnson III tests of cognitive abilities. Intelligence 36: 502–25. [Google Scholar] [CrossRef]
- Kim, Seonghoon, and Leonard S. Feldt. 2010. The estimation of the IRT reliability coefficient and its lower and upper bounds, with comparisons to CTT reliability statistics. Asia Pacific Education Review 11: 179–88. [Google Scholar] [CrossRef]
- Køber, Petter Kristian. 2016. Fra sesjonsplikt til verneplikt for kvinner—motivasjon og seleksjon på sesjon del 1 for årskullene 1992–1997 [From Mandatory Muster to Mandatory Conscription for Women—Motivation and Selection on Muster Part 1 for Birth Cohorts 1992–1997]. FFI-Rapport 2016/00014. Kjeller: Forsvarets forskningsinstitutt (FFI). [Google Scholar]
- Køber, Petter Kristian. 2020. Motivasjon for førstegangstjeneste—en kvantitativ analyse av sesjonsdata 2009–2019 [Motivation for Conscription—A Quantitative Analysis of Mustering Data 2009–2019]. FFI Note 20/01634. Kjeller: Forsvarets Forskningsinstitutt (FFI). [Google Scholar]
- Køber, Petter Kristian, Ole Christian Lang-Ree, Kari V. Stubberud, and Monica Martinussen. 2017. Predicting Basic Military Performance for Conscripts in the Norwegian Armed Forces. Military Psychology 29: 560–69. [Google Scholar] [CrossRef][Green Version]
- Kristensen, Petter, and Tor Bjerkedal. 2007. Explaining the relation between birth order and intelligence. Science 316: 1717. [Google Scholar] [CrossRef]
- Kvist, Ann Valentin, and Jan-Eric Gustafsson. 2008. The relation between fluid intelligence and the general factor as a function of cultural background: A test of Cattell’s Investment theory. Intelligence 36: 422–36. [Google Scholar] [CrossRef]
- Lakin, Joni M., and James L. Gambrell. 2014. Sex differences in fluid reasoning: Manifest and latent estimates from the cognitive abilities test. Journal of Intelligence 2: 36–55. [Google Scholar] [CrossRef]
- Lim, Tock Keng. 1994. Gender-related differences in intelligence: Application of confirmatory factor analysis. Intelligence 19: 179–92. [Google Scholar] [CrossRef]
- Lopez Rivas, Gabriel E., Stephen Stark, and Oleksandr S. Chernyshenko. 2009. The Effects of Referent Item Parameters on Differential Item Functioning Detection Using the Free Baseline Likelihood Ratio Test. Applied Psychological Measurement 33: 251–65. [Google Scholar] [CrossRef]
- Lynn, Richard, and Paul Irwing. 2004. Sex differences on the progressive matrices: A meta-analysis. Intelligence 32: 481–98. [Google Scholar] [CrossRef]
- Mackintosh, Nicholas J., and E. S. Bennett. 2005. What do Raven’s Matrices measure? An analysis in terms of sex differences. Intelligence 33: 663–74. [Google Scholar] [CrossRef]
- Marshalek, Brachia, David F. Lohman, and Richard E. Snow. 1983. The complexity continuum in the radex and hierarchical models of intelligence. Intelligence 7: 107–27. [Google Scholar] [CrossRef]
- Maydeu-Olivares, Alberto. 2013. Goodness-of-Fit Assessment of Item Response Theory Models. Measurement 11: 71–101. [Google Scholar] [CrossRef]
- Maydeu-Olivares, Alberto, and Harry Joe. 2014. Assessing Approximate Fit in Categorical Data Analysis. Multivariate Behavioral Research 49: 305–28. [Google Scholar] [CrossRef] [PubMed]
- McDonald, Roderick P. 1999. Test Theory: A Unified Treatment, 1st ed. New York: Psychology Press. [Google Scholar] [CrossRef]
- McGrew, Kevin S. 2009. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 37: 1–10. [Google Scholar] [CrossRef]
- Norrøne, Tore. 2016. Utvelgelse av kandidater til Sjøforsvarets grunnleggende befalskurs: En undersøkelse av den prediktive validiteten til seleksjonssystemet. [Selection of Candidates for Navy Basic Leadership Training: A Study of Predictive Validity.]. Master’s thesis, NTNU, Trondheim, Norway. [Google Scholar]
- NOU 2019:3. 2019. Nye sjanser—bedre læring—Kjønnsforskjeller i skoleprestasjoner og utdanningsløp [New Chances—Better Learning—Sex Differences in School Performance and Educational Trajectories]. Technical Report. Oslo: Kunnskapsdepartementet. [Google Scholar]
- Plaisted, Kate, Stuart Bell, and N. J. Mackintosh. 2011. The role of mathematical skill in sex differences on Raven’s Matrices. Personality and Individual Differences 51: 562–65. [Google Scholar] [CrossRef]
- Primi, Ricardo. 2001. Complexity of geometric inductive reasoning tasks contribution to the understanding of fluid intelligence. Intelligence 30: 41–70. [Google Scholar] [CrossRef]
- Raven, John C. 1941. Standardization of progressive matrices, 1938. British Journal of Medical Psychology 19: 137–50. [Google Scholar] [CrossRef]
- Reynolds, Matthew R., Daniel B. Hajovsky, and Jacqueline M. Caemmerer. 2022. The sexes do not differ in general intelligence, but they do in some specifics. Intelligence 92: 101651. [Google Scholar] [CrossRef]
- Sackett, Paul R., Charlene Zhang, Christopher M. Berry, and Filip Lievens. 2022. Revisiting meta-analytic estimates of validity in personnel selection: Addressing systematic overcorrection for restriction of range. Journal of Applied Psychology 107: 2040–68. [Google Scholar] [CrossRef]
- Skoglund, Tom Hilding, Monica Martinussen, and Ole Christian Lang-Ree. 2014. Papir vs. PC [Paper vs. PC]. Tidsskrift for Norsk Psykologiforening 51: 450–52. [Google Scholar]
- Snow, Richard E. 1981. Aptitude processes. In Aptitude, Learning and Instruction: Vol. 1. Cognitive Process Analyses of Aptitude. Edited by Richard E. Snow, Pat-Anthony Federico and William E. Montague. San Diego: Navy Personnel Research and Development Center, chp. 2. pp. 27–63. [Google Scholar]
- Stark, Stephen, Oleksandr S. Chernyshenko, and Fritz Drasgow. 2006. Detecting differential item functioning with confirmatory factor analysis and item response theory: Toward a unified strategy. Journal of Applied Psychology 91: 1292–306. [Google Scholar] [CrossRef]
- Steinmayr, Ricarda, André Beauducel, and Birgit Spinath. 2010. Do sex differences in a faceted model of fluid and crystallized intelligence depend on the method applied? Intelligence 38: 101–10. [Google Scholar] [CrossRef]
- Strand, Steve, Ian J. Deary, and Pauline Smith. 2006. Sex differences in Cognitive Abilities Test scores: A UK national picture. British Journal of Educational Psychology 76: 463–80. [Google Scholar] [CrossRef] [PubMed]
- Sundet, Jon Martin, Dag G. Barlaug, and Tore M. Torjussen. 2004. The end of the Flynn effect? A study of secular trends in mean intelligence test scores of Norwegian conscripts during half a century. Intelligence 32: 349–62. [Google Scholar] [CrossRef]
- Sundet, Jon Martin, Ingrid Borren, and Kristian Tambs. 2008. The Flynn effect is partly caused by changing fertility patterns. Intelligence 36: 183–91. [Google Scholar] [CrossRef]
- Sundet, Jon Martin, Kristian Tambs, Jennifer R. Harris, Per Magnus, and Tore M. Torjussen. 2005. Resolving the genetic and environmental sources of the correlation between height and intelligence: A study of nearly 2600 Norwegian male twin pairs. Twin Research and Human Genetics 8: 307–11. [Google Scholar] [CrossRef] [PubMed]
- Sundet, Jon Martin, Kristian Tambs, Per Magnus, and Kåre Berg. 1988. On the question of secular trends in the heritability of intelligence test scores: A study of Norwegian twins. Intelligence 12: 47–59. [Google Scholar] [CrossRef]
- Sundet, Jon Martin, Willy Eriksen, Ingrid Borren, and Kristian Tambs. 2010. The Flynn effect in sibships: Investigating the role of age differences between siblings. Intelligence 38: 38–44. [Google Scholar] [CrossRef]
- Tay, Louis, Adam W. Meade, and Mengyang Cao. 2015. An Overview and Practical Guide to IRT Measurement Equivalence Analysis. Organizational Research Methods 18: 3–46. [Google Scholar] [CrossRef]
- Thrane, Vidkunn Coucheron. 1977. Evneprøving av Utskrivingspliktige i Norge 1950–53 [Ability Testing of Norwegian Conscripts 1950–53]. INAS Arbeidsrapport nr. 26. Technical Report. Oslo: Institutt for Anvendt Sosialvitenskapelig Forskning. [Google Scholar]
- Vik, Joar Sæterdal. 2013. Har seleksjon noen betydning? En studie av seleksjonens prediktive validitet. [Does Selection Matter? A Study on the Predictive Validity of the Selection]. Master’s thesis, Universitetet i Tromsø, Tromsø, Norway. [Google Scholar]
- Waschl, Nicolette, and Nicholas R. Burns. 2020. Sex differences in inductive reasoning: A research synthesis using meta-analytic techniques. Personality and Individual Differences 164: 109959. [Google Scholar] [CrossRef]


| Cohort | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|
| n | 3921 | 18,238 | 19,597 | 17,668 | 18,649 | 17,569 | 14,011 |
| Female | 28% | 27% | 31% | 31% | 34% | 38% | 34% |
| Male | 72% | 73% | 69% | 69% | 66% | 62% | 66% |
| Birth year | 1992–1993 | 1993–1994 | 1994–1995 | 1995–1996 | 1996–1997 | 1997–1998 | 1998–1999 |
| Cohort | Group | df | p | RMSEA (2.5%, 97.5%) | SRMSR | |
|---|---|---|---|---|---|---|
| 2011 | Female | 460.999 | 299 | .001> | 0.022 (0.017, 0.027) | 0.039 |
| Male | 719.818 | 299 | .001> | 0.022 (0.020, 0.025) | 0.035 | |
| 2012 | Female | 878.534 | 299 | .001> | 0.020 (0.018, 0.022) | 0.028 |
| Male | 2302.478 | 299 | .001> | 0.022 (0.021, 0.024) | 0.034 | |
| 2013 | Female | 961.704 | 299 | .001> | 0.019 (0.017, 0.021) | 0.025 |
| Male | 2433.951 | 299 | .001> | 0.023 (0.022, 0.024) | 0.031 | |
| 2014 | Female | 982.257 | 299 | .001> | 0.020 (0.018, 0.022) | 0.026 |
| Male | 2188.407 | 299 | .001> | 0.022 (0.021, 0.023) | 0.030 | |
| 2015 | Female | 836.257 | 299 | .001> | 0.016 (0.015, 0.018) | 0.022 |
| Male | 1969.806 | 299 | .001> | 0.021 (0.020, 0.022) | 0.028 | |
| 2016 | Female | 869.110 | 299 | .001> | 0.017 (0.015, 0.018) | 0.022 |
| Male | 1931.236 | 299 | .001> | 0.022 (0.021, 0.023) | 0.030 | |
| 2017 | Female | 818.726 | 299 | .001> | 0.019 (0.017, 0.021) | 0.026 |
| Male | 1656.481 | 299 | .001> | 0.021 (0.020, 0.022) | 0.031 |
| Cohort | Test Reliability | Marginal Reliability | ||
|---|---|---|---|---|
| Female | Male | Female | Male | |
| 2011 | .70 (.58, .83) | .77 (.74, .79) | .70 (.68, .73) | .75 (.73, .76) |
| 2012 | .72 (.70, .73) | .77 (.72, .81) | .72 (.71, .73) | .75 (.74, .75) |
| 2013 | .70 (.69, .72) | .77 (.69, .85) | .71 (.70, .72) | .75 (.74, .75) |
| 2014 | .71 (.69, .73) | .76 (.75, .77) | .71 (.70, .72) | .74 (.73, .75) |
| 2015 | .69 (.68, .71) | .73 (.72, .75) | .70 (.69, .71) | .72 (.71, .73) |
| 2016 | .69 (.67, .71) | .74 (.73, .76) | .70 (.69, .71) | .73 (.72, .74) |
| 2017 | .73 (.71, .76) | .77 (.72, .81) | .73 (.72, .74) | .75 (.74, .75) |
| Item | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | DIF |
|---|---|---|---|---|---|---|---|---|
| 11 | o | o | 2 | |||||
| 12 | 0 | |||||||
| 13 | 0 | |||||||
| 14 | 0 | |||||||
| 15 | o | 1 | ||||||
| 16 | 0 | |||||||
| 17 | o | o | o | 3 | ||||
| 18 | 0 | |||||||
| 19 | o | o | o | o | o | 5 | ||
| 20 | 0 | |||||||
| 21 | o | o | o | o | 4 | |||
| 22 | 0 | |||||||
| 23 | o | o | o | o | o | o | o | 7 |
| 24 | 0 | |||||||
| 25 | o | o | o | o | 4 | |||
| 26 | o | 1 | ||||||
| 27 | 0 | |||||||
| 28 | o | 1 | ||||||
| 29 | o | o | o | o | o | o | o | 7 |
| 30 | o | o | 2 | |||||
| 31 | o | o | o | o | o | o | 6 | |
| 32 | o | o | o | o | o | o | 6 | |
| 33 | o | o | 2 | |||||
| 34 | o | o | o | o | o | o | 6 | |
| 35 | 0 | |||||||
| 36 | o | 1 | ||||||
| DIF | 2 | 7 | 13 | 12 | 8 | 7 | 9 |
| Cohort | Model | AIC | BIC | RMSEA (2.5%, 97.5%) | SRMSR.F | SRMSR.M |
|---|---|---|---|---|---|---|
| 2011 | Constrained | 73,262 | 73,601 | 0.016 (0.015, 0.018) | 0.042 | 0.036 |
| Partial | 73,222 | 73,586 | 0.016 (0.014, 0.017) | 0.041 | 0.036 | |
| Configural | 73,220 | 73,872 | 0.016 (0.014, 0.017) | 0.039 | 0.035 | |
| 2012 | Constrained | 339,083 | 339,505 | 0.016 (0.015, 0.017) | 0.029 | 0.035 |
| Partial | 338,807 | 339,338 | 0.015 (0.015, 0.016) | 0.029 | 0.034 | |
| Configural | 338,724 | 339,536 | 0.015 (0.015, 0.016) | 0.028 | 0.034 | |
| 2013 | Constrained | 375,974 | 376,401 | 0.016 (0.016, 0.017) | 0.026 | 0.033 |
| Partial | 375,465 | 376,098 | 0.015 (0.015, 0.016) | 0.026 | 0.032 | |
| Configural | 375,426 | 376,249 | 0.015 (0.015, 0.016) | 0.025 | 0.031 | |
| 2014 | Constrained | 341,680 | 342,102 | 0.016 (0.015, 0.017) | 0.027 | 0.031 |
| Partial | 341,319 | 341,929 | 0.015 (0.014, 0.016) | 0.026 | 0.031 | |
| Configural | 341,334 | 342,147 | 0.015 (0.015, 0.016) | 0.026 | 0.030 | |
| 2015 | Constrained | 351,901 | 352,326 | 0.015 (0.014, 0.015) | 0.023 | 0.029 |
| Partial | 351,566 | 352,118 | 0.014 (0.013, 0.014) | 0.022 | 0.028 | |
| Configural | 351,540 | 352,360 | 0.014 (0.013, 0.014) | 0.022 | 0.028 | |
| 2016 | Constrained | 331,109 | 331,530 | 0.015 (0.014, 0.015) | 0.023 | 0.031 |
| Partial | 330,872 | 331,403 | 0.014 (0.014, 0.015) | 0.022 | 0.031 | |
| Configural | 33,0845 | 331,657 | 0.014 (0.014, 0.015) | 0.022 | 0.030 | |
| 2017 | Constrained | 278,244 | 278,655 | 0.015 (0.015, 0.016) | 0.026 | 0.033 |
| Partial | 277,944 | 278,492 | 0.014 (0.014, 0.015) | 0.025 | 0.032 | |
| Configural | 277,938 | 278,730 | 0.014 (0.014, 0.015) | 0.026 | 0.031 |
| −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| TI.F | 0.56–0.82 | 1.33–1.66 | 2.89–3.05 | 4.00–4.74 | 4.18–5.32 | 3.28–4.19 | 2.32–2.81 | 1.53–1.86 | 0.99–1.14 | 0.59–0.64 |
| TI.M | 0.55–0.81 | 1.31–1.62 | 2.81–2.99 | 3.97–4.71 | 4.25–5.34 | 3.32–4.11 | 2.18–2.69 | 1.44–1.75 | 0.93–1.07 | 0.58–0.61 |
| SE.F | 1.11–1.34 | 0.78–0.87 | 0.57–0.59 | 0.46–0.50 | 0.43–0.49 | 0.49–0.55 | 0.60–0.66 | 0.73–0.81 | 0.94–1.01 | 1.25–1.30 |
| SE.M | 1.11–1.35 | 0.79–0.87 | 0.58–0.60 | 0.46–0.50 | 0.43–0.49 | 0.49–0.55 | 0.61–0.68 | 0.76–0.83 | 0.97–1.04 | 1.28–1.32 |
| Cohort | Means | Variances | DIF | ||
|---|---|---|---|---|---|
| Constr. (2.5%, 97.5%) | Partial (2.5%, 97.5%) | Constr. (2.5%, 97.5%) | Partial (2.5%, 97.5%) | ||
| 2011 | 0.32 (0.22, 0.41) | 0.30 (0.20, 0.39) | 1.62 (1.39, 1.85) | 1.59 (1.36, 1.82) | 2 |
| 2012 | 0.33 (0.28, 0.37) | 0.25 (0.20, 0.30) | 1.52 (1.42, 1.62) | 1.51 (1.40, 1.63) | 7 |
| 2013 | 0.30 (0.25, 0.34) | 0.32 (0.27, 0.37) | 1.63 (1.53, 1.73) | 1.69 (1.55, 1.82) | 13 |
| 2014 | 0.24 (0.20, 0.29) | 0.15 (0.10, 0.20) | 1.45 (1.36, 1.55) | 1.35 (1.23, 1.46) | 12 |
| 2015 | 0.27 (0.23, 0.31) | 0.24 (0.19, 0.28) | 1.36 (1.28, 1.44) | 1.38 (1.27, 1.48) | 8 |
| 2016 | 0.32 (0.28, 0.36) | 0.28 (0.24, 0.33) | 1.48 (1.39, 1.57) | 1.42 (1.32, 1.52) | 7 |
| 2017 | 0.25 (0.21, 0.29) | 0.19 (0.14, 0.24) | 1.36 (1.27, 1.45) | 1.32 (1.21, 1.42) | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Helland-Riise, F.; Norrøne, T.N.; Andersson, B. Large-Scale Item-Level Analysis of the Figural Matrices Test in the Norwegian Armed Forces: Examining Measurement Precision and Sex Bias. J. Intell. 2024, 12, 82. https://doi.org/10.3390/jintelligence12090082
Helland-Riise F, Norrøne TN, Andersson B. Large-Scale Item-Level Analysis of the Figural Matrices Test in the Norwegian Armed Forces: Examining Measurement Precision and Sex Bias. Journal of Intelligence. 2024; 12(9):82. https://doi.org/10.3390/jintelligence12090082
Chicago/Turabian StyleHelland-Riise, Fredrik, Tore Nøttestad Norrøne, and Björn Andersson. 2024. "Large-Scale Item-Level Analysis of the Figural Matrices Test in the Norwegian Armed Forces: Examining Measurement Precision and Sex Bias" Journal of Intelligence 12, no. 9: 82. https://doi.org/10.3390/jintelligence12090082
APA StyleHelland-Riise, F., Norrøne, T. N., & Andersson, B. (2024). Large-Scale Item-Level Analysis of the Figural Matrices Test in the Norwegian Armed Forces: Examining Measurement Precision and Sex Bias. Journal of Intelligence, 12(9), 82. https://doi.org/10.3390/jintelligence12090082





