Abstract
The PISA 2022 literacy assessment highlights a significant decline in math performance among most OECD countries, with the magnitude of this decline being approximately three times that of the previous round. Remarkably, Hong Kong, Macao, Taipei, Singapore, Japan, and Korea ranked in the top six among all participating countries or economies, with Taipei, Singapore, Japan, and Korea also demonstrating improved performance. Given the widespread concern about the factors influencing secondary-school students’ mathematical literacy, this paper adopts machine learning and the SHapley Additive exPlanations (SHAP) method to analyze 34,968 samples and 151 features from six East Asian education systems within the PISA 2022 dataset, aiming to pinpoint the crucial factors that affect middle-school students’ mathematical literacy. First, the XGBoost model has the highest prediction accuracy for math literacy performance. Second, 15 variables were identified as significant predictors of mathematical literacy across the student population, particularly variables such as mathematics self-efficacy (MATHEFF) and expected occupational status (BSMJ). Third, mathematics self-efficacy was determined to be the most influential factor. Fourth, the factors influencing mathematical literacy vary among individual students, including the key influencing factors, the direction (positive or negative) of their impact, and the extent of this influence. Finally, based on our findings, four recommendations are proffered to enhance the mathematical literacy performance of secondary-school students.
1. Introduction
The Program for International Student Assessment (PISA) is a global assessment program initiated by the Organization for Economic Co-operation and Development (OECD) to evaluate the reading, mathematics, and science literacy among 15-year-old students using standardized tests and background questionnaires (OECD and UNESCO Institute for Statistics 2003). Since 2000, PISA has been conducted every three years, with each iteration focusing on a specific domain. In 2021, the primary domain was intended to be mathematics literacy. However, due to the COVID-19 pandemic, PISA 2021 was rescheduled to 2022 and included creative thinking as an additional component of the assessment for the first time (OECD 2023b). During prior evaluations, the mean math literacy score among Organization for Economic Co-operation and Development (OECD) countries exhibited minimal variation, fluctuating within a range of 4 points. However, the results from the Program for International Student Assessment (PISA) in 2022 indicated that the average scores of 35 OECD countries, with the exception of Costa Rica and Spain, were approximately 15 points lower compared to those in 2018. This drop is more than three times as large as the fluctuations in scores of previous rounds. Notably, among the 81 participating countries and economies, the top 6 were the six East Asian education systems (Hong Kong, Macao, Taipei, Singapore, Japan, and Korea). Moreover, Taipei, Singapore, Japan, and Korea have also improved their grades. Apart from the fact that they all belong to the East Asian cultural sphere, are there any other factors that have contributed to their mathematical excellence? In other words, what are the pivotal elements that impact secondary-school students’ mathematical literacy? Moreover, mathematical literacy is an essential competency for secondary-school students in the 21st century to navigate the evolving challenges in their professional and social lives. By discerning these key influences, educators can devise targeted and practical interventions to enhance individual mathematical proficiency and better equip students for future challenges.
The PISA test employs a two-stage sampling method. The first stage uses probability proportional to size (PPS) based on school size, while the second stage involves random sampling of students within the selected schools (OECD 2003). This process generates a multilevel dataset. Consequently, existing studies have primarily utilized statistical learning methods such as multilevel linear modeling (HLM) for analyzing PISA data (Tourón et al. 2019; You et al. 2021; Lezhnina and Kismihók 2022; Bhutoria and Aljabri 2022; Hu and Yu 2021; Hu and Wang 2022). However, this study involved 34,968 samples and 152 variables (before data preprocessing), making machine learning methods more suitable for handling complex data with numerous feature dimensions and nonlinear relationships between variables (Hilbert et al. 2021). On the one hand, educational applications related to machine learning techniques, particularly performance prediction, focus more on improving model forecasting ability than on model explanation (Munir et al. 2022); on the other hand, although there is also some literature on applying machine learning methods to examine factors influencing academic performance (Lee 2022; Bernardo et al. 2022; Wang et al. 2023a; Gómez-Talal et al. 2024), they primarily explore the influencing factors for all samples, paying less attention to individual and multiple samples. Therefore, further exploration of machine learning explanations in the field of education is needed. This study identifies significant influences affecting mathematical literacy through machine learning and the SHAP method, addressing the following questions:
- (1)
- Which machine learning model is best for predicting middle-school students’ math literacy?
- (2)
- What are the important factors that affect mathematical literacy performance?
Moreover, previous literature has identified several variables that influence math literacy. These variables are broadly categorized into five categories in the PISA dataset: individual student, household context, school community, education systems, and macro society (Wang et al. 2023b). Since Singapore only completed the student questionnaire, school questionnaire, and creative thinking questionnaire (OECD 2023c), this article focuses on student, family, and school factors.
1.1. Student Factors
Student variables, including demographic characteristics, students’ psychological factors, learning opportunities, and school experiences, all exert a certain degree of impact on their mathematical literacy.
Among demographic characteristics, gender (Melkonian et al. 2019) and grade level have a significant effect on student scores. There exists a disparity between male and female students in their performance in different areas of mathematics. Male students are more dominant than females in space and shape (Liu and Wilson 2009). Nevertheless, the differences in students’ grades due to gender are not independent; rather, they are associated with the state (Zhang et al. 2022) and age (Lindberg et al. 2010). Additionally, as students progress to higher grades, their grades tend to increase (Aguayo-Téllez and Martínez-Rodríguez 2020; Spörlein and Schlueter 2018).
Regarding students’ psychology, studies have indicated that cognitive factors such as a growth mindset (Bernardo 2021) and creative thinking (de Vink et al. 2023; Sebastian and Huang 2016) can effectively raise scores. In addition to cognitive traits, non-cognitive variables such as self-concept (Pinquart and Ebeling 2020), self-efficacy (confidence) (Rodríguez et al. 2017), motivation (Pitsia et al. 2017), and positive attitudes toward learning (Bernardo 2021; Gjicali and Lipnevich 2021) are equally beneficial. In particular, self-efficacy is considered the best predictor (Stankov et al. 2012), and the impact of motivation is moderated through emotional support and self-efficacy (Skaalvik et al. 2015). However, non-cognitive features such as math anxiety (Barroso et al. 2021) may have an adverse effect. Concerning the relationship between subjective well-being and student scores, although some literature has found a positive connection (Yao et al. 2018), Bücker et al. (2018) disagree, arguing that students who are superior in math do not necessarily have a high level of well-being, and poor students do not necessarily have a lower level of well-being.
Regarding learning opportunities, the judicious utilization of Information and Communication Technology (ICT) is beneficial (Kim 2018). Students who use ICT moderately for recreation perform better than those who use it heavily (Xiao and Sun 2022). However, the availability and use of ICT both in and out of school might be detrimental (Courtney et al. 2022), while positive attitudes toward ICT could have a positive impact (Wijaya et al. 2022b). Beyond the use of ICT, students who receive early childhood education (ECE) generally have higher scores than those who do not (Giannelli and Rapallini 2016). Interestingly, an earlier start in ECE is not necessarily better. In general, pupils starting ECE at age 3 are better than those starting at 0–2, which may be related to the developmental issues of children (Laaninen et al. 2024).
Finally, features related to the school experience, such as absenteeism, truancy (Yamamura 2019; Fernández-Gutiérrez et al. 2020), and grade repetition (Salas-Velasco et al. 2021; Luschei and Jeong 2021) etc., are not conducive to promoting students’ mathematics grades.
1.2. Family Factors
Factors such as family socio-economic and cultural status, parental education level, and parents’ occupational status play an integral role in math literacy (Kriegbaum and Spinath 2016; Tanskanen et al. 2016). These variables are usually positively correlated with it (Sulis et al. 2020; Xiao and Sun 2021; Wang et al. 2022; Zhu et al. 2018), implying that improving these conditions contributes to student literacy. Moreover, home education resources, such as the availability of Information and Communication Technology (ICT), are also associated with it (Dockery et al. 2020; Tan 2017; Brow 2019). However, views on the impact of home ICT availability are inconsistent. Giannelli and Rapallini (2016) concluded that it is beneficial for students, while X. Hu et al. (2018) held the opposite opinion. Finally, the support provided by parents, including emotional support (Karakus et al. 2023), academic support (Levpušček and Zupančič 2009; Smith and Hausafus 1998), parental involvement (Lerner et al. 2022) and appropriate parental expectations (Daucourt et al. 2021; Tan 2017), all contribute positively to children’s achievements. In particular, parental expectation influences them through direct effects (Rodríguez et al. 2017) and indirect impacts (Pinquart and Ebeling 2020; Wijaya et al. 2022a).
1.3. School Factors
The school variables related to math grades primarily consist of within-classroom factors, school characteristics (Wang et al. 2023b), and teacher-related features.
For instance, larger class sizes generally promote students’ literacy in mathematics (Fung et al. 2018; Tan and Hew 2019), but different viewpoints have been found (Pivovarova and Powers 2019; Erdogdu 2022). Additionally, Denny and Oppedisano (2013) suggested that the significance of class size is linked to the method of analysis used. Apart from class size, the number of teachers is also an important factor in the improvement of math accomplishments. A modest increase in the student-teacher ratio is generally favorable (Gamazo and Martínez-Abad 2020; Erdogdu 2022), while Bokhove and Hampden-Thompson (2022), on the other hand, concluded that the student-teacher ratio does not have a significant impact.
Regarding school characteristics, it has been demonstrated that mathematical literacy is strongly associated with school Information and Communication Technology (ICT) usage (Juhaňák et al. 2018; Wang and Wang 2023), and it is considered beneficial (Hu et al. 2018), even though Eickelmann et al. (2012) and Posso (2016) hold the opposite view. Generally, students in urban schools are more literate than those in rural areas (Dockery et al. 2020; Fernández-Gutiérrez et al. 2020), although Bokhove and Hampden-Thompson (2022) hold a different stance, while Bhutoria and Aljabri (2022) found that its impact is not significant. As for school size, Gümüş et al. (2022) argued that larger schools are better, while Erdogdu (2022) disagreed. In addition, a strong sense of school belonging (Evans and Field 2020) and moderate school competition (Rudolf and Lee 2023) also relate to it. Finally, school bullying is generally considered to harm mathematical achievements (Konishi et al. 2010), and this effect acts indirectly by reducing students’ subjective well-being in school.
Research indicates that students’ perception of teacher support (Ma et al. 2021) and access to teacher support (Mammadov and Schroeder 2023), as well as feedback (Forsythe and Johnson 2017), have a positive effect on their literacy; however, the use of written teacher feedback may be disadvantageous, suggesting that the effect of teacher feedback on mathematical literacy is related to the form of feedback (Selvaraj et al. 2021). Furthermore, high-quality teacher-student relationships are thought to enhance students’ mathematical literacy, and this effect is indirectly achieved by increasing teachers’ self-efficacy (Hajovsky et al. 2020). Regarding cognitive activation (You et al. 2021), Lee (2021) found that cognitive activation was positively associated with students’ mathematics results in Confucian areas. At the same time, it was also noted that the effect was related to the frequency (Caro et al. 2016) and the activity type of cognitive activation (Tourón et al. 2019).
Finally, the purpose of this study is to reveal the important factors affecting mathematics literacy by considering numerous features and highlighting the explanation ability of machine learning approaches in the field of pedagogy. At the same time, the findings of global explanation also provide data support for the upgrading of the education system, and the results of local explanation assist in the development of personalized teaching in the context of artificial intelligence.
2. Materials and Methods
2.1. The Data Sources and Processing
2.1.1. Data Sources
PISA 2022 employs 10 plausible values (PVs) to represent each student’s mathematical literacy, aiming to assess their abilities more accurately. Additionally, the PISA data analysis manual states that “the use of one plausible value or five plausible values does not really have a substantial impact on a large sample.” (OECD 2009) Therefore, the first plausible value (PV1MATH) was selected as each student’s math literacy score. The dataset was obtained from the PISA 2022 of six East Asian education systems (Hong Kong, Macao, Taipei, Singapore, Japan, and Korea), with a total of 34,968 middle-school student samples. From it, 151 characteristics related to individual students (77), household backgrounds (17), and school community (including teachers) (57) were selected as input variables, and PV1MATH was used as an output variable.
2.1.2. Data Processing
Data processing mainly encompasses the steps of selecting features and handling missing values (Figure 1), and the detailed process is as follows. First, samples with a missing rate greater than 70% are excluded. After excluding samples with null values exceeding 70% from the selected 34,968 samples, 34,495 samples remained. Second, features are selected. This study chooses 151 characteristics related to student factors (77), household factors (17), and school factors (57) as independent variables. Among them, student variables contain factors such as grade, math anxiety, and self-efficacy; family features include indicators such as ESCS, family support, and parental expectations; and school variables are related to the sense of belonging, teacher feedback and support, class size, etc. Third, features with a missing rate of more than 70% are eliminated. After removing features with nulls of more than 70% from the selected 151 input variables, 124 features are retained. Fourth, variables with all missing data for each country/region are excluded separately. Some countries/regions in the six East Asian education systems did not participate in the optional questionnaire. For example, Japan, Korea, Singapore, and Taipei did not engage in the well-being questionnaire (OECD 2023a), and the data for them are missing. Thus, this study excludes the characteristics of all missing data for each of them and retains 78 variables. Fifth, variables with moderate/strong multicollinearity are removed. Some of the included variables may have collinearity. For example, ESCS is derived from the highest parental occupation status (HISEI), highest education of parents in years (PAREDINT), and home possessions (HOMEPOS). To avoid covariance among the features reducing the prediction performance of methods, six variables (ICTWKDY, HOMEPOS, PAREDINT, ICTAVSCH, ICTAVHOM, and MCLSIZE) with moderate covariance are excluded, ultimately leaving 72 independent variables (see Table S2). Sixth, the KNN algorithm (K = 8) (Bernardo et al. 2023) is used to complete the missing values. Finally, a feature dataset consisting of 34,495 samples and 72 variables is obtained. Seventh, the dataset is divided into the training and validating datasets in a ratio of 80:20. In this case, the sample size of the training dataset and validating dataset are 27,596 and 6,899, respectively.
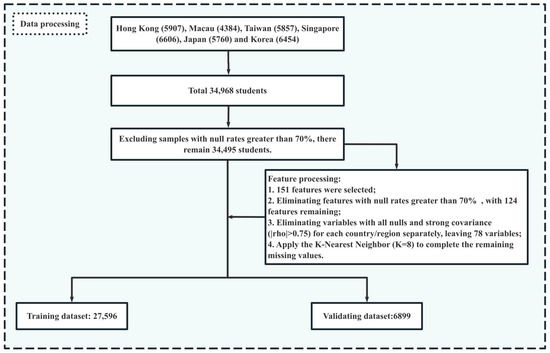
Figure 1.
Flowchart of data processing.
2.2. Methods
2.2.1. Machine Learning Methods
Reference is made to the models commonly used in performance prediction (Munir et al. 2022). Multiple Linear Regression (MLR) (Zhou 2021), Support Vector Regression (SVR) (Li 2023), Decision Tree (DT) (Zhou 2021), Random Forest (RF) (Segal 2004), and XGBoost (Acıslı-Celik and Yesilkanat 2023) were included. Next, GridSearchCV was applied to exhaustively enumerate the given combinations of hyperparameters to determine a set of optimal hyperparameters for the five algorithms. Then, with the help of metrics such as Mean Absolute Percentage Error (MAPE) and Pearson’s Correlation Coefficient (PCCs), the prediction ability of the five optimal models in PISA 2022 mathematical literacy of Hong Kong, Macao, Taipei, Singapore, Japan, and Korea was assessed. After comparing their prediction performance, it was found that the XGBoost model was considered the best.
- (1)
- Multiple linear regression (MLR)
Multiple linear regression is a predictive modeling technique. It employs curves or surfaces to fit some known data points, with the objective of minimizing the difference in distance from the curve or surface to the data points. For a given dataset , where , the loss function can be defined as follows:
The current task is transformed into minimization , i.e.,:
Then, the gradient descent method is employed to minimize the objective function (loss function).
- (2)
- Support vector machine regression (SVR)
Given a dataset , we aim to learn a regression model that is as close as possible to the data points , here and b are the model parameters. In the support vector machine regression algorithm, the loss function is computed only when the absolute value of the difference between and y is more than the error . Therefore, the support vector machine regression problem can be written in the following form:
where C is a regularization constant, , and by introducing slack variables and , the above problem can be written as:
Then, the Lagrange multipliers are introduced to obtain the Lagrange function. The optimal solution to the original problem is obtained by solving its dual problem.
- (3)
- Decision tree (DT)
A regression tree has continuous predictive values, and the average of all samples at a leaf node is usually taken as the prediction value for that node. Its generation is a process of recursively constructing a binary tree. For a given dataset , the j-th variable and its value s are chosen as the cutoff variable and cutoff point, and two regions are defined:
Then, find the optimal cutoff variable j and cutoff point s. Specifically, solve for them.
The optimal cut-point s can be found for a fixed input variable j. The optimal cut-point s can be found for a fixed input variable j.
Iterate over all input variables to find the optimal cutoff variable j, forming a pair (j, s). Sequentially, the space is divided into two regions. Then, repeat the above division process for each region until the stopping condition is satisfied.
- (4)
- Random forest (RF)
Random forest is a combination of bagging and decision trees (Figure 2). The main idea is to train several decision tree models (learners) separately and then let all the learners decide the output of the test samples with an equal voting mechanism. In addition, the training samples of each learner are randomly selected, i.e., an equal number of data are randomly drawn from the original training dataset with replacement as the training samples; and when building the decision tree, a portion of the features is randomly selected from the features to build the decision tree. For the regression problem, Random Forest uses the CART regression tree as an individual learner and adopts the mean of the outputs of all CART regression trees as the final prediction result.
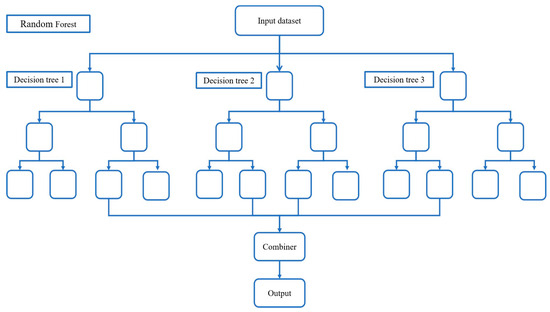
Figure 2.
A random forest consisting of three decision trees.
- (5)
- XGBoost
Extreme Gradient Boosting (XGBoost) was proposed by (T. Chen and Guestrin 2016). Although the popularity of neural networks has increased dramatically in recent years, XGBoost still demonstrates unparalleled and unique advantages in the face of limited training samples, short training cycles, or inexperience in tuning. It is also better at handling structured tabular data and model explanations. XGBoost is a supervised learning algorithm based on Gradient Tree Boosting, which can solve problems such as classification and regression. First, it assigns an initial weight to each training sample. In each iteration, XGBoost trains a decision tree. Second, it adjusts the weights of training samples according to the forecast ability of decision trees. Then, it trains the next round of the weak learner (base learner) on the adjusted dataset and repeats the above process until it reaches the preset stopping condition. Finally, a strong learner is constructed by combining all weak learners through a specific combining strategy.
Assuming that the training dataset is , the model contains K decision trees. Then, the XGBoost model is defined as follows:
denotes the K-th decision tree, and is the first K-1 base learner that has completed training and is fixed. Its objective function is:
represents the loss function, which is used to evaluate the error between the actual value and the model prediction, and is the regular term; T is the leaf nodes of tree ; is a vector consisting of the output values of all leaf nodes (prediction values); and are the hyperparameters. For a given sample , its forecast is obtained by summing the outputs of the K decision trees.
2.2.2. SHAP Method
Considering the extant literature on predicting student accomplishments based on machine learning methods, most of them focus on the capability of model forecast (Munir et al. 2022) and lack sufficient attention to the explanation of model outputs. The article applies the SHAP method to explain how different factors affect the generation of forecast values (mathematical literacy). SHapley Additive exPlanation (SHAP) is a method for explaining machine learning models based on cooperative game theory. It explains the output of the model by calculating how much each feature contributes to the prediction value. The formula is shown below:
represents the prediction value of the i-th sample and is the average of the predicted values of all samples, and is the SHAP value of the j-th feature in the i-th sample, which is used to reflect the extent to which feature j contributes to the model output of sample i. means that feature j has a positive effect on the predicted value of sample i; denotes that feature j hurts sample i and m is the total number of features. There are several variants of the SHAP method, for example, TreeSHAP (Lundberg and Lee 2017), which is particularly suitable for tree-based methods such as XGBoost. In addition, the TreeSHAP method is widely popular for its fast computational speed and high accuracy. Therefore, this paper primarily explains the output results of the XGBoost model with the help of the TreeSHAP method.
3. Results
3.1. Model Training and Prediction Ability
To make the model have a better prediction performance (accuracy), all combinations of the given hyperparameters were exhaustively enumerated using GridSearchCV (5-fold cross-validation by default), and a set of optimal hyperparameters was obtained for Multiple Linear Regression (MLR), Support Vector Regression (SVR), Decision Tree (DT), Random Forest (RF), and XGBoost, respectively (See Table 1). Then, the forecast capability of the optimal hyperparameter models on the validating dataset was compared (see Table 2 and Figure 3). The model evaluation metrics include Mean Square Error (MSE), Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), Coefficient of Determination and Pearson Correlation Coefficients (PCCs). In particular, PCCs are used to measure the degree of linear correlation between model outputs and actual values.

Table 1.
Set of hyperparameters for different methods.

Table 2.
Assessment metrics of optimal parameter models for different models.
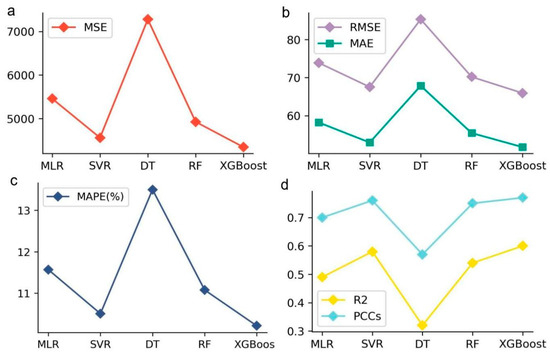
Figure 3.
Model evaluation metrics for different methods on the validating dataset. (a) Mean Square Error (MSE). (b) Root Mean Square Error (RMSE) and Mean Absolute Error (MAE). (c) Mean Absolute Percentage Error (MAPE). (d) Coefficient of Determination and Pearson Correlation Coefficients (PCCs).
In general, when the MAPE is less than 10%, the model is considered to have good predictive ability, and when the MAPE is between 10% to 20%, the predictive effect of the model is considered to be acceptable. As can be seen from Table 2 and Figure 3c, the MAPE of all the models on the validating dataset is between 10% to 15%, which implies that the prediction ability of these models is acceptable. In particular, the evaluation indicators of the XGBoost model (MSE = 4344.98, RMSE = 65.92, MAE = 51.72, and MAPE = 10.21%) are lower than those of MLR, SVR, DT, and RF. Moreover, its coefficient of determination (), and Pearson’s correlation coefficients (PCCs = 0.77) are also superior to the other four models. In addition, this study also gives the prediction performance of the XGBoost model on the Hong Kong, Korea, US, and Spain datasets, and the results show that the prediction ability is within the acceptable range for all regions except Spain (see Figures S1–S4, Table S2). Based on the above analysis, it can be seen that the XGBoost model is the most superior regression model for predicting the mathematical literacy of the PISA 2022 in Hong Kong, Macao, Taipei, Singapore, Japan, and Korea.
3.2. Model Explanation
The SHAP method provides two types of explanations, including global model explanation and local model explanation. The global explanation aims to assess the contribution of each feature to the predicted outcome for all samples. The SHAP summary bar plot determines the importance of the feature to the prediction value by calculating the average of the absolute values of the SHAP values of all samples for each feature. The SHAP summary dot plot presents the SHAP values for each sample. In addition, the SHAP partial dependence plot gives the specific contribution of single features to the model output. The local explanation is concerned with evaluating the contribution of each feature to the prediction results for a specific individual sample and multiple samples.
3.2.1. The Number of Key Influencing Factors
In feature importance analysis, the top 10 (Bernardo et al. 2022), top 15 (Bernardo et al. 2023), and top 20 (Chen et al. 2021) variables are considered to be important influences on students’ literacy. In this study, after identifying XGBoost as the optimal model for predicting math literacy in middle-school students, the SHAP method was employed to evaluate the contribution of each variable to the predictions (math literacy). Subsequently, by comparing the prediction performance (using a validating dataset) of the XGBoost model with varying numbers of features (top 5, top 10, top 15, top 20, top 30, top 40, top 50, top 60, and the full set of features (72)), the key influence numbers were determined. From Table 3 and Figure 4, it can be seen that, on the one hand, the prediction accuracy of the 15-feature model was within an acceptable range (MAPE = 10.95%); on the other hand, the Mean Absolute Percentage Error (MAPE = 10.95%) and Pearson correlation coefficients (PCCs = 0.73) of the 15-feature model were slightly inferior compared to those of the 72-feature model (MAPE = 10.25%, PCCs = 0.77). In addition, the top 15 variables, in terms of feature importance, were able to explain the influence of the educational system on students’ math literacy (Bernardo et al. 2023). Therefore, in this paper, the number of key factors affecting math literacy was set at 15.

Table 3.
Prediction capability of XGBoost with a different number of features.
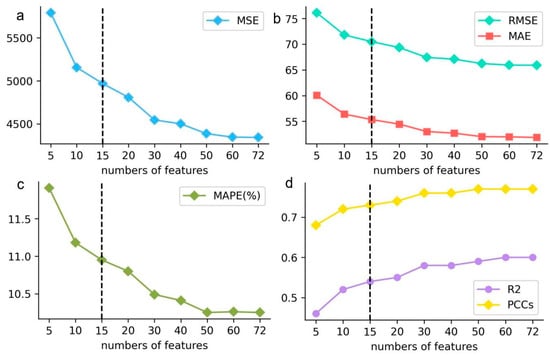
Figure 4.
Prediction ability of XGBoost with a different number of features.
3.2.2. All Samples Analysis
The SHAP summary bar plot ranks the variables by the mean of the absolute values of all students’ SHAP values. On the one hand, the color of the bar represents whether the independent variable positively or negatively affects the forecasts, with red showing a positive contribution and blue the negative. For example, mathematical self-efficacy (MATHEFF) and mathematical anxiety (ANXMAT) have positive and negative impacts on mathematical literacy, respectively (Figure 5). On the other hand, the length of the bar indicates the importance of the feature, with a longer bar indicating that the feature contributes more to the model outputs. For example, mathematical self-efficacy (MATHEFF) has the greatest contribution (Figure 5). The dot plot shows the SHAP value for every sample (Figure 6). Math scores increase as the SHAP value of the feature increases. Each student has one dot on the line of each feature, and these dots are stacked vertically to show the density. The color of the dots changing from blue to red indicates the actual value of the variable changes from small to large. In addition, the SHAP partial dependence plot (Figure 7) gives the contribution of the signal input variable to predictions. A dot represents one student. The x-axis represents the actual value of the independent variable, and the y-axis is the SHAP value of that variable. For example, both MATHEFF > −0.5 and ANXMAT < 0 tend to increase math accomplishments, while MATHEFF < −0.5 and ANXMAT > 0 tend to decrease. Finally, the key factors influencing PISA 2022 mathematics literacy in Hong Kong, Macao, Taipei, Singapore, Japan, and Korea and their contributions are presented in detail below.
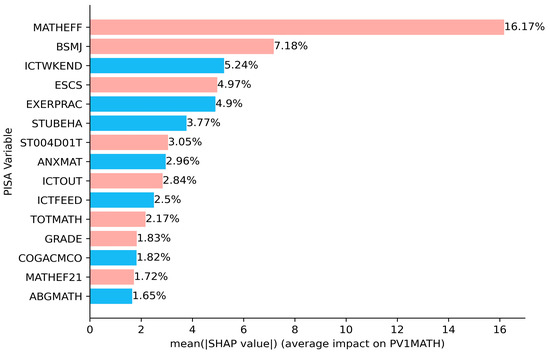
Figure 5.
SHAP summary bar plot.
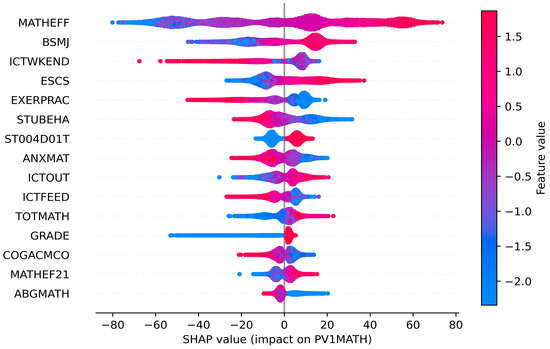
Figure 6.
SHAP summary dot plot.
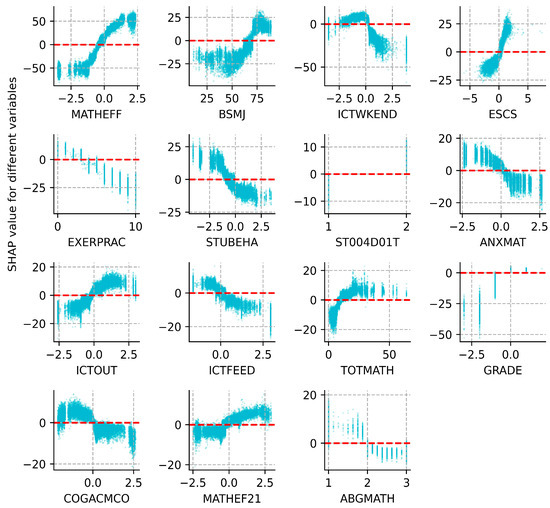
Figure 7.
SHAP partial dependence plot.
- Key influencing factors
- (1)
- Student factors
Student factors related to mathematical literacy include demographic variables such as student gender (ST004D01T) and grade level (GRADE), as well as psychological factors such as mathematical self-efficacy (MATHEFF, MATHEF21), expected occupational status (BSMJ) and math anxiety (ANXMAT). In addition, variables related to learning opportunities are the frequency of using Information and Communication Technology (ICT) for leisure activities on weekends (ICTWKEND), participation in physical activity before and after school (EXERPRAC), the frequency of receiving support and feedback from teachers and classmates with the help of ICT (ICTFEED), and use of ICT outside the classroom for learning activities (ICTOUT). Meanwhile, the school experience focuses on factors that disrupt the school climate, such as truancy and alcoholism (STUBEHA).
ST004D01T refers to student gender. On the one hand, there is a positive contribution to math literacy (Figure 5); on the other hand, when ST004D01T = 1, the SHAP value is below 0, and the individual’s prediction value will be lower than the average of all the samples without considering the effects of other features. In contrast, when ST004D01T = 2, the prediction of math literacy is greater than the mean of all samples (Figure 5). GRADE indicates comparison to modal grade in the country. It exhibits a positive relationship with their accomplishments, i.e., the higher the grade level the student is in, the better the math accomplishments generally are. In particular, GRADE > 0 tends to increase students’ scores; conversely, it inclines to reduce them (Figure 7).
MATHEFF represents mathematics self-efficacy in doing a range of formal and applied mathematics tasks. MATHEF21 denotes mathematical reasoning and 21st-century mathematics tasks. They show a positive relationship with students’ math scores. Meanwhile, MATHEFF > 0 and MATHEF21 > 0 are both favorable to enhance the prediction. BSMJ refers to the students’ expected occupational status, and higher scores on this variable indicate higher levels of a student’s expected occupational status. When BSMJ > 70, most of the students’ SHAP values are larger than 0, i.e., while the effect of other independent variables is not taken into account, there is an increase in math literacy. ANXMAT means mathematics anxiety, and it shows a negative effect. At the same time, ANXMAT < 0 tends to boost students’ accomplishments.
The frequency of ICT activity during a weekend day (ICTWKEND), the days of exercising or practicing a sport before or after school (EXERPRAC), and ICTFEED, which indicates the support or feedback from teachers and other students via ICT, all show a significant negative relationship with pupils’ attainment. This indicates that as these variables increase, their accomplishment declines. However, the use of ICT for school activities outside of the classroom (ICTOUT) generates different influences, which means an appropriate increase in the use of ICT for school-related activities contributes to student grades. Furthermore, ICTWKEND > 0, EXERPRAC > 4, ICTFEED > 0, and ICTOUT < 0 all tend to boost the scores.
STUBEHA means student-related factors affecting school climate, such as student truancy and student use of alcohol or illegal drugs, and it is harmful to their math accomplishments. Alternatively, when STUBEHA < -0.5, most samples have SHAP values less than 0, which suggests that the math grades rise.
- (2)
- Family factors
The index of economic, social, and cultural status (ESCS) is based on three indicators: highest parental occupation status (HISEI), highest education of parents in years (PAREDINT), and home possessions (HOMEPOS). Typically, math literacy shows an upward trend as ESCS improves. And if ECSE < 0, it would tend to lower the scores.
- (3)
- School factors
They can be broadly grouped into within-classroom factors (TOTMATH), school characteristics (ABGMATH), and teacher factors (COGACMCO). The total number of mathematics teachers at school (TOTMATH) has a positive association with the predicted scores, and TOTMATH < 0 tends to reduce their literacy. However, the ability grouping for mathematics classes (ABGMATH) is harmful, revealing that in mathematics classes, blindly teaching students in groups according to their abilities or grades does not always foster an increase in math accomplishments. As for teacher factors, cognitive activation in mathematics (COGACMCO) does not act as a positive influence, as can be seen in Figure 7. In other words, teachers’ moderate use of cognitive activation activities is beneficial to the individual’s success, while excessive or abusive use of cognitive activation activities may lead to a decrease.
- 2.
- Contribution of key influencing factors
The extent to which each significant factor contributed to the PISA 2022 math literacy in Hong Kong, Macao, Taipei, Singapore, Japan, and Korea, in descending order, is as follows: MATHEFF (16.17%), MATHEF21 (1.72%) > BSMJ (7.18%) > ESCS (4.97%) > ICTWKEND (5.24%) > EXERPRAC (4.9%) > STUBEHA (3.77%) > ST004D01T (3.05%) > ANXMAT (2.96%) > ICTOUT (2.84%) > ICTFEED (2.5%) > TOTMATH (2.17%) > GRADE (1.83%) > COGACMCO (1.82%) > ABGMATH (1.65%) (see Figure 5). Mathematics self-efficacy in expressing and applying math to solve practical problems in mathematics had the most significant effect on mathematics literacy, followed by expected occupational status, then the use of ICT for recreational activities on weekends, and so on. Lastly, the school’s ability grouping for mathematics classes had the least impact.
3.2.3. Specific and Multiple Sample Analysis
Beyond the global model explanation, SHAP analysis also provides a local model explanation for single or multiple students. Figure 8 and Figure 9 show the localized bar graphs of a top-performing student A and a low-performing student B , respectively. is the prediction value, and presents the mean of the model outputs of all samples . The lengths of the red and blue bars indicate the extent of the contribution of each variable to the forecasts, where the red bar shows a positive contribution, and the blue bar shows the opposite. Thus, the forecasts of mathematical literacy of student A and student B are 665.988 and 360.925. The variables ESCS, BSMJ, and STUBEHA increase the scores of student A by 21.64, 14.29, and 11.14, respectively, from the mean scores of all samples. ICTSCH increases the literacy of student B by 9.94. Similarly, ST004D01T results in a decrease of 6.41 for student A compared to the mean score (); MATHEFF, ICTWKEND, and BSMJ lead to the forecast of student B to decline by 26.84, 26.68, and 20.63, respectively.
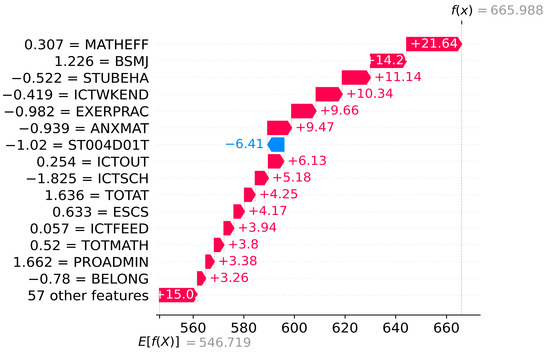
Figure 8.
Waterfall plot for student A.
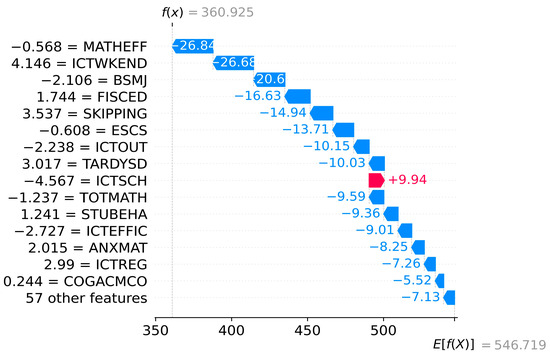
Figure 9.
Waterfall plot for student B.
In the Force plot, the x-axis indicates each student, while the y-axis represents the SHAP value of each feature, i.e., the extent to which it contributes to the prediction value. The features marked in purple are all factors that boost mathematic accomplishments, while the variables marked in green all decrease. Figure 10 presents a force plot consisting of SHAP values of 100 samples, where the first 50 samples belong to top-performing students in mathematics and the last 50 are low-performing students. It can be seen from left to right that the number of features that enhance mathematical literacy gradually decreases.
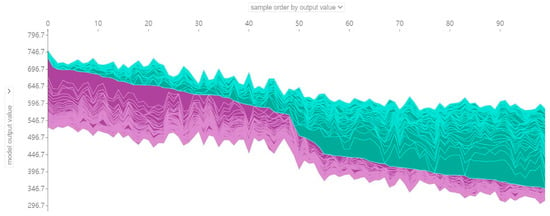
Figure 10.
Force plot for the 100 students.
4. Discussion
- (1)
- XGBoost is the best model for predicting the mathematical literacy of middle-school students.
Several studies have utilized Support Vector Machines (SVM) (Gorostiaga and Rojo-Álvarez 2016) and Random Forest (RF) (Bernardo et al. 2022) to predict students’ mathematics literacy. This paper compares the predicting capability of five algorithms, including SVM, RF, and XGBoost models in PISA 2022 mathematics literacy scores in Hong Kong, Macao, Taipei, Singapore, Japan, and Korea, and finds that XGBoost is the optimal model.
- (2)
- A total of 15 variables, including math self-efficacy, are key influences on math literacy.
The global model explanation identifies 15 factors that are important in determining the math literacy of the whole sample, including math self-efficacy (MATHEFF, MATHEF21), expected occupational status (BSMJ), frequency of participation in leisure activities via Information and Communication Technology (ICT) (ICTWKEND), and so on. Among these variables, eight variables, such as math self-efficacy, expected occupational status, and family’s socio-economic and cultural status (ESCS), contribute positively to mathematical literacy, while seven variables, such as the use of ICT for leisure activities (ICTWKEND), participation in physical activity (EXERPRAC), and math anxiety (ANXMAT) have the opposite contribution. Moreover, these variables are primarily related to student, family, and school factors and are dominated by individual student factors.
In terms of student factors, the larger the value of gender (ST004D01T), the better their attainment, which signifies that boys outperform girls in math literacy accomplishments overall (Liu and Wilson 2009; Gevrek et al. 2020). The contribution of grades to it is positive, which says that students tend to perform better as they move up the grade scale (Aguayo-Téllez and Martínez-Rodríguez 2020). The reason for this is that students in higher grades have a broader base of mathematical knowledge than students in lower grades, and breadth of knowledge tends to show a positive link to their grades (Barnard-Brak et al. 2018).
Both MATHEFF and MATHEF21 are relevant to student self-efficacy. In general, students with stronger self-efficacy are favored, and this finding is consistent with the results of X. Wang et al. (2024), Brow (2019), and Zhao and Ding (2019). Furthermore, the higher the expected occupation status (BSMJ), the more excellent their math outcomes (Bernardo et al. 2022; Tourón et al. 2018). Also, the contribution of BSMJ is followed by MATHEFF, which demonstrates that it is critical to encourage students to engage in activities that foster intrinsic motivation to raise the level of educational and occupational aspirations (Michael and Kyriakides 2023). Nevertheless, students with increased levels of anxiety in math (ANXMAT) perform worse (Barroso et al. 2021; Fan et al. 2019; Cheung 2017). When the value of ANXMAT is more than 0, it tends to a drop in the model outcome, which implies that excessive math anxiety is detrimental.
Regarding learning opportunities, the frequency of ICT activity on weekends (ICTWKEND) is not conducive. This phenomenon is explained by the fact that students who spend too much time on online social networks significantly negatively affect other domains of learning (Cheema and Zhang 2013; Posso 2016). On the contrary, the use of ICT for school activities outside of the classroom (ICTOUT) is beneficial since using ICT for learning relevant activities is useful to their accomplishments (Skryabin et al. 2015). Hence, there is still a need for further exploration to reveal the connection between ICT and pupils’ performance. ICTFEED describes the frequency of students’ use of ICT in various activities related to support or feedback, which may generate a disadvantageous effect. Several studies have shown that teacher support facilitates students’ academic performance (Ma et al. 2021; Mammadov and Schroeder 2023), and students’ positive attitudes toward peer and teacher feedback also contribute to it (Forsythe and Johnson 2017). Yet, Selvaraj et al. (2021) note that although teacher feedback can contribute to it, the form of the feedback, especially written form, may adversely reflect on or be a barrier to student learning. Consequently, the links between the form of feedback and students’ performance in mathematical literacy remain to be thoroughly analyzed. Exercising or practicing a sport before or after school (EXERPRAC) yields a slight negative effect, which may be related to the fact that physical activity reduces the time available for study (Aksoy and Link 2000).
Lastly, regarding school experiences, student-related factors affecting school climate (STUBEHA) are hazardous to student grades, which suggests that curbing undesirable behaviors such as truancy is beneficial (Fernández-Gutiérrez et al. 2020; Yamamura 2019; Sälzer and Heine 2016).
Family factors like the index of economic, social, and cultural status (ESCS) contribute favorably, and enhancing it helps to upgrade students’ mathematics grades (Sulis et al. 2020; Xiao and Sun 2021; Wang et al. 2022; Zhu et al. 2018), as more educated parents can provide more assistance in terms of occupational status and economic resources to their children than less educated (Useem 1992).
As for school factors, TOTMATH expresses the total number of mathematics teachers at school. At TOTMATH < 0, their mathematical grades will decline due to a shortage of teachers is harmful to students’ mathematics study (Bokhove and Hampden-Thompson 2022). In the alternative, some countries, to improve the scores of underperforming students, match them into smaller classrooms for learning (Wang et al. 2023b). Second, ABGMATH reflects the extent to which school mathematics programs are adapted to students of different ability levels. Although Slavin (1987) found that grouping students according to their ability or grades was useful in promoting their math scores, the research by Betts and Shkolnik (2000) stated that school policies that grouped students by ability nearly contributed positively to student literacy, while in heterogeneous classes, middle and poor students tended to perform better in math than their peers in same-ability classes (Linchevski and Kutscher 1998), which may help to explain the result that ABGMATH contributed negatively to math scores. Regarding cognitive activation in mathematics (COGACMC), unlike the findings of Lee (2021), who reports that cognitive activation shows a positive relationship with students’ literacy in Confucian areas, this essay discovers that COGACMC is damaging to their grades, and this gap may link to the frequency (Caro et al. 2016) and type (Tourón et al. 2019) of cognitive activation activities implemented by teachers.
- (3)
- Math self-efficacy is the most significant influence on math literacy.
Among the important factors affecting students’ literacy in mathematics, self-efficacy in applying mathematics to solve real-world problems (16.17%) and self-efficacy in engaging in mathematical reasoning and solving 21st-century mathematical problems (1.72%) contribute the most. This is followed by expected occupation status (7.18%), and finally, ability grouping for mathematics classes (1.65%), i.e., math self-efficacy has the most significant impact on mathematical literacy (You et al. 2021). Additionally, mathematical self-efficacy makes a positive contribution to math literacy. Combining the above two points, it can be concluded that enhancing math self-efficacy is one of the effective ways to improve students’ mathematical literacy.
- (4)
- Differences in key influences affecting math literacy and the extent of their contribution across individuals.
After a detailed analysis of the factors affecting the mathematics literacy of individual students as well as multiple students, it was found that, first, there are significant differences in the key influencing factors between students (see Figure 8 and Figure 9). Second, the same factor may make diametrically opposed contributions to the mathematics grades of different students (see Figure 8, Figure 9 and Figure 10). For instance, math self-efficacy (MATHEFF) may positively contribute to the model output of student A (top-performing student), while it shows a negative connection to student B (low-performing student). Third, the same factor contributes differently to the mathematics scores of different students. For example, support or feedback via ICT (ICTFEED) improves the mathematics scores of student A and student B by 8.01 and 8.34 points, respectively, from the average score of all samples. Meanwhile, the above results can provide valuable data support for personalized education based on artificial intelligence technology (Cao et al. 2024).
5. Conclusions and Limitations
This paper employs machine learning and the SHAP method to analyze 34,968 samples and 151 features from PISA 2022 in Hong Kong, Macao, Taipei, Singapore, Japan, and Korea, aiming to identify the key factors affecting middle-school students’ literacy in mathematics. It has several advantages. First, machine learning techniques in the field of education primarily focus on the prediction ability of the model and pay less attention to its explanatory nature. The article applies the SHAP method to explain the model output by calculating the extent to which each variable contributes to the forecasts. Second, important factors affecting mathematical literacy performance are identified by considering many features to obtain more comprehensive and insightful analysis results. Third, the global model explanation of the SHAP method can help provide specific and actionable ideas for improving the educational system in terms of enhancing students’ performance in mathematical literacy. Fourth, the dominant factors affecting the mathematical literacy of a specific individual, as revealed by the local model explanation, can provide a valuable database for the implementation of personalized instruction in the context of AI-assisted education.
There are 4 conclusions that can be obtained. First, the XGBoost model is considered the best regression algorithm for predicting mathematics literacy. Second, the results of the global model explanation show that the key factors affecting the mathematical literacy performance of all students include 15 variables, such as mathematical self-efficacy (MATHEFF, MATHEF21), expected occupation status (BSMJ), leisure activities with the help of ICT (ICTWKEND) and so on. Among them, mathematics self-efficacy (MATHEFF, MATHEF21), expected occupational status (BSMJ), family’s economic, social, and cultural status (ESCS), use of ICT for learning activities outside the classroom (ICTOUT), number of mathematics teachers in the school (TOTMATH), grade level (GRADE), and gender (ST004D01T) have a positive impact. Conversely, recreational activities through ICT (ICTWKEND), frequency of participation in sports (EXERPRAC), math anxiety (ANXMAT), disruptive behaviors such as truancy and alcohol abuse (STUBEHA), use of ICT to receive support and feedback from teachers and peers (ICTFEED), the ability grouping for mathematics classes (ABGMATH), and cognitive activation to encourage students to do mathematical thinking (COGACMCO) show a negative relationship. Third, math self-efficacy has the most significant effect on students’ math literacy. Fourth, important influences are not identical across individuals; the same factor may have positive or negative effects on various students and does not affect different students’ mathematical literacy to the same extent.
This study captures many samples and features, as well as the complex relationships between them through machine learning, and comprehends these relationships with the aid of SHAP methods to more profoundly and comprehensively reveal the important factors affecting mathematical literacy. In addition, the results of this kind of research have some insights into enhancing students’ mathematical literacy.
First, mathematical self-efficacy (MATHEFF, MATHEF21) plays a positive role in mathematical literacy and ranks first in terms of the degree of its influence. Therefore, teachers should pay attention to cultivating students’ self-efficacy in their daily teaching. For example, setting up reasonable problems and scenarios to help students gain a successful experience and improve their self-efficacy.
Second, the expected occupation status (BSMJ) is just after MATHEFF in terms of its importance to mathematical literacy and plays a positive role. In teachers’ instruction and extracurricular activities, emphasis should be placed on stimulating students’ intrinsic motivation to learn and raising the level of expected occupation.
Third, the frequency of ICT activity-weekend (ICTWKEND), exercising or practicing a sport before or after school (EXERPRAC), and mathematics anxiety (ANXMAT) have a negative effect on mathematics literacy. On the one hand, the larger the value of ICTWKEND and EXERPRAC, the worse the literacy. The possible reason is that students spend too much time on online networks or outside the classroom engaging in activities that are not related to academics. The school, parents, and teachers should rationalize the students’ time for study, rest, and recreation and help students build a healthy view of time. On the other hand, the larger the value of math anxiety, the worse the performance of mathematics literacy. Therefore, schools, parents, and teachers should view students’ academic scores correctly to avoid causing unnecessary anxiety to students. Moreover, some methods to reduce math anxiety should be taught to help students relieve math anxiety.
Fourth, the results of the SHAP local model explanation show that there are some differences in the key influence variables and their degree of influence across individuals. For this reason, when conditions permit, recommendations for individuals can be given based on the key factors it provides for influencing a specific individual and combined with other AI techniques to truly personalize education and teaching.
There are also some limitations. Regarding the data, first, the PISA dataset is derived from subjective responses from students, parents, school administrators, and teachers, which may affect the objectivity of the data. Second, the PISA data are characterized by multiple levels of nesting. However, machine learning neglects the interaction of student-level data with school-level data. Once again, the article mainly focuses on data from six East Asian education systems and only examines the prediction performance of the model on the U.S. and Spanish PISA 2022 datasets. In the future, we can consider incorporating data from more countries (regions) as well as from different years to test the prediction ability of the model. Finally, the data used in the SHAP partial dependence plot, such as MATHEFF, MATHEF21, and ANXMAT, are derived variables based on weighted likelihood estimates (WLE) and normalized to [0, 1]. This means that they do not directly reflect the specific impact of the raw data for each feature on math literacy. Regarding model selection, the study only compares the prediction ability of five machine learning methods, such as Support Vector Machine and XGBoost. Future research can consider introducing deep learning techniques to improve prediction accuracy. As for the model explanation, the SHAP method did not fully consider the causal relationship between features. Future research can try to adopt a model explanation method that considers the causal relationship between features to obtain a deeper understanding.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/jintelligence12100093/s1, Figure S1: Comparison of Hong Kong math literacy performance scores estimated by the XGBoost algorithm with the actual results; Figure S2: Comparison of Korea math literacy performance scores estimated by the XGBoost algorithm with actual results; Figure S3: Comparison of U.S. math literacy performance scores estimated by the XGBoost algorithm with actual results; Figure S4: Comparison of Spain math literacy performance scores estimated by the XGBoost algorithm with actual results; Table S1. 72 variables used for model training; Table S2: Prediction accuracy of XGBoost on PISA math literacy performance in Hong Kong, Korea, the United States and Spain.
Author Contributions
Conceptualization, Y.H., Y.Z. and J.C.; Data curation, D.W.; Investigation, Y.Z.; Methodology, Y.H. and D.W.; Project administration, Y.Z.; Software, Y.H.; Validation, J.C.; Visualization, J.C.; Writing–original draft, Y.H.; Writing–review and editing, Y.H. and D.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “the 2024 Innovation Project of Guangxi Graduate Education, “A Study on Measuring Digital Literacy of Mathematics Teacher Trainees” (XYCSR2024073)”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Acknowledgments
Research for this paper was partially supported by the 2024 Innovation Project of Guangxi Graduate Education (XYCSR2024073) and the Key Project of Guangxi Higher Education Undergraduate Education Teaching Reform Project (2023JGZ107), and I would like to thank all who participated in this research.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Acıslı-Celik, Sibel, and Cafer Mert Yesilkanat. 2023. Predicting science achievement scores with machine learning algorithms: A case study of OECD PISA 2015–2018 data. Neural Computing and Applications 35: 21201–28. [Google Scholar] [CrossRef]
- Aguayo-Téllez, Ernesto, and Flor E. Martínez-Rodríguez. 2020. Early school entrance and middle-run academic performance in Mexico: Evidence for 15-year-old students from the PISA test. Large-Scale Assessments in Education 8: 11. [Google Scholar] [CrossRef]
- Aksoy, Tevfik, and Charles R Link. 2000. A panel analysis of student mathematics achievement in the US in the 1990s: Does increasing the amount of time in learning activities affect math achievement? Economics of Education Review 19: 261–77. [Google Scholar] [CrossRef]
- Barnard-Brak, Lucy, William Y. Lan, and Zhanxia Yang. 2018. Differences in mathematics achievement according to opportunity to learn: A 4pL item response theory examination. Studies in Educational Evaluation 56: 1–7. [Google Scholar] [CrossRef]
- Barroso, Connie, Colleen M. Ganley, Amanda L. McGraw, Elyssa A. Geer, Sara A. Hart, and Mia C. Daucourt. 2021. A Meta-Analysis of the Relation Between Math Anxiety and Math Achievement. Psychological Bulletin 147: 134–68. [Google Scholar] [CrossRef]
- Bernardo, Allan B. I. 2021. Socioeconomic status moderates the relationship between growth mindset and learning in mathematics and science: Evidence from PISA 2018 Philippine data. International Journal of School and Educational Psychology 9: 208–22. [Google Scholar] [CrossRef]
- Bernardo, Allan B. I., Macario O. Cordel, Marissa Ortiz Calleja, Jude Michael M. Teves, Sashmir A. Yap, and Unisse C. Chua. 2023. Profiling low-proficiency science students in the Philippines using machine learning. Humanities and Social Sciences Communications 10: 192. [Google Scholar] [CrossRef]
- Bernardo, Allan B. I., Macario O. Cordel, Minie Rose C. Lapinid, Jude Michael M. Teves, Sashmir A. Yap, and Unisse C. Chua. 2022. Contrasting Profiles of Low-Performing Mathematics Students in Public and Private Schools in the Philippines: Insights from Machine Learning. Journal of Intelligence 10: 61. [Google Scholar] [CrossRef]
- Betts, Julian R., and Jamie L. Shkolnik. 2000. The effects of ability grouping on student achievement and resource allocation in secondary schools. Economics of Education Review 19: 1–15. Available online: www.elsevier.com/locate/econedurev (accessed on 17 December 2023). [CrossRef]
- Bhutoria, Aditi, and Nayyaf Aljabri. 2022. Patterns of cognitive returns to Information and Communication Technology (ICT) use of 15-year-olds: Global evidence from a Hierarchical Linear Modeling approach using PISA 2018. Computers & Education 181: 104447. [Google Scholar] [CrossRef]
- Bokhove, Christian, and Gillian Hampden-Thompson. 2022. Country and school family composition’s effects on mathematics achievement. School Effectiveness and School Improvement 33: 280–302. [Google Scholar] [CrossRef]
- Brow, Mark V. 2019. Significant predictors of mathematical literacy for top-tiered countries/economies, Canada, and the United States on PISA 2012: Case for the sparse regression model. British Journal of Educational Psychology 89: 726–49. [Google Scholar] [CrossRef] [PubMed]
- Bücker, Susanne, Sevim Nuraydin, Bianca A. Simonsmeier, Michael Schneider, and Maike Luhmann. 2018. Subjective well-being and academic achievement: A. meta-analysis. Journal of Research in Personality 74: 83–94. [Google Scholar] [CrossRef]
- Cao, Canxi, Tongxin Zhang, and Tao Xin. 2024. The effect of reading engagement on scientific literacy—An analysis based on the XGBoost method. Frontiers in Psychology 15: 1329724. [Google Scholar] [CrossRef] [PubMed]
- Caro, Daniel H., Jenny Lenkeit, and Leonidas Kyriakides. 2016. Teaching strategies and differential effectiveness across learning contexts: Evidence from PISA 2012. Studies in Educational Evaluation 49: 30–41. [Google Scholar] [CrossRef]
- Cheema, Jehanzeb R., and Bo Zhang. 2013. Quantity and quality of computer use and academic achievement: Evidence from a large-scale international test program. International Journal of Education and Development using Information and Communication Technology (IJEDICT) 9: 95–106. [Google Scholar]
- Chen, Jiangping, Yang Zhang, Yueer Wei, and Jie Hu. 2021. Discrimination of the Contextual Features of Top Performers in Scientific Literacy Using a Machine Learning Approach. Research in Science Education 51: 129–58. [Google Scholar] [CrossRef]
- Chen, Tianqi, and Carlos Guestrin. 2016. XGBoost: A Scalable Tree Boosting System. Paper presented at the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, August 13–17; pp. 785–94. [Google Scholar] [CrossRef]
- Cheung, Kwok Cheung. 2017. The effects of resilience in learning variables on mathematical literacy performance: A study of learning characteristics of the academic resilient and advantaged low achievers in Shanghai, Singapore, Hong Kong, Taiwan and Korea. Educational Psychology 37: 965–82. [Google Scholar] [CrossRef]
- Courtney, Matthew, Mehmet Karakus, Zara Ersozlu, and Kaidar Nurumov. 2022. The influence of ICT use and related attitudes on students’ math and science performance: Multilevel analyses of the last decade’s PISA surveys. Large-Scale Assessments in Education 10: 8. [Google Scholar] [CrossRef]
- Daucourt, Mia C., Amy R. Napoli, Jamie M. Quinn, Sarah G. Wood, and Sara A. Hart. 2021. The Home Math Environment and Math Achievement: A Meta-Analysis. Psychological Bulletin 147: 565–96. [Google Scholar] [CrossRef] [PubMed]
- Denny, Kevin, and Veruska Oppedisano. 2013. The surprising effect of larger class sizes: Evidence using two identification strategies. Labour Economics 23: 57–65. [Google Scholar] [CrossRef]
- de Vink, Isabelle C., Lisette Hornstra, and Evelyn H. Kroesbergen. 2023. Latent Profile Analysis of Working Memory: Relations with Creativity and Academic Achievement. Creativity Research Journal 35: 1–17. [Google Scholar] [CrossRef]
- Dockery, Alfred Michael, Paul Koshy, and Ian W. Li. 2020. Culture, migration and educational performance: A focus on gender outcomes using Australian PISA tests. The Australian Educational Researcher 47: 39–59. [Google Scholar] [CrossRef]
- Eickelmann, Birgit, Kerstin Drossel, Heike Wendt, and Wilfried Bos. 2012. ICT-use in primary schools and children’s mathematics achievement-a multi-level approach to compare educational systems through an international lens with TIMSS data. Paper presented at Joint AARE APERA International Conference, WERA Focal Meeting, Sydney, Australia, December 2–6, vol. 2012. [Google Scholar]
- Erdogdu, Funda. 2022. Potential predictors of student attainment: A longitudinal study at global level. Education and Information Technologies 27: 9689–711. [Google Scholar] [CrossRef]
- Evans, Danielle, and Andy P. Field. 2020. Maths attitudes, school affect and teacher characteristics as predictors of maths attainment trajectories in primary and secondary education. Royal Society Open Science 7: 200975. [Google Scholar] [CrossRef]
- Fan, Xizhen, Ronald K. Hambleton, and Minqiang Zhang. 2019. Profiles of mathematics anxiety among 15-year-old students: A cross-cultural study using multi-group latent profile analysis. Frontiers in Psychology 10: 1217. [Google Scholar] [CrossRef]
- Fernández-Gutiérrez, Marcos, Gregorio Gimenez, and Jorge Calero. 2020. Is the use of ICT in education leading to higher student outcomes? Analysis from the Spanish Autonomous Communities. Computers & Education 157: 103969. [Google Scholar] [CrossRef]
- Forsythe, Alex, and Sophie Johnson. 2017. Thanks, but no-thanks for the feedback. Assessment & Evaluation in Higher Education 42: 850–59. [Google Scholar]
- Fung, Francis, Cheng Yong Tan, and Gaowei Chen. 2018. Student engagement and mathematics achievement: Unraveling main and interactive effects. Psychology in the Schools 55: 815–31. [Google Scholar] [CrossRef]
- Gamazo, Adriana, and Fernando Martínez-Abad. 2020. An Exploration of Factors Linked to Academic Performance in PISA 2018 Through Data Mining Techniques. Frontiers in Psychology 11: 575167. [Google Scholar] [CrossRef] [PubMed]
- Gevrek, Z. Eylem, Deniz Gevrek, and Christian Neumeier. 2020. Explaining the gender gaps in mathematics achievement and attitudes: The role of societal gender equality. Economics of Education Review 76: 101978. [Google Scholar] [CrossRef]
- Giannelli, Gianna Claudia, and Chiara Rapallini. 2016. Immigrant student performance in Math: Does it matter where you come from? Economics of Education Review 52: 291–304. [Google Scholar] [CrossRef]
- Gjicali, Kalina, and Anastasiya A. Lipnevich. 2021. Got math attitude? (In)direct effects of student mathematics attitudes on intentions, behavioral engagement, and mathematics performance in the U.S. PISA. Contemporary Educational Psychology 67: 102019. [Google Scholar] [CrossRef]
- Gorostiaga, Arantza, and José Luis Rojo-Álvarez. 2016. On the use of conventional and statistical-learning techniques for the analysis of PISA results in Spain. Neurocomputing 171: 625–37. [Google Scholar] [CrossRef]
- Gómez-Talal, Ismael, Luis Bote-Curiel, and José Luis Rojo-Álvarez. 2024. Understanding the disparities in Mathematics performance: An interpretability-based examination. Engineering Applications of Artificial Intelligence 133: 108109. [Google Scholar] [CrossRef]
- Gümüş, Sedat, Mehmet Şükrü Bellibaş, and Marcus Pietsch. 2022. School leadership and achievement gaps based on socioeconomic status: A search for socially just instructional leadership. Journal of Educational Administration 60: 419–38. [Google Scholar] [CrossRef]
- Hajovsky, Daniel B., Kari A. Oyen, Steven R. Chesnut, and Susan J. Curtin. 2020. Teacher–student relationship quality and math achievement: The mediating role of teacher self-efficacy. Psychology in the Schools 57: 111–34. [Google Scholar] [CrossRef]
- Hilbert, Sven, Stefan Coors, Elisabeth Kraus, Bernd Bischl, Alfred Lindl, Mario Frei, Johannes Wild, Stefan Krauss, David Goretzko, and Clemens Stachl. 2021. Machine learning for the educational sciences. Review of Education 9: e3310. [Google Scholar] [CrossRef]
- Hu, Jie, and Rushi Yu. 2021. Influence of students’ perceptions of instruction quality on their digital reading performance in 29 OECD countries: A multilevel analysis. Computers & Education 189: 104591. [Google Scholar] [CrossRef]
- Hu, Jie, and Yanyu Wang. 2022. The effects of ICT-based social media on adolescents’ digital reading performance: A longitudinal study of PISA 2009, PISA 2012, PISA 2015 and PISA 2018. Computers & Education 175: 104342. [Google Scholar] [CrossRef]
- Hu, Xiang, Yang Gong, Chun Lai, and Frederick K. S. Leung. 2018. The relationship between ICT and student literacy in mathematics, reading, and science across 44 countries: A multilevel analysis. Computers & Education 125: 1–13. [Google Scholar] [CrossRef]
- Juhaňák, Libor, Jiří Zounek, Klára Záleská, Ondřej Bárta, and Kristýna Vlčková. 2018. The Relationship between Students’ ICT Use and Their School Performance: Evidence from PISA 2015 in the Czech Republic. Orbis Scholae 12: 37–64. [Google Scholar] [CrossRef]
- Karakus, Mehmet, Matthew Courtney, and Hasan Aydin. 2023. Understanding the academic achievement of the first- and second-generation immigrant students: A multi-level analysis of PISA 2018 data. Educational Assessment, Evaluation and Accountability 35: 233–78. [Google Scholar] [CrossRef]
- Kim, Sunha. 2018. ICT and the UN’s sustainable development goal for education: Using ICT to boost the math performance of immigrant youths in the US. Sustainability 10: 4584. [Google Scholar] [CrossRef]
- Konishi, Chiaki, Shelley Hymel, Bruno D. Zumbo, and Zhen Li. 2010. Do School Bullying and Student—Teacher Relationships Matter for Academic Achievement? A Multilevel Analysis. Canadian Journal of School Psychology 25: 19–39. [Google Scholar] [CrossRef]
- Kriegbaum, Katharina, and Birgit Spinath. 2016. Explaining Social Disparities in Mathematical Achievement: The Role of Motivation. European Journal of Personality 30: 45–63. [Google Scholar] [CrossRef]
- Laaninen, Markus, Nevena Kulic, and Jani Erola. 2024. Age of entry into early childhood education and care, literacy and reduction of educational inequality in Nordic countries. European Societies 26: 1–30. [Google Scholar] [CrossRef]
- Lee, Hanol. 2022. What drives the performance of Chinese urban and rural secondary schools: A machine learning approach using PISA 2018. Cities 123: 103609. [Google Scholar] [CrossRef]
- Lee, Jihyun. 2021. Teacher–student relationships and academic achievement in Confucian educational countries/systems from PISA 2012 perspectives. Educational Psychology 41: 764–85. [Google Scholar] [CrossRef]
- Lerner, Rachel E., Wendy S. Grolnick, Alessandra J. Caruso, and Madeline R. Levitt. 2022. Parental involvement and children’s academics: The roles of autonomy support and parents’ motivation for involvement. Contemporary Educational Psychology 68: 102039. [Google Scholar] [CrossRef]
- Levpušček, Melita Puklek, and Maja Zupančič. 2009. Math achievement in early adolescence: The role of parental involvement, teachers’ behavior, and students’ motivational beliefs about math. The Journal of Early Adolescence 29: 541–70. [Google Scholar] [CrossRef]
- Lezhnina, Olga, and Gábor Kismihók. 2022. Combining statistical and machine learning methods to explore German students’ attitudes towards ICT in PISA. International Journal of Research & Method in Education 45: 180–99. [Google Scholar] [CrossRef]
- Li, Hang. 2023. Machine Learning Methods. Berlin: Springer Nature. [Google Scholar]
- Linchevski, Liora, and Bilha Kutscher. 1998. Tell Me with Whom You’re Learning, and I’ll Tell You How Much You’ve Learned: Mixed-Ability versus Same-Ability Grouping in Mathematics. Journal for Research in Mathematics Education 29: 533–54. [Google Scholar] [CrossRef]
- Lindberg, Sara M., Janet Shibley Hyde, Marcia C. Linn, and Jennifer L. Petersen. 2010. New Trends in Gender and Mathematics Performance: A Meta-Analysis. Psychological Bulletin 136: 1123. [Google Scholar] [CrossRef]
- Liu, Ou Lydia, and Mark Wilson. 2009. Gender differences in large-scale math assessments: PISA trend 2000 and 2003. Applied Measurement in Education 22: 164–84. [Google Scholar] [CrossRef]
- Lundberg, Scott M., and Su-In Lee. 2017. A unified approach to interpreting model predictions. Advances in Neural Information Processing Systems 30: 4765–4774. [Google Scholar]
- Luschei, Thomas F., and Dong Wook Jeong. 2021. School Governance and Student Achievement: Cross-National Evidence From the 2015 PISA. Educational Administration Quarterly 57: 331–71. [Google Scholar] [CrossRef]
- Ma, Lihong, Haifeng Luo, and Leifeng Xiao. 2021. Perceived teacher support, self-concept, enjoyment and achievement in reading: A multilevel mediation model based on PISA 2018. Learning and Individual Differences 85: 101947. [Google Scholar] [CrossRef]
- Mammadov, Sakhavat, and Kayla Schroeder. 2023. A meta-analytic review of the relationships between autonomy support and positive learning outcomes. Contemporary Educational Psychology 75: 102235. [Google Scholar] [CrossRef]
- Melkonian, Michael, Shaljan Areepattamannil, Luisa Menano, and Patricia Fildago. 2019. Examining acculturation orientations and perceived cultural distance among immigrant adolescents in Portugal: Links to performance in reading, mathematics, and science. Social Psychology of Education 22: 969–89. [Google Scholar] [CrossRef]
- Michael, Demos, and Leonidas Kyriakides. 2023. Mediating effects of motivation and socioeconomic status on reading achievement: A secondary analysis of PISA 2018. Large-Scale Assessments in Education 11: 31. [Google Scholar] [CrossRef]
- Munir, Hussan, Bahtijar Vogel, and Andreas Jacobsson. 2022. Artificial Intelligence and Machine Learning Approaches in Digital Education: A Systematic Revision. Information 13: 203. [Google Scholar] [CrossRef]
- OECD. 2003. Literacy Skills for the World of Tomorrow-Further Results from Pisa 2000 Executive Summary Organisation for Economic co-Operation and Development Unesco Institute for Statistics. Available online: www.copyright.com (accessed on 24 March 2024).
- OECD. 2009. PISA Data Analysis Manual: SPSS. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- OECD. 2023a. PISA 2022 Results. Paris: OECD Publishing, vol. I. [Google Scholar] [CrossRef]
- OECD. 2023b. PISA 2022 Results (Volume II): Learning During–and From–Disruption. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- OECD. 2023c. PISA 2022 Technical Report. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- OECD, and UNESCO Institute for Statistics. 2003. Literacy Skills for the World of Tomorrow. Available online: https://www.oecd-ilibrary.org/content/publication/9789264102873-en (accessed on 12 March 2024).
- Pinquart, Martin, and Markus Ebeling. 2020. Parental Educational Expectations and Academic Achievement in Children and Adolescents—A Meta-analysis. Educational Psychology Review 32: 463–80. [Google Scholar] [CrossRef]
- Pitsia, Vasiliki, Andy Biggart, and Anastasios Karakolidis. 2017. The role of students’ self-beliefs, motivation and attitudes in predicting mathematics achievement: A multilevel analysis of the Programme for International Student Assessment data. Learning and Individual Differences 55: 163–73. [Google Scholar] [CrossRef]
- Pivovarova, Margarita, and Jeanne M. Powers. 2019. Generational status, immigrant concentration and academic achievement: Comparing first and second-generation immigrants with third-plus generation students. Large-Scale Assessments in Education 7: 7. [Google Scholar] [CrossRef]
- Posso, Alberto. 2016. Internet Usage and Educational Outcomes Among 15-Year-Old Australian Students. International Journal of Communication 10. Available online: http://ijoc.org (accessed on 15 June 2024).
- Rodríguez, Susana, Isabel Piñeiro, Ma Luisa Gómez-Taibo, Bibiana Regueiro, Iris Estévez, and Antonio Valle. 2017. Un modelo explicativo del rendimiento en matemáticas: Percepción de la implicación parental y motivación académica. Psicothema 29: 184–90. [Google Scholar] [CrossRef]
- Rudolf, Robert, and Jieun Lee. 2023. School climate, academic performance, and adolescent well-being in Korea: The roles of competition and cooperation. Child Indicators Research 16: 917–40. [Google Scholar] [CrossRef]
- Salas-Velasco, Manuel, Dolores Moreno-Herrero, and José Sánchez-Campillo. 2021. Positive Geographical Spillovers of Human Capital on Student Learning Outcomes. Applied Spatial Analysis and Policy 14: 415–43. [Google Scholar] [CrossRef]
- Sälzer, Christine, and Jörg-Henrik Heine. 2016. Students’ skipping behavior on truancy items and (school) subjects and its relation to test performance in PISA 2012. International Journal of Educational Development 46: 103–13. [Google Scholar] [CrossRef]
- Sebastian, James, and Haigen Huang. 2016. Examining the relationship of a survey based measure of math creativity with math achievement: Cross-national evidence from PISA 2012. International Journal of Educational Research 80: 74–92. [Google Scholar] [CrossRef]
- Segal, Mark R. 2004. Machine Learning Benchmarks and Random Forest Regression. San Francisco: UCSF Center for Bioinformatics and Molecular Biostatistics. Available online: https://escholarship.org/uc/item/35x3v9t4 (accessed on 23 September 2024).
- Selvaraj, Anne Malar, Hazita Azman, and Wahiza Wahi. 2021. Teachers’ feedback practice and students’ academic achievement: A systematic literature review. International Journal of Learning, Teaching and Educational Research 20: 308–322. [Google Scholar] [CrossRef]
- Skaalvik, Einar M., Roger A. Federici, and Robert M. Klassen. 2015. Mathematics achievement and self-efficacy: Relations with motivation for mathematics. International Journal of Educational Research 72: 129–36. [Google Scholar] [CrossRef]
- Skryabin, Maxim, JingJing Zhang, Luman Liu, and Danhui Zhang. 2015. How the ICT development level and usage influence student achievement in reading, mathematics, and science. Computers & Education 85: 49–58. [Google Scholar] [CrossRef]
- Slavin, Robert E. 1987. Ability Grouping and Student Achievement in Elementary Schools: A Best-Evidence Synthesis. Review of Educational Research 57: 293–336. [Google Scholar] [CrossRef]
- Smith, Frances M., and Cheryl O. Hausafus. 1998. Relationship of family support and ethnic minority students’ achievement in science and mathematics. Science Education 82: 111–25. [Google Scholar] [CrossRef]
- Spörlein, Christoph, and Elmar Schlueter. 2018. How education systems shape cross-national ethnic inequality in math competence scores: Moving beyond mean differences. PLoS ONE 13: e0193738. [Google Scholar] [CrossRef] [PubMed]
- Stankov, Lazar, Jihyun Lee, Wenshu Luo, and David J. Hogan. 2012. Confidence: A better predictor of academic achievement than self-efficacy, self-concept and anxiety? Learning and Individual Differences 22: 747–58. [Google Scholar] [CrossRef]
- Sulis, Isabella, Francesca Giambona, and Mariano Porcu. 2020. Adjusted indicators of quality and equity for monitoring the education systems over time. Insights on EU15 countries from PISA surveys. Socio-Economic Planning Sciences 69: 100714. [Google Scholar] [CrossRef]
- Tan, Cheng Yong. 2017. Do parental attitudes toward and expectations for their children’s education and future jobs matter for their children’s school achievement? British Educational Research Journal 43: 1111–30. [Google Scholar] [CrossRef]
- Tan, Cheng Yong, and Khe Foon Hew. 2019. The Impact of Digital Divides on Student Mathematics Achievement in Confucian Heritage Cultures: A Critical Examination Using PISA 2012 Data. International Journal of Science and Mathematics Education 17: 1213–32. [Google Scholar] [CrossRef]
- Tanskanen, Antti O., Jani Erola, and Johanna Kallio. 2016. Parental Resources, Sibship Size, and Educational Performance in 20 Countries: Evidence for the Compensation Model. Cross-Cultural Research 50: 452–77. [Google Scholar] [CrossRef] [PubMed]
- Tourón, Javier, Emelina López González, Luis Lizasoain, M. J. Pedro, and Enrique Navarro Asencio. 2018. Spanish High and Low achievers in Science in PISA 2015: Impact analysis of some contextual variables. Revista de Educacion 148: 156–84. [Google Scholar] [CrossRef]
- Tourón, Javier, Enrique Navarro-Asencio, Luis Lizasoain, Emelina López-González, and María José García-San Pedro. 2019. How teachers’ practices and students’ attitudes towards technology affect mathematics achievement: Results and insights from PISA 2012. Research Papers in Education 34: 263–75. [Google Scholar] [CrossRef]
- Useem, Elizabeth L. 1992. Middle Schools and Math Groups: Parents’ Involvement in Children’s Placement. Sociology of Education 65: 263–79. [Google Scholar] [CrossRef]
- Wang, Faming, Ronnel B. King, and Shing On Leung. 2023a. Why do East Asian students do so well in mathematics? A machine learning study. International Journal of Science and Mathematics Education 21: 691–711. [Google Scholar] [CrossRef]
- Wang, Faming, Yaping Liu, and Shing On Leung. 2022. Disciplinary Climate, Opportunity to Learn, and Mathe-matics Achievement: An Analysis Using Doubly Latent Multilevel Structural Equation Modeling. School Effectiveness and School Improvement 33: 479–96. [Google Scholar] [CrossRef]
- Wang, Xiaofang Sarah, Laura B. Perry, Anabela Malpique, and Tobias Ide. 2023b. Factors predicting mathematics achievement in PISA: A systematic review. Large-Scale Assessments in Education 11: 24. [Google Scholar] [CrossRef]
- Wang, Xuran, Richard T. Houang, William H. Schmidt, and Kimberly S. Kelly. 2024. Relationship between Opportunity to Learn, Mathematics Self-Efficacy, and Math Performance: Evidence from PISA 2012 in 63 Countries and Economies. International Journal of Science and Mathematics Education 22: 1–26. [Google Scholar] [CrossRef]
- Wang, Yajing, and Yashuang Wang. 2023. Exploring the relationship between educational ICT resources, student engagement, and academic performance: A multilevel structural equation analysis based on PISA 2018 data. Studies in Educational Evaluation 79: 101308. [Google Scholar] [CrossRef]
- Wijaya, Tommy Tanu, Imam Fitri Rahmadi, Siti Chotimah, Jailani Jailani, and Dhoriva Urwatul Wutsqa. 2022a. A Case Study of Factors That Affect Secondary School Mathematics Achievement: Teacher-Parent Support, Stress Levels, and Students’ Well-Being. International Journal of Environmental Research and Public Health 19: 16247. [Google Scholar] [CrossRef]
- Wijaya, Tommy Tanu, Yiming Cao, Robert Weinhandl, and Maximus Tamur. 2022b. A Meta-Analysis of the Effects of E-Books on students’ mathematics achievement. Heliyon 8: e09432. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Feiya, and Li Sun. 2021. Students’ Motivation and Affection Profiles and Their Relation to Mathematics Achievement, Persistence, and Behaviors. Frontiers in Psychology 11: 533593. [Google Scholar] [CrossRef]
- Xiao, Feiya, and Li Sun. 2022. Profiles of student ICT use and their relations to background, motivational factors, and academic achievement. Journal of Research on Technology in Education 54: 456–72. [Google Scholar] [CrossRef]
- Yamamura, Eiji. 2019. Gender wage gap and its effect on test scores of immigrant students. Journal of Economic Studies 46: 872–87. [Google Scholar] [CrossRef]
- Yao, Yiling, Qiping Kong, and Jinfa Cai. 2018. Investigating Elementary and Middle School Students’ Subjective Well-Being and Mathematical Performance in Shanghai. International Journal of Science and Mathematics Education 16: 107–27. [Google Scholar] [CrossRef]
- You, Sukkyung, Eui Kyung Kim, Sun Ah Lim, and Myley Dang. 2021. Student and Teacher Characteristics on Student Math Achievement. Journal of Pacific Rim Psychology 15: 1834490921991428. [Google Scholar] [CrossRef]
- Zhang, Yuan, Shannon Russell, and Sean Kelly. 2022. Engagement, achievement, and teacher classroom practices in mathematics: Insights from TIMSS 2011 and PISA 2012. Studies in Educational Evaluation 73: 101146. [Google Scholar] [CrossRef]
- Zhao, Yuyang, and Cody Ding. 2019. The association between students mathematic knowledge and factors related to students, parents, and school: A cross-cultural comparison study. International Journal of Educational Research 93: 210–17. [Google Scholar] [CrossRef]
- Zhou, Zhi-Hua. 2021. Machine Learning. Berlin: Springer Nature. [Google Scholar]
- Zhu, Yan, Gabriele Kaiser, and Jinfa Cai. 2018. Gender equity in mathematical achievement: The case of China. Educational Studies in Mathematics 99: 245–60. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).