Implicit Processing of Numerical Order: Evidence from a Continuous Interocular Flash Suppression Study
Abstract
1. Introduction
1.1. Implicit Processing of Ordinality
1.2. Ordinality and Numerosity
1.3. The Current Study
2. Experiment 1
2.1. Material and Method
2.1.1. Participants
2.1.2. Experimental Task
2.1.3. Stimuli
Prime Stimuli
Mask Stimuli
Target Stimuli
2.1.4. Apparatus
2.1.5. Procedure
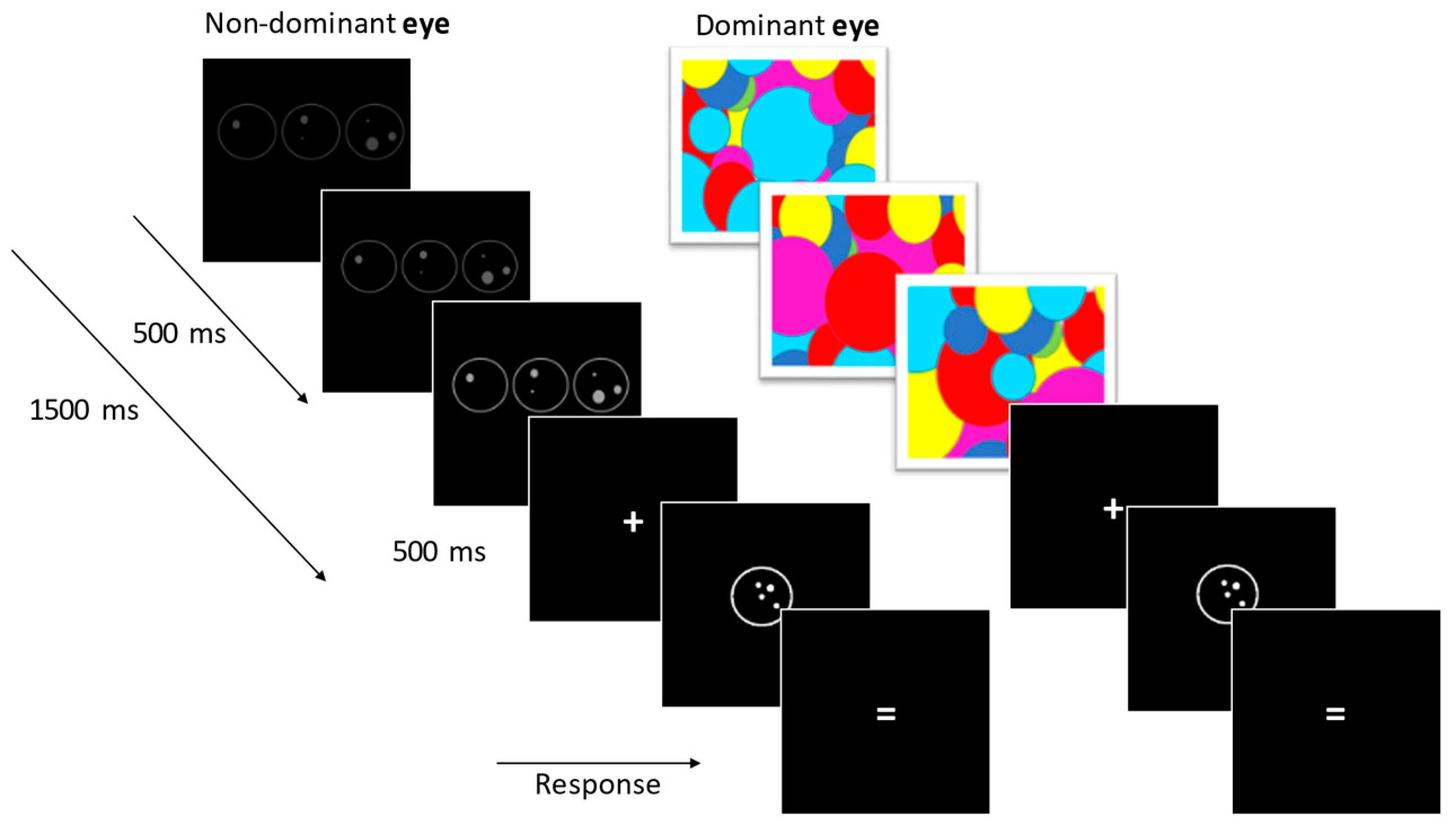
CFS Ordered Priming Task
Objective Test Block
2.1.6. Data Analysis
Modeling Strategy
2.2. Model Results and Discussion
3. Experiment 2
3.1. Materials and Method
3.1.1. Participants
3.1.2. Prime Contrast
3.1.3. Objective Test Block
3.1.4. Data Analysis
Bayesian Statistical Analyses
3.2. Results and Discussion
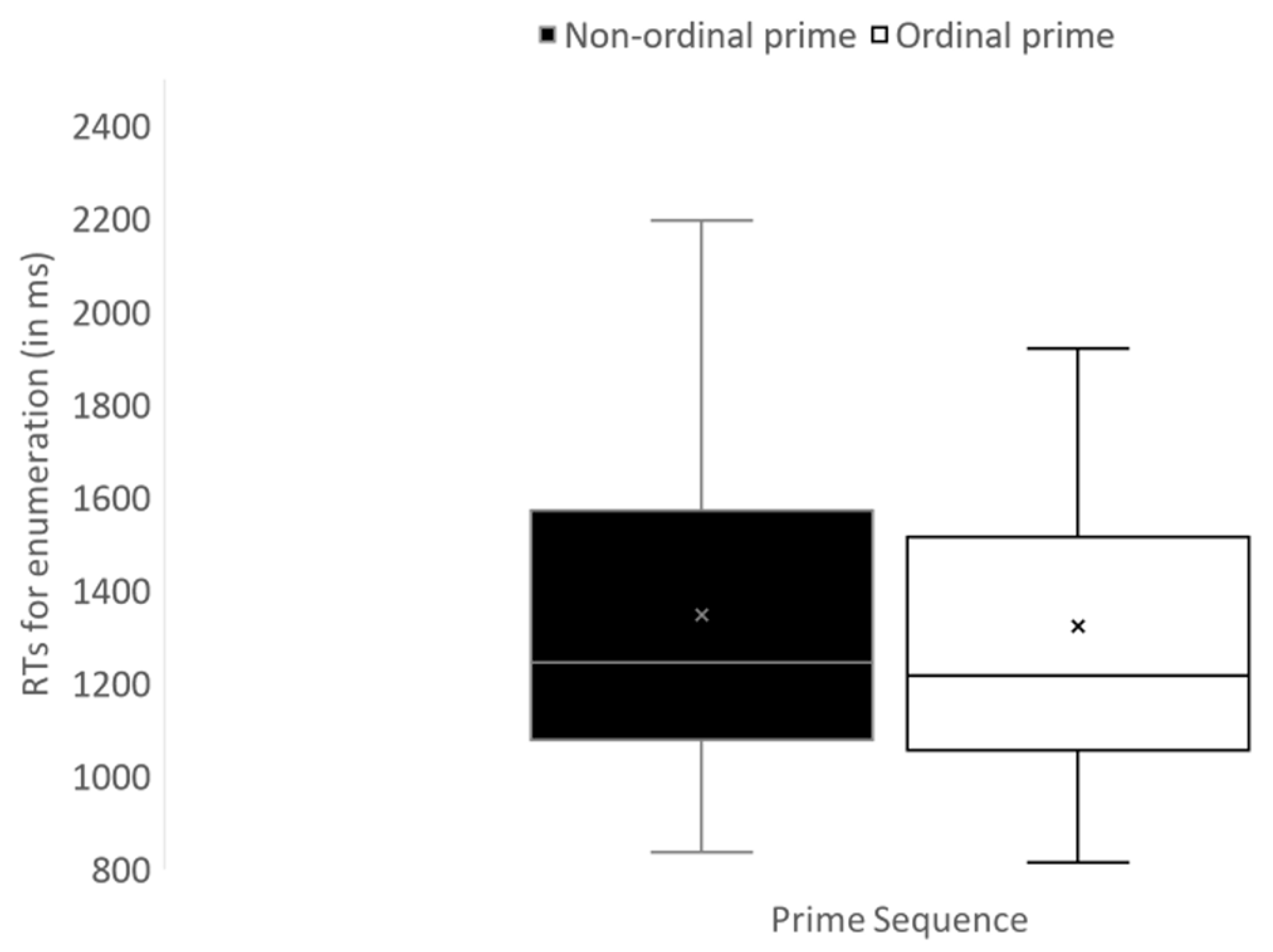
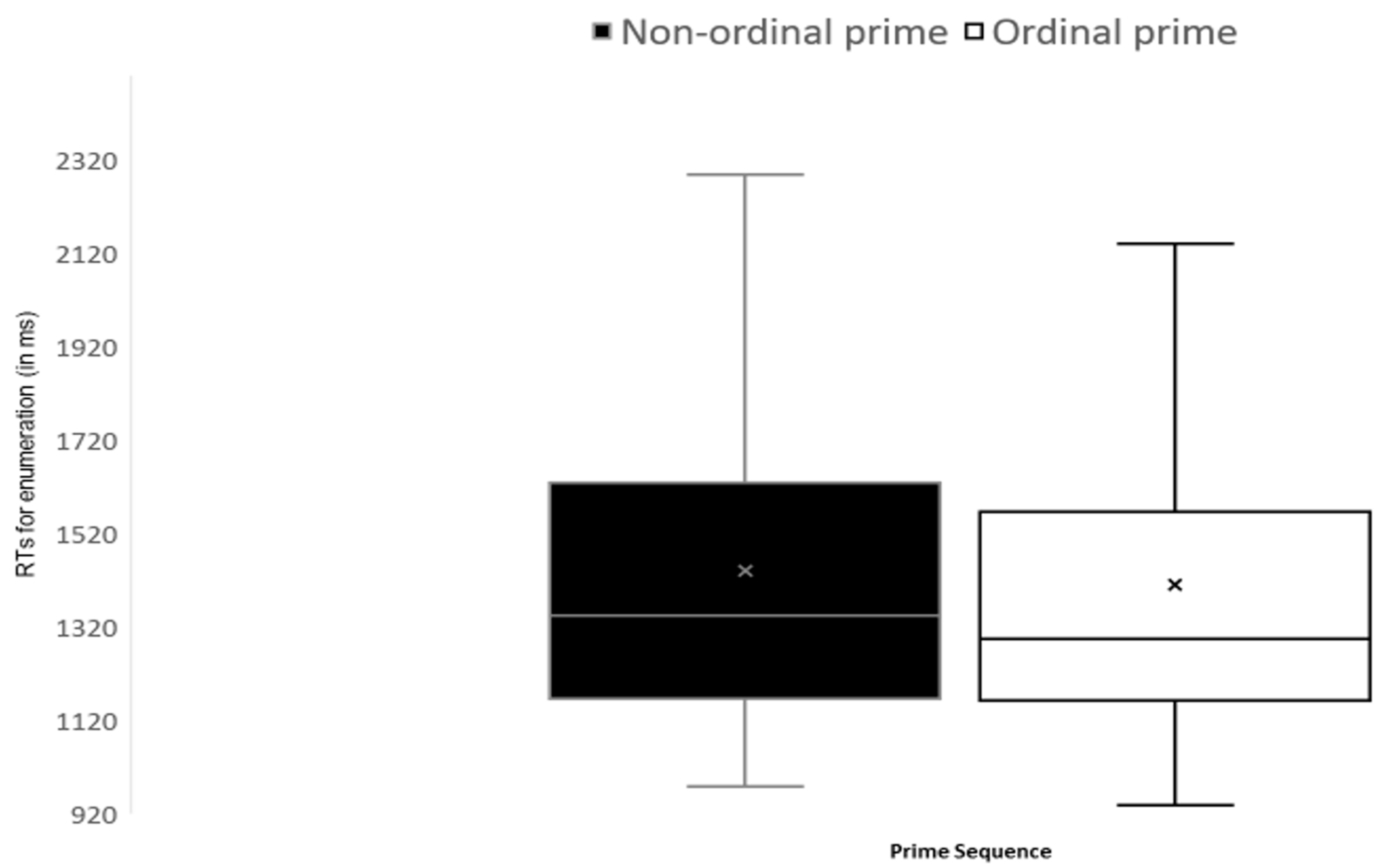
3.2.1. The Significant Effect of Implicitly Presented Ordered Sequences on Numerical Enumeration (i.e., Main Effect of Order of the Primes)
3.2.2. The Non-Significant Effect of Implicitly Presented Numerical Ratios on Numerical Enumeration (i.e., the Main Effect of Ratio of the Ordered Primes)
3.2.3. The Non-Significant Effect of an Implicitly Presented Different Direction on Numerical Enumeration (i.e., the Main Effect of Direction of the Ordered Primes)
3.3. Discussion
4. General Discussion
Numerical Order Is Implicitly Processed
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Description of Non-Symbolic Numerical Stimuli
Appendix B. Detailed Description of ICC Method
References
- Bahrami, Bahador, Petra Vetter, Eva Spolaore, Silvia Pagano, Brian Butterworth, and Geraint Rees. 2010. Unconscious numerical priming despite interocular suppression. Psychological Science 21: 224–33. [Google Scholar] [CrossRef] [PubMed]
- Bargh, John A., and Tanya L. Chartrand. 2000. The mind in the middle: A practical guide to priming and automaticity research. In Handbook of Research Methods in Social and Personality Psychology. Edited by Harry T. Reis and Charles M. Judd. Cambridge: Cambridge University Press, pp. 253–85. [Google Scholar]
- Bar-Shai, Noam, Tamar Keasar, and Avi Shmida. 2011. The use of numerical information by bees in foraging tasks. Behavioral Ecology 22: 317–25. [Google Scholar] [CrossRef]
- Bickel, Robert. 2007. Multilevel Analysis for Applied Research, It’s Just Regression. New York: Guil-ford. [Google Scholar]
- Bonato, Mario, Marco Zorzi, and Carlo Umiltà. 2012. When time is space: Evidence for a mental time line. Neuroscience & Biobehavioral Reviews 36: 2257–73. [Google Scholar]
- Brannon, Elizabeth M. 2002. The development of ordinal numerical knowledge in infancy. Cognition 83: 223–40. [Google Scholar] [CrossRef] [PubMed]
- Brannon, Elizabeth M., and Herbert S. Terrace. 2000. Representation of the numerosities 1–9 by rhesus macaques (Macaca mulatta). Journal of Experimental Psychology: Animal Behavior Processes 26: 31–49. [Google Scholar] [CrossRef]
- Bregman, Albert S., and Jeffrey Campbell. 1971. Primary auditory stream segregation and perception of order in rapid sequences of tones. Journal of Experimental Psychology 89: 244–49. [Google Scholar] [CrossRef]
- Cai, Yuxuan, Shir Hofstetter, Jelle van Dijk, Wietske Zuiderbaan, Wietske van der Zwaag, Ben M. Harvey, and Serge O. Dumoulin. 2021. Topographic numerosity maps cover subitizing and estimation ranges. Nature Communications 12: 3374. [Google Scholar] [CrossRef]
- Cantlon, Jessica F., and Elizabeth M. Brannon. 2006. Shared system for ordering small and large numbers in monkeys and humans. Psychological Science 17: 401–6. [Google Scholar] [CrossRef]
- Cantlon, Jessica F., Michael L. Platt, and Elizabeth M. Brannon. 2009. Beyond the numbers domain. Trends in Cognitive Sciences 13: 83–91. [Google Scholar] [CrossRef]
- Carey, Susan. 2009. Where our number concepts come from. The Journal of Philosophy 106: 220–54. [Google Scholar] [CrossRef]
- Cassia, Viola Macchi, Marta Picozzi, Luisa Girelli, and Maria Dolores de Hevia. 2012. Increasing magnitude counts more: Asymmetrical processing of ordinality in 4-month-old infants. Cognition 124: 183–93. [Google Scholar] [CrossRef] [PubMed]
- Cicchini, Guido Marco, Giovanni Anobile, and David C. Burr. 2014. Compressive mapping of number to space reflects dynamic encoding mechanisms, not static logarithmic transform. Proceedings of the National Academy of Sciences of the United States of America 111: 7867–72. [Google Scholar] [CrossRef]
- Cicchini, Guido Marco, Giovanni Anobile, and David C. Burr. 2016. Spontaneous perception of numerosity in humans. Nature Communications 7: 12536. [Google Scholar] [CrossRef] [PubMed]
- Cooper, Robert G., and Catherine Sophian. 1984. Early number development: Discovering number space with addition and subtraction. In Origin of Cognitive Skills. vol. 1—Book, Section. Edited by Catherine Sophian. Mahwah: Lawrence Erlbaum, pp. 157–92. [Google Scholar]
- Corbett, Jennifer E., Jason Fischer, and David Whitney. 2011. Facilitating stable representations: Serial dependence in vision. PLoS ONE 6: e16701. [Google Scholar] [CrossRef] [PubMed]
- de Hevia, Maria Dolores. 2021. How the Human Mind Grounds Numerical Quantities on Space. Child Development Perspectives 15: 44–50. [Google Scholar] [CrossRef]
- de Hevia, Maria Dolores, and Elizabeth S. Spelke. 2010. Number-Space Mapping in Human Infants. Psychological Science 21: 653–60. [Google Scholar] [CrossRef]
- de Hevia, Maria Dolores, Margaret Addabbo, Elena Nava, Emanuela Croci, Luisa Girelli, and Viola Macchi Cassia. 2017. Infants’ detection of increasing numerical order comes before detection of decreasing number. Cognition 158: 177–88. [Google Scholar] [CrossRef]
- De Houwer, Jan, and Agnes Moors. 2012. How to define and examine implicit processes. Implicit and Explicit Processes in the Psychology of Science 183–98. [Google Scholar] [CrossRef]
- Dehaene, Stanislas. 1992. Varieties of numerical abilities. Cognition 44: 1–42. [Google Scholar] [CrossRef]
- Dehaene, Stanislas. 1997. The Number Sense: How the Mind Creates Mathematics. Oxford: Oxford University Press. [Google Scholar]
- Dehaene, Stanislas, Florent Meyniel, Catherine Wacongne, Liping Wang, and Christophe Pallier. 2015. The neural representation of sequences: From transition probabilities to algebraic patterns and linguistic trees. Neuron 88: 2–19. [Google Scholar] [CrossRef]
- Dehaene, Stanislas, Lionel Naccache, Gurvan Le Clec’H, Etienne Koechlin, Michael Mueller, Ghislaine Dehaene-Lambertz, Pierre-Francois van de Moortele, and Denis Le Bihan. 1998. Imaging unconscious semantic priming. Nature 395: 597–600. [Google Scholar] [CrossRef] [PubMed]
- Dehaene, Stanislas, Serge Bossini, and Pascal Giraux. 1993. The mental representation of parity and number magnitude. Journal of Experimental Psychology: General 122: 371. [Google Scholar] [CrossRef]
- Dere, Ekrem, Joseph P. Huston, and Maria A. De Souza Silva. 2005. Episodic-like memory in mice: Simultaneous assessment of object, place and temporal order memory. Brain Research Protocols 16: 10–19. [Google Scholar] [CrossRef] [PubMed]
- Feigenson, Lisa, Stanislas Dehaene, and Elizabeth Spelke. 2004. Core systems of number. Trends in Cognitive Sciences 8: 307–14. [Google Scholar] [CrossRef]
- Feigenson, Lisa, Susan Carey, and Marc Hauser. 2002. The representations underlying infants’ choice of more: Object files versus analog magnitudes. Psychological Science 13: 150–56. [Google Scholar] [CrossRef] [PubMed]
- Ferrigno, Stephen, Julian Jara-Ettinger, Steven T. Piantadosi, and Jessica F. Cantlon. 2017. Universal and uniquely human factors in spontaneous number perception. Nature Communications 8: 13968. [Google Scholar] [CrossRef]
- Fischer, Martin H., Richard A. Mills, and Samuel Shaki. 2010. How to cook a SNARC: Number placement in text rapidly changes spatial–numerical associations. Brain and Cognition 72: 333–36. [Google Scholar] [CrossRef]
- Fischer, Martin H., Samuel Shaki, and Alexander Cruise. 2009. It Takes Just One Word to Quash a SNARC. Experimental Psychology 56: 361–66. [Google Scholar] [CrossRef]
- Fló, Ana. 2021. Evidence of ordinal position encoding of sequences extracted from continuous speech. Cognition 213: 104646. [Google Scholar] [CrossRef]
- Gevers, Wim, Bert Reynvoet, and Wim Fias. 2003. The mental representation of ordinal sequences is spatially organized. Cognition 87: 87–95. [Google Scholar] [CrossRef]
- Gilad, Sharon, Ming Meng, and Pawan Sinha. 2009. Role of ordinal contrast relationships in face encoding. Proceedings of the National Academy of Sciences of the United States of America 106: 5353–58. [Google Scholar] [CrossRef] [PubMed]
- Göbel, Silke M., Samuel Shaki, and Martin H. Fischer. 2011. The cultural number line: A review of cultural and linguistic influences on the development of number processing. Journal of Cross-Cultural Psychology 42: 543–65. [Google Scholar] [CrossRef]
- Greenwald, Anthony G., Mark R. Klinger, and Eric S. Schuh. 1995. Activation by marginally perceptible (“subliminal”) stimuli: Dissociation of unconscious from conscious cognition. Journal of Experimental Psychology: General 124: 22–42. [Google Scholar] [CrossRef] [PubMed]
- Halberda, Justin, Michèle M. M. Mazzocco, and Lisa Feigenson. 2008. Individual differences in non-verbal number acuity correlate with maths achievement. Nature 455: 665. [Google Scholar] [CrossRef]
- Harvey, Ben M., and Serge O. Dumoulin. 2017. Network of topographic numerosity maps in human association cortex. Nature Human Behavior 1: 36. [Google Scholar] [CrossRef]
- Heck, Ronald H., and Scott L. Thomas. 2015. An Introduction to Multilevel Modeling Techniques: MLM and SEM Approaches Using Mplus. New York: Routledge. [Google Scholar]
- Heck, Ronald H., and Tingting Reid. 2017. Using multilevel regression to examine hierarchical data: Investigating differences in reading performance between immigrant and native-born children. Culturay Educación 29: 619–65. [Google Scholar] [CrossRef]
- Henik, Avishai, and Joseph Tzelgov. 1982. Is three greater than five: The relation between physical and semantic size in comparison tasks. Memory & Cognition 10: 389–95. [Google Scholar]
- Hesselmann, Guido, and André Knops. 2014. No Conclusive Evidence for Numerical Priming Under Interocular Suppression. Psychological Science 25: 2116–19. [Google Scholar] [CrossRef]
- Hesselmann, Guido, Nancy Darcy, Philipp Sterzer, and André Knops. 2015. Exploring the boundary conditions of unconscious numerical priming effects with continuous flash suppression. Consciousness and Cognition 31: 60–72. [Google Scholar] [CrossRef]
- Hogan, Dennis P. 1978. The variable order of events in the life course. American Sociological Review 43: 573–86. [Google Scholar]
- Hutchison, Jane E., Daniel Ansari, Samuel Zheng, Stefanie De Jesus, and Ian M. Lyons. 2020. The relation between subitizable symbolic and non-symbolic number processing over the kindergarten school year. Developmental Science 23: e12884. [Google Scholar] [CrossRef]
- Ischebeck, Anja, Stefan Heim, Christian Siedentopf, Laura Zamarian, Michael Schocke, Christian Kremser, Karl Egger, Hans Strenge, Filip Scheperjans, and Margarete Delazer. 2008. Are numbers special? Comparing the generation of verbal materials from ordered categories (months) to numbers and other categories (animals) in an fMRI study. Human Brain Mapping 29: 894–904. [Google Scholar] [CrossRef] [PubMed]
- Jacob, Simon N., and Andreas Nieder. 2008. The ABC of cardinal and ordinal number representations. Trends in Cognitive Sciences 12: 41–43. [Google Scholar] [CrossRef]
- JASP Team. 2017. JASP (Version 0.8.1.2) [Computer Software]. Available online: https://jasp-stats.org/ (accessed on 18 March 2023).
- Jeffreys, Harold. 1961. The Theory of Probability. Oxford: Oxford University Press. [Google Scholar]
- Kadosh, Roi Cohen, Kathrin Cohen Kadosh, and Avishai Henik. 2008. When brightness counts: The neuronal correlate of numerical-luminance interference. Cerebral Cortex 18: 337–43. [Google Scholar] [CrossRef] [PubMed]
- Kadosh, Roi Cohen, Kathrin Cohen Kadosh, Teresa Schuhmann, Amanda Kaas, Rainer Goebel, Avishai Henik, and Alexander T. Sack. 2007. Virtual dyscalculia induced by parietal-lobe TMS impairs automatic magnitude processing. Current Biology 17: 689–93. [Google Scholar] [CrossRef]
- Kaufmann, Liane, Stephan E. Vogel, Michael Starke, Christian Kremser, and Marc Schocke. 2009. Numerical and non-numerical ordinality processing in children with and without developmental dyscalculia: Evidence from fMRI. Cognitive Development 24: 486–94. [Google Scholar] [CrossRef]
- Koechlin, Etienne, Lionel Naccache, Eliza Block, and Stanislas Dehaene. 1999. Primed numbers: Exploring the modularity of numerical representations with masked and unmasked semantic priming. Journal of Experimental Psychology: Human Perception and Performance 25: 1882. [Google Scholar] [CrossRef]
- Koenderink, Jan J., Andrea J. van Doorn, Astrid M. L. Kappers, and James T. Todd. 2002. Pappus in optical space. Perception & Psychophysics 64: 380–91. [Google Scholar]
- Kouider, Sid, and Stanislas Dehaene. 2007. Levels of processing during non-conscious perception: A critical review of visual masking. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 362: 857–75. [Google Scholar] [CrossRef]
- Krajcsi, Attila, Eszter Szabó, and István Ákos Mórocz. 2013. Subitizing Is Sensitive to the Arrangement of Objects. Experimental Psychology 60: 227–34. [Google Scholar] [CrossRef]
- Krajcsi, Attila, Gábor Lengyel, and Petia Kojouharova. 2016. The Source of the Symbolic Numerical Distance and Size Effects. Frontiers in Psychology 7: 1795. Available online: https://www.frontiersin.org/articles/10.3389/fpsyg.2016 (accessed on 13 August 2017).
- Krajcsi, Attila, Gábor Lengyel, and Petia Kojouharova. 2018. Symbolic Number Comparison Is Not Processed by the Analog Number System: Different Symbolic and Non-symbolic Numerical Distance and Size Effects. Frontiers in Psychology 9: 124. Available online: https://www.frontiersin.org/articles/10.3389/fpsyg.2018.00124 (accessed on 18 March 2023).
- Lashley, Karl Spencer. 1951. The Problem of Serial Order in Behavior. Oxford: Bobbs-Merrill, vol. 21. [Google Scholar]
- Leibovich, Tali, Liana Diesendruck, Orly Rubinsten, and Avishai Henik. 2013. The importance of being relevant: Modulation of magnitude representations. Frontiers in Psychology 4: 369. Available online: https://www.frontiersin.org/articles/10.3389/fpsyg.2013.00369 (accessed on 13 April 2023).
- Lewkowicz, David J., and Iris Berent. 2009. Sequence learning in 4-month-old infants: Do infants represent ordinal information. Child Development 80: 1811–23. [Google Scholar] [CrossRef]
- Lyons, Ian M., and Daniel Ansari. 2015. Numerical order processing in children: From reversing the distance-effect to predicting arithmetic. Mind, Brain, and Education 9: 207–21. [Google Scholar] [CrossRef]
- Lyons, Ian M., and Sian L. Beilock. 2011. Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition 121: 256–61. [Google Scholar] [CrossRef] [PubMed]
- Lyons, Ian M., and Sian L. Beilock. 2013. Ordinality and the nature of symbolic numbers. Journal of Neuroscience 33: 17052–61. [Google Scholar] [CrossRef] [PubMed]
- Moors, Pieter, Guido Hesselmann, Johan Wagemans, and Raymond van Ee. 2017. Continuous Flash Suppression: Stimulus Fractionation rather than Integration. Trends in Cognitive Sciences 21: 719–21. [Google Scholar] [CrossRef]
- Muthén, Bengt O., and Albert Satorra. 1995. Complex sample data in structural equation modeling. Sociological Methodology 25: 267–316. [Google Scholar] [CrossRef]
- Namboodiri, Vijay Mohan K., Marco A. Huertas, Kevin J. Monk, Harel Z. Shouval, and Marshall G. Hussain Shuler. 2015. Visually cued action timing in the primary visual cortex. Neuron 86: 319–30. [Google Scholar] [CrossRef]
- Nguyen, Vincent A., Ian P. Howard, and Robert S. Allison. 2005. Detection of the depth order of defocused images. Vision Research 45: 1003–11. [Google Scholar] [CrossRef]
- Nieder, Andreas. 2005. Counting on neurons: The neurobiology of numerical competence. Nature Reviews Neuroscience 6: 177–90. [Google Scholar] [CrossRef]
- Nieder, Andreas, and Stanislas Dehaene. 2009. Representation of number in the brain. Annual Review of Neuroscience 32: 185–208. [Google Scholar] [CrossRef]
- Osborne, Jason W., and Amy Overbay. 2004. The power of outliers (and why researchers should always check for them). Practical Assessment, Research, and Evaluation 9: 6. [Google Scholar]
- Pepperberg, Irene M. 2006. Ordinality and inferential abilities of a grey parrot (Psittacus erithacus). Journal of Comparative Psychology 120: 205. [Google Scholar] [CrossRef] [PubMed]
- Petrazzini, Maria Elena Miletto, Tyrone Lucon-Xiccato, Christian Agrillo, and Angelo Bisazza. 2015. Use of ordinal information by fish. Scientific Reports 5: 15497. [Google Scholar] [CrossRef] [PubMed]
- Pfuhl, Gerit, and Robert Biegler. 2012. Ordinality and novel sequence learning in jackdaws. Animal Cognition 15: 833–49. [Google Scholar] [CrossRef] [PubMed]
- Piazza, Manuela. 2010. Neurocognitive start-up tools for symbolic number representations. Trends in Cognitive Sciences 14: 542–51. [Google Scholar] [CrossRef] [PubMed]
- Picozzi, Marta, Maria Dolores de Hevia, Luisa Girelli, and Viola Macchi Cassia. 2010. Seven-month-olds detect ordinal numerical relationships within temporal sequences. Journal of Experimental Child Psychology 107: 359–67. [Google Scholar] [CrossRef] [PubMed]
- Pinhas, Michal, David J. Paulsen, Marty G. Woldorff, and Elizabeth M. Brannon. 2023. Neurophysiological signatures of approximate number system acuity in preschoolers. Trends in Neuroscience and Education 30: 100197. [Google Scholar] [CrossRef]
- Reber, Arthur S. 1989. Implicit learning and tacit knowledge. Journal of Experimental Psychology: General 118: 219. [Google Scholar] [CrossRef]
- Reynvoet, Bert, Marc Brysbaert, and Wim Fias. 2002. Semantic priming in number naming. The Quarterly Journal of Experimental Psychology: Section A 55: 1127–39. [Google Scholar] [CrossRef]
- Roggeman, Chantal, Tom Verguts, and Wim Fias. 2007. Priming reveals differential coding of symbolic and non-symbolic quantities. Cognition 105: 380–94. [Google Scholar] [CrossRef]
- Rubinsten, Orly, and Avishai Henik. 2005. Automatic activation of internal magnitudes: A study of developmental dyscalculia. Neuropsychology 19: 641. [Google Scholar] [CrossRef]
- Rubinsten, Orly, and Dana Sury. 2011. Processing ordinality and quantity: The case of developmental dyscaculia. PLoS ONE 6: e24079. [Google Scholar] [CrossRef] [PubMed]
- Rubinsten, Orly, Dana Sury, Dmitri Lavro, and Andrea Berger. 2013. Processing ordinality and quantity: ERP evidence of separate mechanisms. Brain and Cognition 82: 201–12. [Google Scholar] [CrossRef] [PubMed]
- Schacter, Daniel L. 1987. Memory, amnesia, and frontal lobe dysfunction. Psychobiology 15: 21–36. [Google Scholar] [CrossRef]
- Schneider, Walter, and Richard M. Shiffrin. 1977. Controlled and automatic human information processing: I. Detection, search, and attention. Psychological Review 84: 1. [Google Scholar] [CrossRef]
- Sella, Francesco, and Daniela Lucangeli. 2020. The knowledge of the preceding number reveals a mature understanding of the number sequence. Cognition 194: 104104. [Google Scholar] [CrossRef]
- Shaki, Samuel, Martin H. Fischer, and Silke M. Göbel. 2012. Direction counts: A comparative study of spatially directional counting biases in cultures with different reading directions. Journal of Experimental Child Psychology 112: 275–81. [Google Scholar] [CrossRef] [PubMed]
- Shaki, Samuel, Martin H. Fischer, and William M. Petrusic. 2009. Reading habits for both words and numbers contribute to the SNARC effect. Psychonomic Bulletin & Review 16: 328–31. [Google Scholar]
- Shanks, David R. 2016. Regressive research: The pitfalls of post hoc data selection in the study of unconscious mental processes. Psychonomic Bulletin & Review 1–24. [Google Scholar] [CrossRef]
- Sklar, Asael Y., Nir Levy, Ariel Goldstein, Roi Mandel, Anat Maril, and Ran R. Hassin. 2012. Reading and doing arithmetic nonconsciously. Proceedings of the National Academy of Sciences 109: 19614–19. [Google Scholar] [CrossRef]
- Snijders, Tom, and Roel Bosker. 1999. Multilevel Analysis—An Introduction to Basic and Advanced Multilevel Modeling. London: Sage Publications. [Google Scholar]
- Sommerauer, Gerrit, Karl-Heinz Grass, Roland H. Grabner, and Stephan E. Vogel. 2020. The semantic control network mediates the relationship between symbolic numerical order processing and arithmetic performance in children. Neuropsychologia 141: 107405. [Google Scholar] [CrossRef]
- Spelke, Elizabeth S., and Katherine D. Kinzler. 2007. Core knowledge. Developmental Science 10: 89–96. [Google Scholar] [CrossRef] [PubMed]
- Stein, Timo, Vanessa Utz, and Filip Van Opstal. 2020. Unconscious semantic priming from pictures under backward masking and continuous flash suppression. Consciousness and Cognition 78: 102864. [Google Scholar] [CrossRef] [PubMed]
- Suanda, Sumarga H., Whitney Tompson, and Elizabeth M. Brannon. 2008. Changes in the ability to detect ordinal numerical relationships between 9 and 11 months of age. Infancy 13: 308–37. [Google Scholar] [CrossRef] [PubMed]
- Sury, Dana, and Orly Rubinstan. 2011. Ordinal processing in numerical and non-numerical information. In Reading, Writing, Mathematics and the Developing Brain: Listening to Many Voices. vol. 1–Book, Section. Edited by Zvia Breznitz, Orly Rubinsten, Victoria J. Molfese and Denis L. Molfese. Berlin: Springer. [Google Scholar]
- Sury, Dana, and Orly Rubinsten. 2019. Children automatically process order: Evidence from an ‘ordinal Stroop’ task. Cognitive Development 52: 100812. [Google Scholar] [CrossRef]
- Suzuki, Kotaro, and Tessei Kobayashi. 2000. Numerical competence in rats (Rattus norvegicus): Davis and Bradford 1986 extended. Journal of Comparative Psychology 114: 73. [Google Scholar] [CrossRef]
- Terrace, Herbert S. 2005. The simultaneous chain: A new approach to serial learning. Trends in Cognitive Sciences 9: 202–10. [Google Scholar] [CrossRef]
- Tsuchiya, Naotsugu, and Christof Koch. 2005. Continuous flash suppression reduces negative afterimages. Nature Neuroscience 8: 1096–101. [Google Scholar] [CrossRef]
- Tzelgov, Joseph, Joachim Meyer, and Avishai Henik. 1992. Automatic and intentional processing of numerical information. Journal of Experimental Psychology: Learning, Memory, and Cognition 18: 166. [Google Scholar] [CrossRef]
- vanMarle, Kristy. 2013. Infants use different mechanisms to make small and large number ordinal judgments. Journal of Experimental Child Psychology 114: 102–10. [Google Scholar] [CrossRef]
- Viswanathan, Pooja, and Andreas Nieder. 2013. Neuronal correlates of a visual “sense of number” in primate parietal and prefrontal cortices. Proceedings of the National Academy of Sciences of the United States of America 110: 11187–92. [Google Scholar] [CrossRef]
- Vogel, Stephan E., Nikolaus Koren, Stefan Falb, Martina Haselwander, Anna Spradley, Philip Schadenbauer, Sandra Tanzmeister, and Roland H. Grabner. 2019. Automatic and intentional processing of numerical order and its relationship to arithmetic performance. Acta Psychologica 193: 30–41. [Google Scholar] [CrossRef] [PubMed]
- Vogel, Stephan E., Trent Haigh, Gerrit Sommerauer, Melanie Spindler, Clemens Brunner, Ian M. Lyons, and Roland H. Grabner. 2017. Processing the Order of Symbolic Numbers: A Reliable and Unique Predictor of Arithmetic Fluency. Journal of Numerical Cognition 3: 288–308. [Google Scholar] [CrossRef]
- Wagenmakers, Eric-Jan, Jonathon Love, Maarten Marsman, Tahira Jamil, Alexander Ly, Josine Verhagen, Ravi Selker, Quentin F. Gronau, Damian Dropmann, Bruno Boutin, and et al. 2017. Bayesian inference for psychology. Part II: Example applications with JASP. Psychonomic Bulletin & Review 1–19. [Google Scholar] [CrossRef]
- Walsh, Vincent. 2003. A theory of magnitude: Common cortical metrics of time, space and quantity. Trends in Cognitive Sciences 7: 483–88. [Google Scholar] [CrossRef] [PubMed]
- Whelan, Robert. 2008. Effective analysis of reaction time data. The Psychological Record 58: 475–82. [Google Scholar] [CrossRef]
- Wood, Guilherme, Klaus Willmes, Hans-Christoph Nuerk, and Martin H. Fischer. 2008. On the cognitive link between space and number: A meta-analysis of the SNARC effect. Psychology Science Quarterly 50: 489–525. [Google Scholar]
- Yang, Eunice, and Randolph Blake. 2012. Deconstructing continuous flash suppression. Journal of Vision 12: 8. [Google Scholar] [CrossRef]
- Zacks, Jeffrey M., and Barbara Tversky. 2001. Event structure in perception and conception. Psychological bulletin 127: 3. [Google Scholar] [CrossRef]
- Zohar-Shai, Bar, Joseph Tzelgov, Avi Karni, and Orly Rubinsten. 2017. It does exist! A left-to-right spatial–numerical association of response codes (SNARC) effect among native Hebrew speakers. Journal of Experimental Psychology: Human Perception and Performance 43: 719. [Google Scholar] [CrossRef]
| Ratio | 0.7 | 0.5 | ||||||
|---|---|---|---|---|---|---|---|---|
| Sequence presented as prime | Target | Sequence presented as prime | Target | |||||
| Position | First | Second | Third | First | Second | Third | ||
| 3 | 4 | 6 | 9 | 2 | 4 | 8 | 16 | |
| 4 | 6 | 9 | 13 | 3 | 6 | 12 | 24 | |
| 5 | 7 | 10 | 15 | 4 | 8 | 16 | 32 | |
| 6 | 9 | 13 | 19 | 5 | 10 | 20 | 40 | |
| Target’s Value | RT | Deviations of Enumeration |
|---|---|---|
| 9 | 1319 (430) | 0.26 (0.17) |
| 13 | 1367 (406) | 0.37 (0.33) |
| 15 | 1360 (360) | 0.31 (0.17) |
| 16 | 1371 (407) | 0.36 (0.30) |
| 19 | 1353 (410) | 0.34 (0.20) |
| 24 | 1320 (381) | 0.40 (0.31) |
| 32 | 1295 (381) | 0.35 (0.20) |
| 40 | 1281 (357) | 0.34 (0.21) |
| Model 1: All Students | Model 2: Unawareness Subgroup | ||||
|---|---|---|---|---|---|
| Estimate | S.E. | Estimate | S.E. | ||
| Level One | Order | −0.014 ~ | 0.009 | −0.023 * | 0.012 |
| Ratio | −0.059 * | 0.029 | −0.062 ~ | 0.036 | |
| Residual Variance | 0.232 *** | 0.020 | 0.250 *** | 0.029 | |
| Level Two | Accuracy | −0.004 | 0.003 | −0.009 ~ | 0.006 |
| Mean Response Time 1 | 1.558 *** | 0.163 | 1.810 *** | 0.282 | |
| Residual Variance | 0.100 *** | 0.021 | 0.126 *** | 0.033 | |
| Sample N | 69 | 41 | |||
| Model Fit | AIC = 13,113; BIC = 13,137 | AIC = 904; BIC = 9115 | |||
| Target’s Value | RT | Deviations of Enumeration |
|---|---|---|
| 9 | 1414 (413) | 0.30 (0.23) |
| 13 | 1479 (454) | 0.38 (0.25) |
| 15 | 1471 (463) | 0.33 (0.22) |
| 16 | 1445 (404) | 0.33 (0.21) |
| 19 | 1409 (420) | 0.31 (0.22) |
| 24 | 1414 (361) | 0.31 (0.18) |
| 32 | 1357 (379) | 0.29 (0.17) |
| 40 | 1335 (387) | 0.25 (0.13) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sury, D.; Rubinsten, O. Implicit Processing of Numerical Order: Evidence from a Continuous Interocular Flash Suppression Study. J. Intell. 2023, 11, 96. https://doi.org/10.3390/jintelligence11050096
Sury D, Rubinsten O. Implicit Processing of Numerical Order: Evidence from a Continuous Interocular Flash Suppression Study. Journal of Intelligence. 2023; 11(5):96. https://doi.org/10.3390/jintelligence11050096
Chicago/Turabian StyleSury, Dana, and Orly Rubinsten. 2023. "Implicit Processing of Numerical Order: Evidence from a Continuous Interocular Flash Suppression Study" Journal of Intelligence 11, no. 5: 96. https://doi.org/10.3390/jintelligence11050096
APA StyleSury, D., & Rubinsten, O. (2023). Implicit Processing of Numerical Order: Evidence from a Continuous Interocular Flash Suppression Study. Journal of Intelligence, 11(5), 96. https://doi.org/10.3390/jintelligence11050096





