Construction and Validation of the HeiQ: An Operation-Oriented Figural Matrices Test
Abstract
1. Introduction
- Distractors and the attractor were generated so that the attractor cannot be identified by using a counting strategy (Mittring and Rost 2008);
- Distractors and the attractor were generated so that they are of a similar visual appearance (Arendasy and Sommer 2013);
- All distractors were generated so that they were plausible solutions to the item (Gierl et al. 2017; Haladyna et al. 2002; Haladyna and Rodriguez 2013): plausibility was achieved by applying some, but not all of the item’s underlying operations correctly when generating a distractor (Guttman and Schlesinger 1967) and by applying additional operation(s) in accordance with possible misconceptions about the operations used in the respective item (Case and Swanson 2002);
- Each possible correct/incorrect combination of the item’s underlying operations was reflected by one particular distractor, so that distractor selection would be informative with regard to which operations were correctly applied and which were incorrectly applied (Guttman and Schlesinger 1967).
2. Materials and Methods
2.1. Participants
2.2. Materials
2.2.1. Construction of the Heidelberg Figural Matrices Test (HeiQ)
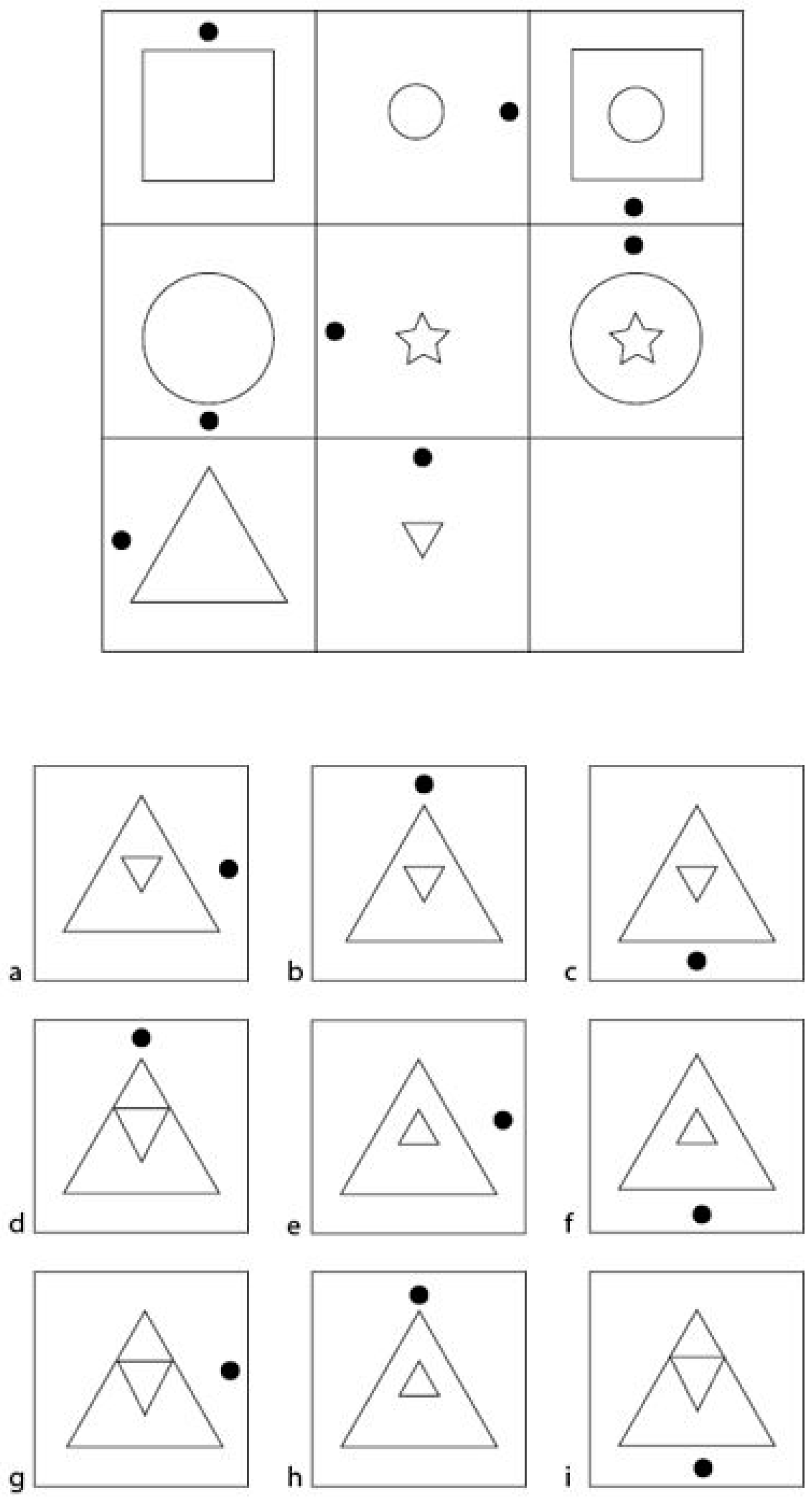
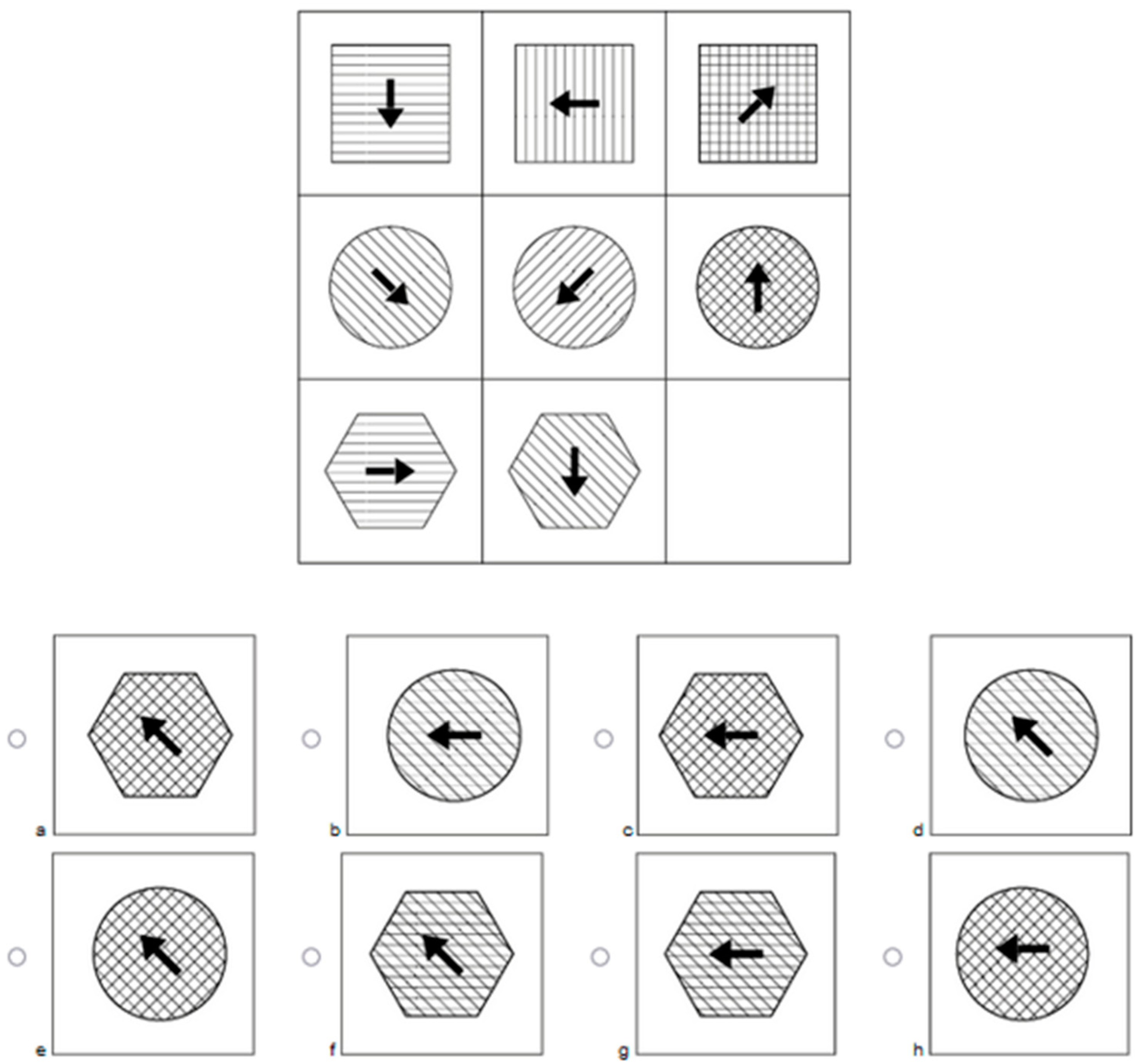
Operations
- Identity (ID): The same figure is repeatedly displayed in each cell of a row/column, (Figure 2a);
- Addition (AD): The figures of the first two cells (row-/column-wise) are added together to form the third figure (Figure 2b);
- Subtraction (SU): The figure of the second cells (row-/column-wise) is deducted from the figure in the first cell of the same row/column to form the figure in the third cell (Figure 2c);
- Intersection (IN): The third figure consists of only those elements of the figures that are displayed in both the first and the second cell (Figure 2d);
- Unique addition (UA): The third figure is made up only of those elements of the figures that are displayed in either the first or the second cell. Elements that are found in both figures are omitted (Figure 2e);
- Seriation (SE): The rule of change from the first to the second cell (e.g., movement, rotation, change in size, or addition of elements) is applied to the figure in the second cell to generate the figure for the third cell (Figure 2f);
- Variation of open Gestalts (VO): In each row/column, three one-dimensional figures (e.g., a line, curve, or arrow) are presented. These figures are then repeated in the other rows/columns, although not necessarily in the same order (Figure 2g). Open Gestalts in this case refers to the “one-dimensional” appearance (Hornke et al. 2000);
- Variation of closed Gestalts (VC): In each column/row, three different figures are presented (for instance, one square, one circle, and one pentagon; see Figure 2h). The order with which the three figures appear within their respective column or row is randomly determined. Closed Gestalts refer to figures of two-dimensional nature (Hornke et al. 2000), such as squares, rectangles, or other visually “closed” figures.
Item Construction
Distractor Generation
Balanced Occurrence of Figural Elements
Informative Content of Distractors
2.2.2. Berlin Intelligence Structure Test Short Form (BIS-S)
2.2.3. Intelligence Structure Test 2000R (I-S-T 2000R)
2.2.4. Raven Advanced Progressive Matrices (RAPM)
2.2.5. Need for Cognition (NFC) Scale
2.3. Procedure
3. Results
3.1. Percentage of Items Solved
3.2. Missing Responses
3.3. Measurement Models
3.4. Reliability
3.5. Validity
3.6. Operation-Specific Indicators
4. Discussion
4.1. Considerations on Bypassing Strategies Other Than Response Elimination
4.2. Future Applications and Opportunities of the Operation-Level Test Scoring
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Item | Outfit Mean-Square | Infit Mean-Square | Differential Item Functioning | Item Difficulty |
|---|---|---|---|---|
| 1 | 1.513 | 1.367 | 1.976 * | −0.027 |
| 2 | 0.989 | 1.014 | 1.554 | −0.430 |
| 3 | 1.020 | 0.985 | −1.068 | −0.048 |
| 4 | 0.695 | 0.841 | −0.305 | −0.662 |
| 5 | 1.521 | 1.316 | 0.373 | 0.246 |
| 6 | 0.737 | 0.859 | 0.384 | −2.395 |
| 7 | 1.176 | 1.117 | 0.755 | 0.349 |
| 8 | 1.167 | 1.148 | 0.602 | 0.068 |
| 9 | 1.361 | 1.193 | 0.397 | −0.882 |
| 10 | 0.949 | 0.959 | 1.000 | −1.964 |
| 11 | 0.960 | 0.913 | −1.458 | 0.947 |
| 12 | 1.065 | 1.050 | −1.663 | 0.623 |
| 13 | 0.802 | 0.856 | −0.939 | −0.838 |
| 14 | 1.062 | 1.068 | −0.935 | −1.413 |
| 15 | 0.914 | 0.903 | −2.190 * | −0.420 |
| 16 | 0.839 | 0.924 | −0.701 | −0.407 |
| 17 | 0.749 | 0.807 | −0.344 | −0.932 |
| 18 | 1.227 | 1.194 | 0.432 | −1.301 |
| 19 | 1.311 | 1.019 | 0.455 | −1.366 |
| 20 | 0.590 | 0.796 | −0.464 | −1.434 |
| 21 | 1.034 | 0.934 | −1.796 | −0.922 |
| 22 | 0.815 | 0.855 | −0.821 | −0.228 |
| 23 | 0.821 | 0.882 | −1.105 | −1.788 |
| 24 | 0.672 | 0.752 | −2.559 * | 0.078 |
| 25 | 1.117 | 1.094 | 2.307 * | −0.344 |
| 26 | 0.983 | 0.932 | −1.878 | −1.012 |
| 27 | 0.851 | 0.930 | −1.360 | −0.668 |
| 28 | 0.895 | 0.937 | −0.848 | 0.548 |
| 29 | 0.868 | 0.895 | −0.673 | −0.913 |
| 30 | 1.437 | 1.215 | 0.122 | 1.146 |
| 31 | 1.235 | 1.141 | −0.239 | −0.061 |
| 32 | 0.885 | 0.895 | −1.836 | 0.546 |
| 33 | 0.978 | 1.005 | 1.361 | −1.145 |
| 34 | 1.058 | 1.007 | −1.102 | −0.494 |
| 35 | 1.666 | 1.396 | 6.102 * | −0.437 |
| 36 | 0.809 | 0.877 | −0.881 | −0.386 |
| 37 | 0.846 | 0.890 | −0.335 | 0.212 |
| 38 | 1.435 | 1.330 | −0.118 | 0.136 |
| 39 | 0.783 | 0.837 | −1.425 | −0.073 |
| 40 | 0.780 | 0.815 | −0.137 | 0.039 |
| 41 | 0.697 | 0.765 | −0.968 | 0.481 |
| 42 | 1.109 | 0.998 | 0.967 | 0.395 |
| 43 | 0.977 | 1.037 | 1.196 | −0.678 |
| 44 | 0.765 | 0.802 | 0.826 | 0.308 |
| 45 | 0.936 | 0.986 | 2.588 * | −0.204 |
| 46 | 0.856 | 0.896 | 2.396 * | −0.221 |
| 47 | 0.970 | 0.975 | 1.006 | −0.206 |
| 48 | 0.957 | 0.966 | 2.155 * | −0.213 |
| Measure | M | SD | Range | Skewness | Curtosis | 1 | 2 | 3.1 | 3.2 |
|---|---|---|---|---|---|---|---|---|---|
| HeiQ | 26.87 | 10.68 | 3–47 | 0.04 | −1.03 | ||||
| BIS-S | 97.63 | 18.23 | 55–145 | −0.27 | −0.30 | 0.58 *** (0.70) | |||
| I-S-T 2000R | |||||||||
| Reasoning | 113.53 | 21.89 | 62–153 | −0.18 | −0.64 | 0.73 *** (0.79) | - | ||
| Knowledge | 54.72 | 11.76 | 21–78 | −0.42 | −0.09 | 0.43 ** (0.47) | - | 0.53 *** (0.58) | |
| RAPM | 23.64 | 6.58 | 9–35 | −0.34 | −0.90 | 0.81 *** (0.90) | - | 0.73 *** (0.81) | 0.36 ** (0.41) |
References
- Arendasy, Martin E., and Markus Sommer. 2013. Reducing response elimination strategies enhances the construct validity of figural matrices. Intelligence 41: 234–43. [Google Scholar] [CrossRef]
- Arthur, Winfred, and David J. Woehr. 1993. A confirmatory factor analytic study examining the dimensionality of the Raven’s Advanced Progressive Matrices. Educational and Psychological Measurement 53: 471–78. [Google Scholar] [CrossRef]
- Beauducel, André, and Martin Kersting. 2002. Fluid and crystallized intelligence and the Berlin Model of Intelligence Structure (BIS). European Journal of Psychological Assessment 18: 97–112. [Google Scholar] [CrossRef]
- Becker, Nicolas, Franzis Preckel, Julia Karbach, Nathalie Raffel, and Frank M. Spinath. 2014. Die Matrizenkonstruktionsaufgabe. Diagnostica 61: 22–33. [Google Scholar] [CrossRef]
- Becker, Nicolas, Florian Schmitz, Anke Falk, Jasmin Feldbrügge, Daniel R. Recktenwald, Oliver Wilhelm, Franzis Preckel, and Frank M. Spinath. 2016. Preventing Response Elimination Strategies Improves the Convergent Validity of Figural Matrices. Journal of Intelligence 4: 2. [Google Scholar] [CrossRef]
- Beißert, Hanna, Meike Köhler, Marina Rempel, and Constanze Beierlein. 2015. Eine Deutschsprachige Kurzskala zur Messung des Konstrukts Need for Cognition (NFC-K). Mannheim: GESIS—Leibniz-Institut für Sozialwissenschaften. [Google Scholar] [CrossRef]
- Bethell-Fox, Charles E., David F. Lohman, and Richard E. Snow. 1984. Adaptive reasoning: Componential and eye movement analysis of geometric analogy performance. Intelligence 8: 205–38. [Google Scholar] [CrossRef]
- Bors, Douglas A., and François Vigneau. 2003. The effect of practice on Raven’s Advanced Progressive Matrices. Learning and Individual Differences 13: 291–312. [Google Scholar] [CrossRef]
- Brown, Anna, and Tim J. Croudace. 2015. Scoring and estimating score precision using multidimensional IRT models. In Handbook of Item Response Theory Modeling: Applications to Typical Performance Assessment. Multivariate Applications Series; New York: Routledge/Taylor & Francis Group, pp. 307–33. [Google Scholar]
- Cacioppo, John T., and Richard E. Petty. 1982. The need for cognition. Journal of Personality and Social Psychology 42: 116–31. [Google Scholar] [CrossRef]
- Carpenter, Patricia A., Marcel A. Just, and Peter Shell. 1990. What one intelligence test measures: A theoretical account of the processing in the Raven Progressive Matrices Test. Psychological Review 97: 404–31. [Google Scholar] [CrossRef]
- Case, Susan, and David Swanson. 2002. Constructing Written Test Questions for the Basic and Clinical Sciences. Philadelphia: National Board of Examiners. [Google Scholar]
- Cattell, Raymond B. 1963. Theory of fluid and crystallized intelligence: A critical experiment (No. 1). Journal of Educational Psychology 54: 1–22. [Google Scholar] [CrossRef]
- Danner, Daniel, Dirk Hagemann, Andrea Schankin, Marieke Hager, and Joachim Funke. 2011. Beyond IQ: A latent state trait analysis of general intelligence, dynamic decision making, and implicit learning. Intelligence 39: 323–34. [Google Scholar] [CrossRef]
- Deary, Ian J., Steve Strand, Pauline Smith, and Cres Fernandes. 2007. Intelligence and educational achievement. Intelligence 35: 13–21. [Google Scholar] [CrossRef]
- Formann, Anton K. 1973. Die Konstruktion eines neuen Matrizentest und die Untersuchung des Lösungsverhaltens mit Hilfe des Linearen Logistischen Testmodells. Unpublished Ph.D. dissertation, Universität Wien, Vienna, Austria. [Google Scholar]
- Formann, Anton K., and Karl Piswanger. 1979. WMT Wiener Matrizen-Test. Weinheim: Beltz. [Google Scholar]
- Forthmann, Boris, Natalie Förster, Birgit Schütze, Karin Hebbecker, Janis Flessner, Martin T. Peters, and Elmar Souvignier. 2020. How Much g Is in the Distractor? Re-Thinking Item-Analysis of Multiple-Choice Items. Journal of Intelligence 8: 11. [Google Scholar] [CrossRef]
- Freund, Philipp A., Stefan Hofer, and Heinz Holling. 2008. Explaining and Controlling for the Psychometric Properties of Computer-Generated Figural Matrix Items. Thousand Oaks: SAGE Publications, Applied Psychological Measurement 32. [Google Scholar]
- Gierl, Mark J., Okan Bulut, Qi Guo, and Xinxin Zhang. 2017. Developing, Analyzing, and Using Distractors for Multiple-Choice Tests in Education: A Comprehensive Review. Review of Educational Research 87: 1082–116. [Google Scholar] [CrossRef]
- Gonthier, Corentin, and Jean-Luc Roulin. 2020. Intraindividual strategy shifts in Raven’s matrices, and their dependence on working memory capacity and need for cognition. Journal of Experimental Psychology: General 149: 564–79. [Google Scholar] [CrossRef]
- Gottfredson, Linda S., and Ian J. Deary. 2004. Intelligence Predicts Health and Longevity, but Why? (No. 1). Oxford: Blackwell Publishing, Current Directions in Psychological Science 13. [Google Scholar]
- Guttman, Louis, and I. M. Schlesinger. 1967. Systematic Construction of Distractors for Ability and Achievement Test Items. Educational and Psychological Measurement 27: 569–80. [Google Scholar] [CrossRef]
- Haladyna, Thomas M., and Michael Rodriguez. 2013. Developing and Validating Test Items. London: Routledge. [Google Scholar] [CrossRef]
- Haladyna, Thomas M., and Steven M. Downing. 1989. A Taxonomy of Multiple-Choice Item-Writing Rules. Applied Measurement in Education 2: 37–50. [Google Scholar] [CrossRef]
- Haladyna, Thomas M., Steven M. Downing, and Michael C. Rodriguez. 2002. A review of multiple-choice item-writing guidelines for classroom assessment. Applied Measurement in Education 15: 309–34. [Google Scholar] [CrossRef]
- Hayes, Taylor R., Alexander A. Petrov, and Per B. Sederberg. 2011. A novel method for analyzing sequential eye movements reveals strategic influence on Raven’s Advanced Progressive Matrices. Journal of Vision 11: 10. [Google Scholar] [CrossRef]
- Heydasch, Timo. 2014. The Hagen Matrices Test (HMT). DataCite, Unpublished. [Google Scholar]
- Horn, John L. 1968. Organization of abilities and the development of intelligence. Psychological Review 75: 242–59. [Google Scholar] [CrossRef] [PubMed]
- Horn, John L., and Raymond B. Cattell. 1967. Age Differences in Fluid and Crystallized Intelligence (No. 2). Amsterdam: Elsevier Science. [Google Scholar]
- Hornke, Lutz F., and Michael W. Habon. 1986. Rule-Based Item Bank Construction and Evaluation Within the Linear Logistic Framework. Applied Psychological Measurement 10: 369–80. [Google Scholar] [CrossRef]
- Hornke, Lutz F., Anja Küppers, and Stefan Etzel. 2000. Konstruktion und Evaluation eines adaptiven Matrizentests. Diagnostica 46: 182–88. [Google Scholar] [CrossRef]
- Hossiep, Rüdiger, Daniela Turck, and Michele Hasella. 1999. BOMAT—Advanced—Bochumer Matrizentest. Goettingen: Hogrefe. [Google Scholar]
- Hu, Li-tze, and Peter M. Bentler. 1999. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal 6: 1–55. [Google Scholar] [CrossRef]
- Jäger, Adolf Otto, Heinz-Martin Süß, and André Beauducel. 1997. Mehrdimensionale Intelligenzdiagnostik Mit Dem “Berliner Intelligenzstruktur-Test” (BIS-Test, Form 4). Goettingen: Hogrefe Verlag für Psychologie. [Google Scholar]
- Jarosz, Andrew F., and Jennifer Wiley. 2012. Why does working memory capacity predict RAPM performance? A possible role of distraction. Intelligence 40: 427–38. [Google Scholar] [CrossRef]
- Jendryczko, David, Jana Scharfen, and Heinz Holling. 2019. The Impact of Situational Test Anxiety on Retest Effects in Cognitive Ability Testing: A Structural Equation Modeling Approach. Journal of Intelligence 7: 22. [Google Scholar] [CrossRef]
- Klauer, Karl-Josef, ed. 1978. Handbuch der Pädagogischen Diagnostik. Düsseldorf: Pädagogischer Verlag Schwann. [Google Scholar]
- La Torre, Jimmy de, and Tzur Karelitz. 2009. Impact of diagnosticity on the adequacy of models for cognitive diagnosis under a linear attribute structure: A simulation study. Journal of Educational Measurement 46: 450–69. [Google Scholar] [CrossRef]
- Laurence, Paulo G., and Elizeu C. Macedo. 2022. Cognitive strategies in matrix-reasoning tasks: State of the art. Psychonomic Bulletin & Review. [Google Scholar] [CrossRef]
- Leiner, D. J. 2019. SoSci Survey (version 3.4.03). Computer Software. Available online: https://www.soscisurvey.de (accessed on 15 September 2020).
- Liepmann, Detlev, André Beauducel, Burkhard Brocke, and Rudolf Amthauer. 2001. Intelligenz-Struktur-Test 2000 R. I-S-T 2000 R—[Intelligence Structure Test 2000 R]. Göttingen: Hogrefe. [Google Scholar]
- Marshalek, Brachia, David F. Lohman, and Richard E. Snow. 1983. The complexity continuum in the radex and hierarchical models of intelligence. Intelligence 7: 107–27. [Google Scholar] [CrossRef]
- McGrew, Kevin S. 2009. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 37: 1–10. [Google Scholar] [CrossRef]
- McNeish, Daniel. 2018. Thanks coefficient alpha, we’ll take it from here. Psychological Methods 23: 412–33. [Google Scholar] [CrossRef] [PubMed]
- Meng, Xiao-Li, Robert Rosenthal, and Donald B. Rubin. 1992. Comparing correlated correlation coefficients. Psychological Bulletin 111: 172–75. [Google Scholar] [CrossRef]
- Mittring, Gert, and Detlef H. Rost. 2008. Die verflixten Distraktoren. Diagnostica 54: 193–201. [Google Scholar] [CrossRef]
- Muthén, Linda K., and Bengt O. Muthén. 2017. Mplus User’s Guide, 8th ed. Los Angeles: Muthén & Muthén. [Google Scholar]
- Naglieri, Jack A. 2003. NNAT Naglieri Nonverbal Ability Test. Individual Administration. Stimulus Book. San Antonio: The Psychological Corporation. [Google Scholar]
- Pohl, Steffi, Linda Gräfe, and Norman Rose. 2013. Dealing With Omitted and Not-Reached Items in Competence Tests: Evaluating Approaches Accounting for Missing Responses in Item Response Theory Models. Educational and Psychological Measurement 74: 423–52. [Google Scholar] [CrossRef]
- Preckel, Franzis. 2003. Diagnostik Intellektueller Hochbegabung: Testentwicklung zur Erfassung der Fluiden Intelligenz. Zugl.: Münster, University, Diss. 2002 u.d.T.: Preckel. Franzis: Regelgeleitete Entwicklung eines figuralen Matrizentests zur Erfassung intellektueller Hochbegabung, Hochbegabung. Göttingen: Hogrefe Verl. für Psychologie. [Google Scholar]
- Rammstedt, Beatrice, Christoph Kemper, Mira Klein, Constanze Beierlein, and A. Kovaleva. 2012. Eine kurze Skala zur Messung der fünf Dimensionen der Persönlichkeit: Big-Five-Inventory-10 (BFI-10) (GESIS Working Papers 2012|23). Köln: GESIS. [Google Scholar]
- Rasch, Georg. 1960. Studies in Mathematical Psychology: I. Probabilistic Models for Some Intelligence and Attainment Tests. New York: Nielsen & Lydiche. [Google Scholar]
- Raven, John C. 1976. Advanced Progressive Matrices, Set II. New York: Oxford University Press. [Google Scholar]
- Raven, John C., John H. Court, and Jean Raven. 1994. Manual for Raven’s Progressive Matrices and Mill Hill Vocabulary Scales. In Advanced Progressive Matrices. New York: Oxford Psychologists Press. [Google Scholar]
- Schmidt, Frank L., and John Hunter. 2004. General mental ability in the world of work: Occupational attainment and job performance. Journal of Personality and Social Psychology 86: 162–73. [Google Scholar] [CrossRef]
- Schneider, W. Joel, and Kevin S. McGrew. 2012. The Cattell-Horn-Carroll model of intelligence. In Contemporary Intellectual Assessment: Theories, Tests, and Issues, 3rd ed. New York: The Guilford Press, pp. 99–144. [Google Scholar]
- Schott, Franz, and Hans-Jürgen W. Wieberg. 1984. Regelgeleitete Itemkonstruktion [Rule-governed construction of items.]. Diagnostica 30: 47–66. [Google Scholar]
- Storme, Martin, Nils Myszkowski, Simon Baron, and David Bernard. 2019. Same Test, Better Scores: Boosting the Reliability of Short Online Intelligence Recruitment Tests with Nested Logit Item Response Theory Models. Journal of Intelligence 7: 17. [Google Scholar] [CrossRef] [PubMed]
- Tarrant, Marie, James Ware, and Ahmed M. Mohammed. 2009. An assessment of functioning and non-functioning distractors in multiple-choice questions: A descriptive analysis. BMC Medical Education 9: 40. [Google Scholar] [CrossRef]
- The International Cognitive Ability Resource Team. 2014. Available online: https://icar-project.com/ (accessed on 6 April 2023).
- Undeutsch, Nicole. 2010. Zwei neue Subtests für das “Self-Assessment” Psychologie Durch Regelgeleitete Konstruktion. Wien: Diplomarbeit, Universität Wien, DataCite. [Google Scholar]
- Waschl, Nicolette A., Ted Nettelbeck, Simon A. Jackson, and Nicholas R. Burns. 2016. Dimensionality of the Raven’s Advanced Progressive Matrices: Sex differences and visuospatial ability. Personality and Individual Differences 100: 157–66. [Google Scholar] [CrossRef]
- Wheaton, Blair, Bengt Muthén, Duane F. Alwin, and Gene F. Summers. 1977. Assessing Reliability and Stability in Panel Models. Sociological Methodology 8: 84–136. [Google Scholar] [CrossRef]
- Wise, Steven L. 2017. Rapid-Guessing Behavior: Its Identification, Interpretation, and Implications. Educational Measurement: Issues and Practice 36: 52–61. [Google Scholar] [CrossRef]
- Wise, Steven L., and Christine E. DeMars. 2010. Examinee Noneffort and the Validity of Program Assessment Results. Educational Assessment 15: 27–41. [Google Scholar] [CrossRef]
- Yu, Ching-Yun. 2002. Evaluating Cutoff Criteria of Model Fit Indices for Latent Variable Models with Binary and Continuous Outcomes. Doctoral dissertation, University of California, Los Angeles, CA, USA. [Google Scholar]

| Sub-Sample | N | Age | Gender (Female (%)) | Population | Location | Cognitive Measures | Additional Questionnaires | Academic | |
|---|---|---|---|---|---|---|---|---|---|
| M | SD | ||||||||
| 1 | 155 | 23.81 | 5.49 | 112 (72.3) | University | Online | |||
| 2 | 107 | 24.18 | 3.42 | 72 (67.3) | University of Applied Sciences | Online | NFC | GPA | |
| 3 | 126 | 24.66 | 4.47 | 92 (73.0) | University of Applied Sciences | Online | NFC | GPA | |
| 4 | 216 | 26.02 | 11.18 | 136 (63.0) | University and general population | In person | BIS-S | NFC | GPA |
| 5 | 79 | 33.81 | 13.54 | 40 (50.6) | General population | Online | I-S-T 2000R RAPM | NFC | GPA |
| Response Option | Addition | Identification | Seriation | Operations Correct |
|---|---|---|---|---|
| A | 0 | 1 | 1 | 2 |
| B | 1 | 0 | 0 | 1 |
| C | 0 | 1 | 0 | 1 |
| D | 1 | 0 | 1 | 2 |
| E | 0 | 0 | 1 | 1 |
| F | 1 | 1 | 1 | 3 |
| G | 1 | 1 | 0 | 2 |
| H | 0 | 0 | 0 | 0 |
| Item | Correctly Solved (in %) | Valid Responses (N) |
|---|---|---|
| 1 | 50.66 | 677 |
| 2 | 60.59 | 680 |
| 3 | 51.19 | 670 |
| 4 | 66.03 | 680 |
| 5 | 43.91 | 681 |
| 6 | 93.27 | 683 |
| 7 | 41.38 | 679 |
| 8 | 48.32 | 683 |
| 9 | 70.90 | 677 |
| 10 | 89.00 | 682 |
| 11 | 27.71 | 682 |
| 12 | 34.85 | 680 |
| 13 | 69.96 | 679 |
| 14 | 81.11 | 683 |
| 15 | 60.35 | 681 |
| 16 | 60.03 | 683 |
| 17 | 71.98 | 678 |
| 18 | 79.18 | 682 |
| 19 | 80.32 | 681 |
| 20 | 81.47 | 680 |
| 21 | 71.76 | 680 |
| 22 | 55.67 | 670 |
| 23 | 86.78 | 681 |
| 24 | 48.07 | 672 |
| 25 | 58,49 | 677 |
| 26 | 73.63 | 675 |
| 27 | 66.17 | 677 |
| 28 | 36.61 | 672 |
| 29 | 71.58 | 665 |
| 30 | 23.72 | 662 |
| 31 | 51.51 | 662 |
| 32 | 36.67 | 660 |
| 33 | 76.28 | 666 |
| 34 | 62.11 | 665 |
| 35 | 60.76 | 660 |
| 36 | 59.51 | 657 |
| 37 | 44.73 | 626 |
| 38 | 46.63 | 489 |
| 39 | 51.81 | 635 |
| 40 | 49.03 | 620 |
| 41 | 38.21 | 602 |
| 42 | 40.27 | 596 |
| 43 | 66.39 | 607 |
| 44 | 42.37 | 557 |
| 45 | 55.06 | 563 |
| 46 | 55.50 | 564 |
| 47 | 55.12 | 557 |
| 48 | 55.29 | 539 |
| Model | χ2 | df | p | CFI | RMSEA | χ2/df |
|---|---|---|---|---|---|---|
| 3542.68 | 1127 | <.001 | 0.88 | 0.056 | 3.14 |
| Variable | Sample Size (N) | Correlation | |
|---|---|---|---|
| RAPM | 76 | 0.81 *** (0.90) | |
| BIS-S | 215 | 0.58 *** (0.70) | |
| I-S-T 2000R | 76 | ||
| Reasoning | |||
| Overall | 0.73 *** (0.79) | ||
| Verbal | 0.42 *** (0.49) | ||
| Numeric | 0.66 *** (0.71) | ||
| Figural | 0.63 *** (0.79) | ||
| Knowledge | |||
| Overall | 0.43 ** (0.47) | ||
| Verbal | 0.23 (0.27) | ||
| Numeric | 0.51 *** (0.61) | ||
| Figural | 0.39 *** (0.48) |
| Variable | Sample Size | Correlation | |
|---|---|---|---|
| High School | |||
| GPA | 472 (264) | −0.38 *** (−0.48 ***) | |
| Mathematics | 194 (126) | 0.48 *** (48 ***) | |
| German | 192 (125) | 0.20 ** (0.22 *) | |
| English | 186 (118) | 0.17 * (0.20 *) | |
| Biology | 142 (91) | 0.32 ***(0.44 ***) | |
| Arts | 107 (64) | 0.08 (0.17) |
| Operation | M | SD | Alpha | 1 | 2 | 3 | 4 | 5 | 6 | 7 | HeiQ | BIS |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Addition | 81.69 | 15.23 | 0.68 | 0.74 *** (0.93) | 0.38 *** (0.51) | |||||||
| Subtraction | 77.86 | 19.51 | 0.77 | 0.67 | 0.83 *** (0.98) | 0.55 *** (0.70) | ||||||
| Identification | 91.93 | 11.08 | 0.66 | 0.61 | 0.62 | 0.55 *** (0.70) | 0.32 *** (0.44) | |||||
| Variation of Open Gestalts | 77.95 | 16.38 | 0.64 | 0.63 | 0.64 | 0.61 | 0.72 *** (0.93) | 0.42 *** (0.58) | ||||
| Variation of Closed Gestalts | 78.05 | 15.98 | 0.62 | 0.62 | 0.63 | 0.56 | 0.65 | 0.72 *** (0.95) | 0.40 *** (0.56) | |||
| Intersection | 63.44 | 20.21 | 0.69 | 0.58 | 0.65 | 0.47 | 0.56 | 0.54 | 0.81 *** (0.99) | 0.42 *** (0.56) | ||
| Unique Addition | 61.79 | 24.44 | 0.80 | 0.61 | 0.72 | 0.50 | 0.59 | 0.56 | 0.72 | 0.84 *** (0.97) | 0.51 *** (0.63) | |
| Seriation | 76.60 | 19.16 | 0.73 | 0.65 | 0.72 | 0.57 | 0.64 | 0.62 | 0.66 | 0.69 | 0.80 *** (0.97) | 0.53 *** (0.69) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pallentin, V.S.; Danner, D.; Rummel, J. Construction and Validation of the HeiQ: An Operation-Oriented Figural Matrices Test. J. Intell. 2023, 11, 73. https://doi.org/10.3390/jintelligence11040073
Pallentin VS, Danner D, Rummel J. Construction and Validation of the HeiQ: An Operation-Oriented Figural Matrices Test. Journal of Intelligence. 2023; 11(4):73. https://doi.org/10.3390/jintelligence11040073
Chicago/Turabian StylePallentin, Vanessa S., Daniel Danner, and Jan Rummel. 2023. "Construction and Validation of the HeiQ: An Operation-Oriented Figural Matrices Test" Journal of Intelligence 11, no. 4: 73. https://doi.org/10.3390/jintelligence11040073
APA StylePallentin, V. S., Danner, D., & Rummel, J. (2023). Construction and Validation of the HeiQ: An Operation-Oriented Figural Matrices Test. Journal of Intelligence, 11(4), 73. https://doi.org/10.3390/jintelligence11040073





