Basic Symbolic Number Skills, but Not Formal Mathematics Performance, Longitudinally Predict Mathematics Anxiety in the First Years of Primary School
Abstract
:1. Introduction
1.1. The Emergence of MA
1.2. The Aims of the Current Study
2. Method
2.1. Participants
2.2. Materials
2.2.1. Measures of Socioeconomic Status and Cognitive Ability
Northern Ireland Multiple Deprivation Measure
Parental Education
Verbal and Non-Verbal Intelligence
Order Working Memory (WM) Task
Daily Event Task
2.2.2. Measures of Basic Numerical Skills at the Start of the First School Year
Number Ordering2
Counting
Non-Symbolic Addition
Number Comparison
Number Line Task
Mathematics Performance
Mathematical Anxiety
2.3. Procedure
2.4. Power Analysis
3. Results
3.1. Concurrent MA and Math Performance at T3
3.2. Longitudinal Relations between T1 and T2 Basic Skills and T3 Math Performance
3.3. Longitudinal Relations between T1 and T2 Basic Skills and MA at T3
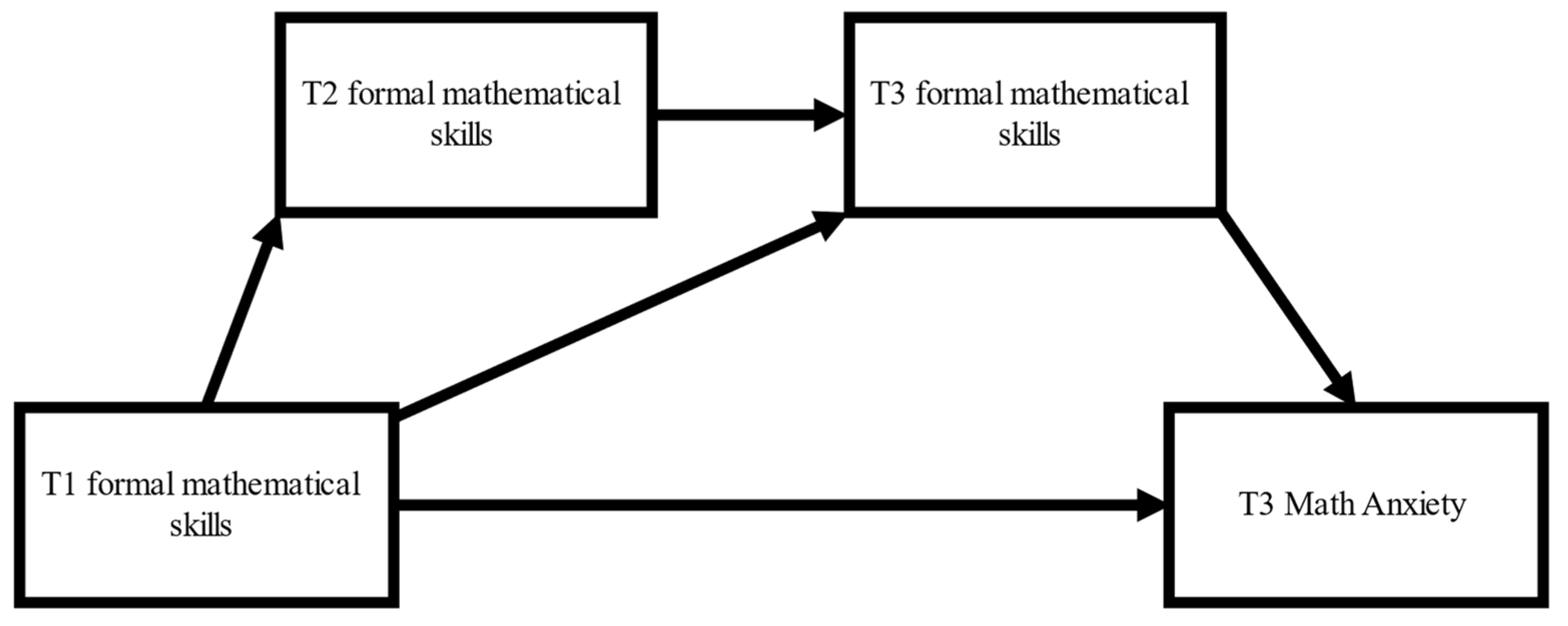
3.4. Longitudinal Relations between Formal Mathematical Skills at Different Time Points and between Formal Mathematics Skills and MA
3.5. Indirect Effects of Early Formal Math Skills on T3 MA
4. Discussion
4.1. Limitations and Future Directions
4.2. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | The original sample consisted of ninety children at T1. At T2, two of the children moved schools, and one further participant was withdrawn from the study. At T3, a further 27 children did not take part in the study. Three of these children moved to another school. The remaining 24 children did not take part because their parent(s) did not give consent for their child to take part. The children who did not take part at T3 were not all from the same class (children in the study came from eight different classes across four different schools); the number of children from each of the eight classes who did not take part in the study at T3 ranged from 1–5. Despite the high drop-out rate in the study, children who dropped out did not differ from the final sample in their basic characteristics (see Table S1 in Supplementary Materials). |
| 2 | Reaction time data was recorded for only three tasks (number comparison, daily events, and number ordering at T2). We did not analyse these results further, as reliability estimates for RT for young children tend to be lower than those for accuracy. |
| 3 | Due to high attrition rates at Time 3, our final sample size was slightly smaller than this. |
References
- Aagten-Murphy, David, Claudia Attucci, Niki Daniel, Elena Klaric, David Burr, and Elizabeth Pellicano. 2015. Numerical estimation in children with autism. Autism Research 8: 668–81. [Google Scholar] [CrossRef]
- Aarnos, Eila, and Päivi Perkkilä. 2012. Early signs of mathematics anxiety? Procedia-Social and Behavioral Sciences 46: 1495–99. [Google Scholar] [CrossRef]
- Ashcraft, Mark H. 2002. Math anxiety: Personal, educational, and cognitive consequences. Current Directions in Psychological Science 11: 181–85. [Google Scholar] [CrossRef]
- Ashcraft, Mark H., and Jeremy A. Krause. 2007. Working memory, math performance, and math anxiety. Psychonomic Bulletin & Review 14: 243–48. [Google Scholar] [CrossRef]
- Ashcraft, Mark H., and Kelly S. Ridley. 2005. Math anxiety and its cognitive consequences: A tutorial review. In The Handbook of Mathematical Cognition. London: Psychology Press, pp. 315–27. [Google Scholar]
- Ashcraft, Mark H., Elizabeth P. Kirk, and Derek Hopko. 1998. On the cognitive consequences of mathematics anxiety. In Studies in Developmental Psychology. The Development of Mathematical Skills. Edited by C. Donlan. London: Psychology Press/Taylor and Francis (UK), pp. 175–96. [Google Scholar]
- Attout, Lucie, and Steve Majerus. 2018. Serial order working memory and numerical ordinal processing share common processes and predict arithmetic abilities. British Journal of Developmental Psychology 36: 285–98. [Google Scholar] [CrossRef]
- Attout, Lucie, Marie-Pascale Noël, and Steve Majerus. 2014. The relationship between working memory for serial order and numerical development: A longitudinal study. Developmental Psychology 50: 1667. [Google Scholar] [CrossRef]
- Barroso, Connie, Colleen M. Ganley, Amanda L. McGraw, Elyssa A. Geer, Sara A. Hart, and Mia C. Daucourt. 2021. A meta-analysis of the relation between math anxiety and math achievement. Psychological Bulletin 147: 134. [Google Scholar] [CrossRef] [PubMed]
- Beilock, Sian L., and Daniel T. Willingham. 2014. Math anxiety: Can teachers help students reduce it? ask the cognitive scientist. American Educator 38: 28. [Google Scholar]
- Brankaer, Carmen, Pol Ghesquière, and Bert De Smedt. 2017. Symbolic magnitude processing in elementary school children: A group administered paper-and-pencil measure (SYMP Test). Behavior Research Methods 49: 1361–73. [Google Scholar] [CrossRef]
- Cain-Caston, Marlene. 1993. Parent and student attitudes toward mathematics as they relate to third grade mathematics achievement. Journal of Instructional Psychology 20: 96–119. [Google Scholar]
- Cargnelutti, Elisa, Carlo Tomasetto, and Maria Chiara Passolunghi. 2017a. How is anxiety related to math performance in young students? A longitudinal study of Grade 2 to Grade 3 children. Cognition and Emotion 31: 755–64. [Google Scholar] [CrossRef]
- Cargnelutti, Elisa, Carlo Tomasetto, and Maria Chiara Passolunghi. 2017b. The interplay between affective and cognitive factors in shaping early proficiency in mathematics. Trends in Neuroscience and Education 8: 28–36. [Google Scholar] [CrossRef]
- Chen, Qixuan, and Jingguang Li. 2014. Association between individual differences in non-symbolic number acuity and math performance: A meta-analysis. Acta Psychologica 148: 163–72. [Google Scholar] [CrossRef] [PubMed]
- Ching, Boby Ho-Hong. 2017. Mathematics anxiety and working memory: Longitudinal associations with mathematical performance in Chinese children. Contemporary Educational Psychology 51: 99–113. [Google Scholar] [CrossRef]
- Ching, Boby Ho-Hong, Kenneth Hong Cheng Kong, Hannah Xiaohan Wu, and Tiffany Ting Chen. 2020. Examining the reciprocal relations of mathematics anxiety to quantitative reasoning and number knowledge in Chinese children. Contemporary Educational Psychology 63: 101919. [Google Scholar] [CrossRef]
- Cohen, Jacob. 1988. Statistical Power Analysis for the Behavioral Sciences. New York: Routledge Academic (USA). [Google Scholar]
- Council for the Curriculum, Examinations and Assessment. 2019. Assessment Arrangements for Key Stage 1 and 2. Available online: https://ccea.org.uk/downloads/docs/ccea-asset/Curriculum/The%20Northern%20Ireland%20Curriculum%20-%20Primary.pdf (accessed on 6 March 2022).
- Council for the Curriculum, Examinations and Assessment. 2020. Mathematics and Numeracy: Key Stage 1. Available online: https://ccea.org.uk/downloads/docs/ccea-asset/Resource/Key%20Stage%201%20Statutory%20Requirements%20for%20Mathematics%20and%20Numeracy.pdf (accessed on 6 March 2022).
- Devine, Amy, Francesca Hill, Emma Carey, and Dénes Szűcs. 2018. Cognitive and emotional math problems largely dissociate: Prevalence of developmental dyscalculia and mathematics anxiety. Journal of Educational Psychology 110: 431–44. [Google Scholar] [CrossRef]
- Devine, Amy, Kayleigh Fawcett, Dénes Szűcs, and Ann Dowker. 2012. Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behavioral and Brain Functions 8: 1–9. [Google Scholar] [CrossRef]
- Dietrich, Julia F., Stefan Huber, Korbinian Moeller, and Elise Klein. 2015. The influence of math anxiety on symbolic and non-symbolic magnitude processing. Frontiers in Psychology 6: 1621. [Google Scholar] [CrossRef]
- Dowker, Ann, Amar Sarkar, and Chung Yen Looi. 2016. Mathematics anxiety: What have we learned in 60 years? Frontiers in Psychology 7: 508. [Google Scholar] [CrossRef]
- Dowker, Ann, Karina Bennett, and Louise Smith. 2012. Attitudes to mathematics in primary school children. Child Development Research 2012: 124939. [Google Scholar] [CrossRef]
- Dreger, Ralph Mason, and Lewis R. Aiken Jr. 1957. The identification of number anxiety in a college population. Journal of Educational Psychology 48: 344–51. [Google Scholar] [CrossRef]
- Fazio, Lisa K., Drew H. Bailey, Clarissa A. Thompson, and Robert S. Siegler. 2014. Relations of different types of numerical magnitude representations to each other and to mathematics achievement. Journal of Experimental Child Psychology 123: 53–72. [Google Scholar] [CrossRef] [PubMed]
- Finell, Jonatan, Ellen Sammallahti, Johan Korhonen, Hanna Eklöf, and Bert Jonsson. 2022. Working Memory and its mediating role on the relationship of math anxiety and math performance: A meta-analysis. Frontiers in Psychology 12: 798090. [Google Scholar] [CrossRef] [PubMed]
- Friedman, William J. 1990. Children’s representations of the pattern of daily activities. Child Development 61: 1399–412. [Google Scholar] [CrossRef]
- Friso-Van den Bos, Ilona, Sanne H. G. Van der Ven, Evelyn H. Kroesbergen, and Johannes E. H. Van Luit. 2013. Working memory and mathematics in primary school children: A meta-analysis. Educational Research Review 10: 29–44. [Google Scholar] [CrossRef]
- Ganley, Colleen M., and Amanda L. McGraw. 2016. The development and validation of a revised version of the math anxiety scale for young children. Frontiers in Psychology 7: 1181. [Google Scholar] [CrossRef]
- Gilmore, Camilla K., Shannon E. McCarthy, and Elizabeth S. Spelke. 2010. Non-symbolic arithmetic abilities and mathematics achievement in the first year of formal schooling. Cognition 115: 394–406. [Google Scholar] [CrossRef]
- Ginsburg, Herbert, and Arthur J. Baroody. 2003. TEMA-3: Test of Early Mathematics Ability. Austin: Pro-ed. [Google Scholar]
- Gunderson, Elizabeth A., Daeun Park, Erin A. Maloney, Sian L. Beilock, and Susan C. Levine. 2018. Reciprocal relations among motivational frameworks, math anxiety, and math achievement in early elementary school. Journal of Cognition and Development 19: 21–46. [Google Scholar] [CrossRef]
- Halberda, Justin, Michèle M. M. Mazzocco, and Lisa Feigenson. 2008. Individual differences in non-verbal number acuity correlate with maths achievement. Nature 455: 665–68. [Google Scholar] [CrossRef]
- Hannula, Minna M., and Erno Lehtinen. 2005. Spontaneous focusing on numerosity and mathematical skills of young children. Learning and Instruction 15: 237–56. [Google Scholar] [CrossRef]
- Harari, Rachel R., Rose K. Vukovic, and Sean P. Bailey. 2013. Mathematics anxiety in young children: An exploratory study. The Journal of Experimental Education 81: 538–55. [Google Scholar] [CrossRef]
- Hembree, Ray. 1990. The nature, effects, and relief of mathematics anxiety. Journal for Research in Mathematics Education 21: 33–46. [Google Scholar] [CrossRef]
- Hill, Francesca, Irene C. Mammarella, Amy Devine, Sara Caviola, Maria Chiara Passolunghi, and Dénes Szűcs. 2016. Maths anxiety in primary and secondary school students: Gender differences, developmental changes and anxiety specificity. Learning and Individual Differences 48: 45–53. [Google Scholar] [CrossRef]
- Hodder Education. n.d. Mathematics Assessment for Learning and Teaching. Available online: https://www.hoddereducation.co.uk/malt (accessed on 6 March 2022).
- Jameson, Molly M. 2013. The development and validation of the Children’s Anxiety in Math Scale. Journal of Psychoeducational. [Google Scholar] [CrossRef]
- Krinzinger, Helga, Liane Kaufmann, and Klaus Willmes. 2009. Math anxiety and math ability in early primary school years. Journal of Psychoeducational Assessment 27: 206–25. [Google Scholar] [CrossRef]
- Lauer, Jillian E., Alena G. Esposito, and Patricia J. Bauer. 2018. Domain-specific anxiety relates to children’s math and spatial performance. Developmental Psychology 54: 2126. [Google Scholar] [CrossRef]
- Lee, Kerry, and Rebecca Bull. 2016. Developmental changes in working memory, updating, and math achievement. Journal of Educational Psychology 108: 869. [Google Scholar] [CrossRef]
- Levy, Helen, Peter A. Ubel, Amanda J. Dillard, David R. Weir, and Angela Fagerlin. 2014. Health numeracy: The importance of domain in assessing numeracy. Medical Decision Making 34: 107–15. [Google Scholar] [CrossRef]
- Liang, Yuan, Lijin Zhang, Xu Duan, Guoqiang Wu, and Hao Yan. 2023. Longitudinal association between non-symbolic numerical representation and emerging math competence: The dynamic mediation effect from cardinal knowledge to ordinal skills. Cognitive Development 66: 101339. [Google Scholar] [CrossRef]
- Lyons, Ian M., and Daniel Ansari. 2015. Numerical order processing in children: From reversing the distance-effect to predicting arithmetic. Mind, Brain, and Education 9: 207–21. [Google Scholar] [CrossRef]
- Lyons, Ian M., and Sian L. Beilock. 2011. Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition 121: 256–61. [Google Scholar] [CrossRef]
- Lyons, Ian M., Gavin R. Price, Anniek Vaessen, Leo Blomert, and Daniel Ansari. 2014. Numerical predictors of arithmetic success in grades 1–6. Developmental Science 17: 714–26. [Google Scholar] [CrossRef]
- Ma, Xin. 1999. A meta-analysis of the relationship between anxiety toward mathematics and achievement in mathematics. Journal for Research in Mathematics Education 30: 520–40. [Google Scholar] [CrossRef]
- Majerus, Steve, Martine Poncelet, Christelle Greffe, and Martial Van der Linden. 2006. Relations between vocabulary development and verbal short-term memory: The relative importance of short-term memory for serial order and item information. Journal of Experimental Child Psychology 93: 95–119. [Google Scholar] [CrossRef]
- Malone, Stephanie A., Verena E. Pritchard, and Charles Hulme. 2021. Separable effects of the approximate number system, symbolic number knowledge, and number ordering ability on early arithmetic development. Journal of Experimental Child Psychology 208: 105120. [Google Scholar] [CrossRef] [PubMed]
- Maloney, Erin A., Daniel Ansari, and Jonathan A. Fugelsang. 2011. Rapid communication: The effect of mathematics anxiety on the processing of numerical magnitude. Quarterly Journal of Experimental Psychology 64: 10–16. [Google Scholar] [CrossRef] [PubMed]
- Mononen, Riikka, Markku Niemivirta, Johan Korhonen, Marcus Lindskog, and Anna Tapola. 2022. Developmental relations between mathematics anxiety, symbolic numerical magnitude processing and arithmetic skills from first to second grade. Cognition and Emotion 36: 452–72. [Google Scholar] [CrossRef]
- Morsanyi, Kinga, Bianca M. C. W. van Bers, Patrick Aaron O’Connor, and Teresa McCormack. 2020. The role of numerical and non-numerical ordering abilities in mathematics and reading in middle childhood. Contemporary Educational Psychology 62: 101895. [Google Scholar] [CrossRef]
- Morsanyi, Kinga, Chiara Busdraghi, and Caterina Primi. 2014. Mathematical anxiety is linked to reduced cognitive reflection: A potential road from discomfort in the mathematics classroom to susceptibility to biases. Behavioral and Brain Functions 10: 1–13. [Google Scholar] [CrossRef]
- Morsanyi, Kinga, Eileen O’Mahony, and Teresa McCormack. 2017. Number comparison and number ordering as predictors of arithmetic performance in adults: Exploring the link between the two skills, and investigating the question of domain-specificity. Quarterly Journal of Experimental Psychology 70: 2497–517. [Google Scholar] [CrossRef]
- Namkung, Jessica M., Peng Peng, and Xin Lin. 2019a. The relation between mathematics anxiety and mathematics performance among school-aged students: A meta-analysis. Review of Educational Research 89: 459–96. [Google Scholar] [CrossRef]
- Namkung, Jessica M., Peng Peng, J. Marc Goodrich, and Victoria Molfese. 2019b. Exploring growth trajectories of informal and formal mathematics skills among prekindergarten children struggling with mathematics. Learning Disability Quarterly, 80–91. [Google Scholar] [CrossRef]
- National Numeracy. 2015. Why Is Numeracy Important? Available online: https://www.nationalnumeracy.org.uk/why-numeracy-important (accessed on 6 March 2022).
- Northern Ireland Statistics and Research Agency. 2010. Northern Ireland Multiple Deprivation Measure 2010: Blueprint Document; February. Available online: http://www.nisra.gov.uk/deprivation/archive/Updateof2005Measures/NIMDM_2010_Blueprint_Document.pdf (accessed on 6 March 2022).
- Nosworthy, Nadia, Stephanie Bugden, Lisa Archibald, Barrie Evans, and Daniel Ansari. 2013. A two-minute paper-and-pencil test of symbolic and nonsymbolic numerical magnitude processing explains variability in primary school children’s arithmetic competence. PLoS ONE 8: e67918. [Google Scholar] [CrossRef] [PubMed]
- Núñez-Peña, M. Isabel, and Macarena Suarez-Pellicioni. 2014. Less precise representation of numerical magnitude in high math-anxious individuals: An ERP study of the size and distance effects. Biological Psychology 103: 176–83. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, Patrick Aaron, Kinga Morsanyi, and Teresa McCormack. 2018. Young children’s non-numerical ordering ability at the start of formal education longitudinally predicts their symbolic number skills and academic achievement in maths. Developmental Science 21: e12645. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, Patrick Aaron, Kinga Morsanyi, and Teresa McCormack. 2019. The stability of individual differences in basic mathematics-related skills in young children at the start of formal education. Mind, Brain, and Education 13: 234–44. [Google Scholar] [CrossRef]
- Passolunghi, Maria Chiara, Chiara De Vita, and Sandra Pellizzoni. 2020. Math anxiety and math achievement: The effects of emotional and math strategy training. Developmental Science 23: e12964. [Google Scholar] [CrossRef]
- Peng, Peng, Jessica Namkung, Marcia Barnes, and Congying Sun. 2016. A meta-analysis of mathematics and working memory: Moderating effects of working memory domain, type of mathematics skill, and sample characteristics. Journal of Educational Psychology 108: 455–73. [Google Scholar] [CrossRef]
- Piazza, Manuela, Andrea Facoetti, Anna Noemi Trussardi, Ilaria Berteletti, Stefano Conte, Daniela Lucangeli, Stanislas Dehaene, and Marco Zorzi. 2010. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition 116: 33–41. [Google Scholar] [CrossRef]
- Preacher, Kristopher J., and Andrew F. Hayes. 2008. Asymptotic and resampling strategies for assessing and comparing indirect effects in multiple mediator models. Behavior Research Methods 40: 879–91. [Google Scholar] [CrossRef]
- Primi, Caterina, Maria Anna Donati, Francesca Chiesi, and Kinga Morsanyi. 2018. Are there gender differences in cognitive reflection? Invariance and differences related to mathematics. Thinking & Reasoning 24: 258–79. [Google Scholar] [CrossRef]
- Primi, Caterina, Maria A. Donati, Viola A. Izzo, Veronica Guardabassi, Patrick Aaron O’Connor, Carlo Tomasetto, and Kinga Morsanyi. 2020. The Early Elementary School Abbreviated Math Anxiety Scale (the EES-AMAS): A new adapted version of the AMAS to measure math anxiety in young children. Frontiers in Psychology 11: 1014. [Google Scholar] [CrossRef]
- Ramirez, Gerardo, Elizabeth A. Gunderson, Susan C. Levine, and Sian L. Beilock. 2013. Math anxiety, working memory, and math achievement in early elementary school. Journal of Cognition and Development 14: 187–202. [Google Scholar] [CrossRef]
- Ramirez, Gerardo, Hyesang Chang, Erin A. Maloney, Susan C. Levine, and Sian L. Beilock. 2016. On the relationship between math anxiety and math achievement in early elementary school: The role of problem solving strategies. Journal of Experimental Child Psychology 141: 83–100. [Google Scholar] [CrossRef]
- Richardson, Frank C., and Richard M. Suinn. 1972. The mathematics anxiety rating scale: Psychometric data. Journal of Counseling Psychology 19: 551–54. [Google Scholar] [CrossRef]
- Rolison, Jonathan J., Kinga Morsanyi, and Ellen Peters. 2020. Understanding health risk comprehension: The role of math anxiety, subjective numeracy, and objective numeracy. Medical Decision Making 40: 222–34. [Google Scholar] [CrossRef] [PubMed]
- Rolison, Jonathan J., Kinga Morsanyi, and Patrick A. O’Connor. 2016. Can I count on getting better? Association between math anxiety and poorer understanding of medical risk reductions. Medical Decision Making 36: 876–86. [Google Scholar] [CrossRef] [PubMed]
- Sasanguie, Delphine, and Helene Vos. 2018. Sasanguie, Delphine, and Helene Vos. About why there is a shift from cardinal to ordinal processing in the association with arithmetic between first and second grade. Developmental Science 21: e12653. [Google Scholar] [CrossRef]
- Sasanguie, Delphine, Ian M. Lyons, Bert De Smedt, and Bert Reynvoet. 2017. Unpacking symbolic number comparison and its relation with arithmetic in adults. Cognition 165: 26–38. [Google Scholar] [CrossRef] [PubMed]
- Sattler, Jerome M., and R. Dumont. 2004. Assessment of Children: WISC-IV and WPPSI-III Supplement. San Diego: Jerome M. Sattler, Publisher. [Google Scholar]
- Schneider, Michael, Kassandra Beeres, Leyla Coban, Simon Merz, S. Susan Schmidt, Johannes Stricker, and Bert De Smedt. 2017. Associations of non-symbolic and symbolic numerical magnitude processing with mathematical competence: A meta-analysis. Developmental Science 20: e12372. [Google Scholar] [CrossRef] [PubMed]
- Schneider, Michael, Simon Merz, Johannes Stricker, Bert De Smedt, Joke Torbeyns, Lieven Verschaffel, and Koen Luwel. 2018. Associations of number line estimation with mathematical competence: A meta-analysis. Child Development 89: 1467–84. [Google Scholar] [CrossRef] [PubMed]
- Song, Charlene Shujie, Chang Xu, Erin A. Maloney, Sheri-Lynn Skwarchuk, Sabrina Di Lonardo Burr, Anne Lafay, Judith Wylie, Helena P. Osana, Heather Douglas, and Jo-Anne LeFevre. 2021. Longitudinal relations between young students’ feelings about mathematics and arithmetic performance. Cognitive Development 59: 101078. [Google Scholar] [CrossRef]
- Strenze, Tarmo. 2007. Intelligence and socioeconomic success: A meta-analytic review of longitudinal research. Intelligence 35: 401–26. [Google Scholar] [CrossRef]
- Szczygiel, Monika. 2020. Gender, general anxiety, math anxiety and math achievement in early school-age children. Issues in Educational Research 30: 1126–42. Available online: http://www.iier.org.au/iier30/szczygiel.pdf (accessed on 1 September 2023).
- Tankersley, Karen. 1993. Teaching Math Their Way. Educational Leadership 50: 12–13. [Google Scholar]
- Thomas, G., and A. Dowker. 2000. Mathematics anxiety and related factors in young children. In British Psychological Society Developmental Section Conference. Bristol: University of Bristol. [Google Scholar]
- Tomasetto, Carlo, Kinga Morsanyi, Veronica Guardabassi, and Patrick Aaron O’Connor. 2021. Math anxiety interferes with learning novel mathematics contents in early elementary school. Journal of Educational Psychology 113: 315–29. [Google Scholar] [CrossRef]
- Vogel, Stephan E., Alicia Remark, and Daniel Ansari. 2015. Differential processing of symbolic numerical magnitude and order in first-grade children. Journal of Experimental Child Psychology 129: 26–39. [Google Scholar] [CrossRef]
- Vukovic, Rose K., Michael J. Kieffer, Sean P. Bailey, and Rachel R. Harari. 2013a. Mathematics anxiety in young children: Concurrent and longitudinal associations with mathematical performance. Contemporary Educational Psychology 38: 1–10. [Google Scholar] [CrossRef]
- Vukovic, Rose K., Steven O. Roberts, and Linnie Green Wright. 2013b. From parental involvement to children’s mathematical performance: The role of mathematics anxiety. Early Education & Development 24: 446–67. [Google Scholar] [CrossRef]
- Wang, Zhe, Sara Ann Hart, Yulia Kovas, Sarah Lukowski, Brooke Soden, Lee A. Thompson, Robert Plomin, Grainne McLoughlin, Christopher W. Bartlett, Ian M. Lyons, and et al. 2014. Who is afraid of math? Two sources of genetic variance for mathematical anxiety. Journal of Child Psychology and Psychiatry 55: 1056–64. [Google Scholar] [CrossRef]
- Wechsler, David. 2003. Wechsler Preschool and Primary Scale of Intelligence—Third UK Edition (WPPSI-III). Columbus: Psychological Corp. [Google Scholar]
- Williams, Julian. 2005. Mathematics Assessment for Learning and Teaching. London: Hodder Education. [Google Scholar]
- Wood, Guilherme, Pedro Pinheiro-Chagas, Annelise Julio-Costa, Letícia Rettore Micheli, Helga Krinzinger, Liane Kaufmann, Klaus Willmes, and Vitor Geraldi Haase. 2012. Math anxiety questionnaire: Similar latent structure in Brazilian and German school children. Child Development Research 2012: 610912. [Google Scholar] [CrossRef]
- Woodcock, Richard W., Kevin S. McGrew, and Nancy Mather. 2001. Woodcock-Johnson III NU Complete. Rolling Meadows: Riverside Publishing. [Google Scholar]
- Wu, Sarah S., Erik G. Willcutt, Emily Escovar, and Vinod Menon. 2014. Mathematics achievement and anxiety and their relation to internalizing and externalizing behaviors. Journal of Learning Disabilities 47: 503–14. [Google Scholar] [CrossRef] [PubMed]
- Wu, Sarah S., Maria Barth, Hitha Amin, Vanessa Malcarne, and Vinod Menon. 2012. Math anxiety in second and third graders and its relation to mathematics achievement. Frontiers in Psychology 3: 162. [Google Scholar] [CrossRef] [PubMed]
- Xenidou-Dervou, Iro, Dylan Molenaar, Daniel Ansari, Menno van der Schoot, and Ernest C. D. M. van Lieshout. 2017. Nonsymbolic and symbolic magnitude comparison skills as longitudinal predictors of mathematical achievement. Learning and Instruction 50: 1–13. [Google Scholar] [CrossRef]
- Yeo, Joseph Kai Kow. 2005. Anxiety and performance on mathematical problem solving of secondary two students in Singapore. The Mathematics Educator 8: 71–83. [Google Scholar]
- Zhang, Jing, Nan Zhao, and Qi Ping Kong. 2019. The relationship between math anxiety and math performance: A meta-analytic investigation. Frontiers in Psychology 10: 1613. [Google Scholar] [CrossRef]

| Mean (SD) | Range | D | |
|---|---|---|---|
| Parental education (Median) | 5 | 0–6 | <0.001 |
| Deprivation (Median) | 10.09 | 1.85–62.91 | <0.001 |
| Vocabulary (T1) | 15.93 (7.03) | 7–32 | 0.030 |
| Block design (T1) | 24.40 (3.37) | 16–30 | 0.011 |
| OPQ (T1) | 44.12 (7.18) | 26–56 | 0.200 |
| Order WM (T1) | 9.93 (4.36) | 1–16 | <0.001 |
| Order WM (T2) | 11.23 (4.34) | 1–19 | <0.001 |
| Daily events (T1) | 0.66 (.12) | 0.46–0.96 | <0.001 |
| Daily events (T2) | 0.77 (.12) | 0.46–1 | 0.003 |
| Number ordering (T1) | 0.85 (.28) | 0–1 | <0.001 |
| Number ordering (T2) | 0.76 (.20) | 0.38–1 | <0.001 |
| Counting (T1) | 0.20 (2.72) | −8.21–3 | <0.001 |
| Counting (T2) | 0.32 (1.83) | −9.28–1 | <0.001 |
| Non-symbolic addition (T1) | 0.56 (0.11) | 0.30–0.88 | 0.002 |
| Non-symbolic addition (T2) | 0.66 (0.14) | 0.33–0.96 | 0.178 |
| Number comparison (T1) | 0.71 (0.19) | 0.40–1 | 0.008 |
| Number comparison (T2) | 0.97 (0.04) | 0.75–1 | <0.001 |
| Number line estimation (T1) | 199.36 (78.52) | 64–453 | 0.023 |
| Number line estimation (T2) | 120.24 (42.82) | 42.222 | 0.200 |
| CMAQ-R | 34.30 (13.30) | 16–70 | 0.200 |
| EES-AMAS | 19.53 (9.18) | 9–39 | <0.001 |
| Math Performance at T1 | 23.24 (4.88) | 1–28 | <0.001 |
| Math Performance at T2 (raw score) | 21.74 (4.71) | 7–29 | 0.001 |
| Math Performance at T3 (raw score) | 27.43 (7.15) | 13–40 | 0.200 |
| Math Performance at T3 (standardised score) | 106.10 (11.49) | 86–130 | 0.200 |
| Math Anxiety | |||
|---|---|---|---|
| r | BF10 | BF01 | |
| Formal math performance (Raw) | −0.31 * | 5.380 | 0.186 |
| Counting and understanding number | −0.35 ** | 12.434 | 0.080 |
| Knowing and using number facts | −0.30 * | 4.418 | 0.226 |
| Calculating | −0.28 * | 3.210 | 0.312 |
| Understanding shape | −0.07 | 0.263 | 3.807 |
| Measuring | −0.07 | 0.267 | 3.748 |
| Handling data | −0.08 | 0.289 | 3.464 |
| Formal Math Performance (T3) | Math Anxiety (T3) | |||||
|---|---|---|---|---|---|---|
| r | BF10 | BF01 | r | BF10 | BF01 | |
| OPQ (T1) | 0.21 | 1.03 | 0.97 | 0.01 | 0.15 | 6.55 |
| Order WM (T1) | 0.28 * | 3.23 | 0.31 | 0.07 | 0.11 | 8.89 |
| Order WM (T2) | 0.30 * | 4.62 | 0.22 | 0.08 | 0.11 | 9.41 |
| Daily events (T1) | 0.41 ** | 62.23 | 0.02 | −0.12 | 0.40 | 2.47 |
| Daily events (T2) | 0.39 ** | 30.95 | 0.03 | −0.01 | 0.17 | 6.01 |
| Number ordering (T1) | 0.25 | 1.73 | 0.58 | 0.13 | 0.09 | 11.45 |
| Number ordering (T2) | 0.49 *** | 663.18 | <0.01 | −0.35 ** | 13.56 | 0.07 |
| Counting (T1) | 0.44 *** | 143.21 | <0.01 | −0.24 | 1.67 | 0.60 |
| Counting (T2) | 0.20 | 0.95 | 1.05 | −0.17 | 0.63 | 1.60 |
| Non-symbolic addition (T1) | 0.23 | 1.39 | 0.72 | −0.22 | 1.26 | 0.79 |
| Non-symbolic addition (T2) | 0.45 *** | 197.52 | <0.01 | −0.22 | 1.15 | 0.87 |
| Number comparison (T1) | 0.14 | 0.49 | 2.05 | −0.37 ** | 20.90 | 0.05 |
| Number comparison (T2) | 0.32 * | 6.25 | 0.16 | −0.04 | 0.21 | 4.87 |
| Number line estimation (T1) | 0.35 ** | 12.60 | 0.08 | 0.12 | 0.38 | 2.61 |
| Number line estimation (T2) | 0.16 | 0.60 | 1.67 | 0.07 | 0.26 | 3.83 |
| Formal math performance (T1) | 0.47 ** | 340.31 | <0.001 | 0.02 | 0.15 | 6.79 |
| Formal math performance (T2) | 0.58 ** | 28,939.12 | <0.001 | −0.19 | 0.82 | 1.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Connor, P.A.; Morsanyi, K.; McCormack, T. Basic Symbolic Number Skills, but Not Formal Mathematics Performance, Longitudinally Predict Mathematics Anxiety in the First Years of Primary School. J. Intell. 2023, 11, 211. https://doi.org/10.3390/jintelligence11110211
O’Connor PA, Morsanyi K, McCormack T. Basic Symbolic Number Skills, but Not Formal Mathematics Performance, Longitudinally Predict Mathematics Anxiety in the First Years of Primary School. Journal of Intelligence. 2023; 11(11):211. https://doi.org/10.3390/jintelligence11110211
Chicago/Turabian StyleO’Connor, Patrick A., Kinga Morsanyi, and Teresa McCormack. 2023. "Basic Symbolic Number Skills, but Not Formal Mathematics Performance, Longitudinally Predict Mathematics Anxiety in the First Years of Primary School" Journal of Intelligence 11, no. 11: 211. https://doi.org/10.3390/jintelligence11110211
APA StyleO’Connor, P. A., Morsanyi, K., & McCormack, T. (2023). Basic Symbolic Number Skills, but Not Formal Mathematics Performance, Longitudinally Predict Mathematics Anxiety in the First Years of Primary School. Journal of Intelligence, 11(11), 211. https://doi.org/10.3390/jintelligence11110211





