A Psychometric Network Analysis of CHC Intelligence Measures: Implications for Research, Theory, and Interpretation of Broad CHC Scores “Beyond g”
Abstract
1. Introduction
2. Literature Review
2.1. The beyond g Position: The Promise of Broad CHC Scores in Intelligence Testing Interpretation
2.2. The g-Centric Position: Broad CHC Scores Are of Trivial Value beyond the Global IQ Score
2.3. The Problem of Conflating Theoretical and Psychometric g
2.4. The Application of Non-g Emergent Property Network Models to IQ Batteries
2.4.1. Limitations of Common Cause Factor Models of Intelligence
2.4.2. The Potential of Psychometric Network Models of Intelligence Tests
2.4.3. Prior PNA of IQ Batteries
2.5. Current Study
3. Materials and Methods
3.1. Participants
3.2. Measures
3.3. Data Analysis
3.3.1. Score Metric and Analysis Software
3.3.2. PNA Methods
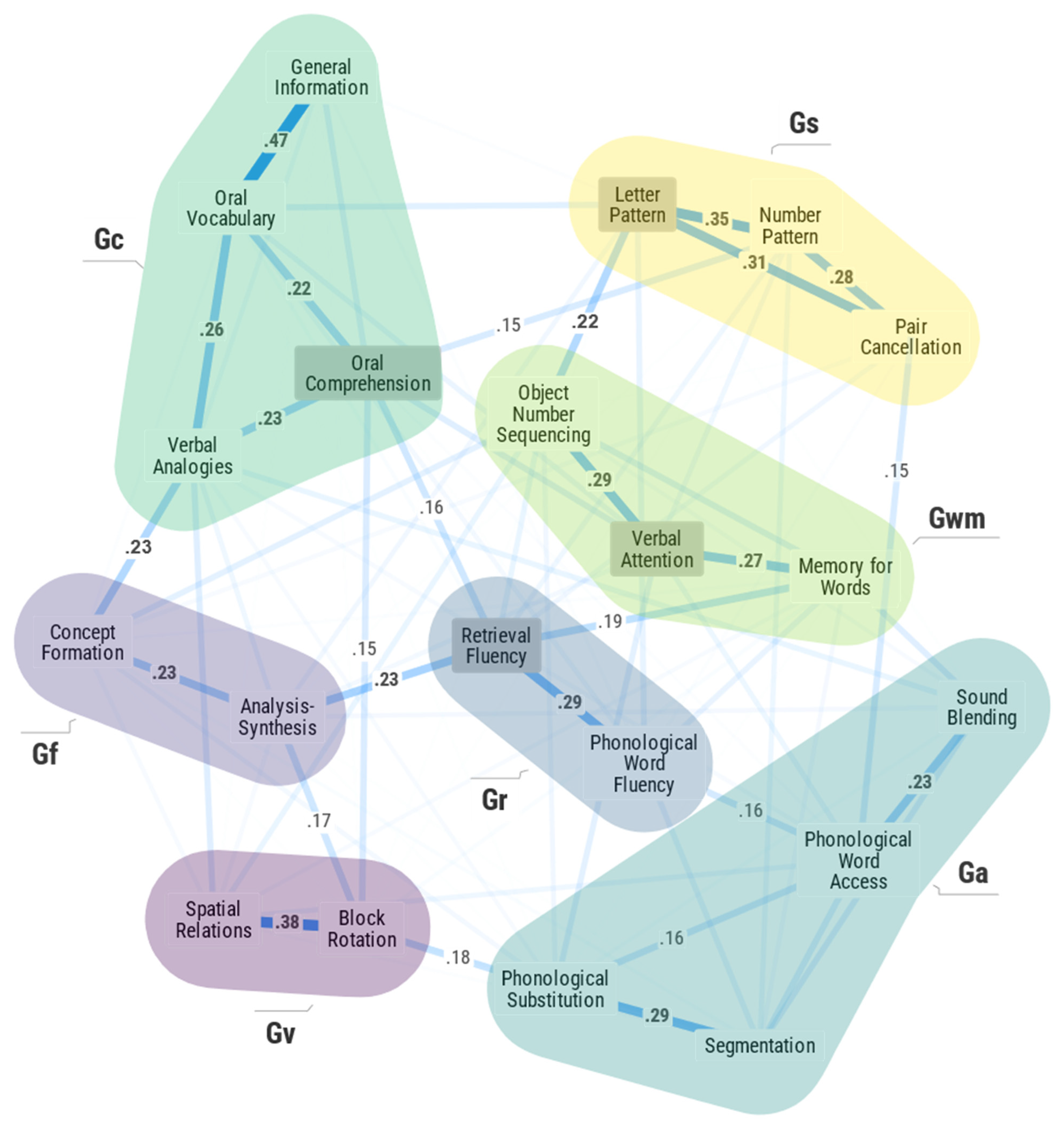
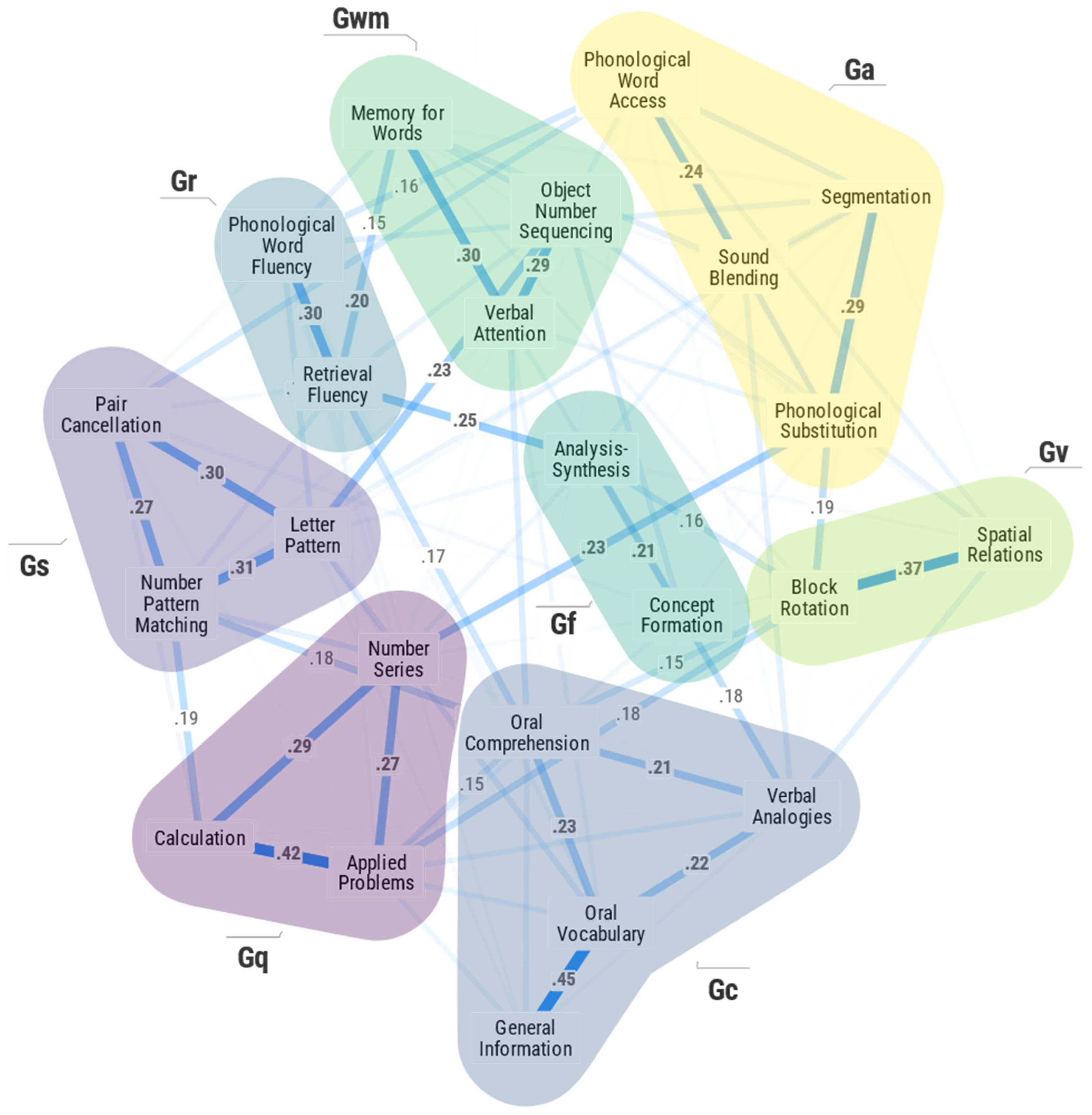
4. Results
4.1. PNA Models
4.2. PNA Model Centrality Metrics
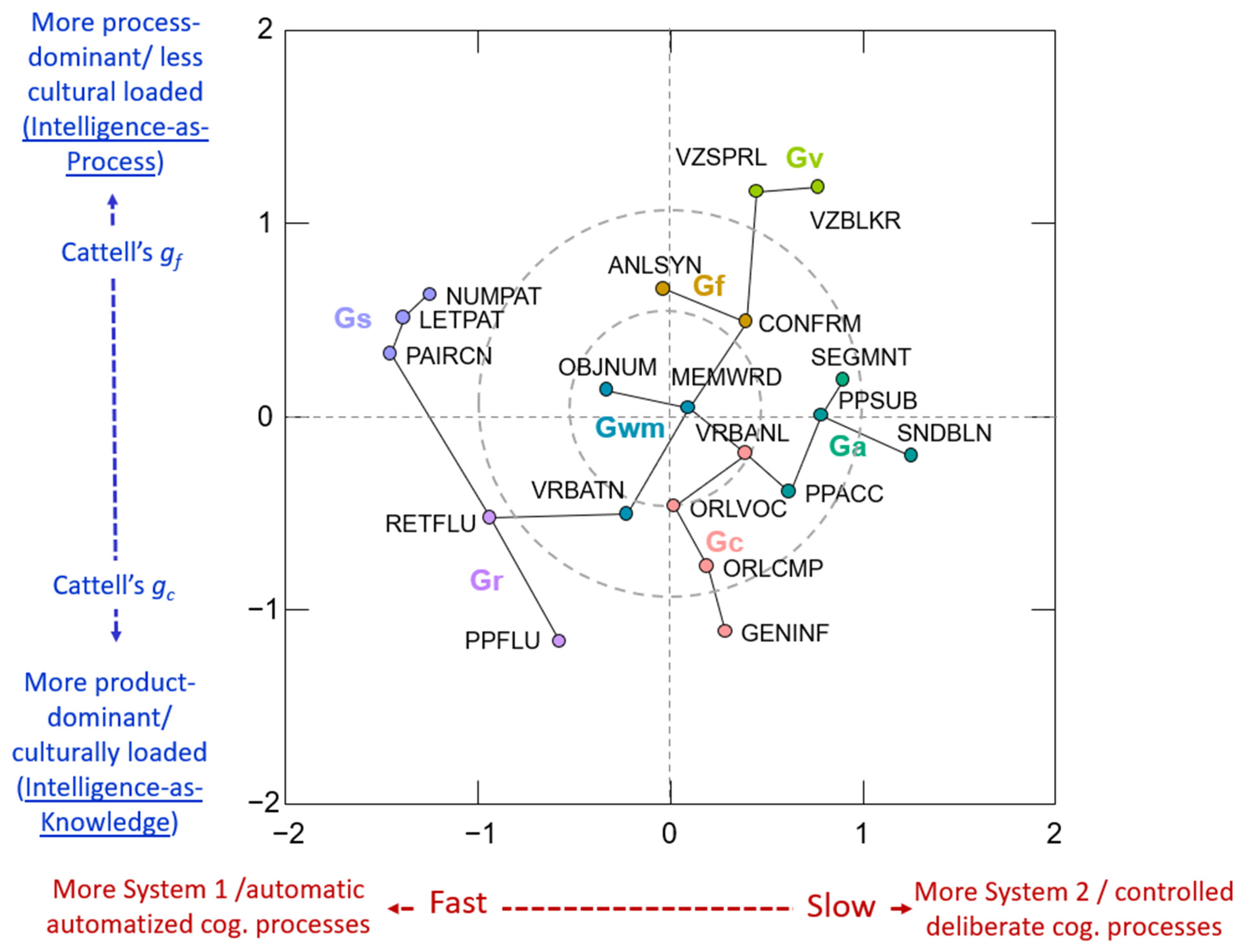
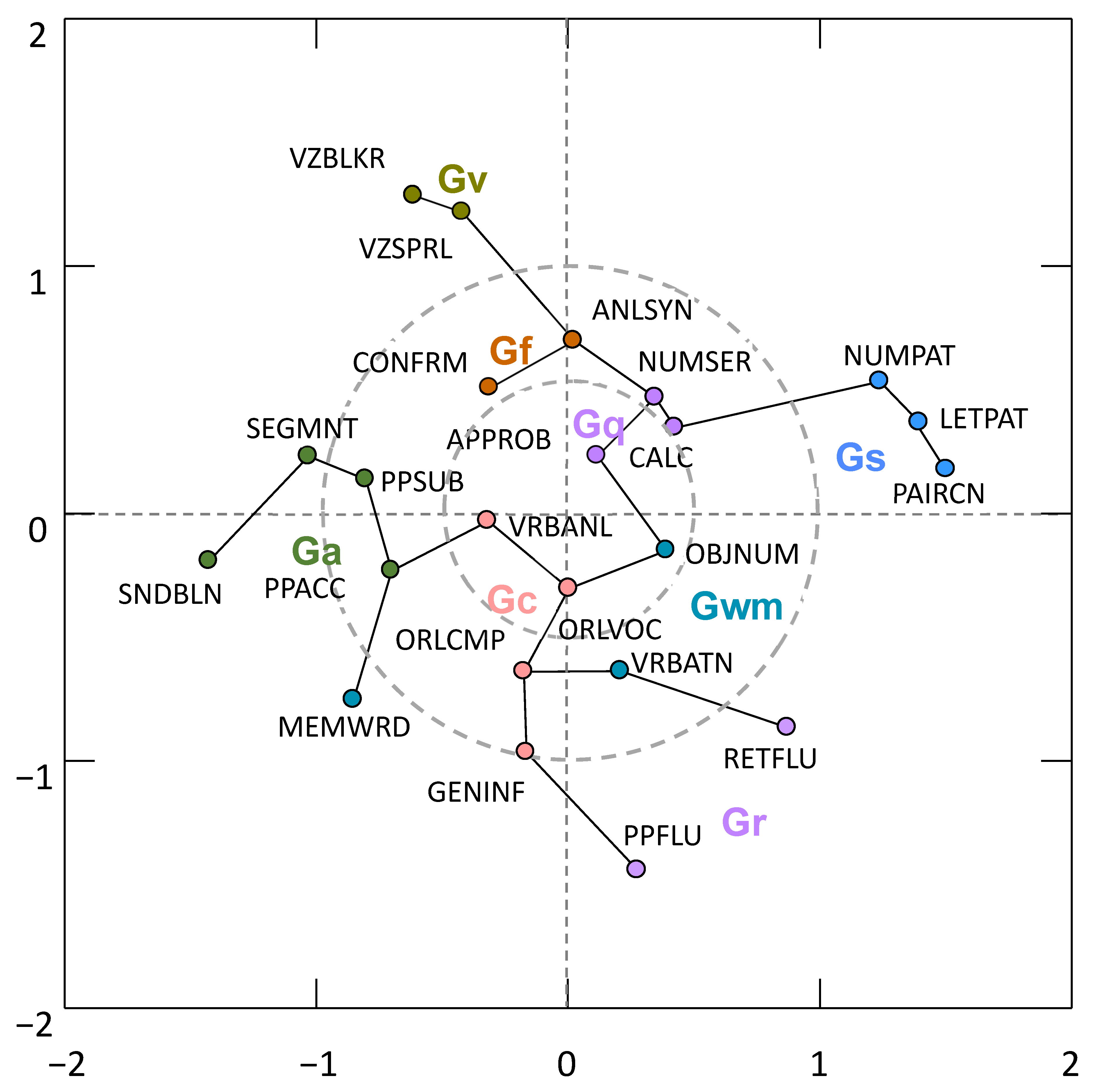
4.3. Complimentary MDS and MST Analysis
5. Discussion
5.1. Implications for Theories of Intelligence and Cognitive Abilities
5.1.1. Implications for CHC Theory
5.1.2. Possible Intermediate Cognitive Ability or Processing Dimensions
5.1.3. Is Cognitive Processing Efficiency or Attentional Control the Key Component of Intelligence?
5.1.4. Why Is Oral Comprehension Most Central in the CHC Network Model?
5.2. The Implication of a CHC Network Model of Intelligence for Interventions
5.3. Implications for Intelligence Testing Interpretation
5.3.1. Interpretation of Broad CHC Scores in Intelligence Testing
5.3.2. Implications for Interpretation of Select WJ IV Tests and Clusters
5.4. Methodological Implications for the PNA Investigation of Intelligence Tests
6. Limitations and Future Directions
7. Concluding Comments
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | The intelligence “test” and CHC factor and theory literature can be confusing. There are IQ test scores, individual subtests, individual tests, CHC factors, abilities, scores, etc. In this paper, the following terms and definitions are used. The commonly referred to “subtests” (e.g., Wechsler subtests) are referred to as individual tests, or just tests. Tests are the smallest individual measure that provides obtained scores for interpretation. Some tests may be comprised of subtests, that are mini-tests for which no derived score is provided. Subtests are typically combined to form a test (e.g., WJ IV General Information test consists of the “what” and “where” subtests). Two or more tests are typically combined into composite or index scores (e.g., Wechsler Processing Speed Index) that represent broad stratum II abilities as per CHC theory (e.g., Gs). These are called broad CHC scores. Broad CHC stratum II theoretical constructs are called broad CHC abilities. The combination of tests that provide a total composite IQ score representing general intelligence (g) is called the global IQ. A self-contained published battery of tests is called an IQ battery, not an IQ test. |
| 2 | Henceforth in this paper, for economy of writing, in the analysis and results sections the different WJ IV tests or subtests are referred to as the WJ IV measures. Measures designates the WJ IV test and subtest scores used in the PNA analysis. |
| 3 | It is often misunderstood that Horn and Carroll’s broad Gf and Gc abilities are not isomorphic with Cattell’s two gf/gc general capacities, constructs that are more consistent with the notion of general intelligence (g) as articulated by Cattell’s mentor, Spearman (see Schneider and McGrew 2018). The gf/gc notation used here refers to Cattell’s two general types of intelligences. Ackerman’s complete PPIK theory of intelligence includes the broad constructs of intelligence-as-process, personality, interests, and intelligence-as-knowledge. |
References
- Ackerman, Phillip L. 1996. A theory of adult intellectual development: Process, personality, interests, and knowledge. Intelligence 22: 227–57. [Google Scholar] [CrossRef]
- Ackerman, Phillip L. 2018. Intelligence-as-process, personality, interests, and intelligence-as-knowledge: A framework for adult intellectual development. In Contemporary Intellectual Assessment: Theories, Tests, and Issues, 4th ed. Edited by Dawn P. Flanagan and Erin M. McDonough. New York: The Guilford Press, pp. 225–41. [Google Scholar]
- Alfonso, Vincent C., Dawn P. Flanagan, and Suzan Radwan. 2005. The impact of the Cattell-Horn-Carroll Theory on test development and interpretation of cognitive and academic abilities. In Contemporary Intellectual Assessment: Theories, Tests, and Issues, 2nd ed. Edited by Dawn P. Flanagan and Patti L. Harrison. New York: Guilford Press, pp. 185–202. [Google Scholar]
- Angelelli, Paola, Daniele L. Romano, Chiara V. Marinelli, Lluigi Macchitella, and Pierluigi Zoccolotti. 2021. The simple view of reading in children acquiring a regular orthography (Italian): A network analysis approach. Frontiers in Psychology 12: 686914. [Google Scholar] [CrossRef] [PubMed]
- Barrouillet, Pierre. 2011. Dual-process theories and cognitive development: Advances and challenges. Developmental Review 31: 79–85. [Google Scholar] [CrossRef]
- Beaujean, A. Alexander, Nicholas Benson, Ryan McGill, and Stefan C. Dombrowski. 2018. A misuse of IQ scores: Using the Dual Discrepancy/Consistency Model for identifying specific learning disabilities. Journal of Intelligence 6: 36. [Google Scholar] [CrossRef] [PubMed]
- Borsboom, Denny, Marie K. Deserno, Mijke Rhemtulla, Sacha Epskamp, Eiko I. Fried, Richard J. McNally, Donald J. Robinaugh, Marco Perugini, Jonas Dalege, Giulio Costantini, and et al. 2021. Network analysis of multivariate data in psychological science. Nature Reviews Methods Primers 1: 58. [Google Scholar] [CrossRef]
- Box, George E. P., and Norman R. Draper. 2007. Response Surfaces, Mixtures, and Ridge Analyses, 2nd ed. Hoboken: John Wiley. [Google Scholar]
- Bressler, Steven L., and Vinod Menon. 2010. Large-scale brain networks in cognition: Emerging methods and principles. Trends in Cognitive Sciences 14: 277–90. [Google Scholar] [CrossRef]
- Bringmann, Laura F., Casper Albers, Claudi Bockting, Denny Borsboom, Eva Ceulemans, Angélique Cramer, Sacha Epskamp, Markus I. Eronen, Eellen Hamaker, Peter Kuppens, and et al. 2022. Psychopathological networks: Theory, methods and practice. Behaviour Research and Therapy 149: 104011. [Google Scholar] [CrossRef]
- Bringmann, Laura F., Timon Elmer, Sacha Epskamp, Robert W. Krause, David Schoch, Marieke Wichers, Johanna T. W. Wigman, and Evelien Snippe. 2019. What do centrality measures measure in psychological networks? Journal of Abnormal Psychology 128: 892–903. [Google Scholar] [CrossRef]
- Bulut, Okan, Damien C. Cormier, Alexandra M. Aquilina, and Hatice C. Bulut. 2021. Age and sex invariance of the Woodcock-Johnson IV tests of cognitive abilities: Evidence from psychometric network modeling. Journal of Intelligence 9: 35. [Google Scholar] [CrossRef]
- Burgoyne, Alexander P., Cody A. Mashburn, Jason S. Tsukahara, and Randall W. Engle. 2022. Attention control and process overlap theory: Searching for cognitive processes underpinning the positive manifold. Intelligence 91: 101629. [Google Scholar] [CrossRef]
- Caemmerer, Jacqueline M., Danika L. S. Maddocks, Timothy Z. Keith, and Matthew R. Reynolds. 2018. Effects of cognitive abilities on child and youth academic achievement: Evidence from the WISC-V and WIAT-III. Intelligence 68: 6–20. [Google Scholar] [CrossRef]
- Caemmerer, Jacqueline M., Timothy Z. Keith, and Matthew R. Reynolds. 2020. Beyond individual intelligence tests: Application of Cattell-Horn-Carroll Theory. Intelligence 79: 101433. [Google Scholar] [CrossRef]
- Canivez, Gary L. 2013a. Incremental criterion validity of WAIS–IV factor index scores: Relationships with WIAT–II and WIAT–III subtest and composite scores. Psychological Assessment 25: 484–95. [Google Scholar] [CrossRef]
- Canivez, Gary L. 2013b. Psychometric versus actuarial interpretation of intelligence and related aptitude batteries. In The Oxford Handbook of Child Psychological Assessment. Edited by Donald H. Saklofske, Cecil R. Reynolds and Vicki L. Schwean. Oxford: Oxford University Press, pp. 84–112. [Google Scholar]
- Canivez, Gary L., and Ryan J. McGill. 2016. Factor structure of the Differential Ability Scales–Second Edition: Exploratory and hierarchical factor analyses with the core subtests. Psychological Assessment 28: 1475–88. [Google Scholar] [CrossRef]
- Canivez, Gary L., Marley W. Watkins, and Stefan C. Dombrowski. 2016. Factor structure of the Wechsler Intelligence Scale for Children–Fifth Edition: Exploratory factor analyses with the 16 primary and secondary subtests. Psychological Assessment 28: 975–86. [Google Scholar] [CrossRef] [PubMed]
- Carroll, John B. 1993. Human Cognitive Abilities: A Survey of Factor-Analytic Studies. Cambridge: Cambridge University Press. [Google Scholar] [CrossRef]
- Carroll, John B. 2003. The higher-stratum structure of cognitive abilities: Current evidence supports g and about ten broad factors. In The Scientific Study of General Intelligence: Tribute to Arthur R. Jensen. Edited by Helmuth Nyborg. Oxford: Pergamon, pp. 5–22. [Google Scholar]
- Cattell, Raymond B. 1943. The measurement of adult intelligence. Psychological Bulletin 40: 153–93. [Google Scholar] [CrossRef]
- Cattell, Raymond B. 1971. Abilities: Its Structure, Growth and Action. Boston: Houghton Mifflin. [Google Scholar]
- Cattell, Raymond B. 1987. Intelligence: Its Structure, Growth and Action. Amsterdam: Elsevier. [Google Scholar]
- Cattell, Raymond B. 1998. Where is intelligence? Some answers from the triadic theory. In Human Cognitive Abilities in Theory and Practice. Edited by John J. McArdle and Richard W. Woodcock. Mahwah: Erlbaum, pp. 29–38. [Google Scholar]
- Christo, Catherine, and Jenny Ponzuric. 2017. CASP position paper: Specific learning disabilities and patterns of strengths and weaknesses. Contemporary School Psychology 21: 7–9. [Google Scholar] [CrossRef]
- Cohen, Arie, Catherine A. Fiorello, and Frank H. Farley. 2006. The cylindrical structure of the Wechsler Intelligence Scale for Children–IV: A retest of the Guttman model of intelligence. Intelligence 34: 587–91. [Google Scholar] [CrossRef]
- Comrey, Andrew L. 1988. Factor-analytic methods of scale development in personality and clinical psychology. Journal of Consulting and Clinical Psychology 56: 754–61. [Google Scholar] [CrossRef]
- Conway, Andrew R. A., and Kristof Kovacs. 2015. New and emerging models of human intelligence. WIREs Cognitive Science 6: 419–26. [Google Scholar] [CrossRef] [PubMed]
- Conway, Andrew R. A., Kristof Kovacs, Han Hao, Kevin P. Rosales, and Jean-Paul Snijder. 2021. Individual differences in attention and intelligence: A united cognitive/psychometric approach. Journal of Intelligence 9: 34. [Google Scholar] [CrossRef] [PubMed]
- Cormier, Damien C., Kevin S. McGrew, Okan Bulut, and Allyson Funamoto. 2017a. Revisiting the relations between the WJ-IV measures of Cattell-Horn-Carroll (CHC) cognitive abilities and reading achievement during the school-age years. Journal of Psychoeducational Assessment 35: 731–54. [Google Scholar] [CrossRef]
- Cormier, Damien C., Okan Bulut, Kevin S. McGrew, and Deepak Singh. 2017b. Exploring the relations between Cattell-Horn-Carroll (CHC) cognitive abilities and mathematics achievement: CHC abilities and mathematics. Applied Cognitive Psychology 31: 530–38. [Google Scholar] [CrossRef]
- Cormier, Damien C., Okan Bulut, Kevin S. McGrew, and Jessica Frison. 2016. The role of Cattell-Horn-Carroll (CHC) cognitive abilities in predicting writing achievement during the school-age years: CHC abilities and writing. Psychology in the Schools 53: 787–803. [Google Scholar] [CrossRef]
- Costantini, Giulo, Sacha Epskamp, Denny Borsboom, Marco Perugini, René Mõttus, Lourens J. Waldorp, and Angélique O. Cramer. 2015. State of the aRt personality research: A tutorial on network analysis of personality data in R. Journal of Research in Personality 54: 13–29. [Google Scholar] [CrossRef]
- Cowan, Nelson. 2014. Working memory underpins cognitive development, learning, and education. Educational Psychology Review 26: 197–223. [Google Scholar] [CrossRef]
- De Alwis, Duneesha, Sandra Hale, and Joel Myerson. 2014. Extended cascade models of age and individual differences in children’s fluid intelligence. Intelligence 46: 84–93. [Google Scholar] [CrossRef]
- De Neys, Wim, and Gordon Pennycook. 2019. Logic, fast and slow: Advances in dual-process theorizing. Current Directions in Psychological Science 28: 503–9. [Google Scholar] [CrossRef]
- Deary, Ian J. 2012. Intelligence. Annual Review of Psychology 63: 453–82. [Google Scholar] [CrossRef]
- Decker, Scott L., Rachel M. Bridges, Jessica C. Luedke, and Michael J. Eason. 2021. Dimensional evaluation of cognitive measures: Methodological confounds and theoretical concerns. Journal of Psychoeducational Assessment 39: 3–27. [Google Scholar] [CrossRef]
- Demetriou, Andreas, George Spanoudis, Michael Shayer, Sanne van der Ven, Christopher R. Brydges, Evelyn Kroesbergen, Gal Podjarny, and H. Lee Swanson. 2014. Relations between speed, working memory, and intelligence from preschool to adulthood: Structural equation modeling of 14 studies. Intelligence 46: 107–21. [Google Scholar] [CrossRef]
- Dombrowski, Stefan C., Alexander A. Beaujean, Ryan J. McGill, and Nicholas F. Benson. 2019a. The Woodcock-Johnson IV Tests of Achievement provides too many scores for clinical interpretation. Journal of Psychoeducational Assessment 37: 819–36. [Google Scholar] [CrossRef]
- Dombrowski, Stefan C., Ryan J. McGill, Ryan L. Farmer, John H. Kranzler, and Gary L. Canivez. 2021. Beyond the rhetoric of evidence-based assessment: A framework for critical thinking in clinical practice. School Psychology Review 51: 1–14. [Google Scholar] [CrossRef]
- Dombrowski, Stefan C., Ryan J. McGill, and Gary L. Canivez. 2017. Exploratory and hierarchical factor analysis of the WJ-IV Cognitive at school age. Psychological Assessment 29: 394–407. [Google Scholar] [CrossRef]
- Dombrowski, Stefan C., Ryan J. McGill, and Gary L. Canivez. 2018a. An alternative conceptualization of the theoretical structure of the Woodcock-Johnson IV Tests of Cognitive Abilities at school age: A confirmatory factor analytic investigation. Archives of Scientific Psychology 6: 1–13. [Google Scholar] [CrossRef]
- Dombrowski, Stefan C., Ryan J. McGill, and Gary L. Canivez. 2018b. Hierarchical exploratory factor analyses of the Woodcock-Johnson IV full test battery: Implications for CHC application in school psychology. School Psychology Quarterly 33: 235–50. [Google Scholar] [CrossRef] [PubMed]
- Dombrowski, Stefan C., Ryan J. McGill, Gary L. Canivez, and Christina H. Peterson. 2019b. Investigating the theoretical structure of the Differential Ability Scales—Second Edition through hierarchical exploratory factor analysis. Journal of Psychoeducational Assessment 37: 91–104. [Google Scholar] [CrossRef]
- Epskamp, Sacha, Angélique O. J. Cramer, Lourens J. Waldorp, Verena D. Schmittmann, and Denny Borsboom. 2012. qgraph: Network Visualizations of Relationships in Psychometric Data. Journal of Statistical Software 48. [Google Scholar] [CrossRef]
- Epskamp, S., Mijke Rhemtulla, and Denny Borsboom. 2017. Generalized network psychometrics: Combining network and latent variable models. Psychometrika 82: 904–927. [Google Scholar] [CrossRef]
- Epskamp, S., and Eiko I. Fried. 2018. A tutorial on regularized partial correlation networks. Psychological Methods 23: 617–34. [Google Scholar] [CrossRef] [PubMed]
- Epskamp, Sacha, Denny Borsboom, and Eiko I. Fried. 2018a. Estimating psychological networks and their accuracy: A tutorial paper. Behavior Research Methods 50: 195–212. [Google Scholar] [CrossRef] [PubMed]
- Epskamp, Sacha, Gunter K. J. Maris, Lourens J. Waldorp, and Denny Borsboom. 2018b. Network psychometrics. In The Wiley Handbook of Psychometric Testing, 1st ed. Edited by Paul Irwing, Tom Booth and David J. Hughes. Hoboken: Wiley, pp. 953–86. [Google Scholar] [CrossRef]
- Eronen, Markus I., and Laura F. Bringmann. 2021. The theory crisis in psychology: How to move forward. Perspectives on Psychological Science 16: 779–88. [Google Scholar] [CrossRef] [PubMed]
- Evans, Jeffrey J., Randy G. Floyd, Kevin S. McGrew, and Maria H. Leforgee. 2002. The relations between measures of Cattell-Horn-Carroll (CHC) cognitive abilities and reading achievement during childhood and adolescence. School Psychology Review 31: 246–62. [Google Scholar] [CrossRef]
- Farmer, Ryan L., Imad Zaheer, Gary J. Duhon, and Stephanie Ghazal. 2021a. Reducing low-value practices: A functional-contextual consideration to aid in de-implementation efforts. Canadian Journal of School Psychology 36: 166–85. [Google Scholar] [CrossRef]
- Farmer, Ryan L., Ryan J. McGill, Stefan C. Dombrowski, and Gary L. Canivez. 2021b. Why questionable assessment practices remain popular in school psychology: Instructional materials as pedagogic vehicles. Canadian Journal of School Psychology 36: 98–114. [Google Scholar] [CrossRef]
- Farrell, Peter. 2010. School psychology: Learning lessons from history and moving forward. School Psychology International 31: 581–98. [Google Scholar] [CrossRef]
- Fiorello, Catherine A., Dawn P. Flanagan, and James B. Hale. 2014. Response to the special issue: The utility of the pattern of the strengths and weaknesses approach. Learning Disabilities: A Multidisciplinary Journal 20: 55–59. [Google Scholar] [CrossRef]
- Flanagan, Dawn P., and W. Joel Schneider. 2016. Cross-Battery Assessment? XBA PSW? A case of mistaken identity: A commentary on Kranzler and colleagues’ “Classification agreement analysis of Cross-Battery Assessment in the identification of specific learning disorders in children and youth”. International Journal of School and Educational Psychology 4: 137–45. [Google Scholar] [CrossRef]
- Floyd, Randy G., Jeffery J. Evans, and Kevin S. McGrew. 2003. Relations between measures of Cattell-Horn-Carroll (CHC) cognitive abilities and mathematics achievement across the school-age years. Psychology in the Schools 40: 155–71. [Google Scholar] [CrossRef]
- Floyd, Randy G., Kevin S. McGrew, Amberly Barry, Fawziya Rafael, and Joshua Rogers. 2009. General and specific effects on Cattell-Horn-Carroll broad ability composites: Analysis of the Woodcock–Johnson III Normative Update Cattell-Horn-Carroll factor clusters across development. School Psychology Review 38: 249–65. [Google Scholar] [CrossRef]
- Floyd, Randy G., Kevin S. McGrew, and Jeffery J. Evans. 2008. The relative contributions of the Cattell-Horn-Carroll cognitive abilities in explaining writing achievement during childhood and adolescence. Psychology in the Schools 45: 132–44. [Google Scholar] [CrossRef]
- Floyd, Randy G., Timothy Z. Keith, Gordon E. Taub, and Kevin S. McGrew. 2007. Cattell-Horn-Carroll cognitive abilities and their effects on reading decoding skills: g has indirect effects, more specific abilities have direct effects. School Psychology Quarterly 22: 200–33. [Google Scholar] [CrossRef]
- Fried, Eiko I. 2020. Lack of theory building and testing impedes progress in the factor and network literature. Psychological Inquiry 31: 271–88. [Google Scholar] [CrossRef]
- Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. 2008. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9: 432–41. [Google Scholar] [CrossRef]
- Fry, Astrid F., and Sandra Hale. 1996. Processing speed, working memory, and fluid intelligence: Evidence for a developmental cascade. Psychological Science 7: 237–41. [Google Scholar] [CrossRef]
- Gordon, Deborah M. 2010. Ant Encounters: Interaction Networks and Colony Behavior. Princeton: Princeton University Press. [Google Scholar]
- Green, C. Shawn, and Nora S. Newcombe. 2020. Cognitive training: How evidence, controversies, and challenges inform education policy. Policy Insights from the Behavioral and Brain Sciences 7: 80–86. [Google Scholar] [CrossRef]
- Gustafsson, Jan-Eric. 1984. A unifying model for the structure of intellectual abilities. Intelligence 8: 179–203. [Google Scholar] [CrossRef]
- Guttman, Louis. 1954. A new approach to factor analysis: The Radex. In Mathematical Thinking in the Social Sciences. Edited by Paul F. Lazarsfeld. New York: Free Press, pp. 258–348. [Google Scholar]
- Guttman, Ruth, and Charles W. Greenbaum. 1998. Facet theory: Its development and current status. European Psychologist 3: 13–36. [Google Scholar] [CrossRef]
- Hajovsky, Daniel B., Matthew R. Reynolds, Randy G. Floyd, Joshua J. Turek, and Timothy Z. Keith. 2014. A multigroup investigation of latent cognitive abilities and reading achievement relations. School Psychology Review 43: 385–406. [Google Scholar] [CrossRef]
- Hampshire, Adam, Roger R. Highfield, Beth L. Parkin, and Adrian M. Owen. 2012. Fractionating human intelligence. Neuron 76: 1225–37. [Google Scholar] [CrossRef] [PubMed]
- Hart, Bernard, and Charles Spearman. 1912. General ability, its existence and nature. British Journal of Psychology 5: 51–84. [Google Scholar] [CrossRef]
- Haslbeck, Jonas M. B., Oisín Ryan, Donald J. Robinaugh, Lourens J. Waldorp, and Denny Borsboom. 2021. Modeling psychopathology: From data models to formal theories. Psychological Methods 27: 930–57. [Google Scholar] [CrossRef] [PubMed]
- Holden, La Tasha R., and Sara A. Hart. 2021. Intelligence can be used to make a more equitable society but only when properly defined and applied. Journal of Intelligence 9: 57. [Google Scholar] [CrossRef]
- Hunt, Earl B. 2011. Human Intelligence. Cambridge: Cambridge University Press. [Google Scholar]
- Isvoranu, Adela-Maria, and Sacha Epskamp. 2021. Which estimation method to choose in network psychometrics? Deriving guidelines for applied researchers. Psychological Methods. Advance online publication. [Google Scholar] [CrossRef]
- Jaeggi, Susanne M., Martin Buschkuehl, John Jonides, and Priti Shah. 2011. Short- and long-term benefits of cognitive training. Proceedings of the National Academy of Sciences 108: 10081–86. [Google Scholar] [CrossRef]
- JASP Team. 2022. JASP (0.16.3). Available online: https://jasp-stats.org/ (accessed on 4 October 2021).
- Jensen, Arthur R. 1998. The g Factor: The Science of Mental Ability. New York: Praeger. [Google Scholar]
- Jensen, Arthur R. 2002. Psychometric g: Definition and substantiation. In The General Factor of Intelligence: How General Is It? Edited by Robert J. Sternberg and Elena L. Grigorenko. Mahwah: Lawrence Erlbaum Associates, pp. 39–53. ISBN 9780415652445. [Google Scholar]
- Jimerson, Shane R., Matthew K. Burns, and Amanda M. VanDerHeyden. 2016. Handbook of Response to Intervention. New York: Springer. [Google Scholar] [CrossRef]
- Jones, Payton J., Patrick Mair, and Richard J. McNally. 2018. Visualizing psychological networks: A tutorial in R. Frontiers in Psychology 9: 1742. [Google Scholar] [CrossRef]
- Kahneman, Daniel. 2011. Thinking, Fast and Slow. Basingstoke: Macmillan. [Google Scholar]
- Kail, Robert V. 2007. Longitudinal evidence that increases in processing speed and working memory enhance children’s reasoning. Psychological Science 18: 312–13. [Google Scholar] [CrossRef]
- Kan, Kees-Jan, Han L. J. van der Maas, and Stephen Z. Levine. 2019. Extending psychometric network analysis: Empirical evidence against g in favor of mutualism? Intelligence 73: 52–62. [Google Scholar] [CrossRef]
- Kane, Michael J., and Jennifer C. McVay. 2012. What mind wandering reveals about executive-control abilities and failures. Current Directions in Psychological Science 21: 348–54. [Google Scholar] [CrossRef]
- Kaufman, Alan S., Susan E. Raiford, and Diane L. Coalson. 2016. Intelligent Testing with the WISC-V. Hoboken: Wiley. [Google Scholar]
- Keith, Timothy Z. 1999. Effects of general and specific abilities on student achievement: Similarities and differences across ethnic groups. School Psychology Quarterly 14: 239–62. [Google Scholar] [CrossRef]
- Keith, Timothy Z., and Mathew R. Reynolds. 2010. Cattell-Horn-Carroll abilities and cognitive tests: What we’ve learned from 20 years of research. Psychology in the Schools 47: 635–50. [Google Scholar] [CrossRef]
- Keith, Timothy Z., and Mathew R. Reynolds. 2018. Using confirmatory factor analysis to aid in understanding the constructs measured by intelligence tests. In Contemporary Intellectual Assessment: Theories, Tests, and Issues, 4th ed. New York: The Guilford Press, pp. 853–900. [Google Scholar]
- Keith, Timothy Z., and Stephen B. Dunbar. 1984. Hierarchical factor analysis of the K-ABC: Testing alternate models. The Journal of Special Education 18: 367–75. [Google Scholar] [CrossRef]
- Kievit, Roger A., Simon W. Davis, John Griffiths, Marta M. Correia, Cam-CAN, and Richard N. Henson. 2016. A watershed model of individual differences in fluid intelligence. Neuropsychologia 91: 186–98. [Google Scholar] [CrossRef] [PubMed]
- Kim, Young-Suk G. 2016. Direct and mediated effects of language and cognitive skills on comprehension of oral narrative texts (listening comprehension) for children. Journal of Experimental Child Psychology 141: 101–20. [Google Scholar] [CrossRef]
- Kovacs, Kristof, and Andrew R. A. Conway. 2019. A unified cognitive/differential approach to human intelligence: Implications for IQ testing. Journal of Applied Research in Memory and Cognition 8: 255–72. [Google Scholar] [CrossRef]
- Kovacs, Kristof, and Andrew R. Conway. 2016. Process overlap theory: A unified account of the general factor of intelligence. Psychological Inquiry 27: 151–77. [Google Scholar] [CrossRef]
- Kranzler, John H., and Randy G. Floyd. 2020. Assessing Intelligence in Children and Adolescents: A Practical Guide for Evidence-Based Assessment, 2nd ed. Lanham: Rowman and Littlefield. [Google Scholar]
- Kranzler, John H., Randy G. Floyd, Nicolas Benson, Brian Zaboski, and Lia Thibodaux. 2016. Classification agreement analysis of Cross-Battery Assessment in the identification of specific learning disorders in children and youth. International Journal of School and Educational Psychology 4: 124–36. [Google Scholar] [CrossRef]
- Kyllonen, Patrick C., and Raymond E. Christal. 1990. Reasoning ability is (little more than) working-memory capacity? Intelligence 14: 389–433. [Google Scholar] [CrossRef]
- Letina, Srebrenka, Tessa F. Blanken, Marie K. Deserno, and Denny Borsboom. 2019. Expanding network analysis tools in psychological networks: Minimal spanning trees, participation coefficients, and motif analysis applied to a network of 26 psychological attributes. Complexity 2019: 1–27. [Google Scholar] [CrossRef]
- Lubinski, David. 2004. Introduction to the special section on cognitive abilities: 100 years after Spearman’s (1904) ‘General intelligence, objectively determined and measured’. Journal of Personality and Social Psychology 86: 96. [Google Scholar] [CrossRef]
- Lunansky, Gabriela, Jasper Naberman, Claudia D. van Borkulo, Chen Chen, Li Wang, and Denny Borsboom. 2022. Intervening on psychopathology networks: Evaluating intervention targets through simulations. Methods 204: 29–37. [Google Scholar] [CrossRef]
- Lutz, Antoine, Heleen A. Slagter, John D. Dunne, and Richard J. Davidson. 2008. Attention regulation and monitoring in meditation. Trends in Cognitive Sciences 12: 163–69. [Google Scholar] [CrossRef]
- Maki, Kathrin E., John H. Kranzler, and Mary E. Moody. 2022. Dual discrepancy/consistency pattern of strengths and weaknesses method of specific learning disability identification: Classification accuracy when combining clinical judgment with assessment data. Journal of School Psychology 92: 33–48. [Google Scholar] [CrossRef] [PubMed]
- Mascolo, Jennifer T., Dawn P. Flanagan, and Vincent C. Alfonso, eds. 2014. Essentials of Planning, Selecting, and Tailoring Interventions for Unique Learners. Hoboken: John Wiley and Sons. [Google Scholar]
- Mather, Nancy, and Barbara J. Wendling. 2014. Woodcock-Johnson IV Tests of Oral Language: Examiner’s manual. Rolling Meadows: Riverside. [Google Scholar]
- McGill, Ryan J. 2018. Confronting the base rate problem: More ups and downs for cognitive scatter analysis. Contemporary School Psychology 22: 384–93. [Google Scholar] [CrossRef]
- McGill, Ryan J., and Randy T. Busse. 2017. When theory trumps science: A critique of the PSW model for SLD identification. Contemporary School Psychology 21: 10–18. [Google Scholar] [CrossRef]
- McGill, Ryan J., Stefan C. Dombrowski, and Gary L. Canivez. 2018. Cognitive profile analysis in school psychology: History, issues, and continued concerns. Journal of School Psychology 71: 108–21. [Google Scholar] [CrossRef] [PubMed]
- McGrew, Kevin S. 1997. Analysis of the major intelligence batteries according to a proposed comprehensive Gf-Gc framework. In Contemporary Intellectual Assessment: Theories, Tests, and Issues. New York: Guilford Press, pp. 151–79. [Google Scholar]
- McGrew, Kevin S. 2005. The Cattell-Horn-Carroll theory of cognitive abilities: Past, present, and future. In Contemporary Intellectual Assessment. Theories, Tests, and Issues, 2nd ed. Edited by Dawn P. Flanagan and Patti L. Harrison. New York: Guilford Press, pp. 136–81. [Google Scholar]
- McGrew, Kevin S. 2009. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 37: 1–10. [Google Scholar] [CrossRef]
- McGrew, Kevin S. 2013. The Science behind Interactive Metronome—An Integration of Brain Clock, Temporal Processing, Brain Network and Neurocognitive Research and Theory. No. 2. Mind Hub Pub. Institute for Applied Psychometrics. Available online: http://www.iapsych.com/articles/mindhubpub2.pdf (accessed on 9 October 2022).
- McGrew, Kevin S., and Barbara J. Wendling. 2010. Cattell-Horn-Carroll cognitive-achievement relations: What we have learned from the past 20 years of research. Psychology in the Schools 47: 651–75. [Google Scholar] [CrossRef]
- McGrew, Kevin S., and Dawn P. Flanagan. 1998. The Intelligence Test Desk Reference (ITDR): Gf-Gc Cross-Battery Assessment. Boston: Allyn & Bacon. [Google Scholar]
- McGrew, Kevin S., and Gary L. Hessler. 1995. The relationship between the WJ-R Gf-Gc cognitive clusters and mathematics achievement across the life-span. Journal of Psychoeducational Assessment 13: 21–38. [Google Scholar] [CrossRef]
- McGrew, Kevin S., and Susan N. Knopik. 1993. The relationship between the WJ-R Gf-Gc cognitive clusters and writing achievement across the life-span. School Psychology Review 22: 687–95. [Google Scholar] [CrossRef]
- McGrew, Kevin S., Dawn P. Flanagan, Timothy Z. Keith, and Mike Vanderwood. 1997. Beyond g: The impact of Gf-Gc specific cognitive abilities research on the future use and interpretation of intelligence tests in the schools. School Psychology Review 26: 189–210. [Google Scholar] [CrossRef]
- McGrew, Kevin S., Erica M. LaForte, and Fredrick A. Schrank. 2014. Woodcock-Johnson IV Technical Manual. Rolling Meadows: Riverside. [Google Scholar]
- McVay, Jennifer C., and Michael J. Kane. 2012. Why does working memory capacity predict variation in reading comprehension? On the influence of mind wandering and executive attention. Journal of Experimental Psychology: General 141: 302–20. [Google Scholar] [CrossRef] [PubMed]
- Messick, Samuel. 1995. Validity of psychological assessment: Validation of inferences from persons’ responses and performances as scientific inquiry into score meaning. American Psychologist 50: 741–49. [Google Scholar] [CrossRef]
- Meyer, Emily M., and Matthew R. Reynolds. 2017. Scores in space: Multidimensional scaling of the WISC-V. Journal of Psychoeducational Assessment 36: 562–75. [Google Scholar] [CrossRef]
- Neal, Zachary P., and Jennifer W. Neal. 2021. Out of bounds? The boundary specification problem for centrality in psychological networks. Psychological Methods. Advance online publication. [Google Scholar] [CrossRef]
- Nelson, Jason M., Gary L. Canivez, and Marley W. Watkins. 2013. Structural and incremental validity of the Wechsler Adult Intelligence Scale–Fourth Edition with a clinical sample. Psychological Assessment 25: 618–30. [Google Scholar] [CrossRef]
- Neubeck, Markus, Julia Karbach, and Tanja Könen. 2022. Network models of cognitive abilities in younger and older adults. Intelligence 90: 101601. [Google Scholar] [CrossRef]
- Niileksela, Christopher R., Matthew R. Reynolds, Timothy Z. Keith, and Kevin S. McGrew. 2016. A special validity study of the Woodcock–Johnson IV. In WJ IV Clinical Use and Interpretation. Amsterdam: Elsevier, pp. 65–106. [Google Scholar] [CrossRef]
- Osada, Nobuko. 2004. Listening comprehension research: A brief review of the past thirty years. Dialogue 3: 53–66. [Google Scholar]
- Pedersen, Thomas L. 2022a. ggforce: Accelerating “ggplot2” [R package]. Available online: ggforce.data-imaginist.com (accessed on 20 August 2022).
- Pedersen, Thomas L. 2022b. tidygraph: A Tidy API for Graph Manipulation [R Package]. Available online: https://tidygraph.data-imaginist.com (accessed on 20 August 2022).
- Protzko, John, and Roberto Colom. 2021a. A new beginning of intelligence research. Designing the playground. Intelligence 87: 101559. [Google Scholar] [CrossRef]
- Protzko, John, and Roberto Colom. 2021b. Testing the structure of human cognitive ability using evidence obtained from the impact of brain lesions over abilities. Intelligence 89: 101581. [Google Scholar] [CrossRef]
- Reynolds, Matthew R., and Christopher R. Niileksela. 2015. Test Review: Schrank, Fredrick A., McGrew, Kevin S., and Mather, Nancy 2014. Woodcock-Johnson IV Tests of Cognitive Abilities. Journal of Psychoeducational Assessment 33: 381–90. [Google Scholar] [CrossRef]
- Reynolds, Matthew R., and Joshua J. Turek. 2012. A dynamic developmental link between verbal comprehension-knowledge (Gc) and reading comprehension: Verbal comprehension-knowledge drives positive change in reading comprehension. Journal of School Psychology 50: 841–63. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, Matthew R., and Timothy Z. Keith. 2017. Multi-group and hierarchical confirmatory factor analysis of the Wechsler Intelligence Scale for Children—Fifth Edition: What does it measure? Intelligence 62: 31–47. [Google Scholar] [CrossRef]
- Reynolds, Mathew R., Timothy Z. Keith, Dawn P. Flanagan, and Vincent C. Alfonso. 2013. A cross-battery, reference variable, confirmatory factor analytic investigation of the CHC taxonomy. Journal of School Psychology 51: 535–55. [Google Scholar] [CrossRef] [PubMed]
- Robinaugh, Donald J., Alexander J. Millner, and Richard J. McNally. 2016. Identifying highly influential nodes in the complicated grief network. Journal of Abnormal Psychology 125: 747–57. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Torres, Ana M., Victor Peralta, Gustavo J. Gil-Berrozpe, Gisela Mezquida, María Ribeiro, Mariola Molina-García, Silvia Amoretti, Antonio Lobo, Ana González-Pinto, Jessica Merchán-Naranjo, and et al. 2022. The network structure of cognitive deficits in first episode psychosis patients. Schizophrenia Research 244: 46–54. [Google Scholar] [CrossRef]
- Savi, Alexander O., Maarten Marsman, and Han L. J. van der Maas. 2021. Evolving networks of human intelligence. Intelligence 88: 101567. [Google Scholar] [CrossRef]
- Schmank, Christopher J., Sara A. Goring, Kristof Kovacs, and Andrew R. A. Conway. 2019. Psychometric network analysis of the Hungarian WAIS. Journal of Intelligence 7: 21. [Google Scholar] [CrossRef]
- Schmank, Christopher J., Sara A. Goring, Kristof Kovacs, and Andrew R. A. Conway. 2021. Investigating the structure of intelligence using latent variable and psychometric network modeling: A commentary and reanalysis. Journal of Intelligence 9: 8. [Google Scholar] [CrossRef] [PubMed]
- Schneider, W. Joel. 2016. Strengths and weaknesses of the Woodcock-Johnson IV Tests of Cognitive Abilities: Best practice from a scientist-practitioner perspective. In WJ IV Clinical Use and Interpretation. Edited by D. P. Flanagan and V. C. Alfonso. Cambridge: Academic Press, pp. 191–210. [Google Scholar]
- Schneider, W. Joel, and Kevin S. McGrew. 2012. The Cattell-Horn-Carroll model of intelligence. In Contemporary Intellectual Assessment: Theories, Tests and Issues, 3rd ed. Edited by Dawn P. Flanagan and Patti L. Harrison. New York: Guilford Press, pp. 99–144. [Google Scholar]
- Schneider, W. Joel, and Kevin S. McGrew. 2013. Cognitive performance models: Individual differences in the ability to process information. In Handbook of Educational Theories. Edited by Beverly Irby, Genevieve H. Brown, Rafael Laro-Alecio and Shirley Jackson. Charlotte: Information Age Publishing, pp. 767–82. [Google Scholar]
- Schneider, W. Joel, and Kevin S. McGrew. 2018. The Cattell-Horn-Carroll theory of cognitive abilities. In Contemporary Intellectual Assessment: Theories, Tests and Issues, 4th ed. Edited by Dawn P. Flanagan and Erin M. McDonough. New York: Guilford Press, pp. 73–130. [Google Scholar]
- Schneider, W. Joel, John D. Mayer, and Daniel A. Newman. 2016. Integrating hot and cool intelligences: Thinking broadly about broad abilities. Journal of Intelligence 4: 1. [Google Scholar] [CrossRef]
- Schrank, Fredrick A., Kevin S. McGrew, and Nancy Mather. 2015. Woodcock-Johnson IV Tests of Early Cognitive and Academic Development. Rolling Meadows: Riverside. [Google Scholar]
- Sedlmeier, Peter, Juliane Eberth, Marcus Schwarz, Doreen Zimmermann, Frederik Haarig, Sonia Jaeger, and Sonja Kunze. 2012. The psychological effects of meditation: A meta-analysis. Psychological Bulletin 138: 1139–71. [Google Scholar] [CrossRef]
- Shipstead, Zach, Kenny L. Hicks, and Randall W. Engle. 2012. Cogmed working memory training: Does the evidence support the claims? Journal of Applied Research in Memory and Cognition 1: 185–93. [Google Scholar] [CrossRef]
- Simons, Daniel J., Walter R. Boot, Neil Charness, Susan E. Gathercole, Christopher F. Chabris, David Z. Hambrick, and Elizabeth A. L. Stine-Morrow. 2016. Do “brain training” programs work? Psychological Science in the Public Interest 17: 103–86. [Google Scholar] [CrossRef]
- Smallwood, Jonathan. 2010. Why the global availability of mind wandering necessitates resource competition: Reply to McVay and Kane (2010). Psychological Bulletin 136: 202–7. [Google Scholar] [CrossRef]
- Spearman, Charles E. 1923. The Nature of “Intelligence” and the Principles of Cognition. Basingstoke: MacMillan. [Google Scholar]
- Spearman, Charles E. 1927. The Abilities of Man: Their Nature and Measurement. Basingstoke: MacMillan. [Google Scholar] [CrossRef]
- Spencer, Steven J., Christine Logel, and Paul G. Davies. 2016. Stereotype threat. Annual Review of Psychology 67: 415–37. [Google Scholar] [CrossRef] [PubMed]
- Steele, Claude M., and Joshua Aronson. 1995. Stereotype threat and the intellectual test performance of African Americans. Journal of Personality and Social Psychology 69: 797–811. [Google Scholar] [CrossRef]
- Taub, Gordon E., Kevin S. McGrew, and Timothy Z. Keith. 2007. Improvements in interval time tracking and effects on reading achievement. Psychology in the Schools 44: 849–63. [Google Scholar] [CrossRef]
- Taub, Gordon E., Timothy Z. Keith, Randy G. Floyd, and Kevin S. McGrew. 2008. Effects of general and broad cognitive abilities on mathematics achievement. School Psychology Quarterly 23: 187–98. [Google Scholar] [CrossRef]
- Taylor, W. Pat, Jeremy Miciak, Jack M. Fletcher, and David J. Francis. 2017. Cognitive discrepancy models for specific learning disabilities identification: Simulations of psychometric limitations. Psychological Assessment 29: 446–57. [Google Scholar] [CrossRef]
- Tourva, Anna, and George Spanoudis. 2020. Speed of processing, control of processing, working memory and crystallized and fluid intelligence: Evidence for a developmental cascade. Intelligence 83: 101503. [Google Scholar] [CrossRef]
- Unsworth, Nash, Ashley L. Miller, and Matthew K. Robison. 2021a. Are individual differences in attention control related to working memory capacity? A latent variable mega-analysis. Journal of Experimental Psychology: General 150: 160. [Google Scholar] [CrossRef]
- Unsworth, Nash, Mattjew K. Robison, and Ashley L. Miller. 2021b. Individual differences in lapses of attention: A latent variable analysis. Journal of Experimental Psychology: General 150: 1303–31. [Google Scholar] [CrossRef]
- van der Maas, Han L. J., Alexander O. Savi, Abe Hofman, Kees-Jan Kan, and Maarten Marsman. 2019. The network approach to general intelligence. In General and Specific Mental Abilities. Edited by D. J. McFarland. Cambridge: Cambridge Scholars Publishing, pp. 108–31. [Google Scholar]
- van der Maas, Han L. J., Conor V. Dolan, Raul P. P. P. Grasman, Jelte M. Wicherts, Hilde M. Huizenga, and Maartje E. J. Raijmakers. 2006. A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychological Review 113: 842–61. [Google Scholar] [CrossRef] [PubMed]
- van der Maas, Han L. J., Kees-Jan Kan, and Denny Borsboom. 2014. Intelligence is what the intelligence test measures. Seriously. Journal of Intelligence 2: 12–15. [Google Scholar] [CrossRef]
- van der Maas, Han L. J., Kees-Jan Kan, Maartem Marsman, and Claire E. Stevenson. 2017. Network models for cognitive development and intelligence. Journal of Intelligence 5: 16. [Google Scholar] [CrossRef]
- Vanderwood, Mike L., Kevin S. McGrew, Dawn P. Flanagan, and Timothy Z. Keith. 2002. The contribution of general and specific cognitive abilities to reading achievement. Learning and Individual Differences 13: 159–88. [Google Scholar] [CrossRef]
- Villarreal, Victor. 2015. Test Review: Schrank, Fredrick A., Mather, Nancy, and McGrew, Kevin S. (2014). Woodcock-Johnson IV Tests of Achievement. Journal of Psychoeducational Assessment 33: 391–98. [Google Scholar] [CrossRef]
- von Bastian, Claudia C., Chris Blais, Gene A. Brewer, Máté Gyurkovics, Craig Hedge, Patrycja Kałamała, Matt E. Meier, Klaus Oberauer, Alodie Rey-Mermet, Jeffrey N. Rouder, and et al. 2020. Advancing the Understanding of Individual Differences in Attentional Control: Theoretical, Methodological, and Analytical Considerations [Preprint]. PsyArXiv. Available online: https://doi.org/10.31234/osf.io/x3b9k (accessed on 4 October 2021).
- Wickham, Hadley. 2016. ggplot2: Elegant Graphics for Data Analysis. Berlin/Heidelberg: Springer. [Google Scholar]
- Wilke, Claus O. 2020. ggtext: Improved Text Rendering Support for ggplot2. Available online: CRAN.R-project.org/package=ggtext (accessed on 20 August 2022).
- Wilkinson, Leland. 2010. SYSTAT. Wiley Interdisciplinary Reviews: Computational Statistics 2: 256–57. [Google Scholar] [CrossRef]
- Woodcock, Richard W., Kevin S. McGrew, and Nancy Mather. 2001. Woodcock-Johnson III. Rolling Meadows: Riverside Publishing. [Google Scholar]
- Woodcock, Richard W., Kevin S. McGrew, Fredrick A. Schrank, and Nancy Mather. 2007. Woodcock-Johnson III Normative Update. Rolling Meadows: Riverside Publishing. [Google Scholar]
- Zoccolotti, Pierlluigi, Paola Angelelli, Chiara V. Marinelli, and Daniele L. Romano. 2021. A network analysis of the relationship among reading, spelling and maths skills. Brain Sciences 11: 656. [Google Scholar] [CrossRef]
| Gender | White | Black | Indigenous | Asian/Pacific Islander | Other |
|---|---|---|---|---|---|
| Male | 1261 (38.7%) | 214 (6.6%) | 9 (0.3%) | 73 (2.2%) | 41 (1.3%) |
| Female | 1265 (38.8%) | 274 (8.4%) | 14 (0.4%) | 74 (2.3%) | 33 (1.0%) |
| Network Relative Centrality Characteristic Metrics | |||||||
|---|---|---|---|---|---|---|---|
| 20 Measure Primary Model | 23 Measure Sensitivity Model | ||||||
| WJ IV Measure | CHC Domain | Between. | Close. | Strength | Between. | Close. | Strength |
| Analysis-Synthesis | Gf | 0.35 | 0.84 | 0.82 | 0.12 | 0.77 | 0.73 |
| Concept Formation | Gf | 0.29 | 0.80 | 0.65 | 0.06 | 0.71 | 0.64 |
| Verbal Analogies | Gc/Gf | 0.94 | 0.87 | 0.84 | 0.32 | 0.84 | 0.76 |
| General Information | Gc | 0.12 | 0.73 | 0.65 | 0.00 | 0.66 | 0.64 |
| Oral Comprehension | Gc | 1.00 | 1.00 | 0.98 | 1.00 | 1.00 | 1.00 |
| Oral Vocabulary | Gc | 0.88 | 0.82 | 0.88 | 0.47 | 0.75 | 0.81 |
| Block Rotation | Gv | 0.53 | 0.90 | 0.90 | 0.47 | 0.90 | 0.89 |
| Spatial Relations | Gv | 0.12 | 0.82 | 0.76 | 0.06 | 0.82 | 0.67 |
| Phon. Proc.-Word Access | Ga | 0.41 | 0.79 | 0.77 | 0.15 | 0.74 | 0.67 |
| Phon. Proc.-Substitution | Ga | 0.65 | 0.79 | 0.87 | 0.47 | 0.80 | 0.83 |
| Segmentation | Ga | 0.18 | 0.73 | 0.69 | 0.03 | 0.71 | 0.62 |
| Sound Blending | Ga | 0.35 | 0.78 | 0.64 | 0.21 | 0.77 | 0.66 |
| Phon. Proc.-Word Fluency | Gr | 0.24 | 0.87 | 0.78 | 0.06 | 0.79 | 0.74 |
| Retrieval Fluency | Gr | 0.65 | 0.92 | 0.96 | 0.35 | 0.86 | 0.92 |
| Object-Number Seq. | Gwm | 0.41 | 0.86 | 0.73 | 0.21 | 0.82 | 0.64 |
| Memory for Words | Gwm | 0.29 | 0.81 | 0.79 | 0.12 | 0.73 | 0.75 |
| Verbal Attention | Gwm | 0.77 | 0.95 | 0.97 | 0.47 | 0.85 | 0.88 |
| Letter-Pattern Matching | Gs | 1.00 | 0.93 | 1.00 | 0.68 | 0.92 | 0.94 |
| Number-Pattern Matching | Gs | 0.18 | 0.85 | 0.86 | 0.32 | 0.88 | 0.90 |
| Pair Cancellation | Gs | 0.18 | 0.81 | 0.67 | 0.18 | 0.83 | 0.71 |
| Number Series | Gq | 0.44 | 0.82 | 0.96 | |||
| Applied Problems | Gq | 0.18 | 0.85 | 0.81 | |||
| Calculation | Gq | 0.15 | 0.82 | 0.73 | |||
| 23-Variable Sensitivity Analysis Model | ||||
|---|---|---|---|---|
| 20 Variable Primary Model | Betweenness | Closeness | Strength | g-Loading (PCA) |
| Betweenness | .84 | .58 | .69 | .43 |
| Closeness | .77 | .88 | .81 | −.05 |
| Strength | .81 | .74 | .93 | .02 |
| g-loading (PCA) | .10 | −.24 | −.15 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McGrew, K.S.; Schneider, W.J.; Decker, S.L.; Bulut, O. A Psychometric Network Analysis of CHC Intelligence Measures: Implications for Research, Theory, and Interpretation of Broad CHC Scores “Beyond g”. J. Intell. 2023, 11, 19. https://doi.org/10.3390/jintelligence11010019
McGrew KS, Schneider WJ, Decker SL, Bulut O. A Psychometric Network Analysis of CHC Intelligence Measures: Implications for Research, Theory, and Interpretation of Broad CHC Scores “Beyond g”. Journal of Intelligence. 2023; 11(1):19. https://doi.org/10.3390/jintelligence11010019
Chicago/Turabian StyleMcGrew, Kevin S., W. Joel Schneider, Scott L. Decker, and Okan Bulut. 2023. "A Psychometric Network Analysis of CHC Intelligence Measures: Implications for Research, Theory, and Interpretation of Broad CHC Scores “Beyond g”" Journal of Intelligence 11, no. 1: 19. https://doi.org/10.3390/jintelligence11010019
APA StyleMcGrew, K. S., Schneider, W. J., Decker, S. L., & Bulut, O. (2023). A Psychometric Network Analysis of CHC Intelligence Measures: Implications for Research, Theory, and Interpretation of Broad CHC Scores “Beyond g”. Journal of Intelligence, 11(1), 19. https://doi.org/10.3390/jintelligence11010019








