Effects of Fractional Derivatives with Different Orders in SIS Epidemic Models
Abstract
:1. Introduction
2. Caputo Fractional Epidemic Models
2.1. Solutions
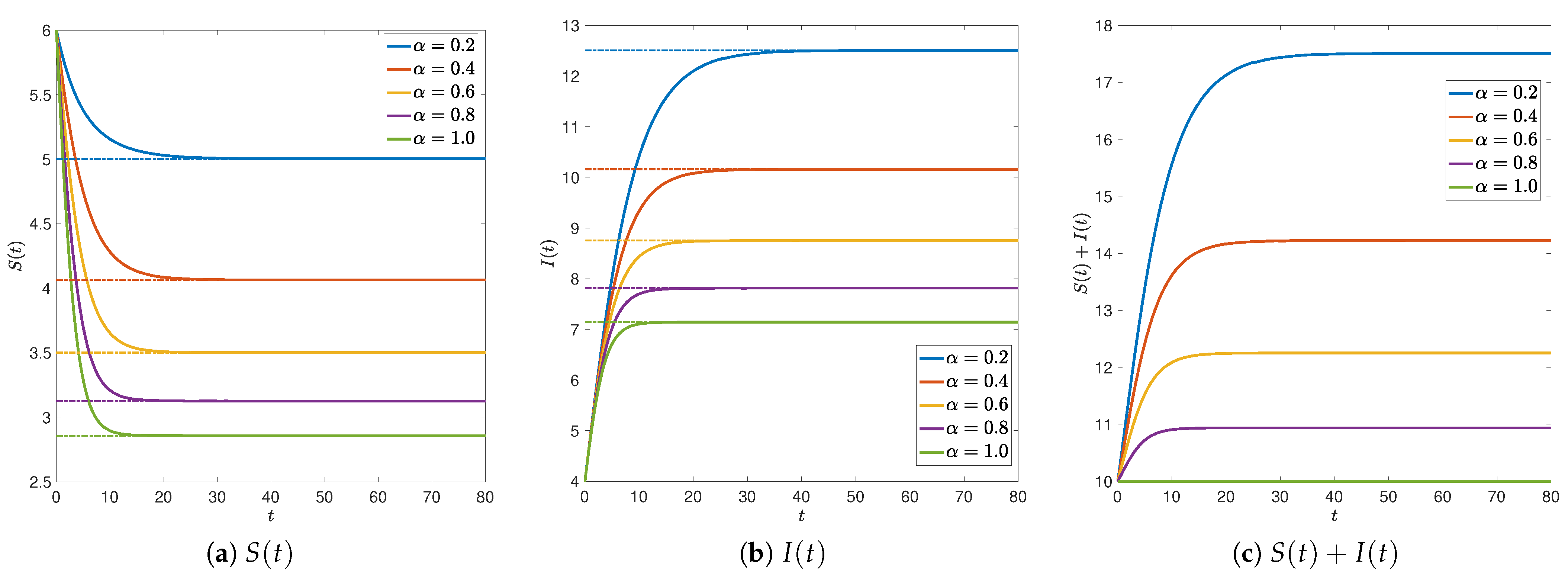
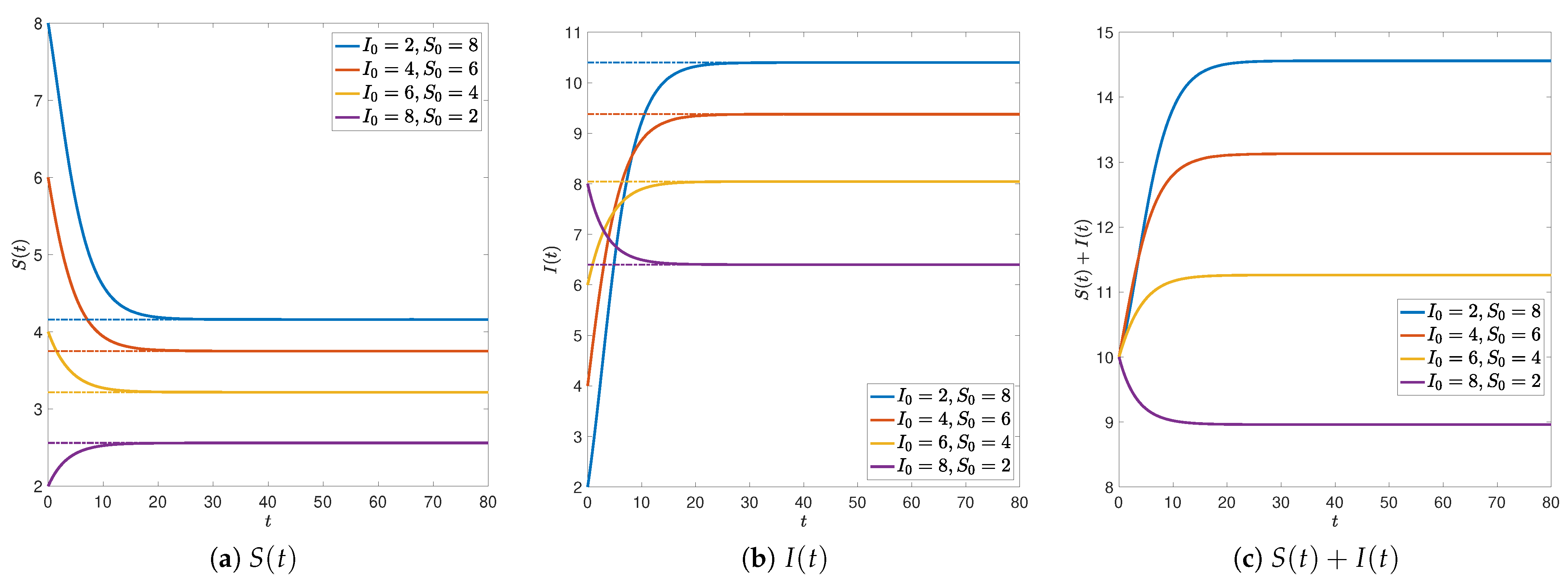
2.2. Numerical Simulations
3. Caputo–Fabrizio Fractional Epidemic Models
3.1. Solutions and Equilibria
Equilibria
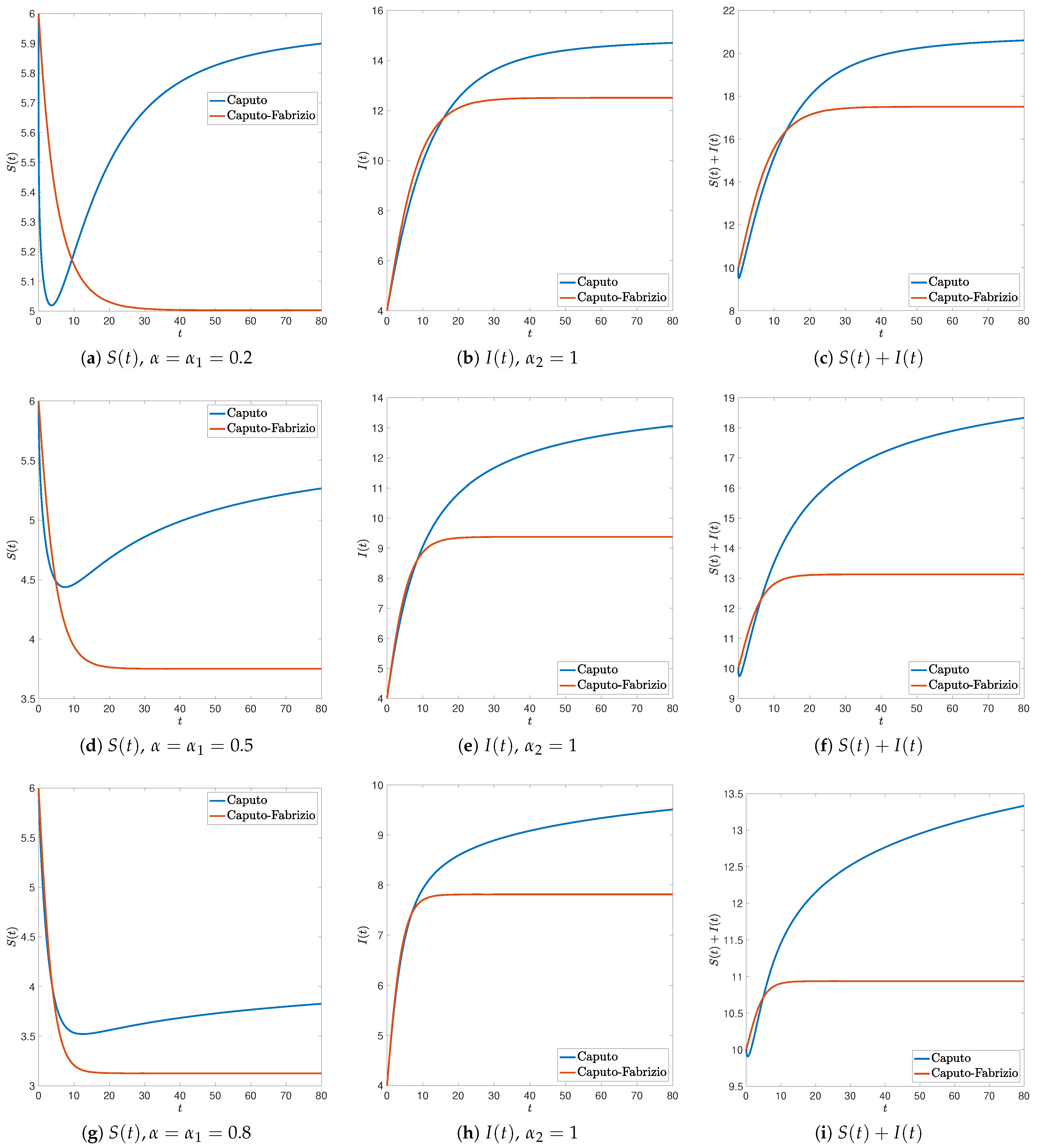
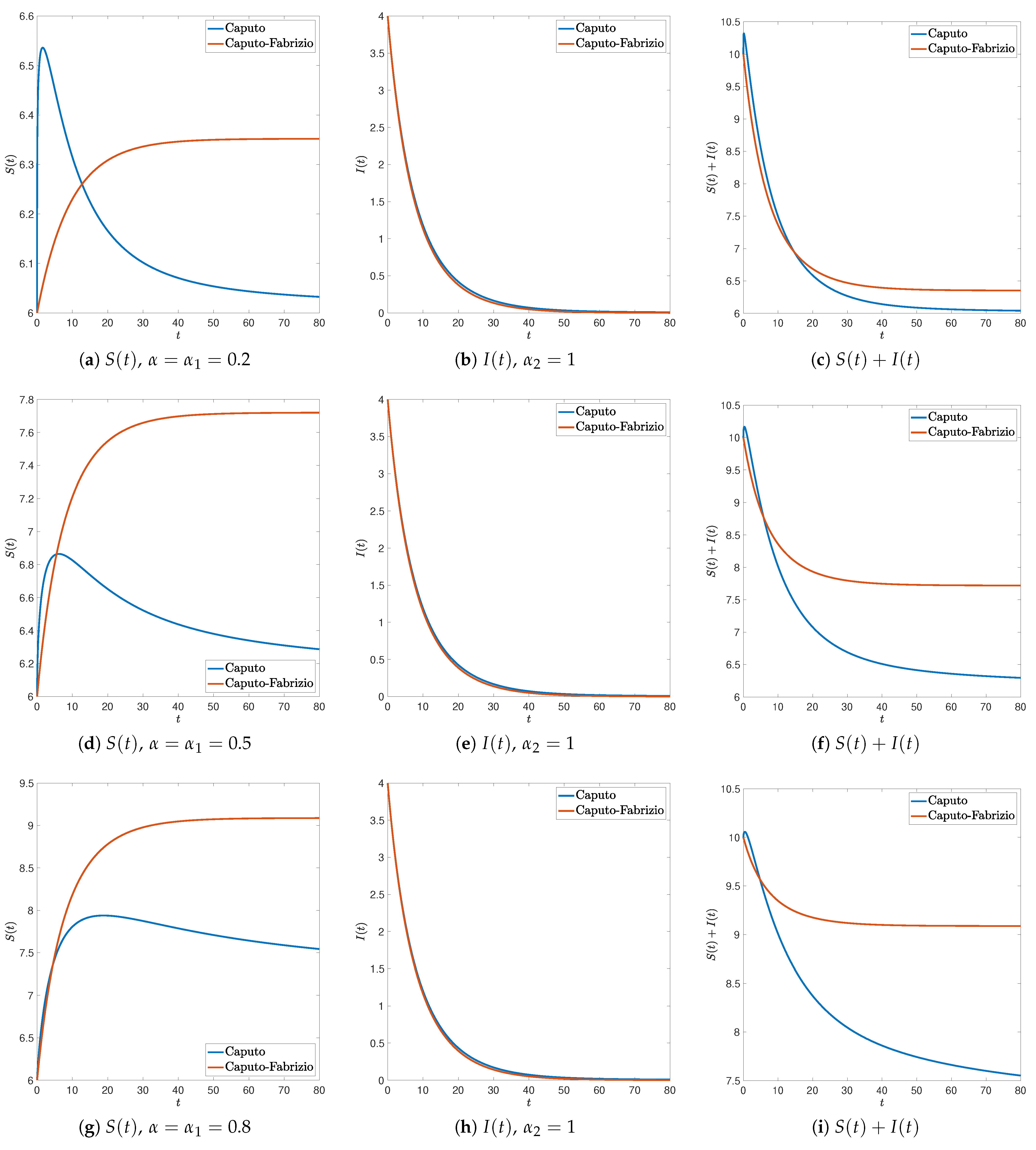
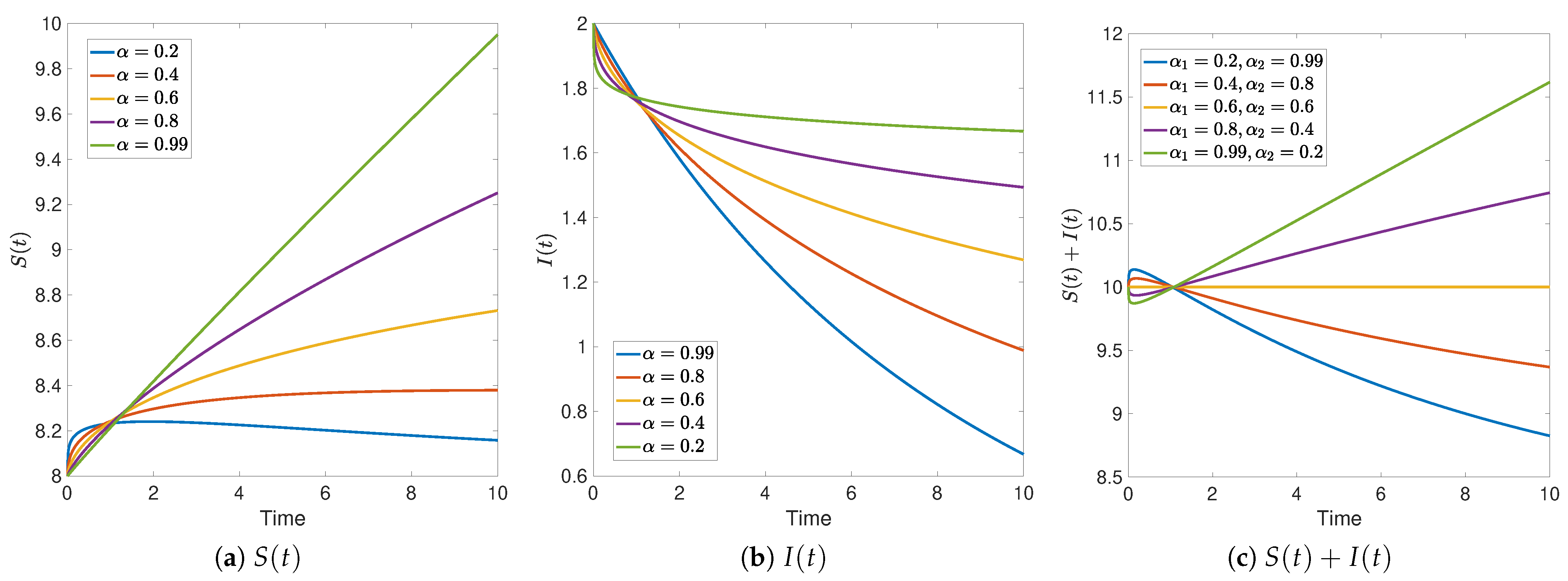
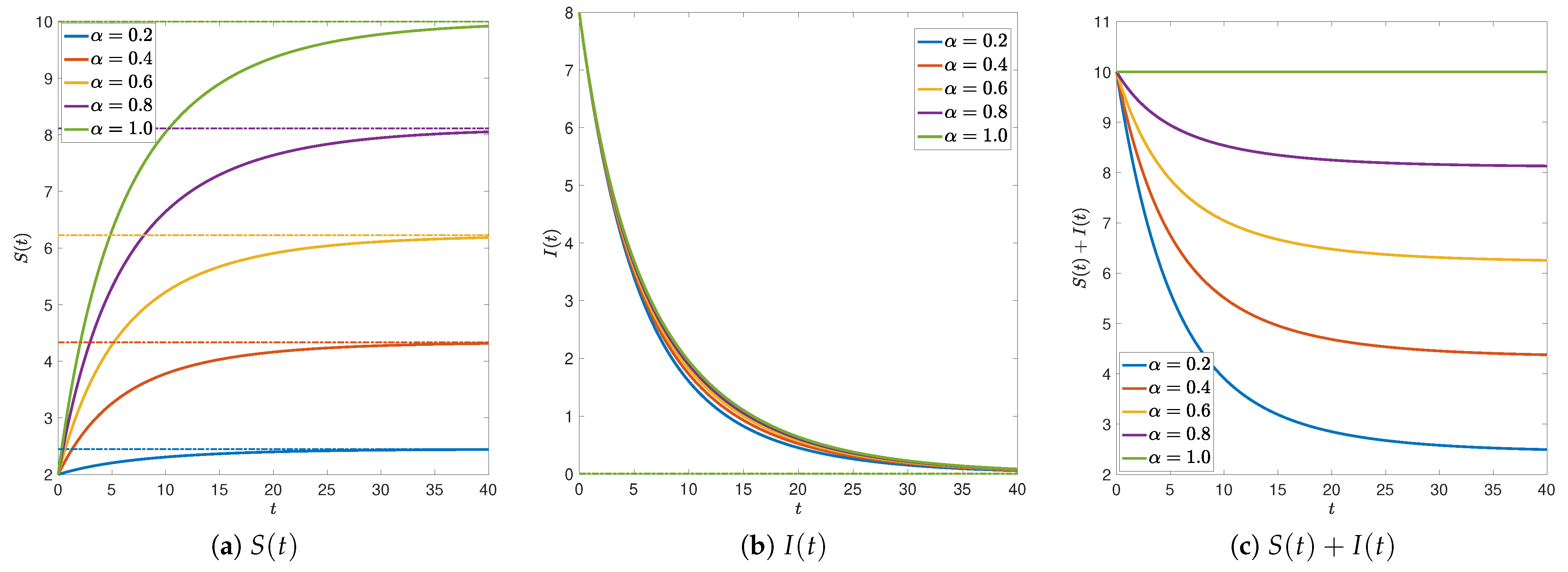
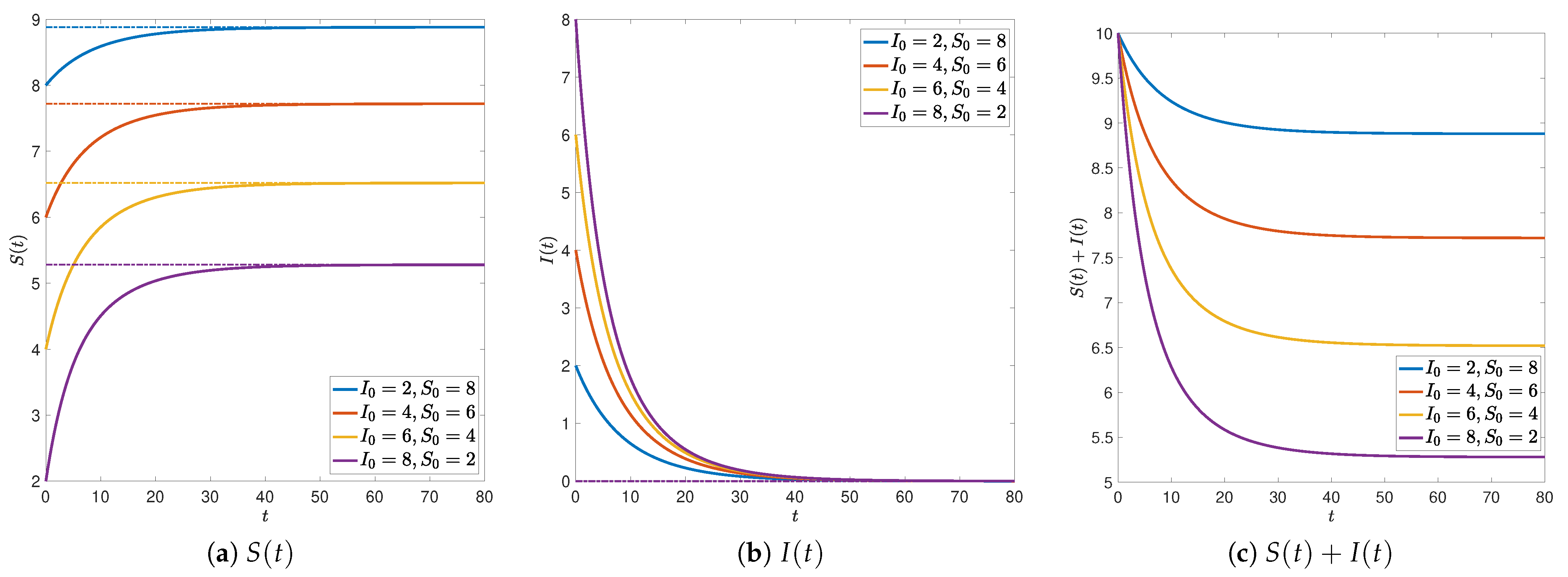
3.2. Numerical Simulations
Comparison between Caputo SIS Model and Caputo–Fabrizio SIS Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A 1927, 115, 700–721. [Google Scholar]
- Hethcote, H.W. Three basic epidemiological models. In Applied Mathematical Ecology (Trieste, 1986); Biomathematics; Springer: Berlin, Germany, 1989; Volume 18, pp. 119–144. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, F.; Yu, Q.; Li, T. Review of fractional epidemic models. Appl. Math. Model. 2021, 97, 281–307. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Li, C.; Lü, J. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 2007, 48, 409–416. [Google Scholar] [CrossRef]
- Yavuz, M.; Sene, N. Stability analysis and numerical computation of the fractional predator–prey model with the harvesting rate. Fractal Fract. 2020, 4, 35. [Google Scholar] [CrossRef]
- Daşbaşi, B. Stability analysis of the hiv model through incommensurate fractional-order nonlinear system. Chaos Solitons Fractals 2020, 137, 109870. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Fract. Calc. Appl. Anal. 2008, 11, 4–14, reprinted in Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Verhulst, P.F. Notice sur la loi que la population suit dans son accroissement. Corresp. Math. Phys. 1838, 10, 113–126. [Google Scholar]
- Verhulst, P.F. Recherches mathématiques sur la loi d’accroissement de la population. J. Econ. 1845, 12, 276. [Google Scholar]
- Verhulst, P.F. Deuxième mémoire sur la loi d’accroissement de la population. Mémoires De L’académie Royale des Sciences des Lettres et des Beaux-Arts de Belgique 1847, 20, 1–32. [Google Scholar]
- Balzotti, C.; D’Ovidio, M.; Loreti, P. Fractional SIS Epidemic Models. Fractal Fract. 2020, 4, 44. [Google Scholar] [CrossRef]
- El-Saka, H. The fractional-order SIR and SIRS epidemic models with variable population size. Math. Sci. Lett. 2013, 2, 195. [Google Scholar] [CrossRef]
- Hassouna, M.; Ouhadan, A.; El Kinani, E.H. On the solution of fractional order SIS epidemic model. Chaos Solitons Fractals 2018, 117, 168–174. [Google Scholar] [CrossRef] [PubMed]
- D’Ovidio, M.; Loreti, P. Solutions of fractional logistic equations by Euler’s numbers. Phys. A 2018, 506, 1081–1092. [Google Scholar] [CrossRef] [Green Version]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematical Models in Epidemiology; Texts in Applied Mathematics; Springer: New York, NY, USA, 2019; Volume 69. [Google Scholar] [CrossRef]
- Giga, Y.; Liu, Q.; Mitake, H. On a discrete scheme for time fractional fully nonlinear evolution equations. Asymptot. Anal. 2020, 120, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Kumar, D.; Singh, J.; Al Qurashi, M.; Baleanu, D. A new fractional SIRS-SI malaria disease model with application of vaccines, antimalarial drugs, and spraying. Adv. Differ. Equ. 2019, 2019, 278. [Google Scholar] [CrossRef] [Green Version]
- Yavuz, M.; Özdemir, N. Analysis of an epidemic spreading model with exponential decay law. Math. Sci. Appl. E-Notes 2020, 8, 142–154. [Google Scholar] [CrossRef] [Green Version]
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; Tata McGraw-Hill Education: New Delhi, India, 1955. [Google Scholar]
- Mainardi, F.; Gorenflo, R. Time-fractional derivatives in relaxation processes: A tutorial survey. Fract. Calc. Appl. Anal. 2007, 10, 269–308. [Google Scholar]
- Higazy, M.; Alyami, M.A. New Caputo-Fabrizio fractional order SEIASqEqHR model for COVID-19 epidemic transmission with genetic algorithm based control strategy. Alex. Eng. J. 2020, 59, 4719–4736. [Google Scholar] [CrossRef]
- Khan, S.A.; Shah, K.; Kumam, P.; Seadawy, A.; Zaman, G.; Shah, Z. Study of mathematical model of Hepatitis B under Caputo-Fabrizo derivative. AIMS Math. 2021, 6, 195–209. [Google Scholar] [CrossRef]
- Moore, E.J.; Sirisubtawee, S.; Koonprasert, S. A Caputo-Fabrizio fractional differential equation model for HIV/AIDS with treatment compartment. Adv. Differ. Equ. 2019, 200, 20. [Google Scholar] [CrossRef] [Green Version]
- Ullah, S.; Khan, M.A.; Farooq, M.; Hammouch, Z.; Baleanu, D. A fractional model for the dynamics of tuberculosis infection using Caputo-Fabrizio derivative. Discret. Contin. Dyn. Syst. Ser. S 2020, 13, 975–993. [Google Scholar] [CrossRef] [Green Version]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Progr. Fract. Differ. Appl 2015, 1, 87–92. [Google Scholar]
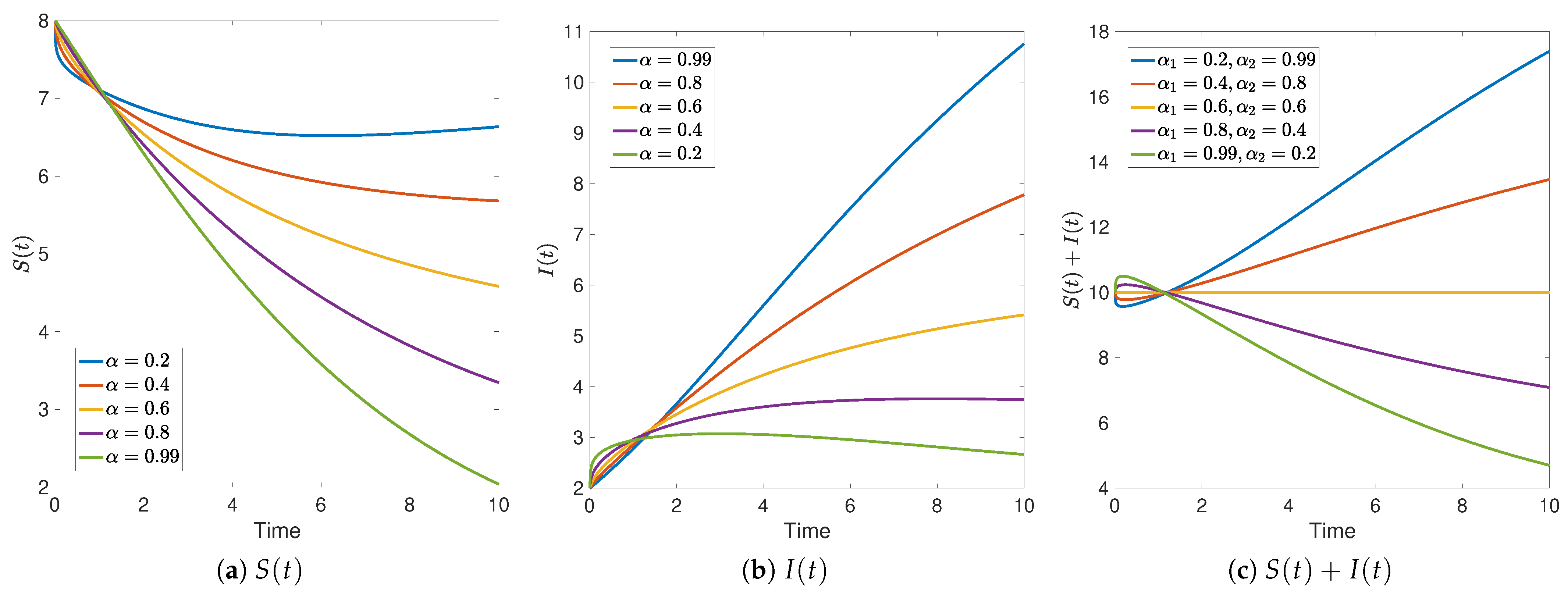
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balzotti, C.; D’Ovidio, M.; Lai, A.C.; Loreti, P. Effects of Fractional Derivatives with Different Orders in SIS Epidemic Models. Computation 2021, 9, 89. https://doi.org/10.3390/computation9080089
Balzotti C, D’Ovidio M, Lai AC, Loreti P. Effects of Fractional Derivatives with Different Orders in SIS Epidemic Models. Computation. 2021; 9(8):89. https://doi.org/10.3390/computation9080089
Chicago/Turabian StyleBalzotti, Caterina, Mirko D’Ovidio, Anna Chiara Lai, and Paola Loreti. 2021. "Effects of Fractional Derivatives with Different Orders in SIS Epidemic Models" Computation 9, no. 8: 89. https://doi.org/10.3390/computation9080089
APA StyleBalzotti, C., D’Ovidio, M., Lai, A. C., & Loreti, P. (2021). Effects of Fractional Derivatives with Different Orders in SIS Epidemic Models. Computation, 9(8), 89. https://doi.org/10.3390/computation9080089