Abstract
The center of an F-graph contains at least two vertices, and the distance between any two central vertices is equal to the radius. In this short note, we describe one way of constructing these graphs.
MSC:
05C12; 05C90
1. Introduction
One class of frequently studied central problems in the application of graphs is facility location problems. A cluster of emergency facilities, such as a hospital, a fire station or, a police station, has to locate to a new habitation. We aim to minimize the response time between the facility and the location of a possible emergency. Thus, these facilities are separated as much as possible to minimize the interference [1,2,3]. The simple model of location facilities with those two conditions is an F-graph. The central vertices of F-graphs are as separated as much as possible to minimize the interference between corresponding facilities.
Our terminology and notation are based on [4,5] excluding those given here. Here, we consider nonempty, finite, connected, and undirected graphs without loops and multiple edges. Let denote the distance between the vertices u and v of a graph . The eccentricity is the maximum distance between v and any other vertex u of G; that is, . The minimum eccentricity among the vertices of G is the radius , and the set of vertices of G with eccentricity is the center. The distance between a vertex and a nonempty subset S of is the minimum of the distance for every .
Buckley and Lewinter define a graph G as an F-graph (the ‘F’ denotes ‘far’) if its center and for all is ; see, e.g., [6]. They also show the existence of such graphs with a prescribed radius and diameter. Kyš gives a necessary and sufficient condition for a graph to be an F-graph [7]. Figure 1 shows an example of an F-graph G, whose radius is , and the center is the set .
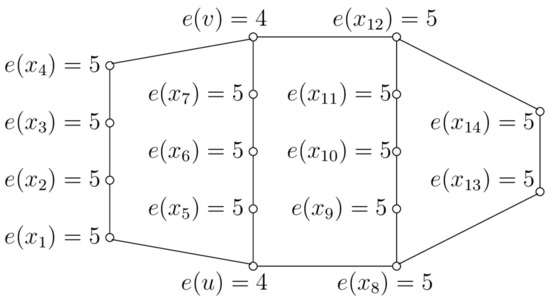
Figure 1.
Example of F-graph G with center .
2. Construction of F-Graph
The purpose of this note is to propose a construction for connecting two F-graphs, and such that the resulting graph G will also be an F-graph. Let G be a graph with and a center and k be a natural number . We denote by the set of all vertices v, where .
Lemma 1.
Let G be an F-graph with and k be a natural number . Then, the F-graph G contains a nonempty set as a subset of .
Proof.
Following from the definition of an F-graph, for every , , and the center contains at least two vertices. Thus, there is at least one shortest path of length r between two different central vertices. There is at least one vertex on this path such that the distance between this vertex and at least one of these two central vertices is k. Thus, is nonempty. □
Lemma 2.
Let G be an F-graph with an even radius . Then, for every vertex v where there exists a vertex u in such that .
Proof.
Suppose . Assume to the contrary that there exists , where such that for every , there is . Suppose that v lies on the shortest path P between two central vertices. Clearly, there is a vertex x from in the middle of P. Thus, leads to a contradiction. On the other hand, suppose that v does not lie on the shortest path between central vertices. There is just one such vertex where . For every , is and . Every shortest path from to v contains a vertex y from the ; thus, leads to a contradiction.
Suppose is a central vertex; thus, . On shortest path P between and other central vertex lies vertex y from the and . Therefore, the proof holds for this case.
Now, suppose . There is a vertex such that . The shortest path from v to c contains a vertex such that (Lemma 1); thus, . □
Lemma 3.
Let G be an F-graph with an odd radius . Then, for every vertex v such that and , there exists a vertex u in such that .
Proof.
Suppose . Assume to the contrary that there exists where and such that for every vertex, is . Suppose that v lies on a shortest path P between two central vertices . Clearly, there are vertices from such that . Thus, or leads to a contradiction. On the other hand, suppose that v does not lie on the shortest path between the central vertices. There is just one such vertex that . For every , is and . Every shortest path from to v contains a vertex y from ; thus, leads to a contradiction.
Suppose is a central vertex; thus, . On the shortest path P between other central vertices lies vertex y from such that . Thus, the proof holds for this case.
Suppose . There is a vertex such that . The shortest path from v to c contains a vertex , where or (Lemma 1); thus, . □
Theorem 1.
Let and be two F-graphs with centers and , respectively, and . Then, there exists an F-graph G with and , containing and as induced subgraphs.
Proof.
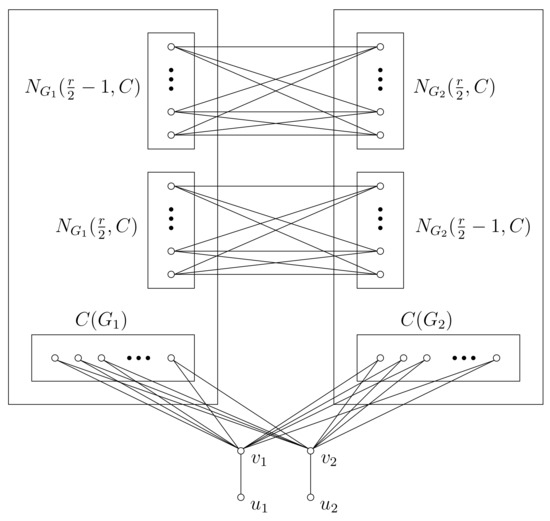
We constructed the graph for even radius as illustrated in Figure 2. The construction is based directly on the definition of the F-graph, and, as such, the center contains at least two vertices, and the distance between any two central vertices is equal to the radius. First, it is necessary to ensure that the distance between the central vertices of both graphs is . Following from Lemma 1, the F-graph contains nonempty sets and , and contains nonempty sets and . We constructed a complete bipartite graph such that the set is the first partition and is the second partition, as well as a complete bipartite graph with sets and as partitions. Then, for the set of vertices , it holds that for every . It is then necessary to ensure that for every vertex , it holds that . For every vertex, and ; thus, it holds that (Lemma 2). We added four nodes, , to . Each vertex is connected by a path with a length of to nodes and . Finally, we added two disjoint paths, and , with a length of . Following from the construction, graph G is an F-graph.

Figure 2.
Construction of the even radius.
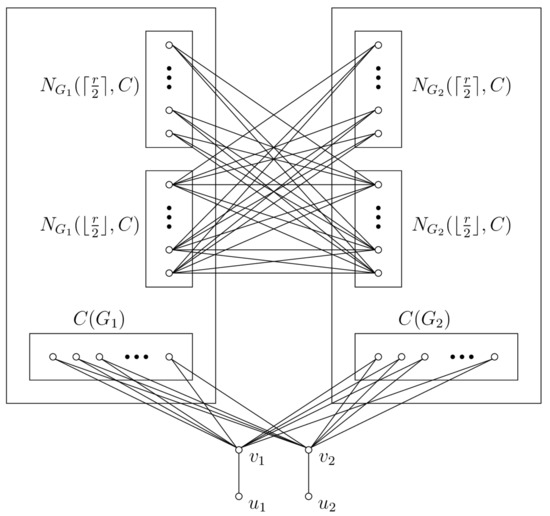
Suppose the radius is odd, as shown in Figure 3. It is necessary to ensure that the distance between the central vertices of both graphs is and, at the same time, that the distance of the vertex from the center to the non-central vertex of the graph is (). The existence of sets and is a continuation of Lemma 1. We constructed a complete bipartite graph with those sets as partitions. If there existed the set , then we constructed a complete bipartite graph with and as partitions. Similarly, if there existed the set , then we constructed a complete bipartite graph with and as partitions. Thus, for the set of vertices , it holds that for every . Following this, it is necessary to ensure that for every vertex , it holds that . For every vertex, and ; thus, it holds that (Lemma 3). We added four nodes, , to . Each vertex from the is connected by a path with a length of with to and by a path with a length of to vertex . Each vertex from the is connected by a path with a length of to vertex and by a path with a length of to vertex . Finally, we added two disjoint paths, and , with a length of . Following from the construction, the graph G is an F-graph. □

Figure 3.
Construction of the odd radius.
F-graphs represent an ideal model for the relocation of emergency facilities to housing estates, towns, etc. Such a model is difficult to apply directly in practice. F-graphs can serve as stepping stones to real applications.
Author Contributions
Conceptualization, V.L.; methodology, V.L.; investigation, V.L.; formal analysis, V.L.; writing—original draft preparation, V.L. and R.V.; writing—review and editing, V.L. and R.V. Both authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the project SANET II of OPVaI-VA/DP/2018/1.1.3-05 (ITMS2014+ code 313011W988).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the anonymous referees and Editors for their careful reading, valuable comments, and helpful suggestions, which helped significantly in improving the presentation of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Binay, K.B.; Minati, D.; Subhas, C.N.; Sasanka, R. Constant work-space algorithms for facility location problems. Discret. Appl. Math. 2020, 283, 456–472. [Google Scholar]
- Buckley, F. Facility location problems. Coll. Math. J. 1987, 18, 24–32. [Google Scholar]
- Buckley, F.; Lewinter, M. Graphs with all diametral paths through distant central nodes. Math. Comput. Model. 1993, 17, 35–41. [Google Scholar] [CrossRef]
- Buckley, F.; Lewinter, M. Introductory Graph Theory with Aplications; Waveland Press, Inc.: Long Grove, IL, USA, 2013. [Google Scholar]
- Buckley, F.; Harary, F. Distance in Graphs; Addison-Wesley: Redwood City, CA, USA, 1990. [Google Scholar]
- Nazeer, W.; Kang, S.M.; Nazeer, S.; Munir, M.; Kousar, I.; Sehar, A.; Kwun, Y.C. On center, periphery and average eccentricity for the convex polytopes. Symmetry 2016, 8, 145. [Google Scholar] [CrossRef] [Green Version]
- Kyš, P. Graphs with equidistant central nodes. Australas. J. Comb. 1996, 17, 149–156. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).