RuSseL: A Self-Consistent Field Theory Code for Inhomogeneous Polymer Interphases
Abstract
1. Introduction
- density profiles of each chain type
- density profiles of specific chain segments; that is, chain ends, or any other segment specified by the user
2. Model Space
2.1. Geometries and Interfaces
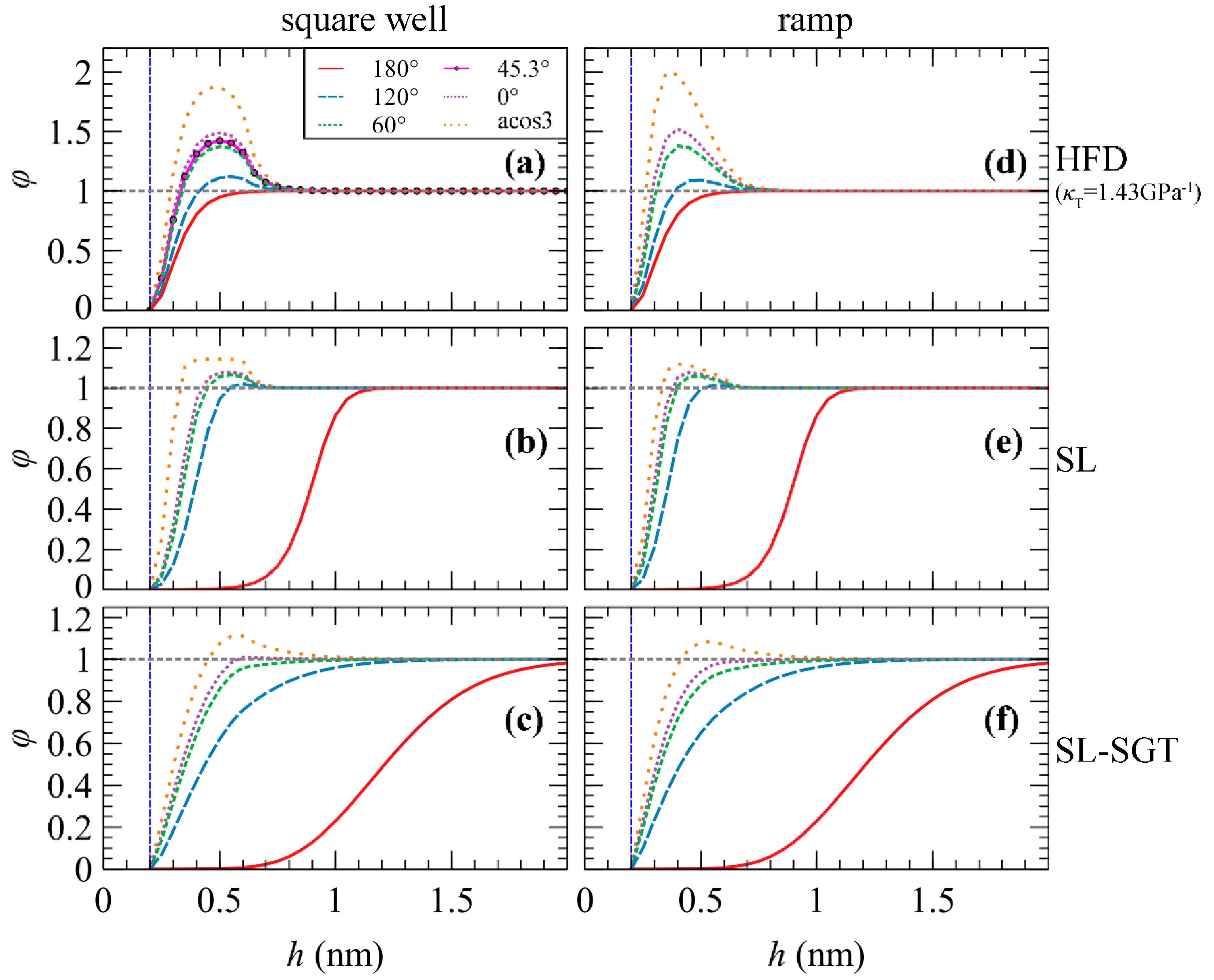
2.2. Polymer–Solid Interactions
3. Computational Details
3.1. Mathematical Formulation
3.2. Discretization of the Edwards PDE
3.2.1. Semi-Implicit Finite Differences Discretization
3.2.2. Implicit Finite Differences Discretization
3.3. Boundary Conditions
3.3.1. Dirichlet–Dirichlet System
3.3.2. Neumann–Neumann System
3.4. Solving the Linear System of Equations
4. Code Structure and Description
4.1. Input Files
- the contour length and spatial discretization (Δh, ΔΝc)
- the kind of discretization (uniform, nonuniform)
- the integration method (Simpson’s method, rectangle rule)
- the field relaxation parameter amix, which depends on the isothermal compressibility, κT, of the bulk polymer and the length of the polymer chains [27]
- the chain contour stepping method for the solution of the time-dependent PDE must be specified, that is, semi-implicit (also known as “Crank–Nicholson”) or implicit (see Section 3.2.1 and Section 3.2.2) [51].
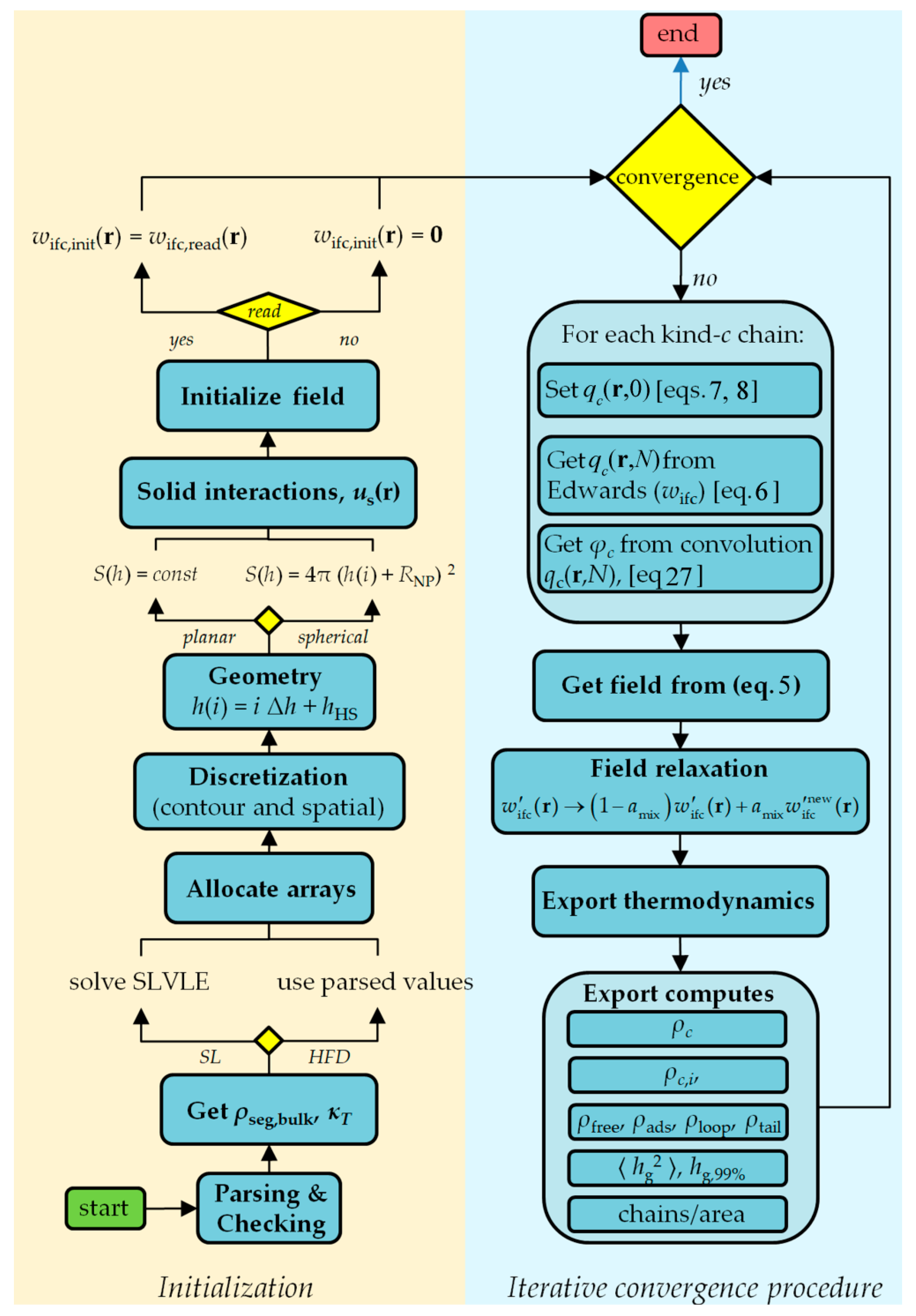
4.2. Code Flow
5. Export Computes
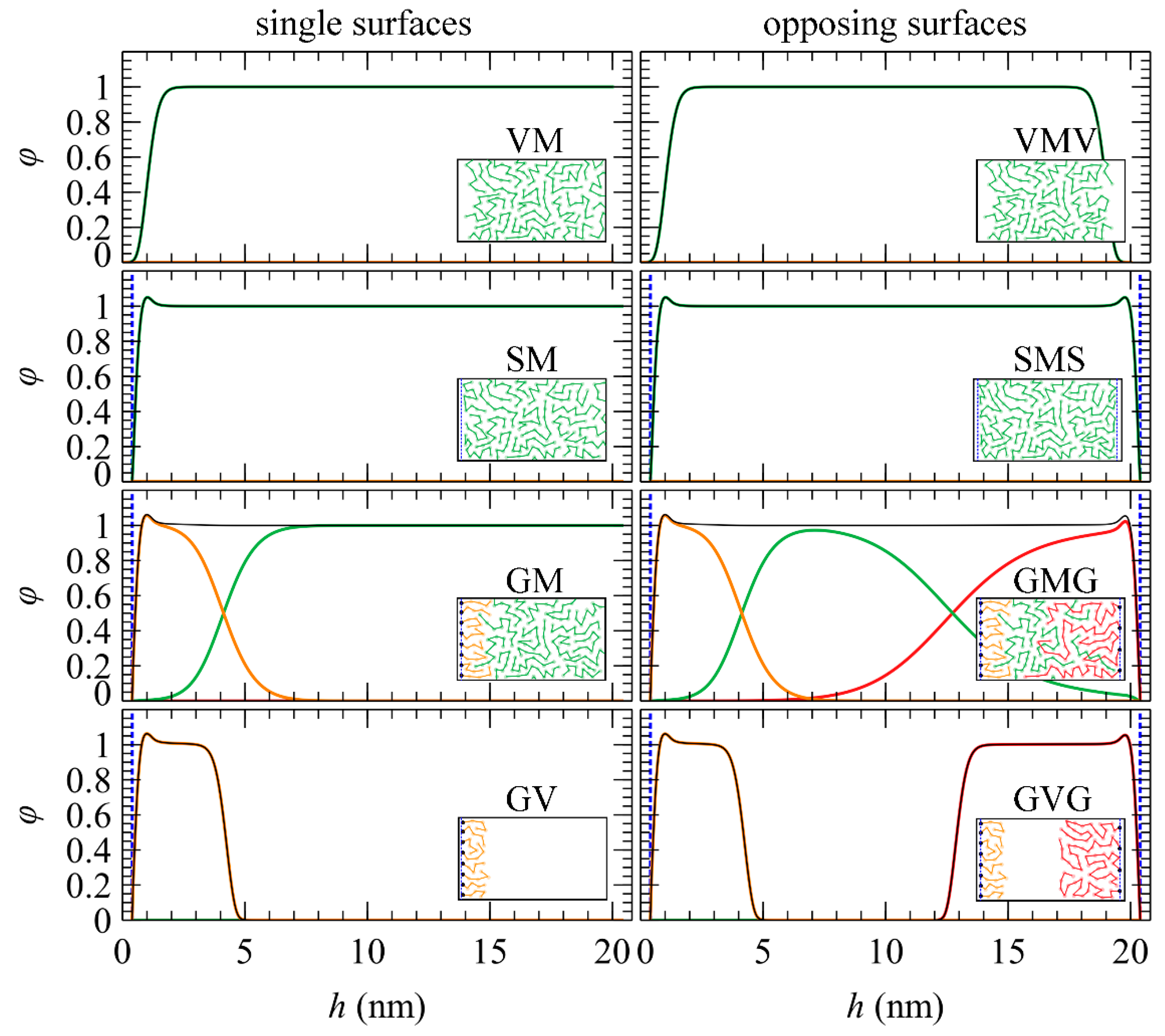
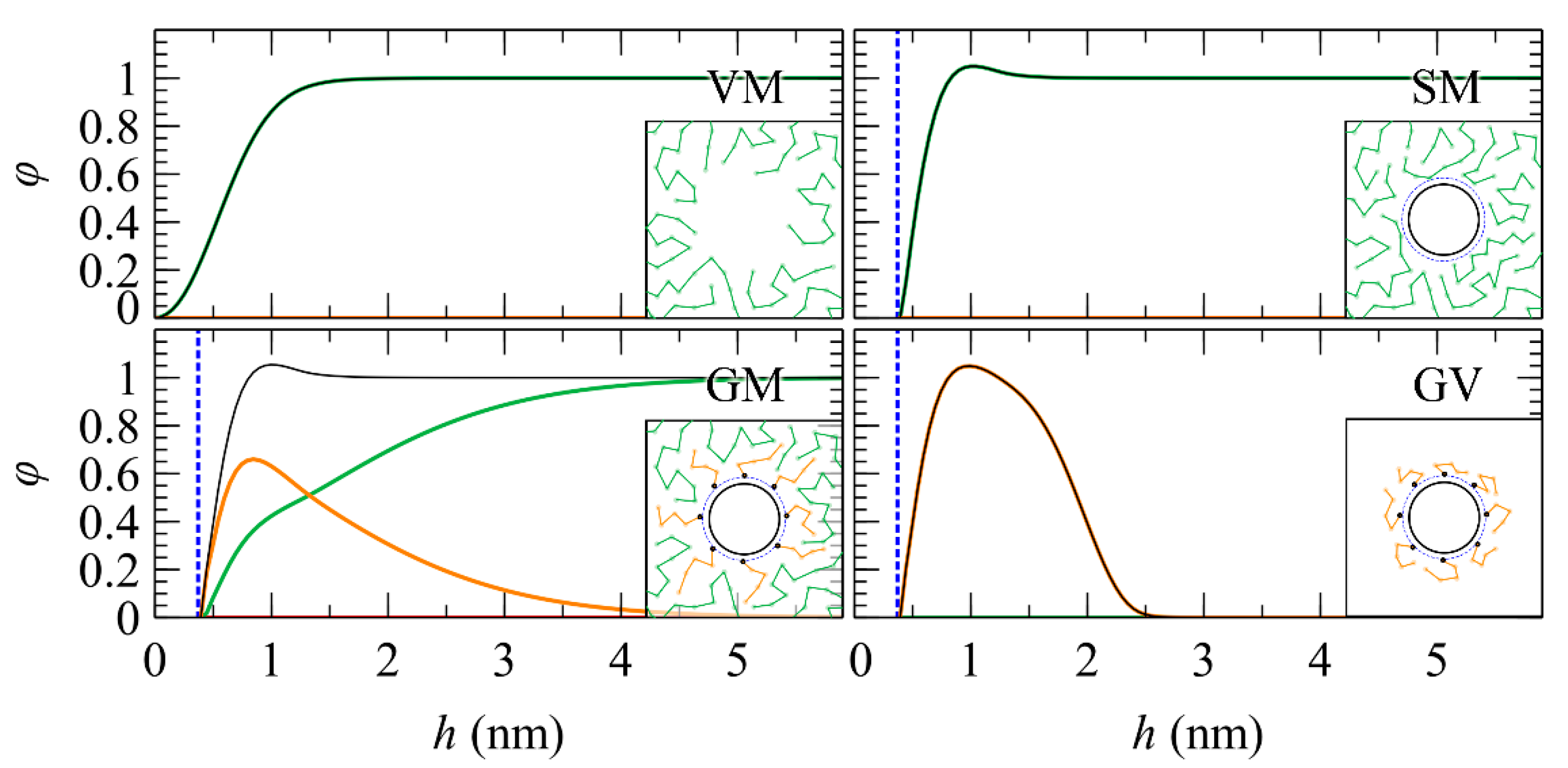
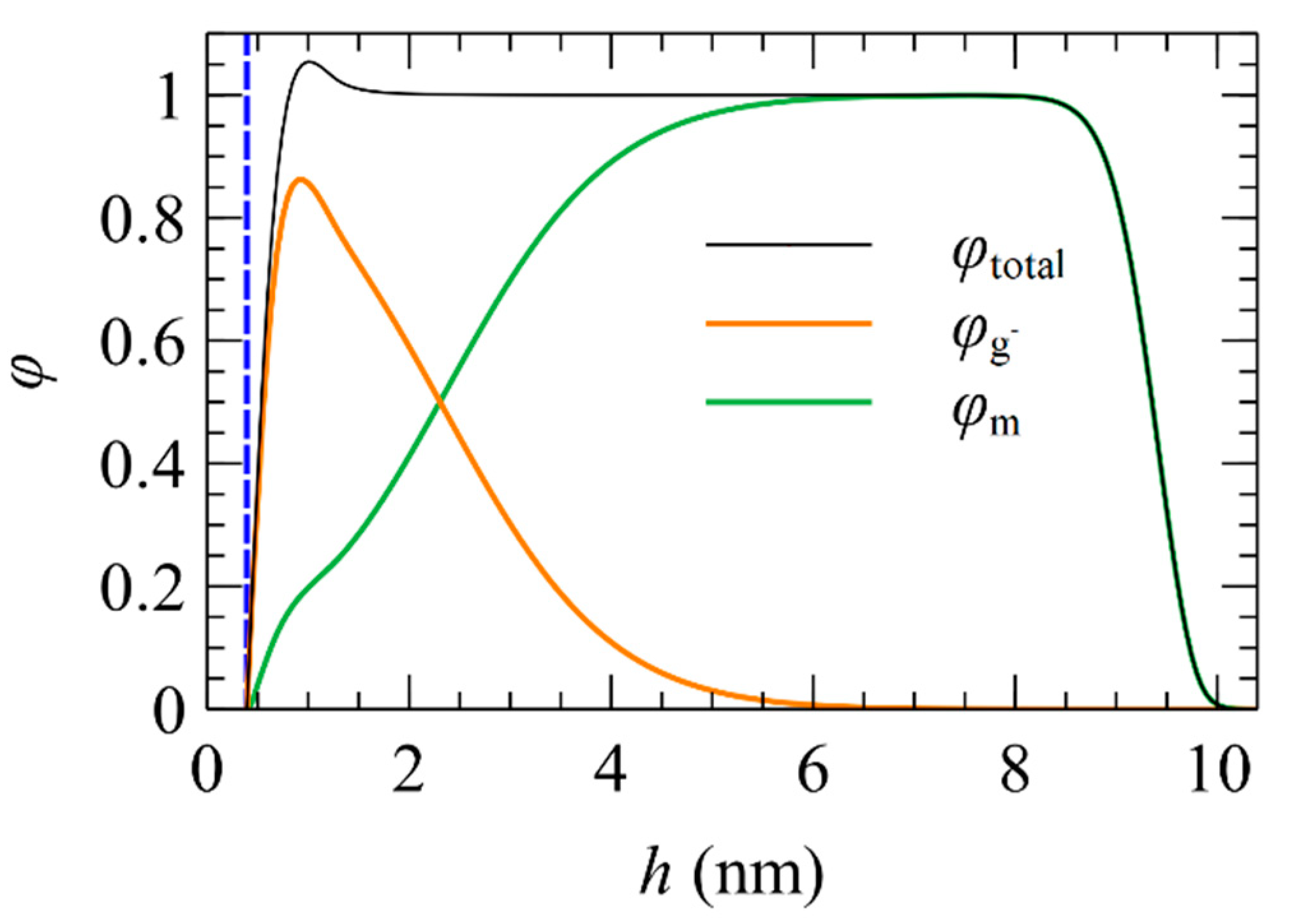
5.1. Total and Partial Density Profiles
5.2. Brush Thickness
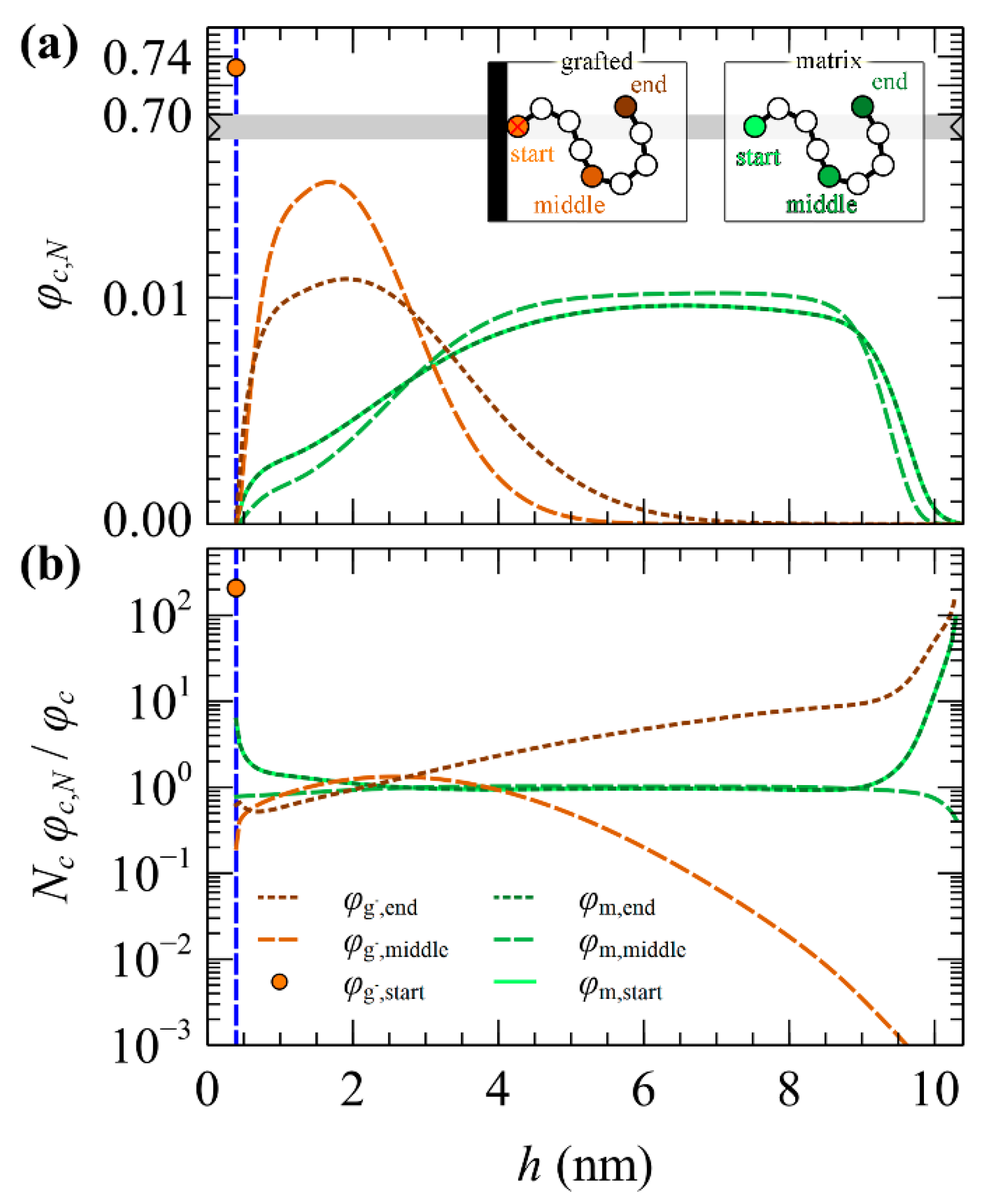
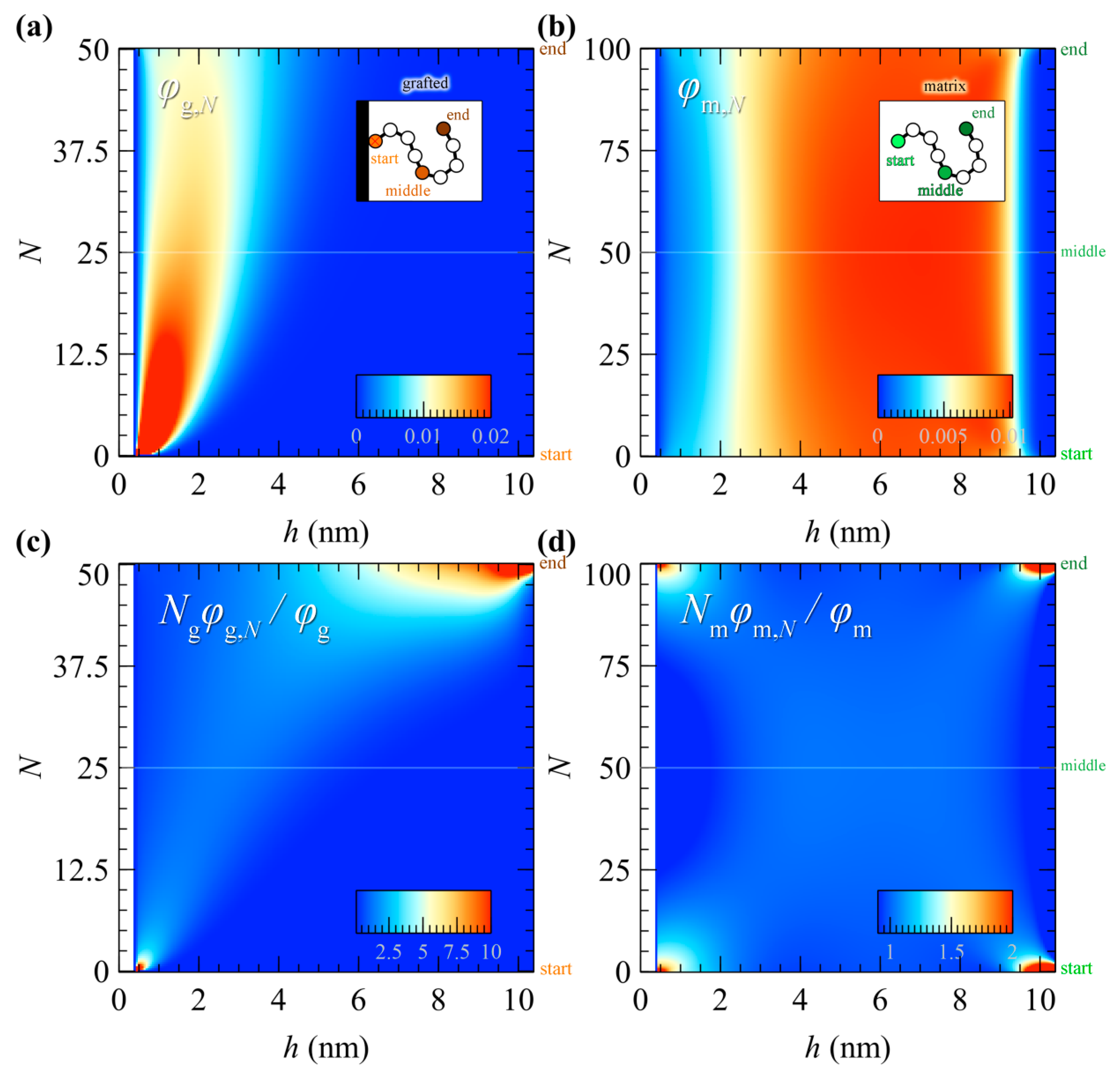
5.3. Profiles of Individual Chain Segments
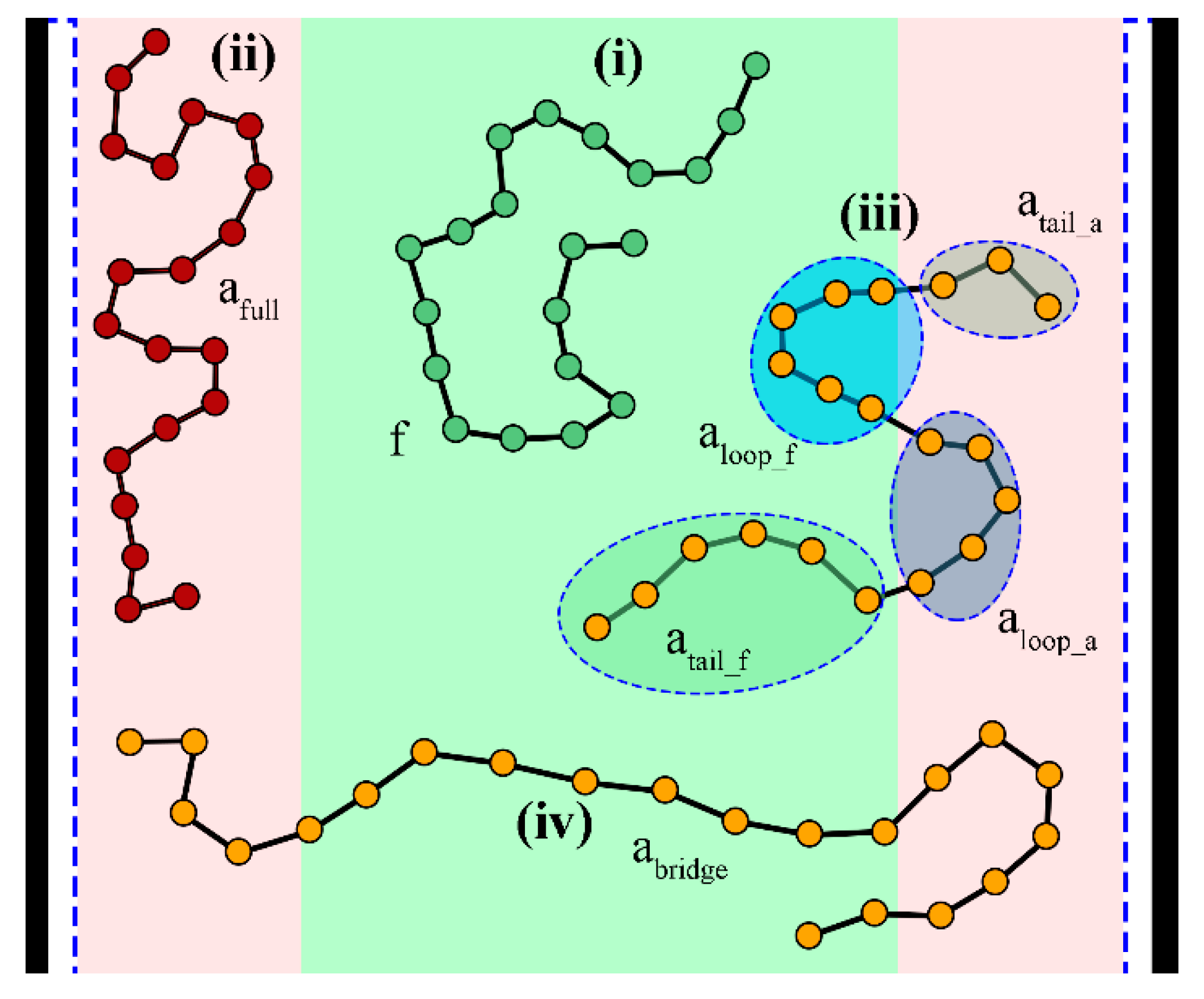
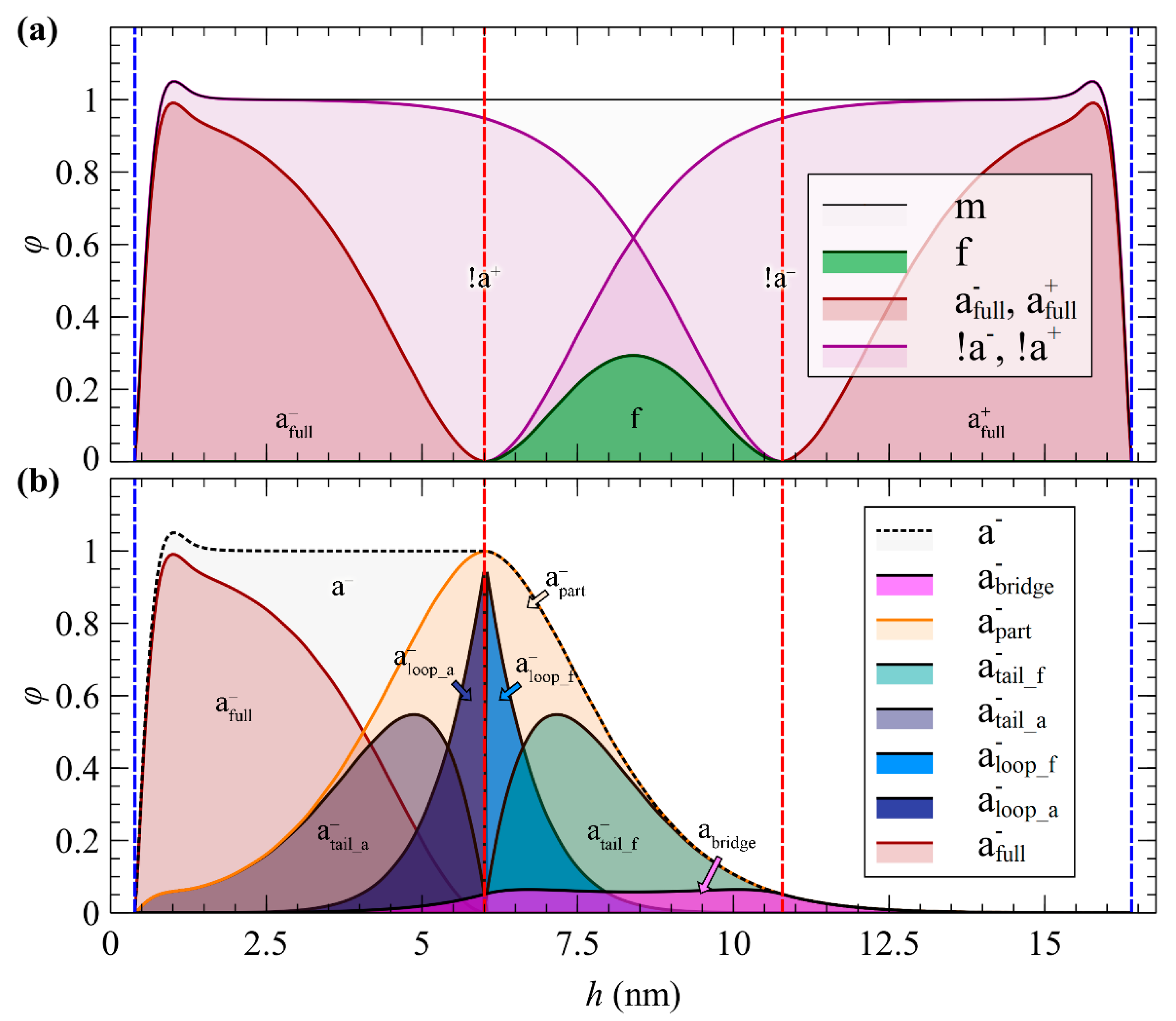
5.4. Distinction between Adsorbed and Free Segments
- Solid adsorption: hads can be tuned based on the peaks of the density profile (e.g., in Ref. [37], hads was set equal to 0.6 nm, the distance between the first two peaks of the polyethylene/graphite density profile), or based on the strength of polymer–solid interactions (e.g., in Ref. [28], hads was set equal to 1.28 nm, where the PS-Silica interactions, as described by the Hamaker potential, become very weak).
- Segregation at polymer–vacuum interfaces: In Ref. [11], hads was set equal to a distance where the reduced density φ reaches 0.5.
- Brush penetration: hads can also be set to the span of the grafted brush, hg,99%, in order to quantify the tendency of matrix chains to penetrate the brushes, or the tendencies of opposing brushes to penetrate each other.
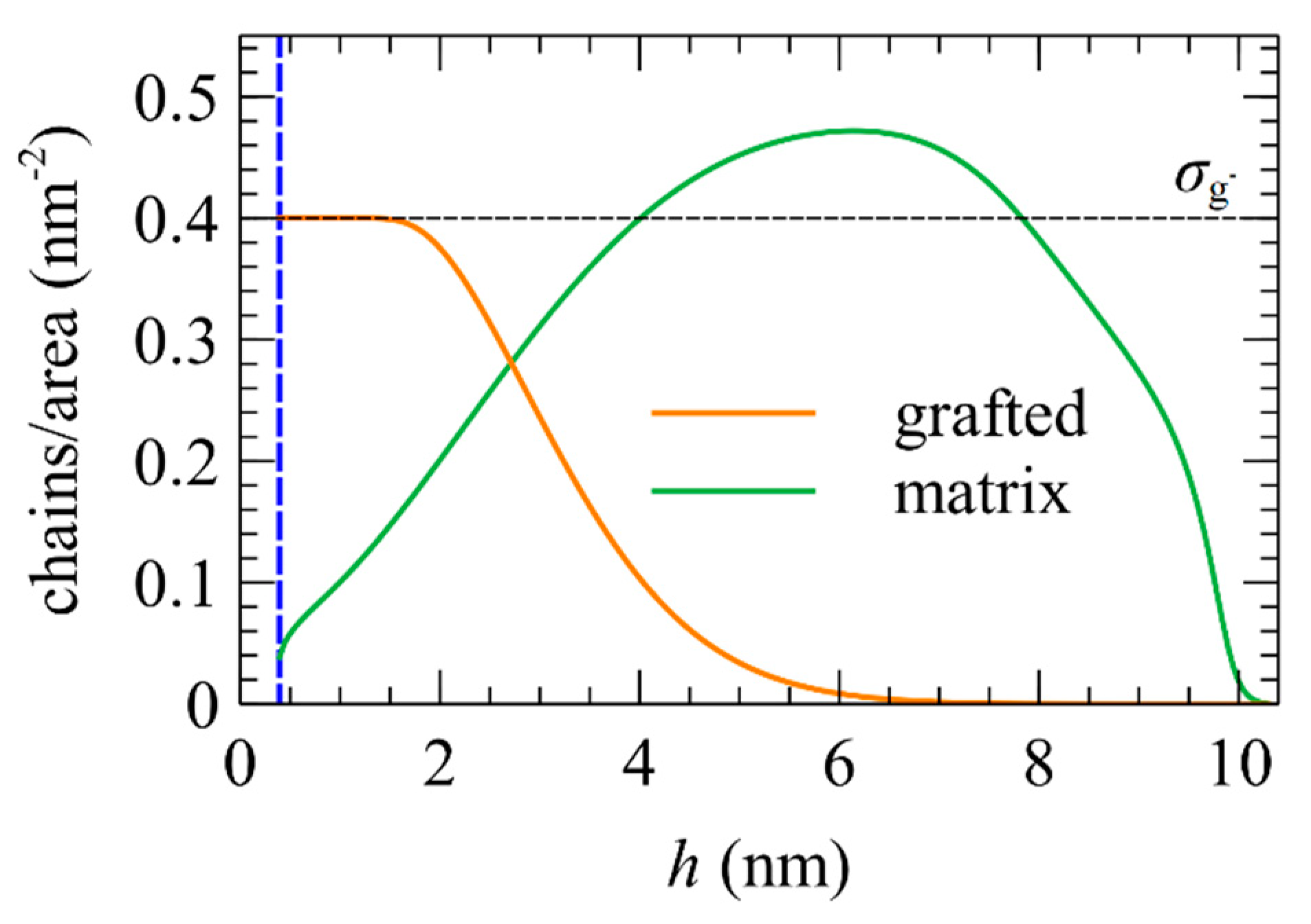
5.5. Chains/Area
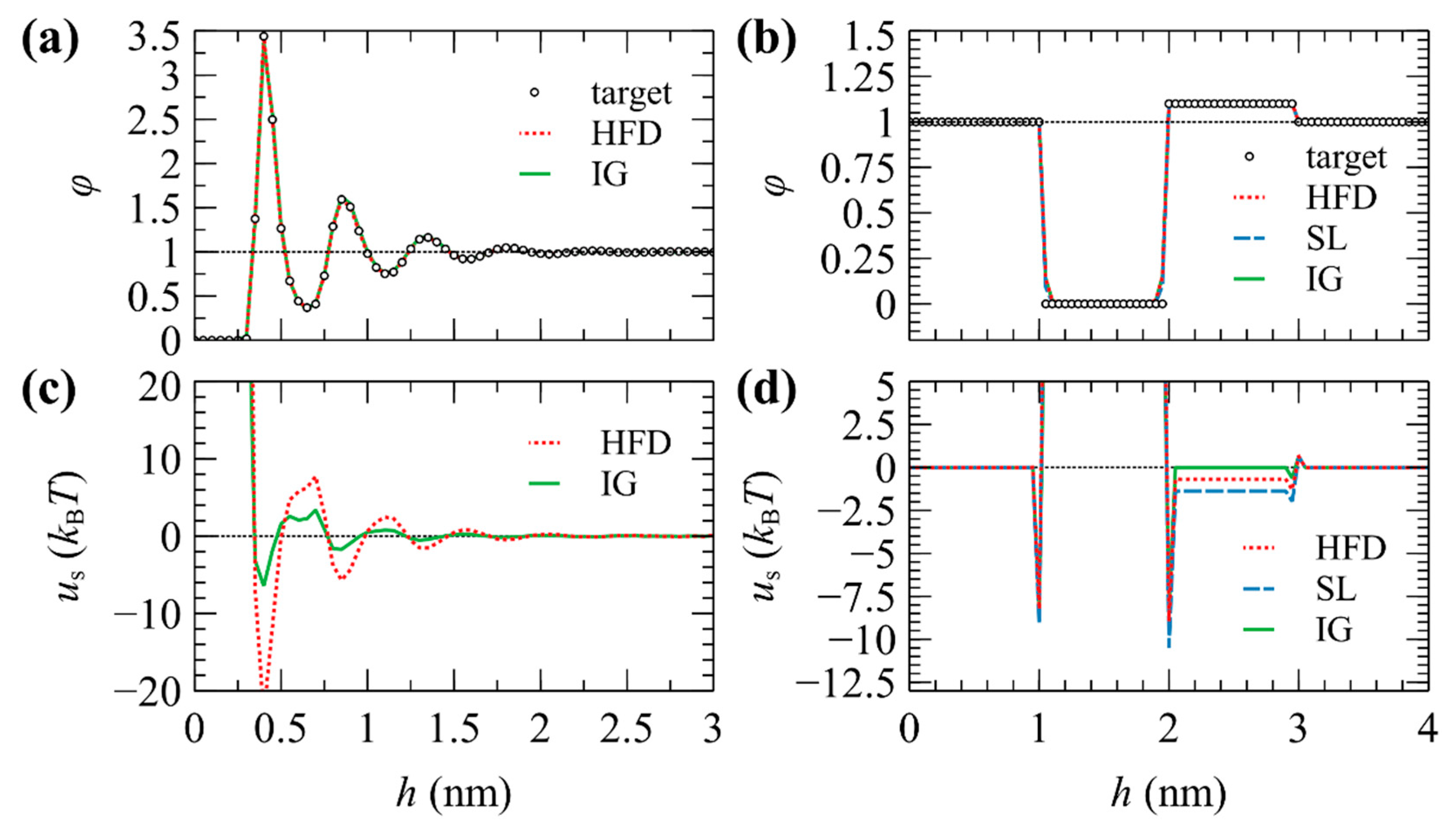
5.6. Free Energy Density Components
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, L.-T.; Xie, X.-M. Computational modeling and simulation of nanoparticle self-assembly in polymeric systems: Structures, properties and external field effects. Prog. Polym. Sci. 2013, 38, 369–405. [Google Scholar] [CrossRef]
- Zeng, Q.H.; Yu, A.B.; Lu, G.Q. Multiscale modeling and simulation of polymer nanocomposites. Prog. Polym. Sci. 2008, 33, 191–269. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Español, P.; Warren, P.B. Perspective: Dissipative particle dynamics. J. Chem. Phys. 2017, 146, 150901. [Google Scholar] [CrossRef]
- Bore, S.L.; Kolli, H.B.; De Nicola, A.; Byshkin, M.; Kawakatsu, T.; Milano, G.; Cascella, M. Hybrid particle-field molecular dynamics under constant pressure. J. Chem. Phys. 2020, 152. [Google Scholar] [CrossRef] [PubMed]
- Caputo, S.; Hristov, V.; De Nicola, A.; Herbst, H.; Pizzirusso, A.; Donati, G.; Munaò, G.; Albunia, A.R.; Milano, G. Efficient Hybrid Particle-Field Coarse-Grained Model of Polymer Filler Interactions: Multiscale Hierarchical Structure of Carbon Black Particles in Contact with Polyethylene. J. Chem. Theory Comput. 2021, 17, 1755–1770. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Vogiatzis, G.G.; Megariotis, G.; Tzoumanekas, C.; Theodorou, D.N. Multiscale Simulations of Graphite-Capped Polyethylene Melts: Brownian Dynamics/Kinetic Monte Carlo Compared to Atomistic Calculations and Experiment. Macromolecules 2019, 52, 7503–7523. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Lakkas, A.T.; Megariotis, G.; Theodorou, D.N. Mesoscopic Simulations of Free Surfaces of Molten Polyethylene: Brownian Dynamics/kinetic Monte Carlo Coupled with Square Gradient Theory and Compared to Atomistic Calculations and Experiment. Macromolecules 2018, 51, 9798–9815. [Google Scholar] [CrossRef]
- Lo Verso, F.; Egorov, S.A.; Milchev, A.; Binder, K. Spherical polymer brushes under good solvent conditions: Molecular dynamics results compared to density functional theory. J. Chem. Phys. 2010, 133, 184901. [Google Scholar] [CrossRef] [PubMed]
- Theodorou, D.N.; Vogiatzis, G.G.; Kritikos, G. Self-consistent-field study of adsorption and desorption kinetics of polyethylene melts on graphite and comparison with atomistic simulations. Macromolecules 2014, 47, 6964–6981. [Google Scholar] [CrossRef]
- Lakkas, A.T.; Sgouros, A.P.; Theodorou, D.N. Self-Consistent Field Theory Coupled with Square Gradient Theory of Free Surfaces of Molten Polymers and Compared to Atomistic Simulations and Experiment. Macromolecules 2019, 52, 5337–5356. [Google Scholar] [CrossRef]
- Müller, M. Phase diagram of a mixed polymer brush. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2002, 65, 1–4. [Google Scholar] [CrossRef]
- Trombly, D.M.; Ganesan, V. Curvature effects upon interactions of polymer-grafted nanoparticles in chemically identical polymer matrices. J. Chem. Phys. 2010, 133, 154904. [Google Scholar] [CrossRef] [PubMed]
- Müller, M.; Schmid, F. Incorporating fluctuations and dynamics in self-consistent field theories for polymer blends. Adv. Polym. Sci. 2005, 185, 1–58. [Google Scholar]
- Ouaknin, G.; Laachi, N.; Delaney, K.; Fredrickson, G.H.; Gibou, F. Self-consistent field theory simulations of polymers on arbitrary domains. J. Comput. Phys. 2016, 327, 168–185. [Google Scholar] [CrossRef]
- Arora, A.; Qin, J.; Morse, D.C.; Delaney, K.T.; Fredrickson, G.H.; Bates, F.S.; Dorfman, K.D. Broadly Accessible Self-Consistent Field Theory for Block Polymer Materials Discovery. Macromolecules 2016, 49, 4675–4690. [Google Scholar] [CrossRef]
- Rasmussen, K.; Kalosakas, G. Improved numerical algorithm for exploring block copolymer mesophases. J. Polym. Sci. Part B Polym. Phys. 2002, 40, 1777–1783. [Google Scholar] [CrossRef]
- Drolet, F.; Fredrickson, G.H. Combinatorial screening of complex block copolymer assembly with self-consistent field theory. Phys. Rev. Lett. 1999, 83, 4317–4320. [Google Scholar] [CrossRef]
- Drolet, F.; Fredrickson, G.H. Optimizing chain bridging in complex block copolymers. Macromolecules 2001, 34, 5317–5324. [Google Scholar] [CrossRef]
- Kim, J.U.; Matsen, M.W. Finite-stretching corrections to the Milner-Witten-Cates theory for polymer brushes. Eur. Phys. J. E 2007, 23, 135–144. [Google Scholar] [CrossRef]
- Vigil, D.L.; García-Cervera, C.J.; Delaney, K.T.; Fredrickson, G.H. Linear Scaling Self-Consistent Field Theory with Spectral Contour Accuracy. ACS Macro Lett. 2019, 8, 1402–1406. [Google Scholar] [CrossRef]
- Ackerman, D.M.; Delaney, K.; Fredrickson, G.H.; Ganapathysubramanian, B. A finite element approach to self-consistent field theory calculations of multiblock polymers. J. Comput. Phys. 2017, 331, 280–296. [Google Scholar] [CrossRef]
- Huttom, D.V. Fundamentals of Finite Element Analysis; McGraw Hill: New York, NY, USA, 2004; ISBN 0-07-112231-1. [Google Scholar]
- Smith, I.M.; Griffiths, D.V.; Margetts, L. Programming the Finite Element Method, 5th ed.; Wiley: West Sussex, UK, 2014; ISBN 9781119973348. [Google Scholar]
- Revelas, C.J.; Sgouros, A.P.; Lakkas, A.T.; Theodorou, D.N. A Three-Dimensional Finite Element Methodology for Addressing Heterogeneous Polymer Systems with Simulations Based on Self-Consistent Field Theory. In Proceedings of the International Conference of Computational Methods In Science and Engineering 2020 (ICCMSE 2020), Heraklion, Crete, Greece, 27 April–3 May 2020; p. 130002. [Google Scholar]
- Daoulas, K.C.; Müller, M. Exploring thermodynamic stability of the stalk fusion-intermediate with three-dimensional self-consistent field theory calculations. Soft Matter 2013, 9, 4097–4102. [Google Scholar] [CrossRef]
- Lakkas, A.T.; Sgouros, A.P.; Revelas, C.J.; Theodorou, D.N. Structure and Thermodynamics of Grafted Silica/Polystyrene Nanocomposites Investigated Through Self-Consistent Field Theory. Soft Matter 2021, 17, 4077–4097. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Revelas, C.J.; Lakkas, A.T.; Theodorou, D.N. Potential of Mean Force between Bare or Grafted Silica/Polystyrene Surfaces from Self-Consistent Field Theory. Polymers (Basel) 2021, 13, 1197. [Google Scholar] [CrossRef]
- Cheong, G.K.; Chawla, A.; Morse, D.C.; Dorfman, K.D. Open-source code for self-consistent field theory calculations of block polymer phase behavior on graphics processing units. Eur. Phys. J. E 2020, 43, 15. [Google Scholar] [CrossRef]
- Price-Whelan, A.M. SCF 1991. Available online: https://github.com/adrn/scf_fortran (accessed on 10 May 2021).
- Bilchak, C.R.; Buenning, E.; Asai, M.; Zhang, K.; Durning, C.J.; Kumar, S.K.; Huang, Y.; Benicewicz, B.C.; Gidley, D.W.; Cheng, S.; et al. Polymer-Grafted Nanoparticle Membranes with Controllable Free Volume. Macromolecules 2017, 50, 7111–7120. [Google Scholar] [CrossRef]
- Daoulas, K.C.; Theodorou, D.N.; Harmandaris, V.A.; Karayiannis, N.C.; Mavrantzas, V.G. Self-consistent-field study of compressible semiflexible melts adsorbed on a solid substrate and comparison with atomistic simulations. Macromolecules 2005, 38, 7134–7149. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Vogiatzis, G.G.; Kritikos, G.; Boziki, A.; Nikolakopoulou, A.; Liveris, D.; Theodorou, D.N. Molecular Simulations of Free and Graphite Capped Polyethylene Films: Estimation of the Interfacial Free Energies. Macromolecules 2017, 50, 8827–8844. [Google Scholar] [CrossRef]
- Theodorou, D.N. Variable-Density Model of Polymer Melt/Solid Interfaces: Structure, Adhesion Tension, and Surface Forces. Macromolecules 1989, 22, 4589–4597. [Google Scholar] [CrossRef]
- Vogiatzis, G.G.; Theodorou, D.N. Structure of polymer layers grafted to nanoparticles in silica-polystyrene nanocomposites. Macromolecules 2013, 46, 4670–4683. [Google Scholar] [CrossRef]
- Hamaker, H.C. The London—van der Waals attraction between spherical particles. Physica 1937, 4, 1058–1072. [Google Scholar] [CrossRef]
- Daoulas, K.C.; Harmandaris, V.A.; Mavrantzas, V.G. Detailed Atomistic Simulation of a Polymer/Solid Interface: Structure, Density and Conformation of a Thin Film of Polyethylene Melt Adsorbed on Graphite. Macromolecules 2005, 38, 5780–5795. [Google Scholar] [CrossRef]
- Magda, J.J.; Tirrell, M.; Davis, H.T. Molecular dynamics of narrow, liquid-filled pores. J. Chem. Phys. 1985, 83, 1888–1901. [Google Scholar] [CrossRef]
- Bilchak, C.R.; Jhalaria, M.; Huang, Y.; Abbas, Z.; Midya, J.; Benedetti, F.M.; Parisi, D.; Egger, W.; Dickmann, M.; Minelli, M.; et al. Tuning Selectivities in Gas Separation Membranes Based on Polymer-Grafted Nanoparticles. ACS Nano 2020, 14, 17174–17183. [Google Scholar] [CrossRef]
- Mansfield, K.F.; Theodorou, D.N. Atomistic Simulation of a Glassy Polymer/Graphite Interface. Macromolecules 1991, 24, 4295–4309. [Google Scholar] [CrossRef]
- Hong, K.M.; Noolandi, J. Conformational Entropy Effects in a Compressible Lattice Fluid Theory of Polymers. Macromolecules 1981, 14, 1229–1234. [Google Scholar] [CrossRef]
- Fredrickson, G.H. The Equilibrium Theory of Inhomogeneous Polymers; International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Theodorou, D.N. Polymers at Surfaces and Interfaces. Comput. Simul. Surf. Interfaces 2003, 329–419. [Google Scholar] [CrossRef]
- Higham, N.J. Accuracy and Stability of Numerical Algorithms; Society for Industrial and Applied Mathematics: University City, PA, USA, 2002; ISBN 978-0-89871-521-7. [Google Scholar]
- Datta, B.N. Numerical Linear Algebra and Applications, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010; ISBN 0898716853. [Google Scholar]
- Vogiatzis, G.G.; Voyiatzis, E.; Theodorou, D.N. Monte Carlo simulations of a coarse grained model for an athermal all-polystyrene nanocomposite system. Eur. Polym. J. 2011, 47, 699–712. [Google Scholar] [CrossRef]
- Helfand, E.; Tagami, Y. Theory of the interface between immiscible polymers. II. J. Chem. Phys. 1972, 56, 3592–3601. [Google Scholar] [CrossRef]
- Poser, C.I.; Sanchez, I.C. Surface tension theory of pure liquids and polymer melts. J. Colloid Interface Sci. 1979, 69, 539–548. [Google Scholar] [CrossRef]
- Lin, H.; Duan, Y.Y.; Min, Q. Gradient theory modeling of surface tension for pure fluids and binary mixtures. Fluid Phase Equilib. 2007, 254, 75–90. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C—The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 1992; ISBN 0521431085. [Google Scholar]
- Wu, D.T.; Fredrickson, G.H.; Carton, J.-P.; Ajdari, A.; Leibler, L. Distribution of chain ends at the surface of a polymer melt: Compensation effects and surface tension. J. Polym. Sci. Part B Polym. Phys. 1995, 33, 2373–2389. [Google Scholar] [CrossRef]
- Theodorou, D.N. Lattice Models for Bulk Polymers at Interfaces. Macromolecules 1988, 21, 1391–1400. [Google Scholar] [CrossRef]
- Chapman, W.G.; Gubbins, K.E.; Jackson, G.; Radosz, M. SAFT: Equation-of-state solution model for associating fluids. Fluid Phase Equilib. 1989, 52, 31–38. [Google Scholar] [CrossRef]
| State | Symbol(α) | Reduced SegmentDensity | Restricted Part. Function | DirichletNodes, qc(h, N) = 0 |
|---|---|---|---|---|
| free | f | |||
| adsorbed fully | ||||
| not adsorbed | ||||
| adsorbed | - | - | ||
| adsorbed partially | - | - | ||
| loops | - | |||
| tails outside the adsorbed region | - | - | ||
| tails inside the adsorbed region | - | - | ||
| bridges | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Revelas, C.J.; Sgouros, A.P.; Lakkas, A.T.; Theodorou, D.N. RuSseL: A Self-Consistent Field Theory Code for Inhomogeneous Polymer Interphases. Computation 2021, 9, 57. https://doi.org/10.3390/computation9050057
Revelas CJ, Sgouros AP, Lakkas AT, Theodorou DN. RuSseL: A Self-Consistent Field Theory Code for Inhomogeneous Polymer Interphases. Computation. 2021; 9(5):57. https://doi.org/10.3390/computation9050057
Chicago/Turabian StyleRevelas, Constantinos J., Aristotelis P. Sgouros, Apostolos T. Lakkas, and Doros N. Theodorou. 2021. "RuSseL: A Self-Consistent Field Theory Code for Inhomogeneous Polymer Interphases" Computation 9, no. 5: 57. https://doi.org/10.3390/computation9050057
APA StyleRevelas, C. J., Sgouros, A. P., Lakkas, A. T., & Theodorou, D. N. (2021). RuSseL: A Self-Consistent Field Theory Code for Inhomogeneous Polymer Interphases. Computation, 9(5), 57. https://doi.org/10.3390/computation9050057






