The Use of Fragility Curves in the Life-Cycle Assessment of Deteriorating Bridge Structures

Abstract

Within the context of structure deterioration studies, we propose a new numerical method based on the use of fragility curves. In particular, the present work aims to theoretically study the degradation of concrete bridge structures subjected to aggressive environments. A simple probabilistic method based on fragility curves is presented which allows the forecasting of the lifetime of the considered structural system and the best monitoring time. The method was applied to investigate the degradation of a concrete bridge used as a case study. A Monte Carlo numerical procedure was used to simulate the variation over time of the residual resistant section and the ultimate bending moment of the deck of the case study. Within this context, fragility curves are used as reliable indicators of possible monitoring scenarios. In comparison with other methods, the main advantage of the proposed approach is the small amount of computing time required to obtain rapid assessment of reliability and deterioration level of the considered structure.

1. Introduction

During their life spans, structures that are subjected to an aggressive environment can suffer deterioration of their component materials. Such damage may reduce the mechanical characteristics of the system and, with them, even its reliability. Due to high randomness, associated with the occurrence of critical attacks in the environment, it is suggested that the deterioration of structures and of structural materials is studied from a probabilistic point of view. Each probabilistic approach requires a series of reliable experimental data and a coherent and significant definition of the physical aspects of the phenomenon. It is known that managing both these aspects is not simple.

In the last decade, many scientific papers were published which aimed to better define uncertainties within the context of engineering problems and to select the most suitable approaches. As described by Ang [1], first of all it is necessary to understand if the uncertainty is random (associated with natural randomness) or epistemic (associated with imperfect knowledge) and then to take one of the most appropriate approaches ([1] provides a framework for modelling and treatment of uncertainties). In general, the treatment of uncertainties can be performed through a probabilistic modelling [2,3,4] or a fuzzy approach [5,6,7].

In probabilistic methods (more suitable for a type of random uncertainty), the forecast of future damage is often evaluated with static or dynamic structural analyses, linear or not, based on the application of Monte Carlo simulations of the behavior over time of structures and structural elements affected by a certain deterioration. The application of this technique aims to formulate a reliable forecast of the evolution of the damage thanks to the creation of a large samples that can be considered a statistical truth [8]. Methods of this type require the formulation of an adequate time-dependent deterioration law and require a significant amount of computational time.

In the approaches based on the fuzzy theory (more suitable for an epistemic uncertainty), the variables lose the dichotomous character present in Aristotle’s logic (true or false) that distinguishes the probabilistic approach; instead, variables become nuanced, on the basis of a membership function. Generally, this approach requires a less important computational time but an expert is required for an adequate construction of membership functions.

Moreover, the prediction of the structural deterioration is also approached by Bayesian inference. In this approach, the degree of confidence in the initial hypothesis increases with the increase in the observations obtained and used in improving the formulated hypothesis. The application of this methodology requires experience and once again a fair amount of computational time [9].

At last, another approach was used that exploits Markovian processes. Through this the prediction of damage evolution is described as the probability of transition through different performance states of the structure. The computational time of this methodology is not excessive, but requires qualified skills in model design and verification of results [10,11,12].

Some of these methods are used in combination with multilevel neural networks, able to learn if properly trained, and to provide different intervention strategies functional to different scenarios of occurrence. These tools require high computational skill and significant computation times [13].

A useful tool for overcoming the problems of the previously listed methods (typically the high calculation time consuming) is provided by the fragility curves. Fragility curves were initially introduced and developed in the seismic risk assessments of nuclear power plants [14,15]. Later, they were widely used in the seismic risk analysis of buildings, infrastructures or urban agglomerations; indeed, research in this field is still widespread at the present.

As an example, we can mention the use of fragility curves for the study of the seismic vulnerability of underground structures [16], subsea structures [17] or buildings. Using the fragility curves, Flora et al. [18] studied the improvement of the seismic vulnerability of an existing building when its structural behavior is modified through the placement of seismic isolation devices. Akhoondi and Behnamfar [19] study the seismic fragility curves of a steel structure taking into account the soil–structure interactions and the uncertainty of the geotechnical parameters. Ansaria et al. [20] studied the effect of the flexibility of the foundation elements on the seismic vulnerability curves of a reinforced concrete high-rise building.

As noted, most of the papers concern the seismic field; indeed, there are relatively few publications that try to use the fragility curves tool in other engineering fields. Rush et al.’s [21] study, through fragility curves, pointed out the vulnerability of steel columns in the presence of fire. Dunn et al. [22] used fragility curves to investigate the resilience of a public electricity transmission network in the event of failures due to windstorm hazards. Singha et al. [23] proposed an assessment method for the fragility curves of steel columns subjected to blast loads.

Regarding fragility curves, a more critical point of view is instead summarized in Grigoriu and Radu [24] which shows, by using a hypothetical seismic site, how the shapes of the seismic fragility curves are sensitive to the particular parameters used during their construction and to the dimensions of the sample used in the analysis.

Here, the proposed research aims to apply the general concept of fragility curves to assess the decay of structures subject to deterioration. In the seismic field, the fragility curves express the probability of overcoming damage levels as a function of the intensity of the earthquake. The authors want to generalize this definition by adapting it to the scope of building durability analyses. In this new context, the traumatic event for the structure is not the earthquake, but the natural deterioration of the structure, caused by the corrosion of the reinforcements.

In more detail, the fragility curve defines the probability of a system to overcome a certain damage threshold, $\overline{m}$, at a certain time $\overline{T}$. According to the specific damage process that is analyzed in turn, this threshold may correspond to the thickness of the lost surface material due to salt decay, the strain-rate induced by the creep behavior, or other significant parameters.

For some years, the authors have been working on the development of a methodology that is able to predict, in probabilistic terms, the evolution of deterioration in a structure even in the presence of a low sample size [25]. In planning maintenance strategies, the forecast of the time taken to reach a certain level of damage also becomes important. This prediction, which might help in choosing sustainable maintenance scenarios, can also be inferred from the fragility curves.

Therefore, the objectives that the authors intend to achieve with the proposed method are: the possible planning of sustainable monitoring scenarios, defined in number and time intervals, and the forecast of the time required to reach possible damage thresholds that are significant for the reliability of the entire structural system.

To show the flexibility of the proposed method and its limitations, the authors choose as a case study a reinforced concrete bridge built in the 1950s over the Corace River in Calabria (Southern Italy). In this paper, a section of the bridge deck was investigated. The bridge is a significant example of reinforced concrete construction both from static and sectional points of view, as it has structural elements of reduced thickness, which could represent a problem from the point of view of durability.

As far as we know, this is the first time that the method of fragility curves is used in predicting the degradation of reinforced concrete structures.

The authors wish to emphasize the methodological nature of this publication. The paper wishes to enlighten the use of fragility curves in the life-cycle assessment of the deteriorating bridge structures and the errors that are made in basing such curves on a few experimental data. Therefore, to test the proposed methodology, the authors use a method of simulation of deterioration over time, already validated in the literature [14,15,16,17,18,19,20,21,22,23,24,25,26]: the so-called fragility curves for the “statistical truth”.

The temporal deterioration of the bridge will be analyzed by the application of a Monte Carlo simulation, which involves the generation of a statistical sample of high sample size of the geometric and mechanical characteristics of the bridge moment by moment. From the data set thus obtained, random samples of limited size will be extracted which can accurately interpret the results of a monitoring campaign. The proposed methodology will be applied to these data in order to investigate possible temporal maintenance scenarios.

We remark that the main contribution of this paper is to provide a numerical approach which requires a small amount of computing time to achieve the objectives described above.

The paper is organized as follows. Section 2 illustrates the method of the fragility curves in predicting the service life of a structure and the construction of the same in both theoretical and experimental forms, reporting basic concepts and definitions. Section 3 presents the case study of the reinforced concrete bridge over the Corace River in Calabria. Section 4 covers the simulation of deterioration over the time addressed and the fragility curves are constructed as “statistical truth” and are introduced in the application of the fragility curves as indicators of possible monitoring scenarios and to forecast the achievement of a possible reliability limit. Section 5 reports concluding remarks.

2. Fragility Curves for Predicting Service Life

In this section, basic concepts and definitions are recalled for the reader’s convenience.

2.1. Stochastic Modelling of the Deterioration Process

The deterioration process of the structural system can be described through a parameter defined as the loss of performance reached by the system at that instant t*.

The high randomness associated with the occurrence of the deterioration of a structural system in the natural environment suggests considering the damage parameter assumed as a random variable (r.v.) and associating an appropriate probability distribution with it.

From this point of view, the deterioration process can be considered as a stochastic process in the chosen random variable.

The choice of the parameter, m, is indicative of the evolution of the degradation of the structural system and the choice of the distribution of probabilities are not easy choices [25,26,27]. Degradation usually depends on the presence of numerous contributing causes that are not easily reproducible in the laboratory and with numerical modelling. However, this deterioration causes changes in the resistance parameters such as the sectional area, the resisting moment, the maximum stress, the deformation, etc. These parameters can be verified using scheduled monitoring actions. Starting from data collected on similar structural typologies, it is possible to study the temporal evolution of these parameters and search for plausible probabilistic modelling.

The temporal variations of the chosen r.v, m, depend on the instant t* in which it is registered. Therefore, at any instant t*, it can be modelled with a probability density function (p.d.f.) which depends on the variable itself and on the instant t* (e.g., t* = 5, 15, …, years).

The choice of the probabilistic distribution suitable for modelling a given random variable must certainly be assessed both on the basis of classical statistical tests such as Chi square, Kolmogorov–Smirnov, SN* etc. [28,29], and on the physical interpretation of the studied phenomenon and on the characteristics of the distribution functions in the tails, which are the descriptors of the behavior of rare events and, therefore, not easy to detect experimentally [26,30,31,32]. This aspect can be studied by analyzing the behavior of the hazard rate function connected to the chosen distribution function (details are given in [26]):

$${\varphi }_m\left(M\right)dM=Pr\left\{M<m\le M+dM|m>M\right\} \forall t^{*},$$

(1)

where m is the damage parameter chosen and assumed as r.v. in probabilistic modelling, while M represents all the values that the r.v. can assume in the evolution of the process.

For the sake of completeness, we say that (1) is a conditional probability that describes the risk of an event greater than the one already recorded (m > M), even if for an infinitesimal quantity (m ≤ M + dM).

2.2. Structural Reliability Function vs. Fragility Curves

Reliability R(t) describes the performance of a system over time and is defined as the probability that the system will not fail within a certain time t [28]. There, the author extends this definition by assuming that $\overline{R}\left(t\right)$ is the probability that a given system will not exceed a given damage threshold $\overline{m}$ within the time t [26,31]. Therefore, the reliability can be quantified by a new r.v., $\overline{T}$, defined as the time required to reach or, to exceed, a certain damage threshold $\overline{m}$.

Therefore, the reliability function becomes:

$$\overline{R}\left(t\right)=Pr\left\{\overline{T}>t\right\}=1-F_{\overline{T}}\left(t\right),$$

(2)

where $F_{\overline{T}}\left(t\right)$ is the cumulative distribution function of the r.v. $\overline{T}$. The probability distribution $F_{\overline{T}}\left(t\right)$ is able to associate the probable time of occurrence $\overline{m}$ with each level of damage. Therefore, it has the value of a fragility curve in predicting the evolution over time of a certain parameter of structural deterioration [32,33].

Considering that the probability density function $f_{\overline{T}}\left(t\right)$ exists and using (2), the hazard rate function ${\varphi }_{\overline{T}}\left(t\right)$ can be defined as follows [28]:

$${\varphi }_{\overline{T}}\left(t\right)=\frac{Pr\left\{t<\overline{T}\le t+dt|\overline{T}>t\right\}}{dt}=\frac{f_{\overline{T}}\left(t\right)}{1-F_{\overline{T}}\left(t\right)}=\frac{f_{\overline{T}}\left(t\right)}{\overline{R}\left(t\right)},$$

(3)

The aforementioned function (3) describes the occurrence probability of rare events; in this case, it describes the probability that the passage of the threshold $\overline{m}$ occurs at the instant t + dt, immediately following today (“today” = instant $\overline{T}$) and if that has not happened, it will therefore be useful in choosing the probability distribution that best describes the theoretical fragility curves.

2.3. The Construction of the Experimental Fragility Curves

The construction of the fragility curves for each level of damage considered starts with the modelling, with the appropriate p.d.f. and at each instant t*, the chosen r.v.

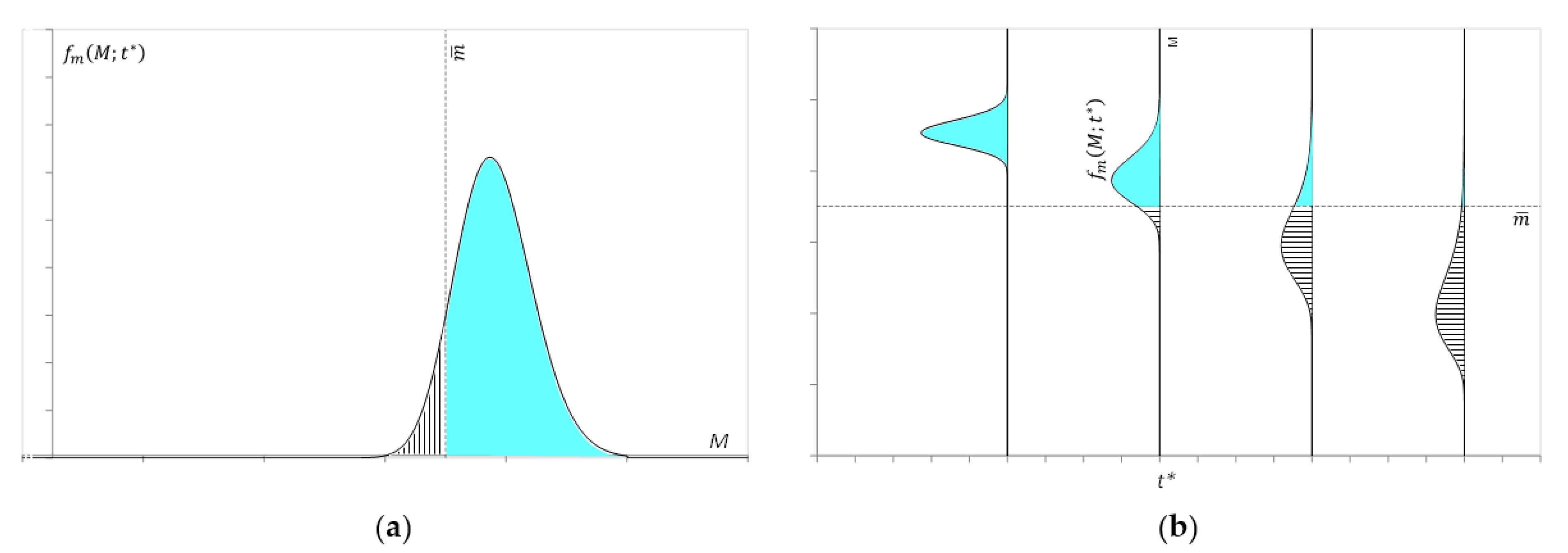
As already mentioned, the fragility curve defines the probability of a system to overcome a certain damage threshold, $\overline{m}$, at a certain time $\overline{T}$. Therefore, once the damage threshold $\overline{m}$ has been defined, the probability that it is reached in the instant t*, is described by the area underlying the p.d.f. at the left of the threshold. On the other hand, the probability of exceeding this threshold is described by the area underlying the p.d.f. at the right of the threshold itself (Figure 1a).

If the construction of reaching or crossing threshold for the chosen random variable is performed for each instant of monitoring and represented (as in Figure 1b), there is an immediate perception of how the construction of the fragility curve linked to the experimental evidence, or an experimental fragility curve $F_{\overline{T}}\left(t^{*}\right)$ is possible.

The area above the damage threshold $\overline{m}$ is easily calculated using the survival function,

$${\Im }_m\left(M, t^{*}\right)=Pr\left\{m>M\right\}=1-F_m\left(M, t^{*}\right),$$

(4)

where $F_m\left(M,t^{*}\right)$ is the cumulative probability distribution of m at each instant, t*. It describes the probability that the variable, m, and assumes values are greater than a certain value M—in our case, M =$\overline{m}$.

Moreover, the area below the threshold $\overline{m}$ is given by the cumulative distribution $F_m\left(M,t^{*}\right)=Pr\left\{m\le M\right\}$, which describes the probability that m can assume values not greater than M—in our case, M =$\overline{m}$.

The calculation of $F_m\left(M,t^{*}\right)$, by the calculation of its complementary ${\Im }_m\left(M,t^{*}\right)$, is possible through the numerical integration of the probability density function $f_m\left(M,t^{*}\right),$ respectively, in the intervals (−∞; $\overline{m}$] e ($\overline{m}$; +∞). In this way, the areas calculated on different thresholds $\overline{m}$ provide the experimental fragility curves, $F_{\overline{T}}\left(t^{*}\right)$, for each of the established damage thresholds. The integration of probability density can be carried out by commercial software of statistics; here, a FORTRAN code exploiting routines from IMSL Fortran Numerical Library in simple precision was used by the authors. In particular, for function minimization the Rosenbrock’s method routine provided therein was chosen.

If the r.v. investigated increases over time (loss of system performance), the fragility curves will be constructed using survival functions, ${\Im }_m\left(M,t^{*}\right)$. Conversely, if the r.v. investigated decreases over time (residual resistance capacity), the fragility curves will be constructed using the cumulative distribution function.

2.4. Theoretical Fragility Functions

The theoretical modelling of the experimental fragility curves also requires attention in the choice of probability distributions. Undoubtedly, the method of a good fitting with minimum square deviation is one of the ways to address this, but also, in this case, the solutions mentioned above do not guarantee a good interpretation of the physical phenomenon, especially regarding rare events. Once again, a further comprehension of what could be the evolution of the phenomenon investigated over time would be of greater value. The fragility curve describes the probability of exceeding a certain damage over time, damage that seems to increase when time is increasing (except for maintenance interventions). Therefore, if this damage has not yet occurred at that instant t*, it is very likely that it will occur in the immediate future and this probability increases with time. Therefore, in this case the probability distribution to be chosen will be a distribution at extreme values: a Gamma distribution or a Weibull distribution. Both these distributions have an increasing hazard rate function, respectively, tending to be an asymptotic value in the Gamma distribution and tending to an infinite value in the Weibull distribution.

Given that the more time that goes by, the more the probability of exceeding a certain threshold becomes pressing, the authors decided to model the experimental fragility curves with a Weibull distribution [26,30,33]. Although aware that this cannot be the only solution, above all they underline the need to always understand the phenomenon that is attempted to be modelled before proceeding with the choice of a possible distribution.

The Weibull distribution chosen here has the following form [26]:

$$F_{\overline{T}}\left(t\right)=1-\exp \left[-{\left(\rho t\right)}^{\alpha }\right],$$

(5)

where α and ρ are, respectively, the shape parameter and the scale parameter of the distribution.

3. Case Study

The methodology presented here is applied to the study of deterioration induced by aggressive environmental agents in a reinforced concrete bridge beam.

The beam to be studied is the section of the bridge deck on the Corace River (Calabria Region, South Italy) built in 1955 [34].

The work is one of the most daring Maillart typologies ever created by Adriano Galli. It is the first example of a vaulted concrete road bridge with a thin deck-stiffened arch to have been built in Southern Italy. It is over 170 m with two access viaducts formed by a deck with three sturdy continuous beams arranged on four supports and one mighty, yet slender, central arch of 80.7 m.

Figure 2 shows the dimensions of the bridge [35,36]; the arch span is 80.7 m.

Table 1. Distribution of the steel reinforcement in the beam, in the arch and in the columns (the upper, $A_s^{\prime }$, and downer, $A_s$, steel area is expressed in a number of steel bars per diameter—for instance, 21 bars of 28 mm of diameter: 21ø28).

Distribution of the Steel Reinforcement in the Structural Elements
Distribution at the top ${A^{\prime }}_s$ and at the bottom $A_s$ reinforcement along the beam
${A^{\prime }}_s$	21ø28	48ø28	42ø28	30ø28	24ø28	48ø28	48ø28	45ø28	33ø28
$A_s$	21ø28	30ø28	42ø28	24ø28	24ø28	21ø28	36ø28	27ø28	24ø28
Reinforcement along the arch bridge: 45 (on the top) + 45ø28 (on the bottom of the section)
Reinforcement along the columns: 3 × 8ø18

presents the distribution of steel reinforcement into different sections of the bridge.

Due to the landslide failures that occurred in 2010, the bridge is now constantly monitored by the Calabria Region. These data are not currently available. However, the bridge also shows a widespread deterioration of the structural elements due to aggressive environmental attacks.

The prediction of the residual useful life of an operational bridge implies knowledge of its level of degradation and its temporal evolution.

To set up a probabilistic prediction model of the evolution of deterioration, measures to quantify the degradation collected throughout the life of the structure are required. Extended and coordinated data collection campaigns are not always carried out regularly. The parameters measured in the monitoring actions are different and often aimed at investigating precise and nongeneralized aspects.

The most frequent survey parameters are the geometric survey of the system, the survey of surface degradation with a reduction in the sectional area, the survey of the crack pattern, and the survey of deformation.

Therefore, if the evaluation of the loss of performance regarding the cross section of a bridge is needed, significant parameters could be the detection of the residual resistant sectional steel area, A_s, of the reinforcement iron and the variation of the relative ultimate bending moment M_z.

To investigate the loss of performance over time in terms of residual resistant section steel area, the approach proposed in Section 2 proves to be sufficiently efficient and easy to apply. Unfortunately, due to the inability to directly access to the Calabria Region database and the desire to demonstrate the effectiveness of the proposed approach using the characteristics of a real bridge, it is necessary to resort to a simulation of the possible deterioration behavior of the bridge over the years through the application of a Monte Carlo simulation.

4. Simulation of Deterioration by Fragility Curves

In the following section, the approach introduced in Section 2 is applied to the case study presented in Section 3.

In this section, the deterioration suffered by the Section 5 of the beam (Figure 2b), in terms of residual resistant section and ultimate bending moment, is simulated here using a Monte Carlo numerical procedure, implemented by an appropriate probabilistic law of degradation [4,37], which allows one to simulate the variations over time of the two investigated parameters.

The parameters investigated are M_z and A_s and their variation over time will be assumed as random variables.

In particular, the M_z variable was assumed as the damage variable by the authors because the flexural verification of the deck (part of the structure on which the application is focused) is the most important safety verification. The value of M_z depends directly on the shape of the section and the amount of steel reinforcement present (A_s). The corrosion phenomenon, modifying the steel resistance, leads in time to a modification of the M_z value and of the structural safety.

To proceed with the simulation of monitoring actions at different time intervals, samples of reduced sizes will be randomly extracted from the simulated data and will be used in the construction of the fragility curves of predicting the time to reach or exceed a certain level of performance of the structure.

4.1. Simulation of Deterioration

The probabilistic evaluation of the reduction in resistant area over time can be studied as:

$$A_s^{\prime }\left(t\right)=A_{s0}^{\prime }\left[1-\delta \left(t\right)\right],$$

(6)

where $A_{s0}^{\prime }$ is the initial resistant area of the reinforcement bars, while δ = δ (t)∈[0;1] describes the time-dependent deterioration process using the law [38]:

$$\delta \left(t\right)=\{\begin{array}{c}{\omega }^{1-\rho }{\tau }^{\rho } , \tau \le \omega \\ 1-{\left(1-\omega \right)}^{1-\rho }{\left(1-\tau \right)}^{\rho } , \omega <\tau <1 \\ 1 , \tau \ge 1\end{array},$$

(7)

where τ = t/T_f, is the normalized instant of time at which the threshold δ = 1 is reached—that is, the collapse time—ρ is the parameter that describes the rate of deterioration, and ω describes the bending point of the curve constituting law (7). The parameters ρ and ω and the probable collapse time suffer from uncertainty and it is advisable to assume them as random variables [37].

Table 2. Damage law parameters and their probability distributions governed by the means and standard deviations reported here.

Parameter	Mean Value μ	Stand. dev. σ	Distribution
ρ	1.80	0.40	Lognormal
ω	0.55	0.20	Lognormal
Tf	130	22	Weibull

reports the average values and standard deviations assumed for the variables involved. These values have been taken from the literature [2,38].

The assumed damage variable assumed is, as mentioned, the ultimate bending moment, M_z, of the Section 5 in Figure 2. In the calculation of the M_z the design yield stress of the projected steel maintained constant f_sd (Class FeB38k, f_sd = 326 MPa). As initial ultimate bending moment is assumed:

$$M_{z0}=A_{s0}^{\prime }·f_{sd}·\left(d-0.4X_0\right),$$

(8)

where $A_{s0}^{\prime }$ is the initial resistant area of the tensile reinforcement, $f_{sd}$ the yield point under stress of the projected steel, d is the height of the resistant section, and X₀ is the position of the neutral axis of the undeteriorated section.

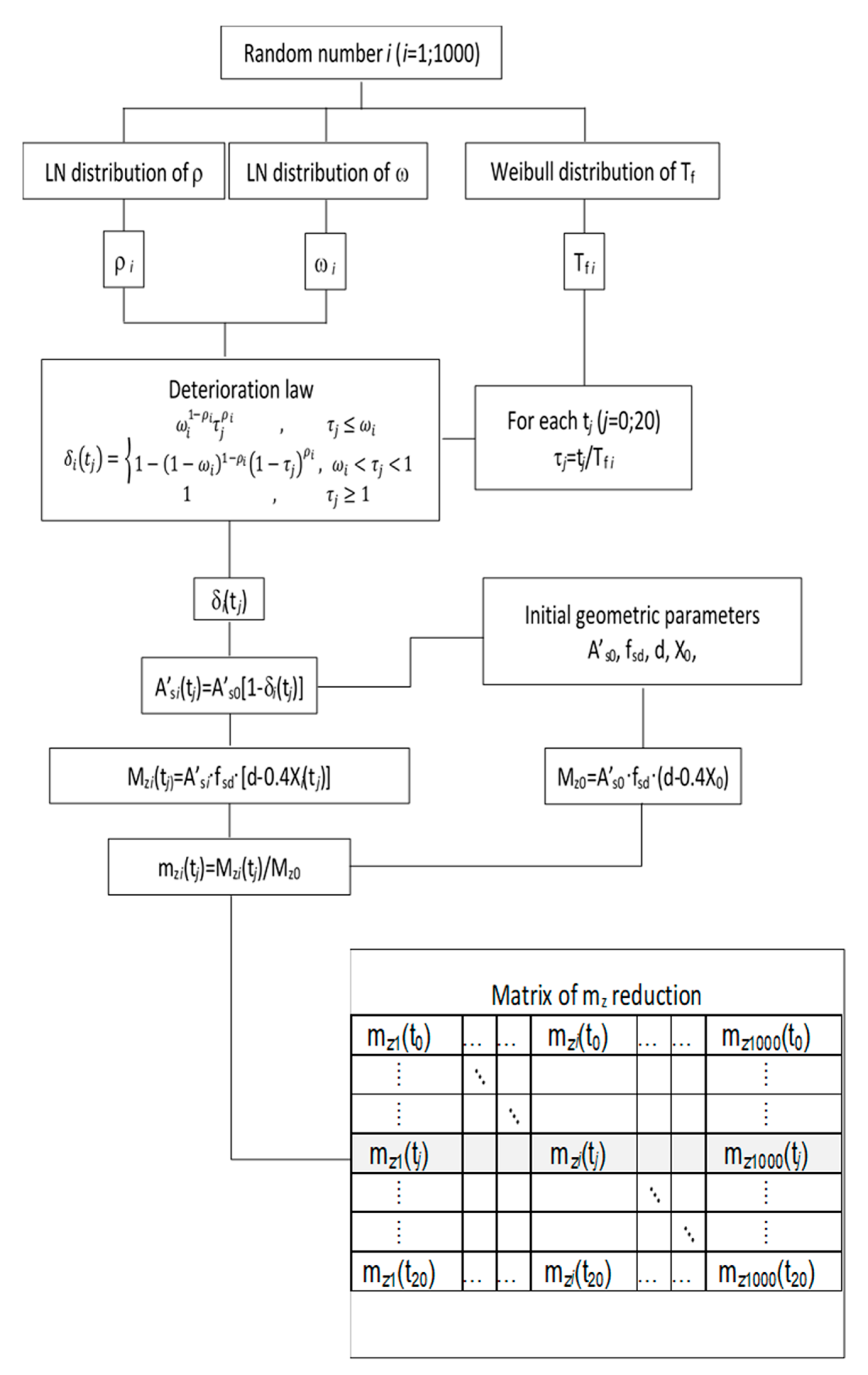
With the random extraction of 1000 numbers and the application of Equations (6) and (7), it is possible to construct the simulation of the ultimate bending moment behavior over time (Figure 3).

$$M_z\left(t\right)=A_s^{\prime }\left(t\right)·f_{sd}·\left[d-0.4X\left(t\right)\right],$$

(9)

where $A_s^{\prime }\left(t\right)$ is the residual resistant area at instant t, given by the Equation (6), $f_{sd}$ is the design yield stress for steel, d is the height of the resistant section, which remains unchanged, and X(t) is the position of the neutral axis at the instant t.

For a better understanding of the results, we proceed with the normalization of M_z(t):

$$m_z\left(t\right)=M_z\left(t\right)/\left(M_{z0}\right),$$

(10)

where $M_z\left(t\right)$ is the ultimate bending moment at the instant t, and M_z0 is the initial ultimate bending moment.

If an investigation of 100 years of life in 5-year steps were to be carried out, it would create a matrix of 21,000 samples of m_z (Figure 3). In the flow chart of Figure 3, t₀ corresponds to the initial state of the bridge; therefore, t₀ = 0 years, while t₂₀ corresponds to the state of the bridge after 100 years of service life—therefore, t₂₀ = 100 years.

From the proposed procedure, for each instant of time t_j, 1000 samples are generated with different levels of deterioration, leading to different m_zi values (Figure 3). Therefore, for each t_j a distribution of possible values of m_zi can be built. This distribution will be characterized by a mean and a standard deviation. Using these mean and standard deviation of the m_z it is possible to construct, for each instant t (row of the matrix in Figure 3), the probability distribution of the occurrence for different levels of deterioration. 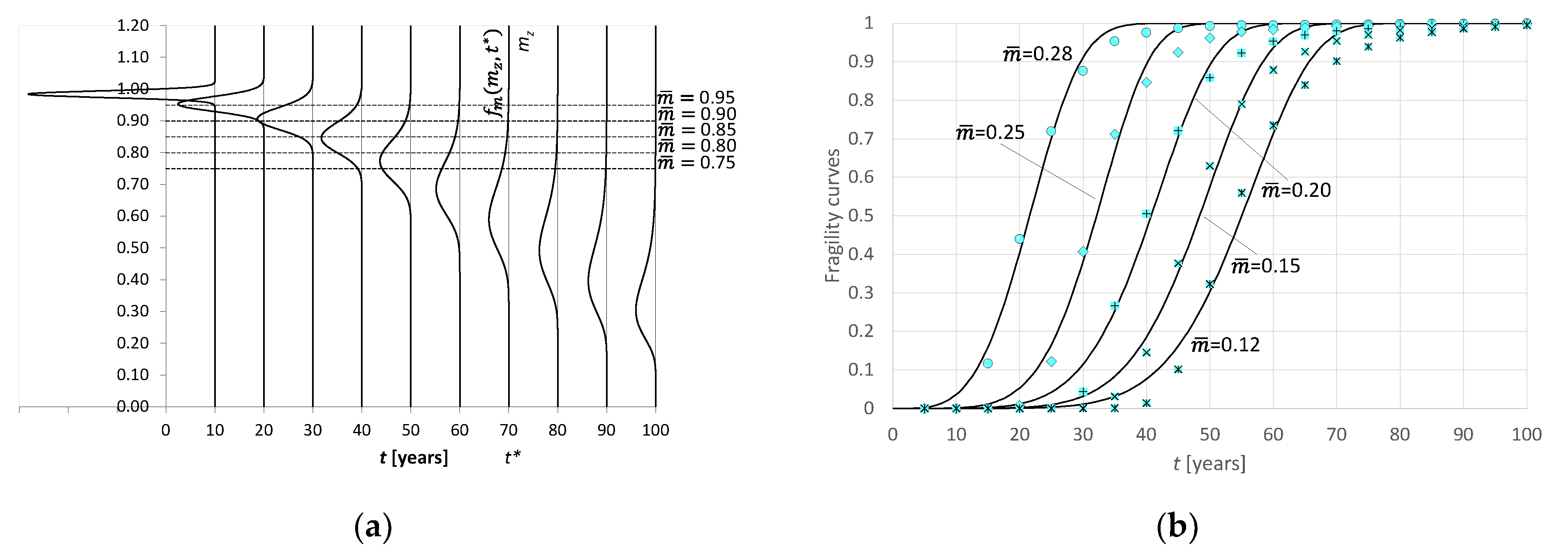Figure 4a shows the probability of collapse obtained by the simulation for certain levels of structural demand. They are built over 100 years of service life of the bridge and in steps of 5 years.

Instead, using the mean and standard deviation of the values present in the columns of the matrix in Figure 3, it is possible to define, in probabilistic form, the possible trend from the performance loss over time. Figure 4b shows the temporal variations for the parameter m_z.

These curves allow us to evaluate the reliability over time of the bridge cross section with respect to a specific performance demand or, on the contrary, to evaluate the remaining service time before reaching potentially dangerous performance thresholds if no maintenance is carried out.

4.2. Construction of Fragility Curves as “Statistical Truth”

The data obtained from the previous simulation will now be taken as experimental data. They will be used to simulate the data collected in monitoring actions throughout the life-cycle of the structure, characterized by different measurement intervals.

The first step is the construction of fragility curves that can represent a statistical truth as they are built based on a sample size. They are to be used as a comparison to quantify the degree of error that could be made when acting with a limited number of monitoring actions.

All the samples constructed with the simulation previously introduced, for each row of the matrix of Figure 3 and for each instant of life t*, allowed us to construct the density of probability of occurrence $f_m\left(m_z;t^{*}\right)$ (Figure 5a) and the relative fragility curves both experimental and theoretical, $F_{\overline{T}}^m\left(t\right)$ (Figure 5b).

In Figure 4a, it can be seen that the variation of the considered parameter is descending; therefore, for the construction of the fragility curves the considered areas are the areas underlying the probability density functions and below the considered threshold, defined by the cumulative distribution $F_m\left(m_z;t^{*}\right)$ (dashed areas in Figure 1b).

The damage thresholds chosen for the construction of the fragility curves are:

• $\overline{m}$ = 0.95; $\overline{m}$= 0.90; $\overline{m}$= 0.85; $\overline{m}$= 0.80; $\overline{m}$= 0.75.

The choice is based on the achievement of possible potentially dangerous states of damage, which correspond to potential performance losses of a percentage between 5% and 25%.

Consequently, the constructed curves describe the probability o the studied system not being able to guarantee, at any instant t, an ultimate bending moment greater than or equal to $\overline{m}$.

4.3. Fragility Curves as Indicators of Possible Monitoring Scenarios

Once constructed the statistical truth, it may now be interesting to verify the error that could be made if the fragility curves were constructed on the basis of monitoring performed at different intervals of time and with a limited sampling of investigations.

The situation described is very frequent in professional practice. In this context, 1000 experimental measurements (samples) are rarely available; therefore, the intent is to verify the validity of the proposed procedure if a small number of samples is available.

To simulate these actions, 10 random samples were extracted from the probability distributions of m_z (Figure 4a) referring to certain instants of life of the structure (e.g., 10, 15, 20, 25, 30, and 40 years) as many detections of the degradation operated in a hypothetical monitoring action. To better grasp the epistemic and random uncertainties that may be inherent in the experimental data, the extracted samples were further altered with a random procedure (addition of a percentage of random error subtraction). The choice of 10 samples was based on the authors’ previous experience in this field. In the following, we will call this analysis experimental in the sense that it simulates experimental data. The influence of the number of samples on the accuracy of the results is evident in Figure 6a. The further one moves away from the initial state (t₀), the greater the dispersion of the statistical data becomes, highlighting the need to plan a more extensive sampling as the service life of the bridge increases.

The influence of the width and frequency of the investigation intervals on the accuracy of the results will be discussed below.

Following the procedure illustrated in Section 2.2, for each scenario and for each instant of monitoring, the 10 detections were modelled with a Lognormal (LN) distribution and the respective fragility curves were calculated (Figure 6).

Three plausible monitoring scenarios equivalent to ten key points for each monitoring and a few monitoring actions throughout the service life of the structure were chosen to verify the extent of the forecast error in which it could occur:

scenario 1: 10, 15, 20, 25, 30, 40, 50 years;

scenario 2: 10, 20, 30, 40, 50 years;

scenario 3: 10, 20, 50 years.

From the data modelling of the first 50 years of the life of the structure, it was seen that the significant thresholds for m_z could correspond to:

• $\overline{m}$ = 0.95 (95% of m_z0); $\overline{m}$ = 0.85 (85% of m_z0); $\overline{m}$ = 0.75 (75% of m_z0).

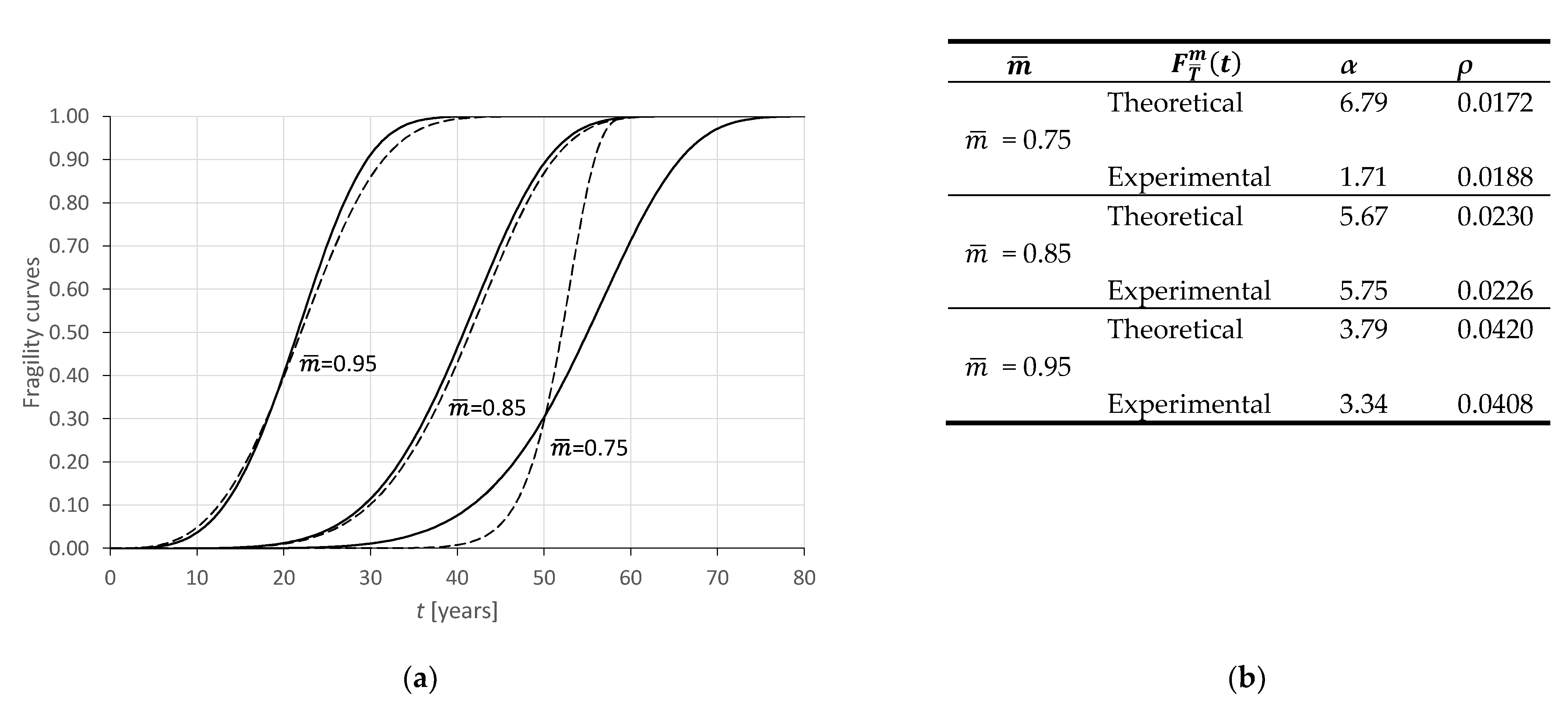
Scenario 1

Figure 7 shows the comparison between the fragility curves built on the basis of seven monitoring instants and 10 samples analyzed for each instant and the fragility curves built on a large sample size, which we have called “statistical truth” (solid lines).

Figure 7 shows a certain difficulty in detecting the highest loss of performance, in fact the biggest error is found in the modelling of the normalized residual ultimate bending moment which is lower than $\overline{m}$ = 0.75, even if after 50 years of life it could still be predicted as being safe. This might happen because, for the scenarios created, the probability of reaching high performance loss thresholds is still too low; therefore, modelling is affected by this fact.

Scenario 2

In scenario 2, the number of monitoring actions is reduced to five and regular intervals of 10 years are expected.

Figure 8 shows the comparison between the fragility curves built for scenario 2 and the statistical truth curves (solid line).

The situation is not very different from the previous one. The forecasting ability loses a bit of accuracy for the threshold $\overline{m}$ = 0.75 but remains good. However, the error made is always high for the threshold $\overline{m}$ = 0.75. The consideration that can be made is the same as for scenario 1: the probability of exceeding 50 years is still very low and the modelling is somewhat compromised.

Scenario 3

For scenario 3, the number of monitoring actions is reduced to three with regular 20-year intervals.

In this case, a greater forecast error is detected and unfortunately, it does not predict safety for the three thresholds. Therefore, few monitoring actions are not able to provide a correct prediction about the probability of reaching the investigated damage threshold.

In conclusion, the forecasts for reaching the threshold $\overline{m}$ = 0.95 are better captured by frequent monitoring in the first construction phase (Figure 7a and Figure 8a). For the intermediate threshold $\overline{m}$ = 0.85, monitoring at regular intervals, even if infrequent, can reach a good degree of prediction (Figure 7a and Figure 8a), whereas it is somewhat compromised for monitoring at too long intervals (Figure 9a). For the lowest residual capacity threshold, $\overline{m}$ = 0.75, the monitoring should be extended beyond the limit of 50 years of useful life.

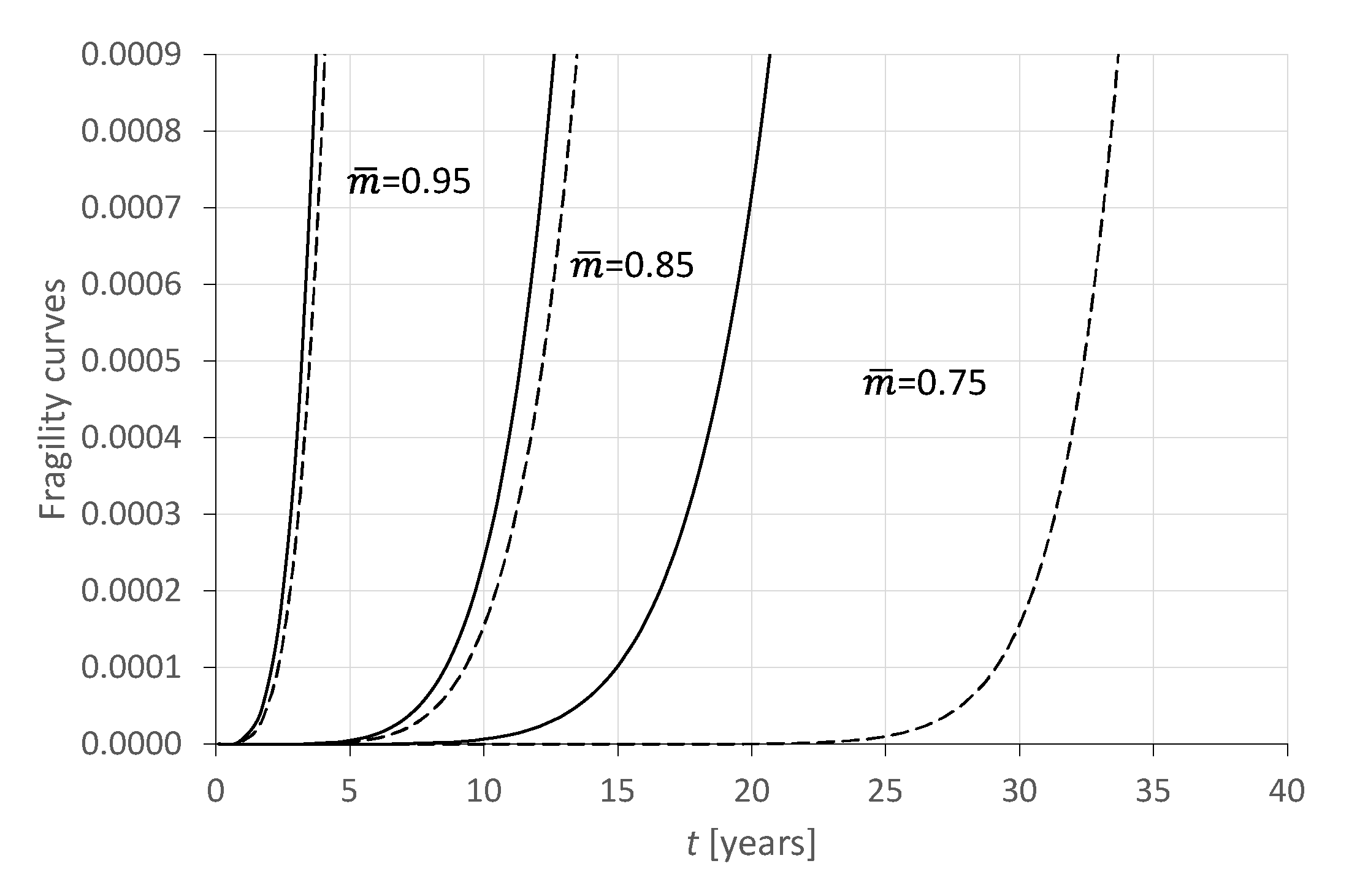
From Figure 10, it is clear that the error made in certain cases can be important for example for the threshold $\overline{m}$ = 0.75; in fact, the critical threshold would be reached at 33.67 years with a probability equal to 9 × 10⁻⁴. However, the statistical truth would say that at 33.67 years the probability of reaching the 0.75 threshold increases to 0.024. This is definitely not to be overlooked. To consider any uncertainties, a time interval could be established within which it is better to schedule maintenance in relative safety.

At each maintenance intervention, it will be appropriate to update the fragility curves with the insertion of data relating to postintervention monitoring, to improve the forecast of future damage.

5. Concluding Remarks

Infrastructure monitoring surveys can easily detect the reduction in the resistant section of the reinforcement bars of a deck beam and, consequently, the ultimate bending moment. By collecting a certain number of damage surveys for each monitoring moment, it is possible to construct experimental and theoretical fragility curves capable of describing the possible evolution of deterioration over time.

The main contribution of this work is to show how to construct these curves from a rather small amount of data, showing a rather interesting application flexibility. Indeed, this allows the presented method to be easily used on municipal and territorial scales in order to obtain a rapid assessment of the reliability and deterioration level of the considered structure.

The obtained results enlighten as to how the quality of the results is sensitive to subjective choices that cannot be circumvented—for example, the choice of damage thresholds or the sample size.

The computed fragility curves are able to predict the evolution times of the degradation; if the curves in their tails are analyzed (ex.: from 0.00 to 9 × 10⁻⁴), they are able to give indications on the possible achievement of this threshold of damage (Figure 10), albeit with a very small probability, but this is not to be excluded.

So, it seems possible to plan maintenance scenarios whenever the probability of occurrence reaches a value of 9 × 10⁻⁴ with awareness of the possible level of damage achieved.

Remarkably, even though the choice of damage thresholds is a critical point of this application, investigating multiple thresholds does not entail an expensive computational calculation. This is a further significant advantage of the presented approach.

Future developments of this research will be aimed at the application of the fragility curves in the study of road infrastructures on which it is possible to access the diagnostic monitoring data, the planning of possible maintenance scenarios programmed on the basis of the results obtained from the fragility curves, the upgrade of the curves themselves based on data obtained from maintenance, and verification of new damage forecasts.