Revisiting the Homogenized Lattice Boltzmann Method with Applications on Particulate Flows

Abstract

The simulation of surface resolved particles is a valuable tool to gain more insights in the behaviour of particulate flows in engineering processes. In this work the homogenized lattice Boltzmann method as one approach for such direct numerical simulations is revisited and validated for different scenarios. Those include a 3D case of a settling sphere for various Reynolds numbers. On the basis of this dynamic case, different algorithms for the calculation of the momentum exchange between fluid and particle are evaluated along with different forcing schemes. The result is an updated version of the method, which is in good agreement with the benchmark values based on simulations and experiments. The method is then applied for the investigation of the tubular pinch effect discovered by Segré and Silberberg and the simulation of hindered settling. For the latter, the computational domain is equipped with periodic boundaries for both fluid and particles. The results are compared to the model by Richardson and Zaki and are found to be in good agreement. As no explicit contact treatment is applied, this leads to the assumption of sufficient momentum transfer between particles via the surrounding fluid. The implementations are based on the open-source C++ lattice Boltzmann library OpenLB.

1. Introduction

The simulation of particulate flows finds application in many fields as it permits a detailed examination of an engineering process. It allows access to data on particle behaviour, for which experimental measuring is complex or costly. It was already applied for the simulation of solid separation processes by Viduka et al. [1], testing different pulsation profiles of a jigging device, or by Li et al. [2] regarding the separation of soybeans from mustard seeds. The work presented here is the validation and improvement of a method for direct numerical simulation, also depicting the particle’s shape. The industrial relevance of this topic has been shown, e.g., by Champion et al. [3] who showed that particle shape significantly influences the performance of drug carriers. A discussion on the industrial relevance of particle shape for products and processes is also given by Davies [4], who references, e.g., the relevance for the production of rubber, as also stated by Scotti et al. [5].

On the most coarse level, particles can be depicted as a continuum by considering distributions with Euler–Euler approaches utilising an advection–diffusion equation [6,7,8]. Approaches which treat each particle as separate entity yield more details. With the discrete element method (DEM), e.g., separation processes in a cyclone can be studied [9] considering the particles as solid spheres. Furthermore, adsorption processes in a static mixer [10] or packing characteristics of powder [11] are of interest. The DEM can be used together with various approaches and models for the simulation and representation of the fluid. The coupling of DEM particles with a model for a non-Newtonian turbulent fluid is for example relevant in the simulation of anaerobic digestion [12]. A review of applications for DEM simulations is given by Zhu et al. [13].

For more sophisticated studies, hydrodynamic forces on a particle and its shape can be resolved by direct numerical simulations (DNS) [14]. This enables, e.g., the calculation of drag correlations [15]. Focusing on the shape, the investigation of the interaction between particles and a rough surface is possible [16]. At this point, however, proper collision treatment becomes important. For the absence of a significant influence of a fluid, the framework Grains3D [17,18] has been presented to investigate arbitrarily shaped convex particles under the influence of gravity and contact forces applying the Gilbert–Johnson–Keerthi algorithm for contact detection and distance calculation. The framework has later been extended to concave shapes by representing them as glued convex shapes [19]. Considering particles submersed in fluid, a simple approach is the one of glued spheres [20] to approximate various particle shapes and get more information on the distribution of acting forces. For this approximation, however, the accuracy is limited as the required number of spheres increases drastically for better approximations of a shape. To circumvent this problem, the object can be described by several Lagrange points on the surface, at which the hydrodynamic forces are calculated. This points can be independent of the underlying grid, which represents the fluid. This allows for a high accuracy in depiction of the shape, but requires frequent interpolation between fluid and particle points. This common approach is called immersed boundary method (IBM) [21]. One of its advantages is that it can be coupled with various approaches to solve the fluid system like the finite element method, the finite volume method or the lattice Boltzmann method (LBM) [22,23].

The coupled IBM–LBM has been frequently applied for the investigation of fluid structure interaction problems [24]. While many studies of, e.g., vortex induced vibrations [22,25] or the flow around a torus by Wu and Shu [26] only consider simpler geometries with analytical representations, mappings for more complex polygons exist, as discussed by Owen et al. [27]. Nevertheless, more complex structures can be simulated as well as described by Beny and Latt [28], who simulated multiple propellers on a GPU system. In IBM–LBM, it is possible to also consider simple strings as shown by Tian et al [22] who simulated filaments in a flow. A comparative study of IBM approaches was performed by Kang and Hassan [29], who investigated the flow past a cylinder and decaying Taylor–Green vortices.

The homogenized lattice Boltzmann method (HLBM) used in this work, in turn, has very few restrictions regarding the shape, since a voxel representation of almost any object can be chosen for simulations, as shown in [30]. Very thin objects, however, remain problematic, as they may not be captured by the lattice resolution. The main difference between IBM and HLBM is the way the objects are represented. The former employs Lagrangian points, which allows thin structures but requires interpolations and the creation of a distribution of those points on the surface of the object. The latter directly uses points on the fluid grid. The correct depiction of a structure, in this case, mainly depends on the grid resolution.

The LBM proved to be easy to parallelize due to the fact that most calculations are carried out in a strictly local collision step. This has been investigated for the use on computing clusters with GPU systems [31] as well as mixed CPU–GPU systems [32]. For LBM, additional approaches for the simulation of arbitrarily shaped particles are available, which are specific to their method. The most common one is the partially saturated cells method (PSM), in its original version proposed by Noble and Torczynski [33]. It depicts the object on the fluid grid by assigning a linear combination of a no-slip condition and bulk flow to a grid cell depending on its distance to the actual physical particle boundary. This is possible as LBM operates on a mesoscopic level considering the fluid by distributions of fluid-particles in a phase space. There are several aspects to this approach if moving objects are considered, e.g., the refilling of cells that were previously covered by a particle or the chosen no-slip condition. This has been investigated by Peng et al. [34].

Another topic is the way the hydrodynamic force is calculated. The stress integration method, e.g., described in [35,36], is also applicable for other simulation approaches and not specific to LBM but proved to be inefficient [37,38]. An alternative is the momentum exchange algorithm (MEA) [39,40], which calculates differences in the momentum via the mentioned particle distributions in the phase space. For this method, various formulations and improvements have been proposed [41,42,43,44] and are subject to current investigations [34].

In this study three applications are presented. For the first case of a settling sphere, the results are validated against ten Cate et al. [45], who performed simulations of a single sphere for different Reynolds numbers and compared the data to particle imaging velocimetry experiments. In addition, the results are compared to various drag correlations discussed in Section 2.1.

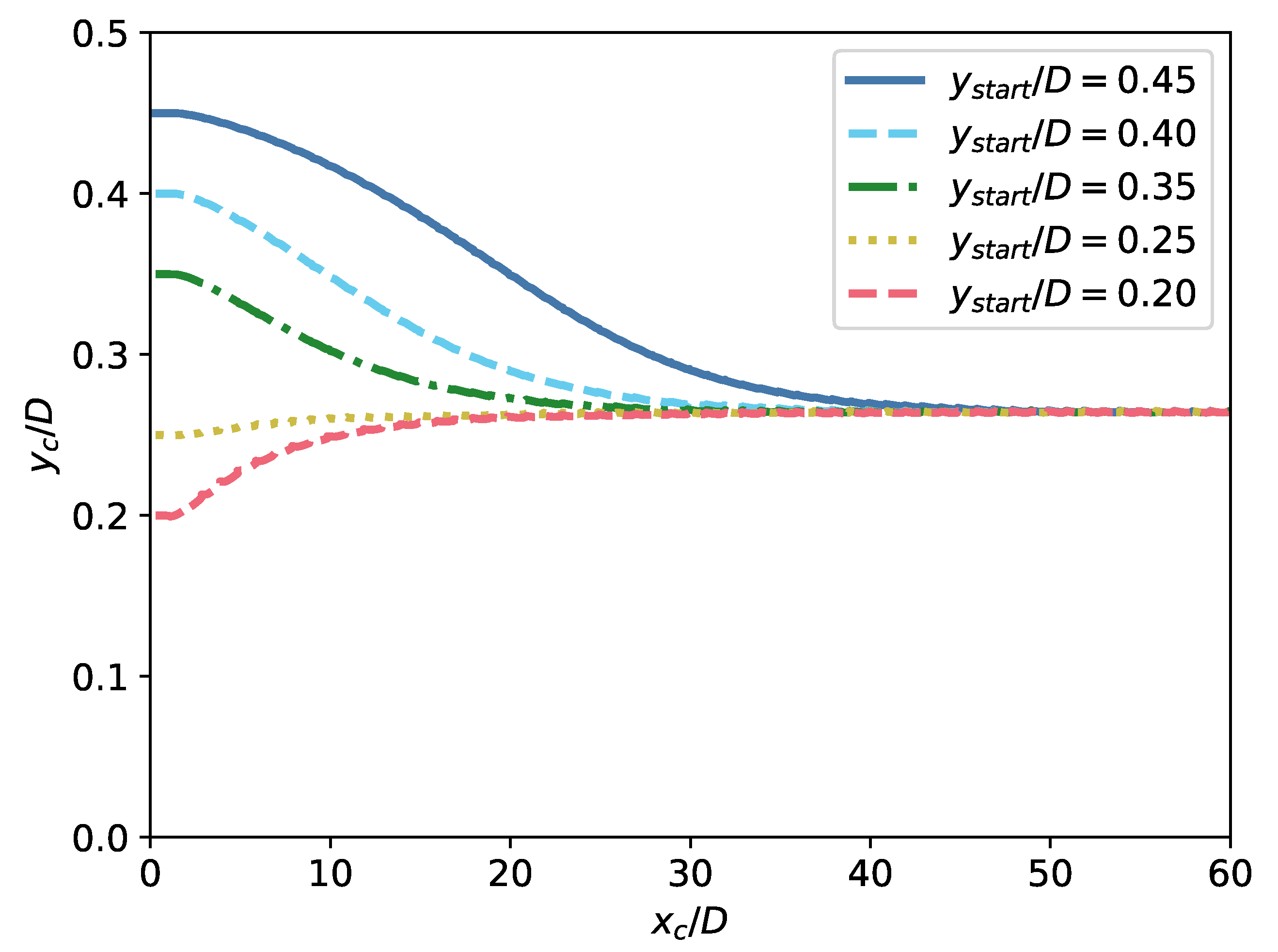
The second case simulates the tubular pinch effect first described by Segré and Silberberg [46]. They found that a neutrally buoyant particle in a tube flow equilibrates at a position between the tube’s center and its wall and that the results for single particles can be extended to mixtures by linear combination [47]. Later, Tachibana et al. [48] found that the equilibrium position depends on the ratio of sphere diameter to tube diameter, which should be larger than $0.2$ for the effect to be clearly visible. Karnis et al. [49] studied further the influence of the Reynolds number and the distance between two spheres on this effect.

The case of hindered settling is also relevant in many applications of process engineering as usually collectives of particles are processed. This is reflected in many studies simulating this case [50,51,52,53]. The results are usually compared to an empirical correlation found by Richardson and Zaki [54]. However, more correlations exist as discussed in Section 2.2. The results in this study are compared to different correlations to give a better overview.

In this work, the HLBM proposed by Krause et al. [30,55] is applied. Contrary to other approaches for moving objects, HLBM does not represent objects by a sharp no-slip boundary but rather with interior fluid utilising a forcing scheme and a transition region to mimic such a condition. This is a similarity to the IBM and leads to the need for further research as existing MEA approaches are developed for no-slip boundaries in the first place. Therefore, a novel momentum loss algorithm (MLA) is tested in this study. The semi-locality (depending on the chosen approach for the calculation of hydrodynamic forces) of the HLBM allows for an easy and efficient implementation on parallel systems without the need of costly interpolations. On the other hand, no refilling of cells is required as in PSM approaches. Besides the new MLA the HLBM is revisited and for the first time evaluated for different forcing schemes and methods for the calculation of hydrodynamic forces. To the knowledge of the authors such a comparative study for HLBM has not been performed before. This finally leads to a new improved scheme, which is validated for the simple case of a settling sphere but also tested for the application in hindered settling simulations and the tubular pinch effect. The results are compared to common experimentally determined correlations and reference simulations. This shows the range of applicability of the presented method, e.g., regarding the Reynolds number. Such tests are currently not found in literature for HLBM, however, this information is of interest when choosing a proper simulation approach depending on an application. Therefore, additionally different cases are examined for the first time with HLBM, which is important as, e.g., the tubular pinch effect can’t be reproduced by all approaches for DNS particle simulations as stated by Li et al. [35] and Peng et al. [34]. Additionally, considering the case of hindered settling the investigation of particle interactions, first mentioned by Krause et al [55], is continued, which was not found in other publications. To the knowledge of the authors, the investigations and findings for HLBM presented in this work have not been shown before.

The remainder of this paper is organized as follows: in Section 2 the physical background and correlations found in the literature are discussed. Then, in Section 3 the methods used for the simulations are discussed along with various forcing and MEA schemes to be tested. Finally, in Section 4 the results of the numerical investigation are presented and the conclusion is drawn in Section 5. All simulations presented are performed with the open-source lattice Boltzmann C++ framework OpenLB [56].

2. Modelling

This study focuses on two component systems of rigid particles submersed in a water-like fluid. The latter is described by the incompressible Navier–Stokes equations, given by

$$\begin{array}{cccc}\hfill \frac{\partial u_{\mathrm{f}}}{\partial t}+(u_{\mathrm{f}}·\nabla )u_{\mathrm{f}}-\nu \Delta u_{\mathrm{f}}+\frac{1}{{\rho }_{\mathrm{f}}}\nabla p& =F_{\mathrm{f}}\hfill & \hfill & \mathrm{in}\Omega \times I,\hfill \\ \hfill \nabla ·u_{\mathrm{f}}& =0\hfill & \hfill & \mathrm{in}\Omega \times I.\hfill \end{array}$$

(1)

The equations are defined on a spatial domain $\Omega \in {\mathbb{R}}^d$ of dimension $d\in 2,3$ and a time interval $I\subseteq \mathbb{R}$. The fluid velocity is denoted by $u_{\mathrm{f}}:\Omega \times I\to {\mathbb{R}}^d$, while $p:\Omega \times I\to \mathbb{R}$ describes the pressure, ${\rho }_{\mathrm{f}}\in {\mathbb{R}}_{>0}$ the fluid’s density and $\nu \in {\mathbb{R}}_{>0}$ its kinematic viscosity. $F_{\mathrm{f}}:\Omega \times I\to {\mathbb{R}}^d$ represents the total of external forces acting on the fluid.

The dynamics of the second component, the rigid particles, are governed by the equations based on Newton’s second law of motion

$$m_{\mathrm{p}}\frac{\partial u_{\mathrm{p}}}{\partial t}=F_{\mathrm{p}}\mathrm{and}{J}_{\mathrm{p}}\frac{\partial {\omega }_{\mathrm{p}}}{\partial t}=T_{\mathrm{p}}.$$

(2)

With the particle mass $m_{\mathrm{p}}\in {\mathbb{R}}_{>0}$, the particle velocity $u_{\mathrm{p}}:\Omega \times I\to {\mathbb{R}}^d$ and the force acting on the particle $F_{\mathrm{p}}:\Omega \times I\to {\mathbb{R}}^d$, the trajectory of motion can be calculated. The rotational behaviour is modelled analogously with the moment of inertia $J_{\mathrm{p}}\in {\mathbb{R}}^{\widehat{d}}$, the angular velocity ${\omega }_{\mathrm{p}}:\Omega \times I\to {\mathbb{R}}^{\widehat{d}}$ and the torque $T_{\mathrm{p}}:\Omega \times I\to {\mathbb{R}}^{\widehat{d}}$. Here $\widehat{d}=1$ for $d=2$ and $\widehat{d}=3$ for $d=3$.

In this study, only the gravitational and buoyancy forces are considered as external forces. They are given by $F^{\mathrm{G}}=(0,0,m_{\mathrm{p}}g)$ and $F^{\mathrm{B}}=(0,0,-m_{\mathrm{p}}\frac{{\rho }_{\mathrm{f}}}{{\rho }_{\mathrm{p}}}g)$ for $d=3$ ($F^{\mathrm{G}}=(0,m_{\mathrm{p}}g)$ and $F^{\mathrm{B}}=(0,-m_{\mathrm{p}}\frac{{\rho }_{\mathrm{f}}}{{\rho }_{\mathrm{p}}}g)$ for $d=2$) for a gravitational acceleration of g. This means, forces regarding particle-particle and particle-wall contact are neglected in this study and momentum between particles is only transferred via the fluid. As most cases consider only single particles with no relevant wall contact this is reasonable. The only exception is the investigation of hindered settling in Section 4.3. Here the system is discretized with a decent resolution to allow for sufficient momentum transfer via the fluid. Along with the hydrodynamic force $F^{\mathrm{H}}:\Omega \times I\to {\mathbb{R}}^d$ accounting for the momentum transfer between fluid and particles, the combined forces are given by

$$F_{\mathrm{f}}=F^{\mathrm{H}},F_{\mathrm{p}}=F^{\mathrm{G}}-F^{\mathrm{B}}-F^{\mathrm{H}}\mathrm{and}{T}_{\mathrm{p}}=r\times \left(-F^{\mathrm{H}}\right),$$

(3)

for a vector $r\in {\mathbb{R}}^d$ denoting the distance to the center of mass of a particle.

2.1. Drag Force

While in this study a DNS approach is chosen, for methods considering the particles as single points the hydrodynamic force has to be modelled. This is done via a drag force, accounting for the resistance an object experiences when moving relative to a surrounding fluid. It is defined by

$$F^{\mathrm{D}}=\frac{1}{2}{\rho }_{\mathrm{f}}{(u_{\mathrm{p}}-u_{\mathrm{f}})}^2{C}_{D}A,$$

(4)

with $A\in {\mathbb{R}}_{>0}$ being the area of the projection of the object in flow direction. While the determination of the drag coefficient $C_D\in \mathbb{R}$ for various shapes is subject to current research [57,58], for spheres many correlations depending on the Reynolds number $\mathrm{Re}$ have been given. The latter is defined as

$$\mathrm{Re}=\frac{d_{\mathrm{p}}\parallel u_{\mathrm{p}}\parallel }{\nu },$$

(5)

for the cases considered in this work, with a particle’s diameter $d_{\mathrm{p}}\in {\mathbb{R}}_{>0}$. For small Reynolds numbers the drag coefficient is described by Stokes’ law [59]

$$C_D=\frac{24}{\mathrm{Re}},\mathrm{for}\mathrm{Re}<1.$$

(6)

While in the Newton regime between $\mathrm{Re}={10}^3$ and $\mathrm{Re}={10}^5$ the coefficient is defined by $C_D=0.44$, many correlations exist for the transition region of Reynolds numbers between 1 and ${10}^3$. Notable here is among others the contribution by Abraham [60], who took the boundary layer into account for a theoretical derivation, leading to

$$C_D={\left(0.5407+\sqrt{\frac{24}{\mathrm{Re}}}\right)}^2,\mathrm{for}0<\mathrm{Re}<5000.$$

(7)

Schiller and Naumann [61] used an empirical approach to obtain the commonly used approximation of

$$C_D=\frac{24}{\mathrm{Re}}\left(1+0.15{\mathrm{Re}}^{0.687}\right),\mathrm{for}\mathrm{Re}<800$$

(8)

for the drag coefficient. As many more correlations can be found, the authors refer to Dey et al. [62] for a comprehensive overview.

2.2. Hindered Settling

The above mentioned drag correlations consider the case of free settling, more precisely the settling of a single sphere in an infinitely extended medium. In practical applications, collectives of particles are more common, which leads to the case of hindered settling caused by interactions between particles. The empirical correlations developed in many past studies proved to be sensible approaches in modeling such behaviour.

The oldest recapitulated here is the one by Steinour [63], who investigated spheres consisting of tapioca and glass, for a solid volume fraction $\varphi$ of up to $49.8\%$. The experimental conditions correspond to $\mathrm{Re}=0.0025$ and $\mathrm{Re}=0.0026$, leading to

$$u_{\mathrm{Steinour}}\left(\varphi \right)=u_{\mathrm{S}}{(1-\varphi )}^2{e}^{-4.19\varphi }.$$

(9)

The hindered settling velocity is here expressed relative to the terminal settling velocity according to Stokes’ $u_{\mathrm{S}}$, obtained by inserting Equation (6) in Equation (4).

Another correlation was found by Oliver [64]. In the experiments with Kallodoc particles, Reynolds numbers up to $0.39$ were reached with solid volume fractions up to $35\%$. The results are reflected in the formula for the hindered settling velocity given by

$$u_{\mathrm{O}}\left(\varphi \right)=u_{\mathrm{S}}\left(1-0.75{\varphi }^{\frac{1}{3}}\right)(1-2.15\varphi ).$$

(10)

One of the most commonly used expressions was found in investigations performed by Richardson and Zaki, who approached the topic from both, an analytical [54] and an experimental [65] perspective. Their formulation was subject to many adaptions regarding accuracy, convenience and extension of applicability [66,67,68,69]. In the original form it is given by $u_{\mathrm{RZ}}\left(\varphi \right)=u_{\mathrm{S}}{(1-\varphi )}^n$, with

$$n=\left\{\begin{array}{cc}4.65\hfill & \mathrm{for}\mathrm{Re}<0.2\hfill \\ 4.35{\mathrm{Re}}^{-0.03}\hfill & \mathrm{for}0.2<\mathrm{Re}<1\hfill \\ 4.45{\mathrm{Re}}^{-0.1}\hfill & \mathrm{for}1<\mathrm{Re}<500\hfill \\ 2.39\hfill & \mathrm{for}500<\mathrm{Re}\hfill \end{array}\right..$$

(11)

In a more comprehensive study taking also the results of other authors into account along with their findings, Barnea and Mizrahi [70] concluded with the general correlation

$$u_{\mathrm{BM}}\left(\varphi \right)=u_{\mathrm{S}}\frac{1-\varphi }{(1+{\varphi }^{\frac{1}{3}})e^{\frac{5\varphi }{3(1-\varphi )}}},$$

(12)

which is independent of the Reynolds number. While this is the finding for the creeping flow regime ($\mathrm{Re}\ll 1$), Barnea and Mizrahi suggest the application of drag correlations beyond Stokes’ law. Therefore in contrast to other publications, for higher Re the hindered settling velocity is not based on $u_{\mathrm{S}}$ anymore, but on a terminal settling velocity determined, e.g., by Equation (8).

3. Methods

For the simulations, the lattice Boltzmann method was applied, which operates on a uniform cubical grid ${\Omega }_{\mathrm{h}}$ approximating the computational domain. This structure is, together with the discrete phase space, spanned by the d spatial dimensions and a discrete set of q velocities $c_i\in {\mathbb{R}}^d,i=0,\cdots ,q-1$, denoted as lattice. The latter is usually labeled as DdQq. Choosing commonly used sets, the simulations in this study were performed on a D2Q9 and a D3Q19 lattice. As usual, the computations were conducted in lattice units meaning all values were scaled such that the grid spacing and time step size became $\delta x^{\mathrm{L}}=1$ and $\delta t^{\mathrm{L}}=1$, respectively. The superscript ${}^{\mathrm{L}}$ indicates that a value is given in lattice units. For reasons of readability, all values in this section were assumed to be in lattice units if not stated otherwise omitting the superscript.

The propagation of particle distributions $f_i:{\Omega }_{\mathrm{h}}\times I_{\mathrm{h}}\to \mathbb{R},i=0,\cdots ,q-1$, for a discretized time interval $I_{\mathrm{h}}$, on the given lattice is described by the lattice Boltzmann equation. Together with the Bhatnagar—Gross—Krook (BGK) collision operator [71] it reads

$$f_i(x+c_i,t+1)-f_i(x,t)=-\frac{1}{\tau }\left(f_i(x,t)-f_i^{\mathrm{eq}}(\rho ,u)\right),\mathrm{for}x\in {\Omega }_{\mathrm{h}},t\in I_{\mathrm{h}},i=0,\cdots ,q-1.$$

(13)

The lattice relaxation time $\tau$ is related to the lattice kinematic viscosity by

$$\nu =c_{\mathrm{s}}^2\left(\tau -\frac{1}{2}\right).$$

(14)

Beside a streaming of particle distributions, Equation (13) describes the relaxation of a system towards an equilibrium state given by the discrete Maxwell–Boltzmann distribution

$$f_i^{\mathrm{eq}}(\rho ,u)=w_i\rho \left(1+\frac{c_i·u}{c_{\mathrm{s}}^2}+\frac{{\left(c_i·u\right)}^2}{2c_{\mathrm{s}}^4}+\frac{u^2}{2c_{\mathrm{s}}^2}\right),\mathrm{for}i=0,\cdots ,q-1.$$

(15)

Here, $w_i$ are weights originating from a Gauss–Hermite quadrature rule and $c_{\mathrm{s}}=\frac{1}{\sqrt{3}}$ is the lattice speed of sound, valid for both lattice configurations used in this work. The density and velocity on a grid point can be calculated by moments of the discrete distributions

$$\rho (x,t)=\sum _{i=0}^{q-1}{f}_i(x,t)\mathrm{and}u(x,t)=\frac{1}{\rho }\sum _{i=0}^{q-1}{c}_i{f}_i(x,t),\mathrm{for}x\in {\Omega }_{\mathrm{h}},t\in I_{\mathrm{h}},$$

(16)

respectively. Furthermore, the pressure p is related to the density $\rho$ in LBM by $p(x,t)=\rho (x,t)c_{\mathrm{s}}^2$. In the rest of this section, the arguments for density and velocity are omitted for better comprehensibility. For a more comprehensive overview on this simulation approach, the authors refer to [23].

3.1. Homogenized Lattice Boltzmann Method

The DNS simulations in this study were performed utilizing the HLBM, which was first published by Krause et al. [55] and was extended to 3D by Trunk et al. [30]. The extensions of the method to the standard LBM with BGK collision could be divided into three parts. Namely, the representation of an object on the lattice, the forcing scheme applied to the fluid to account for the particles’ presence and a method to calculate the exchanged momentum between an object and fluid for the calculation of forces acting on the object. From this point, the trajectory of a particle is calculated according to Equation (2) in combination with a velocity-Verlet algorithm [72,73].

Object Representation. The depiction of arbitrary shapes within the HLBM is described in detail by Trunk et al. [30]. Here, only a brief overview is given. From a voxel representation of the object, which did not necessarily have the same spatial resolution as the lattice, parameters like the moment of inertia and the mass were calculated. For a smooth transition between fluid and particle domain, a Gaussian filter was applied. If an analytical representation of the shape was given, a smooth transition could also be defined utilizing trigonometric functions as described by Krause et al. [55]. This led to a mapping function $d_{\mathrm{B}}:\Omega \times I\to [0,1]$, which took on the value of 0 in the fluid domain and 1 in the area covered by the object. In the transition region it yielded values in between. Along with the current position of the object $x_{\mathrm{p}}\in \Omega$ this defined a domain $B\left(t\right)=\{x\in \Omega :d_{\mathrm{B}}(x,t)\ne 0\}$ which was covered by the body. To account for the presence of particles, the velocity used in the equilibrium distribution Equation (15) was replaced by the convex combination

$$\tilde{u}(x,t)=u(x,t)+d_{\mathrm{B}}(x,t)\left(u_{\mathrm{p}}(x,t)-u(x,t)\right)\mathrm{for}x\in B\left(t\right),t\in I_{\mathrm{h}}.$$

(17)

The velocity difference $\Delta u=\tilde{u}-u$ could be used in forcing schemes as stated in the next Section.

Forcing Schemes. As the effect on the fluid is given via a velocity difference, in previous publications a forcing scheme according to Shan and Chen [74] has been chosen, which only modifies the velocity inserted in the Maxwell–Boltzmann distribution. In this study, several forcing schemes (proposed by Shan and Chen [74], Guo et al. [75] and Kupershtokh et al. [76]) were considered (see Section 3.2) and then tested in Section 4.1.

Momentum Exchange. Various methods to calculate the exchanged momentum are given in Section 3.3 and are applied in Section 4.1. They were evaluated regarding the accuracy of the velocity profile of a falling sphere. In previous publications [30,55] an adapted version of the momentum exchange according to Ladd [39,40] was used.

3.2. Forcing Schemes

To incorporate a force in LBM, the definition of the velocity handed to the Maxwell–Boltzmann distribution, from now on labeled $u^{\mathrm{eq}}$, was modified and/or a source term $S_i$ was added to the right hand side of Equation (13). In all cases, the fluid velocity given in Equation (16) was redefined in the presence of a force $F$ to

$$u=\frac{1}{\rho }\sum _{i=0}^{q-1}{c}_i{f}_i(x,t)+\frac{F\delta t}{2\rho },\mathrm{for}x\in {\Omega }_{\mathrm{h}},t\in I_{\mathrm{h}}.$$

(18)

For a more comprehensive discussion on forcing schemes the authors again refer to Krüger et al. [23], however, the three forcing schemes used in this study are briefly summarized here.

The approach of Shan and Chen [74] only modifies the equilibrium velocity to

$$u^{\mathrm{eq}}=\frac{1}{\rho }\sum _{i=0}^{q-1}{c}_i{f}_i(x,t)+\tau \frac{F}{\rho },\mathrm{for}x\in {\Omega }_{\mathrm{h}},t\in I_{\mathrm{h}}.$$

(19)

This scheme originates from methods for multi-component and multi-phase flows, but is also applicable to single-component systems. It is frequently used due to its simplicity and performance advantage, however, a dependency of the results on $\tau$ is found, e.g., by Huang et al. [77] examining various forcing schemes for multi-phase LBM. Along with this scheme, a velocity shift method is proposed by Shan and Chen [74], which states $F=\frac{\rho }{\tau }\Delta u$. Guo et al. [75] proposed a scheme modifying both the velocity and the source term to

$$u^{\mathrm{eq}}=\frac{1}{\rho }\sum _{i=0}^{q-1}{c}_i{f}_i(x,t)+\frac{F\delta t}{2\rho },\mathrm{for}x\in {\Omega }_{\mathrm{h}},t\in I_{\mathrm{h}},$$

(20)

$$S_i(x,t)=\left(1-\frac{\delta t}{2\tau }\right)w_i\left(\frac{c_i-u}{c_{\mathrm{s}}^2}+\frac{\left(c_i·u\right)c_i}{c_{\mathrm{s}}^4}\right)·F,\mathrm{for}x\in {\Omega }_{\mathrm{h}},t\in I_{\mathrm{h}}.$$

(21)

At last, the exact difference method (EDM) by Kupershtokh et al. [76] only introduces a source term $S_i(x,t)=f_i^{\mathrm{eq}}(\rho ,u+\Delta u)-f_i^{\mathrm{eq}}(\rho ,u)$ to the system. The velocity difference $\Delta u$ it is based upon is calculated by $\Delta u=F\delta t/\rho$, since $\delta t=\delta x=1$ in lattice units as stated before. In this approach the velocity $u$ remains just as defined in Equation (16).

3.3. Methods for Momentum Exchange

In this study, different schemes for the momentum exchange between fluid and particle are also discussed. The first is an adaptation of the MEA by Ladd [39,40] which has been applied in [30,55]. As shown in [37,38], it can be written as

$$F^{\mathrm{H}}\left(t\right)=\sum _{x\in B\left(t\right)}\sum _{i=1}^{q-1}{c}_i\left(f_i(x+c_i,t)+f_{\overline{i}}(x,t)\right),\mathrm{for}t\in I_{\mathrm{h}}.$$

(22)

Here $f_{\overline{i}}$ is defined as distribution function according to the velocity $c_{\overline{i}}$, which is opposite to $c_i$, i.e., $c_{\overline{i}}=-c_i$. Various Improvements have been suggested [41,78], as this approach fails, e.g., in the simulation of the tubular pinch effect described by Segré and Silberberg [46,47], as stated by Peng et al. [34]. In their study, they compared different MEA approaches and tested them along with other aspects of moving boundary implementations. One of the most common approaches is the one by Wen et al. [42]

$$F^{\mathrm{H}}\left(t\right)=\sum _{x\in B\left(t\right)}\sum _{i=1}^{q-1}\left(c_i-u_{\mathrm{p}}\right)f_i(x+c_i,t)+\left(c_i+u_{\mathrm{p}}\right)f_{\overline{i}}(x,t),\mathrm{for}t\in I_{\mathrm{h}}.$$

(23)

It incorporates the particle velocity for higher accuracy and in order to achieve Galilean invariance.

Lastly, a new approach is proposed by the authors denoted as momentum loss algorithm. As in the HLBM objects are depicted with interior fluid rather than with a sharp no-slip boundary, the investigation for alternative approaches to calculate exchanged momentum is of interest. Examined in this work is the method of computing the momentum directly from the introduced forcing for the approaches by Kupershtokh et al. [76] and Shan and Chen [74]. For the latter this means

$$F^{\mathrm{H}}\left(t\right)=\frac{1}{\tau }\sum _{x\in B\left(t\right)}\sum _{i=1}^{q-1}{c}_i\left(f_i^{\mathrm{eq}}(\rho ,\tilde{u})-f_i^{\mathrm{eq}}(\rho ,u)\right),\mathrm{for}t\in I_{\mathrm{h}},$$

(24)

while for the EDM it is slightly different namely,

$$F^{\mathrm{H}}\left(t\right)=\sum _{x\in B\left(t\right)}\sum _{i=1}^{q-1}{c}_i\left(f_i^{\mathrm{eq}}(\rho ,\tilde{u})-f_i^{\mathrm{eq}}(\rho ,u)\right),\mathrm{for}t\in I_{\mathrm{h}}.$$

(25)

The forcing schemes and methods for momentum exchange discussed in this section allow for a comparative study. The previously used HLBM approach is based on the forcing introduced by Shan and Chen [74] and the momentum exchange by Ladd [39,40]. According to literature [34], there are methods available which yield a higher accuracy. This will be investigated in Section 4.1 leading to an updated version of HLBM which is expected to yield higher accuracy.

4. Results and Discussion of Numerical Experiments

In this Section, various schemes for forcing and momentum exchange are tested along with the remaining HLBM implementation. In Section 4.1 first, the approaches are compared regarding the settling velocity of a sphere and the best performing combination is selected for further validation against existing drag correlations for spheres. Afterwards, the implementation is applied to the cases of a neutrally buoyant particle in a pipe in Section 4.2 and hindered settling in Section 4.3, respectively.

4.1. Settling Sphere

In this section, simulation results are first compared to experimental data by ten Cate et al. [45] for evaluation and validation of the chosen methods and subsequently against empirical correlations discussed in Section 2.1.

4.1.1. Simulation Setup—Comparison to Literature

The settling of a single sphere has been investigated by ten Cate et al. [45] both, experimentally and numerically. Therefore a sphere of diameter $d_{\mathrm{p}}=0.015 \mathrm{m}$ with density ${\rho }_{\mathrm{p}}=1120 \mathrm{kg} {\mathrm{m}}^{-3}$ was placed $0.12 \mathrm{m}$ from the bottom in a container of height $0.16 \mathrm{m}$ and a width and depth of $0.1 \mathrm{m}$, as shown in Figure 1. This setup was used to examine the settling for different Reynolds numbers by varying the fluid density ${\rho }_{\mathrm{f}}$ and dynamic viscosity ${\mu }_{\mathrm{f}}$. The same setup was chosen for the simulations with different discretization parameters for each case. The values were given along with the simulation results of ten Cate et al. [45] for a resolution of four cells per particle radius in

Table 1. Values of the setup of the four cases for a settling sphere investigated by ten Cate et al. [45] along with the deviation of their results to the maximum settling velocity $u_{\infty }$ predicted with the drag correlation by Abraham [60].

Case	${\mathit{\rho }}_f$ in kg m${}^{-3}$	${\mathit{\mu }}_f$ in kg m${}^{-1}$s${}^{-1}$	$\mathrm{Re}$	$\mathit{\delta }\mathit{x}$ in m	$\mathit{\delta }\mathit{t}$ in s	${\mathit{u}}_{\mathit{\infty }}$ in m s${}^{-1}$ (Abraham [60])	Error in %
1	970	$0.373$	$1.5$	$1.671\times {10}^{-3}$	$3.891\times {10}^{-4}$	$0.038$	$10.6$
2	965	$0.212$	$4.1$	$1.645\times {10}^{-3}$	$2.41\times {10}^{-4}$	$0.06$	$5.0$
3	962	$0.113$	$11.6$	$1.61\times {10}^{-3}$	$1.526\times {10}^{-4}$	$0.091$	$4.5$
4	960	$0.058$	$31.9$	$1.559\times {10}^{-3}$	$1.01\times {10}^{-4}$	$0.128$	$5.3$

. The Reynolds number was given in this case according to the values in the table by $\mathrm{Re}$$=d_{\mathrm{p}}{u}_{\infty }{\rho }_{\mathrm{f}}/{\mu }_{\mathrm{f}}$. For the boundaries, a no-slip halfway bounce-back condition [79] was chosen.

In this study, the given setup is investigated for different combinations of forcing and momentum exchange schemes described in Section 3.2 and Section 3.3. Additionally, a convergence study is performed.

4.1.2. Results and Discussion—Comparison to Literature

For reasons of readability, further abbreviations are introduced. Here, GUO and SCF refer to the respective forcing schemes by Guo et al. [75] and Shan and Chen [74] (see Section 3.2). Additionally, MEA-L and MEA-W refer to the momentum exchange algorithms by Ladd [39,40] and Wen et al. [42]. As different resolutions are studied a factor N is introduced to scale the effective grid spacing to $\delta x/N$.

From the simulations, the root mean squared error (RMSE) relative to the maximum absolute velocity of the respective case and the deviation of the maximum settling velocity compared to the one calculated according to the drag correlation by Abraham [60] are given in

Table 2. Different error measures [80] for the four cases described by ten Cate et al. [45] for various combinations of momentum exchange and forcing schemes. The error in terminal velocity is given relative to the analytical values according to Abraham [60]. The results in the table refer to $N=1$.

Case	Forcing	Momentum Exchange	RMSE	PCM	Area between Curves	Error in % Maximum Velocity
1	EDM	MEA-W	$0.04191$	$3.63347$	$0.00386$	$4.69880$
1	EDM	MLA	$0.02722$	$2.17069$	$0.00292$	$4.91581$
1	EDM	MEA-L	$0.04187$	$3.61223$	$0.00386$	$4.71524$
1	GUO	MEA-W	$0.04190$	$3.63317$	$0.00386$	$4.69881$
1	SCF	MEA-W	$0.02616$	$3.86421$	$0.00323$	$6.73646$
1	SCF	MEA-L	$0.02618$	$3.87909$	$0.00323$	$6.73834$
2	EDM	MEA-W	$0.07019$	$1.96464$	$0.00703$	$6.08454$
2	EDM	MLA	$0.11885$	$4.41254$	$0.01115$	$6.71691$
2	EDM	MEA-L	$0.07028$	$1.96609$	$0.00704$	$6.08627$
2	GUO	MEA-W	$0.07019$	$1.96473$	$0.00703$	$6.08455$
2	SCF	MEA-W	$0.10945$	$3.48661$	$0.01082$	$7.83986$
2	SCF	MEA-L	$0.10952$	$3.49102$	$0.01082$	$7.85094$
3	EDM	MEA-W	$0.04287$	$1.50668$	$0.00409$	$6.23779$
3	EDM	MLA	$0.08819$	$2.58684$	$0.01000$	$8.01712$
3	EDM	MEA-L	$0.04289$	$1.50718$	$0.00409$	$6.23545$
3	GUO	MEA-W	$0.04287$	$1.50659$	$0.00409$	$6.23780$
3	SCF	MEA-W	$0.05442$	$2.00959$	$0.00585$	$7.27864$
3	SCF	MEA-L	$0.05443$	$2.00904$	$0.00585$	$7.28794$
4	EDM	MEA-W	$0.02578$	$0.50550$	$0.00271$	$4.88694$
4	EDM	MLA	$0.10395$	$2.71061$	$0.01302$	$9.27789$
4	EDM	MEA-L	$0.02580$	$0.50635$	$0.00271$	$4.89684$
4	GUO	MEA-W	$0.02578$	$0.50551$	$0.00271$	$4.88695$
4	SCF	MEA-W	$0.03347$	$0.86398$	$0.00401$	$5.84097$
4	SCF	MEA-L	$0.03349$	$0.86637$	$0.00402$	$5.84066$

for $N=1$ and in

Table 3. Different error measures [80] for the four cases described by ten Cate et al. [45] for various combinations of momentum exchange and forcing schemes. The error in terminal velocity is given relative to the analytical values according to Abraham [60]. The results in the table refer to $N=8$.

Case	Forcing	Momentum Exchange	RMSE	PCM	Area between Curves	Error in % Maximum Velocity
1	EDM	MEA-W	$0.03241$	$4.35586$	$0.00422$	$8.24923$
1	EDM	MLA	$0.03399$	$2.84034$	$0.00448$	$8.27399$
1	EDM	MEA-L	$0.03241$	$4.35589$	$0.00422$	$8.24930$
1	GUO	MEA-W	$0.03241$	$4.35586$	$0.00422$	$8.24923$
1	SCF	MEA-W	$0.03442$	$4.41524$	$0.00457$	$8.49026$
1	SCF	MEA-L	$0.03442$	$4.41527$	$0.00457$	$8.49039$
2	EDM	MEA-W	$0.03224$	$1.11747$	$0.00347$	$4.32345$
2	EDM	MLA	$0.05467$	$1.03172$	$0.00550$	$4.44263$
2	EDM	MEA-L	$0.03224$	$1.11747$	$0.00347$	$4.32358$
2	GUO	MEA-W	$0.03224$	$1.11748$	$0.00347$	$4.32345$
2	SCF	MEA-W	$0.03326$	$1.10431$	$0.00359$	$4.59350$
2	SCF	MEA-L	$0.03326$	$1.10431$	$0.00359$	$4.59360$
3	EDM	MEA-W	$0.02349$	$0.64709$	$0.00162$	$4.43872$
3	EDM	MLA	$0.06483$	$1.49952$	$0.00563$	$4.83740$
3	EDM	MEA-L	$0.02349$	$0.64703$	$0.00162$	$4.43877$
3	GUO	MEA-W	$0.02349$	$0.64709$	$0.00162$	$4.43872$
3	SCF	MEA-W	$0.02079$	$0.76920$	$0.00152$	$4.67580$
3	SCF	MEA-L	$0.02079$	$0.76898$	$0.00152$	$4.67593$
4	EDM	MEA-W	$0.08260$	$1.06138$	$0.00223$	$4.96350$
4	EDM	MLA	$0.08638$	$1.67762$	$0.00927$	$6.09874$
4	EDM	MEA-L	$0.08259$	$1.06147$	$0.00223$	$4.96360$
4	GUO	MEA-W	$0.08260$	$1.06139$	$0.00223$	$4.96350$
4	SCF	MEA-W	$0.08877$	$1.03403$	$0.00251$	$5.16140$
4	SCF	MEA-L	$0.08875$	$1.03418$	$0.00251$	$5.16147$

for $N=8$. To further compare the whole curves, similarity measures were calculated [80], i.e., a partial curve mapping (PCM) [81] and the area between curves according to Jekel et al. [80]. The latter was less influenced by noisy data or outliers. As reference solution in this calculation, the experimental data of ten Cate et al. [45] were used and approximated by a polynomial fit of 18-th order. The RMSE of the fit for case 1 to 4 was given by $0.01447$, $0.01481$, $0.01838$, and $0.02093$. The values were rounded to six decimal places to demonstrate that some differences (e.g., between MEA-L and MEA-W) were on a negligible level for this case.

For better comprehensibility, the values in Table 2 and Table 3 are averaged over the four cases for each setup in

Table 4. Mean values of the results presented in Table 2 and Table 3. The averages are taken over the four application cases.

N	Forcing	Momentum Exchange	RMSE (Mean)	PCM (Mean)	Area between Curves (Mean)	Error in % Maximum (Mean)
1	EDM	MEA-W	$0.04519$	$1.90257$	$0.00442$	$5.47702$
1	EDM	MLA	$0.08455$	$2.97017$	$0.00927$	$7.23193$
1	EDM	MEA-L	$0.04521$	$1.89796$	$0.00443$	$5.48345$
1	GUO	MEA-W	$0.04519$	$1.90250$	$0.00442$	$5.47703$
1	SCF	MEA-W	$0.05588$	$2.55610$	$0.00598$	$6.92398$
1	SCF	MEA-L	$0.05590$	$2.56138$	$0.00598$	$6.92947$
8	EDM	MEA-W	$0.04268$	$1.79545$	$0.00288$	$5.49373$
8	EDM	MLA	$0.05997$	$1.76230$	$0.00622$	$5.91319$
8	EDM	MEA-L	$0.04268$	$1.79546$	$0.00288$	$5.49381$
8	GUO	MEA-W	$0.04268$	$1.79545$	$0.00288$	$5.49373$
8	SCF	MEA-W	$0.04431$	$1.83069$	$0.00305$	$5.73024$
8	SCF	MEA-L	$0.04430$	$1.83069$	$0.00305$	$5.73035$

. The mean error regarding the maximum settling velocity in the reference was given by $6.35\%$. For the same grid spacing, the combinations EDM and MEA-W, EDM and MEA-L and GUO and MEA-W performed best (about $5.5\%$) with the first one yielding slightly better results. The same holds for the area between the curves, PCM and RMSE. While for smaller grid spacing the results were predominantly better, the same conclusions could be drawn as for $N=1$, with the combination of EDM and MEA-W performing better or equal to all other combinations. Only for PCM, the combination of EDM and MLA yielded the best results while it performed worst in all other cases. Looking only at the results for the cases with lower Reynolds numbers however, this setup yielded the highest accuracy in all values except in the prediction of the maximum settling velocity. This might also be due to the fact that the latter was not calculated from experimental values, but from a given correlation.

A possible reason for this behaviour is that forcing terms for points in the interior of the particle domain did not cancel out in contrast to MEA approaches. While for static objects no difference in the results was observed for the MLA, the error increased with the Reynolds number. This can also be seen in Figure 2. Since the objects did not have strict no-slip boundaries, simply omitting contributions to the force of points beyond the physical boundary was no solution. The transition region between the cells relevant and the ones not relevant for the hydrodynamic force within the particle domain seemed to be dependent on both the discretization parameters and the velocity. Further research in the future is required at this point. In empirical studies the influence of different parameters like grid spacing and the velocity or Reynolds number need to be quantified to deduce further steps in improving the proposed MLA.

Some configurations are plotted in Figure 2 for $N=8$, along with the experimental results by ten Cate et al. [45]. At this point, it can be concluded that all combinations tested in this study yielded reasonable results with the RMSE being the same order of magnitude as the RMSE for the utilized fit. While the application of EDM and MLA should be restricted to low Reynolds numbers only, where it performed best among the considered schemes. The combination of SCF and MEA-L, which was used in previous publications of HLBM [30,55] was among the worst, therefore the overall best performing configuration of EDM and MEA-W was chosen for the remaining calculations.

To further validate the implementation, a convergence study was performed. The experimental order of convergence (EOC) given by

$$EOC(N,\widehat{N})=\frac{log\left(\mathrm{err}\left(\mathrm{N}\right)\right)-\log \left(\mathrm{err}\left(\widehat{\mathrm{N}}\right)\right)}{log\left(N\right)-log\left(\widehat{N}\right)},$$

(26)

was calculated for two different grid spacings $\delta x/N$ and $\delta x/\widehat{N}$ with $N<\widehat{N}$. The function $\mathrm{err}:[1,2,4,8]\to \mathbb{R}$ gives the difference of a chosen error or similarity measure for a given N to the value in the same setup but with a grid spacing according to $N=8$. This way, for each case and setup, two values, i.e., $EOC(1,2)$ and $EOC(2,4)$ were obtained. Averaging all values for the experimental order of convergence of a given combination of schemes for a measure leads to

Table 5. Mean experimental order of convergence (EOC) for different error and similarity measures regarding $N=8$. Results are averaged over all values for a given combination of forcing and momentum exchange scheme as well as all cases.

Forcing	Momentum Exchange	EOC (RMSE)	EOC (RMSE)	EOC (Area between Curves)	EOC (Area between Curves)
EDM	MEA-W	$1.79$	$1.81$	$2.06$	$1.39$
EDM	MLA	$1.37$	$2.00$	$1.49$	$1.66$
EDM	MEA-L	$1.79$	$1.81$	$2.05$	$1.36$
GUO	MEA-W	$1.79$	$1.81$	$2.06$	$1.39$
SCF	MEA-W	$1.57$	$1.03$	$1.72$	$1.55$
SCF	MEA-L	$1.57$	$1.03$	$1.72$	$1.55$

.

The mean EOC values were between 1 and 2 for all schemes, thereby superlinear convergence can be assumed. Similar to the results in previous tables, combinations of EDM or GUO with MEA-W or MEA-L performed best while combinations with SCF were falling behind. The MLA yielded the highest convergence rate for PCM and the maximum settling velocity while it also yielded the worst for the other measures. The results for $\mathrm{Re}=11.6$ with EDM and MEA-W are depicted for different grid spacings according to the parameter N in Figure 3.

The combination of EDM and MEA-W was chosen for all further computations, as it proved best in overall performance. The applicability of the MLA, however, seemed to be limited to some low Reynolds number cases.

Thereby the HLBM was updated, while in previous publications a combination of SCF and MEA-L was used for the calculations the new approach consisting of EDM and MEA-W yielded better results and a higher accuracy.

4.1.3. Simulation Setup—Comparison to Correlations

To check if the drag correlations presented in Section 2.1 can be reproduced by the HLBM, again the setup of a single settling sphere was chosen. It was placed with the center $0.021 \mathrm{m}$ above the bottom of a domain of size $0.0055 \mathrm{m}\times 0.0055 \mathrm{m}\times 0.022 \mathrm{m}$. The top and bottom of the domain were equipped with no-slip boundaries again, but in contrast to the previous case the sides were chosen to be periodic. The densities of the fluid and the sphere were ${\rho }_{\mathrm{f}}=1000 \mathrm{kg} {\mathrm{m}}^{-3}$ and ${\rho }_{\mathrm{p}}=2500 \mathrm{kg} {\mathrm{m}}^{-3}$, respectively. The dynamic viscosity was varied to change the Reynolds number, the sphere had a diameter of $d_{\mathrm{p}}=0.0005 \mathrm{m}$ and the gravitational acceleration was given by $g=9.81 \mathrm{m} {\mathrm{s}}^{-2}$. In this subsection $\mathrm{Re}$ is defined via the given ${\rho }_{\mathrm{f}}$ and $d_{\mathrm{p}}$, while $u_{\infty }$ is defined by the used drag correlation and ${\mu }_{\mathrm{f}}$ as shown in

Table 6. Deviation of of the drag coefficients calculated by homogenized lattice Boltzmann method (HLBM) simulations to different drag correlations.

${\mathit{\mu }}_f$ in kg m${}^{-1}{s}^{-1}$	${\mathit{C}}_D$ (Simulated)	Stokes		Abraham		Schiller and Naumann
		Re	Error in %	Re	Error in %	Re	Error in %
$2.0\times {10}^{-2}$	$86.6942$	$0.26$	$-7.72$	$0.23$	$-24.93$	$0.24$	$-17.33$
$1.5\times {10}^{-2}$	$56.7155$	$0.45$	$7.33$	$0.40$	$-17.98$	$0.42$	$-8.42$
$1.0\times {10}^{-2}$	$29.6648$	$1.02$	$26.31$	$0.84$	$-14.14$	$0.90$	$-2.68$
$5.0\times {10}^{-3}$	$10.5937$	$4.09$	$80.42$	$2.90$	$-9.38$	$3.08$	$2.74$
$2.5\times {10}^{-3}$	$4.5797$	$16.35$	$212.00$	$9.18$	$-1.61$	$9.57$	$6.94$
$1.25\times {10}^{-3}$	$2.2965$	$65.40$	$525.82$	$26.57$	$3.29$	$26.83$	$5.34$
$6.25\times {10}^{-4}$	$1.2539$	$261.60$	$1266.86$	$70.48$	$-0.79$	$69.50$	$-3.52$
$3.125\times {10}^{-4}$	$0.7339$	$1046.40$	$3100.03$	$173.68$	$-11.84$	$170.80$	$-14.74$
$1.5625\times {10}^{-4}$	$0.5213$	$4185.60$	$8992.70$	$404.05$	$-15.27$	$406.40$	$-14.28$
$7.8125\times {10}^{-5}$	$0.4543$	16,742.40	31,595.60	$900.47$	$-8.31$	$948.67$	$1.76$

.

The grid spacing was given by $\delta x=3.125\times {10}^{-5} \mathrm{m}$, this means the particle diameter was equivalent to 8 grid cells. As stated by ten Cate et al. [45], DNS methods experience a non-physical dependency of the drag force on the kinematic viscosity. This has also been investigated by Rohde et al. [82] for a boundary taking the actual, non-voxelized, surface. This effect is described to be less significant for $\mathrm{Re}\gg 1$ and a scaling procedure is proposed to estimate the hydrodynamic radius for the simulation. In this study, the radius and grid spacing were kept fixed, only the temporal discretization was adapted. LBM simulations required the maximum occurring velocity in lattice units to be much smaller than $c_{\mathrm{s}}$ to ensure incompressible flow conditions and stability. Estimating the maximum velocity $u_{\infty }$ by the drag correlation in Equation (8) and choosing the discretization such that this velocity was equivalent to $0.01$ in lattice units finally led to

$$\delta t=\frac{0.01}{u_{\infty }}\delta x.$$

(27)

4.1.4. Results and Discussion—Comparison to Correlations

In all simulations, the sphere reached a stable settling velocity, which was used to calculate the drag coefficient using Equation (4) with the fluid velocity assumed to be zero. The results are presented in Table 6 along with Reynolds numbers according to the terminal velocity of the drag correlations by Stokes, Abraham and Schiller and Naumann, discussed in Section 2.1. Additionally, the deviation in % from the analytical value of the respective correlation is given.

Here, the closest correlation was the one by Schiller and Naumann with an average error of $7.78\%$ calculated from the absolute values of the ones given in Table 6. The results yielded a slightly worse error of $10.75\%$ comparing to Abraham. Additionally, as expected for $\mathrm{Re}<1$ the results were closer to the prediction using Stokes drag.

On the other hand, deviations in this region might also be due to the stronger viscosity dependency for low $\mathrm{Re}$ discussed in Section 4.1.3. Another reason for deviations might be the lattice relaxation time entering the region of under-relaxation [23] for $\mathrm{Re}<1$ and approaching the value of $0.5$ for the high $\mathrm{Re}$ considered here. For a stable simulation $\tau >0.5$ is required [23]. This, however, is related to the chosen discretization. For reasons of comparability between the data points $\delta x$ was kept constant, however, adapting it to achieve a reasonable $\tau$ can presumably improve the results. Increasing the grid resolution and also the gravitational acceleration, Reynolds numbers up to 1591 were reached in tests. At this point, a further increase was limited by available computational resources, as not only did $\delta x$ need to be lowered, but also the domain size had to be increased to allow the particle to reach its terminal velocity. Overall, the results are in good agreement with the discussed correlations, this can be seen in Figure 4, where the Reynolds number was defined via the maximum settling velocity in the simulation.

For further analysis, $\delta t$ was varied by choosing a different lattice velocity to be equivalent to the one calculated by Schiller and Naumann in Equation (27). These results can be used in further simulations for an a-priori estimate of the error regarding the temporal resolution, for cases that allow an estimation of the maximum occurring velocity.

The results in

Table 7. Maximum settling velocity for ${\mu }_{\mathrm{f}}=0.005 \mathrm{k}\mathrm{g} {\mathrm{m}}^{-1} {\mathrm{s}}^{-1}$ for a chosen lattice velocity $u^{\mathrm{L}}$ (see Equation (27)). Additionally, given is the deviation to the velocity obtained with $u^{\mathrm{L}}=0.0025$ and the change of maximum velocity to the value obtained with the next smaller $u^{\mathrm{L}}$.

${\mathit{u}}^L$	$0.0025$	$0.005$	$0.01$	$0.02$	$0.04$	$0.08$	$0.16$
$u_{\infty }$ in $\mathrm{m} {\mathrm{s}}^{-1}$	$0.02975$	$0.03002$	$0.03042$	$0.03102$	$0.031981$	$0.03375$	$0.03768$
Deviation in %	0	$0.89$	$2.24$	$4.25$	$7.50$	$13.45$	$26.64$
Change in %	-	$0.89$	$1.33$	$1.97$	$3.11$	$5.54$	$11.6$

show that $u^{\mathrm{L}}$ should be at least smaller or equal to $0.04$ as this gave a $7.5\%$ deviation from the finest tested temporal resolution. A value of $u^{\mathrm{L}}=0.01$ would be most desirable since from this point on the deviation was smaller than most errors measured in this work. Then again, this meant the computational cost quadruple compared to the just found minimum requirement regarding the lattice velocity, since $u^{\mathrm{L}}$ was directly proportional to $\delta t$. Using $u^{\mathrm{L}}=0.0025$ as a reference was justified as halving $u^{\mathrm{L}}=0.005$ only led to a change below $1\%$ regarding the maximum settling velocity. Overall, almost perfect linear convergence was observed considering the average $EOC=0.97$ regarding the maximum settling velocity. The results are also depicted in Figure 5, where a convergence towards a value in between the predictions by Abraham [60] and Schiller and Naumann [61] is shown.

4.1.5. Further Discussion—Onset of Unsteadiness

Spheres settling under the influence of gravity experience a range of regimes of motion, depending on the density ratio between the spheres and the fluid as well as the Reynolds or Galileo number. This has been shown and experimentally investigated by Horowitz and Williamson [83]. Later, Rahmani and Wachs [84] investigated the same behaviour via simulations. Following their definition of the Galileo number as

$$\mathrm{Ga}=\frac{\sqrt{\left|1-{\rho }_{\mathrm{p}}/{\rho }_{\mathrm{f}}\right|g{d}_{\mathrm{p}}^3}}{\nu },$$

(28)

the simulations presented in Section 4.1.4 cover a range of $\mathrm{Ga}=2.14$ up to $\mathrm{Ga}=548.97$. For this discussion, the size of the domain has been extended to $0.0375$ $\mathrm{m}$ in z-direction. In this context, it is notable that the unsteadiness observed in experiments can only be reproduced in simulations if the setup is not perfectly symmetrical, i.e., if the sphere does not perfectly align with the grid for a domain free of disturbance. Therefore, the sphere is moved $0.3\delta x$ from the center of the domain in x- and y-direction respectively. It can be observed that for $\mathrm{Ga}=137.24$, a sphere follows a slightly oblique path, while all spheres with lower $\mathrm{Ga}$ settle vertically straight, as depicted in Figure 6. This fits the results by Jenny et al. [85], who found the onset of oblique motion at about $\mathrm{Ga}=150$, and Rahmani and Wachs [84].

For higher Galileo numbers, the motion seems to be characterized by an oblique oscillation. However, to ensure this classification, a closer evaluation with a longer settling path is required, especially since Rahmani and Wachs [84] as well as Jenny et al. [85] predicted a chaotic motion for this parameters. The vortex structure shown in Figure 7 also seems to be rather chaotic. A thorough investigation of the different settling regimes including the vortex shedding, which was found as depicted in Figure 7, however, exceeds the scope of the present work at this point.

4.2. Tubular Pinch Effect

In this section, 2D simulations regarding the tubular pinch effect are presented. It was first discovered [46] and then further investigated [47] by Segré and Silberberg. The effect describes the motion of neutrally buoyant particles in a tube flow towards an equilibrium position between the tube’s center and its wall. As reference simulation, results by Li et al. [35] and Inamuro et al. [36] are considered.

4.2.1. Simulation Setup

For all considered cases, the base setup depicted in Figure 8 was the same, only the parameters change. The tube with diameter D and length L was equipped with pressure boundary conditions at front and back. A flow was induced by a pressure difference $\Delta p^{\mathrm{L}}$, considering the relation between pressure and density this was equivalent to setting ${\rho }^{\mathrm{L}}=1\pm p^{\mathrm{L}}/6$, for an initial density of ${\rho }^{\mathrm{L}}=1$ across the domain. For the particle, a periodic boundary was chosen. As contact with the given boundary implementation distorted the particle movement, the particle was always kept one particle diameter $d_{\mathrm{p}}$ away. While pressure boundaries were applied to the fluid domain, the particle experienced the periodic boundary before the actual end of the domain and got cut off one particle diameter before the pressure outlet. The part of the particle having left the domain via this boundary entered the domain also one particle diameter from the pressure inlet. This is done similarly by Li et al. [35] while Inamuro et al. [36] present a boundary condition capable of handling particles passing through it. To account for this difference, the domain was enlarged by $2d_{\mathrm{p}}$ in flow direction so that the domain length stayed the same from perspective of the circle. The top and bottom of the domain had a no-slip condition for the fluid as well as the submersed object. The periodicity for the particles was required to reduce computational load since, as depicted in Figure 9, the domain would require between 15 and 60 times the size, depending on the case. It also allowed us to study the influence of the distance between spheres by varying the domain length as presented by Inamuro et al. [36]. The application of periodicity as described by Li et al. [35] was required as the improved periodic particle boundary presented in Inamuro et al. [36] was formulated for particles represented by a bounce-back boundary and could therefore not be applied straightforward for HLBM.

The calculations in the reference literature were performed in lattice units, therefore the discretization parameters were chosen accordingly. Additionally, all values in this subsection and the one regarding the results of this case are therefore non-dimensionalized by those discretization parameters, just like shown in the references. As no value was affiliated with a unit, the superscript ${}^{\mathrm{L}}$, indicating lattice units, is also dropped in this section for reasons of readability. The viscosity is defined by Equation (14) for a given $\tau$. Since, as also stated by Inamuro et al. [36], the error was proportional to the maximum occuring lattice velocity squared, it was monitored for the presented cases.

The trajectory of the submersed circle is described by the coordinates of its center $(x_{\mathrm{c}},y_{\mathrm{c}})$. All simulations are run for $6\times {10}^{-2}$ time steps to ensure convergence according the the results shown in Figure 9.

4.2.2. Results and Discussion

The results of the simulations are printed in

Table 8. Parameters of the simulations investigating the tubular pinch effect along with the results for multiple cases according to Inamuro et al. [36] and the one described by Li et al. [35].

Case	$\mathit{\tau }$	$\mathbf{\Delta }\mathit{p}$	D	L	${\mathit{d}}_p/\mathit{D}$	${\mathit{y}}_c/\mathit{D}$	Error in %
Inamuro et al. case 2	$1.4$	$8.167\times {10}^{-4}$	200	200	$0.25$	$0.2642$	$-3.33\%$
Inamuro et al. case 6	$0.757$	$2.337\times {10}^{-4}$	200	200	$0.25$	$0.2548$	$-5.83\%$
Inamuro et al. case 11	$1.4$	$1.633\times {10}^{-3}$	200	400	$0.25$	$0.2726$	$-4.35\%$
Inamuro et al. case 14	$0.95$	$3.207\times {10}^{-3}$	100	400	$0.5$	$0.3590$	$-5.48\%$
Li et al.	$0.75$	$2.670\times {10}^{-4}$	100	400	$0.25$	$0.2756$	$-4.10\%$

for different cases with the respective parameters. For each case, the simulations were run for different starting points $y_{\mathrm{start}}/D\in \{0.2,0.25,0.35,0.4,0.45\}$ of the circle and the simulations showed a convergence towards a single position for each case as depicted in Figure 9. The resulting $y_{\mathrm{c}}/D$ was averaged over the last $20,000$ time steps of each simulation and over the results of all starting points.

Inamuro et al. [36] investigated the influence of various parameter like $\mathrm{Re}$, $d_{\mathrm{p}}/D$ and the distance between two circles, which is reflected in the area covered by particles. They found the same relations as Karnis et al. in their experiments [49], namely that the equilibrium position of the circle gets closer to the wall for higher $\mathrm{Re}$, but closer to the center for more distance between two objects and also gets closer to the center for increasing $d_{\mathrm{p}}/D$. Inamuro et al. [36] defined the Reynolds number for this case as the ratio of time- and space-averaged velocity times the distance between the walls to the kinematic viscosity. The values were chosen to approximately achieve a maximum lattice velocity of $u^{\mathrm{L}}=0.04$, this was also found in the current simulations with $u^{\mathrm{L}}\approx 0.041$ across all runs. With an average absolute error of $4.75\%$ across the cases the results showed good agreement to the ones obtained by Inamuro et al. [36]. The most probable source of the deviation was the difference in boundary conditions at the in- and outflow.

With an error of $-4.1\%$, the last case is also in good agreement with Li et al. [35], however, they also stated an error of $5.16\%$ comparing with case 2 of Inamuro et al. [36]. As the parameter did not fully match any of those reference cases, a comparison between the two reference publications is complicated, especially since for the last case in Table 8, a maximum lattice velocity of $u^{\mathrm{L}}\approx 0.096$ was measured.

Additionally, the applicability of the MEA-L was tested for HLBM in this case. As already stated by Li et al. [35] and Peng et al. [34], it was found that the MEA according to Ladd [39,40] is not able to reproduce the tubular pinch effect. In all cases, the circle reached its final position in the middle of the tube.

4.3. Hindered Settling

In this section, the phenomenon of hindered settling is simulated with HLBM. Although there was no explicit collision model implemented, the particles affected each other by momentum transfer via the fluid. This, of course, was only sufficient if the spatial and temporal resolution was chosen fine enough that the transferred momentum prevented an overlapping of particles by several cells. This effect has been observed in previous publications regarding HLBM, e.g., by Krause et al. [55], but has up to now only been described qualitatively. Therefore, the study of hindered settling was used to investigate the occurring error regarding the velocity and solid volume fraction. This case aimed at testing the quality of results without collision model and if the effect could be reproduced at all. Therefore, the simulations were compared to various correlations presented in Section 2.2.

4.3.1. Simulation Setup

For this simulations, random distributions of spheres were created in the bottom half of a domain of size 0.00625 m × 0.00625 m × 0.025 m. The latter was equipped with no-slip boundary conditions at the bottom and top and was periodic for fluid and particles at the sides. The considered solid volume fractions in the bottom half are $5\%$, $10\%$, $15\%$, $20\%$ and $25\%$, which required 373, 746, 1119, 1492 and 1865 spheres, respectively. The starting setup for the solid volume fraction $\varphi =0.2$ is depicted in Figure 10.

The spheres had a diameter of $d_{\mathrm{p}}=0.0005 \mathrm{m}$ and a density of ${\rho }_{\mathrm{p}}=2500 \mathrm{k}\mathrm{g} {\mathrm{m}}^{-3}$, while the physical parameters of the fluid were given by ${\rho }_{\mathrm{f}}=1000 \mathrm{k}\mathrm{g} {\mathrm{m}}^{-3}$ and $\nu ={10}^{-6} {\mathrm{m}}^2 {\mathrm{s}}^{-1}$. To study the effect regarding different Reynolds numbers the gravitational acceleration was varied. For an a-priori estimation of $\mathrm{Re}$, the terminal settling velocity $u_{\infty }$ of a sphere according to Schiller and Naumann was used (see Section 2.1). Investigated are the cases of $\mathrm{Re}=0.53$ ($g=0.056 \mathrm{m} {\mathrm{s}}^{-2}$), $\mathrm{Re}=5.29$ ($g=0.748 \mathrm{m} {\mathrm{s}}^{-2}$) and $\mathrm{Re}=49.64$ ($g=15.22 \mathrm{m} {\mathrm{s}}^{-2}$).

For spatial discretization $\delta x=2.27\times {10}^{-5} \mathrm{m}$ was chosen, thereby the diameter of a sphere was equivalent to 11 grid cells. Furthermore

$$\delta t=\frac{u_{\infty }}{u^{\mathrm{L}}}\delta x$$

(29)

was chosen to ensure a sufficient temporal resolution, with $u^{\mathrm{L}}=0.005$, for all cases.

4.3.2. Results and Discussion

The hindered settling velocity of the particle collective was calculated by tracking the upper front to the clear water zone. Therefore, the settling velocity in direction of gravitation was averaged over the highest $5\%$ of particles. The velocity field during the process is visualized in Figure 11.

Since the number of simulated particles was low compared to an experimental setup, especially for low solid volume fractions, the calculated velocity is prone to oscillations. Therefore, it was further averaged over time, beginning with the first point, for which the absolute of the averaged velocity decreases. The endpoint was defined by the the time the first particle of the considered $5\%$ reached the bottom $15\%$ of the domain. The results of the averaging over the particles for $\mathrm{Re}=49.64$ are depicted in Figure 12 along with the part used for temporal averaging, represented by the dashed line. In the following, this latter average will be denoted as simulated hindered settling velocity $u_{\mathrm{sim}}$.

While a comparison to Steinour [63] resulted in throughout large errors, the deviations to different other correlations based on a single particle settling velocity according to Stokes [59] and to Schiller and Naumann [61] (here denoted by $u_{\mathrm{S}-\mathrm{N}}$) are given in

Table 9. Simulated hindered settling velocity regarding different $\mathrm{Re}$ and $\varphi$ in comparison to different correlations.

$\mathrm{Re}$	$\mathit{\varphi }$	usim in m s${}^{-1}$	Error in % (uRZ, uS)	Error in % (uO, uS)	Error in % (uBM, uS)	Error in % (uRZ, uS-N)	Error in % (uO, uS-N)	Error in % (uBM, uS-N)
$0.53$	$0.05$	$-0.00071$	$-23.38$	$-10.17$	$-3.97$	$-15.90$	$-1.46$	$5.35$
$0.53$	$0.1$	$-0.00055$	$-24.69$	$-16.87$	$-7.46$	$-17.28$	$-8.81$	$1.51$
$0.53$	$0.15$	$-0.00045$	$-20.36$	$-19.03$	$-6.15$	$-12.46$	$-11.18$	$2.95$
$0.53$	$0.2$	$-0.00037$	$-15.63$	$-21.35$	$-5.47$	$-7.19$	$-13.73$	$3.70$
$0.53$	$0.25$	$-0.00031$	$-5.06$	$-18.20$	$0.80$	$4.52$	$-10.27$	$10.57$
$5.29$	$0.05$	$-0.00691$	$-46.58$	$-34.75$	$-30.24$	$-20.82$	$-4.00$	$2.63$
$5.29$	$0.1$	$-0.00551$	$-48.15$	$-37.75$	$-30.71$	$-22.56$	$-8.41$	$1.95$
$5.29$	$0.15$	$-0.00444$	$-48.68$	$-40.61$	$-31.16$	$-22.72$	$-12.61$	$1.29$
$5.29$	$0.2$	$-0.00367$	$-47.08$	$-41.07$	$-29.17$	$-19.62$	$-13.29$	$4.22$
$5.29$	$0.25$	$-0.00295$	$-46.26$	$-41.77$	$-28.24$	$-17.62$	$-14.32$	$5.58$
$49.46$	$0.05$	$-0.06962$	$-74.81$	$-67.71$	$-65.47$	$-18.17$	$3.13$	$10.26$
$49.46$	$0.1$	$-0.05656$	$-76.34$	$-68.63$	$-65.08$	$-21.76$	$0.19$	$11.53$
$49.46$	$0.15$	$-0.04757$	$-76.80$	$-68.71$	$-63.73$	$-21.83$	$-0.06$	$15.84$
$49.46$	$0.2$	$-0.03889$	$-77.69$	$-69.34$	$-63.14$	$-23.30$	$-2.07$	$17.71$
$49.46$	$0.25$	$-0.03300$	$-77.49$	$-68.01$	$-60.58$	$-20.96$	$2.17$	$25.90$

. The best agreement was achieved with the results by Barnea and Mizrahi [70] in combination with the drag correlation by Schiller and Naumann with an average error of $8.07\%$. This was expectable since they already stated to use drag correlations beyond Stokes with their formula for higher Reynolds numbers. For the case of $\mathrm{Re}=0.53$ the used drag correlation had negligible influence as it yielded $4.77\%$ deviation to the results with Stokes and $4.82\%$ to the results in combination with $u_{\mathrm{S}-\mathrm{N}}$. Except for the correlation of Oliver built upon Schiller and Naumann yielding an average error of $7.05\%$, mainly the case of $\mathrm{Re}=49.46$ contributed to the error. This was to be expected since the discretization remained the same, but the spheres moved faster, increasing the possibility of large particle volumes overlapping and thereby making further momentum transfer via the fluid impossible. Additionally, high solid volume fractions seemed to have a negative effect on the results, this is shown in the last column of Table 9. Similar as for the high Reynolds number cases the error likely originated from the missing explicit contact model. For this comparably large number of spheres the occurrence of multiple contacts in a short time was possible, which pushed spheres to overlap each other. Despite these errors it was shown that hindered setting could be simulated with this approach however, with limitations to the solid volume fraction and velocity in combination with spatial and temporal discretization.

In this setup the only boundary conditions applied were periodic boundaries and a bounce-back no-slip condition, which are both mass conserving. Since the collision step executed a standard BGK collision with forcing, which was also mass conserving [23], this was also true for the whole scheme. Additionally, during the simulations no notable accumulation or dilution of mass within the areas covered by particles were observed.

Independent of the used drag formula, the correlation according to Richardson and Zaki [54] yielded the worst results among the more precisely studied ones. The average error was $47.27\%$ for the combination with $u_{\mathrm{S}}$, intended by the originators. However, it dropped to $17.78\%$ using $u_{\mathrm{S}-\mathrm{N}}$. The varying deviations to the drag correlations and obviously also between those correlations show the complexity of this application case.

Many reasons for errors and deviations can be found for this application case. Besides the possible influence of the starting distribution of the spheres, it can also be deduced from Figure 12 that a larger domain with more particles was required for more reliable results. Since the clear water front was not necessarily sharp and easy to track, a broader domain with more particles would smooth oscillations in this chaotic top region. Lowering the percentage of tracked particles e.g., to $2\%$, improved the results in comparison to the correlations, however, it also increased the oscillations. Using the top $5\%$ was a compromise between reliable results and a precise tracking of the front by only considering the uppermost particles. A broader domain and clear water front would therefore be beneficial. The extend of the simulation, however, was limited for DNS approaches due to high computational costs.

Furthermore, the probable main point is that no explicit particle-particle collision model is applied and the momentum is solely exchanged via the fluid. This, of course, can be a main source of error, especially if the particles start to overlap by several cells. The latter is caused by a resolution chosen too coarse in comparison to the velocity of the spheres, so that the repelling effect of momentum exchange via the fluid is diminished. The good agreement, e.g., with the results by Barnea and Mizrahi and the obvious dependency of the simulated hindered settling velocity on $\varphi$ however, show that it is possible to sufficiently depict the effect of hindered settling with the chosen setup. While capable of properly simulating the settling phase, the presented method is not suitable for the study of bed formation, as particles start to overlap once sedimented due to the absence of an explicit collision model. No influence of this nonphysical behaviour back on the settling process was observed.

4.4. Computational Efficiency

The performance of the algorithm has been recently investigated by Bretl et al. [86]. In their study, also based on OpenLB [56], they investigated the speedup S, which was defined as ratio of execution times using a single process $T_1$ to using $n_{\mathrm{p}}$ processes. Comparing to the theoretical value for a code which is $99.5\%$ parallelizable given by

$$S=\frac{T_1}{T_1(0.005+0.995/n_{\mathrm{p}})},$$

(30)

they found the results to be in good agreement. These, however, are results for the algorithm in the case of a single settling particle. Considering the case of hindered settling presented in Section 4.3, the dependency of the performance on the number of simulated objects was studied. As measure, the amount of million lattice site updates per second and core (MLUPps) was used. The cases for $\mathrm{Re}=49.64$ were evaluated with the simulations run on a system equipped with Intel Xeon E5-2660 v3 processors.

Each simulation used a lattice with 83,717,424 cells and took 176,000 time-steps utilizing 80 cores. The results are depicted in Figure 13 together with a fit to a rational function f with

$$f\left(\varphi \right)=\frac{a_1\varphi +a_2}{a_3\varphi +a_4},$$

(31)

and fitting parameters $a_1,a_2,a_3,a_4\in \mathbb{R}$. The function yielded $0.45$ MLUPps for $\varphi =1$ and approached $0.35$ MLUPps asymptotically as $\varphi \to \infty$. Despite the questionable physicality regarding such a solid volume fraction for a set of spherical particles, those numbers were useful to estimate the lower bounds of single core performance for this method. The decrease in MLUPps was to be expected, since for each cell covered by a particle, additional computations regarding the hydrodynamic force were required (see e.g., Equation (23)). The influence of the number of particles on the performance, however, did not only depend on the solid volume fraction, but also on the distribution of the objects. Since for the parallelization MPI was used, each particle was treated by the process responsible for the domain it resided in. As in this simulation the particles accumulated at the bottom of the domain, a small number of processors had to take care of the calculation of hydrodynamic forces for all particles. A discussion on distribution strategies of computational load among the processors (load optimal strategy vs. communication optimal strategy) is given by Henn et al. [87].

5. Conclusions

The homogenized lattice Boltzmann method has been revisited and various forcing schemes and approaches to calculate exchanged momentum have been evaluated. Among the latter is a new proposed algorithm based on the momentum loss on a cell. However, it showed substandard accuracy except in the case of low Reynolds numbers. It is assumed that the hydrodynamic force is overestimated due to effects correlated to the interior fluid. The amount of force contributed by the latter is hardly distinguishable from the amount related to momentum exchanged with the bulk fluid. As most MEAs are constructed for a sharp solid boundary, further research at this point should be considered in the future. Since issues related to the interior fluid also exist for the immersed boundary method, it might be possible to adapt improvements.

Besides this a combination of Kupershtokh forcing and the MEA by Wen et al. [38] gave the overall best results. This finally leads to an updated version of HLBM, for which the results are in good agreement to literature (e.g., regarding the velocity profile of a settling sphere).

Furthermore, the reproducibility of drag correlations was tested yielding an error of $7.78\%$ compared to the one by Schiller and Naumann in the range from $\mathrm{Re}=0.24$ up to $\mathrm{Re}=948.67$. Therefore, the applicability of HLBM for Reynolds numbers up to the Newton regime is shown.

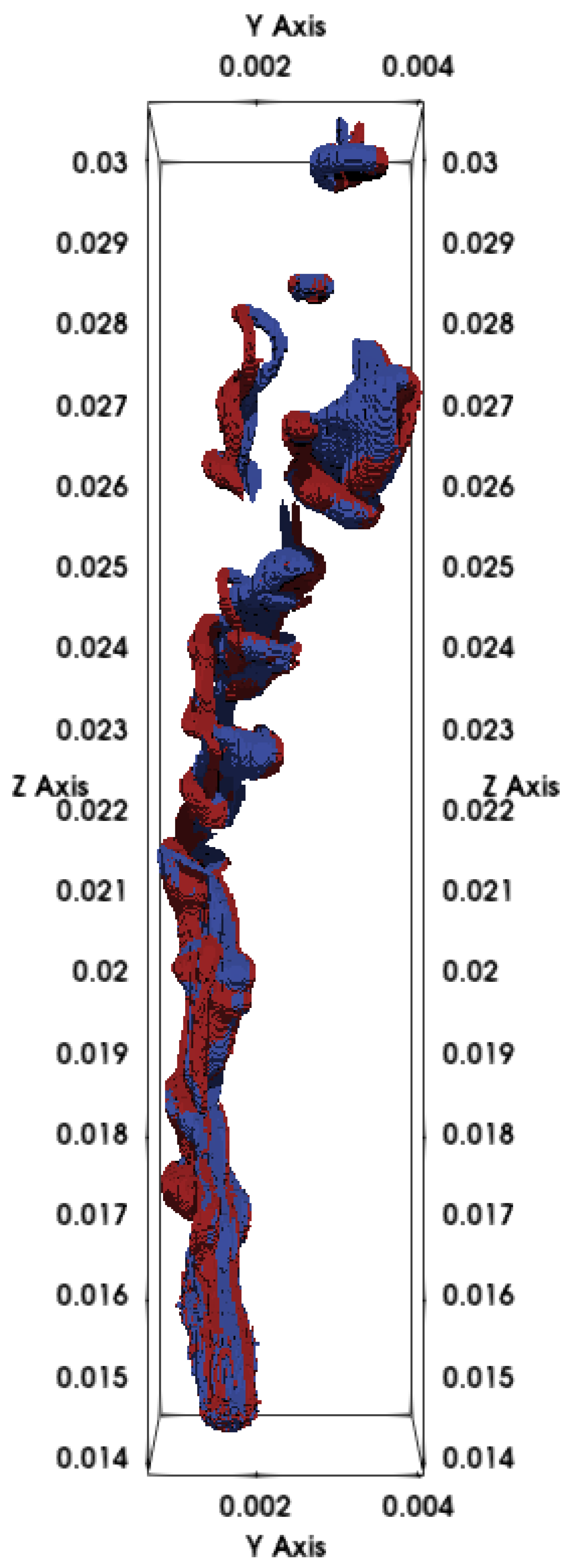
In the next application case, the tubular pinch effect was investigated in 2 dimensions. Here, the error to reference simulations in the literature regarding the influence of the Reynolds number, the ratio of circle to tube diameter and the distance between the circles, never exceeded $5.83\%$.

The authors furthermore showed that the cases of hindered settling can be investigated with HLBM for a sufficient resolution, even without an explicit collision model. With a deviation of $8.07\%$ to the correlation by Barnea and Mizrahi, the results are in excellent agreement, especially considering the error regarding a single settling particle. For more reliable computations regarding hindered settling, particularly for higher Reynolds numbers, and for bed formation processes an additional collision model is mandatory. The implementation of such is planned for future research, especially to evaluate the actual improvement in the quality of results as an effect of the addition of an explicit contact model.

Overall, the updated version of HLBM performed well across all application cases with good agreement to existing literature regarding experimental and theoretical results.