Estimation of Daily Reproduction Numbers during the COVID-19 Outbreak
Abstract
1. Introduction
1.1. Overview and Literature Review
1.2. Calculation of R0
2. Materials and Methods
2.1. The Contagion Mechanism from a First Infectious Case Zero
2.2. The Biphasic Pattern of the Virulence Curve of Coronaviruses
2.3. Relationships between Markovian and ODE SIR Approaches
2.3.1. First Method for Obtaining the SIR Equation from a Deterministic Discrete Mechanism
2.3.2. Second Method for Obtaining the SIR Equation from a Stochastic Discrete Mechanism
+ P(S(t) = k − 1, I(t) = N − k + 1) [f(k − 1) + ρ(N − k + 1)]dt
− P(S(t) = k+1, I(t) = N − k − 1) [µ(k + 1) + ν(k + 1) (N − k − 1)]dt
= − P(S(t) = k, I(t) = N − k) [µk + νk (N − k)−fk-ρ(N − k)]
+ P(S(t) = k − 1, I(t) = N − k + 1) [f(k − 1) + ρ(N − k + 1)]
− P(S(t) = k + 1, I(t) = N − k − 1) [µ(k + 1) + ν(k + 1)(N − k − 1)],
+ P(S(t) = k − 1, I(t) = j + 1) [f(k − 1) + ρ(j + 1)]dt
− P(S(t) = k + 1, I(t) = j − 1) [µ(k + 1) + ν(k + 1)(j − 1)]dt
or, if f = µ, dE(S)/dt ≈ E(I) [−νE(S) + ρ],
3. Results
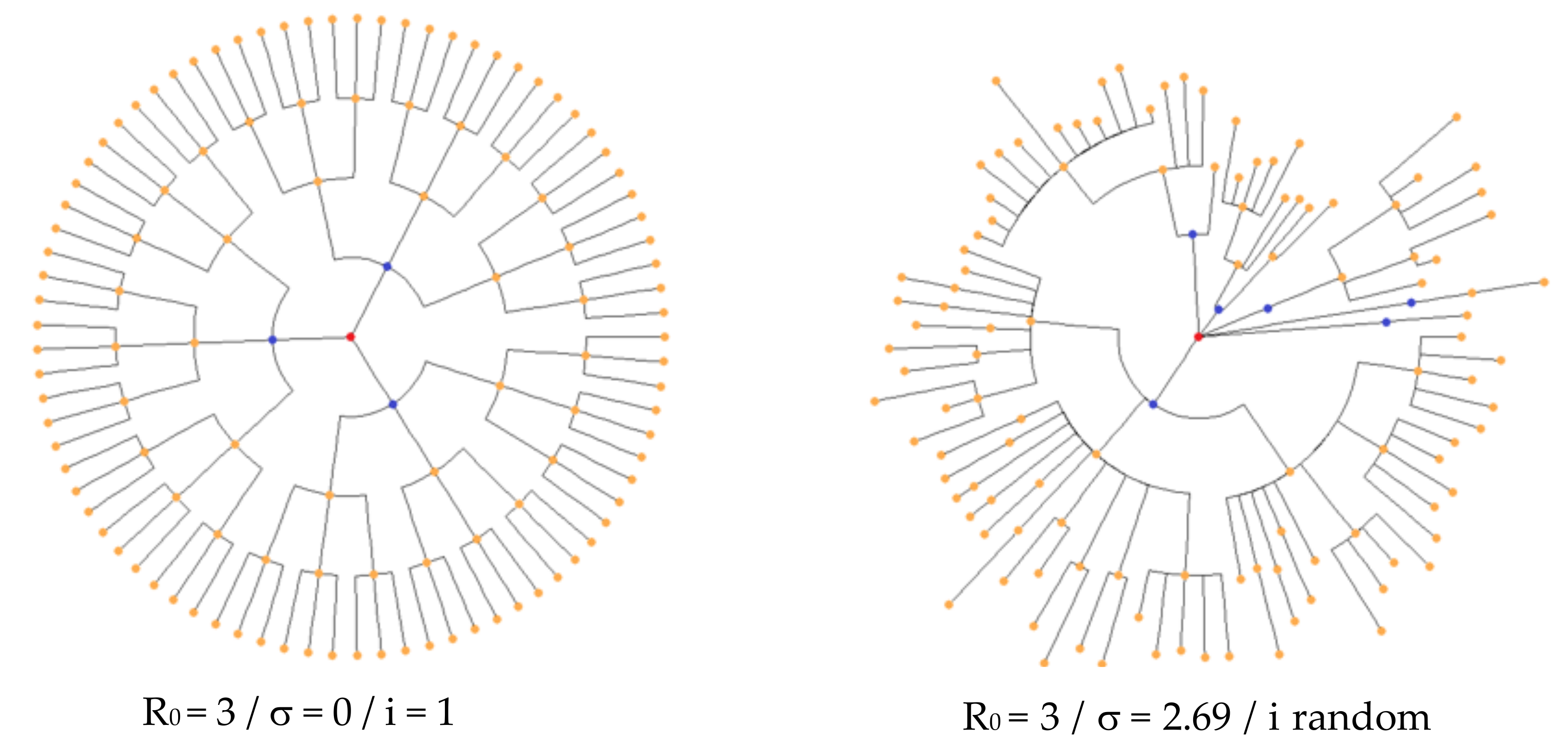
3.1. Distribution of the Daily Reproduction Numbers Rj’s along the Contagiousness Period of an Individual. A Theoretical Example Where They Are Supposed to Be Constant during the Epidemics
3.2. Distribution of the Daily Reproduction Numbers Rj’s When They Are Supposed to Be Random
- 1.
- For a = 0.1, let us randomly and uniformly choose the initial distribution of the daily reproduction numbers R1 in the interval [1.9, 2.1], R2 in [0.95, 1.05] and R3 in [1.9, 2.1] as R1 = 2.1, R2 = 0.95, R3 = 2.1. Then, the transition matrix M1 is equal to:
- 2.
- For a = 1, let us choose the initial R1 in [1, 3], R2 in [0.5, 1.5] and R3 in [1, 3], e.g., R1 = 1, R2 = 1.355 and R3 = 1.1. Then, the transition matrix M1 is equal to:
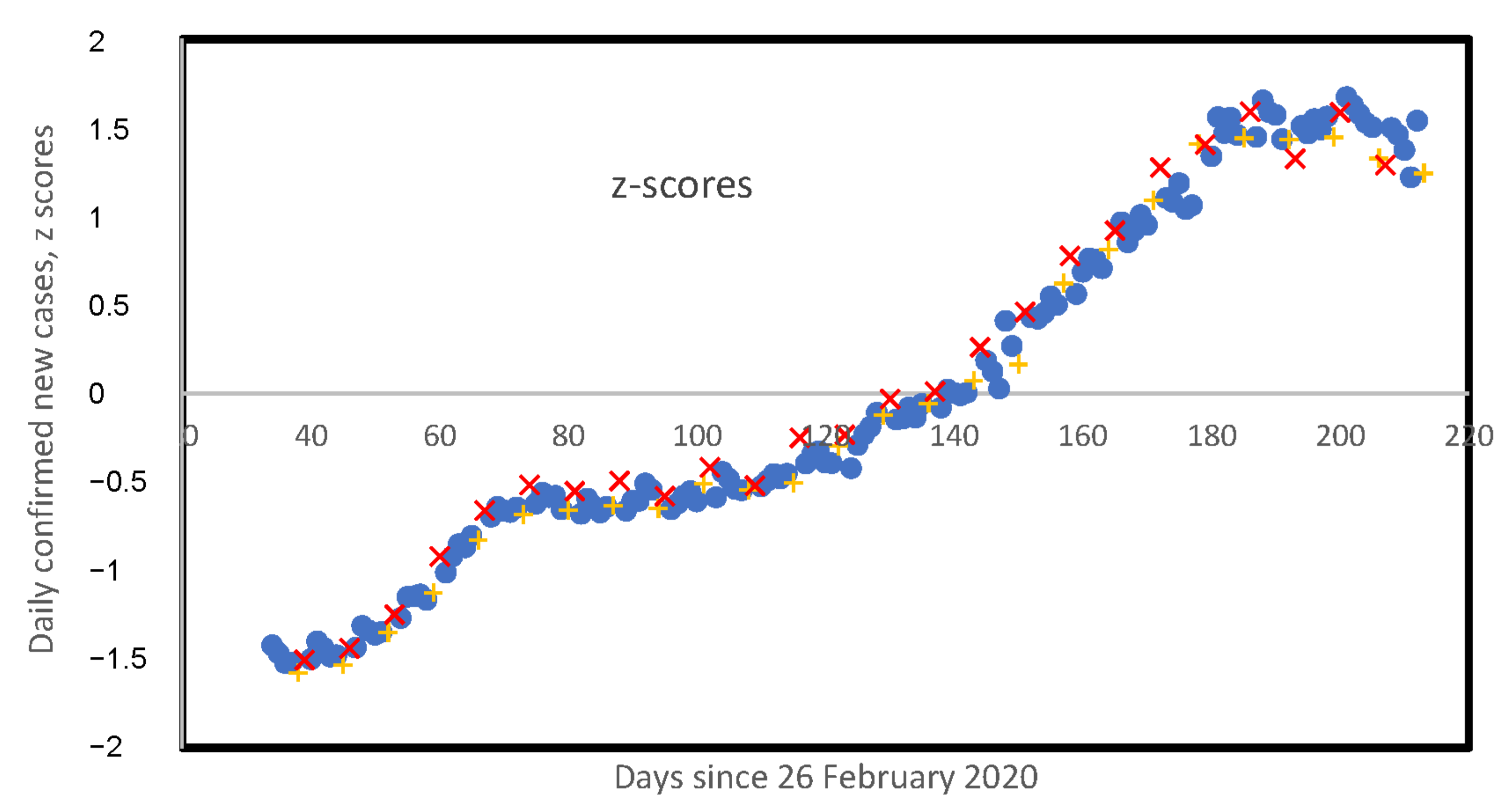
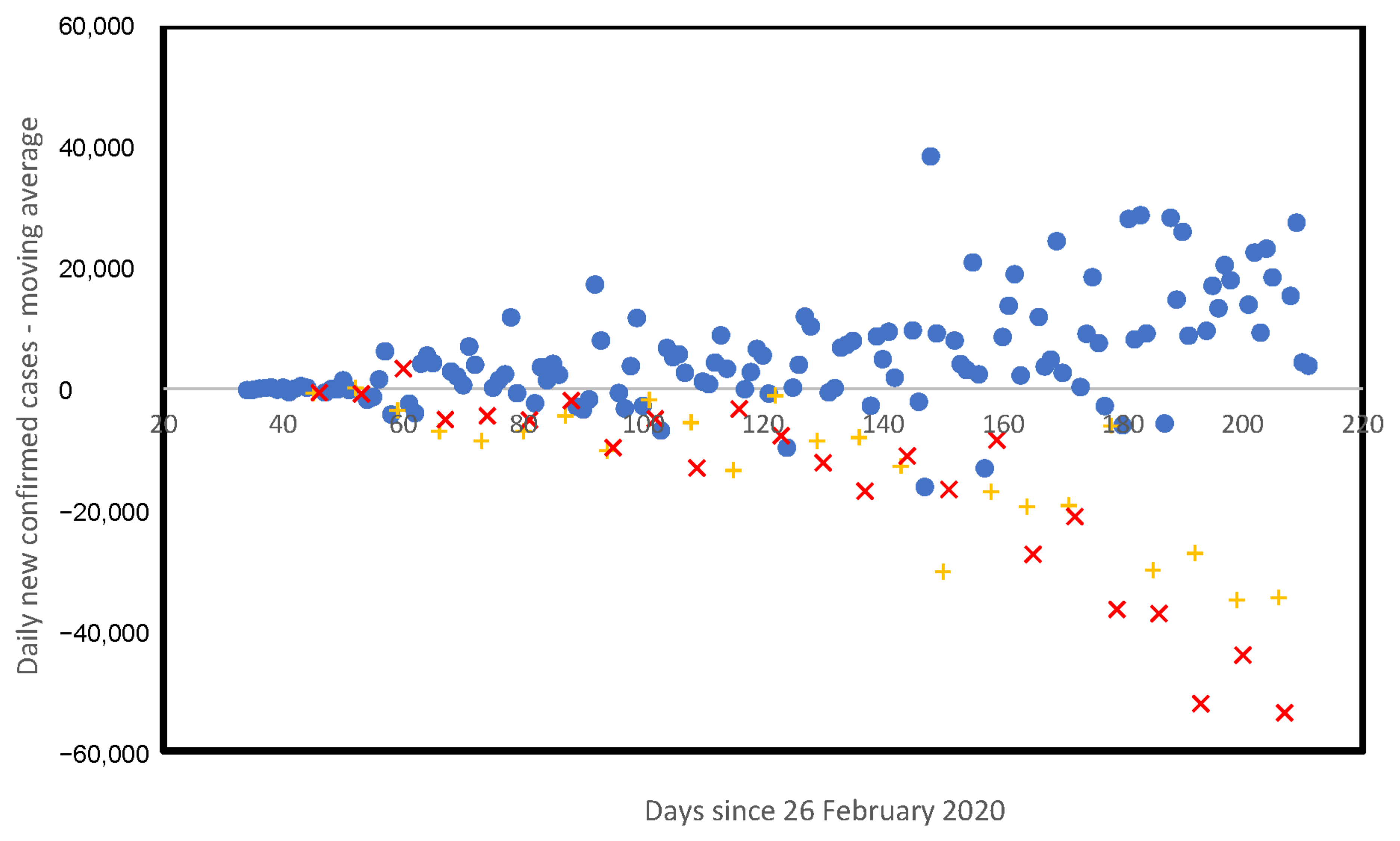
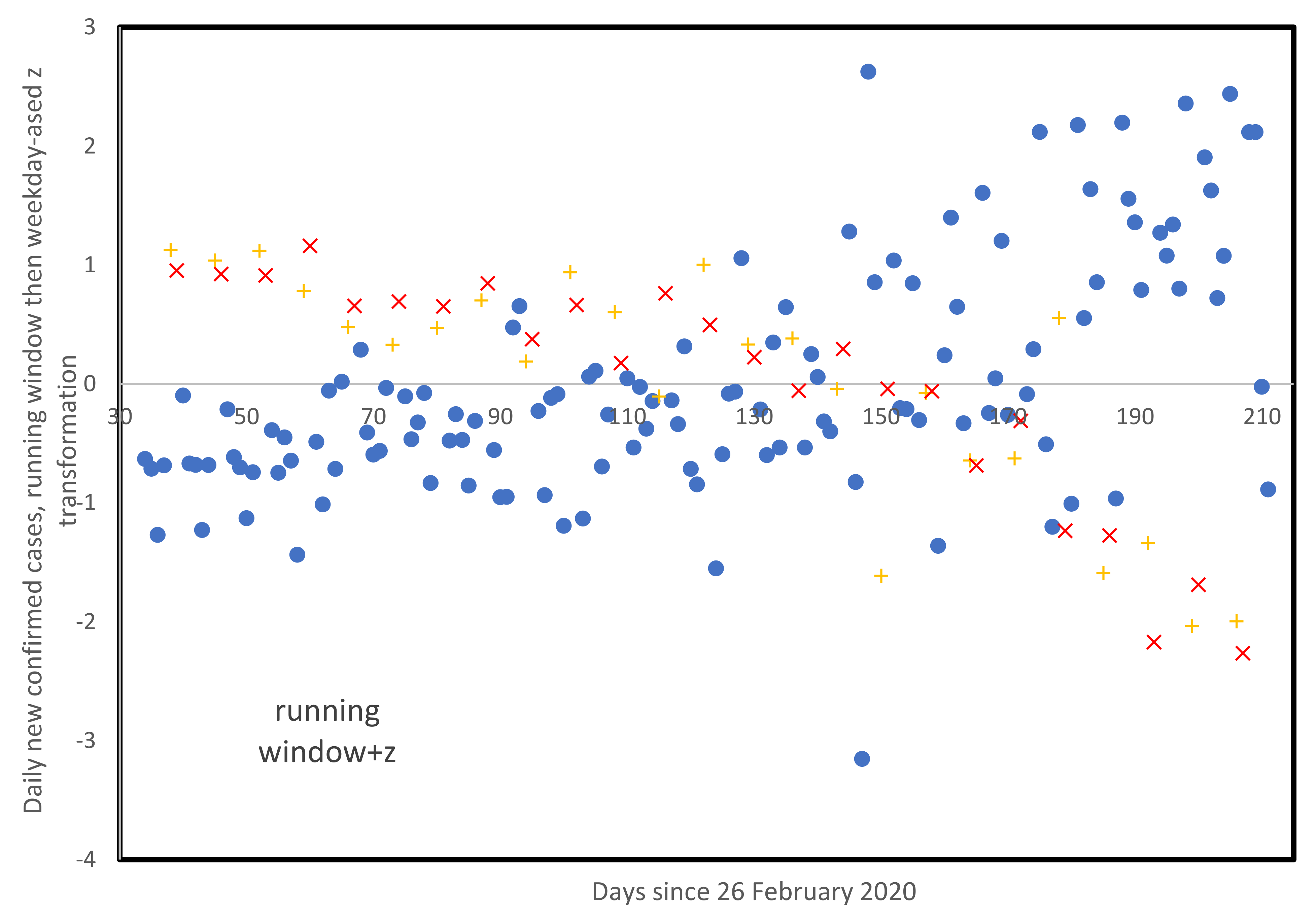
3.3. Distribution of the Daily Reproduction Numbers Rj’s. The Real Example of France
3.4. Calculation of the Rj’s for Different Countries
3.4.1. Chile
3.4.2. Russia
3.4.3. Nigeria
3.5. Weekly Patterns in Daily Infected Cases
4. Discussion
- -
- In the virus transmitter, the transition between the mechanisms of innate (the first defense barrier) and adaptive (the second barrier) immunity may explain a transient decrease in the emission of the pathogenic agent during the phase of contagiousness [15],
- -
- -
- In the recipient of the virus, individual or public policies of prevention, protection, eviction or vaccination, which evolve according to the epidemic severity and the awareness of individuals and socio-political forces, can change the sensitivity of the susceptible individuals [32].
- -
- The hypothesis of spatio-temporal stationarity of the daily reproduction numbers is no longer valid in the case of rapid geo-climatic changes, such as sudden temperature rises, which decrease the virulence of SARS CoV-2 [4], or mutations affecting its transmissibility.
- -
- The still approximate knowledge of the duration r of the period of contagiousness necessitates a more in-depth study at variable durations, by retaining the value of r, which makes all of the daily reproduction numbers positive.
- -
- The choice of uniform random fluctuations of the daily reproduction numbers is based on arguments of simplicity. A more precise study would undoubtedly lead to a unimodal law varying throughout the contagious period, the average of which following a U-shaped curve, of the type observed in the literature on a few real patients [10,54,55,56,57,58].
5. Conclusions and Perspectives
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
- 1.
- Beginning of the pandemic in France from 21 February 2020 to 9 March 2020

- 2.
- Exponential phase in France from 25 October 2020 to 7 November 2020

- 3.
- Beginning of the pandemic in the USA from 21 February 2020 to 5 March 2020

- 4.
- USA exponential phase from 1 November 2020 to 4 November 2020

- 5.
- Beginning of the pandemic in the UK from 23 February 2020 to 7 March 2020

- 6.
- UK exponential phase from 17 October 2020 to 30 October 2020

Appendix C
| All Countries | First Wave | Second Wave | ||||||
|---|---|---|---|---|---|---|---|---|
| No | Country Name | R0 | Rj’s | U-Shape | R0 | Rj’s | U-Shape | |
| 1 | AFGHANISTAN | 0.65 | 0.17; 0.09; 0.39 | YES | 0.04 | −1.38; −0.36; 1.78 | INCR |  |
| 2 | ALGERIA | 1.25 | 3.93; −6.21; 3.53 | YES | 0.91 | 1.28; −1.06; 0.69 | YES | |
| 3 | ARUBA | 5.46 | 10.31; −39.32; 34.47 | YES | 1.10 | 1.54; −1.60; 1.16 | YES | |
| 4 | ANDORRA | 1.36 | 1.00; 0.79; −0.43 | DECR | 0.12 | 4.34; −1.63; −2.59 | DECR | |
| 5 | ANGOLA | 0.63 | 0.33; 1.42; −1.12 | INV | 1.70 | 9.22; −1.58; −5.94 | DECR | |
| 6 | ANTIGUA | 1.92 | 0.00; 1.25; 0.67 | INV | 2.13 | −0.40; 1.33; 1.20 | INV | |
| 7 | ALBANIA | 0.96 | 0.48; 0.50; −0.02 | INV | 0.66 | 1.98; −0.56; −0.76 | DECR | |
| 8 | ARGENTINA | 0.73 | 0.57; −1.28; 1.44 | YES | 0.36 | 1.27; 0.75; −1.66 | DECR | |
| 9 | ARMENIA | 4.43 | 17.99; −36.99; 23.43 | YES | 0.86 | 1.41; −0.97; 0.42 | YES | |
| 10 | AUSTRALIA | 2.79 | −1.02; 3.47; 0.34 | YES | 1.50 | −0.88; 0.68; 1.70 | INCR | |
| 11 | AUSTRIA | 1.17 | −1.78; −0.05; 3.00 | INCR | 2.08 | 0.62; −3.55; 5.01 | YES | |
| 12 | AZERBAIJAN | 1.16 | 1.23; −1.32; 1.25 | YES | 0.37 | 10.36; −6.45; −3.54 | YES | |
| 13 | BAHAMAS | 0.57 | −0.13; −0.98; 1.68 | YES | 1.22 | 0.22; −0.86; 1.86 | YES | |
| 14 | BAHRAIN | 1.10 | −0.74; 0.28; 1.56 | INCR | 1.14 | 1.98; −2.69; 1.85 | YES | |
| 15 | BANGLADESH | 1.04 | 2.37; −2.97; 1.64 | YES | 0.99 | 0.86; −0.69; 0.82 | YES | |
| 16 | BARBADOS | 1.86 | 0.86; −0.64; 1.64 | YES | 1.14 | 0.22; −0.81; 1.73 | YES | |
| 17 | BELARUS | 1.57 | −2.37; −4.58; 8.52 | YES | 1.07 | −0.33; 0.24; 1.16 | INCR | |
| 18 | BELGIUM | 0.43 | 11.66; −15.63; 4.41 | YES | 2.23 | 1.17; −2.39; 3.45 | YES | |
| 19 | BELIZE | 0.99 | 0.80; 0.42; −0.23 | DECR | 0.51 | 1.77; −0.21; −1.05 | DECR | |
| 20 | BENIN | 0.85 | 0.81; 0.47; −0.43 | DECR | 0.85 | 1.17; 0.22; −0.54 | DECR | |
| 21 | BHUTAN | 15.00 | 14.00; 15.00; −14.00 | INV | 1.08 | 0.80; 0.57; −0.29 | DECR | |
| 22 | BOLIVIA | 2.17 | 8.47; −1.17; −5.13 | DECR | 1.61 | 0.96; −0.30; 0.95 | YES | |
| 23 | BOSNIA | 0.09 | −1.06; −1.05; 2.20 | INCR | 1.56 | −0.57; −0.51; 2.64 | INCR | |
| 24 | BOTSWANA | 28.47 | 0.22; 0.00; 28.25 | YES | 28.43 | 0.22; −0.05; 28.26 | YES | |
| 25 | BRAZIL | 0.77 | 0.31; 1.08; −0.62 | INV | 0.46 | 1.21; 0.16; −0.91 | DECR | |
| 26 | BRUNEI | 1.08 | 0.10; −0.15; 1.13 | YES | 1.00 | 1.00; −1.00; 1.00 | YES | |
| 27 | BULGARIA | 5.06 | 14.73; −66.02; 56.35 | YES | 0.75 | 1.34; −0.98; 0.39 | YES | |
| 28 | BURKINA FASO | 1.08 | 0.72; −0.34; 0.70 | YES | 0.94 | 0.31; 0.24; 0.39 | YES | |
| 29 | BURUNDI | 1.33 | 1.33; −0.67; 0.67 | YES | 2.18 | 0.53; 1.80; −0.15 | INV | |
| 30 | CABO VERDE | 0.82 | −0.08; −0.26; 1.16 | YES | 0.19 | 0.56; 1.37; −1.74 | INV | |
| 31 | CAMBODIA | 0.34 | 0.08; 0.25; 0.01 | INV | 0.27 | 0.06; 0.15; 0.06 | INV | |
| 32 | CAMEROON | 2.17 | 2.36; 1.25; −1.44 | DECR | 2.48 | 0.50; −0.25; 2.23 | YES | |
| 33 | CANADA | 1.10 | −0.55; −0.72; 2.37 | YES | 0.44 | 2.36; −0.44; −1.48 | DECR | |
| 34 | CAR | 1.66 | −0.07; 0.64; 1.09 | INCR | 0.33 | 0.44; −0.22; 0.11 | YES | |
| 35 | CHAD | 1.19 | 0.77; −1.15; 1.57 | YES | 0.77 | 1.19; 0.25; −0.67 | DECR | |
| 36 | CHILE | 1.00 | 0.72; 0.17; 0.11 | DECR | 1.64 | 0.37; −4.45; 5.72 | YES | |
| 37 | CHINA | 1.10 | 0.90; −0.49; 0.69 | YES | 0.87 | 1.16; 0.60; −0.89 | DECR | |
| 38 | COLUMBIA | 1.00 | 1.75; −0.86; 0.11 | YES | 1.47 | −1.14; 3.08; −0.47 | INV | |
| 39 | COMOROS | 3.75 | 0.00; −2.75; 6.5 | YES | 1.65 | −0.58; 1.24; 0.99 | INV | |
| 40 | CONGO DEM | 0.03 | −0.37; −0.39; 0.79 | YES | 0.88 | 0.66; 0.74; −0.52 | INV | |
| 41 | CONGO REP | 0.92 | 0.92; 0.92; −0.92 | DECR | 0.39 | −0.12; 0.19; 0.32 | INCR | |
| 42 | COSTA RICA | 0.50 | −2.79; −3.84; 7.13 | YES | 1.26 | 1.21; −0.85; 0.90 | YES | |
| 43 | COTE D’VOIRE | 1.18 | −0.49; −0.63; 2.30 | YES | 2.09 | 4.32; −7.09; 4.86 | YES | |
| 44 | CROTIA | 0.75 | 0.53; 0.79; −0.57 | INV | 0.57 | 0.68; −0.64; 0.53 | YES | |
| 45 | CUBA | 0.48 | −37.25; 16.17; 21.56 | INCR | 0.78 | 0.34; −0.73; 1.17 | YES | |
| 46 | CURACAO | 0.50 | 3.00; −1.00; −1.50 | DECR | 4.19 | 1.93; −4.01; 6.27 | YES | |
| 47 | CYPRUS | 0.69 | 0.27; 2.49; −2.07 | INV | 0.45 | −0.42; 1.76; −0.89 | INV | |
| 48 | CZECH | 0.16 | −0.16; 3.88; −3.56 | INV | 0.88 | 1.88; −1.41; 0.41 | YES | |
| 49 | DENMARK | 0.80 | −0.11; 0.41; 0.50 | INCR | 0.64 | −0.03; 4.65; −3.98 | INV | |
| 50 | DJIBOUTI | 0.17 | 1.23; 0.24; −1.30 | DECR | 0.36 | 0.64; 0.41; −0.69 | DECR | |
| 51 | DOMINICAN | 1.02 | 1.05; −0.31; 0.28 | YES | 1.57 | 0.32; −0.06; 1.31 | YES | |
| 52 | DOMINICA | 7.75 | 2.00; −4.00; 9.75 | YES | 0.67 | −0.36; 0.72; 0.31 | INV | |
| 53 | ECUADOR | 1.46 | −0.47; 1.06; 0.87 | INV | 1.14 | 0.73; −0.14; 0.55 | YES | |
| 54 | EGYPT | 0.84 | 0.30; 0.37; 0.17 | INV | 0.51 | 11.99; −3.76; −7.72 | DECR | |
| 55 | EL SALVADOR | 1.70 | −0.20; 0.59; 1.31 | INCR | 0.66 | −0.76; −14.49; 15.91 | YES | |
| 56 | EQUITORIAL G. | 0.38 | 0.85; −0.20; −0.27 | DECR | 1.48 | 0.81; −0.66; 1.33 | YES | |
| 57 | ERITREA | 1.18 | 1.44; −0.05; −0.21 | DECR | 0.80 | 1.02; 0.20; −0.42 | DECR | |
| 58 | ESTONIA | 0.87 | 1.96; 0.82; −1.91 | DECR | 3.04 | −0.70; −1.80; 5.54 | YES | |
| 59 | ESWATINI | 0.94 | 1.41; −1.42; 0.95 | YES | 0.71 | −0.02; 1.52; −0.79 | INV | |
| 60 | ETHIOPIA | 0.80 | −0.56; −1.45; 2.81 | YES | 1.24 | 0.34; 0.13; 0.77 | YES | |
| 61 | FIJI | 2.00 | 0.00; 1.00; 1.00 | INCR | 0.50 | 0.75; −0.50; 0.25 | YES | |
| 62 | FINLAND | 1.14 | 0.91; −0.42; 0.65 | YES | 2.41 | 0.56; −2.38; 4.23 | YES | |
| 63 | FRANCE | 1.17 | 0.82; 0.10; 0.25 | YES | 2.17 | 0.88; −0.86; 2.15 | YES | |
| 64 | GABON | 0.97 | 0.20; 0.47; 0.30 | INV | 0.19 | −0.51; 0.00; 0.70 | INCR | |
| 65 | GAMBIA | 0.83 | −0.25; 0.43; 0.65 | INCR | 0.37 | −0.38; 0.00; 0.75 | INCR | |
| 66 | GEORGIA | 1.23 | 0.16; 0.43; 0.64 | INCR | 0.79 | 1.52; −0.49; −0.24 | YES | |
| 67 | GERMANY | 0.73 | 0.15; −1.04; 1.62 | YES | 0.79 | 1.15; −0.56; 0.20 | YES | |
| 68 | GHANA | 1.48 | 0.55; 0.70; 0.23 | INV | 0.62 | 0.13; −0.81; 1.30 | YES | |
| 69 | GREECE | 0.71 | 0.33; −0.27; 0.65 | YES | 0.71 | 0.95; 0.28; −0.52 | DECR | |
| 70 | GRENADA | 14.00 | −5.00; 3.00; 16.00 | INCR | 0.10 | −0.15; 0.00; 0.25 | INCR | |
| 71 | GUADELOUPE | 1.35 | 0.00; 0.76; 0.59 | INV | 1.35 | 0.00; 0.76; 0.59 | YES | |
| 72 | GUATEMALA | 0.25 | 2.01; −0.70; −1.06 | YES | 0.27 | 1.19; −0.11; −0.81 | DECR | |
| 73 | GUIANA FRENCH | 0.88 | 1.30; −0.38; −0.04 | YES | 0.43 | 0.99; 0.27; −0.83 | DECR | |
| 74 | GUINEA | 0.46 | 0.65; −0.56; 0.37 | YES | 1.68 | 0.21; 0.68; 0.79 | INCR | |
| 75 | GUINEA BISSAU | 1.14 | 0.06; 1.59; −0.51 | INV | 4.20 | −0.11; 0.04; 4.27 | INCR | |
| 76 | GUYANA | 2.38 | −3.45; −0.20; 6.03 | INCR | 4.23 | −0.53; 0.58; 4.18 | INCR | |
| 77 | HAITI | 0.60 | 0.30; −0.13; 0.43 | YES | 0.61 | 0.32; 0.42; −0.13 | INV | |
| 78 | HONDURAS | 0.57 | −2.94; 3.12; 0.39 | INV | 1.64 | 0.13; 0.54; 0.97 | INCR | |
| 79 | HONGKONG | 0.04 | 0.95; −0.69; −0.22 | YES | 0.24 | 2.50; −8.79; 6.53 | YES | |
| 80 | HUNGARY | 0.90 | 0.66; −0.12; 0.36 | YES | 1.93 | 1.91; −2.72; 2.74 | YES | |
| 81 | ICELAND | 2.28 | −0.85; 3.93; −0.80 | INV | 0.66 | 0.84; 0.22; −0.40 | NO | |
| 82 | INDIA | 0.98 | 1.82; 0.53; −1.37 | DECR | 0.96 | 1.08; −0.57; 0.45 | YES | |
| 83 | INDONESIA | 0.95 | 0.67; 0.88; −0.60 | INV | 0.99 | 1.06; −0.03; −0.03 | YES | |
| 84 | IRAN | 1.04 | 1.73; −0.67; −0.02 | YES | 0.90 | 6.62; −6.62; 0.90 | YES | |
| 85 | IRAQ | 0.77 | 0.15; −0.35; 0.96 | YES | 0.96 | 0.77; −0.40; 0.59 | YES | |
| 86 | IRELAND | 2.16 | −2.83; −5.64; 10.63 | YES | 1.12 | 1.12; −0.39; 0.39 | YES | |
| 87 | ISRAEL | 0.21 | −1.39; 1.08; 0.52 | INV | 1.16 | −0.16; 0.44; 0.88 | INCR | |
| 88 | ITALY | 1.04 | 2.24; −1.85; 0.65 | YES | 3.69 | 1.65; −7.89; 9.93 | YES | |
| 89 | JAMAICA | 0.43 | 0.13; 0.06; 0.24 | YES | 2.47 | −0.34; 2.06; 0.75 | INV | |
| 90 | JAPAN | 1.02 | 0.69; 0.88; −0.55 | INV | 1.16 | 0.61; 0.42; 0.13 | DECR | |
| 91 | JORDAN | 2.53 | 10.82; −18.20; 9.91 | YES | 0.93 | 1.28; 0.57; −0.92 | DECR | |
| 92 | KAZAKHSTAN | 0.60 | 0.53; −5.45; 5.52 | YES | 2.06 | −0.05; 2.37; −1.26 | INV | |
| 93 | KENYA | 1.14 | 0.05; 0.65; 0.44 | INV | 1.18 | 0.47; 1.34; −0.63 | INV | |
| 94 | KOREA REP. | 1.00 | 0.12; 0.87; 0.01 | INV | 1.04 | 0.60; −0.03; 0.47 | YES | |
| 95 | KOSOVO | 1.02 | 1.00; 1.02; −1.00 | INV | 0.99 | 1.31; −0.29; −0.03 | YES | |
| 96 | KUWAIT | 0.88 | 0.5; −0.34; 0.67 | YES | 1.10 | 0.58; −0.84; 1.36 | YES | |
| 97 | KYRGYZSTAN | 0.17 | −0.73; 0.26; 1.64 | INCR | 1.05 | 0.28; −0.32; 1.09 | YES | |
| 98 | LAO PDR | 0.50 | 0.50; 0.50; −0.50 | DECR | 0.15 | 0.33; 0.74; −0.92 | INV | |
| 99 | LATVIA | 0.74 | 1.97; −0.76; −0.47 | YES | 0.50 | 0.40; −0.22; 0.32 | YES | |
| 100 | LEBANON | 1.03 | 0.57; 0.12; 0.34 | YES | 0.90 | 0.23; 0.06; 0.61 | YES | |
| 101 | LESOTHO | 7.08 | −2.86; 7.22; 2.72 | INV | 1.42 | 0.37; 1.51; −0.46 | INV | |
| 102 | LIBERIA | 0.31 | 0.18; −0.04; 0.17 | YES | 4.56 | 0.14; 4.61; −0.19 | INV | |
| 103 | LIBYA | 0.96 | 0.19; −0.71; 1.48 | YES | 0.79 | −0.42; 0.56; 0.65 | INCR | |
| 104 | LITHUANIA | 0.83 | 0.56; 0.11; 0.16 | YES | 2.49 | −0.90; −0.52; 3.91 | INCR | |
| 105 | LUXEMBOURG | 0.24 | −8.55; −3.75; 12.54 | INCR | 1.48 | 1.16; −0.91; 1.23 | YES | |
| 106 | MACAO | 0.29 | 1.14; 2.29; −3.14 | INV | - | - | - | |
| 107 | MADAGASCAR | 0.94 | 0.61; −0.16; 0.49 | YES | 0.75 | 0.38; −1.54; 1.91 | YES | |
| 108 | MALAWI | 1.12 | −0.23; 0.53; 0.82 | INCR | 6.46 | −0.41; 0.99; 5.88 | INCR | |
| 109 | MALAYSIA | 1.25 | 0.38; 2.79; −1.92 | INV | 1.30 | −0.57; 1.82; 0.05 | INV | |
| 110 | MALDIVES | 0.83 | 0.60; −0.53; 0.76 | YES | 1.05 | −0.27; 0.70; 0.62 | INV | |
| 111 | MALI | 0.64 | 0.59; 0.42; −0.37 | DECR | 7.78 | −2.64; −4.96; 15.38 | YES | |
| 112 | MALTA | 1.06 | 1.15; 0.24; −0.33 | DECR | 0.99 | −0.73; 1.81; −0.09 | INV | |
| 113 | MAURITANIA | 1.76 | −0.94; 0.29; 2.41 | INCR | 1.14 | 0.73; −0.41; 0.82 | YES | |
| 114 | MAURITIUS | 4.49 | −4.05; 0.36; 8.18 | INCR | 0.35 | 1.41; 0.53; −1.59 | DECR | |
| 115 | MAYOTTE | 5.46 | −9.46; −2.50; 17.42 | INCR | 1.05 | 0.72; −0.17; 0.50 | YES | |
| 116 | MEXICO | 0.86 | −1.39; 3.07; −0.82 | INV | 2.53 | −0.55; 0.10; 2.98 | INCR | |
| 117 | MOLDOVA | 1.03 | 2.73; −0.67; −1.03 | DECR | 0.36 | 1.27; 0.66; −1.57 | DECR | |
| 118 | MONACO | 3.15 | 0.52; −1.93; 4.56 | YES | 0.54 | 1.02; −0.12; −0.36 | DECR | |
| 119 | MONGOLIA | 10.25 | 1.25; 19.25; −10.25 | INV | 0.68 | 0.91; 0.25; −0.48 | DECR | |
| 120 | MONTENEGRO | 1.37 | 2.94; −3.90; 2.33 | YES | 0.66 | 2.36; 0.26; −1.96 | DECR | |
| 121 | MOROCCO | 0.90 | 0.36; 1.41; −0.87 | INV | 0.95 | 0.95; −0.15; 0.15 | YES | |
| 122 | MOZAMBIQUE | 0.72 | 0.92; 0.001; −0.20 | DECR | 0.70 | 2.46; −2.45; 0.69 | YES | |
| 123 | MYANMAR | 1.12 | −0.75; 1.07; 0.80 | INV | 1.15 | −1.36; −2.17; 4.68 | YES | |
| 124 | NAMIBIA | 0.68 | 1.37; −1.82; 1.13 | YES | 1.22 | −0.26; 0.95; 0.53 | INV | |
| 125 | NEPAL | 0.74 | 0.35; 0.76; −0.37 | INV | 0.78 | 0.11; 0.58; 0.09 | INV | |
| 126 | NETHERLAND | 1.19 | 0.11; 0.11; 0.97 | YES | 1.04 | 1.05; −0.99; 0.98 | YES | |
| 127 | NEW CALEDONIA | 5.00 | −2.00; 2.00; 5.00 | YES | 1.00 | 1.00; −1.00; 1.00 | YES | |
| 128 | NEW ZEALAND | 0.74 | 2.30; −3.40; 1.84 | YES | 0.72 | −0.52; 0.43; 0.81 | INCR | |
| 129 | NICARAGUA | 0.97 | −0.03; 0.97; 0.03 | INV | 1.02 | 0.86; 0.14; 0.02 | DECR | |
| 130 | NIGER | 0.63 | 0.28; −0.12; 0.47 | YES | 2.21 | −0.14; 0.39; 1.96 | INCR | |
| 131 | NIGERIA | 1.13 | 0.16; 0.39; 0.58 | INCR | 1.02 | 1.38; −0.65; 0.29 | YES | |
| 132 | MACEDONIA | 0.74 | 1.83; −1.16; 0.07 | YES | 0.74 | 1.26; −0.10; −0.42 | DECR | |
| 133 | NORWAY | 0.77 | −0.19; −0.61; 1.57 | YES | 2.13 | 6.02; −10.80; 6.91 | YES | |
| 134 | OMAN | 3.70 | 0.39; 0.12; 3.19 | YES | 9.80 | −16.87; 39.41; −12.74 | INV | |
| 135 | PAKISTAN | 1.22 | −0.61; 1.07; 0.76 | INV | 1.19 | 0.55; −0.11; 0.75 | YES | |
| 136 | PALESTINE | 0.96 | −0.18; −0.23; 1.37 | YES | 1.06 | −0.21; 0.18; 1.09 | INCR | |
| 137 | PANAMA | 0.96 | 0.16; 0.56; 0.24 | INV | 0.79 | 1.22; −0.16; −0.27 | DECR | |
| 138 | PAPAU NEW G. | 0.49 | 0.35; −1.96; 2.10 | YES | 0.88 | −0.39; 0.04; 1.23 | INCR | |
| 139 | PARAGUAY | 0.59 | −1.52; 1.90; 0.21 | INV | 1.20 | −3.20;3.06; 1.34 | INV | |
| 140 | PERU | 0.89 | 8.30; −2.47; −4.94 | DECR | 0.53 | 3.98; −4.72; 1.27 | YES | |
| 141 | PHILLIPPINES | 1.15 | 0.89; −0.08; 0.34 | YES | 1.54 | 0.07; 2.84; −1.37 | INV | |
| 142 | POLAND | 0.92 | 2.32; −1.89; 0.49 | YES | 1.31 | 1.71; −1.63; 1.23 | YES | |
| 143 | POLYNESIA | 0.66 | 0.22; 0.20; 0.24 | YES | 0.21 | −1.05; 1.09; 0.17 | INV | |
| 144 | PORTUGAL | 1.56 | −1.34; −8.29; 11.19 | YES | 3.89 | 1.13; −4.00; 6.76 | YES | |
| 145 | QATAR | 0.80 | −0.84; −1.99; 3.63 | YES | 1.03 | 0.62; 0.61; −0.20 | INV | |
| 146 | ROMANIA | 0.88 | 0.90; 0.06; −0.08 | DECR | 0.95 | 1.23; −0.48; 0.20 | YES | |
| 147 | RUSSIA | 1.07 | 1.16; −1.00; 0.91 | YES | 0.87 | 0.83; −5.77; 5.81 | YES | |
| 148 | RWANDA | 1.80 | 3.20; 2.20; −3.60 | DECR | 0.14 | 3.93; −2.75; −1.04 | YES | |
| 149 | SAO TOME | 1.44 | 0.44; 0.64; 0.36 | INV | 2.67 | 2.25; −3.45; 3.87 | YES | |
| 150 | SAN MARINO | 5.10 | 0.28; 1.14;3.68 | INCR | 0.26 | −0.05; 2.32; −2.01 | INV | |
| 151 | SAUDI ARABIA | 0.90 | −1.70; 2.94; −0.34 | INV | 0.98 | −1.05; 0.54; 1.49 | INCR | |
| 152 | SENEGAL | 0.72 | −0.19; 1.48; −0.57 | INV | 1.59 | 0.73; 0.23; 0.63 | YES | |
| 153 | SERBIA | 1.62 | −0.40; 0.47; 1.55 | INCR | 0.82 | 2.02; −0.94; −0.26 | YES | |
| 154 | SEYCHELLES | 0.48 | 0.30; 0.51; −0.33 | INV | 0.54 | 0.38; −0.19; 0.35 | YES | |
| 155 | SIERRA LEONE | 2.23 | −2.93; −0.80; 5.96 | INCR | 1.37 | 0.95; −1.25; 1.67 | YES | |
| 156 | SINGAPORE | 1.33 | 1.15; 0.51; −0.33 | DECR | 2.83 | 1.61; −2.44; 3.66 | YES | |
| 157 | SLOVAK | 0.99 | −2.67; 1.90; 1.76 | INV | 0.74 | 0.97; −0.73; 0.50 | YES | |
| 158 | SLOVENIA | 0.75 | 1.56; −0.71; −0.10 | DECR | 0.64 | 1.47; −0.47; −0.36 | YES | |
| 159 | SOMALIA | 1.18 | −0.16; 1.51; −0.17 | INV | 0.29 | 0.86; 0.57; −1.14 | DECR | |
| 160 | SOUTH AFRICA | 0.87 | 0.22; 0.73; −0.08 | INV | 1.49 | 0.20; −0.04; 1.33 | YES | |
| 161 | SOUTH SUDAN | 0.58 | 0.10; 0.16; 0.32 | INCR | 1.72 | 0.63; −0.63; 1.72 | YES | |
| 162 | SPAIN | 0.38 | −0.18; 0.27; 0.29 | INCR | 0.51 | 1.21; −0.86; 0.16 | YES | |
| 163 | SRI LANKA | 2.13 | 2.73; −0.75; 0.15 | YES | 0.79 | 0.42; 1.00; −0.63 | INV | |
| 164 | ST KITTS NEVIS | 2.00 | 0.00; 1.00; 1.00 | INCR | 1.07 | 0.25; 0.18; 0.64 | YES | |
| 165 | ST LUCIA | 1.13 | −0.53; −0.04; 1.70 | INCR | 1.00 | 1.00; −1.00; 1.00 | YES | |
| 166 | ST VINCENT | 0.04 | −0.29; 0.24; 0.10 | INV | 0.69 | −0.24; 0.35; 0.58 | INCR | |
| 167 | SUDAN | 0.36 | −1.46; 2.34; −0.52 | INV | 2.00 | 0.00; 2.00; 0.00 | INV | |
| 168 | SURINAME | 10.34 | 2.70; 18.77; −11.13 | INV | 1.63 | 2.95; −1.25; −0.07 | YES | |
| 169 | SWEDEN | 0.56 | 0.58; −1.20; 1.18 | YES | 1.21 | 0.67; −0.91; 1.45 | YES | |
| 170 | SWITZERLAND | 1.21 | 1.25; 0.13; −0.17 | DECR | 0.28 | 0.89; 1.18; −1.79 | INV | |
| 171 | SYRIA | 1.43 | 1.39; 4.13; −4.09 | INV | 0.18 | 0.31; −0.68; 0.55 | YES | |
| 172 | TAIWAN | 1.88 | −0.13; 1.38; 0.63 | INV | 0.66 | −5.21; 13.83; −7.96 | INV | |
| 173 | TAJIKISTAN | 1.02 | 0.71; −0.60; 0.91 | YES | 1.49 | 1.83; −0.17; −0.17 | YES | |
| 174 | TANZANIA | 0.91 | −1.50; 0.18; 2.23 | INCR | 1.89 | 3.42; 14.26; −15.79 | INV | |
| 175 | THAILAND | 0.69 | 0.42; 0.07; 0.20 | YES | 2.71 | −1.77; −0.75; 5.23 | INCR | |
| 176 | TIMOR LESTE | 5.00 | 1.00; 0.00; 4.00 | YES | 1.33 | 0.00; 1.00; 0.33 | INV | |
| 177 | TOGO | 0.08 | 6.05; −6.18; 0.21 | YES | 1.14 | 0.18; 0.09; 0.87 | YES | |
| 178 | TRINIDAD | 0.32 | −0.26; 1.46; −0.88 | INV | 0.55 | 0.26; 0.03; 0.26 | YES | |
| 179 | TUNISIA | 1.53 | 0.77; −0.04; 0.80 | YES | 2.77 | −3.21; −2.41; 8.39 | INCR | |
| 180 | TURKEY | 1.15 | −1.50; −1.13; 3.78 | INCR | 2.21 | 19.82; −47.90; 30.29 | YES | |
| 181 | UAE | 0.97 | 2.07; −1.11; 0.01 | YES | 1.15 | 1.25; −0.64; 0.54 | YES | |
| 182 | UGANDA | 0.95 | 0.87; −0.37; 0.45 | YES | 0.64 | 0.44; −0.06; 0.26 | YES | |
| 183 | UKRAINE | 0.96 | 1.35; −1.04; 0.65 | YES | 0.30 | 3.10; 1.07; −1.73 | DECR | |
| 184 | UK | 0.76 | −0.02; −0.76; 1.54 | YES | 1.03 | 0.43; 0.82; −0.22 | INV | |
| 185 | USA | 8.42 | 31.42; −99.18; 76.18 | YES | 0.49 | 3.32; −0.38; −2.45 | DECR | |
| 186 | URUGUAY | 0.63 | 0.71; 0.31; −0.39 | DECR | 1.03 | −0.23; 0.35; 0.91 | INCR | |
| 187 | UZBEKISTAN | 0.95 | 0.04; 0.10; 0.81 | INCR | 0.90 | −0.03; −0.39; 1.32 | YES | |
| 188 | VENEZUELA | 1.54 | 1.65; 2.95; −3.06 | INV | 0.82 | 1.09; −2.53; 2.26 | YES | |
| 189 | VIETNAM | 3.29 | −0.84; −0.39; 4.52 | YES | 1.43 | 0.76; −0.11; 0.78 | YES | |
| 190 | VIRGIN ISLANDS | 0.51 | 0.01; −0.06; 0.56 | YES | 0.33 | 0.44; −0.22; 0.11 | YES | |
| 191 | WEST GAZA | 1.00 | −1.00; −2.00; 4.00 | YES | 0.98 | 0.59; −0.11; 0.50 | YES | |
| 192 | YEMEN | 0.70 | −0.34; 0.17; 0.86 | INCR | 1.50 | 1.00; 0.00; 0.50 | YES | |
| 193 | ZAMBIA | 0.75 | 0.25; −0.13; 0.63 | YES | 1.12 | 1.11; −0.44; 0.45 | YES | |
| 194 | ZIMBABWE | 1.44 | 0.24; 0.60; 0.60 | INCR | 1.62 | 1.08; −1.12; 1.66 | YES | |
References
- Yu, I.T.S.; Li, Y.; Wong, T.W.; Tam, W.; Chan, A.T.; Lee, J.H.W.; Leung, D.Y.C.; Ho, T. Evidence of airborne transmission of the severe acute respiratory syndrome virus. N. Engl. J. Med. 2004, 350, 1731–1739. [Google Scholar] [CrossRef]
- Assiri, A.; McGeer, A.; Perl, T.M.; Price, C.S.; Al Rabeeah, A.A.; Cummings, D.A.T.; Alabdullatif, Z.N.; Assad, M.; Almulhim, A.; Makhdoom, H.; et al. Hospital Outbreak of Middle East Respiratory Syndrome Coronavirus. N. Engl. J. Med. 2013, 369, 407–416. [Google Scholar] [CrossRef] [PubMed]
- Gaunt, E.R.; Hardie, A.; Claas, E.C.J.; Simmonds, P. Epidemiology and Clinical Presentations of the Four Human Coronaviruses 229E, HKU1, NL63, and OC43 Detected over 3 Years Using a Novel Multiplex Real-Time PCR Method. J. Clin. Microbiol. 2010, 48, 2940–2947. [Google Scholar] [CrossRef]
- Demongeot, J.; Flet-Berliac, Y.; Seligmann, H. Temperature decreases spread parameters of the new covid-19 cases dynamics. Biology 2020, 9, 94. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, H.M.; Elbarkouky, R.A.; Omar, O.A.M.; Ragusa, M.A. Models for COVID-19 Daily confirmed cases in different countries. Mathematics 2021, 9, 659. [Google Scholar] [CrossRef]
- Barlow, J.; Vodenska, I. Socio-Economic Impact of the Covid-19 Pandemic in the US. Entropy 2021, 23, 673. [Google Scholar] [CrossRef] [PubMed]
- Seligmann, H.; Iggui, S.; Rachdi, M.; Vuillerme, N.; Demongeot, J. Inverted covariate effects for mutated 2nd vs 1st wave Covid-19: High temperature spread biased for young. Biology 2020, 9, 226. [Google Scholar] [CrossRef]
- Seligmann, H.; Vuillerme, N.; Demongeot, J. Summer COVID-19 Third Wave: Faster High Altitude Spread Suggests High UV Adaptation. Available online: https://www.medrxiv.org/content/10.1101/2020.08.17.20176628v1 (accessed on 22 September 2021).
- Carrat, F.; Vergu, E.; Ferguson, N.M.; Lemaitre, M.; Cauchemez, S.; Leach, S.; Valleron, A.J. Time Lines of Infection and Disease in Human Influenza: A Review of Volunteer. Am. J. Epidemiol. 2008, 167, 775–785. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, D.; Yang, P.; Poon, L.L.M.; Wang, Q. Viral load of SARS-CoV-2 in clinical samples. Lancet Infect. Dis. 2020, 20, 411–412. [Google Scholar] [CrossRef]
- Wölfel, R.; Corman, V.M.; Guggemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.; Jones, T.C.; Vollma, P.; Rothe, C.; et al. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465–469. [Google Scholar] [CrossRef]
- Liu, W.D.; Chang, S.Y.; Wang, J.T.; Tsai, M.J.; Hung, C.C.; Hsu, C.L.; Chang, S.C. Prolonged virus shedding even after seroconversion in a patient with COVID-19. J. Infect. 2020, 81, 318–356. [Google Scholar] [CrossRef]
- Ferretti, L.; Wymant, C.; Kendall, M.; Zhao, L.; Nurtay, A.; Abeler-Dörner, L.; Parker, M.; Bonsall, D.; Fraser, C. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 2020, 368, eabb6936. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Jian, S.W.; Liu, D.P.; Ng, T.C.; Huang, W.T.; Lin, H.H. Contact Tracing Assessment of COVID-19 Transmission Dynamics in Taiwan and Risk at Different Exposure Periods Before and After Symptom Onset. JAMA Intern. Med. 2020, 180, 1156–1163. [Google Scholar] [CrossRef]
- He, X.; Lau, E.H.Y.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.C.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020, 26, 672–675. [Google Scholar] [CrossRef] [PubMed]
- Lacoude, P. Covid-19: Le Début de la Fin? Available online: https://www.contrepoints.org/2020/07/22/376624-covid-19-lx10-debut-dx10-la-fin-1 (accessed on 22 November 2020).
- Delbrück, M. Statistical fluctuations in autocatalytic reactions. J. Chem. Phys. 1940, 8, 120–124. [Google Scholar] [CrossRef]
- De Jesús Rubio, J. Stability Analysis of the Modified Levenberg-Marquardt Algorithm for the Artificial Neural Network Training. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3510–3524. [Google Scholar] [CrossRef] [PubMed]
- de Jesús Rubio, J. Adapting H-Infinity Controller for the Desired Reference Tracking of the Sphere Position in the Maglev Process. Inf. Sci. 2021, 569, 669–686. [Google Scholar] [CrossRef]
- Chiang, H.S.; Chen, M.Y.; Huang, Y.J. Wavelet-Based EEG Processing for Epilepsy Detection Using Fuzzy Entropy and Associative Petri Net. IEEE Access 2019, 7, 103255–103262. [Google Scholar] [CrossRef]
- De Jesús Rubio, J.; Pan, Y.; Pieper, J.; Chen, M.Y.; Sossa Azuela, J.H. Advances in Robots Trajectories Learning via Fast Neural Networks. Front. Neurorobot. 2021, 15, 1–3. [Google Scholar]
- Vargas, D.M. Superpixels extraction by an Intuitionistic fuzzy clustering algorithm. JART 2021, 19, 140–152. [Google Scholar] [CrossRef]
- Soriano, L.A.; Zamora, E.; Vazquez-Nicolas, J.M.; Hernandez, G.; Barraza Madrigal, J.A.; Balderas, D. PD Control Compensation Based on a Cascade Neural Network Applied to a Robot Manipulator. Front. Neurorobot. 2020, 14, 577749. [Google Scholar] [CrossRef] [PubMed]
- Demetrius, L. Boltzmann, Darwin and the directionality theory. Phys. Rep. 2013, 530, 1–86. [Google Scholar] [CrossRef]
- Rhodes, C.J.; Demetrius, L. Evolutionary Entropy Determines Invasion Success in Emergent Epidemics. PLoS ONE 2010, 5, e12951. [Google Scholar] [CrossRef] [PubMed]
- Demongeot, J.; Demetrius, L. Complexity and Stability in Biological Systems. Int. J. Bifurc. Chaos 2015, 25, 40013. [Google Scholar] [CrossRef]
- Garcia, N. Birth and death processes as projections of higher-dimensional Poisson processes. Adv. Appl. Probab. 1995, 4, 911–930. [Google Scholar] [CrossRef]
- Renkulab. COVID-19 Daily Epidemic Forecasting. Available online: https://renkulab.shinyapps.io/COVID-19-Epidemic-Forecasting/_w_e213563a/?tab=ecdc_pred&%20country=France (accessed on 22 November 2020).
- Scire, J.; Nadeau, S.A.; Vaughan, T.; Gavin, B.; Fuchs, S.; Sommer, J.; Koch, K.N.; Misteli, R.; Mundorff, L.; Götz, T.; et al. Reproductive number of the COVID-19 epidemic in Switzerland with a focus on the Cantons of Basel-Stadt and Basel-Landschaft. Swiss Med. Wkly. 2020, 150, w20271. [Google Scholar] [CrossRef]
- Worldometer. Reported Cases and Deaths by Country or Territory. Available online: https://www.worldometers.info/coronavirus/ (accessed on 2 November 2020).
- DW. Coronavirus: Russia Tightens Restrictions, but Avoids Lockdown. 2021. Available online: https://www.dw.com/en/coronavirus-russia-restrictions-pandemic-lockdown/a-55301714 (accessed on 14 October 2021).
- Seligmann, H.; Vuillerme, N.; Demongeot, J. Unpredictable, Counter-Intuitive Geoclimatic and Demographic Correlations of COVID-19 Spread Rates. Biology 2021, 10, 623. [Google Scholar] [CrossRef]
- Breban, R.; Vardavas, R.; Blower, S. Theory versus data: How to calculate R0? PLoS ONE 2007, 2, e282. [Google Scholar] [CrossRef]
- Demetrius, L. Demographic parameters and natural selection. Proc. Natl. Acad. Sci. USA 1974, 71, 4645–4647. [Google Scholar] [CrossRef]
- Demetrius, L. Statistical mechanics and population biology. J. Stat. Phys. 1983, 30, 709–750. [Google Scholar] [CrossRef]
- Demongeot, J.; Demetrius, L. La dérive démographique et la sélection naturelle: Etude empirique de la France (1850–1965). Population 1989, 2, 231–248. [Google Scholar]
- Demongeot, J. Biological boundaries and biological age. Acta Biotheor. 2009, 57, 397–419. [Google Scholar] [CrossRef]
- Gaudart, J.; Ghassani, M.; Mintsa, J.; Rachdi, M.; Waku, J.; Demongeot, J. Demography and Diffusion in epidemics: Malaria and Black Death spread. Acta Biotheor. 2010, 58, 277–305. [Google Scholar] [CrossRef]
- Demongeot, J.; Hansen, O.; Hessami, H.; Jannot, A.S.; Mintsa, J.; Rachdi, M.; Taramasco, C. Random modelling of contagious diseases. Acta Biotheor. 2013, 61, 141–172. [Google Scholar] [CrossRef]
- Wentzell, A.D.; Freidlin, M.I. On small random perturbations of dynamical systems. Russ. Math. Surv. 1970, 25, 1–55. [Google Scholar]
- Donsker, M.D.; Varadhan, S.R.S. Asymptotic evaluation of certain Markov process expectations for large time. I. Comm. Pure Appl. Math. 1975, 28, 1–47. [Google Scholar] [CrossRef]
- Freidlin, M.I.; Wentzell, A.D. Random Perturbations of Dynamical Systems; Springer: New York, NY, USA, 1984. [Google Scholar]
- Scarpino, S.V.; Petri, G. On the predictability of infectious disease outbreaks. Nat. Commun. 2019, 10, 898. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Understanding Unreported Cases in the covid-19 Epidemic Outbreak in Wuhan, China, and Importance of Major Public Health Interventions. Biology 2020, 9, 50. [Google Scholar] [CrossRef] [PubMed]
- Demongeot, J.; Griette, Q.; Magal, P. Computations of the transmission rates in SI epidemic model applied to COVID-19 data in mainland China. R. Soc. Open Sci. 2020, 7, 201878. [Google Scholar] [CrossRef]
- Adam, D.C.; Wu, P.; Wong, J.Y.; Lau, E.H.Y.; Tsang, T.K.; Cauchemez, S.; Leung, G.M.; Cowling, B.J. Clustering and superspreading potential of SARS-CoV-2 infections in Hong Kong. Nat. Med. 2020, 26, 1714–1719. [Google Scholar] [CrossRef]
- Nishiura, H.; Lintona, N.M.; Akhmetzhanov, A.R. Serial interval of novel coronavirus (COVID-19) infections. Int. J. Infect. Dis. 2020, 93, 284–286. [Google Scholar] [CrossRef] [PubMed]
- Gaudart, J.; Landier, J.; Huiart, L.; Legendre, E.; Lehot, L.; Bendiane, M.K.; Chiche, L.; Petitjean, A.; Mosnier, E.; Kirakoya-Samadoulougou, F.; et al. Factors associated with spatial heterogeneity of Covid-19 in France: A nationwide ecological study. Lancet Public Health 2021, 6, e222–e231. [Google Scholar] [CrossRef]
- Bakhta, A.; Boiveau, T.; Maday, Y.; Mula, O. Epidemiological Forecasting with Model Reduction of Compartmental Models. Application to the COVID-19 Pandemic. Biology 2021, 10, 22. [Google Scholar] [CrossRef]
- Roques, L.; Bonnefon, O.; Baudrot, V.; Soubeyrand, S.; Berestycki, H. A parsimonious approach for spatial transmissionand heterogeneity in the COVID-19 propagation. R. Soc. Open Sci. 2020, 7, 201382. [Google Scholar] [CrossRef]
- Griette, Q.; Demongeot, J.; Magal, P. A robust phenomenological approach to investigate COVID-19 data for France. Math. Appl. Sci. Eng. 2021, 3, 149–160. [Google Scholar]
- Griette, Q.; Magal, P. Clarifying predictions for COVID-19 from testing data: The example of New-York State. Infect. Dis. Model. 2021, 6, 273–283. [Google Scholar]
- Oshinubi, K.; Rachdi, M.; Demongeot, J. Analysis of Daily Reproduction Rates of COVID-19 Using Current Health Expenditure as Gross Domestic Product Percentage (CHE/GDP) across Countries. Available online: https://www.medrxiv.org/content/10.1101/2021.08.27.21262737v1 (accessed on 22 September 2021).
- Kawasuji, H.; Takegoshi, Y.; Kaneda, M.; Ueno, A.; Miyajima, Y.; Kawago, K.; Fukui, Y.; Yoshida, Y.; Kimura, M.; Yamada, H.; et al. Transmissibility of COVID-19 depends on the viral load around onset in adult and symptomatic patients. PLoS ONE 2020, 15, e0243597. [Google Scholar] [CrossRef]
- Kim, S.E.; Jeong, H.S.; Yu, Y.; Shin, S.U.; Kim, S.; Oh, T.H.; Kim, U.J.; Kang, S.J.; Jang, H.C.; Jung, S.I.; et al. Viral kinetics of SARS-CoV-2 in asymptomatic carriers and presymptomatic patients. Int. J. Infect. Dis. 2020, 95, 441–443. [Google Scholar] [CrossRef]
- Murphy, B.R.; Rennels, M.B.; Douglas, R.G., Jr.; Betts, R.F.; Couch, R.B.; Cate, T.R., Jr.; Chanock, R.M.; Kendal, A.P.; Maassab, H.F.; Suwanagool, S.; et al. Evaluation of influenza A/Hong Kong/123/77 (H1N1) ts-1A2 and cold-adapted recombinant viruses in seronegative adult volunteers. Infect. Immun. 1980, 29, 348–355. [Google Scholar] [CrossRef]
- Chao, D.L.; Halloran, M.E.; Obenchain, V.J.; Longini, I.M., Jr. FluTE, a Publicly Available Stochastic Influenza Epidemic Simulation Model. PLoS Comput. Biol. 2010, 6, e1000656. [Google Scholar] [CrossRef] [PubMed]
- Itoh, Y.; Shichinohe, S.; Nakayama, M.; Igarashi, M.; Ishii, A.; Ishigaki, H.; Ishida, H.; Kitagawa, N.; Sasamura, T.; Shiohara, M.; et al. Emergence of H7N9 Influenza A Virus Resistant to Neuraminidase Inhibitors in Nonhuman Primates. Antimicrob. Agents Chemother. 2015, 59, 4962–4973. [Google Scholar] [CrossRef]
- Demongeot, J.; Taramasco, C. Evolution of social networks: The example of obesity. Biogerontology 2014, 15, 611–626. [Google Scholar] [CrossRef] [PubMed]
- Demongeot, J.; Hansen, O.; Taramasco, C. Complex systems and contagious social diseases: Example of obesity. Virulence 2015, 7, 129–140. [Google Scholar] [CrossRef][Green Version]
- Demongeot, J.; Jelassi, M.; Taramasco, C. From Susceptibility to Frailty in social networks: The case of obesity. Math. Pop. Stud. 2017, 24, 219–245. [Google Scholar] [CrossRef]
- Oshinubi, K.; Rachdi, M.; Demongeot, J. Analysis of reproduction number R0 of COVID-19 using Current Health Expenditure as Gross Domestic Product percentage (CHE/GDP) across countries. Healthcare 2021, 9, 1247. [Google Scholar] [CrossRef]
- Oshinubi, K.; Rachdi, M.; Demongeot, J. Functional Data Analysis: Transition from Daily Observation of COVID-19 Prevalence in France to Functional Curves. Available online: https://www.medrxiv.org/content/10.1101/2021.09.25.21264106v1 (accessed on 22 September 2021).
- Oshinubi, K.; Ibrahim, F.; Rachdi, M.; Demongeot, J. Modelling of COVID-19 Pandemic vis-à-vis Some Socio-Economic Factors. Available online: https://www.medrxiv.org/content/10.1101/2021.09.30.21264356v1 (accessed on 22 September 2021).
- Oshinubi, K.; Rachdi, M.; Demongeot, J. The application of ARIMA model to analyse incidence pattern in several countries. J. Math. Comput. Sci. 2021, 26, 41–57. [Google Scholar]







| a | Initial Rj’s | t | Xt | Xt+1 | Xt+2 | Resulting R’js | R0 | Distribution Shape, Sign R0 |
|---|---|---|---|---|---|---|---|---|
| 0.1 | 2.1; 0.95; 2.1 | 4 | 15.35 | 31.74 | 113.5 | 2.1; 0.95; 2.1 | 5.15 | U-shape, positive |
| 2; 0.95; 1.9 | 6 | 113.5 | 295.8 | 778.7 | 2.03; 7.6; −16.4 | −6.77 | Inverted U-shape, negative | |
| 2; 1.06; 1.9 | 8 | 778.7 | 2083.7 | 5547 | 2.49; −2.33; 7.39 | 7.55 | U-shape, positive | |
| 1.9; 1.05; 1.9 | 10 | 5547 | 14,207 | 36,776 | 2.69; −16.7; 43.8 | 29.8 | U-shape, positive | |
| 1.9; 0.95; 1.9 | 12 | 36,776 | 93,910 | 240,359 | 2.92; 1.68; −6.7 | −2.1 | Decreased shape, negative | |
| 1.9; 1; 1.9 | 14 | 240,359 | 622,149 | 1,605,227 | 2.3; −4.83; 14.3 | 11.8 | U-shape, positive | |
| 2; 1.05; 1.9 | 16 | 1,605,227 | 4,331,630 | 11,561,153 | 2.76; 27; −70 | −40.2 | Inverted U-shape, negative | |
| 1.9; 1; 1.95 | 18 | 11,561,153 | 29,558,395 | 76,502,587 | 2.5; −6.48; 17.9 | 13.9 | U-shape, positive | |
| 2; 1; 2.1 | 20 | 76,502,587 | 2,076,519 | 556,226,772 | 2.67; −7.6; 19.7 | 14.8 | U-shape, positive | |
| 1 | 1; 1.355; 1.1 | 4 | 4.81 | 9.1 | 18.21 | 1; 1.355; 1.1 | 3.455 | Inverted U-shape, positive |
| 1; 1; 1 | 6 | 18.21 | 32.12 | 59.43 | 2.9; 5.49; −14.7 | −6.31 | Inverted U-shape, negative | |
| 3; 0.5; 2.9 | 8 | 59.43 | 247.16 | 864.34 | 3.7; −33.9; 61.3 | 31.1 | U-shape, positive | |
| 2.6; 0.7; 2.6 | 10 | 864.34 | 2574.82 | 7942 | 3; −1.79; 7.14 | 8.35 | U-shape, positive | |
| 2.5; 0.75; 1.5 | 12 | 7942.2 | 23,083.1 | 67,526.6 | 3.35; 2.54; −11.6 | −5.71 | Decreased shape, negative | |
| 2.4; 0.8; 2.4 | 14 | 67,526.6 | 199,590 | 588,437 | 2.58; −0.5; 4.8 | 6.88 | U-shape, positive | |
| 2; 1; 2 | 16 | 588,437 | 1,511,517 | 4,010,652 | 2.72; −1.08; 3.19 | 4.83 | U-shape, positive | |
| 2.3; 1.15; 2.3 | 18 | 4,010,652 | 12,316,150 | 36,415,885 | 2.88; −7.9; 21.7 | 16.7 | U-shape, positive | |
| 2.8; 0.6; 2 | 20 | 36,415,885 | 117,375,471 | 375,133,150 | 3.7; 4.1; −17 | −9.2 | Inverted U-shape, negative |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demongeot, J.; Oshinubi, K.; Rachdi, M.; Seligmann, H.; Thuderoz, F.; Waku, J. Estimation of Daily Reproduction Numbers during the COVID-19 Outbreak. Computation 2021, 9, 109. https://doi.org/10.3390/computation9100109
Demongeot J, Oshinubi K, Rachdi M, Seligmann H, Thuderoz F, Waku J. Estimation of Daily Reproduction Numbers during the COVID-19 Outbreak. Computation. 2021; 9(10):109. https://doi.org/10.3390/computation9100109
Chicago/Turabian StyleDemongeot, Jacques, Kayode Oshinubi, Mustapha Rachdi, Hervé Seligmann, Florence Thuderoz, and Jules Waku. 2021. "Estimation of Daily Reproduction Numbers during the COVID-19 Outbreak" Computation 9, no. 10: 109. https://doi.org/10.3390/computation9100109
APA StyleDemongeot, J., Oshinubi, K., Rachdi, M., Seligmann, H., Thuderoz, F., & Waku, J. (2021). Estimation of Daily Reproduction Numbers during the COVID-19 Outbreak. Computation, 9(10), 109. https://doi.org/10.3390/computation9100109










