Application of the Robust Fixed Point Iteration Method in Control of the Level of Twin Tanks Liquid
Abstract
1. Introduction
2. Methodology
3. On the Concept of Using of Fixed Point Iteration-Based Control Method
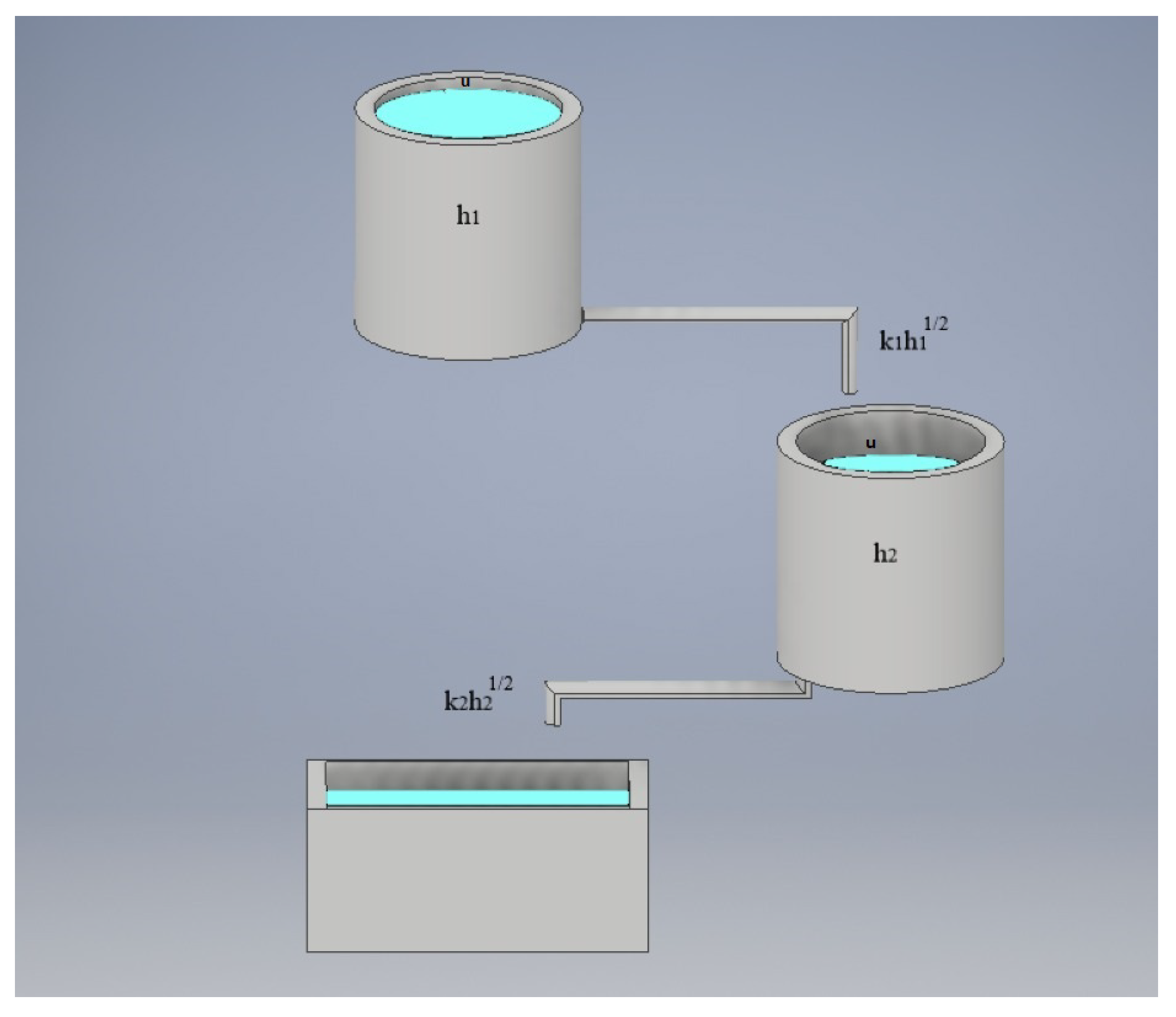
4. Study of Dual Tank Systems
Model Representation
5. Control Task of the Dual Tank System
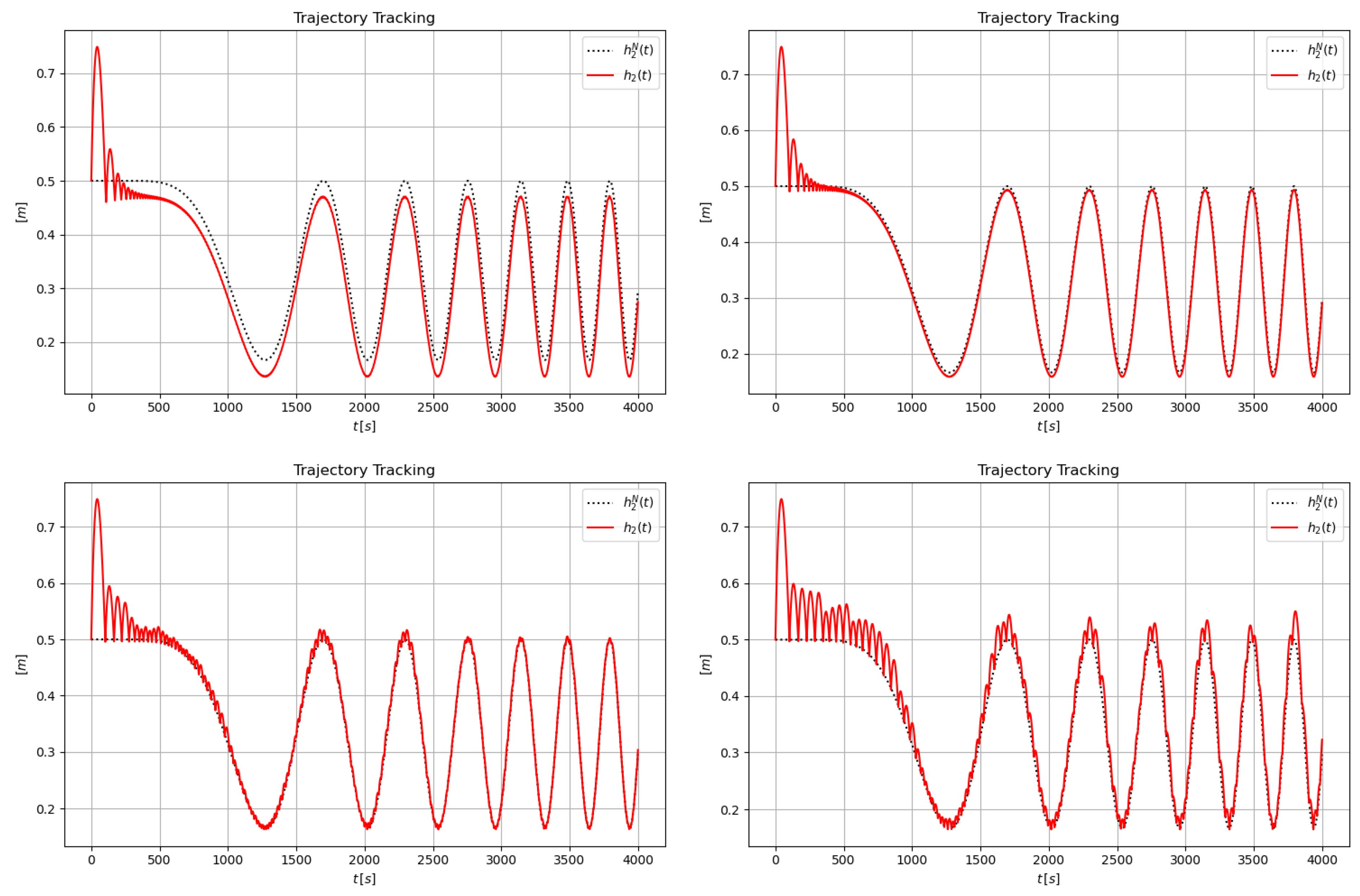
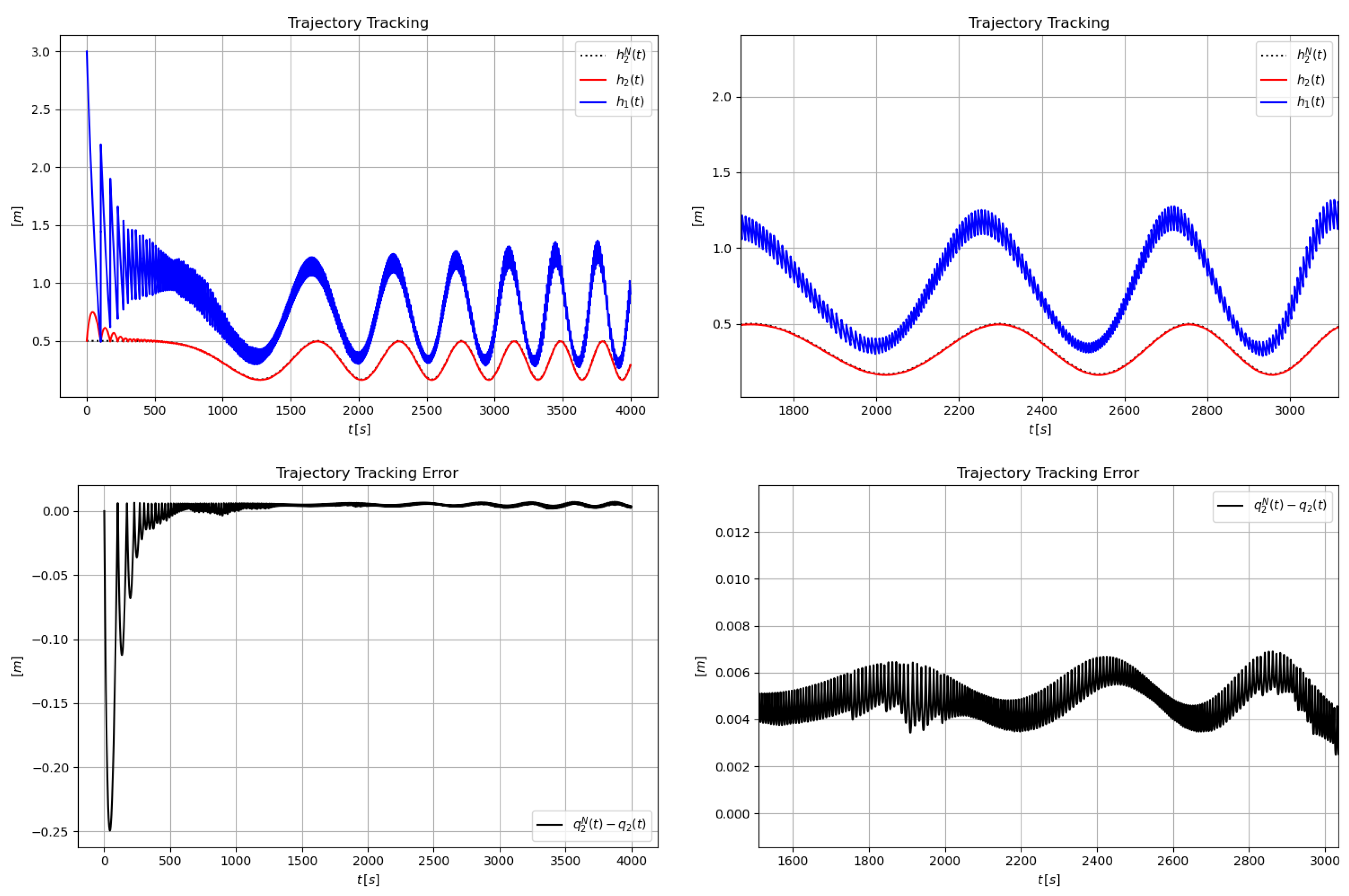
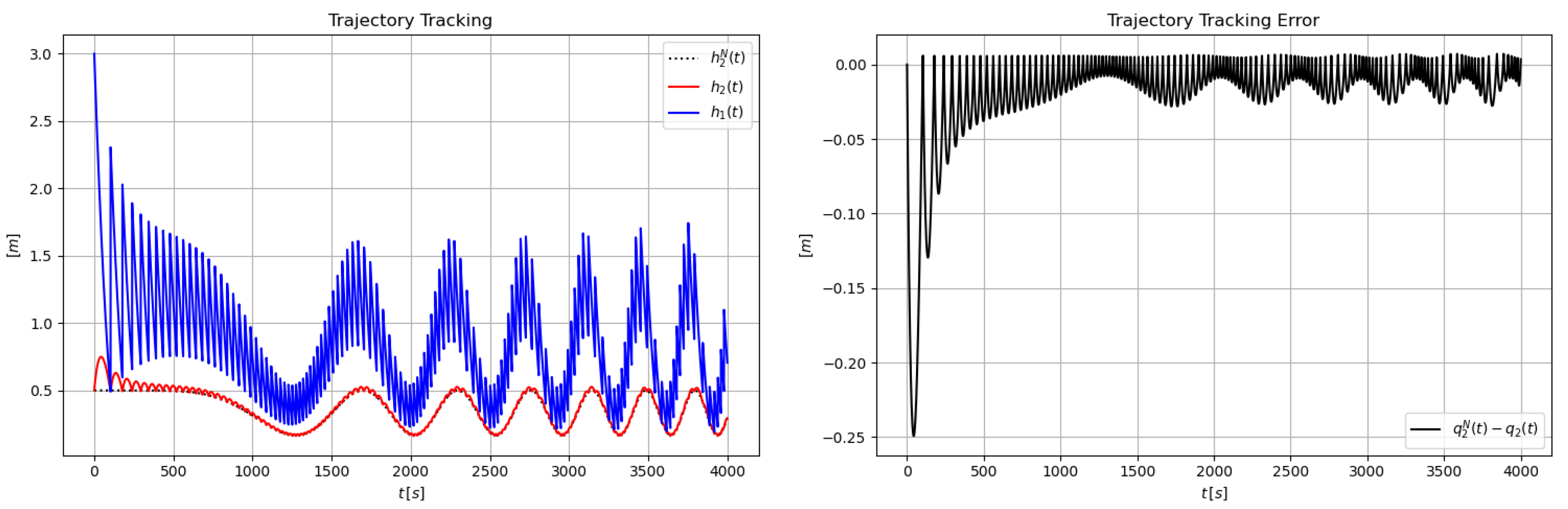
6. Simulation Results for the Coupled Tank
7. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gupta, D. Intelligent techniques for optimization of a two tank system controller. CSI Trans. ICT 2016, 4, 79–82. [Google Scholar] [CrossRef]
- Yu, S.; Lu, X.; Zhou, Y.; Feng, Y.; Qu, T.; Chen, H. Liquid level tracking control of three-tank systems. Int. J. Control Autom. Syst. 2020, 18, 2630–2640. [Google Scholar] [CrossRef]
- Li, X.; Li, Z. The Application of Linear and Nonlinear Water Tanks Case Study in Teaching of Process Control. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 113, p. 012165. [Google Scholar]
- Abukhadra, F. Active disturbance rejection control of a coupled-tank System. J. Eng. 2018, 2018, 7494085. [Google Scholar] [CrossRef]
- Ross, F.E. Automatic Liquid Level Control. U.S. Patent 4,303,406, 1 December 1981. [Google Scholar]
- Farr, J.B. Liquid Level Control with Capacitive Sensors. U.S. Patent 5,145,323, 8 September 1992. [Google Scholar]
- Zhao, J.; Zhang, X. Inverse Tangent Functional Nonlinear Feedback Control and Its Application to Water Tank Level Control. Processes 2020, 8, 347. [Google Scholar] [CrossRef]
- Abbas, H.; Asghar, S.; Qamar, S. Sliding mode control for coupled-tank liquid level control system. In Proceedings of the 10th International Conference on Frontiers of Information Technology, Islamabad, India, 17–19 December 2012; pp. 325–330. [Google Scholar]
- Almutairi, N.B.; Zribi, M. Sliding mode control of coupled tanks. Mechatronics 2006, 16, 427–441. [Google Scholar] [CrossRef]
- Chiriţă, D.; Florescu, A.; Florea, B.C.; Ene, R.; Stoichescu, D.A. Liquid level control for industrial three tanks system based on sliding mode control. Rev. Roum. Sci. Technol. 2015, 4, 437–446. [Google Scholar]
- Delavari, H.; Ranjbar, A. Robust intelligent control of coupled tanks. In Proceedings of the 9th WSEAS International Conference on Automatic Control, Modeling and Simulation, Istanbul, Turkey, 27 May 2007; pp. 1–6. [Google Scholar]
- Echaieb, K.; Gammoudi, R.; Mami, A. A water level control of coupled tank process using a nonlinear control: Tests and measurements. Am. J. Sci. Res. 2012, 56, 111–118. [Google Scholar]
- Phung, T.V.; Tzouanas, V. Design and Control of a Twin Tank Water Process; American Society for Engineering Education: Washington, DC, USA, 2012. [Google Scholar]
- Tijjani, A.S.; Shehu, M.A.; Alsabari, A.M.; Sambo, Y.A.; Tanko, N.L. Performance Analysis for Coupled-Tank System Liquid Level Control using MPC, PI and PI-plus-Feedforward Control Scheme. J. Robot. Autom. 2017, 1, 42–53. [Google Scholar]
- Thabet, H.; Ayadi, M.; Rotella, F. Towards an ultra-local model control of two-tank-system. Int. J. Dyn. Control 2016, 4, 59–66. [Google Scholar] [CrossRef][Green Version]
- Blachuta, M.; Bieda, R.; Grygiel, R. PID Regulatory Control Design for a Double Tank System Based on Time-Scale Separation. In Asian Conference on Intelligent Information and Database Systems, Proceedings of the 11th Asian Conference, ACIIDS, Yogyakarta, Indonesia, 8–11 April 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 420–430. [Google Scholar]
- Blachuta, M.; Bieda, R.; Grygiel, R. High Performance PID Control Design Based on Time-Scale Separation-a Case Study Separation. In Proceedings of the 6th International Conference on Control Engineering & Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Khan, H.; Issa, H.; Tar, J.K. Comparison of the Operation of Fixed Point Iteration-based Adaptive and Robust VS/SM-type Solutions for Controlling Two Coupled Fluid Tanks. In Proceedings of the 20th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 5–7 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (About the Operations in the Abstract Sets and Their Application to Integral Equations). Fund. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Kelley, C. Solving Nonlinear Equations with Newton’s Method, No 1 in Fundamentals of Algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Lyapunov, A. A General Task about the Stability of Motion. Ph.D. Thesis, University of Kazan, Tatarstan, Russia, 1892. (In Russian). [Google Scholar]
- Lyapunov, A. Stability of Motion; Academic Press: New York, NY, USA; London, UK, 1966. [Google Scholar]
- Tar, J.; Bitó, J.; Nádai, L.; Tenreiro Machado, J. Robust Fixed Point Transformations in Adaptive Control Using Local Basin of Attraction. Acta Polytech. Hung. 2009, 6, 21–37. [Google Scholar]
- Khan, H.; Szeghegyi, A.; Tar, J.K. Fixed point transformation-based adaptive optimal control using NLP. In Proceedings of the IEEE 15th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 14–16 September 2017; pp. 000237–000242. [Google Scholar]
- Khan, H.; Tar, J.K. Fine Tuning of the Fixed Point Iteration-Based Matrix Inversion-Free Adaptive Inverse Kinematics Using Abstract Rotations. Punjab Univ. J. Math. 2020, 52, 111–134. [Google Scholar]
- Khan, H.; Galántai, A.; Tar, J.K. Adaptive solution of the inverse kinematic task by fixed point transformation. In Proceedings of the IEEE 15th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 26–28 January 2017; pp. 000247–000252. [Google Scholar]
- Khan, H.; Tar, J.K. On the Implementation of Fixed Point Iteration-based Adaptive Receding Horizon Control for Multiple Degree of Freedom, Higher Order Dynamical Systems. Acta Polytech. Hung. 2019, 16, 135–154. [Google Scholar]
- Dineva, A.; Tar, J.; Várkonyi-Kóczy, A. Novel Generation of Fixed Point Transformation for the Adaptive Control of a Nonlinear Neuron Model. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, (SMC 2015), Hong Kong, China, 10–13 October 2015; pp. 987–992. [Google Scholar]
- Dineva, A.; Tar, J.; Várkonyi-Kóczy, A.; Piuri, V. Generalization of a Sigmoid Generated Fixed Point Transformation from SISO to MIMO Systems. In Proceedings of the IEEE 19th International Conference on Intelligent Engineering Systems, (INES 2015), Bratislava, Slovakia, 3–5 September 2015; pp. 135–140. [Google Scholar]
- Csanádi, B.; Galambos, P.; Tar, J.; Györök, G.; Serester, A. A Novel, Abstract Rotation-based Fixed Point Transformation in Adaptive Control. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC2018), Miyazaki, Japan, 7–10 October 2018; pp. 2577–2582. [Google Scholar]
- Khan, H.; Tar, J.; Rudas, I.; Eigner, G. Adaptive model predictive control based on fixed point iteration. WSEAS Trans. Syst. Control 2017, 12, 347–354. [Google Scholar]
- Khan, H.; Tar, J.; Rudas, I.; Eigner, G. Iterative solution in Adaptive Model Predictive Control by using Fixed-Point Transformation method. Int. J. Math. Models Methods Appl. Sci. 2018, 12, 7–15. [Google Scholar]





| Parameter | Exact Value | Approximate Value |
|---|---|---|
| S | (model parameter) | |
| (model parameter) | ||
| (model parameter) | ||
| (initial height) | Not Applicable | |
| (initial height) | Not Applicable | |
| (control parameter) | Not Applicable | |
| K | (control parameter) | Not Applicable |
| B | (control parameter) | Not Applicable |
| A | (control parameter) | Not Applicable |
| (control parameter) | Not Applicable | |
| (control parameter) | Not Applicable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.; Issa, H.; Tar, J.K. Application of the Robust Fixed Point Iteration Method in Control of the Level of Twin Tanks Liquid. Computation 2020, 8, 96. https://doi.org/10.3390/computation8040096
Khan H, Issa H, Tar JK. Application of the Robust Fixed Point Iteration Method in Control of the Level of Twin Tanks Liquid. Computation. 2020; 8(4):96. https://doi.org/10.3390/computation8040096
Chicago/Turabian StyleKhan, Hamza, Hazem Issa, and József K. Tar. 2020. "Application of the Robust Fixed Point Iteration Method in Control of the Level of Twin Tanks Liquid" Computation 8, no. 4: 96. https://doi.org/10.3390/computation8040096
APA StyleKhan, H., Issa, H., & Tar, J. K. (2020). Application of the Robust Fixed Point Iteration Method in Control of the Level of Twin Tanks Liquid. Computation, 8(4), 96. https://doi.org/10.3390/computation8040096






