Generalized Pattern Search Algorithm for Crustal Modeling

Abstract

In computational seismology, receiver functions represent the impulse response for the earth structure beneath a seismic station and, in general, these are functionals that show several seismic phases in the time-domain related to discontinuities within the crust and the upper mantle. This paper introduces a new technique called generalized pattern search (GPS) for inverting receiver functions to obtain the depth of the crust–mantle discontinuity, i.e., the crustal thickness H, and the ratio of crustal P-wave velocity Vp to S-wave velocity Vs. In particular, the GPS technique, which is a direct search method, does not need derivative or directional vector information. Moreover, the technique allows simultaneous determination of the weights needed for the converted and reverberated phases. Compared to previously introduced variable weights approaches for inverting H-κ stacking of receiver functions, with κ = Vp/Vs, the GPS technique has some advantages in terms of saving computational time and also suitability for simultaneous determination of crustal parameters and associated weights. Finally, the technique is tested using seismic data from the East Africa Rift System and it provides results that are consistent with previously published studies.

1. Introduction

Receiver functions are time series determined by the deconvolution of vertical component seismograms from radial component seismograms [1]. Receiver functions consist of a number of seismic phases, the arrival times of which are correlated to discontinuities in the crust and upper mantle. In other words, receiver functions represent the impulse response of the structure of the earth beneath the seismic station [2]. An algorithm called H-κ stacking of receiver functions has been used to estimate crustal thickness H and crustal Vp/Vs ratio κ, where Vp and Vs represent the P-wave and S-wave velocities, respectively, of the seismic wave in the crust [3]. Since its inception, H-κ stacking has been applied in many crustal structure studies (e.g., [4,5,6]). In some of these studies, the values of weights, which are necessary components for the H-κ stacking procedure, have been assigned through assumptions or using the Monte Carlo simulation technique (e.g., [3,7]) or by using genetic algorithms (GA) [8]. The main objective of this paper is to harness the generalized pattern search (GPS) technique to simultaneously determine optimal or near optimal values of weights along with H and κ values.

Dennis and Torczon [9] introduced a multidirectional search algorithm, and this algorithm was considered a first step towards a general purpose optimization algorithm with promising characteristics for parallel computation [10]. Succeeding work based on the multidirectional search algorithm was then bound for a class of algorithms that allow more flexible computation [11]. Following the multidirectional search algorithm, the generalized pattern search (GPS) has been developed between the 1990s and early 2000s [10,11,12,13,14,15,16]. The GPS is a direct search optimization technique that does not require the gradient or higher derivative of the objective function to solve the optimization problem. Traditional optimization methods, on the other hand, utilize the gradient or higher derivatives information in their search for an optimal solution. The direct methods of pattern search are useful tools when the problem has an objective function that is not differentiable and/or not continuous [16,17,18].

In the next few sections, we provide the method making use of receiver functions inversion and H-κ stacking algorithm followed by the GPS technique. Then, we offer our results of the implementation of the GPS technique for optimal or near optimal receiver function inversion. A discussion and conclusion on the current results and a comparison with previous approaches is provided at the end.

2. Materials and Methods

2.1. Receiver Functions

In the time domain, receiver functions are computed using deconvolution of a vertical component seismic signal from a radial component seismic signal. Since the iterative deconvolution method developed by Ligorria and Ammon [19] is well-established in receiver function processing, we implemented that method for determining the receiver functions in our study. However, we would like to point out that some new algorithms and developments in the area of deconvolution have also been introduced by different researchers more recently. Some of the advances made are in the field of receiver function processing using H-κ stacking. One of these advances, for example, was introduced by Li and co-workers and it introduces a generalized H-κ method with harmonic corrections on Ps and its crustal multiples in receiver functions [20]. Another similar development is the introduction of a new algorithm on generalized iterative deconvolution for receiver function estimation [21]. The new algorithm introduced in that study is described as a generalization of the iterative deconvolution method commonly used as a component of passive array wavefield imaging. Moreover, the authors of that new algorithm claim that their new approach can improve resolution by using an inverse operator tuned to maximize resolution and also that the signal-to-noise ratio of the result can be improved by applying a different convergence criterion than the standard method, which measures the energy left after each iteration.

Under ideal conditions, receiver functions can also be determined in the frequency domain using the ratio of radial component and vertical component seismograms:

$$\mathrm{RF}(\omega )=\frac{\mathrm{R}(\omega )}{\mathrm{V}(\omega )}$$

(1)

where RF(ω) is frequency-domain receiver function; R(ω) and V(ω) are frequency-domain radial and vertical component seismograms, respectively [22]. The time-domain receiver function is obtained by applying inverse Fourier Transform to RF(ω):

rf(t) = RF⁻¹(ω)

(2)

The Supplementary Material associated with this paper discusses some of the details of the practical aspects of computing receiver functions.

2.2. H-κ Stacking

Receiver functions display a number of phases whose arrival times are related with discontinuities in the crust and upper mantle. The phases that are important in crustal studies are depicted in Figure 1a. These phases include the reference direct P wave, P-to-S converted phase (Ps), PpPs phase, and PpSs + PsPs phase. These phases originate from an impinging plane P-wave at the crust–mantle boundary (the Moho). Figure 1b displays the receiver function corresponding to the crustal structure in Figure 1a. The mathematical relationships between crustal thickness and the arrival times t₁, t₂, and t₃ of the different seismic phases are given in the associated Supplementary Material.

H-κ stacking of receiver functions is a technique used to estimate crustal thickness H and crustal Vp-to-Vs ratio κ [3]. Using the relative arrival times t₁, t₂, and t₃ as well as H and κ, we can rewrite the objective function proposed by reference [3] as a maximization problem as follows:

Maximize

$$\mathrm{S}(\mathrm{H},\kappa )={\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{w}}_1{\mathrm{r}}_{\mathrm{j}}\left({\mathrm{t}}_1(\mathrm{H},\kappa )\right)+{\mathrm{w}}_2{\mathrm{r}}_{\mathrm{j}}\left({\mathrm{t}}_2(\mathrm{H},\kappa )\right)}+{\mathrm{w}}_3{\mathrm{r}}_{\mathrm{j}}\left({\mathrm{t}}_3(\mathrm{H},\kappa )\right)$$

(3)

subject to

$${\mathrm{w}}_1+{\mathrm{w}}_2+{\mathrm{w}}_3=1$$

(4)

where w₁, w₂, w₃ are weights. The r_j(t_i), i = 1, 2, 3, are the receiver function amplitude values at the predicted arrival times of the Ps, PpPs, and PsPs + PpSs phases, respectively, for the jth receiver function, and N is the total number of receiver functions used for the seismic station in the study. By performing a grid search through H and κ parameter space, the H and κ values corresponding to the maximum value of the objective function can be determined. The main hypothesis behind H-κ stacking is that the weighted sum stack will attain its maximum value when H and κ acquire their correct values [3].

2.3. Generalized Pattern Search (GPS) Techniques

2.3.1. Pattern Search Methods for Linearly Constrained Minimization Problems

References [15,16] proposed to extend pattern search methods for linearly constrained minimization problems. As a result, a general class of feasible point pattern search algorithms was developed and global convergence to a Karush–Kuhn–Tucker point has been proven to hold for such an approach [14]. For the case of minimization with general constraints and simple bounds, similar pattern search methods employ augmented Lagrangian ([12,24]). The pattern search methods for linearly constrained cases, just like in the case of unconstrained problems, achieve the searching objective without explicit resort to gradient or directional derivative.

In this paper, a pattern search algorithm is implemented for the following kind of optimization problem with linear constraints:

Minimize

f(x)

(5)

subject to

ℓ ≤ Ax ≤ u,

(6)

where f(x) is an objective function; ℓ and u are lower and upper bounds with ℓ ≤ u.

The Generalized Pattern Search (GPS) Algorithm

Here we employed the pattern search algorithm as proposed in reference [14]. A pattern is a matrix P_k which can be partitioned into components as follows:

P_i = [Γ_i L_i]

where Γ_i has some geometrical properties. Pattern search methods advance by managing a series of exploratory moves about the current iterate x_k to choose a new iterate x_i+1 = x_i + s_i, for some feasible step s_i. Let the feasible region for the problem be Ω. For linearly constrained pattern search, the exploratory moves is given in Algorithm 1 below:

Algorithm 1. Exploratory moves for linearly constrained pattern search.

si ∈ ∆iPi = ∆i[Γi Li]. (xi + si) ∈ Ω. If min {f(xi + y) | y ∈ ∆iΓi and(xi + y) ∈ Ω} < f(xi), then f(xi + si) < f(xi).

The generalized pattern search (GPS) algorithm for minimization with linear constraints is displayed in Algorithm 2. In order to define a particular pattern search method, we must specify the pattern P_i, the linearly constrained exploratory moves for generating a feasible step s_i, and the specific algorithms for updating P_i and Δ_i. We also define a trial step s_k to be a vector of the form s_k = Δ_kc_k, where c_k represents a column of the pattern matrix P_i and Δ_i denotes a step length parameter with Δ_i > 0.

Algorithm 2. The generalized pattern search (GPS) method for linearly constrained problems.

Suppose x0 ∈ Ω and Δ0 > 0 be given. For i = 0, 1, …, (a) Compute the objective function f(xi). (b) Determine a step si using a linearly constrained exploratory moves algorithm. (c) If f(xi + si) < f(xi), then xi+1 = xi + si. Otherwise, xi+1 = xi. (d) Update Pi and Δi.

The rules of updating Δ_i are specified in Algorithm 3 below. The goal of updating Δ_i is to make sure that the objective function f(x) decreases as the process continues. An iteration is successful if f(x_i + s_i) < f(x_i); otherwise, the iteration is considered unsuccessful. For any pattern search method to be acceptable, a step needs only to produce a simple decrease, and not a sufficient decrease.

Algorithm 3. Updating Δi.

Let τ ∈ Q, τ > 1, and {w0, w1, …, wL} ⊂ Z, w0 < 0, and wj ≥ 0, j = 1, …, L, where Q is the set of real numbers and Z represents a set of integers. Let θ = τw0, and λi ∈ Λ = {τw1, …, τwL}. (a) If f(xi + si) ≥ f(xi), then Δi+1 = θΔi. (b) If f(xi + si) < f(xi), then Δi+1 = λiΔi.

The conditions on θ and Λ ensure that 0 < θ < 1 and λ_i ≥ 1 for all λ_i ∈ Λ. Thus, if an iteration is successful, it may be possible to increase the step length parameter Δ_i, but Δ_i is not allowed to decrease. The algorithm for updating Δ_i depends on the pattern search method.

2.3.2. Generalized Pattern Search (GPS) Technique for H-κ Inversion

The GPS technique a direct search method that has significant resemblance to the steepest descent method, but unlike the steepest descent scheme, GPS does not require the computation of derivatives or directional vectors on the objective function. H-κ stacking optimization equation has five parameters to be determined if we would like to solve the problem completely. In this case, we apply the generalized pattern search (GPS) technique to solve the H-κ stacking optimization problem entirely.

For objective functions which are not differentiable or not continuous, GPS is an appropriate approach for optimization. It can be used to directly optimize all the five parameters in the problem. The GPS technique is used for solving optimization problems with no information about the gradient of the objective function. Unlike the more traditional optimization methods that use information about the gradient or higher derivatives to search for an optimal point, a direct search algorithm searches for a set of points surrounding a given point, then it looks for one where the value of the objective function is lower than the value at the current iterate point (note that we are considering a minimization problem). In general, direct search techniques are applied to solve problems for which the objective function is neither differentiable nor continuous.

The Minimization Problem for GPS Implementation

H-κ stacking was developed based on exploiting the fact that the amplitudes of the seismic phases in receiver functions attain their maximum values when the correct H and κ values are chosen. H-κ stacking also takes advantage of the signal to noise ratio (SNR) improvement with employing more receiver functions. Thus, it maximizes the stack of receiver functions which identify the correct H and κ values as well as the right set of weights that are appropriate to the quality of available receiver functions. There are two ways to implement the GPS algorithm for our specific problem. We have to either modify the GPS algorithm to work for a maximization problem, or else change the problem from a maximization to a minimization problem. It is easier to convert the maximization problem of H-κ stacking into a minimization problem. Since the expected values of H-κ stacking are either zero or positive, the maximum values of the H-κ stacking are always positive. Multiplication of the H-κ stacking values by −1 will turn the data upside down. Then, the maximum value changes to a minimum value and the minimum value to a maximum. Thus, this will be equivalent to the minimization problem. Therefore, it is possible to find the optimal values for H, κ, w₁, w₂, and w₃ using the GPS technique.

Minimize

$$\overline{{\displaystyle \mathrm{S}}}=-\left[{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{w}}_1{\mathrm{r}}_{\mathrm{j}}\left({\mathrm{t}}_1(\mathrm{H},\kappa )\right)+{\mathrm{w}}_2{\mathrm{r}}_{\mathrm{j}}\left({\mathrm{t}}_2(\mathrm{H},\kappa )\right)}-{\mathrm{w}}_3{\mathrm{r}}_{\mathrm{j}}\left({\mathrm{t}}_3(\mathrm{H},\kappa )\right)\right]$$

(7)

where r_j is the jth receiver function amplitude at the particular expected arrival time, N is the number of receiver functions for the seismic stations, and t₁, t₂, and t₃ are arrival times related to H and κ using Equations (10)–(12) in the Supplementary Material; or, we can minimize the following:

Minimize

$${\displaystyle \overline{\mathrm{S}}\left(\mathrm{x}\right)}=-\left[{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{x}}_3{\mathrm{f}}_1\left({\mathrm{x}}_1,{\mathrm{x}}_2\right)+{\mathrm{x}}_4{\mathrm{f}}_2\left({\mathrm{x}}_1,{\mathrm{x}}_2\right)-{\mathrm{x}}_5{\mathrm{f}}_3\left({\mathrm{x}}_1,{\mathrm{x}}_2\right)}\right]$$

(8)

where f₁, f₂, and f₃ are functions relating t₁, t₂, and t₃, respectively, to x₁ = H and x₂ = κ; and x₃ = w_1, x₄ = w₂ and x₅ = w₃ are weights which are subject to:

$${\mathrm{x}}_3+{\mathrm{x}}_4+{\mathrm{x}}_5=1\left(\mathrm{Linear}\mathrm{Equality}\mathrm{Constraint}\right)$$

(9)

and using the following bounds:

$$0\le {\mathrm{x}}_3\le 1.0$$

(10)

$$0\le {\mathrm{x}}_4\le 1.0$$

(11)

$$0\le {\mathrm{x}}_5\le 1.0$$

(12)

The H-κ receiver function stacking algorithm using GPS has been implemented using MATLAB. The implementation of this algorithm is given in the next subsection (Section 3.1). The receiver functions and their parameters, such as times and amplitudes of the receiver functions, for a given seismic station are obtained from the given seismic signal using the iterative deconvolution method of Ligorria and Amon [19], as mentioned in the previous section (Figure 2), and that helps to determine the parameters of the crustal structure. Figure 2 shows 13 receiver functions, each of which are obtained by the deconvolution of a vertical component seismogram from a radial component seismogram from recorded seismic earthquake data. At each iteration, the H-κ stacking or objective function values are calculated based on the amplitudes of the receiver functions at the three times picked by the H-κ stacking algorithm. The average crustal P-wave velocity (Vp) for the Main Ethiopian Rift, in which station ARBA is situated, is 6.4 km/s ([25,26]) and that value is used for the implementation. More information on seismic station ARBA and the source of data and many other information are found in the Supplementary Material to this article. Researchers making use of the H-κ stacking algorithm have been assigning values for the three weights w₁, w₂, and w₃ a little differently. As a norm, w₁ has been given the greatest weight compared to w₂ and w₃. Some researchers set a value for w₁ greater than w₂ + w₃. However, generally, most studies in the past have made direct or indirect application of the concept of linear equality constraint that we have implemented in the current study, i.e., w₁ + w₂ + w₃ (=x₃ + x₄ + x₅) = 1 (for example, [3,4,27]).

3. Data and Results

3.1. The GPS Implementation

For the GPS implementation, the maximization optimization problem was converted to a minimization optimization problem. The pattern search technique was originally developed for a minimization problem, and so, we can take advantage of previous studies if we convert the problem from a maximization to a minimization optimization problem. The steps of this conversion have already been discussed in the previous sections.

Since there are five different variables to be determined in the H-κ receiver function problem, a mesh size of 1 can offer 10 pattern vectors, each of which equal to a unit-size direction (pattern) vector. If we add the pattern vectors to an initial iterate point, we obtain 10 new iterate (mesh) points. If we apply partial polling of GPS, we calculate objective function values for the new iterate (mesh) points until we obtain an objective function value lower than the objective function at the current iterate. On the other hand, if complete polling is desired, we calculate objective function values at all the new mesh points before seeking to find the mesh point with the smallest objective function value in every iteration. Figure 2 shows receiver functions obtained from seismic data collected in seismic station ARBA which was located close to the town of Arba Minch within the Main Ethiopian Rift. As mentioned in the previous section, more information on seismic station ARBA and other seismic stations as the source of data and many other relevant information are found in the Supplementary Material to this article.

The graphical user interface (GUI) implementation of the GPS algorithm in Figure 3 displays important results from this study. The GUI implementation provides opportunities to display the GPS results. It shows the initial values of the weights and crustal parameters on the top left-hand panel, while it provides the final values of the weights and the crustal parameters at the bottom panel. The graph on the GUI displays the variation of the objective function of the minimization optimization problem versus the number of iterations. The figure particularly shows the GPS inversion results for seismic station ARBA. The initial values are (20, 1.70, 0.34, 0.33, 0.33) and the final values are calculated by the GPS algorithm. The final values of crustal parameters and weights are (30.2, 1.77, 0.6, 0.3, 0.1).

3.2. GPS Convergence Test for the H-κ Inversion

The GPS technique requires considering initial values for the variables to be explored. When we consider initial values for the different variables, especially the crustal parameters, we will be looking at feasible regions. We would be conservative compared to what the expected value for the crustal parameters are, according to global earth models such as CRUST2.0. CRUST2.0 gives global crustal thickness estimates for a very large region of a 2⁰ × 2⁰ ≈ 222 km × 222 km grid over most parts of the Earth [28]. The compilation of CRUST2.0 covers most of Eurasia, North America, and Australia and some areas of Africa and South America and in the oceans.

From previous crustal studies, the crustal thickness in the Main Ethiopian Rift normally varies between about 25 and 35 km ([7,25,26]) and the κ values in the region vary, typically, between about 1.70 and about 1.90 ([7,29]). Thus, here are the range of feasible initial values for the GPS application: H_init = 20–40, κ_init = 1.65–1.95; w_1init, w_2init, w_3init are taken from the range indicated in the previous section. GPS convergence has been tested by observing final parameters and also the final objective function values. We applied the test using not only two extreme initial values but also mixed extreme and some intermediate initial values. This has been performed for the seismic station ARBA.

4. Discussion

It was found that the GPS algorithm converged and offers the same final values irrespective of the initial values.

Table 1. The final values of parameters, weights, and objective function. Fval is the final objective function value.

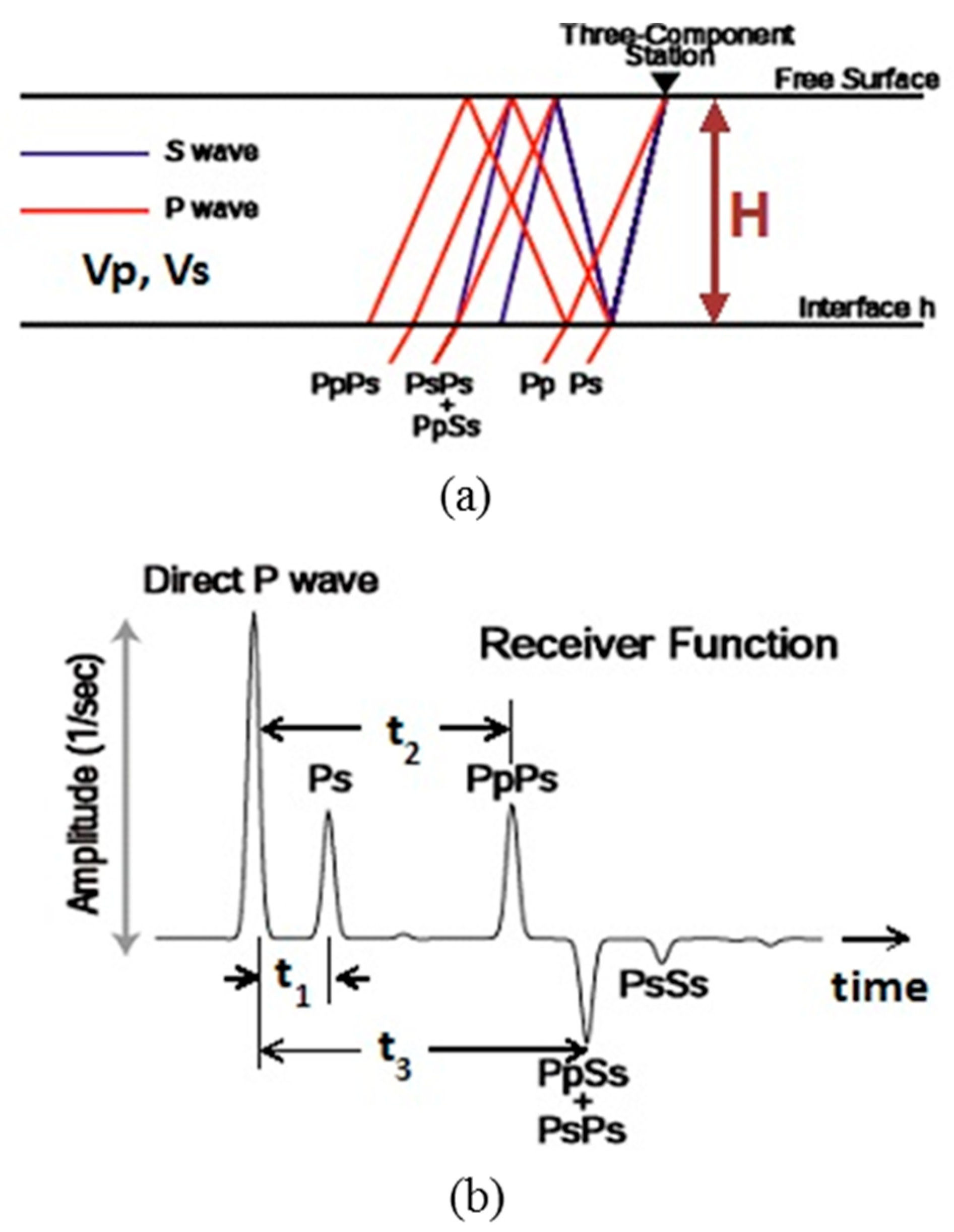
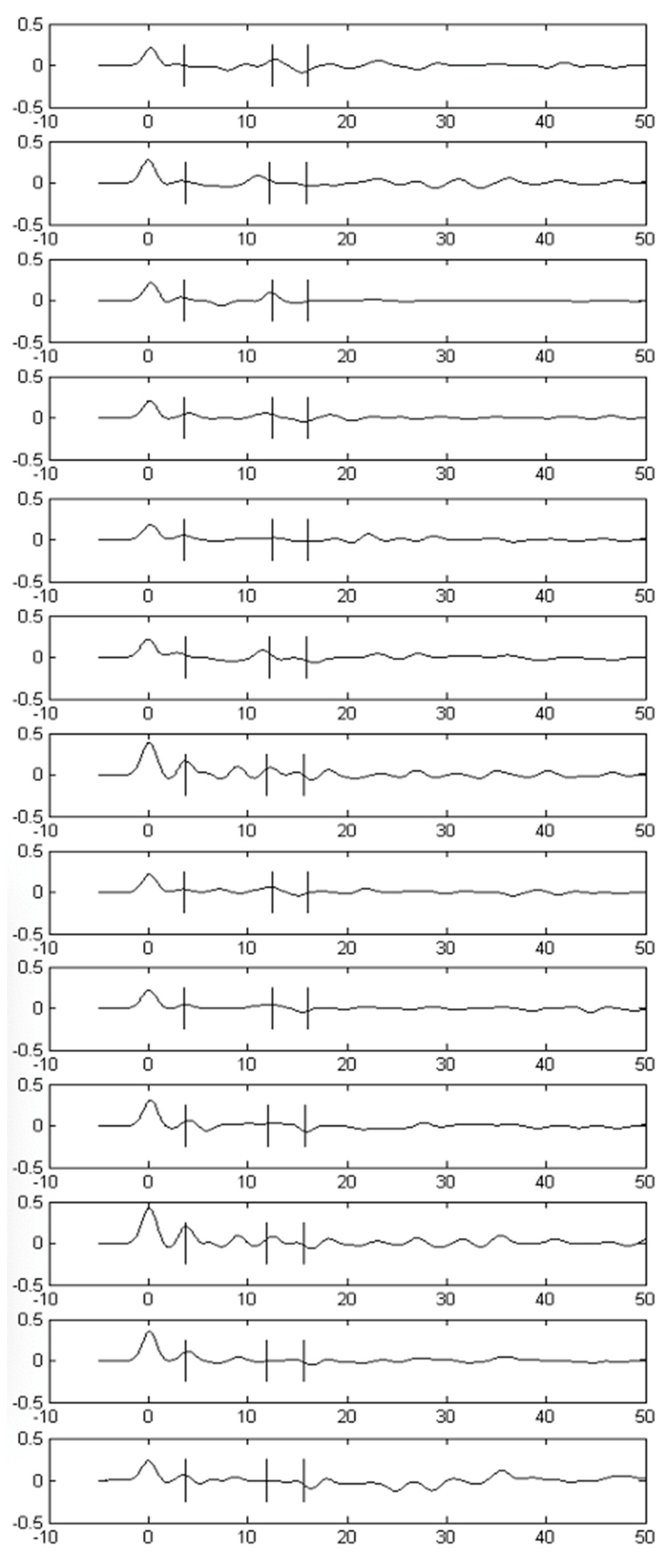
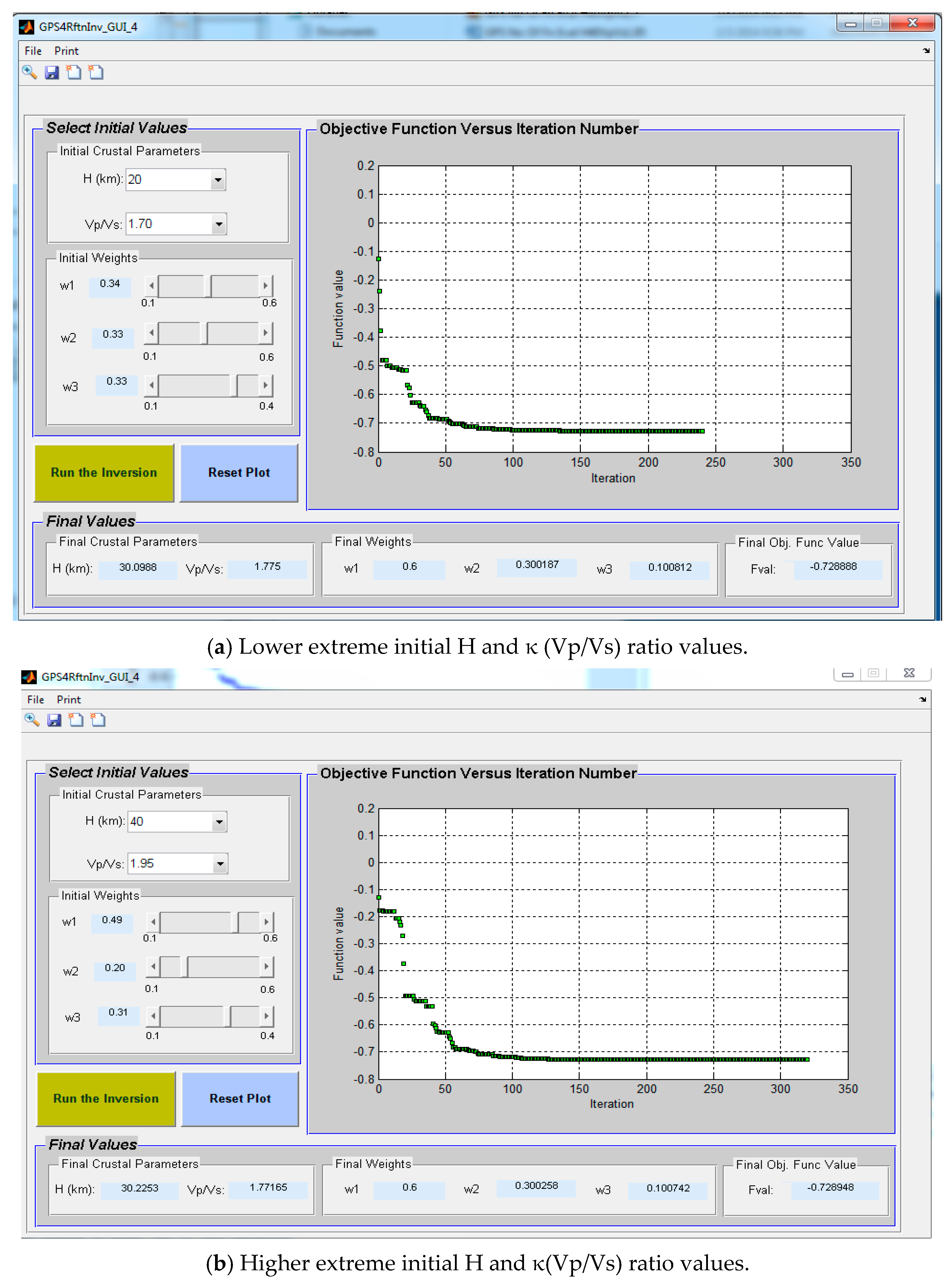
Hopt	30.0988
κopt	1.7750
w1opt	0.6000
w2opt	0.3010
w3opt	0.1000
Fval	−0.7290

summarizes the above results, and the final values for all initial value combinations are the same.

Therefore, the final values are the optimal or near optimal values from the GPS technique.

Table 2. Comparing crustal parameters for the station ARBA from three different approaches.

Different Studies	Optimal H (km)	Optimal Vp/Vs
Genetic algorithm (GA) implementation (Dugda et al., 2012, this study)	29.7	1.77
Monte Carlo (Dugda et al., 2005)	29.8	1.79
GPS technique	30.1	1.78

shows a comparison of optimal crustal parameters for the seismic station ARBA using three different approaches: the Monte Carlo approach (Dugda et al., 2005 [8]), the genetic algorithm (GA), and the GPS technique.

Table 3. Comparing optimal weights for seismic station ARBA from three different approaches.

Different Studies	Optimal w1	Optimal w2	Optimal w3
Genetic algorithm implementation (Dugda et al., 2012, BSSA)	0.5	0.4	0.1
Monte Carlo (Dugda et al., 2005)	0.5	0.4	0.1
GPS technique	0.6	0.3	0.1

provides an appraisal of weights obtained for the seismic station ARBA using the Monte Carlo technique, GA, and GPS. Application of GPS on H-κ stacking of receiver functions enables to almost exhaustively search for the weights w₁, w₂, and w₃ as well as H and κ within the given parameter space. We can observe that the GPS results are repeatable. GPS provides highly repeatable outputs, especially compared to heuristic methods which may need more runs to provide similar results. It is important to note here that our analysis has taken into consideration some potential circumstances that could affect κ values. Recently, some researchers have found that κ values for many seismic stations decrease before the time of a main shock because of crustal area fracture caused by a high stress accumulation [30,31,32]. Fortunately, for the duration of our study, there was no major earthquake in the region where our seismic stations were situated and so there should be no concern about such an effect on our κ values.

The repeatable results are important because the repeatability characteristics would help us check the dependence of the inversion on initial model parameters. If the results are independent of the initial values, we should obtain almost identical results for any initial model. GPS delivers repeatable results, even if it starts at different initial conditions. Thus, the repeatable behavior can be harnessed to use GPS to test initial value dependence of final parameters.

5. Conclusions

In this study, we developed a technique to solve the problem of inverting receiver functions to find optimal crustal parameters and optimal weights using a generalized pattern search (GPS) by setting up the problem as an optimization problem. A previous study utilized the Monte Carlo technique for solving for the weights required to determine crustal parameters using the H-κ stacking of receiver functions ([7]). One major objective of our work has been to develop a system that is suitable for automation besides providing optimal solutions. Our algorithms have been tested using seismic data from more than twenty-five seismic stations and we showed that our results are consistent with previous studies.

Application of GPS on H-κ stacking of receiver functions enables to explore for optimal values just as it is possible to conduct an exhaustive search for the weights w₁, w₂, w₃ as well as H and κ. The GPS method performs the search very quickly because its exploration amounts to finding the steepest descent path without computing the derivative of the objective function. Since it is not computing the derivatives, this makes the GPS faster in its convergence. Moreover, the GPS technique is suitable for objective functions in which finding the derivative is not easy and/or when the objective functions are not continuous. The objective function in this research satisfies both of these last conditions. Finding the derivative for our objective function is not easy and the objective function is not continuous either. Whenever the GPS is successful in its search in the current iteration, its step length increases (in our implementation, the step size Δ doubles) on the next iteration. This is an important factor contributing to the faster convergence of the GPS technique.

Some of the advantages of the GPS technique observed in this research include that outputs and results can be repeated seamlessly, the number of iterations and the number of functions evaluated are the same as long as the machine and initial conditions remain the same, and optimal values do not depend on the initial values. The tool developed utilizing GPS optimizes the given problem and has the following features: it is suitable for automatic processing of seismic data from all stations at the same time; it uses a user-friendly approach based on MATLAB; the approach may not need much knowledge of seismology; and it takes into account the quality of receiver functions through variable weights.

This study confirms that the GPS technique implemented on H-κ stacked receiver function optimization can provide optimal weights as well as optimal crustal parameters H and κ. The optimal crustal parameters and weights produced by the GPS are consistent with the GA results. Results for the station ARBA and others could make it clear that the weights and parameters found by GPS closely match those obtained previously using a different method and also the results from GA implementation.