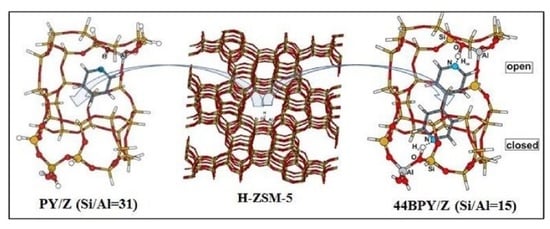
DFT Study of Si/Al Ratio and Confinement Effects on the Energetics and Vibrational Properties of some Aza-Aromatic Molecules Adsorbed on H-ZSM-5 Zeolite
Abstract
1. Introduction
2. Theoretical Calculations
3. Results and Discussion
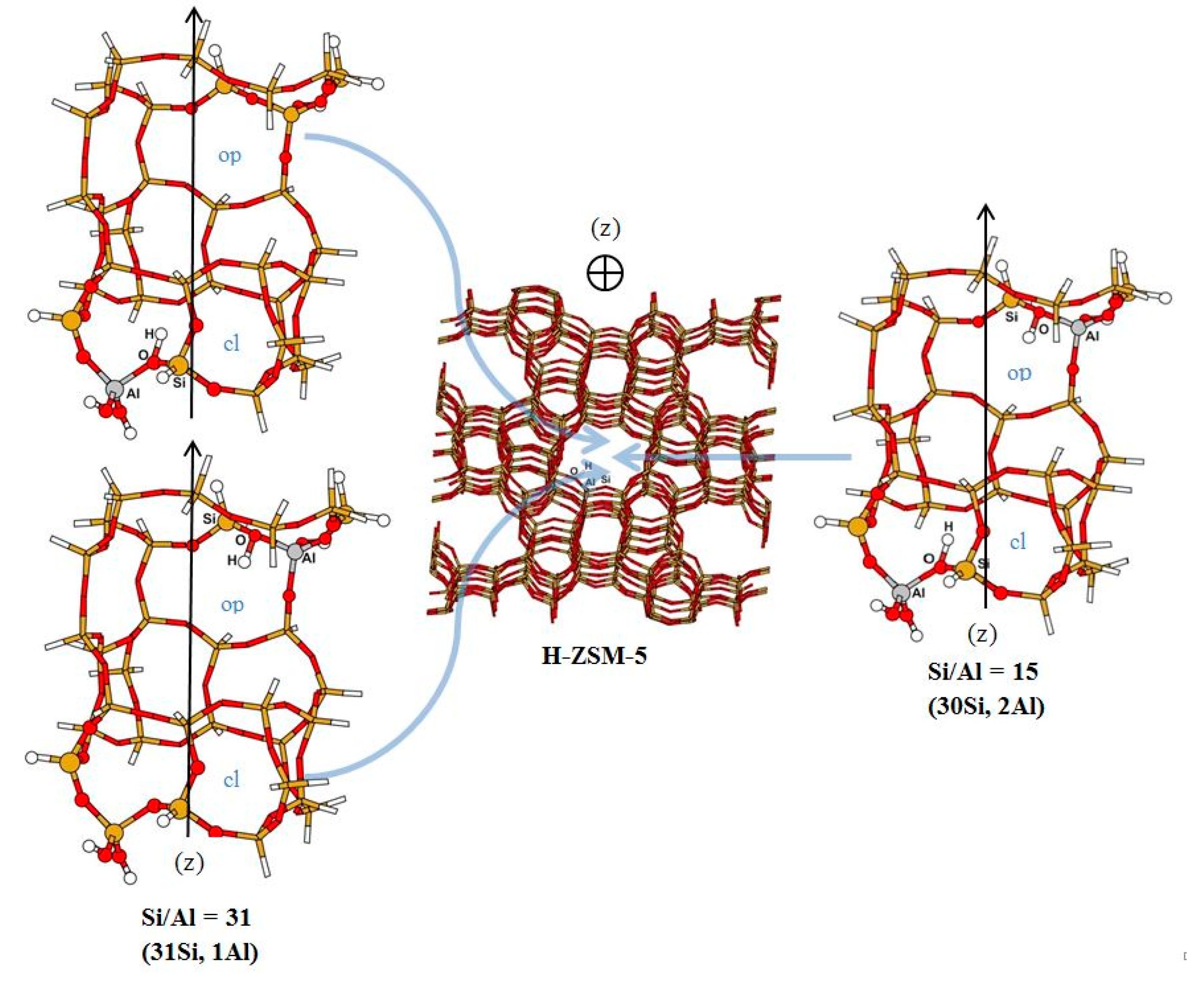
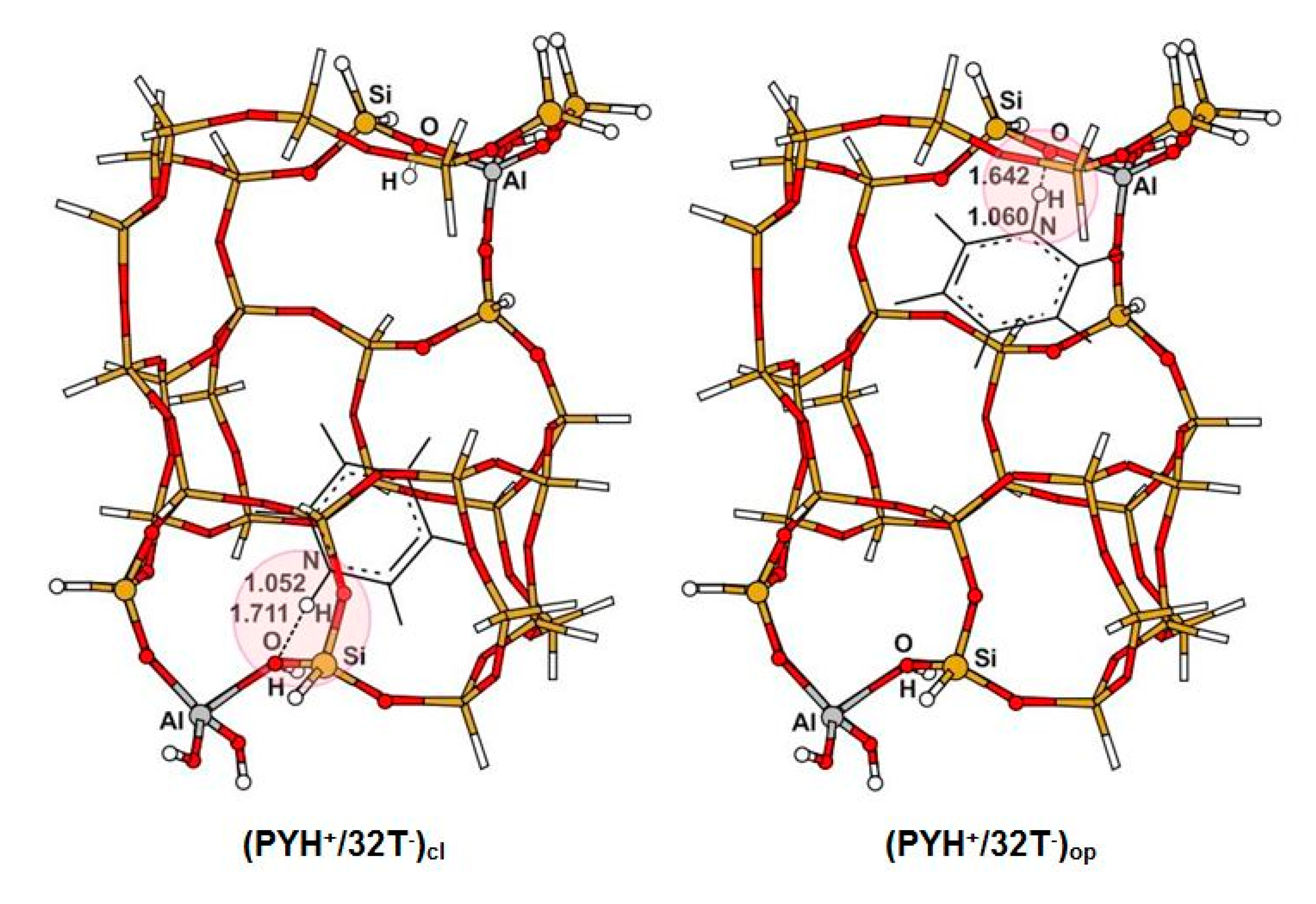
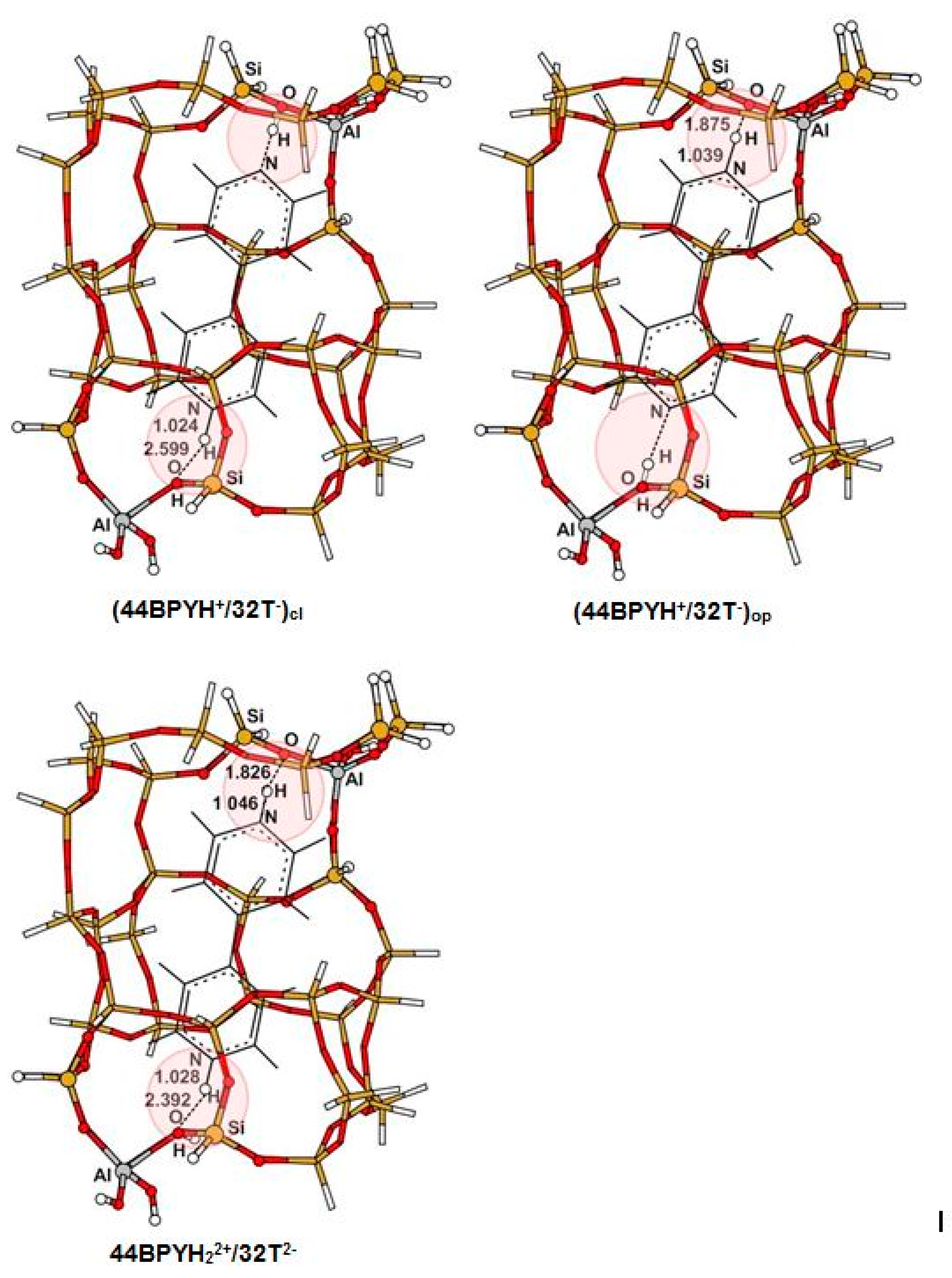
3.1. Structure and Energetic Analysis
3.2. Vibrational Frequencies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bhattacharyya, K.G.; Talukdar, A.K. Catalysis in Petroleum and Petrochemical Industries; Narosa Publishing House: New Dehli, India, 2005. [Google Scholar]
- Auerbach, S.M.; Carrado, K.A.; Dutta, P.K. Handbook of Zeolite Science and Technology; Marcel-Dekker: New York, NY, USA, 2003. [Google Scholar]
- Chen, Y.H. Urea-SCR Technology for deNOx After Treatment of Diesel Exhausts; Springer: New York, NY, USA, 2014. [Google Scholar]
- Martinez, C.; Corma, A. Inorganic molecular sieves: Preparation, Modification and Industrial Application in Catalytic Processes. Coor. Chem. Rev. 2011, 255, 1558–1580. [Google Scholar] [CrossRef]
- Buzzoni, R.; Bordiga, S.; Ricchiardi, G.; Lamberti, C.; Zecchina, A.; Bellussi, G. Interaction of Pyridine with Acidic (H-ZSM5, H-β, H-MORD Zeolites) and Superacidic (H-Nafion Membrane) Systems: An IR Investigation. Langmuir 1996, 12, 930–940. [Google Scholar] [CrossRef]
- Ferwerda, R.; van der Maas, J.H.; van Duijneveldt, F.B. Pyridine Adsorption onto Metal Oxides: An ab Initio Study of Model Systems. J. Mol. Catal. A Chem. 1996, 104, 319–328. [Google Scholar] [CrossRef]
- Moissette, A.; Batonneau, Y.; Brémard, C. Conformation and Protonation of 2,2′-Bipyridine and 4,4′-Bipyridine in Acidic Aqueous Media and Acidic ZSM-5 Zeolites: A Raman Scattering Study. J. Am. Chem. Soc. 2001, 123, 12325–12334. [Google Scholar] [CrossRef]
- Daniell, W.; Topsoe, N.-Y.; Knözinger, H. An FTIR Study of the Surface Acidity of USY Zeolites: Comparison of CO, CD3CN, and C5H5N Probe Molecules. Langmuir 2001, 17, 6233–6239. [Google Scholar] [CrossRef]
- Ehresmann, J.O.; Wang, W.; Herreros, B.; Luigi, D.-P.; Venkatraman, T.N.; Song, W.; Nicholas, J.B.; Haw, J.F. Theoretical and Experimental Investigation of the Effect of Proton Transfer on the 27Al MAS NMR Line Shapes of Zeolite−Adsorbate Complexes: An Independent Measure of Solid Acid Strength. J. Am. Chem. Soc. 2002, 124, 10868–10874. [Google Scholar] [CrossRef]
- Dedecek, J.; Lucero, M.J.; Li, C.; Gao, F.; Klein, P.; Urbanova, M.; Tvaruzkova, Z.; Sazama, P.; Sklenak, S. Complex Analysis of the Aluminum Siting in the Framework of Silicon-Rich Zeolites. A Case Study on Ferrierites. J. Phys. Chem. C 2011, 115, 11056–11064. [Google Scholar] [CrossRef]
- Jobic, H.; Czjzek, M.; van Santen, R.A. Interaction of Water with Hydroxyl Groups in H-Mordenite: A Neutron Inelastic Scattering Study. J. Phys. Chem. 1992, 96, 1540–1542. [Google Scholar] [CrossRef]
- Sauer, J.; Ugliengo, P.; Garrone, E.; Saunders, V.R. Theoretical Study of van der Waals Complexes at Surface Sites in Comparison with the Experiment. Chem. Rev. 1994, 94, 2095–2160. [Google Scholar] [CrossRef]
- Kassab, E.; Jessri, H.; Allavena, M.; White, D. Ab initio Calculations of Carbonyl Adsorption Complexes at Zeolitic Brønsted Sites Simulated by Model Clusters: Role of Modeling. J. Phys. Chem. A 1999, 103, 2766–2774. [Google Scholar] [CrossRef]
- Rozanska, X.; van Santen, R.A.; Hutschka, F. A DFT Study of the Cracking Reaction of Thiophene Activated by Small Zeolitic Clusters. J. Catal. 2001, 200, 79–90. [Google Scholar] [CrossRef]
- Castellà-Ventura, M.; Akacem, Y.; Kassab, E. Vibrational Analysis of Pyridine Adsorption on the Brønsted Acid Sites of Zeolites Based on Density Functional Cluster Calculations. J. Phys. Chem. C 2008, 112, 19045–19054. [Google Scholar]
- Allavena, M.; Seiti, K.; Kassab, E.; Ferenczy, G.; Angyan, J.G. Quantum-Chemical Model Calculations on the Acidic Site of Zeolites Including Madelung-Potential Effects. Chem. Phys. Lett. 1990, 168, 461–467. [Google Scholar] [CrossRef]
- Yuan, S.; Shi, W.; Li, B.; Wang, J.; Jiao, H.; Li, Y.-W. Theoretical ONIOM2 Study on Pyridine Adsorption in the Channels and Intersection of ZSM-5. J. Phys. Chem. A 2005, 109, 2594–2601. [Google Scholar] [CrossRef]
- Boekfa, B.; Choomwattana, S.; Khongpracha, P.; Limtrakul, J. Effects of the Zeolite Framework on the Adsorptions and Hydrogen-Exchange Reactions of Unsaturated Aliphatic, Aromatic, and Heterocyclic Compounds in ZSM-5 Zeolite: A Combination of Perturbation Theory (MP2) and a Newly Developed Density Functional Theory (M06-2X) in ONIOM Scheme. Langmuir 2009, 25, 12990–12999. [Google Scholar]
- Patet, R.E.; Caratzoulas, S.; Vlachos, D.G. Adsorption in Zeolites Using Mechanically Embedded ONIOM Clusters. Phys. Chem. Chem. Phys. 2016, 18, 26094–26106. [Google Scholar] [CrossRef]
- O’Malley, A.J.; Logsdail, A.J.; Sokol, A.A.; Catlow, C.R.A. Modelling Metal Centres, Acid Sites and Reaction Mechanisms in Microporous Catalysts. Faraday Discuss. 2016, 188, 235–255. [Google Scholar] [CrossRef]
- Yi, X.; Li, G.; Huang, L.; Chu, Y.; Liu, Z.; Xia, H.; Zheng, A.; Deng, F. An NMR Scale for Measuring the Base Strength of Solid Catalysts with Pyrrole Probe: A Combined Solid-State NMR Experiment and Theoretical Calculation Study. J. Phys. Chem. C 2017, 121, 3887–3895. [Google Scholar] [CrossRef]
- Nguyen, C.M.; Reyniers, M.F.; Marin, G.B. Theoretical Study of the Adsorption of the Butanol Isomers in H-ZSM-5. J. Phys. Chem. C 2011, 115, 8658–8669. [Google Scholar] [CrossRef]
- Cheng, L.; Curtiss, L.A.; Assary, R.S.; Greeley, J.; Kerber, T.; Sauer, J. Adsorption and Diffusion of Fructose in Zeolite HZSM-5: Selection of Models and Methods for Computational Studies. J. Phys. Chem. C 2011, 115, 21785–21790. [Google Scholar] [CrossRef]
- Boscoboinik, J.A.; Yu, X.; Emmez, E.; Yang, B.; Shaikhutdinov, S.; Fischer, F.D.; Sauer, J.; Freund, H.J. Interaction of Probe Molecules with Bridging Hydroxyls of Two-Dimensional Zeolites: A Surface Science Approach. J. Phys. Chem. C 2013, 117, 13547–13556. [Google Scholar] [CrossRef]
- Liu, C.; Tranca, I.; van Santen, R.A.; Hensen, E.J.M.; Pidko, E.A. Scaling Relations for Acidity and Reactivity of Zeolites. J. Phys. Chem. C 2017, 121, 23520–23530. [Google Scholar] [CrossRef] [PubMed]
- Boronat, M.; Corma, A. What Is Measured When Measuring Acidity in Zeolites with Probe Molecules? ACS Catal. 2019, 9, 1539–1548. [Google Scholar] [CrossRef] [PubMed]
- Kassab, E.; Castellà-Ventura, M.; Akacem, Y. Theoretical Study of 4,4′-Bipyridine Adsorption on the Brønsted Acid Sites of H-ZSM-5 Zeolite. J. Phys. Chem. C 2009, 113, 20388–20395. [Google Scholar] [CrossRef]
- Akacem, Y.; Castellà-Ventura, M.; Kassab, E. Theoretical Study of the Aluminum Distribution Effects on the Double Proton Transfer Mechanisms upon Adsorption of 4,4′-Bipyridine on H-ZSM-5. J. Phys. Chem. A 2012, 116, 1261–1271. [Google Scholar] [CrossRef]
- Castellà-Ventura, M.; Moissette, A.; Kassab, E. A Theoretical Study of the Confinement Effects on the Energetics and Vibrational Properties of 4,4′-Bipyridine Adsorption on H-ZSM-5 Zeolite. Phys. Chem. Chem. Phys. 2018, 20, 6354–6364. [Google Scholar] [CrossRef]
- Nishi, K.; Kamiya, N.; Yokomori, Y. Single-Crystal Structure of a Pyridine Sorption Complex of Zeolite HZSM-5 (H-MFI). Micropor. Mesopor. Mat. 2007, 101, 83–89. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision, D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Parker, L.M.; Bibby, D.M.; Burns, G.R. Fourier-Transform Infrared Study of Pyridine Sorbed on Zeolite HY. J. Chem. Soc. Faraday Trans. 1991, 87, 3319–3323. [Google Scholar] [CrossRef]
- Hendra, P.J.; Passingham, C.; Warnes, G.M.; Burch, R.; Rawlence, D.J. Fourier Transform Raman Spectroscopy in the Study of Species Adsorbed on Catalyst Surfaces. Chem. Phys. Lett. 1989, 164, 178–184. [Google Scholar] [CrossRef]
- Castellà-Ventura, M.; Kassab, E. Vibrational Analysis of Some Transient Species Implicated in the Photoreduction of 4,4′-Bipyridine Based on ab Initio and Density Functional Calculations. J. Raman Spectrosc. 1998, 29, 511–536. [Google Scholar] [CrossRef]
- Klots, T.D. Raman Vapor Spectrum and Vibrational Assignment for Pyridine. Spectrochim. Acta A 1998, 54, 1481–1498. [Google Scholar] [CrossRef]
- Ould-Moussa, L.; Poizat, O.; Castellà-Ventura, M.; Buntinx, G.; Kassab, E. Ab Initio Computations of the Geometrical, Electronic, and Vibrational Properties of the Ground State, the Anion Radical, and the N,N′-Dihydro Cation Radical of 4,4′-Bipyridine Compared to Transient Raman Spectra. J. Phys. Chem. 1996, 100, 2072–2082. [Google Scholar] [CrossRef]
- Zhuang, Z.; Cheng, J.; Wang, X.; Zhao, B.; Han, X.; Luo, Y. Surface-Enhanced Raman Spectroscopy and Density Functional Theory Study on 4,4′-Bipyridine Molecule. Spectrochim. Acta A 2007, 67, 509–516. [Google Scholar] [CrossRef] [PubMed]
| Si/Al | Geometrical Parameters 1 | PY + 32T | 44BPY + 32T | ||||
|---|---|---|---|---|---|---|---|
| PYH+/32T− | 44BPYH+/32T− | 44BPYH22+/32T2− | |||||
| Open | Closed | Open | Closed | Open | Closed | ||
| 31 (31Si,1Al) | NH | 1.060 | 1.052 | 1.036 | 1.024 | ||
| OH | 1.646 | 1.717 | 1.884 | 2.596 | |||
| NO | 2.698 | 2.698 | 2.744 | 3.301 | |||
| NHO | 171.4 | 153.3 | 138.2 | 125.8 | |||
| 15 (30Si,2Al) | NH | 1.060 | 1.052 | 1.039 | 1.024 | 1.046 | 1.028 |
| OH | 1.642 | 1.711 | 1.875 | 2.599 | 1.826 | 2.392 | |
| NO | 2.696 | 2.695 | 2.781 | 3.316 | 2.760 | 3.147 | |
| NHO | 172.0 | 153.8 | 143.7 | 126.9 | 146.7 | 129.5 | |
| Adsorption Complexes | Si/Al = 15 | Si/Al = 31 | ||||
|---|---|---|---|---|---|---|
| Eads | Edisp 1 | Eads | Edisp 1 | |||
| B3LYP | M06-2X-D3 | B3LYP | M06-2X-D3 | |||
| (PYH+/32T−)op | −23.2 | −35.2 | −12.0 | −23.5 | −35.3 | −11.8 |
| (PYH+/32T−)cl | −3.7 | −28.4 | −24.7 | −3.1 | −28.5 | −25.4 |
| (44BPYH+/32T−)op | −0.7 | −44.0 | −43.3 | +3.9 | −36.8 | −40.7 |
| (44BPYH+/32T−)cl | +2.1 | −39.0 | −41.1 | +12.0 | −25.5 | −37.5 |
| 44BPYH22+/32T2− | −3.2 | −44.2 | −41.0 | |||
| Vibrational Modes 1 | PY | PYH+/32T− | |||||
|---|---|---|---|---|---|---|---|
| Exp 2 | Calc 3 | Exp 4,5 | Closed | Open | |||
| Si/Al = 15 Calc 3,5 | Si/Al = 31 Calc 3,5 | Si/Al = 15 Calc 3,5 | Si/Al = 31 Calc 3,5 | ||||
| 1 | 991 | 987 | 1007 (+16)–1015 (+24) | 994 (+7) | 990 (+4) | 994 (+7) | 990 (+4) |
| 12 | 1032 | 1021 | 1025 (−7)–1035 (+3) | 1013 (−8) | 1021 (−1) | 1013 (−8) | 1021 (0) |
| 19b | 1442 | 1446 | 1530 (+88)–1550 (+108) | 1560 (+114) | 1557 (+111) | 1560 (+115) | 1556 (+111) |
| 19a | 1483 | 1487 | 1485 (+2)–1500 (+17) | 1485 (−2) | 1493 (+6) | 1485 (−2) | 1493 (+7) |
| 8b | 1581 | 1591 | 1630 (+40)–1640 (+50) | 1661 (+70) | 1645 (+54) | 1661 (+70) | 1645 (+54) |
| 8a | 1590 | 1595 | 1608 (+27)–1623 (+42) | 1630 (+35) | 1636 (+40) | 1630 (+35) | 1635 (+40) |
| Vibrational Modes 1,2 | 44BPY | 44BPYH+/32T− | |||||
|---|---|---|---|---|---|---|---|
| Exp 3 | Calc 4 | Exp 5,6 Si/Al = 100 | Closed | Open | |||
| Si/Al = 15 Calc 4,6 | Si/Al = 31 Calc 4,6 | Si/Al = 15 Calc 4,6 | Si/Al = 31 Calc 4,6 | ||||
| 6b-B3 | 659 | 663 | 652 (−7) | 647 (−16) | 649 (−14) | 645 (−18) | 642 (−21) |
| 1-A | 762 | 750 | 764 (+2) | 754 (+4) | 752 (+2) | 751 (+1) | 764 (+14) |
| 12-B1 | 989 | 988 | 994 (+5) | 1004 (+15) | 996 (+8) | 1006 (+18) | 999 (+11) |
| 12-A | 1001 | 994 | 1012 (+11) | 1017 (+22) | 1018 (+24) | 1021 (+27) | 1016 (+21) |
| 18a-B1 | 1075 | 1076 | 1064 (−11) | 1075 (−1) | 1076 (0) | 1073 (−3) | 1067 (−9) |
| 18a-A | 1075 | 1079 | 1081 (+6) | 1084 (+5) | 1088 (+9) | 1090 (+11) | 1093 (+14) |
| 9a-B1 | 1218 | 1228 | 1209 (−9) | 1220 (−8) | 1223 (−5) | 1224 (−4) | 1218 (−10) |
| 9a-A | 1216 | 1231 | 1222 (+6) | 1242 (+11) | 1243 (+12) | 1240 (+9) | 1238 (+7) |
| Ω-A | 1300 | 1291 | 1290 (−10) | 1279 (−12) | 1282 (−9) | 1278 (−13) | 1281 (−10) |
| 19a-B1 | 1487 | 1496 | 1516 (+29) | 1502 (+6) | 1502 (+6) | 1505 (+9) | 1500 (+4) |
| 19a-A | 1514 | 1516 | 1531 (+17) | 1534 (+18) | 1533 (+17) | 1533 (+16) | 1526 (+10) |
| 8a-B1 | 1589 | 1608 | 1634 (+45) | 1653 (+45) | 1656 (+48) | 1651 (+43) | 1647 (+39) |
| 8a-A | 1604 | 1614 | 1615 (+11) | 1620 (+5) | 1609 (−6) | 1620 (+6) | 1613 (−1) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castellà-Ventura, M.; Moissette, A.; Kassab, E. DFT Study of Si/Al Ratio and Confinement Effects on the Energetics and Vibrational Properties of some Aza-Aromatic Molecules Adsorbed on H-ZSM-5 Zeolite. Computation 2020, 8, 81. https://doi.org/10.3390/computation8030081
Castellà-Ventura M, Moissette A, Kassab E. DFT Study of Si/Al Ratio and Confinement Effects on the Energetics and Vibrational Properties of some Aza-Aromatic Molecules Adsorbed on H-ZSM-5 Zeolite. Computation. 2020; 8(3):81. https://doi.org/10.3390/computation8030081
Chicago/Turabian StyleCastellà-Ventura, Martine, Alain Moissette, and Emile Kassab. 2020. "DFT Study of Si/Al Ratio and Confinement Effects on the Energetics and Vibrational Properties of some Aza-Aromatic Molecules Adsorbed on H-ZSM-5 Zeolite" Computation 8, no. 3: 81. https://doi.org/10.3390/computation8030081
APA StyleCastellà-Ventura, M., Moissette, A., & Kassab, E. (2020). DFT Study of Si/Al Ratio and Confinement Effects on the Energetics and Vibrational Properties of some Aza-Aromatic Molecules Adsorbed on H-ZSM-5 Zeolite. Computation, 8(3), 81. https://doi.org/10.3390/computation8030081