Non-Intrusive In-Plane-Out-of-Plane Separated Representation in 3D Parametric Elastodynamics
Abstract
1. Introduction
2. Methods
2.1. Non-Intrusive Formulation of the In-Plane-Out-of-Plane Separated Representation
2.2. Separated Representation Constructor
2.2.1. In-Plane Update
2.2.2. Through-The-Thickness Update
3. Problem Formulation
Non-Intrusive Parametric Elastodynamics in Layered Media
- The in-plane update at the enrichment step n useswith everything known except .
- The through-the-thickness update at the enrichment step n useswith everything known except .
- Parametric update. In this case in Equation (32) everything is known except one of the functions depending on the frequency or the parameters , . Introduced into Equation (30) (after this last is integrated into all the variables except the one in which the unknown function is defined) and taking into account the arbitrariness of the associated test function, a scalar algebraic equation that allows calculating the searched function, is obtained.
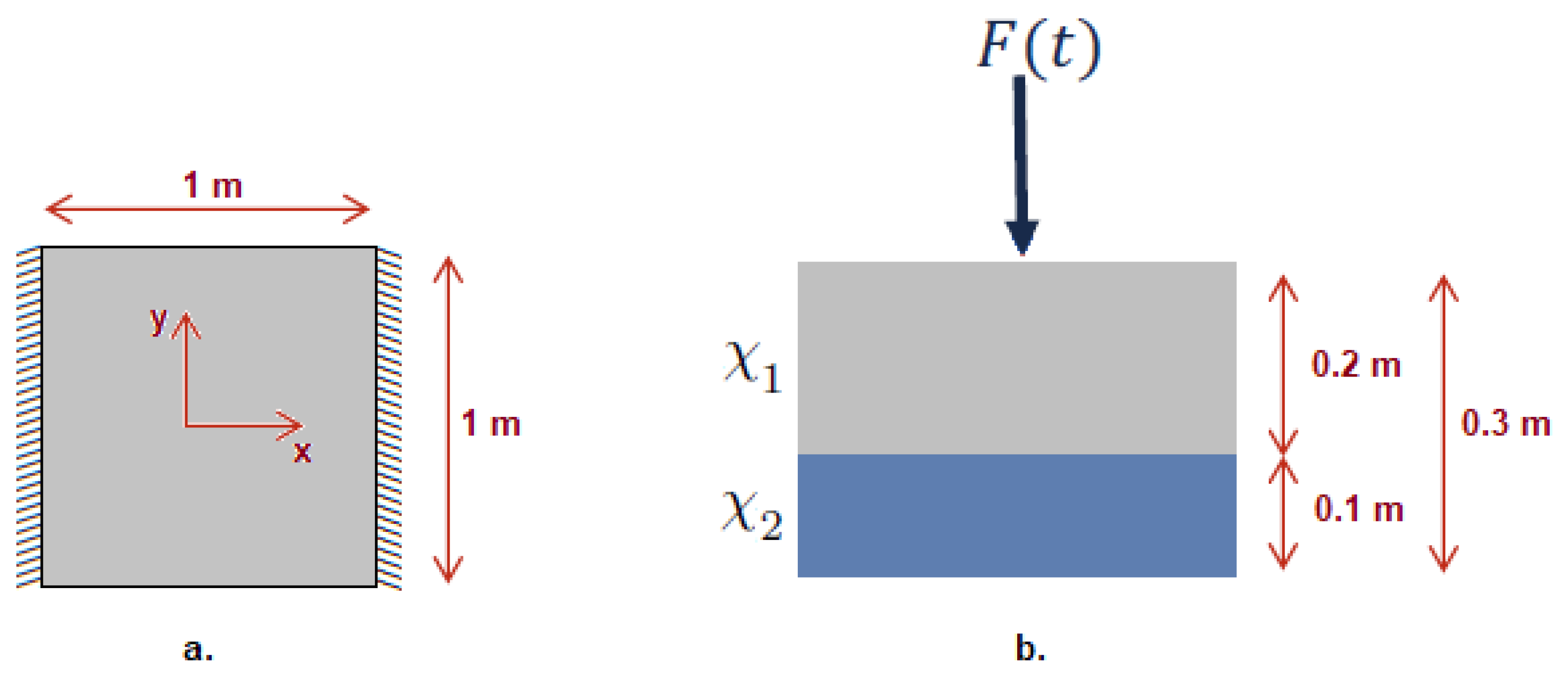
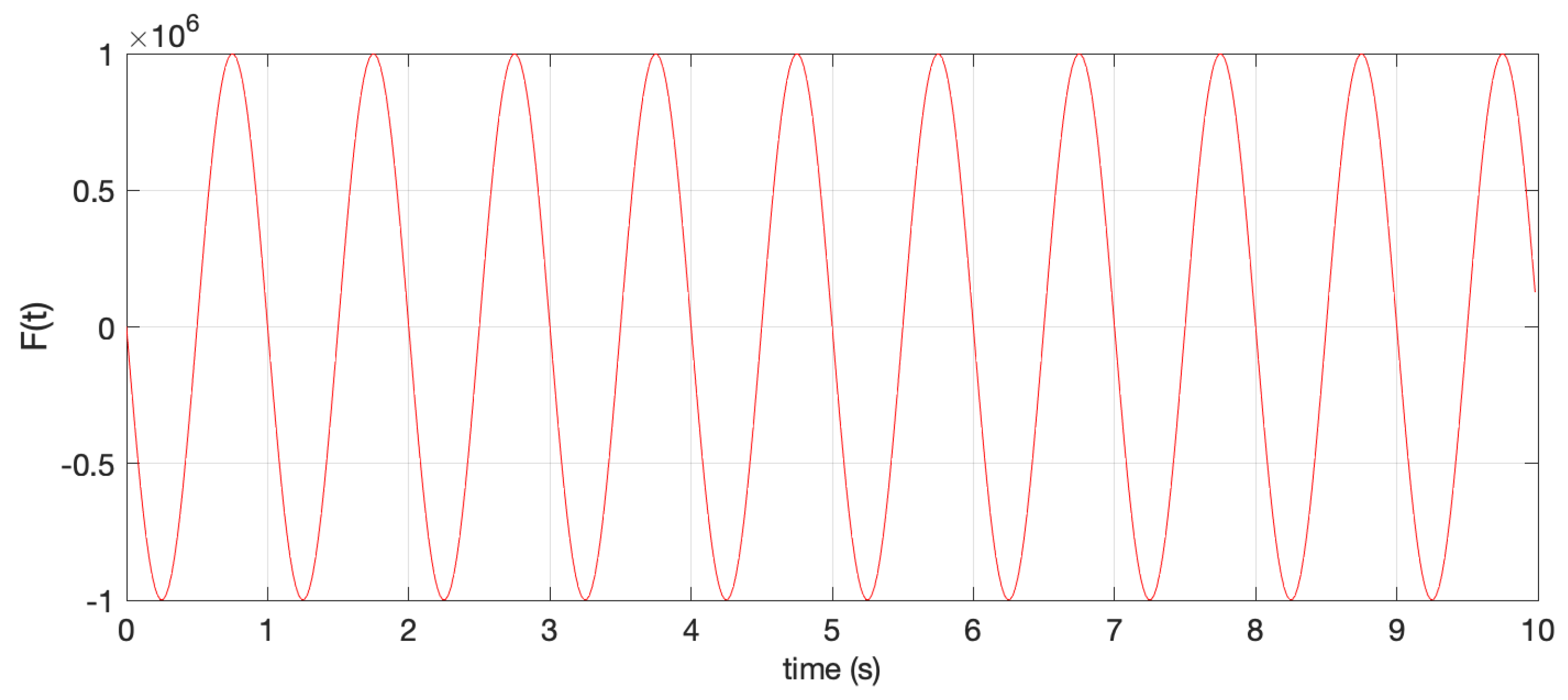
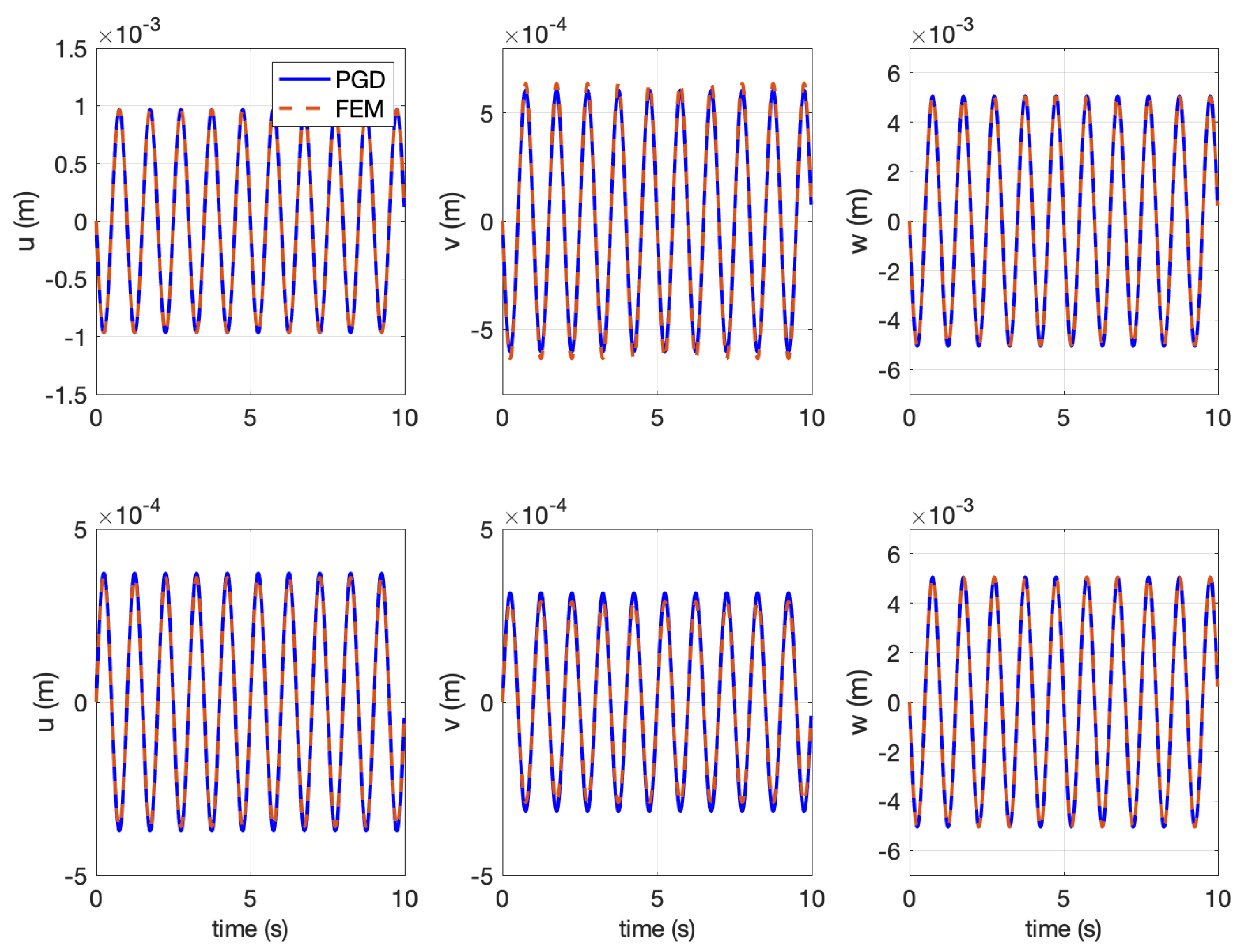
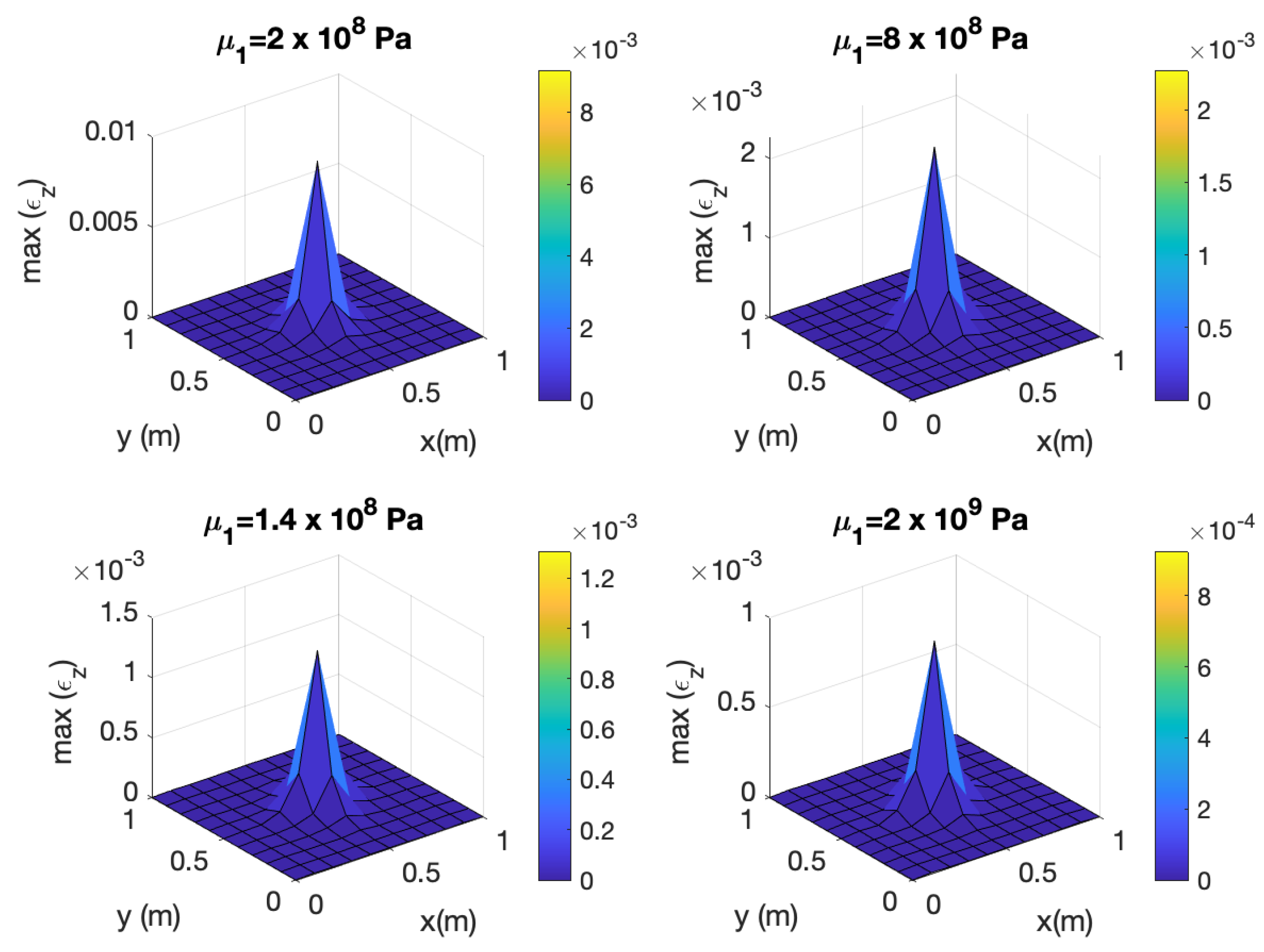
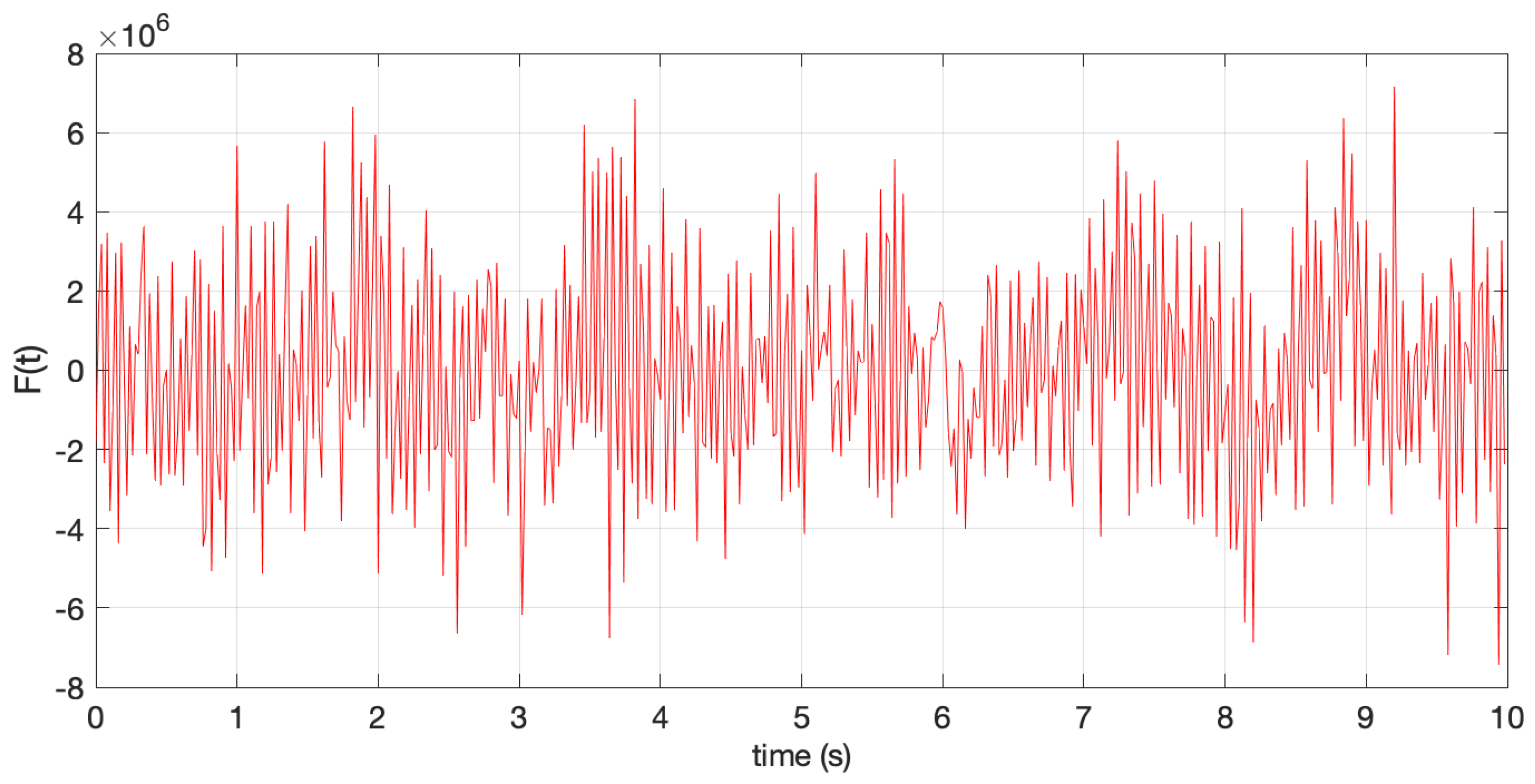
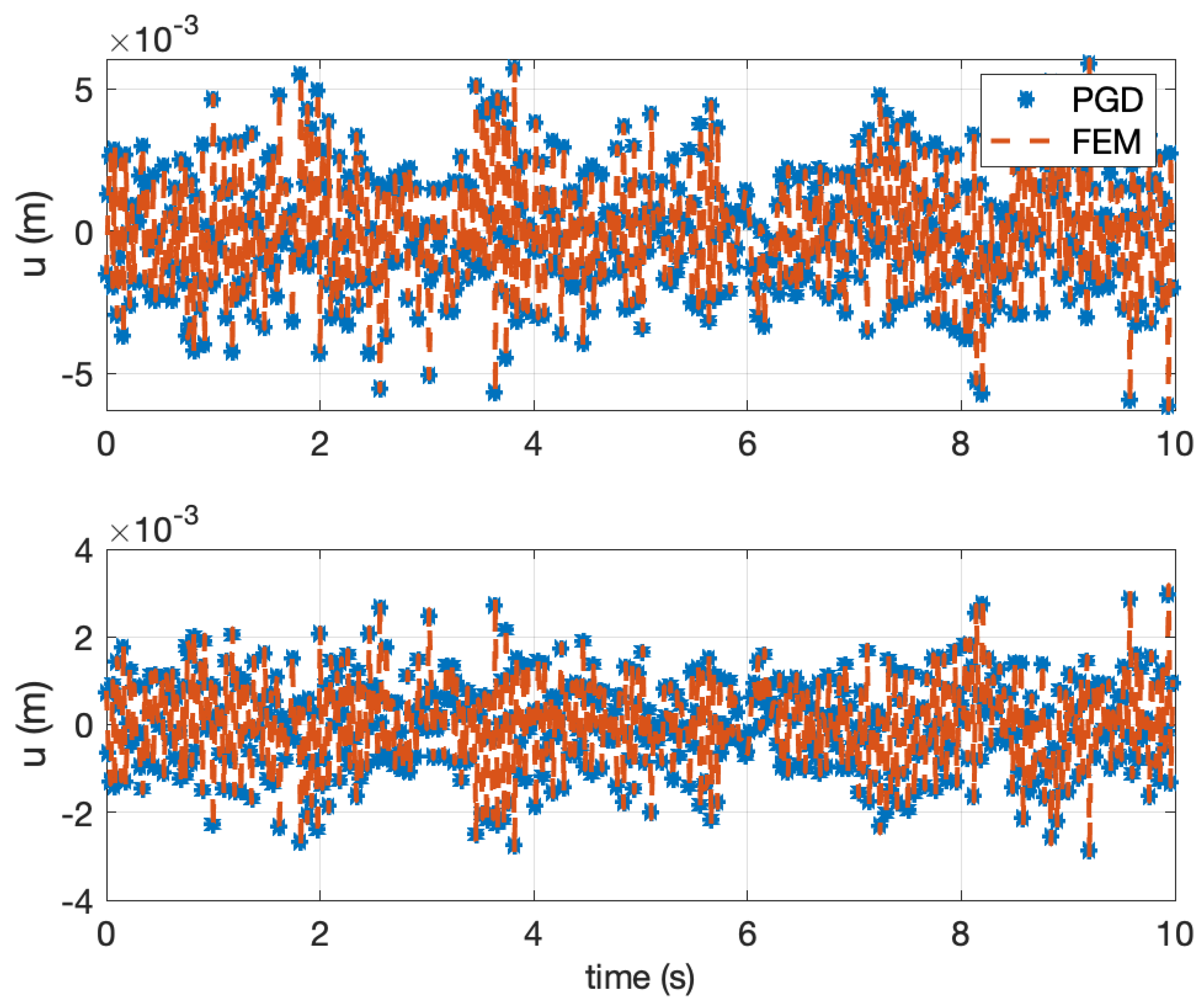
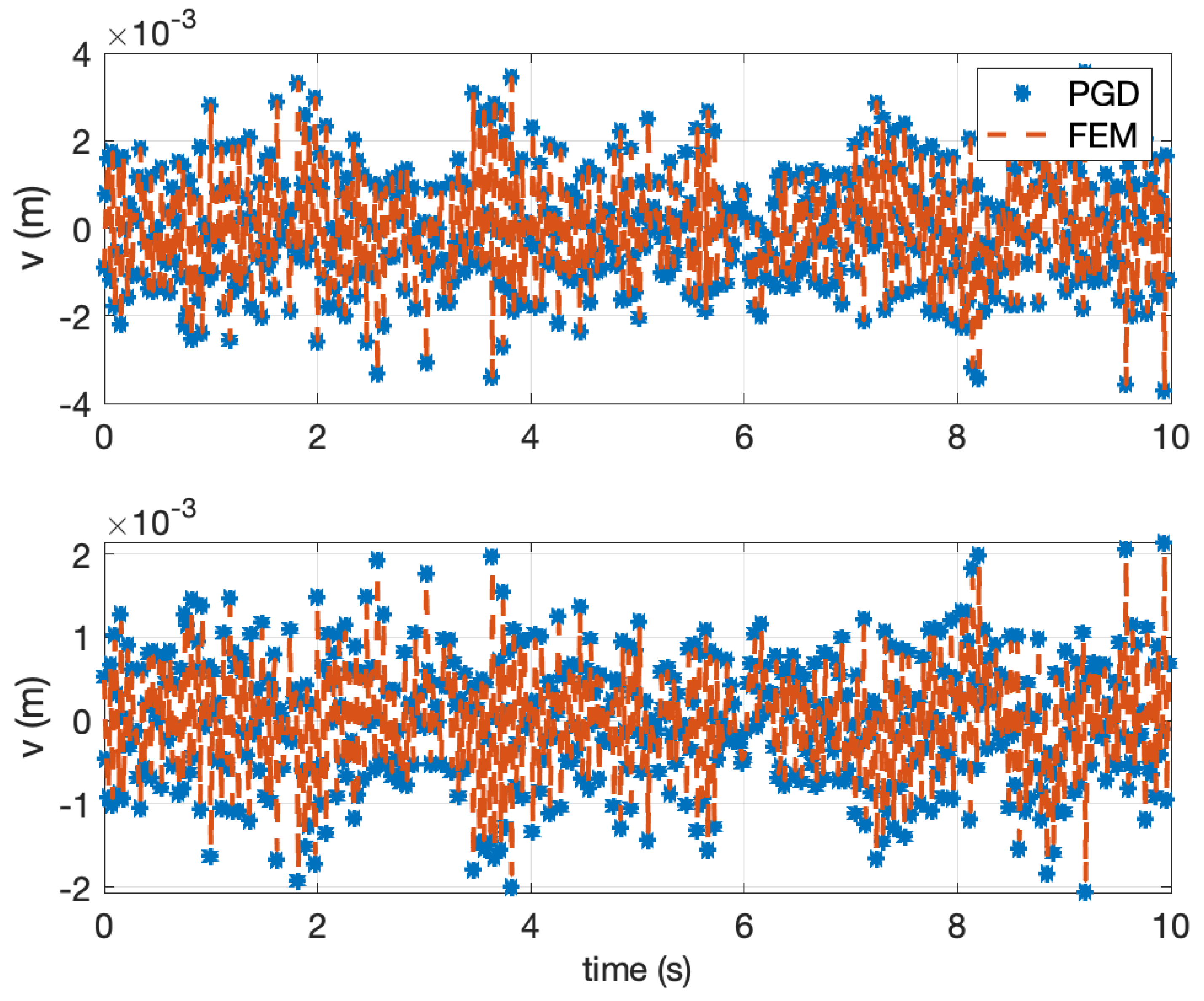
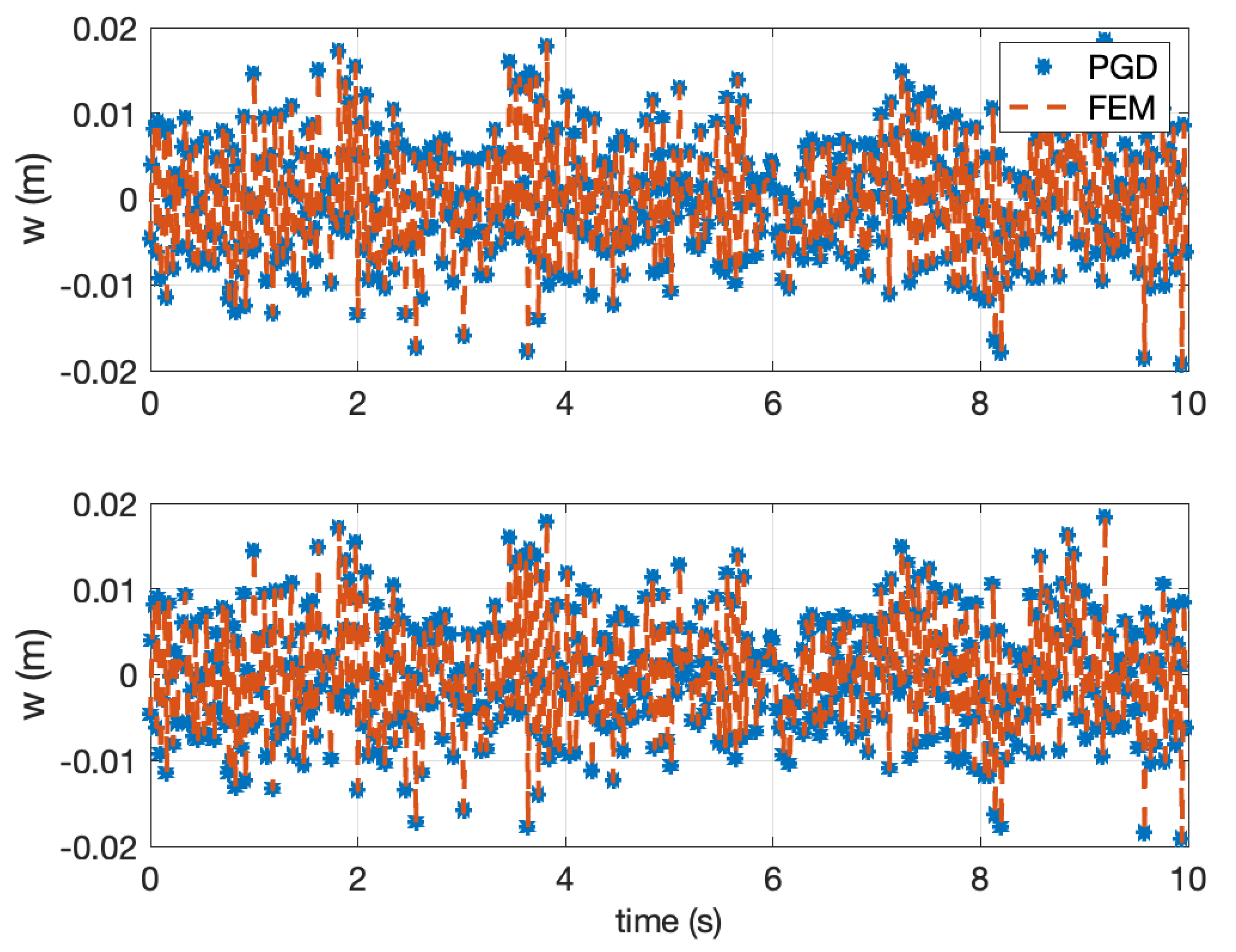
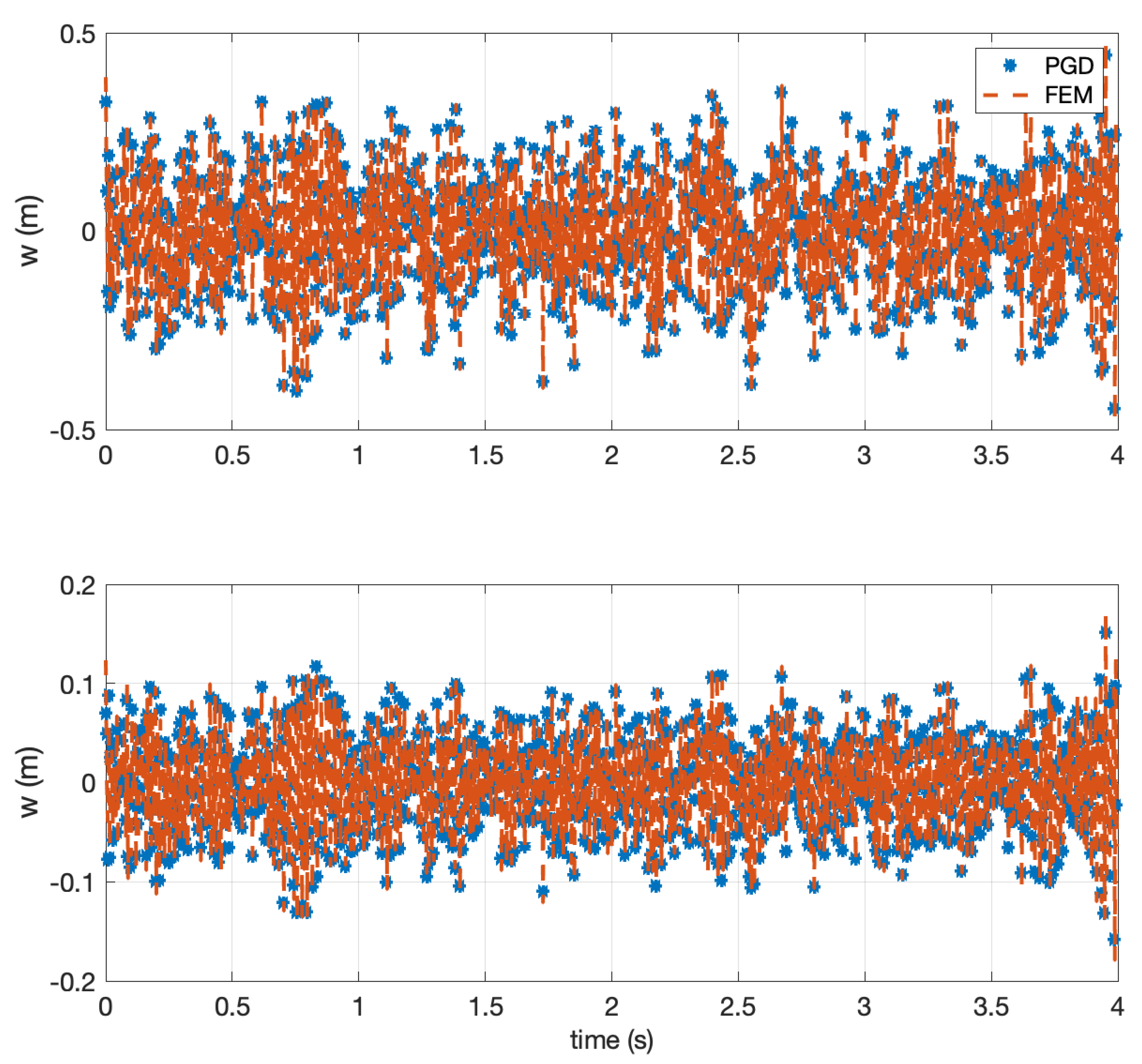
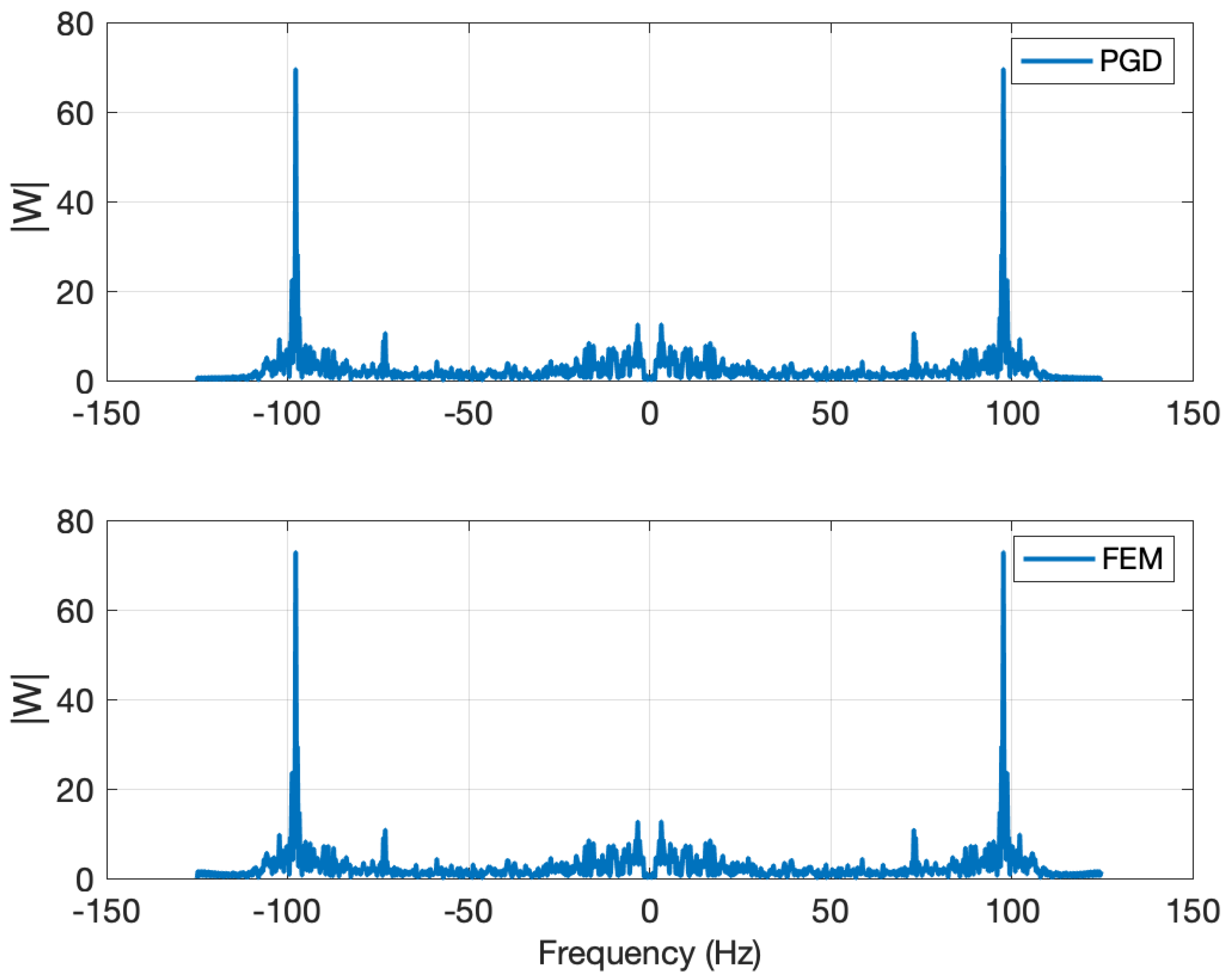
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chinesta, F.; Keunings, R.; Leygue, A. The Proper Generalized Decomposition for Advanced Numerical Simulations; A Primer, Springerbriefs; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Chinesta, F.; Leygue, A.; Bordeu, F.; Aguado, J.V.; Cueto, E.; Gonzalez, D.; Alfaro, I.; Huerta, A. Parametric PGD based computational vademecum for efficient design, optimization and control. Arch. Comput. Methods Eng. 2013, 20, 31–59. [Google Scholar] [CrossRef]
- Bognet, B.; Leygue, A.; Chinesta, F.; Poitou, A.; Bordeu, F. Advanced simulation of models defined in plate geometries: 3D solutions with 2D computational complexity. Comput. Methods Appl. Mech. Eng. 2012, 201, 1–12. [Google Scholar] [CrossRef]
- Bognet, B.; Leygue, A.; Chinesta, F. Separated representations of 3D elastic solutions in shell geometries. Adv. Model. Simul. Eng. Sci. 2014, 1, 4. [Google Scholar] [CrossRef]
- Chinesta, F.; Leygue, A.; Beringhier, M.; Nguyen, L.T.; Grandidier, J.C.; Schrefler, B.; Pesavento, F. Towards a framework for non-linear thermal models in shell domains. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 55–73. [Google Scholar] [CrossRef]
- Vidal, P.; Gallimard, L.; Polit, O. Proper generalized decomposition and layer-wise approach for the modeling of composite plate structures. Int. J. Solids Struct. 2013, 50, 2239–2250. [Google Scholar] [CrossRef]
- Vidal, P.; Gallimard, L.; Polit, O. Shell finite element based on the proper generalized decomposition for the modeling of cylindrical composite structures. Comput. Struct. 2014, 132, 1–11. [Google Scholar] [CrossRef][Green Version]
- Bordeu, F.; Ghnatios, C.; Boulze, D.; Carles, B.; Sireude, D.; Leygue, A.; Chinesta, F. Parametric 3D elastic solutions of beams involved in frame structures. Adv. Aircr. Spacecr. Sci. 2015, 2, 233–248. [Google Scholar] [CrossRef]
- Dumon, A.; Allery, C.; Ammar, A. Proper general decomposition (PGD) for the resolution of Navier-Stokes equations. J. Comput. Phys. 2011, 230, 1387–1407. [Google Scholar] [CrossRef][Green Version]
- Dumon, A.; Allery, C.; Ammar, A. Simulation of heat and mass transport in a square lid-driven cavity with proper generalized decomposition. Numer. Heat Transf. Part B Fundam. 2013, 63, 18–43. [Google Scholar] [CrossRef][Green Version]
- Ghnatios, C.H.; Chinesta, F.; Binetruy, C. 3D Modeling of squeeze flows occurring in composite laminates. Int. J. Mater. Form. 2015, 8, 73–83. [Google Scholar] [CrossRef]
- Leon, A.; De Luca, S.; Leygue, A.; Duval, J.L.; Chinesta, F. Non-intrusive proper generalized decomposition involving space and parameters: Application to the mechanical modeling of 3D woven fabrics. Adv. Model. Simul. Eng. Sci. 2019, 6, 13. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J. Dynamics of Structures; Civil Engineering Series McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar]
- Bathe, J. Conserving energy and momentum in nonlinear dynamics: A simple implicit time integration scheme. Comput. Struct. 2007, 85, 437–445. [Google Scholar] [CrossRef]
- Boucinha, L.; Gravouil, A.; Ammar, A. Space-time proper generalized decompositions for the resolution of transient elastodynamic models. Comput. Methods Appl. Mech. Eng. 2013, 255, 67–88. [Google Scholar] [CrossRef]
- Ladeveze, P. The large time increment method for the analyze of structures with nonlinear constitutive relation described by internal variables. CR Acad. Sci. Paris 1989, 309, 1095–1099. [Google Scholar]
- Ladeveze, P.; Arnaud, L.; Rouch, P.; Blanze, C. The variational theory of complex rays for the calculation of medium-frequency vibrations. Eng. Comput. 1999, 18, 193–214. [Google Scholar] [CrossRef]
- Quaranta, G.; Argerich, C.; Ibanez, R.; Duval, J.L.; Cueto, E.; Chinesta, F. From linear to nonlinear PGD-based parametric structural dynamics. Comptes Rendus Mécanique 2019, 347, 445–454. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Germoso, C.; Quaranta, G.; Duval, J.L.; Chinesta, F. Non-Intrusive In-Plane-Out-of-Plane Separated Representation in 3D Parametric Elastodynamics. Computation 2020, 8, 78. https://doi.org/10.3390/computation8030078
Germoso C, Quaranta G, Duval JL, Chinesta F. Non-Intrusive In-Plane-Out-of-Plane Separated Representation in 3D Parametric Elastodynamics. Computation. 2020; 8(3):78. https://doi.org/10.3390/computation8030078
Chicago/Turabian StyleGermoso, Claudia, Giacomo Quaranta, Jean Louis Duval, and Francisco Chinesta. 2020. "Non-Intrusive In-Plane-Out-of-Plane Separated Representation in 3D Parametric Elastodynamics" Computation 8, no. 3: 78. https://doi.org/10.3390/computation8030078
APA StyleGermoso, C., Quaranta, G., Duval, J. L., & Chinesta, F. (2020). Non-Intrusive In-Plane-Out-of-Plane Separated Representation in 3D Parametric Elastodynamics. Computation, 8(3), 78. https://doi.org/10.3390/computation8030078





