Optimization of the Controls against the Spread of Zika Virus in Populations
Abstract
1. Introduction
2. Mathematical Model
3. Optimization of the Controls
4. Numerical Solution of the Model with Time-Dependent Controls and Cost-Effectiveness Analysis
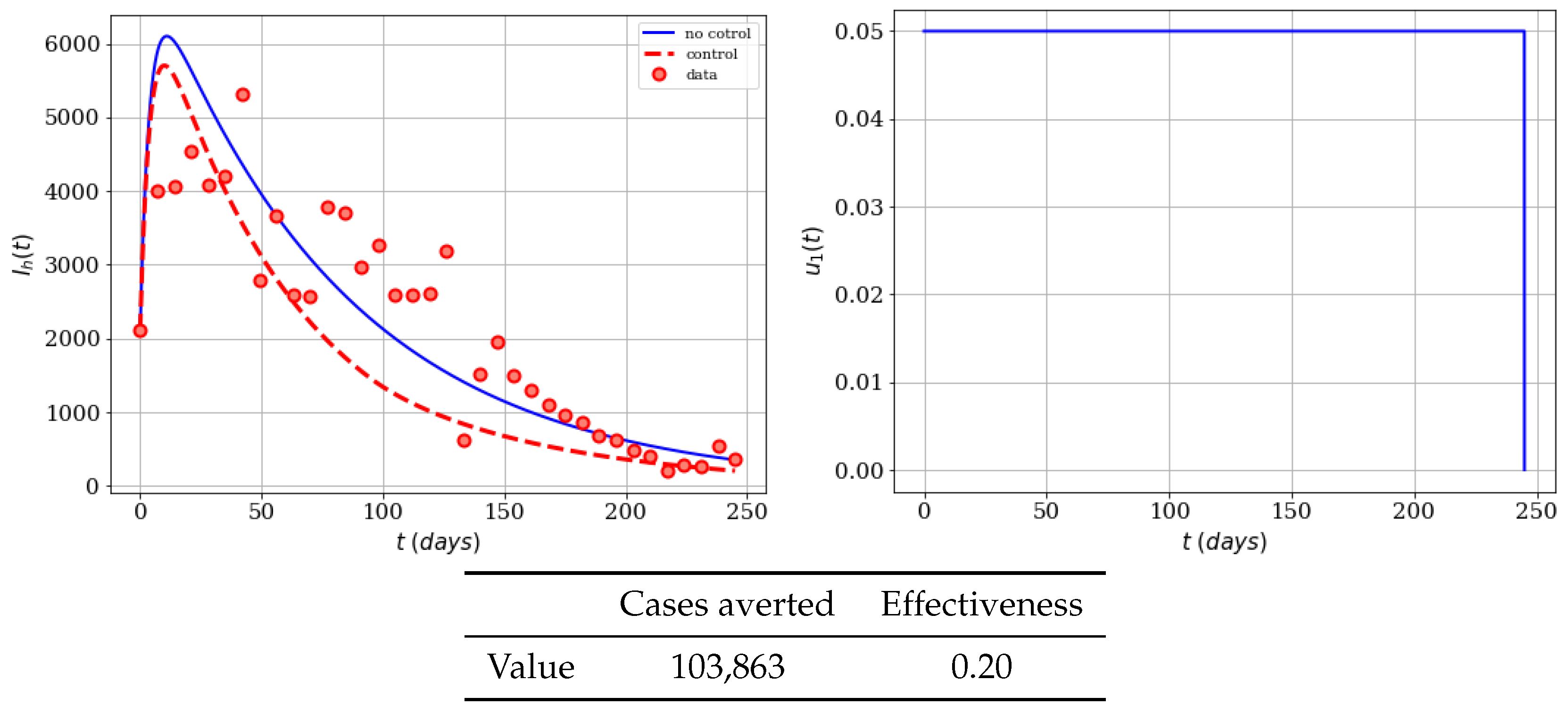
4.1. Mass Educational Campaigns Effects
4.2. Insecticide Spraying Campaign
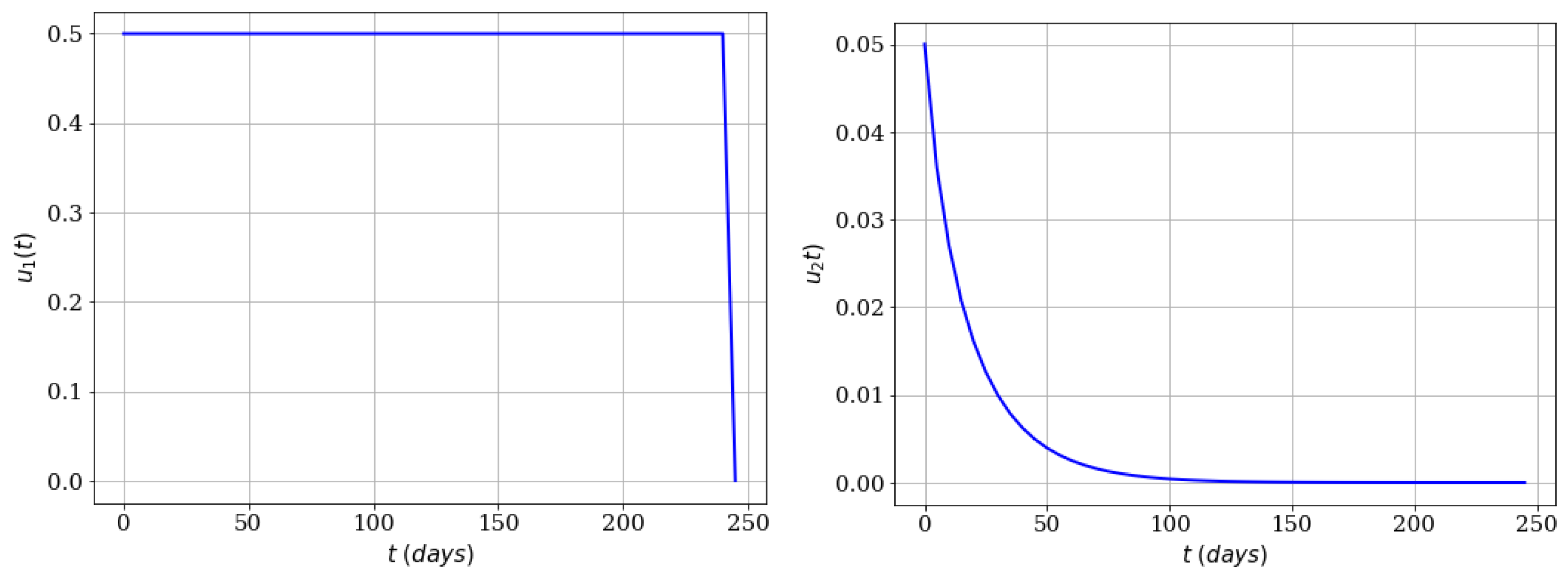
4.3. Mixing the Controls and Including the Infected Mosquitoes
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cerbino-Neto, J.; Mesquita, E.C.; Souza, T.M.L.; Parreira, V.; Wittlin, B.B.; Durovni, B.; Lemos, M.C.F.; Vizzoni, A.; de Filippis, A.M.B.; Sampaio, S.A.; et al. Clinical manifestations of Zika virus infection, Rio de Janeiro, Brazil, 2015. Emerg. Infect. Dis. 2016, 22, 1318. [Google Scholar] [CrossRef] [PubMed]
- González-Parra, G.; Benincasa, T. Mathematical modeling and numerical simulations of Zika in Colombia considering mutation. Math. Comput. Simul. 2019, 163, 1–18. [Google Scholar]
- Dinh, L.; Chowell, G.; Mizumoto, K.; Nishiura, H. Estimating the subcritical transmissibility of the Zika outbreak in the State of Florida, USA, 2016. Theor. Biol. Med Model. 2016, 13, 20. [Google Scholar] [CrossRef] [PubMed]
- Tsetsarkin, K.A.; Kenney, H.; Chen, R.; Liu, G.; Manukyan, H.; Whitehead, S.S.; Laassri, M.; Chumakov, K.; Pletnev, A.G. A full-length infectious cDNA clone of Zika virus from the 2015 epidemic in Brazil as a genetic platform for studies of virus-host interactions and vaccine development. mBio 2016, 7, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Goo, L.; Dowd, K.A.; Smith, A.R.; Pelc, R.S.; DeMaso, C.R.; Pierson, T.C. Zika Virus Is Not Uniquely Stable at Physiological Temperatures Compared to Other Flaviviruses. mBio 2016, 7, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Hethcote, H.W. Mathematics of infectious diseases. SIAM Rev. 2005, 42, 599–653. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology I: An Introduction, Vol. 17 of Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2002. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.; Roberts, M. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2009, 7, 873–885. [Google Scholar] [CrossRef]
- Khan, M.A.; Iqbal, N.; Khan, Y.; Alzahrani, E. A biological mathematical model of vector-host disease with saturated treatment function and optimal control strategies. Math. Biosci. Eng. 2020, 17, 3972. [Google Scholar] [CrossRef]
- Khan, M.; Shah, S.W.; Ullah, S.; Gómez-Aguilar, J. A dynamical model of asymptomatic carrier zika virus with optimal control strategies. Nonlinear Anal. Real World Appl. 2019, 50, 144–170. [Google Scholar] [CrossRef]
- Khan, M.A.; Khan, R.; Khan, Y.; Islam, S. A mathematical analysis of Pine Wilt disease with variable population size and optimal control strategies. Chaos Solitons Fractals 2018, 108, 205–217. [Google Scholar] [CrossRef]
- Khan, M.; Ali, K.; Bonyah, E.; Okosun, K.; Islam, S.; Khan, A. Mathematical modeling and stability analysis of Pine Wilt Disease with optimal control. Sci. Rep. 2017, 7, 3115. [Google Scholar] [CrossRef]
- Götz, T.; Altmeier, N.; Bock, W.; Rockenfeller, R.; Wijaya, K.P. Modeling dengue data from Semarang, Indonesia. Ecol. Complex. 2017, 30, 57–62. [Google Scholar] [CrossRef]
- Bonyah, E.; Khan, M.A.; Okosun, K.; Islam, S. A theoretical model for Zika virus transmission. PLoS ONE 2017, 12, e0185540. [Google Scholar] [CrossRef] [PubMed]
- Luyten, J.; Beutels, P. The social value of vaccination programs: Beyond cost-effectiveness. Health Aff. 2016, 35, 212–218. [Google Scholar] [CrossRef] [PubMed]
- Acedo, L.; Diez-Domingo, J.; Morano, J.A.; Villanueva, R.J. Mathematical modelling of respiratory syncytial virus (RSV): Vaccination strategies and budget applications. Epidemiol. Infect. 2010, 138, 853–860. [Google Scholar] [CrossRef]
- Kumar, A.; Srivastava, P.K. Vaccination and treatment as control interventions in an infectious disease model with their cost optimization. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 334–343. [Google Scholar] [CrossRef]
- Kumar, A.; Srivastava, P.K.; Dong, Y.; Takeuchi, Y. Optimal control of infectious disease: Information-induced vaccination and limited treatment. Phys. A Stat. Mech. Appl. 2020, 542, 123196. [Google Scholar] [CrossRef]
- Barber, L.M.; Schleier, J.J., III; Peterson, R.K. Economic cost analysis of West Nile virus outbreak, Sacramento County, California, USA, 2005. Emerg. Infect. Dis. 2010, 16, 480. [Google Scholar] [CrossRef]
- Keech, M.; Beardsworth, P. The impact of influenza on working days lost. Pharmacoeconomics 2008, 26, 911–924. [Google Scholar] [CrossRef]
- Zohrabian, A.; Meltzer, M.I.; Ratard, R.; Billah, K.; Molinari, N.A.; Roy, K.; Scott, R.D. West Nile virus economic impact, Louisiana, 2002. Emerg. Infect. Dis. 2004, 10, 1736. [Google Scholar] [CrossRef]
- Canali, M.; Rivas-Morales, S.; Beutels, P.; Venturelli, C. The cost of Arbovirus disease prevention in Europe: Area-wide integrated control of tiger mosquito, Aedes albopictus, in Emilia-Romagna, Northern Italy. Int. J. Environ. Res. Public Health 2017, 14, 444. [Google Scholar] [CrossRef]
- Vanderslice, R.; Porter, N.; Williams, S.; Kulungara, A. Functional Relationship Between Public Health and Mosquito Abatement. In Mosquitoes, Communities, and Public Health in Texas; Elsevier: Amsterdam, The Netherlands, 2020; pp. 359–379. [Google Scholar]
- Chen-Charpentier, B.M.; Jackson, M. Direct and indirect optimal control applied to plant virus propagation with seasonality and delays. J. Comput. Appl. Math. 2020, 380, 112983. [Google Scholar] [CrossRef]
- Manore, C.A.; Ostfeld, R.S.; Agusto, F.B.; Gaff, H.; LaDeau, S.L. Defining the risk of Zika and chikungunya virus transmission in human population centers of the eastern United States. PLoS Negl. Trop. Dis. 2017, 11, e0005255. [Google Scholar] [CrossRef]
- Ghosh, D. Zika virus a global emergency. Curr. Sci. 2018, 114, 725. [Google Scholar]
- Kakarla, S.G.; Mopuri, R.; Mutheneni, S.R.; Bhimala, K.R.; Kumaraswamy, S.; Kadiri, M.R.; Gouda, K.C.; Upadhyayula, S.M. Temperature dependent transmission potential model for chikungunya in India. Sci. Total. Environ. 2019, 647, 66–74. [Google Scholar] [CrossRef]
- González-Parra, G.; Dobrovolny, H.M.; Aranda, D.F.; Chen-Charpentier, B.; Rojas, R.A.G. Quantifying rotavirus kinetics in the REH tumor cell line using in vitro data. Virus Res. 2018, 244, 53–63. [Google Scholar] [CrossRef]
- Raue, A.; Kreutz, C.; Maiwald, T.; Bachmann, J.; Schilling, M.; Klingmüller, U.; Timmer, J. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 2009, 25, 1923–1929. [Google Scholar] [CrossRef]
- Moulay, D.; Aziz-Alaoui, M.; Kwon, H.D. Optimal control of chikungunya disease: Larvae reduction, treatment and prevention. Math. Biosci. Eng. 2012, 9, 369–392. [Google Scholar]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; Routledge: Abingdon-on-Thames, UK, 2018. [Google Scholar]
- Keller, H.B. Numerical Methods for Two-Point Boundary-Value Problems; Courier Dover Publications: Mineola, NY, USA, 2018. [Google Scholar]
- Kincaid, D.R.; Cheney, E.W. Numerical Analysis: Mathematics of Scientific Computing; American Mathematical Soc.: Providence, RI, USA, 2002; Volume 2. [Google Scholar]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming; SIAM: Philadelphia, PA, USA, 2010; Volume 19. [Google Scholar]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F. Vaccination models and optimal control strategies to dengue. Math. Biosci. 2014, 247, 1–12. [Google Scholar] [CrossRef]
- Workman, J.T.; Lenhart, S. Optimal Control Applied to Biological Models; Chapman and Hall/CRC: London, UK, 2007. [Google Scholar]
- Boisvert, J.J.; Muir, P.H.; Spiteri, R.J. py_bvp: A universal Python interface for BVP codes. In Proceedings of the 2010 Spring Simulation Multiconference. Society for Computer Simulation International, Orlando, FL, USA, 11–15 April 2010; p. 95. [Google Scholar]
- Kierzenka, J.; Shampine, L.F. A BVP solver based on residual control and the Maltab PSE. ACM Trans. Math. Softw. 2001, 27, 299–316. [Google Scholar] [CrossRef]
- Ascher, U.M.; Mattheij, R.M.; Russell, R.D. Numerical Solution of Boundary Value Problems for Ordinary Differential Equations; SIAM: Philadelphia, PA, USA, 1994; Volume 13. [Google Scholar]
- Moualeu, D.P.; Weiser, M.; Ehrig, R.; Deuflhard, P. Optimal control for a tuberculosis model with undetected cases in Cameroon. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 986–1003. [Google Scholar] [CrossRef]
- Okosun, K.O.; Rachid, O.; Marcus, N. Optimal control strategies and cost-effectiveness analysis of a malaria model. BioSystems 2013, 111, 83–101. [Google Scholar] [CrossRef]
- Kirschner, D.; Lenhart, S.; Serbin, S. Optimal control of the chemotherapy of HIV. J. Math. Biol. 1997, 35, 775–792. [Google Scholar] [CrossRef]
- Mohammed-Awel, J.; Agusto, F.; Mickens, R.E.; Gumel, A.B. Mathematical assessment of the role of vector insecticide resistance and feeding/resting behavior on malaria transmission dynamics: Optimal control analysis. Infect. Dis. Model. 2018, 3, 301–321. [Google Scholar] [CrossRef]
- Rodrigues, P.; Silva, C.J.; Torres, D.F. Cost-effectiveness analysis of optimal control measures for tuberculosis. Bull. Math. Biol. 2014, 76, 2627–2645. [Google Scholar] [CrossRef]





| Parameter | Symbol | Values | Rate |
|---|---|---|---|
| Average-life of the human host | 25 Days | ||
| Average-life of vector | 14 Days | ||
| Average time spent at the infectious stage in the humans | 5 Days | ||
| Time of immunity in the humans | 5 Days | ||
| Transmission of Virus (t) → (t) | |||
| Transmission of Virus (t) → (t) | ≈0.0103791 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Parra, G.; Díaz-Rodríguez, M.; Arenas, A.J. Optimization of the Controls against the Spread of Zika Virus in Populations. Computation 2020, 8, 76. https://doi.org/10.3390/computation8030076
González-Parra G, Díaz-Rodríguez M, Arenas AJ. Optimization of the Controls against the Spread of Zika Virus in Populations. Computation. 2020; 8(3):76. https://doi.org/10.3390/computation8030076
Chicago/Turabian StyleGonzález-Parra, Gilberto, Miguel Díaz-Rodríguez, and Abraham J. Arenas. 2020. "Optimization of the Controls against the Spread of Zika Virus in Populations" Computation 8, no. 3: 76. https://doi.org/10.3390/computation8030076
APA StyleGonzález-Parra, G., Díaz-Rodríguez, M., & Arenas, A. J. (2020). Optimization of the Controls against the Spread of Zika Virus in Populations. Computation, 8(3), 76. https://doi.org/10.3390/computation8030076







