A High-Order Weakly L-Stable Time Integration Scheme with an Application to Burgers’ Equation
Abstract
1. Introduction
2. Preliminary
3. Illustration of the ProposedMethod
3.1. Local Trunction Error
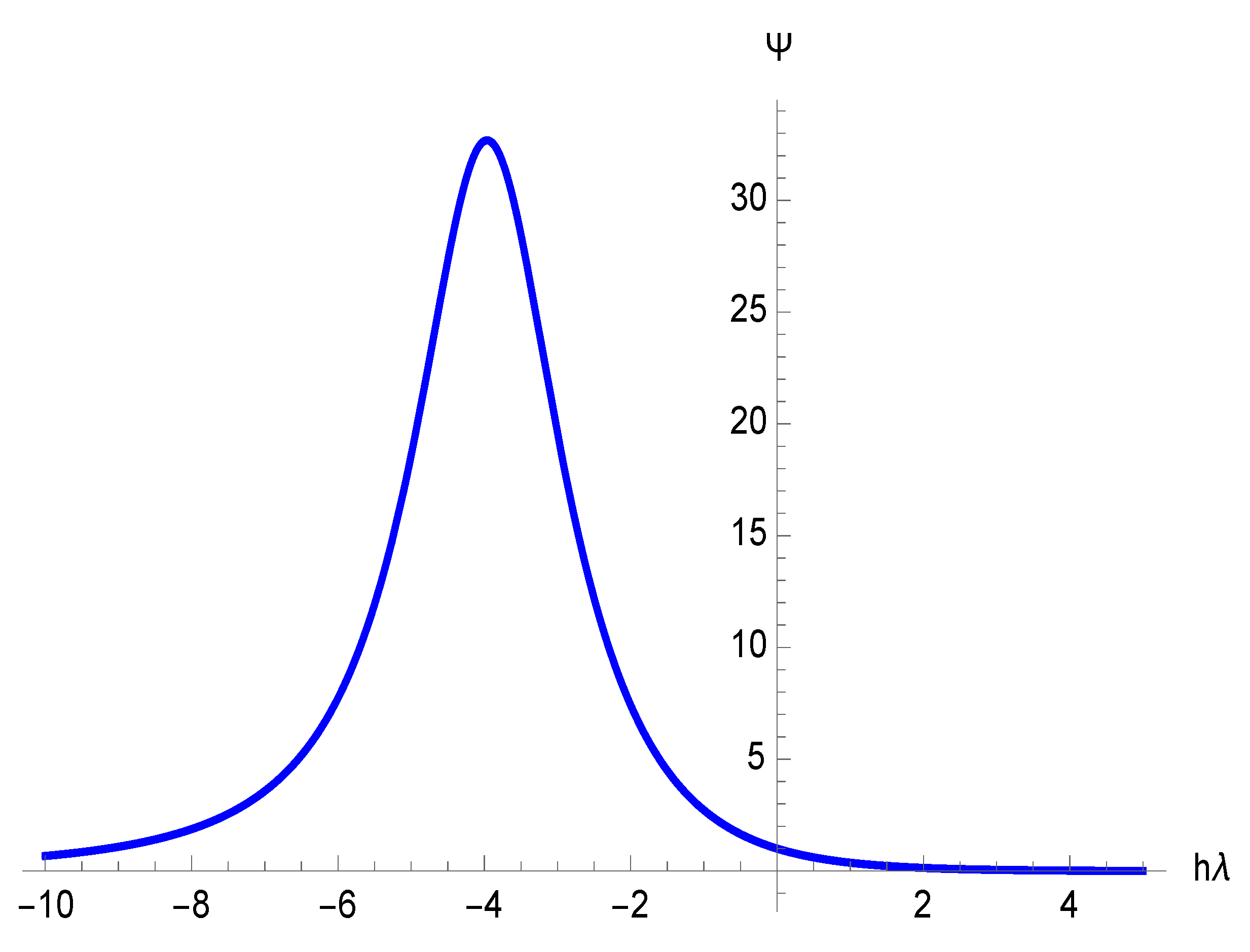
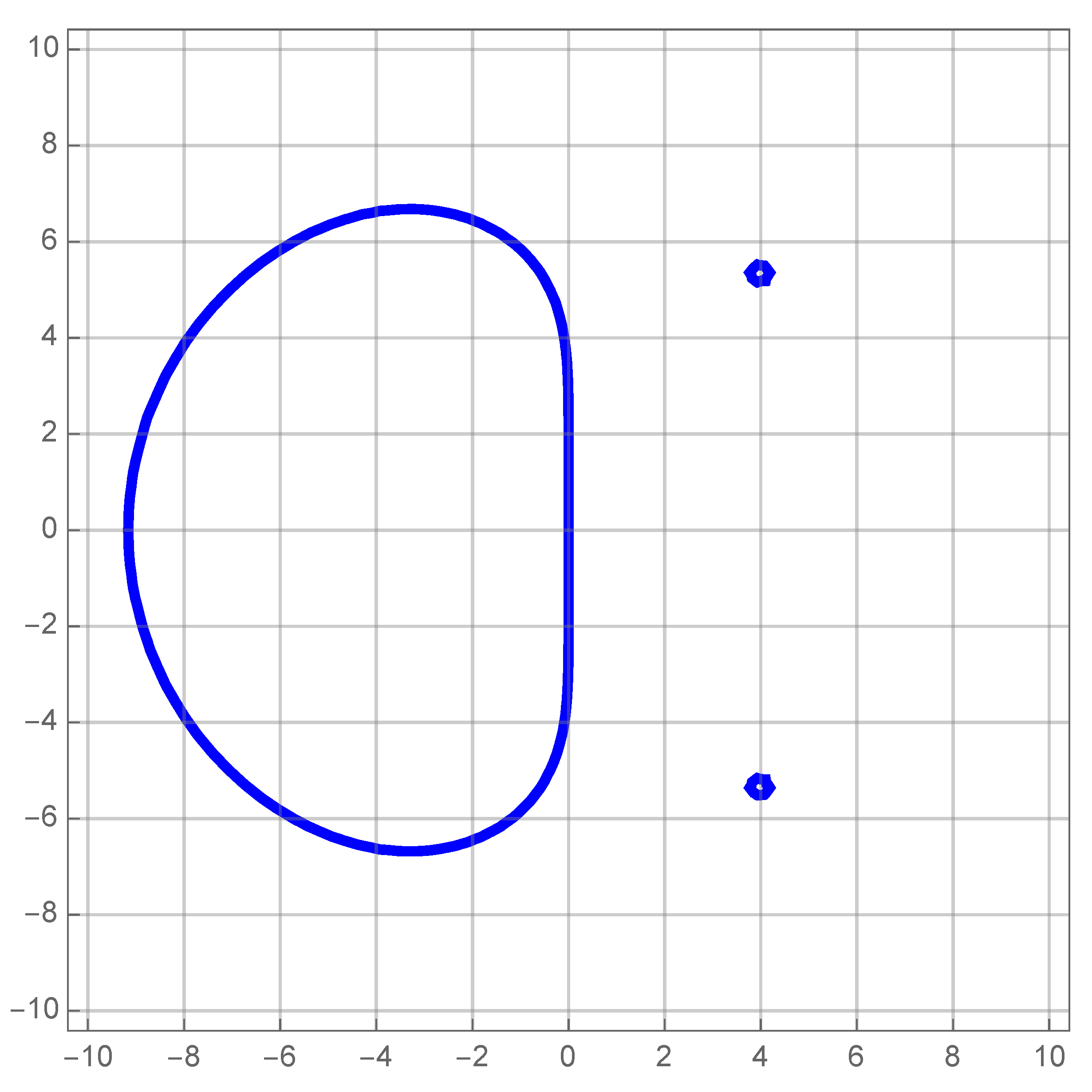
3.2. Stability of the ProposedFormula
3.3. StabilityRegion
4. Application on the Burgers’Equation
4.1. The NumericalScheme
4.2. StabilityAnalysis
5. NumericalExperiment
- (i)
- Mean root square error norm ()
- (ii)
- Maximum error norm ()
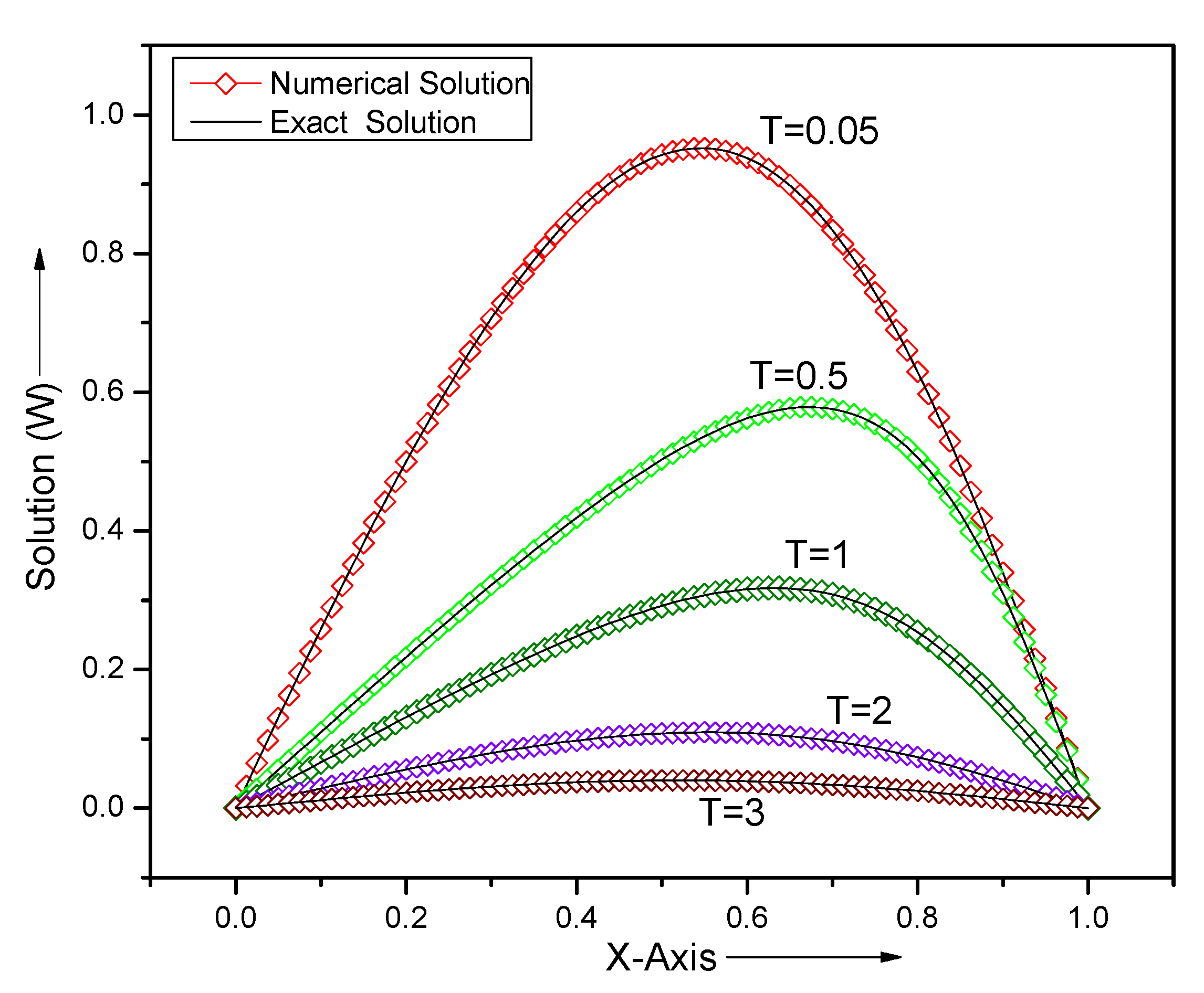
5.1. Example 1
5.2. Example 2
5.3. Example 3
5.4. Example 4
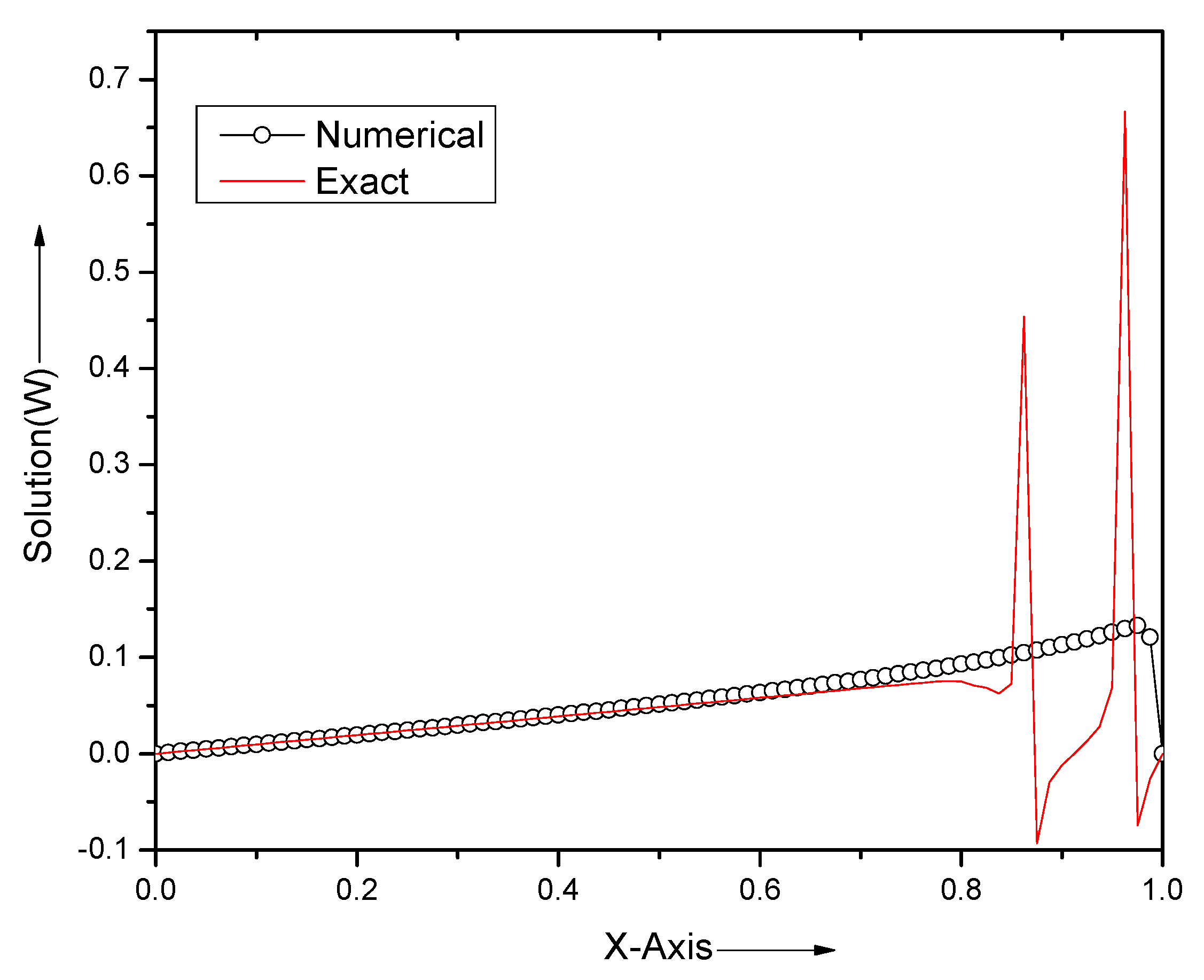
5.5. Example 5
5.6. Example 6
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bateman, H. Some recent researches on the motion of fluids. Mon. Weather Rev. 1915, 252, 163–170. [Google Scholar] [CrossRef]
- Burgers, J.M. Mathematical examples illustrating relations occurring in the theory of turbulent fluid motion, Verh. In Selected Papers of JM Burgers; Springer: Dordrecht, The Netherlands, 1939. [Google Scholar]
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Ryu, S.; Lyu, G.; Do, Y.; Lee, G.W. Improved rainfall nowcasting using Burgers’ equation. J. Hydrol. 2020, 581, 124140. [Google Scholar] [CrossRef]
- Cecchi, M.M.; Nociforo, R.; Patuzzo, P. Burgers problems-Theoretical results. Riv. Mat. Pura Appl. 1997, 21, 159–174. [Google Scholar]
- Benia, Y.; Sadallah, B.K. Existence of solutions to Burgers equations in domains that can be transformed into rectangles. Electron. J. Differ. Equ. 2016, 2016, 1–13. [Google Scholar]
- Tersenov, A.S. On the generalized Burgers equation. Nonlinear Differ. Equ. Appl. NoDEA 2010, 17, 437–452. [Google Scholar] [CrossRef]
- Öziş, T.; Aksan, E.N.; Özdeş, A. A finite element approach for solution of Burgers’ equation. Appl. Math. Comput. 2003, 139, 417–428. [Google Scholar] [CrossRef]
- Dogan, A. A Galerkin finite element approach to Burgers’ equation. Appl. Math. Comput. 2004, 157, 331–346. [Google Scholar] [CrossRef]
- Aksan, E.N. Quadratic B-spline finite element method for numerical solution of the Burgers’ equation. Appl. Math. Comput. 2006, 174, 884–896. [Google Scholar] [CrossRef]
- Saka, B.; Dağ, I. Quartic B-spline collocation method to the numerical solutions of the Burgers’ equation. Chaos Solitons Fractals 2007, 32, 1125–1137. [Google Scholar] [CrossRef]
- Ali, A.H.A. GA Gardner and LRT Gardner, A collocation solution of Burgers’ equation using cubic B-spline finite element. Comput. Methods Appl. Mech. Eng. 1992, 100, 325–337. [Google Scholar] [CrossRef]
- Korkmaz, A.; Aksoy, A.M.; Dag, I. Quartic B-spline differential quadrature method. Int. J. Nonlinear Sci. 2011, 11, 403–411. [Google Scholar]
- Elgindy, K.T.; Dahy, S.A. High-order numerical solution of viscous Burgers’ equation using a Cole-Hopf barycentric Gegenbauer integral pseudospectral method. Math. Methods Appl. Sci. 2018, 41, 6226–6251. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dag, I. Polynomial based differential quadrature method for numerical solution of nonlinear Burgers’ equation. J. Frankl. Inst. 2011, 348, 2863–2875. [Google Scholar] [CrossRef]
- Jiwari, R.; Mittal, R.C.; Sharma, K.K. A numerical scheme based on weighted average differential quadrature method for the numerical solution of Burgers’ equation. Appl. Math. Comput. 2013, 219, 6680–6691. [Google Scholar]
- Pandey, K.; Verma, L.; Verma, A.K. Du Fort-Frankel finite difference scheme for Burgers equation. Arab. J. Math. 2013, 2, 91–101. [Google Scholar] [CrossRef]
- Pandey, K.; Verma, L.; Verma, A.K. On a finite difference scheme for Burgers’ equation. Appl. Math. Comput. 2009, 215, 2206–2214. [Google Scholar]
- Hassanien, I.A.; Salama, A.A.; Hosham, H.A. Fourth-order finite difference method for solving Burgers’ equation. Appl. Math. Comput. 2005, 150, 781–800. [Google Scholar]
- Jiwari, R. A hybrid numerical scheme for the numerical solution of the Burgers’ equation. Comput. Phys. Commun. 2015, 188, 59–67. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Angadi, L.M. Numerical solution of Burgers’ equation using Biorthogonal wavelet-based full approximation scheme. Int. J. Comput. Mater. Sci. Eng. 2019, 8, 1850030. [Google Scholar] [CrossRef]
- Khater, A.H.; Temsah, R.S.; Hassan, M.M. A Chebyshev spectral collocation method for solving Burgers’-type equations. J. Comput. Appl. Math. 2008, 222, 333–350. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Hafez, R.M. Chebyshev collocation treatment of Volterra–Fredholm integral equation with error analysis. Arab. J. Math. 2020, 9, 471–480. [Google Scholar] [CrossRef]
- Doha, E.H.; Abd-Elhameed, W.M.; Elkot, N.A.; Youssri, Y.H. Integral spectral Tchebyshev approach for solving space Riemann-Liouville and Riesz fractional advection-dispersion problems. Adv. Differ. Equ. 2017, 2017, 284. [Google Scholar] [CrossRef][Green Version]
- Gowrisankar, S.; Natesan, S. An efficient robust numerical method for singularly perturbed Burgers’ equation. Appl. Math. Comput. 2019, 346, 385–394. [Google Scholar]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Adv. Comput. Math. 1947, 6, 207–226. [Google Scholar] [CrossRef]
- Lawson, J.D.; Morris, J.L. The extrapolation of first order methods for parabolic partial differential equations. SIAM J. Numer. Anal. 1978, 15, 1212–1224. [Google Scholar] [CrossRef]
- Smith, G.D. Numerical Solution of Partial Differential Equations: Finite Difference Methods; Oxford University Press: Oxford, UK, 1978. [Google Scholar]
- Thomas, J.W. Numerical Partial Differential Equations: Finite Difference Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Morton, K.W. Difference Methods for Initial-Value Problems; John Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Chawla, M.M.; Al-Zanaidi, M.A.; Evans, D.J. Generalized trapezoidal formulas for parabolic equations. Int. J. Comput. Math. 1999, 70, 429–443. [Google Scholar] [CrossRef]
- Chawla, M.M.; Al-Zanaidi, M.A.; Al-Sahhar, M.S. Stabilized fourth order extended methods for the numerical solution of ODEs. Int. J. Comput. Math. 1994, 52, 99–107. [Google Scholar] [CrossRef]
- Chawla, M.M.; Evans, D.J. A new L-stable Simpson-type rule for the diffusion equation. Int. J. Comput. Math. 2005, 82, 601–607. [Google Scholar] [CrossRef]
- Verma, L. L-Stable Derivative-Free Error-Corrected Trapezoidal Rule for Burgers’ Equation with Inconsistent Initial and Boundary Conditions. Int. J. Math. Math. Sci. 2012, 2012, 821907. [Google Scholar] [CrossRef][Green Version]
- Verma, A.K.; Verma, L. Higher order time integration formula with application on Burgers’ equation. Int. J. Comput. Math. 2015, 92, 756–771. [Google Scholar] [CrossRef]
- Hopf, E. The partial differential equation ut + uux = μuxx. Commun. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Cole, J.D. On a quasi-linear parabolic equation occurring in aerodynamics. Q. Appl. Math. 1951, 9, 225–236. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Difference Methods for Ordinary and Partial Differential Equations; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Kutluay, S.; Esen, A.; Dag, I. Numerical solutions of the Burgers’ equation by the least-squares quadratic B-spline finite element method. J. Comput. Appl. Math. 2004, 167, 21–33. [Google Scholar] [CrossRef]
- Asaithambi, A. Numerical solution of the Burgers’ equation by automatic differentiation. Appl. Math. Comput. 2010, 216, 2700–2708. [Google Scholar] [CrossRef]
- Xie, S.S.; Heo, S.; Kim, S.; Woo, G.; Yi, S. Numerical solution of one-dimensional Burgers’ equation using reproducing kernel function. J. Comput. Appl. Math. 2008, 214, 417–434. [Google Scholar] [CrossRef]
- Cecchi, M.M.; Nociforo, R.; Grego, P.P. Space-time finite elements numerical solutions of Burgers’ Problems. Matematiche 1996, 51, 43–57. [Google Scholar]
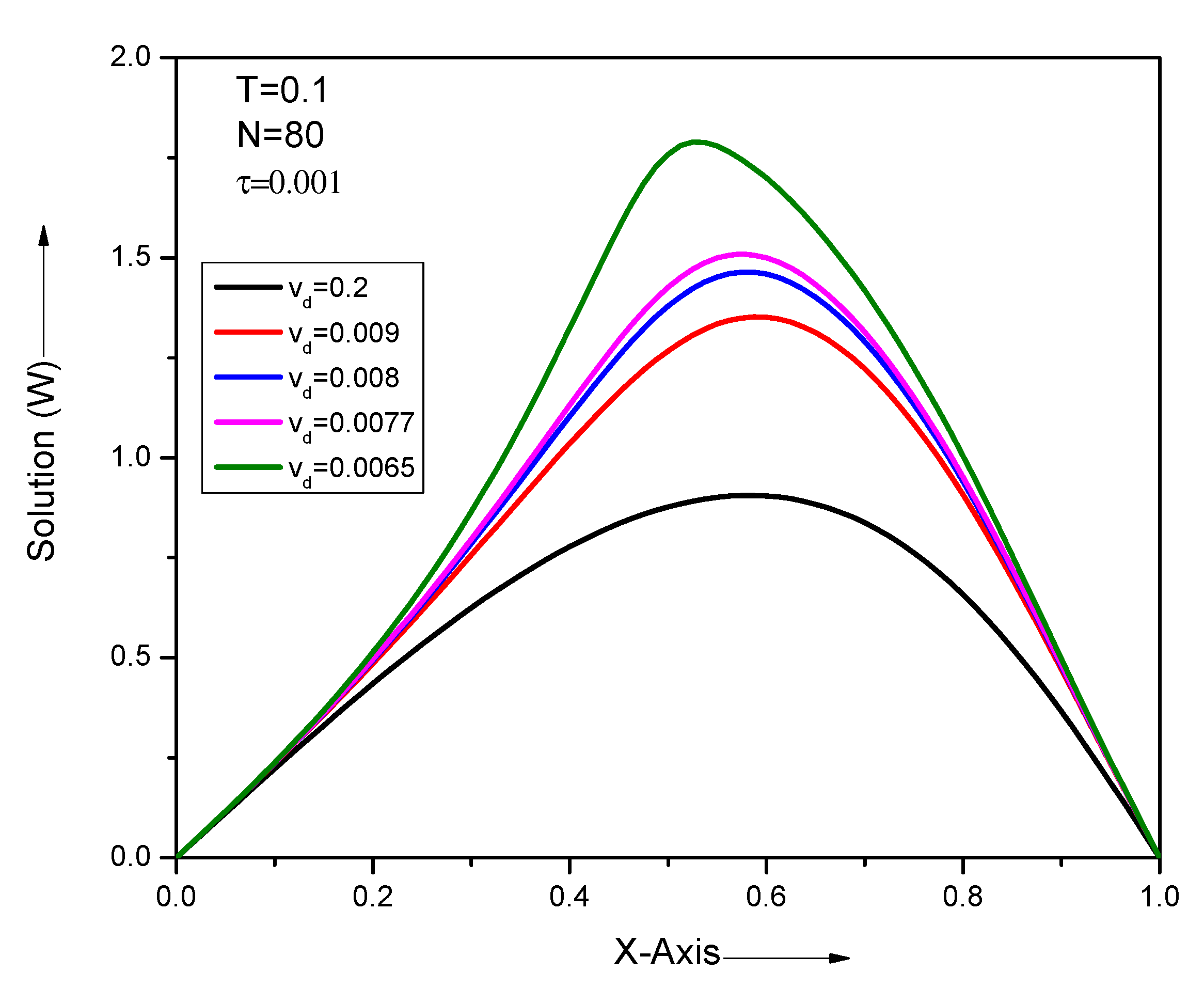
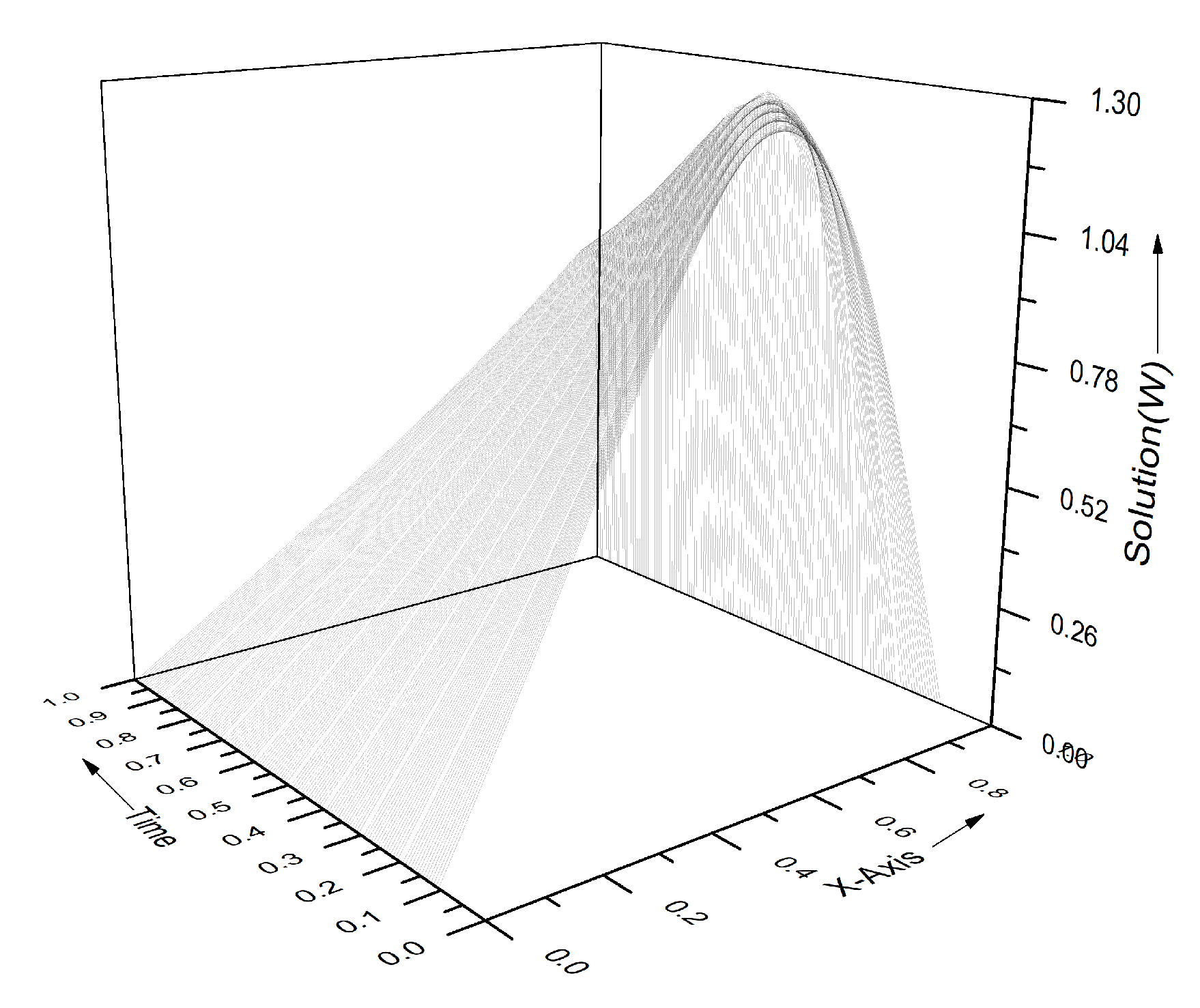
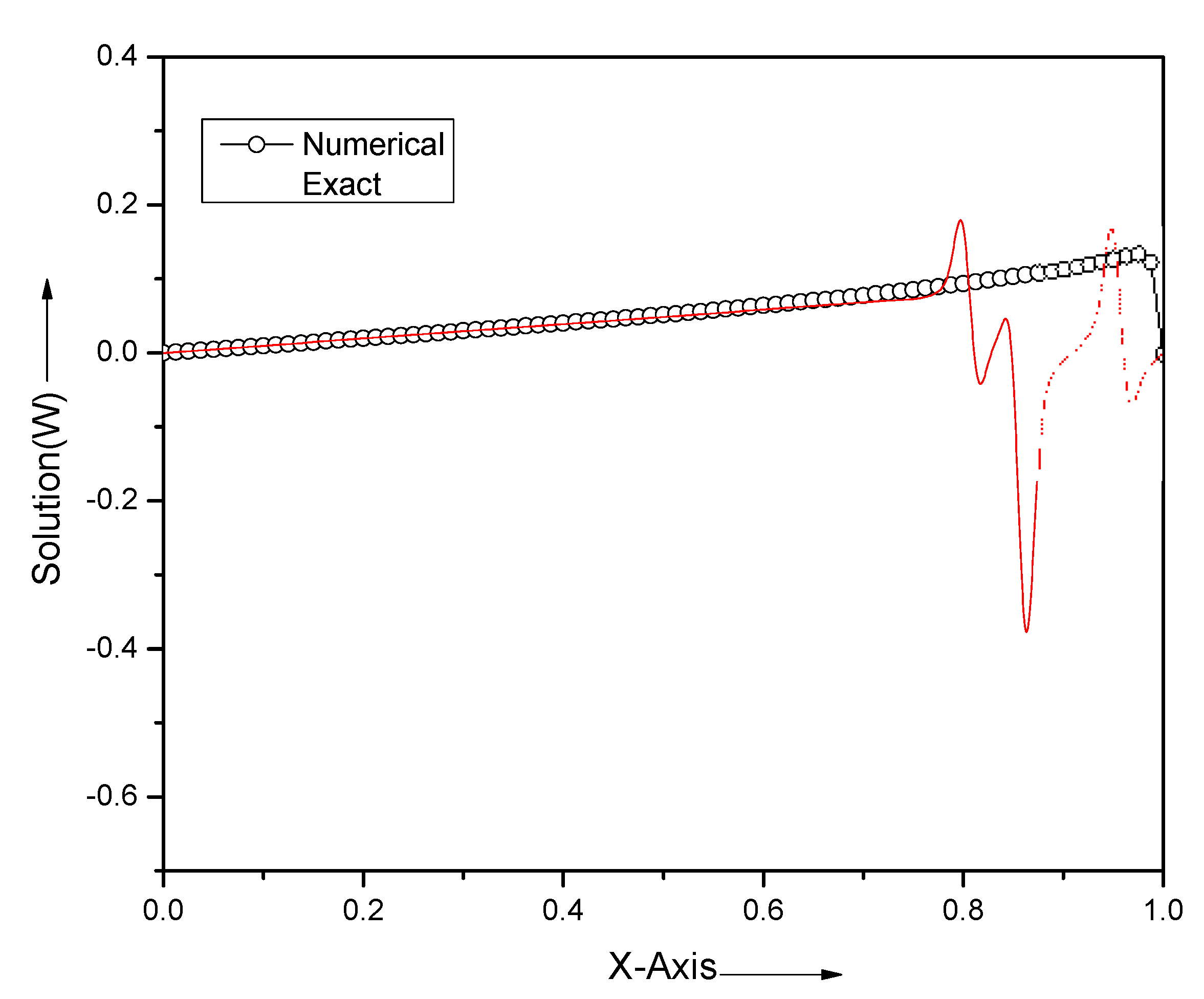
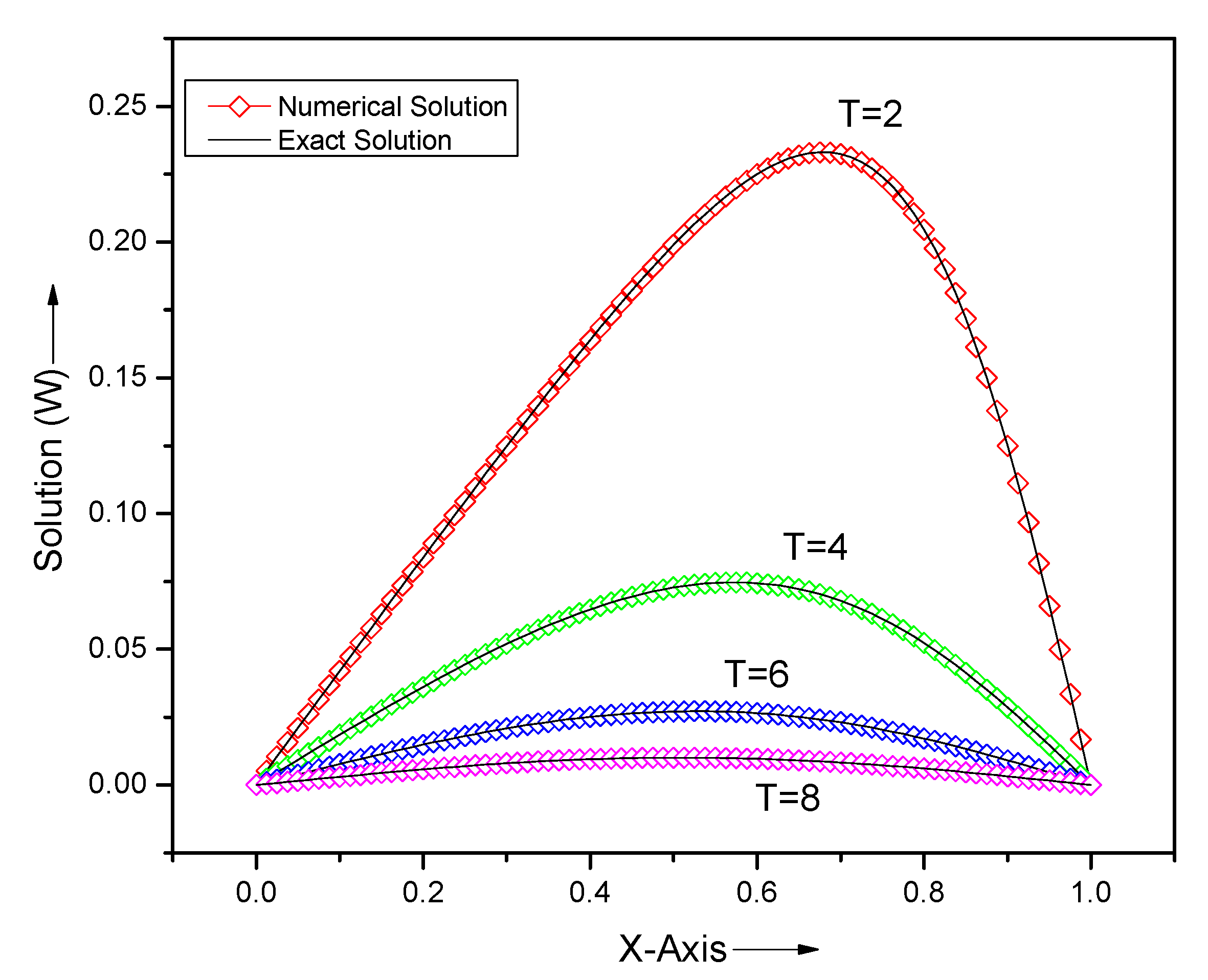

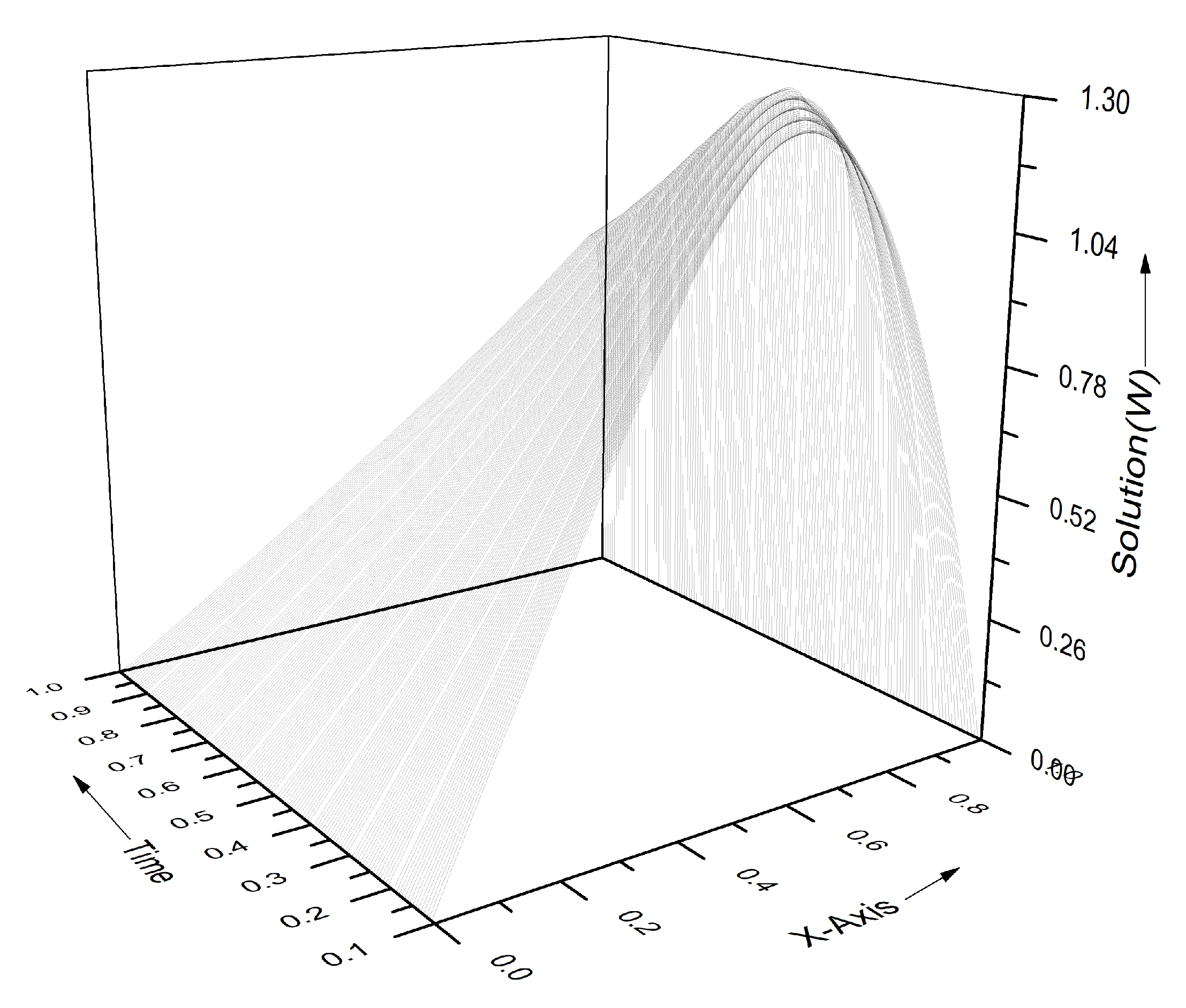
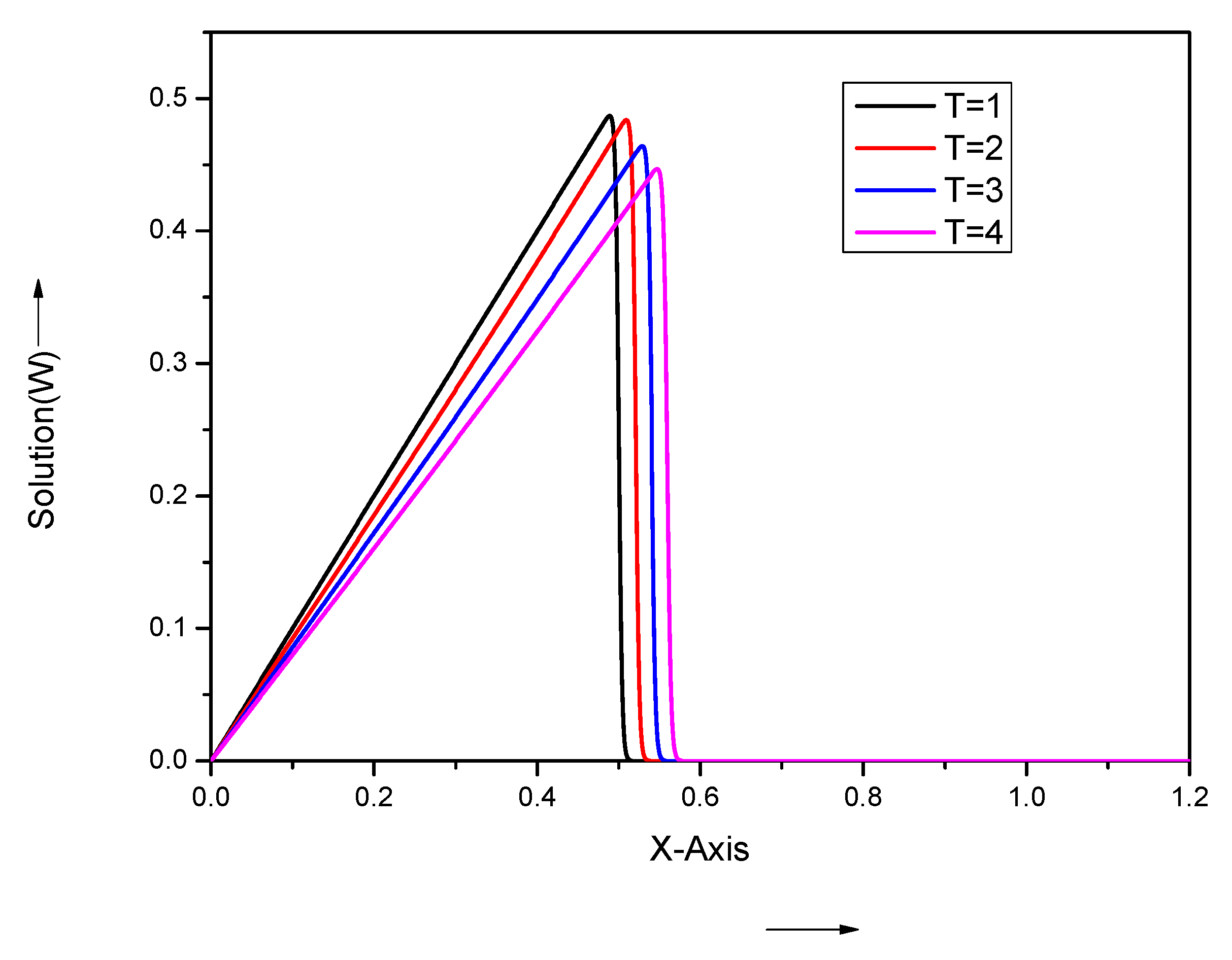
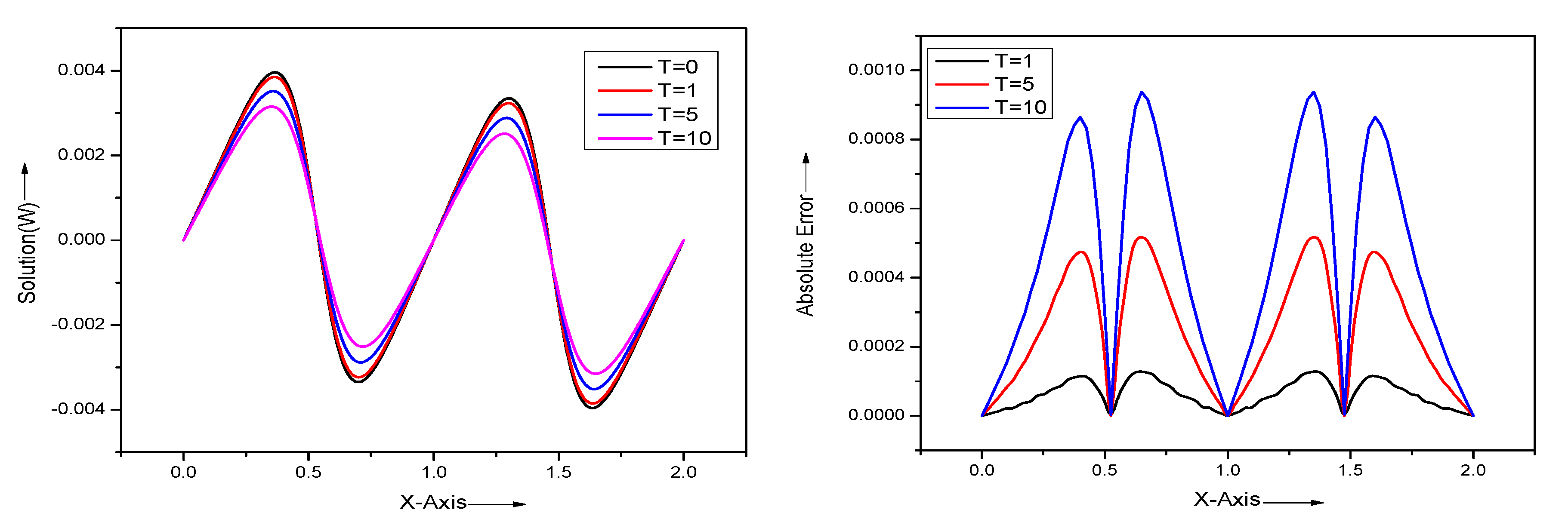
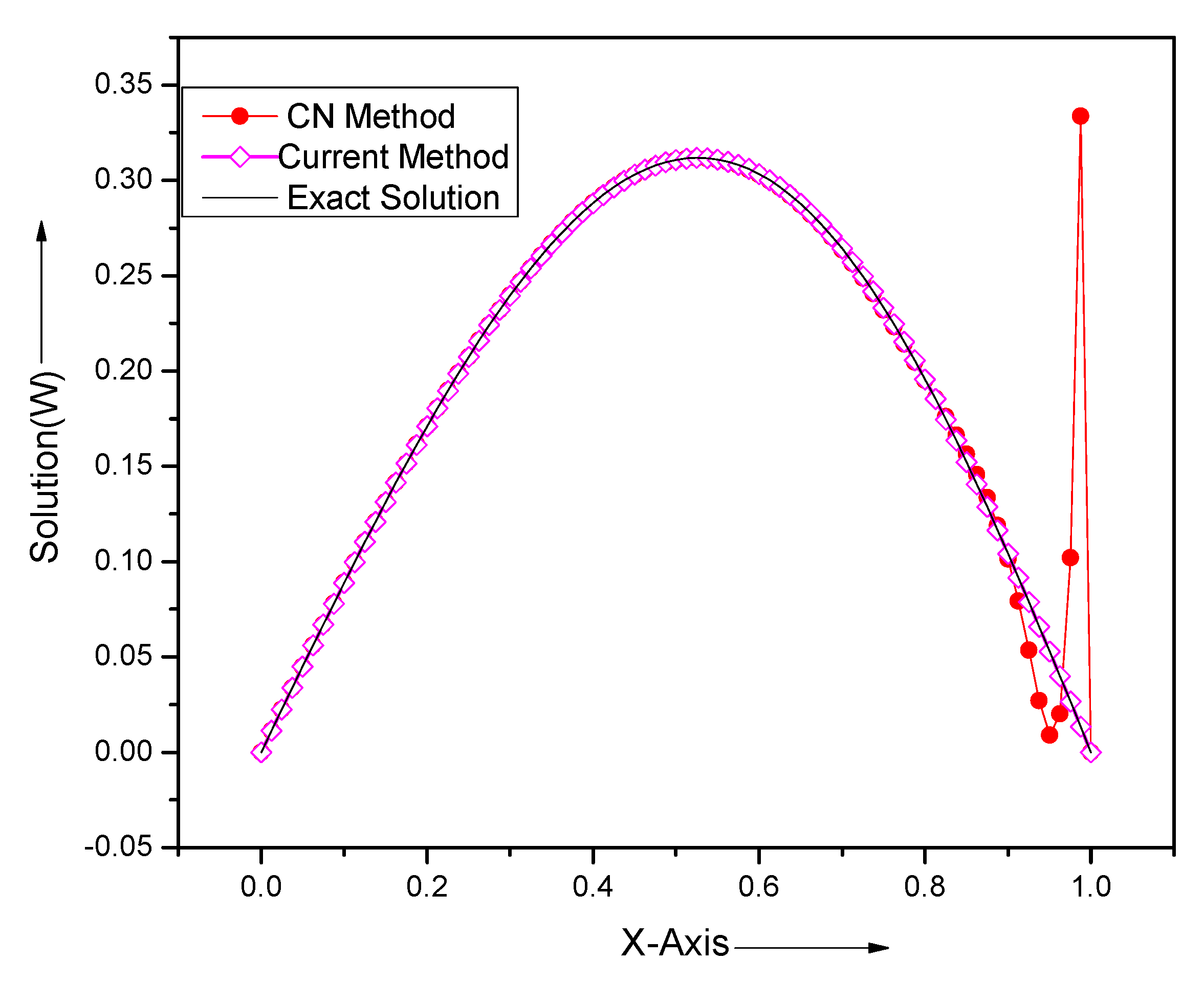

| x | T = 0.001 | T = 0.01 | T = 0.1 | |||
|---|---|---|---|---|---|---|
| 1/10 | 0.305088 | 0.304976 | 0.273239 | 0.273145 | 0.109538 | 0.109509 |
| 2/10 | 0.580565 | 0.580361 | 0.521564 | 0.521393 | 0.209792 | 0.209737 |
| 3/10 | 0.799621 | 0.799363 | 0.721852 | 0.721630 | 0.291896 | 0.291820 |
| 4/10 | 0.940817 | 0.940545 | 0.854590 | 0.854348 | 0.347924 | 0.347834 |
| 5/10 | 0.990174 | 0.989926 | 0.905713 | 0.905483 | 0.371577 | 0.371482 |
| 6/10 | 0.942609 | 0.942407 | 0.868334 | 0.868137 | 0.359046 | 0.358954 |
| 7/10 | 0.802522 | 0.802375 | 0.744098 | 0.743949 | 0.309905 | 0.309827 |
| 8/10 | 0.583466 | 0.583373 | 0.543821 | 0.543723 | 0.227817 | 0.227760 |
| 9/10 | 0.306881 | 0.306837 | 0.286999 | 0.286951 | 0.120687 | 0.120656 |
| 2.71275 × 10 | 2.413 × 10 | 9.54852 × 10 | ||||
| 6.41526 × 10 | 5.82562 × 10 | 2.27535 × 10 | ||||
| x | T | FEM [39] | Asai [40] | ||
|---|---|---|---|---|---|
| 1/4 | 0.4 | 0.31215 | 0.30891 | 0.3087531 | 0.30889 |
| 0.6 | 0.24360 | 0.24076 | 0.2406489 | 0.24074 | |
| 0.8 | 0.19815 | 0.19570 | 0.1956120 | 0.19568 | |
| 1 | 0.16473 | 0.16259 | 0.1625168 | 0.16256 | |
| 3 | 0.02771 | 0.02722 | 0.0271953 | 0.02720 | |
| 2/4 | 0.4 | 0.57293 | 0.56970 | 0.5694998 | 0.56963 |
| 0.6 | 0.45088 | 0.44728 | 0.4470928 | 0.44721 | |
| 0.8 | 0.36286 | 0.35932 | 0.3591441 | 0.35924 | |
| 1 | 0.29532 | 0.29200 | 0.2918410 | 0.29192 | |
| 3 | 0.04097 | 0.04023 | 0.0401946 | 0.04021 | |
| 3/4 | 0.4 | 0.63038 | 0.62567 | 0.6254715 | 0.62544 |
| 0.6 | 0.49268 | 0.48747 | 0.4871652 | 0.48721 | |
| 0.8 | 0.37912 | 0.37415 | 0.3738557 | 0.37392 | |
| 1 | 0.29204 | 0.28766 | 0.2874128 | 0.28747 | |
| 3 | 0.03038 | 0.02979 | 0.0297645 | 0.02977 |
| x | T | ||
|---|---|---|---|
| 1/4 | 5 | 0.046922 | 0.046963 |
| 10 | 0.024202 | 0.024217 | |
| 15 | 0.016300 | 0.016308 | |
| 20 | 0.012236 | 0.012240 | |
| 2/4 | 5 | 0.093998 | 0.093920 |
| 10 | 0.048414 | 0.048421 | |
| 15 | 0.032431 | 0.032439 | |
| 20 | 0.023883 | 0.023889 | |
| 3/4 | 5 | 0.141354 | 0.140832 |
| 10 | 0.071175 | 0.071134 | |
| 15 | 0.044135 | 0.044133 | |
| 20 | 0.029155 | 0.029159 |
| x | T = 0.001 | T = 0.01 | T = 0.1 | |||
|---|---|---|---|---|---|---|
| 1/10 | 0.350947 | 0.350703 | 0.294953 | 0.294822 | 0.112892 | 0.112863 |
| 2/10 | 0.630504 | 0.630240 | 0.553085 | 0.552873 | 0.216252 | 0.216195 |
| 3/10 | 0.830681 | 0.830425 | 0.749751 | 0.749515 | 0.300966 | 0.300887 |
| 4/10 | 0.951242 | 0.951009 | 0.873459 | 0.873232 | 0.358863 | 0.358770 |
| 5/10 | 0.991996 | 0.991794 | 0.919723 | 0.919518 | 0.383422 | 0.383324 |
| 6/10 | 0.952752 | 0.952578 | 0.886239 | 0.886057 | 0.370658 | 0.370563 |
| 7/10 | 0.833318 | 0.833164 | 0.771464 | 0.771302 | 0.320066 | 0.319985 |
| 8/10 | 0.633500 | 0.633351 | 0.576273 | 0.576138 | 0.235371 | 0.235312 |
| 9/10 | 0.353149 | 0.352988 | 0.310136 | 0.310053 | 0.124718 | 0.124687 |
| 2.64275 × 10 | 2.35909 × 10 | 9.85169 × 10 | ||||
| 6.55334 × 10 | 6.07706 × 10 | 2.46429 × 10 | ||||
| x | T | FEM [39] | Asai [40] | ||
|---|---|---|---|---|---|
| 1/4 | 0.4 | 0.32091 | 0.31754 | 0.317374 | 0.31752 |
| 0.6 | 0.24910 | 0.24616 | 0.246045 | 0.24614 | |
| 0.8 | 0.20211 | 0.19958 | 0.199490 | 0.19956 | |
| 1 | 0.16782 | 0.16562 | 0.165549 | 0.16560 | |
| 3 | 0.02828 | 0.02777 | 0.027752 | 0.02776 | |
| 2/4 | 0.4 | 0.58788 | 0.58460 | 0.584404 | 0.58458 |
| 0.6 | 0.46174 | 0.45805 | 0.457862 | 0.45798 | |
| 0.8 | 0.37111 | 0.36748 | 0.367304 | 0.36740 | |
| 1 | 0.30183 | 0.29843 | 0.298267 | 0.29834 | |
| 3 | 0.04185 | 0.41090 | 0.041054 | 0.04107 | |
| 3/4 | 0.4 | 0.65054 | 0.64586 | 0.645660 | 0.64562 |
| 0.6 | 0.50825 | 0.50294 | 0.502629 | 0.50268 | |
| 0.8 | 0.39068 | 0.38557 | 0.385269 | 0.38534 | |
| 1 | 0.30057 | 0.29605 | 0.295794 | 0.29586 | |
| 3 | 0.03106 | 0.03046 | 0.030432 | 0.03044 |
| x | T | ||
|---|---|---|---|
| 1/4 | 5 | 0.047415 | 0.047372 |
| 10 | 0.024336 | 0.024321 | |
| 15 | 0.016362 | 0.016355 | |
| 20 | 0.012272 | 0.012268 | |
| 2/4 | 5 | 0.094814 | 0.094895 |
| 10 | 0.048660 | 0.048653 | |
| 15 | 0.032550 | 0.032542 | |
| 20 | 0.023957 | 0.023951 | |
| 3/4 | 5 | 0.142154 | 0.142693 |
| 10 | 0.071517 | 0.071560 | |
| 15 | 0.044328 | 0.044330 | |
| 20 | 0.029275 | 0.029271 |
| x | T = 1.7 | T = 3.0 | T = 3.5 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| [41] | [41] | [41] | |||||||
| 2/10 | 0.117647 | 0.117660 | 0.11745 | 0.066667 | 0.066669 | 0.06648 | 0.057143 | 0.057144 | 0.05697 |
| 4/10 | 0.235294 | 0.235420 | 0.23456 | 0.133333 | 0.133355 | 0.13295 | 0.114286 | 0.114299 | 0.11394 |
| 6/10 | 0.352909 | 0.353346 | 0.34936 | 0.200000 | 0.200079 | 0.19922 | 0.171429 | 0.171478 | 0.17082 |
| 8/10 | 0.000000 | 0.000000 | 0.00000 | 0.266618 | 0.266808 | 0.26478 | 0.228571 | 0.228690 | 0.22737 |
| 0.50201 | 29.70447 | 0.21289 | 19.00976 | 0.16870 | 16.78871 | ||||
| 0.16675 | 3.59366 | 0.08135 | 2.63510 | 0.06695 | 2.41729 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verma, A.K.; Rawani, M.K.; Agarwal, R.P. A High-Order Weakly L-Stable Time Integration Scheme with an Application to Burgers’ Equation. Computation 2020, 8, 72. https://doi.org/10.3390/computation8030072
Verma AK, Rawani MK, Agarwal RP. A High-Order Weakly L-Stable Time Integration Scheme with an Application to Burgers’ Equation. Computation. 2020; 8(3):72. https://doi.org/10.3390/computation8030072
Chicago/Turabian StyleVerma, Amit Kumar, Mukesh Kumar Rawani, and Ravi P. Agarwal. 2020. "A High-Order Weakly L-Stable Time Integration Scheme with an Application to Burgers’ Equation" Computation 8, no. 3: 72. https://doi.org/10.3390/computation8030072
APA StyleVerma, A. K., Rawani, M. K., & Agarwal, R. P. (2020). A High-Order Weakly L-Stable Time Integration Scheme with an Application to Burgers’ Equation. Computation, 8(3), 72. https://doi.org/10.3390/computation8030072







