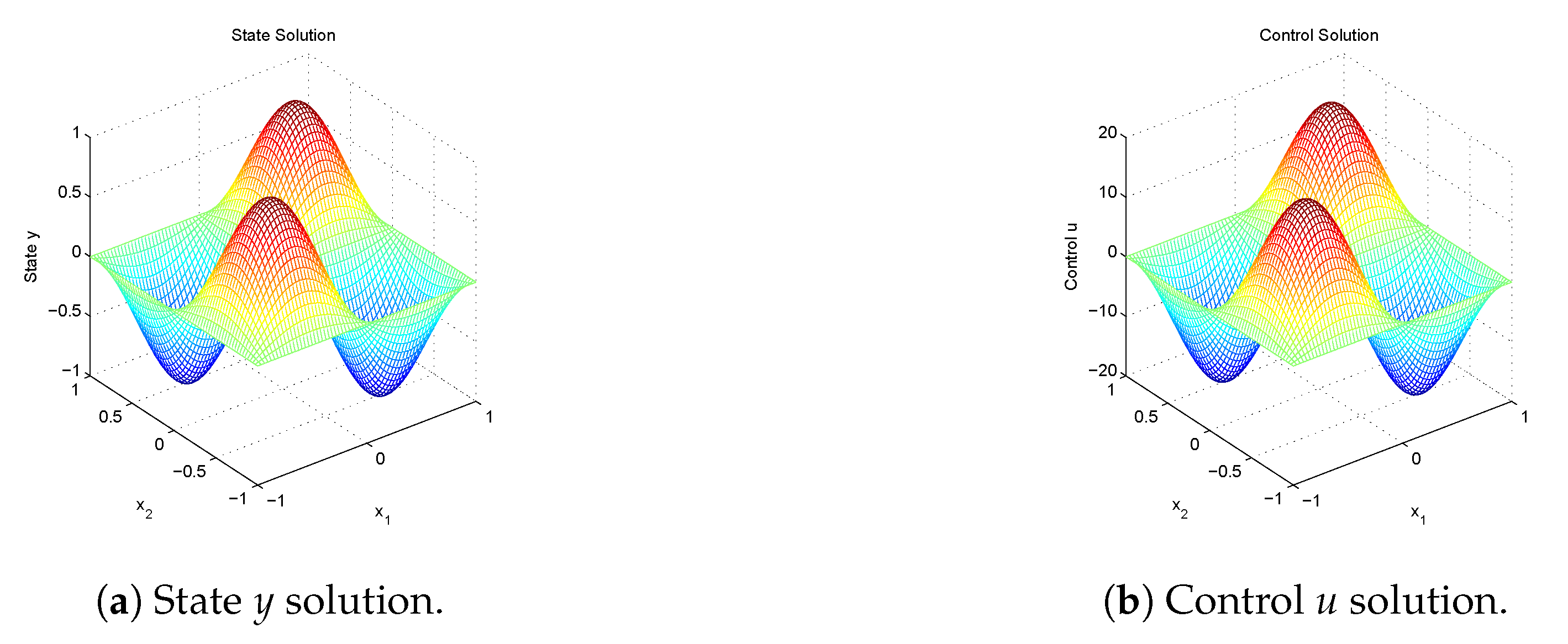1. Introduction
The partial differential equation constrained optimisation problems have over the years become an active research area that has arisen in many application areas that include finance, medicine, modern science and engineering. We refer to [
1,
2] on their theoretical and also to [
3,
4,
5] on their numerical developments. These problems are numerically and analytically challenging to solve. The most clear challenge is that the resulting linear algebraic system is very large such that the only viable way is to get the solution iteratively using specialised methods. The formulation of the linear optimisation problem involves the objective function to minimise subject to the constraints defined by the underlying modelling partial differential equation in a bounded domain
with boundary
. Consider the following elliptic distributed PDE-optimal control problem
subject to the constraints
with
y the state variable,
the desired state known over the domain
and
u the control variable on the right hand side. The parameter
is called the regularisation parameter which measures the cost of the control and is supplied and positive. The size of the regularisation parameter is important in the performances of the iterative solvers. The optimal value of the regularisation parameter
is
; see [
6,
7]. The performance of iterative solvers with the decreasing parameter is the central theme of this study. The solution of the state variable
y must satisfy the PDE over
and must be as close as possible to the desired state
so that the objective function can be minimised.
The optimal control problem Equations (
1) and (
2) has a unique solution
characterised by the following optimality system called the Karush–Kuhn–Tucker (KKT) system [
8,
9]. The first order optimality system of the PDE-optimal control problems consists of a state equation, an adjoint equation and the control equation which is a saddle point problem as given below
The optimality system is achieved through the Lagrange multiplier method which partitions the model problem into three equations, namely, the state
y, control
u and the adjoint,
p which form the saddle point problem. For the numerical solution of the elliptic optimal control problem we apply the finite element method to the system ((
3)–(
5)) to get the linear saddle point problem. The finite element method is the most popular technique for the numerical solution of the PDE-constrained optimisation problems; see [
5,
6,
7] and many more. The finite element method results in the coupled linear algebraic system which has to be solved by the appropriate solvers. The resulting discrete KKT system is
where
is a stiffness matrix, and that and the mass matrix
are both symmetric and positive definite. The vector
is the finite element projection of the desired state
, and
contains the terms arising from the boundaries of the finite element of the state
y.
The finite element discretisation produces a large scale linear algebraic system of Equation (
6) which is indefinite and has poor spectral properties. The numerical solution of such problems is a computational uphill task and has a lot of challenges such that constructing robust and efficient solvers has preoccupied the computational scientific community for decades. The linear algebraic indefinite system is parameter dependent such that the condition number grows when the mesh size and the regularisation parameter approach zero. The well known Krylov and multigrid iterative solvers perform poorly for such systems. In recent years, much effort has been devoted in developing specialised iterative solvers using suitable preconditioners [
3,
6,
7,
10,
11,
12] and appropriate smoothers for the multigrid solvers [
8,
9,
13,
14,
15,
16,
17]. For the development of the efficient multigrid solvers for the distributed optimal control problems, we refer to ([
8,
9,
15,
16,
18,
19]. Several preconditioned strategies have been developed and evolved that accelerate the iterative solvers. These are the block diagonal preconditioner [
6,
20,
21,
22] for the minimum residual (MINRES) solver [
23,
24], and for the generalised minimal residual (GMRES) method, block triangular preconditioners with nonstandard inner products for the conjugate gradient method [
7,
10,
21,
22,
25] and the constraint preconditioner [
7,
11,
21]. The preconditioners were also developed for the two by two reduced block linear system and three by three block system to solve the optimal control problems of the Stokes [
10,
26,
27], parabolic [
28,
29] and convection diffusion [
30] equations. In most cases the application of preconditioners shows robustness and efficiency with the decreasing mesh size but not with the decreasing regularisation parameter. In this study, we focus on the improvement of the block diagonal preconditioner to enhance the performance of the MINRES solver. The MINRES was developed by [
31] and widely used for PDE-constrained optimisation problems. The aim of this paper is to present preconditioners based on the Schur complement approach that seek to achieve an efficient solution of the linear system arising from the discretisation of the PDE- optimal control problems. We give particular attention to preconditioning techniques that achieve robust performances in the MINRES solver with respect to both decreasing mesh size and the regularisation parameter. As the mesh size approaches zero, the dimensions of the problem increase. A mesh-independent performance is always achieved for such systems, but the small values of the regularisation parameter pose a great challenge to the iterative solvers. As the regularisation parameter decreases, the performance of the iterative solver deteriorates, but it improves for large values.
The optimal performance of the preconditioner depends on applying an appropriate approximation of the (1,1) and (3,3)-block entries of the preconditioner. For the preconditioners based on the Schur complement, the (3,3) Schur complement remains one of the challenges to finding a suitable approximation to achieve robustness in terms of parameter changes. The Schur complement approximation developed in [
6] and widely used in literature displays optimal performance for large values of the regularisation parameter, but the performance of it deteriorates as the parameter approaches zero. In [
21,
23] another Schur complement approximation was developed for PDE-constrained optimisation problems which gives convergence of the appropriate iterative method in a number of steps which are independent of the value of the regularisation parameter. The preconditioned iterative solver displays optimal performance for small values of the regularisation parameter. The main contribution of this work is to present a different form of the Schur compliment approximation to achieve an optimal performance of the MINRES solver in terms of iterative counts that are independent of the decreasing mesh size and the regularisation parameter. The clustering of the eigenvalues points to the good convergence properties of the preconditioned solver. We remove the dependency on the regularisation parameters within the preconditioned matrix as in [
21]. We derive and investigate the clustering of the eigenvalues for the Schur compliment approximate and the preconditioned system. The numerical experiments’ outcomes of the proposed approximation are compared with the existing approximations of the Schur complement preconditioner to show its efficiency.
This paper is organised as follows. In
Section 2 we preview the block diagonal preconditioner and investigate the eigenvalue distribution. In
Section 3, we discuss our proposed approximation for the Schur complement and investigate the eigenvalue distribution of the preconditioned system. In
Section 4 we present the numerical experiments to demonstrate how well the proposed approximation works and the conclusion is given.
2. Analysis of the Block Diagonal Preconditioner
We consider the preconditioning strategies for solving the saddle point problem, Equation (
6). The optimal performance of the preconditioned Krylov subspace methods such as MINRES, GMRES and conjugate gradient rely more on the distribution of the eigenvalues of the coefficient matrix. It is well known in numerical analysis that the spectral radius must be bounded by one to guarantee convergence of the iterative solvers. The coefficient matrix of the system (
6) is known to be large, sparse and indefinite with poor spectral properties. This section aims to outline the block diagonal preconditioner that involves the mass matrix and a Schur complement form. We consider a block diagonal preconditioner for the
block coefficient matrix of the Equation (
6). For the
block preconditioners we refer to [
7,
22] and the references therein. The block diagonal preconditioner is given by
where
is the Schur complement form. A good preconditioner must fulfil the assumptions that it is easy to invert, and the linear system
associated with it is easy to solve for any vector
. The approximation of the (3,3) block entry poses more challenges and difficulties. One possible widely used approach as in [
6,
21,
24] is to get the approximation of
S by discarding the term
to obtain
by dropping a term with
with an argument such that for all very small values of
the term
will be dominating. The application of the preconditioner with the approximation
has the shortfall that the iterative solver converges independently of the decreasing mesh size only but not in the decreasing regularisation parameter
. To demonstrate this we need to give the eigenvalue bounds for
as derived in [
6,
21]. We now use the following results, which are Theorems (3.4) and (3.5) in [
6] and used by [
21,
24].
Theorem 1 ([
6]).
For the problem Equation (6) in with the degree of approximation or with the following bounds hold:where and are real constants independent of h but dependent on . Theorem 2 ([
6]).
For the problem Equation (6) in with the degree of approximation or with the following bounds hold:where and are real constants independent of h but dependent on . Theorem 3. The eigenvalues of are bounded as where and are independent of h and but dependent on δ.
Proof of Theorem 3 To find the eigenvalue distribution of
, let
be the eigenvalue, and then
Let
be an eigenvalue of
then the eigenvalue of
is
. This means that
. By using Theorems 1 and 2, there exist positive constants
and
independent of mesh size; we have
This implies that we have
Thus, it follows that there exist constants
and
independent of the mesh size such that
□
It is clear that
has no dependence on
but the eigenvalue lower and upper bounds are dependent on
. The eigenvalue bounds demonstrated by the Theorem 3 above show that the parameter
determines the clustering and distribution of eigenvalues. This clearly shows that if
is too small the eigenvalues are not clustered and
will not be a better approximation. This entails that large values of
,
are a perfect approximation. The current research seeks to construct an approximation whose performance does not rely on both the mesh size and the regularisation parameter. The following theorem in [
6] gives the eigenvalue distribution of the preconditioned coefficient matrix with preconditioner
with the approximation for the Schur complement form
where
Theorem 4 ([
7,
24]).
For approximation, let the preconditioner be defined by Equation (10). Assume that λ is an eigenvalue of the preconditioned matrix . Then or λ satisfies the following bound: For the proof and details we refer to [
7,
24] and references therein.
3. Proposed Schur Complement Preconditioner Approximation
The above Theorem 4 has demonstrated that applying the preconditioner with the Schur complement approximation
results in performance and convergence of the preconditioned iterative solver that are independent of the discretisation mesh size and dependent on the regularisation parameter. It is expected that the convergences of the Krylov methods such as MINRES and GMRES are independent of the mesh size. The crucial task is to develop an efficient preconditioner that gives close eigenvalue bounds of the preconditioned system. The scientific literature on preconditioning optimal control systems includes classical Schur complement based approximations. In [
21] we see the extension of the preconditioner whose effects are independent of the regularisation parameter. This was also used in [
24]. The main task of this section is to briefly discuss the approximation in [
21] and the one we propose in this work, which has the same clustering and distribution of eigenvalues and produces a preconditioned iterative solver that is not sensitive to the changes and decreasing regularisation parameter. The following approximation for
S was developed in [
21]
which reduces to
by discarding the much smaller term
which is a smaller
term than
shown
Section 2 above. To get eigenvalue bounds for
, we follow the same derivation and use the Theorems 1–3 above. The preconditioner involving the Schur complement approximation
is given as follows
There has been development of similarly structured Schur complement approximations to
whose eigenvalue bounds are the same but differ in computational complexities. We have
which is complex based developed by Choi and others in [
32]. In this paper we propose and analyse a robust approximation for
S which has the same eigenvalue bounds but a different eigenvalue distribution within the interval for
as the approximation
which is expected to accelerate the numerical solution. Our proposed approximation for the Schur complement is also derived from
by writing
which similarly reduces to
by discarding a
term this means that the error committed grows much slower. To motivate our choice of the Schur complement approximation, we illustrate the properties of the preconditioned Schur complement and the preconditioned system. We now discuss the derivation of the eigenvalue distribution of
by following the same derivation in [
21].
Theorem 5. The eigenvalues of satisfy the following bounds independent of both mesh size h and regularisation parameter δ
Proof of Theorem 5 is invertible since
M is symmetric and positive definite. Let
be an eigenvalue of
corresponding to eigenvector
; then
Let
be the eigenvalue of
; then
This means that is an eigenvalue of . Now since is similar to the real and symmetric matrix , it is diagonalisable; this means that it describes all the eigenvalues of . It is known that a fraction of the form is bounded between and 1. Hence, which takes the form . Thus, . By this we conclude that is clustered and not dependent on the mesh size h and the regularisation parameter . □
The actual application of the preconditioner in actual computations involving solving two subsystems to accelerate the convergence of Krylov subspace iteration process can be implemented as: Application of Preconditioner .
Algorithm 1.Application of Preconditioner
Let and be any given vector; we can compute the vector and , that is, , using the following procedures:
Since
M and
K are sparse,
L is sparse too, and an added bonus for
and
is that they maintain
-dependency and their bounds are fairly good. The preconditioner involving the Schur complement approximation
is given as follows.
We now derive the eigenvalues distribution of the preconditioned coefficient matrix
with the modified approximation for the Schur complement form. We will use Proposition (2) in [
7] which extends Theorem 4.
Theorem 6 ([
7]).
The eigenvalues of the preconditioned system where and are in the interval Proof of Theorem 5 Let
be the eigenvalue of
and
be an eigenvalue of
corresponding to the eigenvector
. We want to find the eigenvalues bounds for
. We use a different approach from the one in [
21]. We have
The preconditioned coefficient matrix
We consider the eigenvalue problem
If
from Equations (
13) and () we have
and
, then
. Therefore, the corresponding eigenvector is
If
from Equations (
13) and () we have
Substituting Equations (
16) and () into Equation (), we get
Therefore
satisfies
with the corresponding eigenvector
Since
is the eigenvalue of
, then we have
which is
Solving Equation (
18) we get
The values of
derived above agree with the Proposition (2) in [
6] which gives the bounds
. We have that if
are eigenvalues of
then the other eigenvalues of
are
This means that the eigenvalues of
are the eigenvalues of
. From Theorem 5 we have
. Let
and
; substituting in Equations (
19) and () we get
and
Therefore the eigenvalues of the preconditioned coefficient matrix are
□
The Theorem 6 above clearly shows that the eigenvalues of the preconditioned coefficient matrix are clustered and are independent of both the mesh size and the regularisation parameter. The iterative solver is expected to converge with changes in the problem parameters and discretisation parameter. In the next section we carry out numerical tests to verify the theoretical findings and compare the performance of the MINRES solver with the block diagonal preconditioner associated with the three approximations for the Schur complement form.
4. Numerical Results
In this section we present the results of the numerical experiments for solving the problem (Equation (
6)) using the block diagonal preconditioned MINRES method. The main task here is to demonstrate the effectiveness of preconditioner in accelerating the MINRES solver. In this study the numerical experiments began with the
finite element discretisation of the state
y, the adjoint
p and the control
u equations using uniform grids. All simulations and implementations were performed on a Windows 10 platform with Intel
® Core™ i5-3230M CPU@2.6 GHz 6.00 GB speed Intel
® using Matlab 7 programming language. We used the IFISS matlab package developed in [
33] to generate a discrete linear algebraic system. The values of the mesh size
h and the dimensions of
M,
K and
are shown in
Table 1 below
The exact solutions for the distributed optimality system and
are
We give a thumbnail outline of the main task of the paper in the application of the approximation of the Schur complement preconditioner
. The main dominant operations in the application of our proposed block diagonal preconditioner
are 10 fixed Chebyshev semi iterations [
6,
12,
29] for the mass matrix
M in the (1,1) and (2,2) blocks; the (3,3) block is approximated by two cycles of the algebraic multigrid methods for
. This means in total we have two Chebyshev and two algebraic multigrid iterations with two pre and post-smoothing steps of the Jacobi method; similarly for
and
. We test for four regularisation parameters
and
.
We solve the linear algebraic system of saddle point form Equation (
6) using the MINRES with the block diagonal preconditioners
(Equation (
10)),
(Equation (
11)) and
(Equation (
12)) with the three different preconditioner approximations for the Schur complement form
S. Then we compare the performance of the block diagonal preconditioned MINRES method with the three preconditioner approximations for the Schur complement in terms of the number of iterations, CPU time,
error and the value of the objective function. The numerical solution produced by the MINRES with the preconditioner associated with the three Schur complement approximations is the same.
Figure 1 gives the snapshots of the numerical solution,
We now present the eigenvalue distribution of the .
The
Table 2 shows the largest and the smallest eigenvalues of the Schur complement
. The values in
Table 2 clearly show the effects of the preconditioner approximation on the spectral properties of the Schur complement. The eigenvalues of
are clearly dependent on the parameter
; and the eigenvalues of
are bounded between
and 1 though their distribution and are different independent of the parameter
. This confirms the theoretical results and is clearly shown on the figures below.
Figure 2 shows the distribution of eigenvalues for different values of regularisation parameter.
Figure 2 gives the eigenvalue distribution of
for different values of the regularisation parameter at
.
Figure 2a,d,g gives the eigenvalue distribution of
;
Figure 2b,e,h shows the eigenvalue distribution of
; and
Figure 2c,f,i shows the eigenvalue distribution of
for different values of
at
. The eigenvalues are sorted form the smallest to the largest. The most important observation is that the eigenvalue distribution of
is widely spread out as the regularisation parameter decreases. This agrees with the theoretical findings that the eigenvalues depends on the regularisation parameter. Hence the preconditioner approximation performance is not independent of
and deteriorates for small values of
. We also observe that for the approximations
and
the eigenvalue distribution falls with the interval that is given theoretically for the different values of the regularisation parameter. This entails that the clustering of the eigenvalues shown in the
Figure 2 above points to the fast convergence of the iterative solver for all the values of the regularisation parameter.
We now give the numerical experiment results from our MINRES iterative solver preconditioned with the block diagonal preconditioner associated with the three approximations. Since the numerical solutions are the same, we concentrate on the performance in terms of the number of iterations and the CPU time in seconds for comparison purposes.
It is clear from
Table 3 that all these preconditioners associated with the approximations
are robust with respect to mesh size
h, but the approximation
is not robust with respect to the regularisation parameter. The preconditioners associated with approximations
performed efficiently for all the values of
h and
, with
performing slightly better.
The results in
Table 3 and
Table 4 demonstrate the practical applicability of the preconditioners explained theoretically in
Section 2 and
Section 3 and the theoretical prowess of the three approximations of the Schur complement form using the eigenvalue distribution.
Table 3 and
Table 4 give the number of iterations and the CPU time taken by the MINRES preconditioned by block diagonal preconditioners Equations (
10)–(
12) with different values of mesh size and the regularisation parameter, and we compare the effectiveness of the three preconditioners with approximations for the Schur compliment preconditioner. The results clearly show that the preconditioner with
displays mesh-independent convergence but fails on the decreasing values of the regularisation parameter
. The number of iterations and CPU time increase as
. This agrees with the poor eigenvalue distribution of
and that of
. The number of iterations and CPU times produced by the preconditioners associated with
and
are competitive and exhibited parameters
h and
independent of convergence, while both
h and
approached zero. The number of iterations of
and
decreased by the decrease of
, as expected, and those of
decreased further. The results show that these preconditioners are also robust to the mesh size
h and the regularisation parameter
. This agrees with the theoretical results that the eigenvalues are more clustered and distributed more independently of the parameters
h and
than those of
; see
Figure 2. The results of our numerical experiments clearly show that the preconditioners with the approximations
and
are very effective in improving the MINRES in solving elliptic control problems. When compared to other preconditioner approximations in terms of iteration count and computational time,
slightly outperformed them. The preconditioners are more effective with our new approximation, producing more favourable results. We now give the results including the cost functional at
for different values of the objective function for the approximation
and there are the same outputs with the other approximations.
The results in
Table 5 show the behaviour of the cost functional for different values of the regularisation parameter
. It is well known that the
determines how close the state approaches the desired state
. The results provide an interesting observations that
stops increasing at
with
and
decreases with the decrease by a constant factor of the decrease of
. This means that the optimal value of
for the problem is
, becoming very close to the desired state, and also that the control variable
increases as
decreases. This is clear indication that the cost functional will be insensitive to the control variable as
decreases.