Performance and Energy Assessment of a Lattice Boltzmann Method Based Application on the Skylake Processor †
Abstract
1. Introduction and Related Works
2. The Lattice Boltzmann Method
3. Computer Architectures
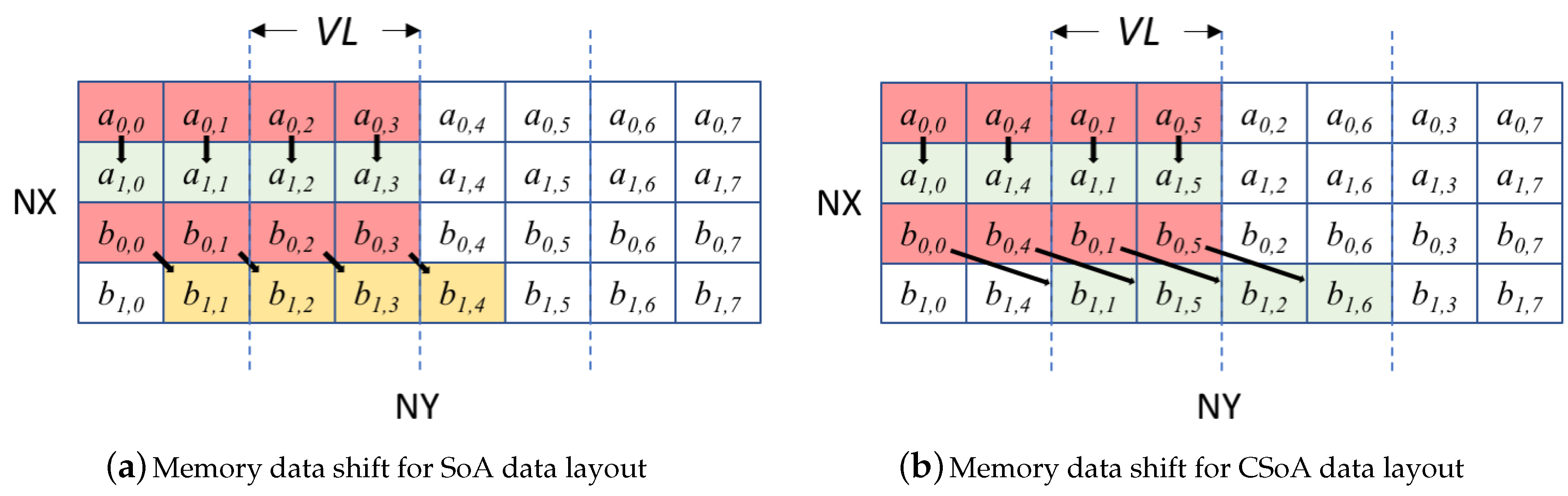
4. Code Optimization for LBM Based Applications
| Algorithm 1: Schematic description of the LBM main loop optimization |
 |
5. Results
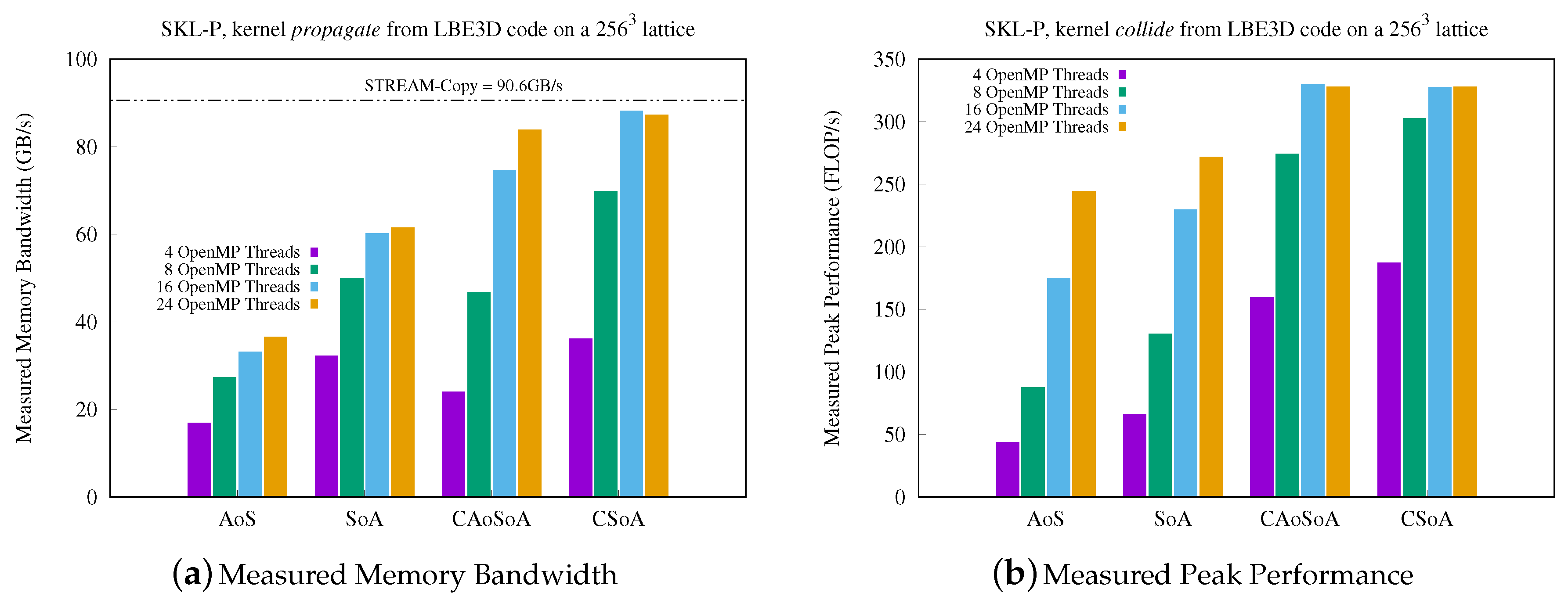
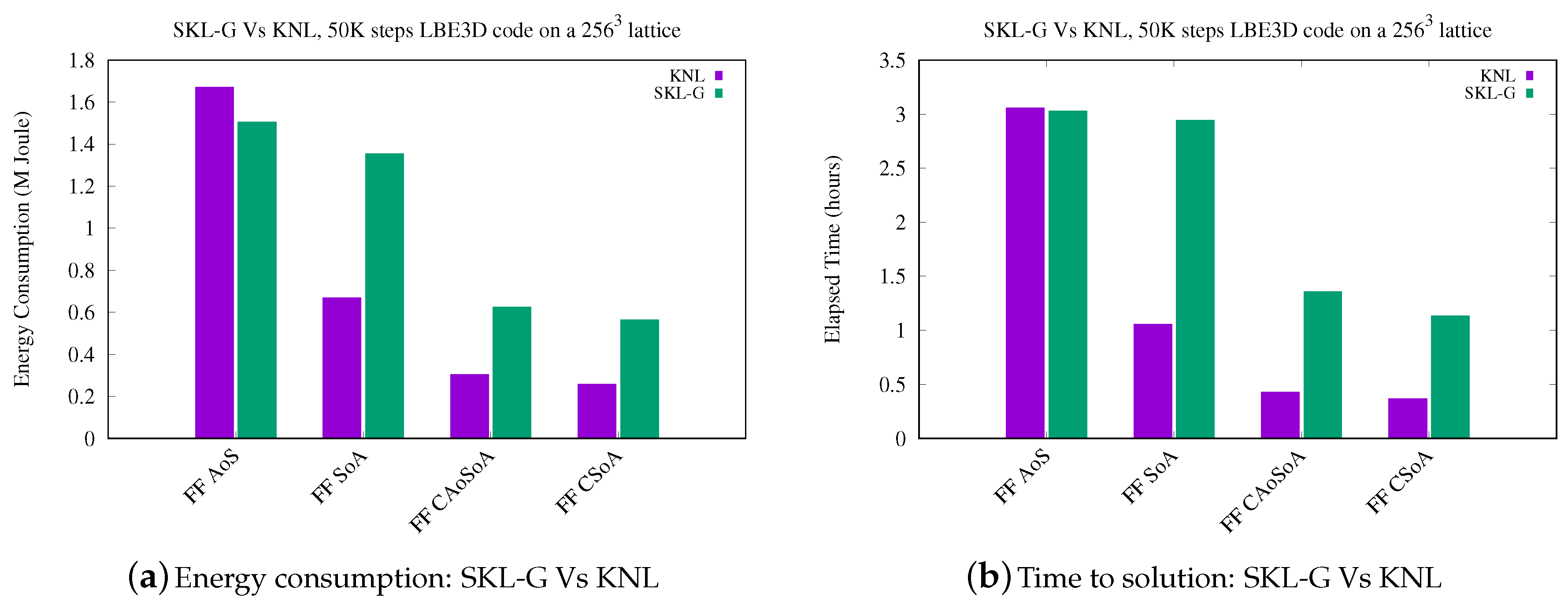
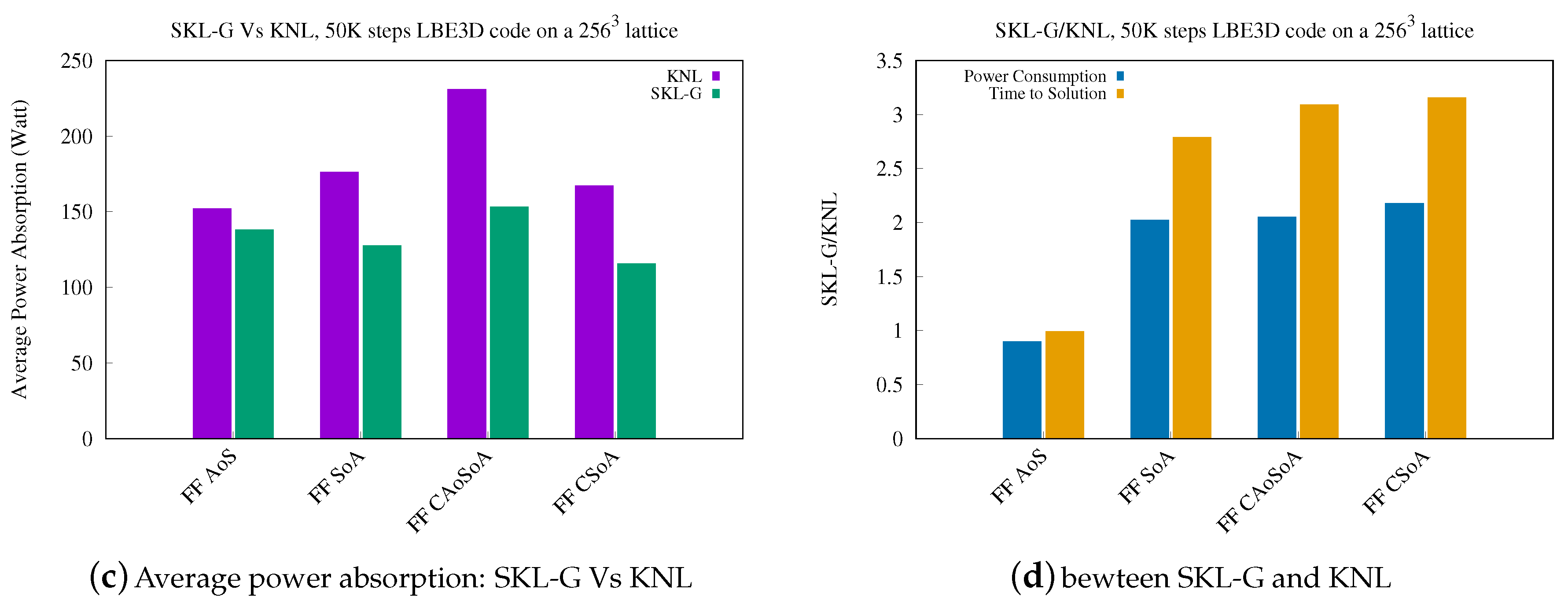
5.1. Analysis of Performance
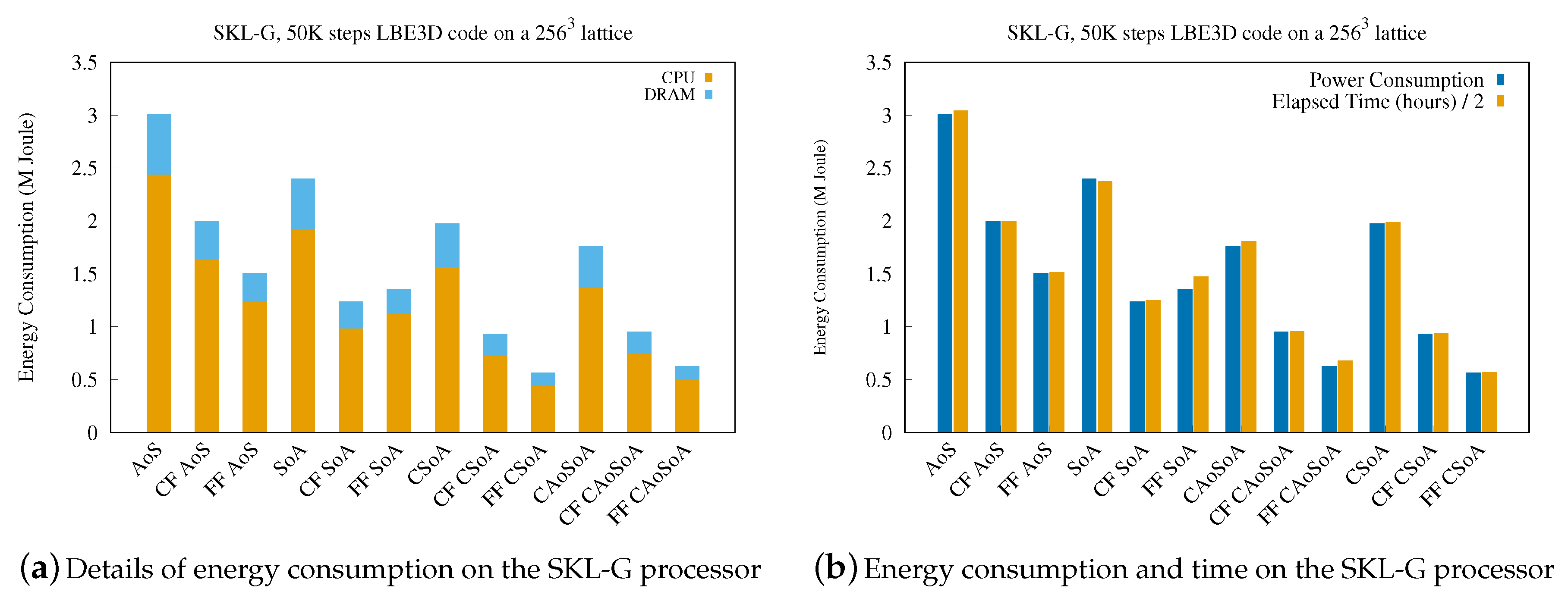
5.2. Analysis of Energy Efficiency
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Girotto, I.; Schifano, S.F.; Calore, E.; Di Staso, G.; Toschi, F. Performance Optimization of D3Q19 Lattice Boltzmann Kernels on Intel KNL. In Proceedings of the INFOCOMP 2018: The Eighth International Conference on Advanced Communications and Computation, Barcelona, Spain, 22–26 July 2018; pp. 31–36. [Google Scholar]
- Girotto, I.; Schifano, S.F.; Calore, E.; Di Staso, G.; Toschi, F. Computational Performances and Energy Efficiency Assessment for a Lattice Boltzmann Method on Intel KNL. Adv. Parallel Comput. 2019, 36, 605–613. [Google Scholar] [CrossRef]
- Calore, E.; Demo, N.; Schifano, S.F.; Tripiccione, R. Experience on Vectorizing Lattice Boltzmann Kernels for Multi- and Many-Core Architectures. In PPAM 2015, Proceedings of the Parallel Processing and Applied Mathematics: 11th International Conference, Krakow, Poland, 6–9 September 2015; Revised Selected Papers, Part I; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2016; pp. 53–62. [Google Scholar] [CrossRef]
- Calore, E.; Gabbana, A.; Schifano, S.F.; Tripiccione, R. Early experience on using Knights Landing processors for Lattice Boltzmann applications. In Proceedings of the Parallel Processing and Applied Mathematics: 12th International Conference (PPAM 2017), Lublin, Poland, 10–13 September 2017; Lecture Notes in Computer Science. Volume 1077, pp. 1–12. [Google Scholar] [CrossRef]
- Calore, E.; Gabbana, A.; Kraus, J.; Schifano, S.F.; Tripiccione, R. Performance and portability of accelerated lattice Boltzmann applications with OpenACC. Concurr. Comput. Pract. Exp. 2016, 28, 3485–3502. [Google Scholar] [CrossRef]
- Eastep, J.; Sylvester, S.; Cantalupo, C.; Geltz, B.; ArdanazAsma, F.; Livingston, A.R.; Keceli, F.; Maiterth, M.; Jana, S. Global Extensible Open Power Manager: A Vehicle for HPC Community Collaboration on Co-Designed Energy Management Solutions. In International Supercomputing Conference; High Performance Computing, ISC 2017, Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10266, pp. 394–412. [Google Scholar] [CrossRef]
- Patki, T.; Lowenthal, D.K.; Sasidharan, A.; Maiterth, M.; Rountree, B.L.; Schulz, M.; de Supinski, B.R. Practical Resource Management in Power-Constrained, High Performance Computing. In Proceedings of the 24th International Symposium on High-Performance Parallel and Distributed Computing (HPDC ’15); Association for Computing Machinery: New York, NY, USA, 2015; pp. 121–132. [Google Scholar] [CrossRef]
- Vysocky, O.; Beseda, M.; Říha, L.; Zapletal, J.; Lysaght, M.; Kannan, V. MERIC and RADAR Generator: Tools for Energy Evaluation and Runtime Tuning of HPC Applications. In High Performance Computing in Science and Engineering ( HPCSE 2017); Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11087. [Google Scholar] [CrossRef]
- Hackenberg, D.; Ilsche, T.; Schuchart, J.; Schöne, R.; Nagel, W.E.; Simon, M.; Georgiou, Y. HDEEM: High Definition Energy Efficiency Monitoring. In Proceedings of the 2014 Energy Efficient Supercomputing Workshop, New Orleans, LA, USA, 16 November 2014; pp. 1–10. [Google Scholar]
- Roberts, S.I.; Wright, S.A.; Fahmy, S.A.; Jarvis, S.A. Metrics for Energy-Aware Software Optimisation. In Proceedings of the 32nd International Conference, ISC High Performance 2017, Frankfurt, Germany, 18–22 June 2017; Volume 10266. [Google Scholar] [CrossRef]
- Roberts, S.I.; Wright, S.A.; Fahmy, S.A.; Jarvis, S.A. The Power-Optimised Software Envelope. ACM Trans. Archit. Code Optim. 2019, 16. [Google Scholar] [CrossRef]
- Padoin, E.L.; de Oliveira, D.A.G.; Velho, P.; Navaux, P.O.A. Time-to-Solution and Energy-to-Solution: A Comparison between ARM and Xeon. In Proceedings of the 2012 Third Workshop on Applications for Multi-Core Architecture, New York, NY, USA, 24–25 October 2012; pp. 48–53. [Google Scholar]
- Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Clarendon University Press: Oxford, UK, 2001; ISBN 978-0-19-850398-9. [Google Scholar]
- Pierre-Gilles de Gennes, F.B.W.; Quéré, D. Capillarity and Wetting Phenomena—Drops, Bubbles, Pearls, Waves; Springer: Cham, Switzerland, 2004; ISBN 978-1-4419-1833-8. [Google Scholar] [CrossRef]
- Sbragaglia, M.; Benzi, R.; Bernaschi, M.; Succi, S. The emergence of supramolecular forces from lattice kinetic models of non-ideal fluids: applications to the rheology of soft glassy materials. Soft Matter 2012, 8, 10773–10782. [Google Scholar] [CrossRef]
- Williams, S.; Carter, J.; Oliker, L.; Shalf, J.; Yelick, K. Optimization of a Lattice Boltzmann computation on stateof-the-art multicore platforms. J. Parallel Distrib. Comput. 2009, 69, 762–777. [Google Scholar] [CrossRef][Green Version]
- Williams, S.; Carter, J.; Oliker, L.; Shalf, J.; Yelick, K.A. Lattice Boltzmann simulation optimization on leading multicore platforms. In Proceedings of the 2008 IEEE International Symposium on Parallel and Distributed Processing, Miami, FL, USA, 14–18 April 2008; pp. 1–14. [Google Scholar] [CrossRef]
- Bernaschi, M.; Fatica, M.; Melchionna, S.; Succi, S.; Kaxiras, E. A flexible high-performance Lattice Boltzmann GPU code for the simulations of fluid flows in complex geometries. Concurr. Comput. Pr. Exper. 2009, 22, 1–14. [Google Scholar] [CrossRef]
- Calore, E.; Gabbana, A.; Schifano, S.F.; Tripiccione, R. Optimization of lattice Boltzmann simulations on heterogeneous computers. Int. J. High Perform. Comput. Appl. 2017, 1–16. [Google Scholar] [CrossRef]
- Product Specifications. Available online: https://ark.intel.com/content/www/us/en/ark.html (accessed on 8 March 2020).
- Weaver, V.; Johnson, M.; Kasichayanula, K.; Ralph, J.; Luszczek, P.; Terpstra, D.; Moore, S. Measuring Energy and Power with PAPI. In Proceedings of the 2012 41st International Conference on Parallel Processing Workshops (ICPPW), Pittsburgh, PA, USA, 10–13 September 2012. [Google Scholar]
- Hackenberg, D.; Schone, R.; Ilsche, T.; Molka, D.; Schuchart, J.; Geyer, R. An Energy Efficiency Feature Survey of the Intel Haswell Processor. In Proceedings of the Parallel and Distributed Processing Symposium Workshop (IPDPSW), 2015 IEEE International, Hyderabad, India, 25–29 May 2015; pp. 896–904. [Google Scholar] [CrossRef]
- Desrochers, S.; Paradis, C.; Weaver, V.M. A Validation of DRAM RAPL Power Measurements. In Proceedings of the Second International Symposium on Memory Systems, 2016 (MEMSYS ’16), Alexandria, VA, USA, 3–6 October 2016; pp. 455–470. [Google Scholar] [CrossRef]
- Calore, E.; Gabbana, A.; Schifano, S.F.; Tripiccione, R. Evaluation of DVFS techniques on modern HPC processors and accelerators for energy-aware applications. Concurr. Comput. Pract. Exp. 2017, 29, 1–19. [Google Scholar] [CrossRef]



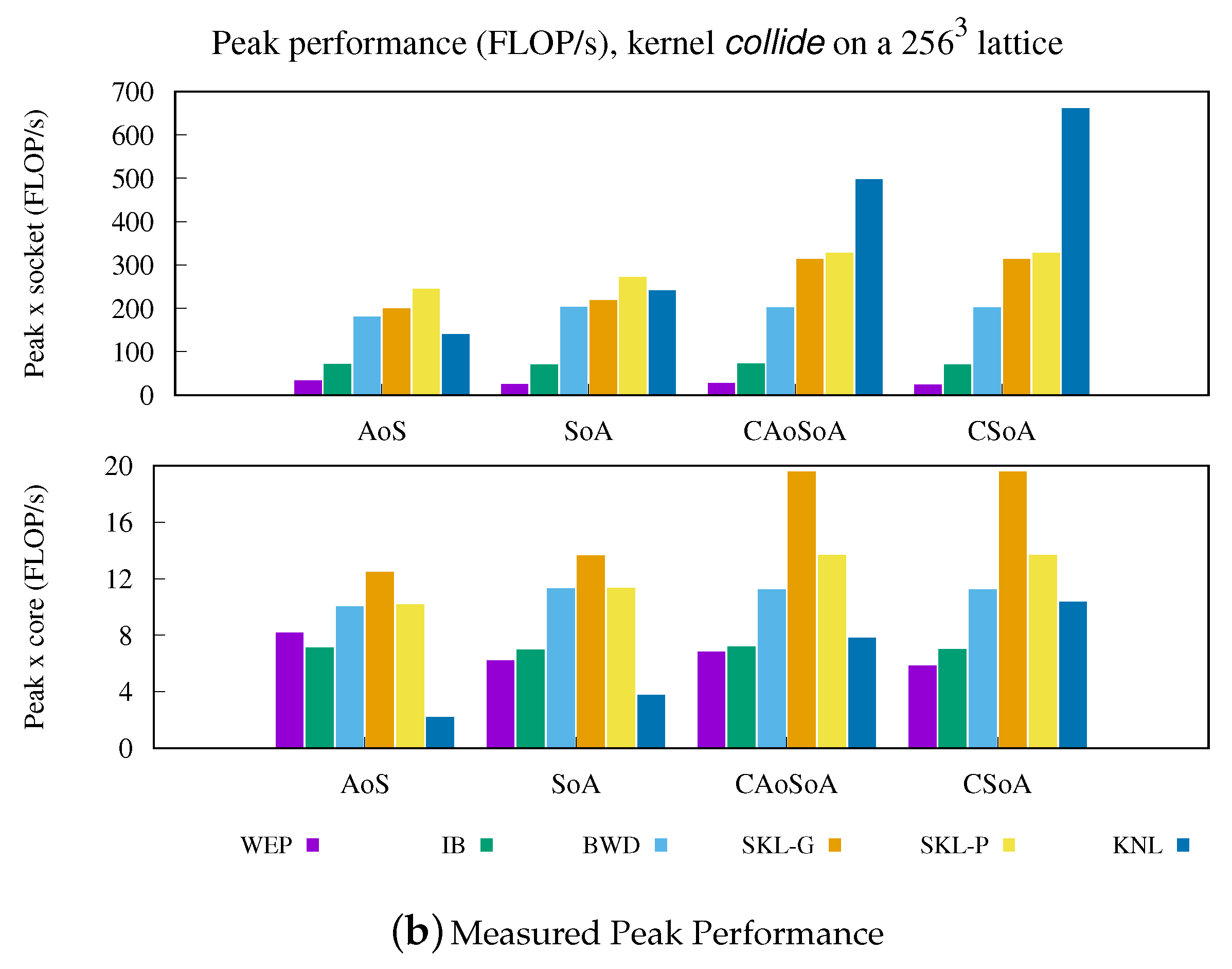
| Host | Proc. Name | Proc. Model | #Cores | Compiler Flags | Short Name | VL |
|---|---|---|---|---|---|---|
| ICTP | Westmere | E5620 @ 2.40GHz | 4 | -sse4 | WEP | 1 |
| ICTP | Ivy Bridge | E5-2680 v2 @ 2.80GHz | 10 | -xavx | IB | 2 |
| CINECA | Broadwell | E5-2697 v4 @ 2.30GHz | 18 | -xavx2 | BWD | 4 |
| CINECA | Knights Landing | Phi7250 @ 1.40GHz | 68 | -xMIC-AVX512 | KNL | 8 |
| INFN | Skylake | Gold 6130 @ 2.10GHz | 16 | -xCORE-AVX512 | SKL-G | 8 |
| INFN | Knights Landing | Phi7230 @ 1.30GHz | 64 | -xMIC-AVX512 | KNL | 8 |
| BSC | Skylake | Platinum 8160 @ 2.10GHz | 24 | -xCORE-AVX512 | SKL-P | 8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Girotto, I.; Schifano, S.F.; Calore, E.; Di Staso, G.; Toschi, F. Performance and Energy Assessment of a Lattice Boltzmann Method Based Application on the Skylake Processor. Computation 2020, 8, 44. https://doi.org/10.3390/computation8020044
Girotto I, Schifano SF, Calore E, Di Staso G, Toschi F. Performance and Energy Assessment of a Lattice Boltzmann Method Based Application on the Skylake Processor. Computation. 2020; 8(2):44. https://doi.org/10.3390/computation8020044
Chicago/Turabian StyleGirotto, Ivan, Sebastiano Fabio Schifano, Enrico Calore, Gianluca Di Staso, and Federico Toschi. 2020. "Performance and Energy Assessment of a Lattice Boltzmann Method Based Application on the Skylake Processor" Computation 8, no. 2: 44. https://doi.org/10.3390/computation8020044
APA StyleGirotto, I., Schifano, S. F., Calore, E., Di Staso, G., & Toschi, F. (2020). Performance and Energy Assessment of a Lattice Boltzmann Method Based Application on the Skylake Processor. Computation, 8(2), 44. https://doi.org/10.3390/computation8020044





