Abstract
Quantum–chemical calculations of the electronic characteristics of carbon and boron-doped silicon polyprismanes were carried out, and the atomic hydrogen adsorption on these structures was analyzed. It was established that silicon polyprismanes doped with boron and carbon retained their metallicity predicted earlier. It was shown that the doping of polyprismanes made them more thermodynamically stable. For the silicon prismanes doped with boron or carbon, hydrogen adsorption was found to be energetically favorable. In the case of boron-doped prismanes, adsorption on the boron impurity was much more advantageous than on the neighboring silicon nodes. For the carbon doping, the adsorption energy of polyprismane with a small diameter weakly depended on the position of the hydrogen atom near the impurity center. However, for the C-doped polyprismanes with a larger diameter, the hydrogen adsorption on the silicon atom belonging to the ring with impurity is more energetically favorable than the adsorption on the silicon atom from the adjacent ring.
1. Introduction
Based on the prismane systems, a special type of strained frame compound, including carbon or silicon, with a non-classical bonding can be obtained [1]. Such compounds are called polyprismanes or [n,m] prismanes, and they can be considered as the folded layers of dehydrogenated carbon (or silicon) rings, where m is the number of vertices of the closed ring and n is the number of layers [2]. Polyprismane can also be considered a special type of single-walled nanotube with a cross-section in the shape of a regular polygon.
In [3,4], by means of density functional theory, structural, energetic, and electronic properties of carbon and silicon polyprismanes based on the regular five, six, seven, and eight-membered rings were calculated. In the case of silicon polyprismanes, regardless of the ring diameter, the results obtained (band structure, the density of electronic states, and electronic transmission coefficients) indicate the manifestation of metallic properties atypical of previously known tetra-coordinated silicon structures. For the carbon polyprismanes, their electronic properties depend on the effective diameter. There is a critical diameter: below this value, carbon polyprismanes are semiconductors, and above the critical diameter, they become metals.
Currently, both carbon and silicon polyprismanes are mainly studied using the various computer-modeling approaches, and the problem of their large-scale synthesis is still open. A number of studies reported the synthesis of elementary prismanes [5,6,7,8,9,10], but there were also some experimental results indicating the existence of rather long unsubstituted carbon nanotubes based on the stacks of the carbon six-membered rings [11], which was confirmed by further numerical calculations [12].
The unusual metallic properties of silicon polyprismanes, demonstrated for the first time in [3], can be applied in the development of measuring equipment elements; for example, tips of a scanning tunneling microscope [13]. Moreover, the chemical reactivity of such silicon needle is reduced due to the lack of free covalent bonds, and therefore, its insensitivity to environmental pollutants. This allows one to achieve atomic resolution in a microscope.
However, a natural question about the stability of the metallic state of silicon polyprismanes under the influences of various factors arises. The analysis presented in [3] confirmed that the metallicity of polyprismanes was retained with the 10% mechanical deformations. Therefore, the primary purpose of the presented study was to analyze the stability of the metallic state of silicon polyprismanes when the impurities were introduced into their framework, and to determine the adsorption capacity of doped polyprismanes, since the doping often leads to an increase in adsorption capacity [14,15,16,17]. It is known that the presence of impurities and defects affects the different properties of low-dimensional structures. Thus, we also tried to provide a comprehensive analysis of the doping effect on the structural, energetic, and electronic characteristics of silicon polyprismanes.
2. Materials and Methods
The supercells of silicon polyprismanes Si5 and Si6 are considered. These supercells contain four elementary cells and are based on the regular pentagon and hexagon, respectively. A boron or carbon atom can replace one of the silicon atoms in such a supercell (see Figure 1). Along the Z-axis of polyprismane, the structure is periodic, and in the XY-plane, the cell sizes are chosen large enough (14 Å) so that there is no interaction with the corresponding periodic images.
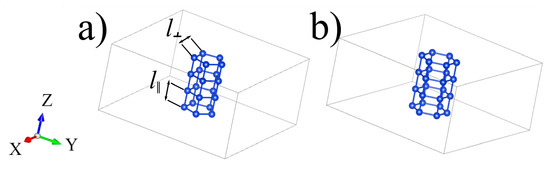
Figure 1.
Supercells of silicon polyprismanes (a) Si5 (b) and Si6 containing four elementary cells. l‖ and l┴ denote interlayer and intralayer bond lengths, respectively.
The calculations are carried out by means of density functional theory using the generalized gradient approximation (GGA) [18] with the PBE functional for the exchange-correlation terms and the basis of plane waves in the Quantum Espresso 6.3 program [19]. Ultrasoft pseudopotentials for silicon, carbon, boron, and hydrogen atoms [20] with a cutoff energy of 60 Ry are used. A Monkhorst-Pack [21] k-point grid of 1 × 1 × 20 is implemented, and the first-order Methfessel-Paxton scheme [22] with a smearing of 0.01 Ry is used. Structural optimization is carried out until all forces become less than 10-4 eV/Å. After the doping of silicon polyprismane with boron or carbon atom, we applied variable cell optimization, i.e., the cell size along the z-axis changed with simultaneous relaxation of atomic positions, until a minimum energy configuration was obtained. Note that the parameters are chosen in such a way that an increase in cutoff energy and a number of k-points does not lead to significant changes in the structural parameters, total energy, and electronic properties of the considered systems. For example, increasing the cutoff energy value to 100 Ry and using a more dense 1 × 1 × 40 k-point grid, will not result in a change in the total energy of the system of more than the 7 × 10−4 Ry.
The hydrogen adsorption energy Eads was calculated as follows
where E(PP) is the total energy of the silicon polyprismane supercell doped with boron or carbon atom, E(PP + H) is the total energy of the system with the adsorbed hydrogen, and E(H) is the energy of the isolated hydrogen atom. Negative values of Eads indicate a decrease in the total energy of the system because of adsorption. The binding energy per atom was calculated using the following formula.
where x, y, and z are the corresponding numbers of silicon, boron, and carbon atoms (y and z can be 0 or 1 depending on the doping type); Nat = x + y + z is the total number of atoms in the system, is the total energy of the system; E(Si), E(B), and E(C) are the energies of the isolated silicon, boron, and carbon atoms, respectively.
3. Results and Discussion
As already noted, the structure of the considered silicon polyprismanes provided them metallic characteristics. First, we calculated the density of electronic states of B-doped and C-doped Si5 and Si6 polyprismanes. The data are presented in Figure 2, which demonstrates a comparison of the density of electronic states for the doped and unsubstituted Si5 and Si6 polyprismane. It is shown that the metallicity of Si5-polyprismane is retained in the both cases: boron and carbon doping. In the case of boron doping, the density of electronic states near the Fermi level decreases in comparison with the case of unsubstituted polyprismane. At the same time, when doped with carbon, the density of electronic states at the Fermi level remains unchanged. Similar results are obtained for the doped Si6 polyprismane.
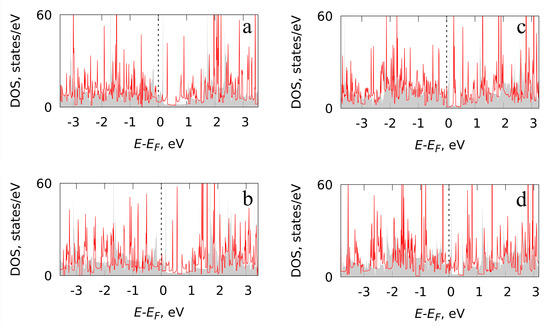
Figure 2.
Density of electronic states for (a) B-doped (b) and C-doped Si5-polyprismane; (c) B-doped (d) and C-doped Si6-polyprismane (red line). The gray filled area corresponds to the unsubstituted Si5 and Si6-polyprismanes.
Binding energies per atom Eb for the pure Si5 and Si6 prismanes as well as for the C and B-doped systems are presented in Table 1. One can see that doping of the silicon polyprismane with boron or carbon atoms leads to a slight increase in the binding energy. In addition, the carbon doping increases Eb more strongly than the doping with boron. Carbon doping of Si5 and Si6 polyprismanes decreases their binding energy in comparison with the case of unsubstituted prismanes by 0.171 and 0.139 eV, respectively.

Table 1.
The binding energy values for the pure Si5 and Si6 silicon prismanes and their carbon and boron-doped analogs.
For the unsubstituted polyprismanes interlayer (l‖) and intralayer (l┴), Si–Si bonds slightly differ from each other: for Si5-polyprismane l┴ = 2.402 Å and l‖ = 2.421 Å, for Si6-polyprismane l┴ = 2.393 Å and l‖ = 2.42 Å. The valence angles in the plane of the silicon ring are equal to 108° for the Si5-polyprismane, and 120° for the Si6-polyprismane; valence angles between the silicon rings for both systems are equal to 90°. From these data, one can conclude that such systems are rather “strained,” since the “strain-free” silicon systems (such as silicon cubic structure) are characterized by the valence angles between neighboring atoms equal to 109.5°.
The prismane doping strongly distorts its structure, and a large scatter in the values of the bond lengths and angles between atoms appears. For the C-doped Si5-polyprismane, the Si-Si bond length l┴ lies in the range 2.333–2.494 Å and l‖ lies in the range 2.401–2.963 Å; Si-C bond length l┴ = 1.945 Å and l‖ = 1.873 Å; and the valence angles between atoms lie in the range 68–132°. For the B-doped Si5-polyprismane, the Si-Si bond length l┴ lies in the range 2.343–2.51 Å and l‖ lies in the range 2.362–2.557 Å; the Si-B bond length l┴ = 2.09 Å and l‖ = 1.937 Å; and the valence angles between atoms lie in the range 68–122°. For the C-doped Si6-polyprismane Si-Si bond length l┴ = 2.38–2.51 Å and l‖ = 2.361–2.693 Å; Si-C bond length l┴ = 1.899 Å and l‖ = 1.922 Å; the valence angles between atoms lie in the range 70–135°. For the B-doped Si6-polyprismane the Si-Si bond length l┴ = 2.35–2.449 Å and l‖ = 2.343–2.542 Å; the Si-C bond length l┴ = 2.049 Å and l‖ = 1.935 Å; the valence angles between atoms lie in the range 69–133°.
Due to the presence of such a spread in the bond lengths and angles between the atoms of the doped prismanes, it is difficult to conclude definitely from this data that the structure is more or less “strained” compared with the unsubstituted polyprismanes. Therefore, we calculated the strain energies for these systems, according to [23,24,25]; i.e., the assessment of the corresponding strain energies was carried out on the basis of the hypothetical homodesmic reactions that required the conversion of each deformed bond or angle into its “stain-free” counterpart.
As the strain-free structures, we chose unit cells of bulk silicon with diamond-like cubic structure, bulk SiC with diamond-like cubic structure, and Si2B2 crystal. The calculated results of the strain energy (SE) are presented in Table 2. The C-doped prismanes have the highest strain energies. The strain energy of C-doped Si5-prismane is higher than the corresponding value of the unsubstituted Si5-prismane by 0.80 eV, and the strain energy of the C-doped Si6-prismane is higher than the corresponding value of the unsubstituted one by 0.88 eV. Note that the most “strained” structures possess rather high thermodynamic stability (see Table 1).

Table 2.
Strain energies (SE) calculated from the homodesmic reactions for the pure and doped Si5 and Si6 polyprismanes.
Next, we studied the adsorption of the hydrogen atom on the B and C-doped silicon polyprismanes. Adsorption on the impurity, and adsorption on the nearest nonequivalent silicon atoms, was considered (see Figure 3). The calculation results are presented in Table 3.
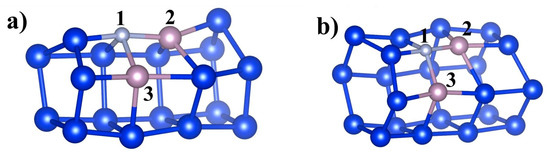
Figure 3.
Designations of various atomic positions involved in the process of hydrogen adsorption on the example of doped Si5 (a) and Si6 (b) polyprismanes: 1—impurity atom (C or B), 2 and 3 nonequivalent positions of the silicon atoms (marked in a different color for clarity). Depicted configurations correspond to the optimized B-doped Si5 and Si6-polyprismanes unit cells.

Table 3.
Adsorption energies (Eads) of the hydrogen atom on the C and B-doped silicon polyprismanes Si5 and Si6 depending on the adsorption site (see Figure 3).
From the results presented in Table 3, one can see that the adsorption of the hydrogen atom on the silicon polyprismanes doped with carbon and boron reduces the total energy of the system. For B-doped Si5 and Si6-polyprismanes, the adsorption of hydrogen to the boron impurity is more energetically favorable than the adsorption on the silicon atom near the dopant. The adsorption energy gain for the Si5 (Si6)-polyprismane is approximately equal to 0.73 eV (0.26 eV) or 0.46 eV (0.03 eV) when hydrogen is bonded to the silicon atom belonging to the ring with impurity or to the adjacent all-silicon ring, respectively. In the case of the C-doped Si5-prismane, the adsorption energy weakly depends on the position of the adsorbed hydrogen atom. Nevertheless, hydrogen adsorption on the silicon atom adjacent to carbon from the neighboring ring is energetically favorable. For the C-doped Si6-prismane, the adsorption of hydrogen on the silicon atom near the impurity that belongs to the same ring is more energetically favorable than on the silicon node from the adjacent hexagon.
4. Conclusions
By means of density functional theory, we studied the effects of B and C-doping on the electronic and energy properties of Si5 and Si6-polyprismanes. The hydrogen adsorption on the doped silicon polyprismanes was analyzed as well. It was found that neither B nor C doping led to a fundamental change in the electronic properties of these polyprismanes; i.e., the metallic nature of such systems was resistant to the presence of considered impurities. Boron and carbon doping decreased the binding energy of polyprismanes. Moreover, C-doped prismanes possessed the lowest binding energy, while their strain energy was rather high.
We analyzed various adsorption types of the hydrogen atom on the polyprismane. Among them were adsorption on the impurity and on the neighboring nonequivalent silicon atoms. It was shown that hydrogen adsorption on doped polyprismanes reduced the total energy of the system. In the case of B-doped polyprismanes, hydrogen adsorption on the impurity was more energetically favorable than on the silicon atom both for Si5 and Si6 nanostructures. For the C-doping in Si5-polyprismanes, the adsorption energy weakly depends on the position of the adsorbed hydrogen atom. At the same time, for the C-doped Si6-polyprismanes, the adsorption energy depends on the position of the hydrogen atom. In this sense, hydrogen adsorption on the silicon atom belonging to the same ring as the carbon atom bonded with it (position 3 in Figure 3) is the most energetically favorable process. Note that in the case of the C-doped Si5 and Si6-polyprismanes, adsorption of hydrogen on a crystal lattice atom (i.e., on a silicon atom) is more energetically favorable (by approximately 0.34 and 1.09 eV for Si5 and Si6-polyprismanes, respectively) than adsorption on a silicon atom in the case of B-doped polyprismanes.
Author Contributions
K.G. performed the conceptualization, methodology, software, investigation, formal analysis, data curation, writing—original draft preparation, visualization. K.K. performed the conceptualization, validation, investigation, resources, writing—review and editing. M.M. was engaged in conceptualization, validation, investigation, resources, writing—original draft preparation, supervision, project administration, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant number 18-72-00183.
Acknowledgments
Mikhail Maslov thanks the DSEPY-RI for the provided computing resources and comprehensive support of the presented study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Minyaev, R.M.; Minkin, V.I.; Gribanova, T.N.; Starikov, A.G.; Hoffmann, R. Poly[n]Prismanes: A Family of Stable Cage Structures with Half-Planar Carbon Centers. J. Org. Chem. 2003, 68, 8588–8594. [Google Scholar] [CrossRef]
- Lewars, E.G. Modeling Marvels: Computational Anticipation of Novel Molecules; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Katin, K.P.; Grishakov, K.S.; Gimaldinova, M.A.; Maslov, M.M. Silicon rebirth: Ab initio prediction of metallic sp3-hybridized silicon allotropes. Comput. Mater. Sci. 2020, 174, 109480. [Google Scholar] [CrossRef]
- Maslov, M.M.; Grishakov, K.S.; Gimaldinova, M.A.; Katin, K.P. Carbon vs silicon polyprismanes: A comparative study of metallic sp3-hybridized allotropes. Fuller. Nanotub. Carbon Nanostruct. 2020, 28, 97–103. [Google Scholar] [CrossRef]
- Katz, T.J.; Acton, N. Synthesis of Prismane. J. Am. Chem. Soc. 1973, 95, 2738–2739. [Google Scholar] [CrossRef]
- Eaton, P.E.; Cole, T.W. Cubane. J. Am. Chem. Soc. 1964, 86, 3157–3158. [Google Scholar] [CrossRef]
- Eaton, P.E.; Or, Y.S.; Branca, S.J. Pentaprismane. J. Am. Chem. Soc. 1981, 103, 2134–2136. [Google Scholar] [CrossRef]
- Matsumoto, H.; Higuchi, K.; Kyushin, S.; Goto, M. Octakis (1,1,2-Trimethylpropyl) Octasilacubane: Synthesis, Molecular Structure, and Unusual Properties. Angew. Chem. Int. Ed. Engl. 1992, 31, 1354–1356. [Google Scholar] [CrossRef]
- Sekiguchi, A.; Yatabe, T.; Kabuto, C.; Sakurai, H. Chemistry of Organosilicon Compounds. 303. The Missing Hexasilaprismane: Synthesis, X-ray Analysis and Photochemical Reactions. J. Am. Chem. Soc. 1993, 115, 5853–5854. [Google Scholar] [CrossRef]
- Koshida, N.; Matsumoto, N. Fabrication and Quantum Properties of Nanostructured Silicon. Mater. Sci. Eng. R 2003, 40, 169–205. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y.; Inoue, S.; Suzuki, T.; Jones, R.O.; Ando, Y. Smallest Carbon Nanotube Is 3 Å in diameter. Phys. Rev. Lett. 2004, 92, 125502. [Google Scholar] [CrossRef]
- Kuzmin, S.; Duley, W.W. Ab Initio Calculations of Some Electronic and Vibrational Properties of Molecules Based on Multi-Layered Stacks of Cyclic C6. Fuller. Nanotub. Carbon Nanostruct. 2012, 20, 730–736. [Google Scholar] [CrossRef]
- Cheung, C.L.; Hafner, J.H.; Lieber, C.M. Carbon nanotube atomic force microscopy tips: Direct growth by chemical vapor deposition and application to high-resolution imaging. PNAS 2000, 97, 3809–3813. [Google Scholar] [CrossRef]
- Zhang, Z.; Cho, K. Ab initio study of hydrogen interaction with pure and nitrogen-doped carbon nanotubes. Phys. Rev. B 2007, 75, 075420. [Google Scholar] [CrossRef]
- Kang, K.Y.; Lee, B.I.; Lee, J.S. Hydrogen adsorption on nitrogen-doped carbon xerogels. Carbon 2009, 47, 1171. [Google Scholar] [CrossRef]
- Dolinskii, I.Y.; Katin, K.P.; Grishakov, K.S.; Prudkovskii, V.S.; Kargin, N.I.; Maslov, M.M. Influence of Mechanical Stretching on Adsorption Properties of Nitrogen-Doped Graphene. Phys. Solid State 2018, 60, 821–825. [Google Scholar] [CrossRef]
- Dolinskii, I.Y.; Grishakov, K.S.; Prudkovskii, V.S. Effect of a Nitrogen Doping and a Mechanical Stress on the Adsorption Capacity of Graphdiene. Phys. Solid State 2019, 61, 274–278. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Dal Corso, A. Pseudopotentials periodic table: From H to Pu. Comput. Mater. Sci. 2014, 95, 337–350. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [PubMed]
- Hehre, W.J.; Radom, L.; Schleyer, P.V.R.; Pople, J.A. Ab Initio Molecular Orbital Theory; Wiley-Interscience: New York, NY, USA, 1986. [Google Scholar]
- Hehre, W.J.; Ditchfield, R.; Radom, L.; Pople, J.A. Molecular orbital theory of the electronic structure of organic compounds. V. Molecular theory of bond separation. J. Am. Chem. Soc. 1970, 92, 4796. [Google Scholar] [CrossRef]
- Dolgonos, G.A.; Mekalka, K. Strain in Nonclassical Silicon Hydrides: An Insight into the “Ultrastability” of Sila-bi[6]Prismane (Si18H12) Cluster with the Endohedrally Trapped Silicon Atom, Si19H12. J. Comp. Chem. 2015, 36, 2095–2102. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).