Recent Progress in Lattice Density Functional Theory

Abstract

Recent developments in the density-functional theory of electron correlations in many-body lattice models are reviewed. The theoretical framework of lattice density-functional theory (LDFT) is briefly recalled, giving emphasis to its universality and to the central role played by the single-particle density-matrix $\gamma$. The Hubbard model and the Anderson single-impurity model are considered as relevant explicit problems for the applications. Real-space and reciprocal-space approximations to the fundamental interaction-energy functional $W\left[\gamma \right]$ are introduced, in the framework of which the most important ground-state properties are derived. The predictions of LDFT are contrasted with available exact analytical results and state-of-the-art numerical calculations. Thus, the goals and limitations of the method are discussed.

1. Introduction

Density-functional theory (DFT) is currently the most widespread method of determining the electronic properties of matter from first principles [1,2]. Formulated initially as a general approach to the inhomogeneous electron gas [3], this theory, although far from being infallible, has demonstrated a remarkable efficiency in the most wide variety of physical and chemical situations. In the meantime, it has become part of most advanced quantum mechanics curricula. The founding idea, both simple and revolutionary at that time, is to replace the wave function by the electron density $\rho (\mathit{r})$ as the basic variable of the many-body problem [4]. From a purely theoretical, fundamental perspective, the beauty of the theory relies, most probably, in its elegance and universality. From a practical perspective, however, the actual breakthrough has been achieved with the Kohn–Sham (KS) scheme, which allows one to obtain the ground-state of any interacting many-body problem from the solution of a set of self-consistent single-particle equations [5]. This formulation, being formally exact, is in principle able to account for all the consequences of electronic correlations within a self-consistent single-particle framework. Clearly, this constitutes a critical paradigm shift which provides a new basis for potentially exact effective single-particle methods. Nevertheless, despite this formal simplification, a central difficulty remains: To render any application of the theory possible, it is necessary to be in possession of a good approximation to the universal kinetic and interaction-energy functionals $T[\rho (\mathit{r})]$ and $W[\rho (\mathit{r})]$, which are not known in an exact explicit form. The most common approximations used in past years are the local density approximation (LDA) [5], the local spin-density approximation (LSDA) [6] and the generalized gradient approximations (GGAs) [7,8,9]. Although successful in countless applications, the above-mentioned local or semilocal functionals have been shown to be unable to provide a satisfactory description of systems where strong electronic correlations play an important role. This concerns, for example, some reaction energies in chemistry [10], the dissociation of closed-shell molecules [11], the physics of heavy-fermion materials [12], high-temperature superconductors [13] and Mott-insulators [14,15,16]. Understanding the physics of strongly correlated systems in the framework of DFT remains therefore a major theoretical challenge.

Several extensions to the early functionals have been developed in order to cope with these difficulties. For example, density functionals based on range separation have been introduced in order to describe nonlocal correlation effects, which are a consequence of the long-range character of the Coulomb interaction [17]. This method has been successfully applied to rare-gas and alkaline-earth-metal dimers, which are bound through weak van der Waals forces [18,19,20,21,22]. Another perspective is provided by the hybrid functionals, which incorporate a portion of the exchange energy given by Hartree–Fock theory and a portion of the exchange and correlation energy obtained in various ways. In this context one should mention Becke’s three-parameter Lee–Yang–Parr (B3LYP) functional [23], the Perdew, Burke, and Ernzerhof functional [24], as well as the screened Coulomb potential functional by Heyd, Scuseria, and Ernzerhof (HSE) [25]. These approaches have been applied to study a number of different molecular properties, including ground-state structures, bond lengths, cohesive energies and vibrational frequencies, which could not be correctly predicted by using other DFT methods. Furthermore, from the perspective of strong electron correlations, one finds applications to actinide and transition-metal oxides, which demonstrate the ability of these functionals to capture the Mott-insulating behavior [26,27,28,29,30]. In this context, one should also mention the studies of the fundamental gap in strongly-correlated Mott insulators by means of the so-called power functional [31,32].

An alternative to the original density-functional perspective is adopted in reduced density-matrix functional theory (RDMFT). In this framework, one considers the complete first-order reduced density matrix (1RDM) $\gamma (\mathit{r},{\mathit{r}}^{\prime })$, rather than only the diagonal density $\rho (\mathit{r})=\gamma (\mathit{r},\mathit{r})$, as the central variable of the many-body problem [33]. This implies that the exact forms of the kinetic-energy and exchange-energy functionals are now available. Therefore, only the correlation part of the interaction energy functional needs to be approximated. Müller [34] and later Goedecker and Umrigar [35], in fact, proposed approximations to the interaction-energy in terms of the 1RDM. These functionals have been used in particular to describe the dissociation of H${}_2$ [36,37], which can be very difficult within DFT. Later on other approximations were proposed to model the potential energy curves of diatomic molecules [36,38,39,40,41,42,43,44]. In this way, RDMFT has grown into an effective approach to the dissociation of closed-shell molecules into open-shell fragments.

Well before the popularization of DFT and its ready-to-use implementations on large computer facilities, there was already a long standing and most successful research activity in condensed-matter theory, whose aim is to understand the properties of strongly correlated fermions on the basis of many-body lattice-model Hamiltonians. Among the most emblematic examples, one should mention the Anderson and Hubbard models [45,46,47,48,49,50], the $sd$ and Kondo models [12], and the models describing superconducting pairing [51]. These Hamiltonians focus on the many-body states that dominate the low temperature physics, particularly when they involve localized orbitals and strong Coulomb repulsions. Despite the simplifications inherent to the model interactions and to the discretized basis set, the physics behind these problems remains highly nontrivial [52]. Under these circumstances, and taking into account the remarkable success of DFT in dealing with the inhomogeneous electron gas in the continuum, it seems quite natural to attempt to adapt and transfer the concepts of DFT to the study of many-body lattice models. This would not only provide us with an alternative approach to the physics of strong correlations but should also be useful for the development of DFT itself.

The existing density functional theories of lattice models can be divided essentially in two categories. The first one uses only the local site occupations $n_i$ as basic variables of the many-body problem. This approach has been introduced by Gunnarsson and Schönhammer, who proposed a local-density approximation in order to study the band-gap problem within a semiconductor model [53,54]. The second type of approach takes into account on equal footing all, diagonal and off-diagonal elements ${\gamma }_{ij}$ of the single-particle density matrix (SPDM) with respect to the lattice sites i and j. This was initially introduced by Schindlmayr and Godby [55]. In a more general framework, it is possible to consider different basic variables and different energy functionals depending on the model under study [56]. More recently, Lima et al. proposed a local approximation in terms of the site occupations $n_i={\gamma }_{ii}$, which is based on the Bethe-ansatz solution of the one-dimensional Hubbard model [57,58]. This functional has been applied to systems far from equilibrium [59], to single impurities [60,61], and to the inhomogeneous Hubbard model [62]. Nevertheless, the problem of electron localization cannot be investigated within a strictly local framework, since the basic variable involves only the local occupations $n_i$, which are strictly the same in the fully localized and delocalized states. Moreover, it is easy to see that any formulation based exclusively on $n_i$ cannot be universal since the associated functionals necessarily depend on the lattice structure. Such restrictions do not apply to functionals which take into account the off-diagonal components ${\gamma }_{ij}$ of the density matrix. The work of Carlsson et al., which belongs to the latter universal perspective [63,64], introduces an interaction-energy functional for the Hubbard model by interpolating between well-established limits. In addition, a functional for the Anderson model is proposed, which relies on a rigorous inequality for the interaction energy. A further interesting density-matrix functional approach is the so-called lattice density-functional theory (LDFT) on which the remainder of this review is focused [65,66,67,68,69,70,71,72].

The rest of the paper is organized as follows. In Section 2, the basic concepts, notation and formalism of the density-functional theory of lattice models are recalled. The main role played by the density matrix ${\gamma }_{ij}$ with respect to the orbitals or lattice sites i and j is discussed. Once ${\gamma }_{ij}$ is regarded as the central variable of the many-body problem, the associated energy functionals and the corresponding variational principle are introduced. Section 3 and Section 4 are devoted to specific applications of LDFT. In Section 3, the single-impurity Anderson model (SIAM) is investigated. Taking advantage of the invariance of the interaction-energy functional $W\left[\gamma \right]$ with respect to unitary transformations, a simple two-level approximation to $W\left[\gamma \right]$ is derived. Subsequently, the LDFT results are compared with exact numerical calculations in order to assess the accuracy of the method. Section 4 concerns the Hubbard model and the development of interaction-energy functionals from both real-space and reciprocal-space perspectives. The first approximation is based on the scaling properties of $W\left[\gamma \right]$ as a function of the degree of delocalization of the electrons in their immediate environment, while the second one exploits a remarkable correlation between W and the single-particle entropy associated to the distribution of Bloch-state occupation numbers. The accuracy of the theory is assessed in applications to a variety of lattices with different dimensions. Finally, Section 5 summarizes the main conclusions.

2. Basic Concepts of Lattice Density Functional Theory

The general many-body Hamiltonian on a lattice or discrete basis set is given by

$$\widehat{H}=\widehat{T}+\widehat{W}=\sum _{\alpha \beta \sigma }{t}_{\alpha \beta }^{\sigma }{\widehat{c}}_{\alpha \sigma }^{†}{\widehat{c}}_{\beta \sigma }+\frac{1}{2}\sum _{\begin{array}{c}\alpha \beta \gamma \delta \\ \sigma {\sigma }^{\prime }\end{array}}{V}_{\alpha \beta \gamma \delta }{\widehat{c}}_{\alpha \sigma }^{†}{\widehat{c}}_{\beta {\sigma }^{\prime }}^{†}{\widehat{c}}_{\delta {\sigma }^{\prime }}{\widehat{c}}_{{\gamma }_{\sigma }},$$

(1)

where ${\widehat{c}}_{\alpha \sigma }^{†}$ creates an electron with spin $\sigma$ in the orbital ${\phi }_{\alpha }$. The single-particle basis set $\left\{{\phi }_{\alpha }(\mathit{r})\right\}$ corresponds, for instance, to localized atomic-like orbitals centered at the lattice sites or to delocalized conduction-band states. The hopping integrals

$$t_{\alpha \beta }^{\sigma }=\int {\mathrm{d}}^{3}r{\phi }_{\alpha }^{\ast }(\mathit{r})\left(-\frac{{\hslash }^2{\nabla }^2}{2m}+v_{\mathrm{ext}}^{\sigma }(\mathit{r})\right){\phi }_{\beta }(\mathit{r})$$

(2)

include contributions of both the kinetic energy and the external potential $v_{\mathrm{ext}}^{\sigma }(\mathit{r})$, which depends on $\sigma$ in the presence of an external magnetic field. Notice that, once the set of basis orbitals $\left\{{\phi }_{\alpha }(\mathit{r})\right\}$ has been chosen, the kinetic-energy contribution to $t_{\alpha \beta }^{\sigma }$ is independent of the problem under study. Thus, $t_{\alpha \beta }^{\sigma }$ is univocally determined by $v_{\mathrm{ext}}^{\sigma }(\mathit{r})$ and vice versa. The electron–electron interaction $\widehat{W}$ is characterized by the integrals

$$V_{\alpha \beta \gamma \delta }=\int \int {\mathrm{d}}^{3}r{\mathrm{d}}^3{r}^{\prime }{\phi }_{\alpha }^{\ast }(\mathit{r}){\phi }_{\beta }^{\ast }({\mathit{r}}^{\prime })w(|\mathit{r}-{\mathit{r}}^{\prime }|){\phi }_{\gamma }(\mathit{r}){\phi }_{\delta }({\mathit{r}}^{\prime }),$$

(3)

where the Coulomb repulsion $w(|\mathit{r}-{\mathit{r}}^{\prime }|)$ is usually approximated as short ranged (e.g., intra-atomic). Obviously, $\widehat{W}$ is universal, i.e., independent of the problem under study. Therefore, from the model perspective, the specific problem under study is defined by the hopping integrals $t_{\alpha \beta }^{\sigma }$ alone. In other words, $t_{\alpha \beta }^{\sigma }$ defines the lattice structure, its dimensionality, and the range and symmetry of the hybridizations. One concludes that in LDFT the hopping integrals $t_{\alpha \beta }^{\sigma }$ play the role given in conventional DFT to the external potential $v_{\mathrm{ext}}^{\sigma }(\mathit{r})$.

To develop a density-functional theory of lattice models, it is necessary to identify the simplest observable that can replace the wave function as the fundamental variable. To this aim, let us first recall that in the inhomogeneous gas the external potential $v_{\mathrm{ext}}^{\sigma }(\mathit{r})$ defines the problem and that it enters the Hamiltonian linearly in a product with the electronic density operator ${\widehat{n}}_{\sigma }(\mathit{r})={\widehat{\psi }}_{\sigma }^{†}(\mathit{r}){\widehat{\psi }}_{\sigma }(\mathit{r})$. This explains why the electronic density ${\rho }_{\sigma }(\mathit{r})=\langle {\widehat{n}}_{\sigma }(\mathit{r})\rangle$ is the simplest fundamental variable in conventional DFT [1,2,3,73,74]. However, as discussed above, in LDFT the hopping integrals $t_{\alpha \beta }^{\sigma }$ define the specific problem under study. According to Equation (1), these integrals $t_{\alpha \beta }^{\sigma }$ enter $\widehat{H}$ in a matrix product with ${\widehat{c}}_{\alpha \sigma }^{†}{\widehat{c}}_{\beta \sigma }$. Therefore, it follows that the single-particle density matrix

$${\gamma }_{\alpha \beta \sigma }=\langle \Psi |{\widehat{c}}_{\alpha \sigma }^{†}{\widehat{c}}_{\beta \sigma }|\Psi \rangle$$

(4)

between the sites $\alpha \beta$ replaces the continuum density ${\rho }_{\sigma }(\mathit{r})$ as the basic variable of the many-body problem on a lattice. A more rigorous theoretical justification for this important property is provided by the lattice version of the Hohenberg–Kohn theorem [71]. It has been indeed shown that, for non-degenerate ground states, the mapping between the wave function $|\Psi \rangle$ and the ground-state density matrix $\gamma$ is injective and therefore invertible. Therefore, it is valid to regard $|\Psi \rangle =|\Psi \left[\gamma \right]\rangle$ and the ground-state expectation value of all observables derived from it as functionals of $\gamma$ [71].

The total energy E of the system can be expressed in terms of $\gamma$ by using the constrained search formalism of Levy and Lieb [27]. In this way, one obtains

$$E\left[\gamma \right]=\underset{\Psi \to \gamma }{min}\langle \Psi |\widehat{H}|\Psi \rangle =T\left[\gamma \right]+W\left[\gamma \right],$$

(5)

where the single-particle energy functional

$$T\left[\gamma \right]=\sum _{\alpha \beta \sigma }{t}_{\alpha \beta }^{\sigma }{\gamma }_{\alpha \beta \sigma }$$

(6)

describes the kinetic and potential energy associated with the electronic motion in the lattice, and

$$W\left[\gamma \right]=\underset{\Psi \to \gamma }{min}\langle \Psi |\widehat{W}|\Psi \rangle =\underset{\Psi \to \gamma }{min}\left\{{\displaystyle \frac{1}{2}}\sum _{\begin{array}{c}\alpha \beta \gamma \delta \\ \sigma {\sigma }^{\prime }\end{array}}{V}_{\alpha \beta \gamma \delta }\langle \Psi |{\widehat{c}}_{\alpha \sigma }^{†}{\widehat{c}}_{\beta {\sigma }^{\prime }}^{†}{\widehat{c}}_{\delta {\sigma }^{\prime }}{\widehat{c}}_{\gamma \sigma }|\Psi \rangle \right\}$$

(7)

is the interaction-energy functional. Notice that $T\left[\gamma \right]$ is explicitly given in terms of matrix elements of $\gamma$. However, the interaction-energy term $W\left[\gamma \right]$ involves a constrained minimization over all N-particle states $|\Psi \rangle$ yielding the given $\gamma$. The minimum in Equation (7), i.e., $W\left[\gamma \right]$ has a clear physical interpretation: it represents the lowest possible value of the interaction energy compatible with a given density matrix $\gamma$. Finally, the variational principle satisfied by E allows one to determine the actual electronic ground-state energy $E_0$ and the corresponding ground-state density matrix ${\gamma }_0$ by the minimization of $E\left[\gamma \right]$ with respect to all physical density matrices $\gamma$.

At this point, the question about the representability, i.e., the mathematical characterization of such physical density matrices, must be raised, since this is the domain of definition of $E\left[\gamma \right]$. It is clear that a physical $\gamma$ is hermitian, has a trace equal to the number of electrons N, and derives from some N-particle state $|\Psi \rangle$. One then also says that $\gamma$ is pure-state N representable. Unfortunately, it is not possible at present to formulate an explicit characterization of pure-state N representable $\gamma$. However, a simple characterization is indeed available for the larger set of density matrices $\gamma$, which derive from mixed states. These are known as ensemble representable density matrices. For this reason, the domain of definition of the functionals in Equations (5)–(7) is extended to include all $\gamma$ of this form [75]. A density matrix $\gamma$ is said to be ensemble representable if a set of pure states $|{\Psi }_m\rangle$ and weights $w_m\ge 0$ with ${\sum }_m{w}_m=1$ exist, such that the mixed state $\widehat{\Gamma }={\sum }_m{w}_m|{\Psi }_m\rangle \langle {\Psi }_m|$ satisfies

$${\gamma }_{\alpha \beta \sigma }=\mathrm{Tr}\left\{\widehat{\Gamma }{\widehat{c}}_{\alpha \sigma }^{†}{\widehat{c}}_{\beta \sigma }\right\}=\sum _m{w}_m\langle {\Psi }_m|{\widehat{c}}_{\alpha \sigma }^{†}{\widehat{c}}_{\beta \sigma }|{\Psi }_m\rangle$$

(8)

for all $\alpha$, $\beta$ and $\sigma$. One can then show that $\gamma$ is ensemble representable if and only if it is hermitian and all its eigenvalues ${\eta }_{k\sigma }$ (occupation numbers) satisfy [1,2]

$$0\le {\eta }_{k\sigma }\le 1\mathrm{with}\sum _{k\sigma }{\eta }_{k\sigma }=N.$$

(9)

The corresponding eigenvectors ${\mathit{u}}_{k\sigma }$ of $\gamma$ are known as natural orbitals. Notice that the occupation numbers ${\eta }_{k\sigma }$ do not necessarily take integer values. In fact, electronic correlations necessarily imply that, unless protected by some particular symmetry, the occupations of basically all single-particle states are fractional in any interacting eigenstate of the Hamiltonian $\widehat{H}$.

Having described the domain of definition of the functionals $E\left[\gamma \right]$ and $W\left[\gamma \right]$, the main challenge is to understand the functional dependence of the interaction energy $W\left[\gamma \right]$. An explicit general expression for $W\left[\gamma \right]$ is not known, since the minimization implied in Equation (7) cannot be performed in practice. To find suitable approximations, it is important to keep in mind, first of all, that $W\left[\gamma \right]$ is independent of the system under study. This means that it only depends on the density matrix $\gamma$ and on the interaction integrals $V_{\alpha \beta \gamma \delta }$, which define the operator $\widehat{W}$. The universality of the interaction energy $W\left[\gamma \right]$ constitutes a fundamental guiding principle along the search for its practical approximations.

The theoretical description of many-body lattice models by using only the orbital occupations $\langle {\widehat{n}}_{\alpha }\rangle ={\gamma }_{\alpha \alpha }$ is formally correct and has provided good results in many applications [53,54,57,59,60,61,76]. However, such a restrictive choice of basic variables spoils the universality of the corresponding functionals. In fact, for given site occupations ${\gamma }_{\alpha \alpha }$, the total energy of a system can be expressed in terms of the on-site energy ${\sum }_{\alpha }{t}_{\alpha \alpha }{\gamma }_{\alpha \alpha }$, which is an explicit function of $\left\{{\gamma }_{\alpha \alpha }\right\}$, and of the functional

$$F\left[\left\{{\gamma }_{\alpha \alpha }\right\}\right]=\underset{\Psi \to \left\{{\gamma }_{\alpha \alpha }\right\}}{min}\left\{\langle \Psi |\sum _{\begin{array}{c}\alpha \ne \beta \\ \sigma \end{array}}{t}_{\alpha \beta }{\widehat{c}}_{\alpha \sigma }^{†}{\widehat{c}}_{\alpha \sigma }+\frac{1}{2}\sum _{\begin{array}{c}\alpha \beta \gamma \delta \\ \sigma {\sigma }^{\prime }\end{array}}{V}_{\alpha \beta \gamma \delta }{\widehat{c}}_{\alpha \sigma }^{†}{\widehat{c}}_{\beta {\sigma }^{\prime }}^{†}{\widehat{c}}_{\delta {\sigma }^{\prime }}{\widehat{c}}_{\gamma \sigma }|\Psi \rangle \right\},$$

(10)

which involves the interaction energy as well as parts of the kinetic energy and the external potential. In this case, the constrained minimization runs over all states $|\Psi \rangle$ which yield the site or orbital occupations $n_{\alpha }={\gamma }_{\alpha \alpha }$ for all $\alpha$. It is important to notice that the off-diagonal hopping integrals $t_{\alpha \beta }$, which describe the electronic motion throughout the lattice, depend on and actually define the lattice under consideration. Therefore, site-occupation approaches are not universal, since the central functional $F\left[\left\{{\gamma }_{\alpha \alpha }\right\}\right]$ depends on the dimensionality of the lattice, on the range of the hopping integrals and on the external potential. This has no significant consequences in problems addressing the effects of inhomogeneities or even disorder in the on-site lattice potentials $t_{\alpha \alpha }$. In fact, in these cases, site-occupation approaches perform very well. However, problems involving correlation-induced changes in the degree of electronic delocalization and in the kinetic energy remain beyond reach, since they require to have access to the off-diagonal elements of $\gamma$.

Taking into account the complete single-particle density-matrix not only allows an accurate description of the kinetic energy $T\left[\gamma \right]$ but also implies that the interaction-energy functional $W\left[\gamma \right]$ is independent of the hopping integrals $t_{\alpha \beta }$. This fundamental universality means that, once a given approximation to $W\left[\gamma \right]$ has been derived, it can in principle be applied to various lattice structures having arbitrary hoppings and site potentials. Nevertheless, $W\left[\gamma \right]$ does depend on the considered many-particle interactions as defined by the parameters $V_{\alpha \beta \gamma \delta }$. In the present review, we focus on the Anderson and Hubbard models, for which explicit approximations to $W\left[\gamma \right]$ are available.

3. The Anderson Model

The single-impurity Anderson model (SIAM)

$$\widehat{H}={\widehat{H}}_{\mathrm{cond}}+{\widehat{H}}_{\mathrm{imp}}+\widehat{W}$$

(11)

describes the physics of a localized magnetic impurity embedded in a free-electron metal [47]. The first term

$${\widehat{H}}_{\mathrm{cond}}=\sum _{\mathit{k}\sigma }{\epsilon }_{\mathit{k}}{\widehat{c}}_{\mathit{k}\sigma }^{†}{\widehat{c}}_{\mathit{k}\sigma }$$

(12)

represents the single-particle band structure of the metallic electrons of the host. The operator ${\widehat{c}}_{\mathit{k}\sigma }^{†}$ (${\widehat{c}}_{\mathit{k}\sigma }$) creates (annihilates) a spin $\sigma$ electron in the delocalized conduction-band state $\mathit{k}$ having the energy ${\epsilon }_{\mathit{k}}$. The second term

$${\widehat{H}}_{\mathrm{imp}}=\sum _{\sigma }{\epsilon }_f{\widehat{n}}_{f\sigma }+\sum _{\mathit{k}\sigma }{V}_{\mathit{k}f}\left({\widehat{c}}_{\mathit{k}\sigma }^{†}{\widehat{f}}_{\sigma }+{\widehat{f}}_{\sigma }^{†}{\widehat{c}}_{\mathit{k}\sigma }\right)$$

(13)

describes the magnetic impurity orbital and its hybridization with the metal. The operator ${\widehat{f}}_{\sigma }^{†}$ (${\widehat{f}}_{\sigma }$) creates (annihilates) a spin $\sigma$ electron in the localized f orbital having an energy ${\epsilon }_f$, and ${\widehat{n}}_{f\sigma }={\widehat{f}}_{\sigma }^{†}{\widehat{f}}_{\sigma }$ counts the magnetic impurity occupation for spin $\sigma$. Notice that the second term in ${\widehat{H}}_{\mathrm{imp}}$ accounts for the charge fluctuations between the impurity orbital and the conduction band, which are proportional to the hybridization matrix-element $V_{\mathit{k}f}$. Finally, the interaction term

$$\widehat{W}=U{\widehat{n}}_{f\uparrow }{\widehat{n}}_{f\downarrow }$$

(14)

takes into account the Coulomb interaction between two electrons occupying the localized f orbital ($U>0$). The SIAM is often used to describe the physics of the Kondo effect, which involves correlated spin and valence fluctuations at the impurity [12]. This behavior results from the interplay between reducing the ground-state average of $\widehat{W}$ and maximizing the hybridization and charge fluctuations between the impurity orbital f and the conduction band. The former favors a correlated state with minimal double occupations $\langle {\widehat{n}}_{f\uparrow }{\widehat{n}}_{f\downarrow }\rangle$ on the f orbital, while the latter favors valence fluctuations which a priori imply an increase of $\langle {\widehat{n}}_{f\uparrow }{\widehat{n}}_{f\downarrow }\rangle$.

To develop a lattice density-functional theory of the SIAM, we follow the work in [71,77], and consider the single-particle energy functional $T\left[\gamma \right]$, which takes the explicit form

$$T\left[\gamma \right]=\sum _{\mathit{k}}{\epsilon }_{\mathit{k}}{\gamma }_{\mathit{k}\mathit{k}}+{\epsilon }_f{\gamma }_{ff}+\sum _{\mathit{k}}{V}_{\mathit{k}f}\left({\gamma }_{\mathit{k}f}+{\gamma }_{f\mathit{k}}\right)$$

(15)

in terms of the matrix elements of $\gamma ={\gamma }_{\uparrow }+{\gamma }_{\downarrow }$. The interaction-energy functional $W\left[\gamma \right]$ can be written as

$$W\left[\gamma \right]=UD\left[\gamma \right],$$

(16)

where $D\left[\gamma \right]$ represents the optimal number of f-level double occupations as a functional of $\gamma$. It involves the minimization

$$D\left[\gamma \right]=\underset{\widehat{\Gamma }\to \gamma }{min}\mathrm{Tr}\left\{\widehat{\Gamma }{\widehat{n}}_{f\uparrow }{\widehat{n}}_{f\downarrow }\right\}=\underset{\widehat{\Gamma }\to \gamma }{min}\sum _m{w}_m\langle {\Psi }_m|{\widehat{n}}_{f\uparrow }{\widehat{n}}_{f\downarrow }|{\Psi }_m\rangle$$

(17)

over all mixed states $\widehat{\Gamma }={\sum }_m{w}_m|{\Psi }_m\rangle \langle {\Psi }_m|$ satisfying the conditions

$$\begin{array}{cc}\hfill {\gamma }_{ff\sigma }& =\sum _m{w}_m\langle {\Psi }_m|{\widehat{f}}_{\sigma }^{†}{\widehat{f}}_{\sigma }|{\Psi }_m\rangle \hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\gamma }_{\mathit{k}f\sigma }& =\sum _m{w}_m\langle {\Psi }_m|{\widehat{c}}_{\mathit{k}\sigma }^{†}{\widehat{f}}_{\sigma }|{\Psi }_m\rangle \hfill \end{array}$$

(19)

and

$${\gamma }_{\mathit{k}{\mathit{k}}^{\prime }\sigma }=\sum _m{w}_m\langle {\Psi }_m|{\widehat{c}}_{\mathit{k}\sigma }^{†}{\widehat{c}}_{{\mathit{k}}^{\prime }\sigma }|{\Psi }_m\rangle$$

(20)

for all $\mathit{k}$, ${\mathit{k}}^{\prime }$ and $\sigma$. In other words, $\widehat{\Gamma }$ runs over all mixed states which yield the given single-particle density matrix $\gamma$ by means of Equations (18)–(20). A simple efficient approximation to $D\left[\gamma \right]$ is presented in the following.

3.1. Two-Level Approximation

A two-level approximation (TLA) $W^{2\mathrm{L}}\left[\gamma \right]=U{D}^{2\mathrm{L}}\left[\gamma \right]$ to the interaction energy has been derived in [71,77] to determine the low-energy properties of the SIAM. The ansatz involves the impurity f orbital and a single conduction-band state s of the form ${\widehat{s}}_{\sigma }^{†}={\sum }_{\mathit{k}}{S}_{\mathit{k}}{\widehat{c}}_{\mathit{k}\sigma }^{†}$, where the coefficients $S_{\mathit{k}}$ are such that the impurity experiences direct charge fluctuations only to this particular orbital. The actual approximation consists in assuming that these two levels are decoupled from the rest of the conduction band for the purpose of deriving the functional dependence of $W^{2\mathrm{L}}\left[\gamma \right]$. In other words, the scattering processes between the conduction-band state s and the rest of the conduction band are neglected while performing the minimization in Equation (17). This assumption is exact in two important limits: first, a totally degenerate (zero band width) conduction spectrum, and, second, a conduction band with widely separated discrete levels. In the first case, it is easy to see that the impurity f orbital couples only to the conduction-band state ${\widehat{s}}_{\sigma }^{†}=A{\sum }_{\mathit{k}}{V}_{\mathit{k}f}{\widehat{c}}_{\mathit{k}\sigma }^{†}$, where A is a normalization constant. In this case, the Hamiltonian of the Anderson model is reducible, since the single-particle states s and f form a two-level subspace, which is decoupled from the rest of the conduction band. For widely separated discrete conduction-band levels, we know from perturbation theory that the dominant charge fluctuations involve the localized impurity state f and the lowest empty or partially occupied conduction band state at the Fermi energy ${\epsilon }_F$. Therefore, these two orbitals define a subsystem which dominates the physics at low energies. The thus motivated two-level ansatz allows one to expresses the number of f-level double occupations D and the resulting interaction energy W in terms of the effective two-level density matrix ${\gamma }^{2\mathrm{L}}$ formed by the impurity f state and the particular conduction-band orbital s.

The two-level problem consisting of the orbitals f and s has been solved exactly in the spin-restricted (SR) half-filled case (i.e., $\mathrm{Tr}\left\{{\gamma }^{2\mathrm{L}}\right\}={\gamma }_{ss}+{\gamma }_{ff}=2$ and ${\gamma }_{\uparrow }={\gamma }_{\downarrow }$) [71], which is the most important one, since the ground state of the SIAM is a singlet [78]. The density matrix ${\gamma }^{2\mathrm{L}}$ of the SR half-filled two-level system is univocally defined by the f-level occupation ${\gamma }_{ff}={\gamma }_{ff\uparrow }+{\gamma }_{ff\downarrow }$ and the degree of charge fluctuations $X=X_{\uparrow }+X_{\downarrow }$ where $X_{\sigma }={|{\gamma }_{sf\sigma }|}^2$. The average f-level double occupation, as given in [77], reads

$$D_{\mathrm{SR}}^{2\mathrm{L}}({\gamma }_{ff},X)=\left\{\begin{array}{cc}{\displaystyle \frac{{\gamma }_{ff}^2}{4}}-{\displaystyle \frac{\sqrt{2\xi }}{4}}·{\displaystyle \frac{2X_{\mathrm{SR}}^0-\sqrt{2\xi }}{1-\sqrt{2\xi }}}\hfill & \mathrm{if}{X}_{\mathrm{SR}}^{\infty }<X\le X_{\mathrm{SR}}^0\hfill \\ D_{\mathrm{SR}}^{\infty }({\gamma }_{ff})=max\left\{{\gamma }_{ff}-1,0\right\}\hfill & \mathrm{if}0\le X\le X_{\mathrm{SR}}^{\infty },\hfill \end{array}\right.$$

(21)

where

$$X_{\mathrm{SR}}^0({\gamma }_{ff})=\frac{1}{2}{\gamma }_{ff}(2-{\gamma }_{ff}),$$

(22)

$$X_{\mathrm{SR}}^{\infty }({\gamma }_{ff})=\left\{\begin{array}{cc}{\gamma }_{ff}\left(1-{\gamma }_{ff}\right)\hfill & \mathrm{if}{\gamma }_{ff}\le 1\hfill \\ \left(2-{\gamma }_{ff}\right)\left({\gamma }_{ff}-1\right)\hfill & \mathrm{if}{\gamma }_{ff}>1,\hfill \end{array}\right.$$

(23)

and

$$\xi =X_{\mathrm{SR}}^0-X.$$

(24)

Knowing that the state s is a linear combination of delocalized $\mathit{k}$ states, one can express the degree of charge fluctuations between the impurity and the conduction band as

$$X_{\sigma }=\sum _{\mathit{k}}{|{\gamma }_{\mathit{k}f\sigma }|}^2.$$

(25)

In this way, $D_{\mathrm{SR}}^{2\mathrm{L}}$ can be regarded as a functional of the single-particle density matrix $\gamma$, irrespectively of the number of $\mathit{k}$ states within the conduction band.

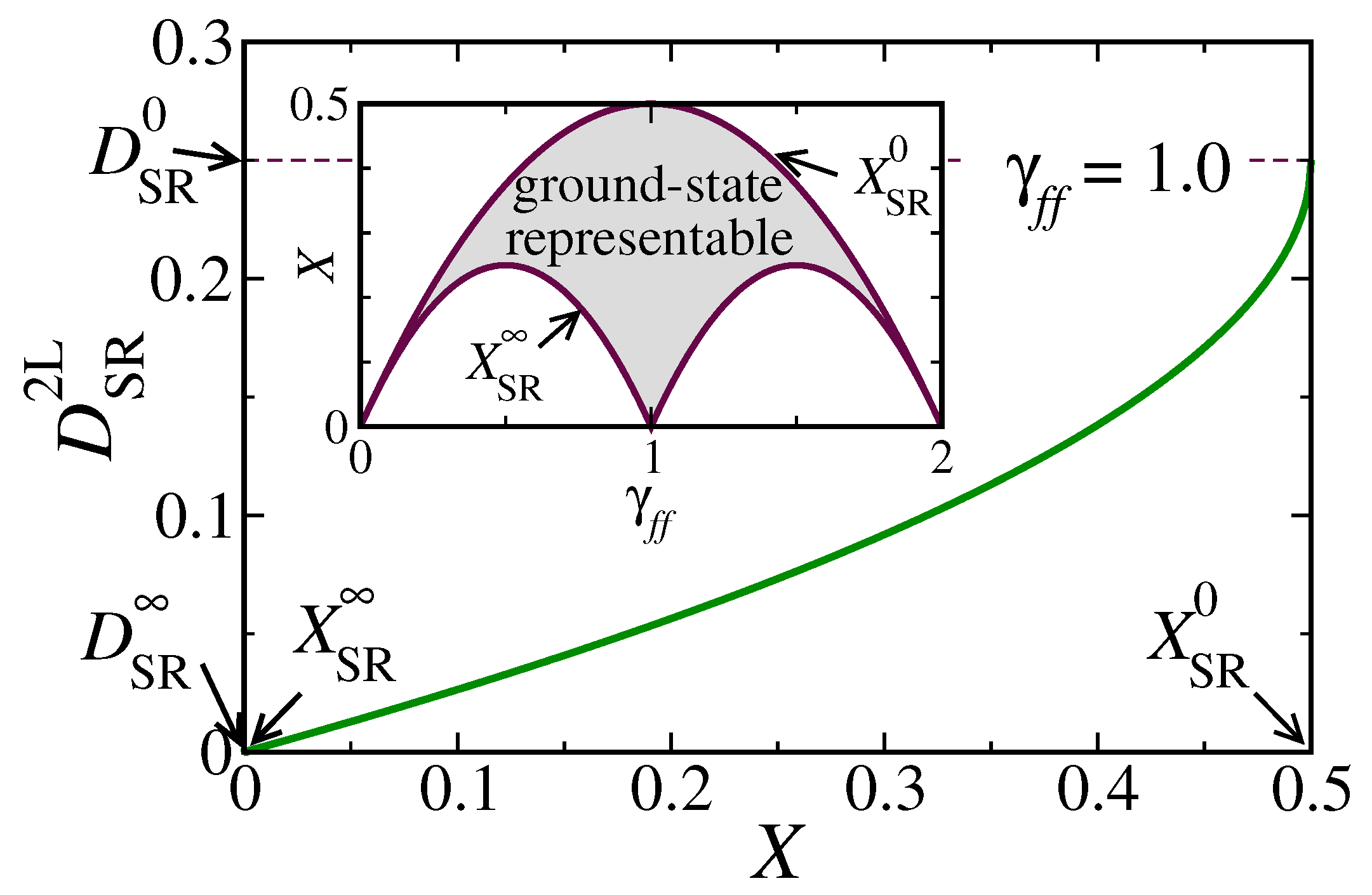
In Figure 1, $D_{\mathrm{SR}}^{2\mathrm{L}}$ is shown as a function of X for the impurity occupation ${\gamma }_{ff}=1$. To understand how $D_{\mathrm{SR}}^{2\mathrm{L}}$ depends on $\gamma$, let us first recall that ensemble representability requires $\gamma$ to be positive definite with eigenvalues ${\eta }_{k\sigma }\in [0,1]$. Consequently, $\gamma -{\gamma }^2$ is also positive definite, and in particular

$$\langle f\sigma |\gamma -{\gamma }^2|f\sigma \rangle ={\gamma }_{ff\sigma }(1-{\gamma }_{ff\sigma })-X_{\sigma }\ge 0.$$

(26)

In the noninteracting limit, the many-body eigenstates $|\Psi \rangle$ are uncorrelated Slater determinants, which implies $\gamma ={\gamma }^2$. In a general case, the inequality in Equation (26) gives us a useful upper bound for the degree of charge fluctuations, namely,

$$X_{\sigma }\le {\gamma }_{ff\sigma }(1-{\gamma }_{ff\sigma })=X_{\sigma }^0$$

(27)

where we have introduced the maximum degree of spin-$\sigma$ charge fluctuations $X_{\sigma }^0$. The previous considerations allow one to characterize the uncorrelated limit by the condition $X_{\sigma }=X_{\sigma }^0$ or $\xi =0$. Using that in the SR case ${\gamma }_{ff\uparrow }={\gamma }_{ff\downarrow }={\gamma }_{ff}/2$ and $X_{\uparrow }=X_{\downarrow }=X/2$, we can write the inequality in Equation (27) as

$$X\le \frac{1}{2}{\gamma }_{ff}(2-{\gamma }_{ff})=X_{\mathrm{SR}}^0({\gamma }_{ff}).$$

(28)

In this case, $D_{\mathrm{SR}}^{2\mathrm{L}}$ takes its maximum value

$$D_{\mathrm{SR}}^0({\gamma }_{ff})=\frac{{\gamma }_{ff}^2}{4},$$

(29)

as predicted by Hartree–Fock theory (see Figure 1). As the degree of charge fluctuations X decreases, $D_{\mathrm{SR}}^{2\mathrm{L}}$ also decreases, since the electrons can correlate thereby reducing double occupations of the impurity state f. The minimum possible value $D_{\mathrm{SR}}^{\infty }({\gamma }_{ff})=max\{{\gamma }_{ff}-1,0\}$ is achieved in the strongly correlated limit, where double occupations (empty states) are suppressed if ${\gamma }_{ff}\le 1$ (${\gamma }_{ff}>1$), while the corresponding degree of charge fluctuations is denoted by $X_{\mathrm{SR}}^{\infty }$ (see the inset of Figure 1).

In [77] the TLA has been extended to the spin polarized case. Taking advantage of the scaling properties of $D\left[\gamma \right]$, one approximates the f-level double occupations for spin-dependent ${\gamma }_{\sigma }$ by the ansatz

$$D^{2\mathrm{L}}({\gamma }_{ff\sigma },X_{\sigma })=D^{\infty }({\gamma }_{ff\sigma })+\left[D^0({\gamma }_{ff\sigma })-D^{\infty }({\gamma }_{ff\sigma })\right]·{\displaystyle \frac{D_{\mathrm{SR}}^{2\mathrm{L}}({\gamma }_{ff},\tilde{X})-D_{\mathrm{SR}}^{\infty }({\gamma }_{ff})}{D_{\mathrm{SR}}^0({\gamma }_{ff})-D_{\mathrm{SR}}^{\infty }({\gamma }_{ff})}},$$

(30)

where

$$D^0({\gamma }_{ff\sigma })={\gamma }_{ff\uparrow }{\gamma }_{ff\downarrow }$$

(31)

and

$$D^{\infty }({\gamma }_{ff\sigma })=max\left\{{\gamma }_{ff}-1,0\right\}$$

(32)

denote, respectively, the f-level double occupations in the weakly and strongly correlated limits [77]. The effective degree of charge fluctuations $\tilde{X}$ scales between the limits $X_{\mathrm{SR}}^0$ and $X_{\mathrm{SR}}^{\infty }$ as

$$\tilde{X}=g·(X_{\mathrm{SR}}^{\infty }-X_{\mathrm{SR}}^0)+X_{\mathrm{SR}}^0$$

(33)

with $g\in [0,1]$ given by

$$g=g_{\uparrow }{g}_{\downarrow }$$

(34)

and

$$g_{\sigma }=\left\{\begin{array}{cc}{\left({\displaystyle \frac{X_{\sigma }^0-X_{\sigma }}{X_{\sigma }^0-X_{\sigma }^{\infty }}}\right)}^{1/2}\hfill & \mathrm{for}{X}_{\sigma }\ge X_{\sigma }^{\infty }\hfill \\ 1\hfill & \mathrm{for}{X}_{\sigma }<X_{\sigma }^{\infty }.\hfill \end{array}\right.$$

(35)

In [77], the following approximation to the degree of charge fluctuations in the strongly correlated limit has been proposed:

$$X_{\sigma }^{\infty }({\gamma }_{ff\sigma })=\left\{\begin{array}{cc}{\gamma }_{ff\sigma }\left(1-{\gamma }_{ff}\right)\hfill & \mathrm{if}{\gamma }_{ff}\le 1\hfill \\ \left(1-{\gamma }_{ff\sigma }\right)\left({\gamma }_{ff}-1\right)\hfill & \mathrm{if}{\gamma }_{ff}>1,\hfill \end{array}\right.$$

(36)

which physically corresponds to the maximum degree of charge fluctuations $X_{\sigma }$ that can be obtained for the given local occupations ${\gamma }_{ff\sigma }$, under the constraint of minimal f-level double occupation $D^{\infty }$.

3.2. Applications to Anderson Rings

The ground state and low-energy spin excitations of the SIAM were investigated by Töws and Pastor [71], Töws and Pastor [77] using the TLA to the interaction-energy functional. The total-energy $E\left[{\gamma }_{\sigma }\right]=T\left[{\gamma }_{\sigma }\right]+U{D}^{2L}\left[{\gamma }_{\sigma }\right]$ has been minimized with respect to ${\gamma }_{\sigma }$ under the constraint of well-defined $S_z$. For an even number of electrons the ground state is obtained by setting $S_z=0$, since this takes into account all possible values of S. The lowest lying triplet state is obtained by setting $S_z=1$, which corresponds to a minimization for $S\ge 1$. As an example, we consider half-filled finite rings having $N_a=11$ atoms ($N_o=N_a+1=12$ orbitals) and $N=N_o=12$ electrons.

The Hamiltonian in Equation (12) of the metallic host can be written in a tight-binding form in terms of the creation and annihilation operators ${\widehat{c}}_{i\sigma }^{†}$ and ${\widehat{c}}_{i\sigma }$ corresponding to atomic-like orbitals centered at the different lattice sites i. Thus, we have

$${\widehat{H}}_{\mathrm{cond}}=-t\sum _{\langle ij\rangle \sigma }{\widehat{c}}_{i\sigma }^{†}{\widehat{c}}_{j\sigma },$$

(37)

where the sum runs over nearest-neighbor (NN) pairs $i,j$ and $t>0$ denotes the NN hopping integral. The corresponding conduction-band Fermi energy at half-band filling is ${\epsilon }_F=0.28t$. The single-particle impurity terms in Equation (13) are given by

$${\widehat{H}}_{\mathrm{imp}}=\sum _{\sigma }{\epsilon }_f{\widehat{n}}_{f\sigma }+\sum _{\sigma }{V}_{sf}\left({\widehat{c}}_{0\sigma }^{†}{\widehat{f}}_{\sigma }+{\widehat{f}}_{\sigma }^{†}{\widehat{c}}_{0\sigma }\right),$$

(38)

where $V_{sf}$ describes the hybridization between the impurity f level and the conduction-band orbital at the impurity atom $i=0$.

The main properties of the singlet ground state and the lowest lying triplet state are shown in Figure 2: interaction energy $W=UD$, impurity occupation ${\gamma }_{ff}$, f-level spin polarization $\langle {\widehat{S}}_{fz}\rangle =({\gamma }_{ff\uparrow }-{\gamma }_{ff\downarrow })/2$ and degree of charge fluctuations $X={\sum }_{\mathit{k}\sigma }{|{\gamma }_{\mathit{k}f\sigma }|}^2$. The complete range of interactions is explored by varying the Coulomb-repulsion strength U at the f orbital from weak to strong electronic correlations. First, one observes that W tends to zero for large $U/t$ since the number of f-level double occupations $D=\langle {\widehat{n}}_{f\uparrow }{\widehat{n}}_{f\downarrow }\rangle$ rapidly vanishes, as expected in strongly correlated states. Notice, moreover, that D is in general much smaller in the triplet than in the singlet state. This can be easily explained by the fact that the f-level spin polarization $\langle {\widehat{S}}_{fz}\rangle \simeq {\gamma }_{ff}/2$ is almost saturated in the former (see the left-hand inset in Figure 2b). To analyze the impurity properties in more detail, it is useful to recall that the conduction-band Fermi level ${\epsilon }_F$ is located above the impurity level: ${\epsilon }_F={\epsilon }_f+0.28t$. Consequently, in the uncorrelated limit ($U/t\to 0$), the ground state corresponds to an $f^1$–$f^2$ intermediate-valence state with ${\gamma }_{ff}>1$. The singlet-triplet excitation implies therefore the transfer of an $f_{\downarrow }$ electron to the Fermi level, which yields ${\gamma }_{ff}<1$ in the triplet (see Figure 2b). In contrast, in the limit of strong correlations, one observes an intermediate valence state with ${\gamma }_{ff}<1$ for both singlet and triplet states. Due to the strong Coulomb repulsion $U/t\gg 1$ no significant double occupations of the f-level take place. In this case, the singlet-triplet excitation involves only the spin degrees of freedom and no charge transfer.

A further interesting property is the degree of charge fluctuations X between the impurity and the conduction band. The right-hand inset of Figure 2b shows X as a function of $U/t$. As already discussed, the ground-state has ${\gamma }_{ff}>1$ for small Coulomb repulsion $U/t$, which means that the main charge fluctuations originate from an $f^2\leftrightarrow f^1$ intermediate-valence state involving singly-occupied and doubly-occupied impurity configurations. As $U/t$ increases, X increases first, until ${\epsilon }_f+U\simeq {\epsilon }_F$, which is the most favorable energy-level configuration concerning charge fluctuations. However, a further increase of U tends to suppress double occupations at the impurity (${\epsilon }_f+U>{\epsilon }_F$). Consequently, X decreases with increasing U. In the strongly correlated limit the impurity double occupations are very effectively suppressed so that the most relevant charge fluctuations in the singlet ground state involve only $f^1\leftrightarrow f^0$ transitions. In the lowest-lying triplet state, X is smaller than in the singlet ground state. This can be understood by noting that the triplet exhibits an almost fully saturated f-level spin polarization. Therefore, only one spin channel contributes to the charge fluctuations between the impurity and the conduction band.

The accuracy of the TLA has been tested by comparing the LDFT results to exact numerical diagonalizations [77,79]. In Figure 2, one observes that in the whole interaction regime, from weak to strong electron correlations, the TLA yields a quite accurate quantitative description of the physical properties both in the ground state and the lowest-lying spin excitation. The relative errors in ${\gamma }_{ff}$, $\langle {\widehat{S}}_{fz}\rangle$ and X are less than $3\%$, $1.2\%$ and $9.6\%$, respectively, while the absolute error in W is less than $0.008t$. This shows that LDFT with the TLA provides an efficient and physically sound approach to the problem of strong electron correlations. Moreover, Figure 3 shows that the singlet-triplet excitation gap $\Delta E=E_{S=1}-E_{S=0}$ and the degree of spin fluctuations ${\sigma }_{\mathrm{sf}}={(\langle {\widehat{S}}_{fz}^2\rangle -{\langle {\widehat{S}}_{fz}\rangle }^2)}^{1/2}$ in the singlet ground state, which are both very sensitive to correlation effects, are also quite accurately reproduced. The singlet-triplet gap $\Delta E$ is particularly interesting since it defines the energy scale which governs the low-temperature physics and is approximately proportional to the Kondo temperature. Concerning $\Delta E$, the largest relative error is about $16\%$. It is also worth noting that in the strongly correlated limit the singlet ground state exhibits a significant local magnetic moment ${\mu }_f={\langle {\mathbf{S}}_f·{\mathbf{S}}_f\rangle }^{1/2}\simeq 0.74$, although the average impurity polarization $\langle {\widehat{S}}_{fz}\rangle$ is strictly zero. This means that the vanishing impurity magnetization is the consequence of spin fluctuations, a subtle indication of spin-charge separation. This contrasts with the usual mean-field approaches, such as the Hartree–Fock approximation, which neglect them and thus lead to an artificial spin-symmetry breaking for sufficiently large $U/t$ (see Figure 2b). Remarkably, the TLA takes correctly into account the fluctuations of a strong local magnetic moment. For these reasons, it provides a simple and accurate tool to describe both ground-state and excited-state properties.

4. The Hubbard Model

The Hubbard model represents a further important challenge in the context of the many-body problem [48,49,50,80], since it describes the physics of correlated electrons in narrow energy bands. The associated Hamiltonian is given by

$$\widehat{H}={\widehat{H}}_0+\widehat{W}.$$

(39)

The first term

$${\widehat{H}}_0=\sum _{i\sigma }{\epsilon }_i{\widehat{n}}_{i\sigma }+\sum _{\langle ij\rangle \sigma }{t}_{ij}{\widehat{c}}_{i\sigma }^{†}{\widehat{c}}_{j\sigma },$$

(40)

represents the single-particle contribution, where ${\epsilon }_i$ denotes the energy level at site i and $t_{ij}$ the hopping integral between NN sites i and j. The operator ${\widehat{c}}_{i\sigma }^{†}$ (${\widehat{c}}_{i\sigma }$) is the usual creation (annihilation) operator for a spin $\sigma$ electron at site i (${\widehat{n}}_{i\sigma }={\widehat{c}}_{i\sigma }^{†}{\widehat{c}}_{i\sigma }$). The hopping integrals $t_{ij}$ characterize the structure of the underlying lattice, as well as the range of interatomic hybridizations. The energy levels ${\epsilon }_i$ can describe both homogeneous and inhomogeneous systems. In the simplest homogeneous Hubbard model, ${\epsilon }_i={\epsilon }_0$ does not depend on the lattice site i. However, more complex situations, including for example lattices composed of different chemical elements or the case where external electric fields are present, are modeled in terms of site-dependent potentials ${\epsilon }_i$. In [70], bipartite lattices have been considered as an example of the inhomogeneous Hubbard model. In this case, the energy levels ${\epsilon }_i$ of the two sublattices A and B differ by the level-splitting $\epsilon$, i.e.,

$${\epsilon }_i=\left\{\begin{array}{c}+\epsilon /2\mathrm{if}i=1(\mathrm{sublattice}{S}_1)\hfill \\ -\epsilon /2\mathrm{if}i=2(\mathrm{sublattice}{S}_2).\hfill \end{array}\right.$$

(41)

The second term

$$\widehat{W}=U\sum _i{\widehat{n}}_{i\uparrow }{\widehat{n}}_{i\downarrow }$$

(42)

accounts for the dominant intra-atomic Coulomb repulsion among the electrons. The strength of the interaction is characterized by the Coulomb integral $U>0$, which is assumed to be independent of the lattice site i.

From a physical point of view, the Hubbard Hamiltonian describes the interplay between two opposite tendencies. On the one hand, the electrons tend to form a bound state and therefore delocalize throughout the lattice in order to reduce their kinetic energy $T={\sum }_{ij\sigma }{t}_{ij}\langle {\widehat{c}}_{i\sigma }^{†}{\widehat{c}}_{j\sigma }\rangle$ by profiting from the interatomic hybridizations. On the other hand, a reduction of the charge fluctuations and of the concomitant Coulomb-repulsion energy is aimed, which favors localized electronic states. In addition, if inhomogeneities are present, the site-dependent potentials ${\epsilon }_i$ give rise to inhomogeneous charge distributions among the atoms, whose nature depends critically on the Coulomb interaction strength. Therefore, the Hubbard model captures the interplay between delocalization, correlations, and density redistributions of interacting electrons in narrow energy-bands.

To derive approximations to the interaction-energy functional $W\left[\gamma \right]$, we consider the Levy–Lieb constraint search. In the case of the Hubbard model, the exact functional takes the form

$$W\left[\gamma \right]=U\underset{\Psi \to \gamma }{min}\left\{\sum _i\langle \Psi |{\widehat{n}}_{i\uparrow }{\widehat{n}}_{i\downarrow }|\Psi \rangle \right\}.$$

(43)

Notice the linearity of $W\left[\gamma \right]$ as a function of U, a rigorous property to be satisfied by any explicit approximation. In the case of a general site dependent interaction, $W\left[\gamma \right]$ remains an homogeneous function of order one of the Coulomb integrals $V_{\alpha \beta \gamma \delta }$. In the following, two successful approximations to the interaction-energy functional $W\left[\gamma \right]$ are presented and discussed. One of them is based on a real-space perspective and on the scaling properties of W. The other one exploits the translational invariance of the homogeneous Hubbard model and adopts a $\mathit{k}$-space perspective. In this case, advantage is taken of some remarkable analogies between the degree of electron correlations and the entropy associated to the occupation-number distribution of the independent delocalized Bloch states.

4.1. Local Perspective to the Interaction-Energy Functional

In previous works, the properties of the exact interaction-energy functional $W\left[\gamma \right]$ have been investigated in both homogeneous and inhomogeneous finite systems [65,66,67,68,69]. These studies have revealed that the dependence of W on the NN bond order ${\gamma }_{12}$ follows a simple approximate scaling relation, which is nearly independent of the system size, lattice dimension and band filling $n=N/N_a$. To illustrate the idea behind this scaling ansatz, it is useful to first consider the domain of v-representability of ${\gamma }_{12}$. This is given by the set of values ${\gamma }_{12}$, which can be obtained from the ground-state of the model for arbitrary parameters. This domain is limited by the condition ${\gamma }_{12}^{\infty }\le {\gamma }_{12}\le {\gamma }_{12}^0$, where the uncorrelated and strongly correlated limits ${\gamma }_{12}^0$ and ${\gamma }_{12}^{\infty }$ correspond to the ground states for $U=0$ and $U\to \infty$. Moreover, it has been shown that both ${\gamma }_{12}^0$ and ${\gamma }_{12}^{\infty }$ increase monotonously with increasing number of electrons N until the single-particle band is half filled [69]. In the weakly correlated limit (${\gamma }_{12}={\gamma }_{12}^0$), the interaction energy is given by its Hartree–Fock value $W^0=U{\sum }_i{\gamma }_{ii\uparrow }{\gamma }_{ii\downarrow }$, since the underlying many-body state is a single Slater determinant. Starting from ${\gamma }_{12}={\gamma }_{12}^0$, W decreases monotonously with decreasing ${\gamma }_{12}$, reaching its lowest possible value $W^{\infty }=U{\sum }_{i}max\{{\gamma }_{ii}-1,0\}$ in the strongly-correlated limit ${\gamma }_{12}={\gamma }_{12}^{\infty }$ [69]. The lower bound ${\gamma }_{12}^{\infty }$ represents the largest amount of interatomic charge fluctuations that can be achieved under the constraint of minimal interaction energy (i.e., minimal double occupations). Physically, the decrease of W with decreasing ${\gamma }_{12}$ illustrates how correlations manage to reduce the Coulomb energy at the expense of kinetic energy and electron delocalization.

The scaling approximation brings the domains of v representability for different band fillings to a common range and scales the interaction energy with respect to its Hartree–Fock and strongly correlated values $W^0$ and $W^{\infty }$. In this way, the scaled interaction energy

$$\omega =\frac{W-W^{\infty }}{W^0-W^{\infty }}$$

(44)

can be regarded as a function of the relative degree of electron delocalization

$$g_{12}=\frac{{\gamma }_{12}-{\gamma }_{12}^{\infty }}{{\gamma }_{12}^0-{\gamma }_{12}^{\infty }}.$$

(45)

As discussed in [70], the scaled interaction energy turns out to be remarkably similar for all considered systems and band fillings. Further investigations on the Hubbard model have shown that the relative change in W caused by a change in $g_{12}$ is also approximately independent of the system size and lattice dimension [65,66,67,68,69,70]. This indicates that the largest part of the dependence of W on ${\gamma }_{12}$ is a consequence of the changes in the domain of representability of ${\gamma }_{ij}$ as defined by the limits of weak and strong correlations. It is therefore reasonable to regard the scaled interaction $\omega$ as a function of the degree of electron delocalization $g_{12}$, which is nearly independent of the system under study, even though the relation between $\omega$ and $g_{12}$ does depend on the charge distribution in inhomogeneous models.

An explicit approximation to W can be obtained, for example, by inferring its functional dependence from a simple reference system which already incorporates the interplay between electronic delocalization, charge transfer and correlations. The simplest system which fulfills this condition is probably the Hubbard dimer. Thus, the scaled dimer approximation has been proposed [70], which is given by

$${\omega }_{\mathrm{sc}}(g_{12},\Delta n)={\omega }_2(g_{12},\Delta n)$$

(46)

or, equivalently,

$$W_{\mathrm{sc}}(g_{12},\Delta n)=W^{\infty }+(W^0-W^{\infty }){\omega }_2(g_{12},\Delta n),$$

(47)

where the exact interaction-energy functional of the Hubbard-dimer ($N=N_a=2$) reads

$${\displaystyle \frac{W_2}{U{N}_a}}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}-{\displaystyle \frac{|{\gamma }_{12}{|}^2}{4}}{\displaystyle \frac{1+\sqrt{1-{(\Delta n/2)}^2-{|{\gamma }_{12}|}^2}}{{(\Delta n/2)}^2+{|{\gamma }_{12}|}^2}},\hfill & \mathrm{if}{\gamma }_{12}^{\infty }<|{\gamma }_{12}|\le {\gamma }_{12}^0\hfill \\ {\displaystyle \frac{\Delta n}{4}},\hfill & \mathrm{if}|{\gamma }_{12}|\le {\gamma }_{12}^{\infty }\hfill \end{array}\right.$$

(48)

and the uncorrelated and strongly-correlated bounds are $W_2^0=U{N}_a[1+{(\Delta n/2)}^2]/4$ and $W_2^{\infty }=U{N}_a\Delta n/4$. It has been shown that $W_{\mathrm{sc}}$ yields a sound approximation to the exact functional W in the complete range from weak ($g_{12}=1$) to strong ($g_{12}=0$) electronic correlations. The largest quantitative deviations are found for intermediate band fillings $n=N/N_a\simeq 0.6$, where $|W-W_{\mathrm{sc}}|/(W^0-W^{\infty })\le 0.1$. In most other cases, the error is in the range of only $|W-W_{\mathrm{sc}}|/(W^0-W^{\infty })\simeq 0.008$–$0.06$ [70]. This is quite remarkable since $W^0$, $W^{\infty }$, ${\gamma }_{12}^0$ and ${\gamma }_{12}^{\infty }$ strongly depend on the size of the system, the band filling n and the charge transfer $\Delta n$. The good general accuracy of the scaled dimer approximation relies ultimately on the universal nature of the interaction-energy functional. In the following, we review a few applications of LDFT in conjunction with this functional.

4.2. Applications of the Scaled Dimer Approximation

As a first application, we consider the inhomogeneous Hubbard model on a bipartite 1D ring having $N_a=14$ sites and half-band filling $n=1$ ($N=14$ electrons). In [70], the ground-state properties are discussed from weak to strong electronic correlations as well as along the crossover from the homogeneous to the strongly ionic regimes. To this aim, two relevant parameters have been varied systematically: the site-dependent potential ${\epsilon }_i$ given in Equation (41), which controls the degree of charge transfer $\Delta n$ between the sublattices, and the Coulomb repulsion strength U, which measures the importance of correlations.

Results for the average number of double occupations per site $W/U{N}_a$, the charge transfer $\Delta n={\gamma }_{22}-{\gamma }_{11}$, and the NN bond order ${\gamma }_{12}$ obtained for different values of the energy-level splitting $\epsilon /t$ are shown in Figure 4 as function of the Coulomb repulsion strength $U/t$. In the homogeneous case ($\epsilon /t=0$), the charge transfer $\Delta n$ between the sublattices is obviously zero. One observes that the interaction energy W and the NN bond order ${\gamma }_{12}$ decrease monotonously with $U/t$, which reflects the reduction of the Coulomb repulsion energy at the expense of kinetic energy. As the level splitting $\epsilon$ between the sublattices increases, for a fixed Coulomb repulsion U, the charge transfer $\Delta n$ and the interaction energy W increase in similar ways. This is due to the fact that inhomogeneous charge distributions necessarily imply larger average double occupations. It is interesting to note that for finite intermediate sublattice level splitting, e.g., $\epsilon /t=1$–16, the system undergoes a qualitative transition between a delocalized charge-density-wave (CDW) state ($\Delta n\simeq 0.9$–$1.6$ and ${\gamma }_{12}\simeq 0.3$–$0.6$) to a nearly localized state having a homogeneous charge distribution ($\Delta n$, ${\gamma }_{12}\to 0$) as the Coulomb interaction strength $U/t$ is increased from weak to strong correlations. Starting from the weakly correlated CDW state and increasing $U/t$, $\Delta n$ decreases as soon as U is of the order of $\epsilon$, reaching a nearly homogeneous charge distribution $\Delta n=0$ for $U\gg \epsilon$. Moreover, for finite $\epsilon /t$, an interesting maximum of ${\gamma }_{12}$ is found for $U\simeq \epsilon$. This can be qualitatively understood by noting that for $U\simeq \epsilon$ the Coulomb repulsion on the doubly occupied sites in sublattice $S_2$ compensates the energy difference between the two sublattices (${\epsilon }_1-{\epsilon }_2=\epsilon$). This allows a nearly freelike motion of the ${\gamma }_{11}$ electrons occupying sublattice $S_1$ together with the ${\gamma }_{22}-1$ electrons in sublattice $S_2$, which occupy already occupied sites (${\gamma }_{11}<1$ and ${\gamma }_{22}>1$ for $\epsilon >0$). With increasing $\epsilon /t$, this effect becomes more pronounced, since both the charge transfer $\Delta n$ in the $U=0$ CDW and the crossover value of U are larger.

Before closing this section, it is important to underline the very good agreement between the results obtained in LDFT using the scaled dimer approximation and the exact results obtained with the Lanczos method. A high accuracy is found for all considered parameter regimes, from weak to strong electronic correlations, and from homogeneous to strongly ionic charge distributions (see Figure 4). The largest absolute discrepancies in the number of double occupations $W/(U{N}_a)$, charge transfer $\Delta n$ and NN bond order ${\gamma }_{12}$ are less than $0.02$, $0.05$ and $0.025$, respectively. Further investigation of the ground-state properties of the Hubbard model in all dimensions $d\le 3$, including dimerized infinite chains, have demonstrated that LDFT reproduces the kinetic, Coulomb and total energies, the local magnetic moments, the charge-excitation gaps, and the charge susceptibilities very accurately [66,67,68,70]. One concludes that LDFT with the scaled dimer approximation is an efficient and accurate method to study the physics of the Hubbard model and, in particular, to describe the interplay between correlation, electron delocalization and charge transfer.

4.3. Reciprocal-Space Perspective

In this section, we focus on the single-band Hubbard model on a periodic lattice and exploit the translational invariance of the system by developing a delocalized $\mathit{k}$-space approach. Periodicity implies that the elements ${\gamma }_{ij\sigma }$ of the SPDM solely depend on the vector ${\mathit{R}}_i-{\mathit{R}}_j$ connecting the lattice sites ${\mathit{R}}_i$ and ${\mathit{R}}_j$. Therefore, applying Bloch’s theorem and knowing that there is only one orbital in the unit cell, one may write

$${\gamma }_{ij\sigma }=\frac{1}{N_a}\sum _{\mathit{k}\in \mathrm{BZ}}{\eta }_{\mathit{k}\sigma }{\mathrm{e}}^{-\mathrm{i}\mathit{k}·({\mathit{R}}_i-{\mathit{R}}_j)}.$$

(49)

This means that any translational-invariant density matrix $\gamma$ can be characterized by its eigenvalues ${\eta }_{\mathit{k}\sigma }$, which represent the average occupation numbers of the natural orbitals. For the given lattice, the occupation numbers ${\eta }_{\mathit{k}\sigma }$ become the fundamental variable in LDFT and all physical observables can be regarded as functionals $\mathcal{O}\left[{\eta }_{\mathit{k}\sigma }\right]$ of ${\eta }_{\mathit{k}\sigma }$. In particular, the kinetic-energy functional is given by

$$T\left[{\eta }_{\mathit{k}\sigma }\right]=\sum _{\mathit{k}\in \mathrm{BZ}}{\epsilon }_{\mathit{k}}{\eta }_{\mathit{k}\sigma },$$

(50)

where ${\epsilon }_{\mathit{k}\sigma }$ is the dispersion relation of the underlying tight-binding model. To obtain the ground-state SPDM of the interacting problem, the energy functional

$$E\left[{\eta }_{\mathit{k}\sigma }\right]=\sum _{\mathit{k}\sigma }{\epsilon }_{\mathit{k}\sigma }{\eta }_{\mathit{k}\sigma }+W\left[{\eta }_{\mathit{k}\sigma }\right]$$

(51)

needs to be minimized, under the constraint of fixed number of spin $\sigma$ electrons $N_{\sigma }={\sum }_{\mathit{k}}{\eta }_{\mathit{k}\sigma }$. This can be done by introducing the Euler–Lagrange functional

$$\mathcal{L}[{\eta }_{\mathit{k}\sigma },{\mu }_{\sigma }]=E\left[{\eta }_{\mathit{k}\sigma }\right]-\sum _{\sigma }{\mu }_{\sigma }\left(\sum _{\mathit{k}\in \mathrm{BZ}}{\eta }_{\mathit{k}\sigma }-N_{\sigma }\right)$$

(52)

and by solving the extremal equations $\partial \mathcal{L}/\partial {\eta }_{\mathit{k}\sigma }=0$ for all $\mathit{k}\sigma$ [66].

To derive a physically sound approximation to the interaction-energy functional $W\left[{\eta }_{\mathit{k}\sigma }\right]$ entering Equation (51), it is very useful to consider two important limiting cases for which $W\left[{\eta }_{\mathit{k}\sigma }\right]$ can be obtained exactly. The first one is when all ${\eta }_{\mathit{k}\sigma }$ are either 0 or 1 and ${\gamma }_{\sigma }$ is idempotent (i.e., ${\gamma }_{\sigma }^2={\gamma }_{\sigma }$). There is only one kind of many-body state which can yield such a $\gamma$, namely, the single Slater determinant consisting of the occupied natural orbitals $\mathit{k}\sigma$. The interaction-energy is then given by $W^0=U{D}^0$, where

$$D^0=\sum _i{\gamma }_{ii\uparrow }{\gamma }_{ii\downarrow }$$

(53)

is the average number of double occupations in an uncorrelated state with the spin density ${\gamma }_{ii\sigma }=n_{i\sigma }$. The second important limiting case concerns scalar density matrices ${\gamma }_{\sigma }=n_{\sigma }\mathbb{1}$, where $n_{\sigma }=N_{\sigma }/N_a$ is the density of electrons with spin $\sigma$. Physically, this corresponds to fully localized electrons since ${\gamma }_{ij}=0$ for $i\ne j$. It is therefore easy to see that the smallest possible interaction energy of the Hubbard model corresponding to a $\mathit{k}$-independent occupation number distribution ${\eta }_{\mathit{k}\sigma }=n_{\sigma }$ is given by $W^{\infty }=U{D}^{\infty }$, where

$$D^{\infty }=\left\{\begin{array}{cc}0\hfill & \mathrm{if}N\le N_a,\hfill \\ N-N_a\hfill & \mathrm{if}N>N_a.\hfill \end{array}\right.$$

(54)

Scalar density matrices representing localized states are particularly relevant in the limit of strong electronic interactions or vanishing hopping integrals.

In this context, it is useful to consider the independent-fermion entropy (IFE)

$$S\left[{\eta }_{\mathit{k}\sigma }\right]=-\sum _{\mathit{k}\sigma }\left[{\eta }_{\mathit{k}\sigma }ln({\eta }_{\mathit{k}\sigma })+(1-{\eta }_{\mathit{k}\sigma })ln(1-{\eta }_{\mathit{k}\sigma })\right]$$

(55)

and its relation to the interaction-energy functional $W\left[{\eta }_{\mathit{k}\sigma }\right]$. $S\left[{\eta }_{\mathit{k}\sigma }\right]$ represents the entropy associated with an arbitrary occupation-number distribution ${\eta }_{\mathit{k}\sigma }$ of fermions, i.e., not necessarily one which matches a specific thermodynamic equilibrium situation [81]. It is interesting to note that at half-band filling $S\left[{\eta }_{\mathit{k}\sigma }\right]$ assumes its extreme values for the same occupation-number distributions ${\eta }_{\mathit{k}\sigma }$ as the interaction energy $W\left[{\eta }_{\mathit{k}\sigma }\right]$. For uncorrelated electrons, we have ${\eta }_{\mathit{k}\sigma }=0$ or 1 for all $\mathit{k}\sigma$ and $S\left[{\eta }_{\mathit{k}\sigma }\right]$ takes its minimum value $S=0$. For localized electrons we have ${\eta }_{\mathit{k}\sigma }=n_{\sigma }$ for all $\mathit{k}$ and thus the IFE assumes its maximal value under the constraint ${\sum }_{\mathit{k}}{\eta }_{\mathit{k}\sigma }/N_a=n_{\sigma }$ (see Equation (55)). If the band is half filled ($n_{\uparrow }+n_{\downarrow }=1$), the maximum value of the IFE reads

$$S^{\infty }=-2N_a[n_{\uparrow }ln(n_{\uparrow })+n_{\downarrow }ln(n_{\downarrow })].$$

(56)

The fact that $S\left[{\eta }_{\mathit{k}\sigma }\right]$ assumes its extremes for the distributions ${\eta }_{\mathit{k}\sigma }$ yielding the extremes of $W\left[{\eta }_{\mathit{k}\sigma }\right]$ suggests that $S\left[{\eta }_{\mathit{k}\sigma }\right]$ could be used as a measure of the degree of electronic correlations. From this perspective, the uncorrelated state with its well-defined natural-orbital occupations ${\eta }_{\mathit{k}\sigma }=0$ or 1 corresponds to a perfectly-ordered zero-entropy or zero-temperature situation. In contrast, the strongly correlated localized state in which all Bloch states are equally probable (${\eta }_{\mathit{k}\sigma }=1/2\forall \mathit{k}\sigma$) corresponds to a fully-disordered maximum-entropy or infinite-temperature situation. It is therefore most interesting to explore to what extent an entropy analogy holds for non-trivial many-body states, where the degree of correlations is not extreme. This would allow us to formulate approximations of $W\left[{\eta }_{\mathit{k}\sigma }\right]$ in terms of $S\left[{\eta }_{\mathit{k}\sigma }\right]$, thus avoiding the certainly more general, but also more difficult to grasp, full functional dependence on the occupation-number distribution ${\eta }_{\mathit{k}\sigma }$.

Exact Lanczos diagonalizations have been performed in [72] to quantify the relation between $W\left[{\eta }_{\mathit{k}\sigma }\right]$ and $S\left[{\eta }_{\mathit{k}\sigma }\right]$ in the half-filled Hubbard model. Different occupation-number distributions ${\eta }_{\mathit{k}\sigma }$, ranging from the weak to the strongly correlated limit, have been obtained by scaling the hopping integrals from $t_{ij}=0$ to $t_{ij}\gg U$. In this way, the complete range of $S\left[{\eta }_{\mathit{k}\sigma }\right]$ has been scanned ($0\le S\le S^{\infty }$). In Figure 5, the relation between the interaction energy $W\left[{\eta }_{\mathit{k}\sigma }\right]$ in the half-filled Hubbard model and the corresponding independent fermion entropy $S\left[{\eta }_{\mathit{k}\sigma }\right]$ is reproduced. Remarkably, one observes that $S\left[{\eta }_{\mathit{k}\sigma }\right]$ captures most of the functional dependence of W on ${\eta }_{\mathit{k}\sigma }$. The relation between W and S is almost independent of the specific size and structure of the systems considered in the exact diagonalizations. The deviations from the common nearly linear trend are always small (below 10%). It has been therefore proposed to approximate the interaction-energy functional of the half-filled Hubbard model by the simple linear relation [72],

$$W\left[{\eta }_{\mathit{k}\sigma }\right]=W^0\left(1-\frac{S\left[{\eta }_{\mathit{k}\sigma }\right]}{S^{\infty }}\right),$$

(57)

where $W^0=U{D}^0$ is the Hartree–Fock value of the interaction energy (see Equation (53)) and $S^{\infty }$ is the upper bound of the IFE given by Equation (56).

Substituting Equation (57) into Equation (51), it is easy to see that the minimization condition $\partial \mathcal{L}/\partial {\eta }_{\mathit{k}\sigma }=0$ for the Euler–Lagrange functional (52) leads to the Fermi–Dirac distribution

$${\eta }_{\mathit{k}\sigma }=\frac{1}{{\mathrm{e}}^{({\epsilon }_{\mathit{k}}-{\mu }_{\sigma })/\vartheta }+1}$$

(58)

for all $\mathit{k}\sigma$, where $\vartheta =U{D}^0/S^{\infty }$ plays the role of an effective temperature which depends on the Coulomb-interaction strength U. Furthermore, all approximations of the interaction-energy functional in terms of the IFE of the form $W=W(S\left[{\eta }_{\mathit{k}\sigma }\right])$ lead to the Fermi–Dirac distribution in Equation (58) of the ground-state occupation numbers ${\eta }_{\mathit{k}\sigma }$. In the general case of a nonlinear relation between W and S, the effective temperature is given by $\vartheta =-\mathrm{d}W/\mathrm{d}S$. This is a limitation since it precludes the IFE approximation to describe any discontinuous jump in ${\eta }_{\mathit{k}\sigma }$ as found, for example, at the Fermi energy of Fermi liquids. In the following, some representative applications of the linear IFE ansatz in Equation (57) are reviewed.

4.4. Application to the Half-Filled Hubbard Model

In Figure 6, the linear IFE-approximation in Equation (57) and exact Lanczos diagonalizations are compared in the case of the half-filled 4 × 4 2D square-lattice ($N_{\uparrow }=N_{\downarrow }=8$) [72]. First, one observes that the IFE approximation yields accurate values for the ground-state energy $E_0$ in the complete interaction range, from weak to strong correlations. Most notably, in the strongly correlated limit, the IFE approximation yields $E_0/N_a=-\alpha t^2/U$, which correctly reproduces the qualitative behavior of localized Heisenberg spins [82,83]. From the IFE approximation, one obtains $\alpha =5.55$, which is only 13% larger than the exact value $\alpha =4.81$ inferred from the Lanczos diagonalizations. It is also interesting to remark that not only the ground-state energy but also the separate contributions of the kinetic energy T and the Coulomb interaction $W=UD$ are reproduced with high accuracy for the most part. Only the double occupations D are significantly underestimated for $U/t<2$. This is a consequence of the degeneracy in the single-particle spectrum of the 4 × 4 finite lattice at the Fermi level ${\epsilon }_F=0$, which leads to fractional occupation numbers ${\eta }_{\mathit{k}\sigma }=1/2$ for $\mathit{k}$ vectors on the Fermi surface, even for $U/t=0$. As a result, one obtains $S>0$ for $U/t=0$. The IFE approximation in Equation (57) correctly predicts $D<D^0$ in this case. However, the actual correlation-induced reduction of D is underestimated for about 30%. Since this effect is a consequence of the degenerate single-particle spectrum, it must be ascribed to the finite size of the system. Therefore, it should not be relevant to infinite periodic lattices, for which the IFE approximation in Equation (57) yields the Hartree–Fock result $D=D^0$ for $U/t\to 0$.

In Figure 6b, the ground-state occupation numbers ${\eta }_{\mathit{k}\sigma }$ are shown as a function of $U/t$ for the different values of $\mathit{k}$. The accuracy of the IFE approximation is quite remarkable. In the non-interacting limit ($U/t=0$), the single-particle states below (above) the Fermi-level ${\epsilon }_F=0$ are occupied (empty), which corresponds to ${\eta }_{\mathit{k}\sigma }=1$ (${\eta }_{\mathit{k}\sigma }=0$). Precisely at ${\epsilon }_F$ we have ${\eta }_{\mathit{k}\sigma }=1/2$ due to the above-discussed finite-size degeneracy. As $U/t$ increases, the occupation numbers below (above) ${\epsilon }_F$ decrease (increase) until, in the strongly correlated limit ($U/t\to \infty$), all natural-orbital occupation numbers are equal and a localized state is reached. Once the ${\eta }_{\mathit{k}\sigma }$ are known, it is rather straightforward to obtain the ground-state SPDM ${\gamma }_{ij\sigma }$ in real space by means of a Fourier transformation. Müller et al. [72], showed that the IFE results for ${\gamma }_{0\delta \sigma }$ follow closely the exact ones. In particular, the transition from a bound state at $U/t=0$, which is characterized by strong interatomic hybridizations ${\gamma }_{01\sigma }$, to a localized state (${\gamma }_{ij\sigma }=0$ for $i\ne j$) is well reproduced.

The IFE approximation has also been applied to the half-filled Hubbard model on infinite hypercubic lattices by introducing an appropriate scaling of the NN hoppings as a function of the dimensionality d ($t_d=t/\sqrt{d}$) [72].

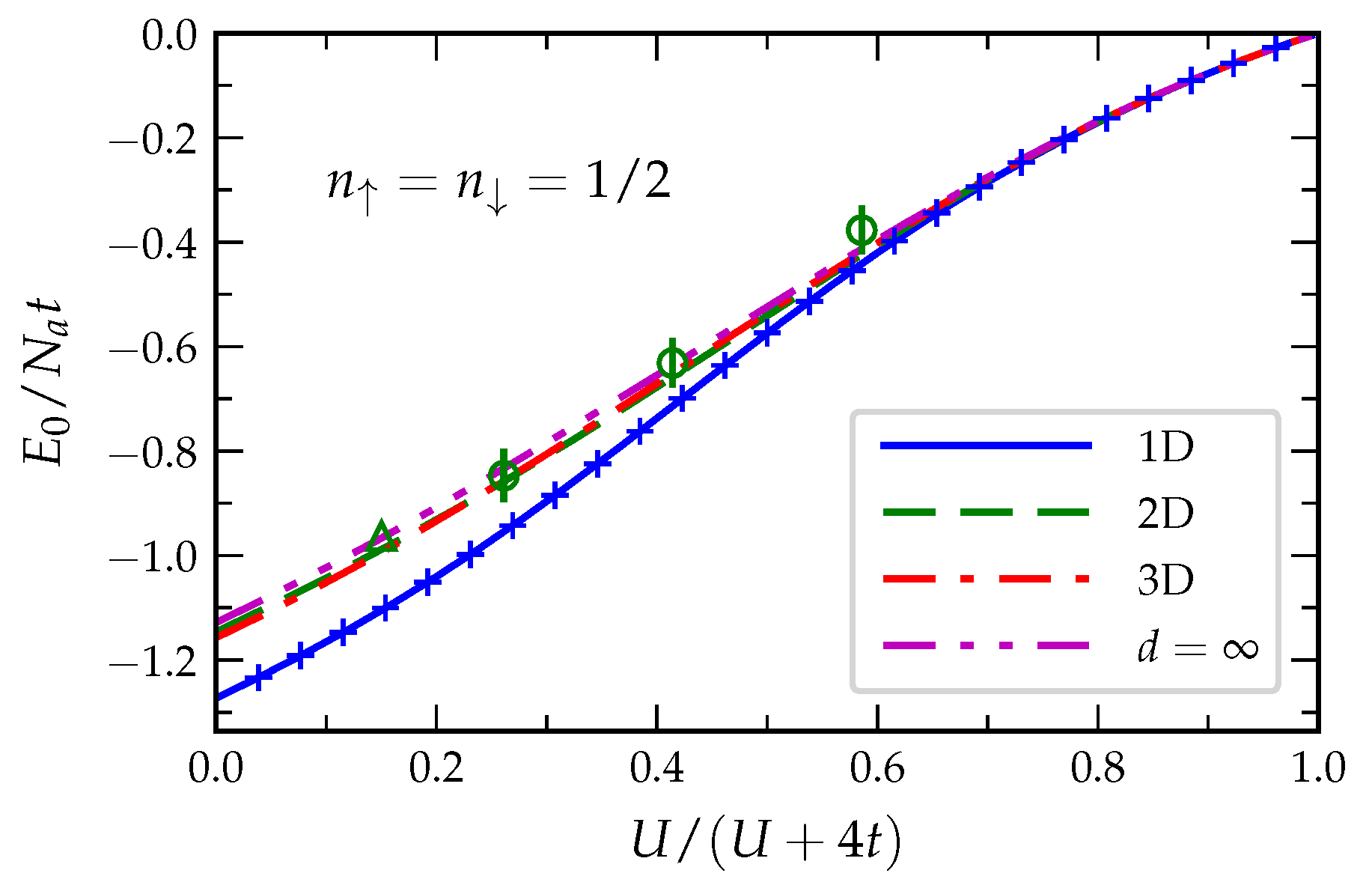
The ground-state energy $E_0$, the average number of double occupations D and the kinetic energy T of the half-filled Hubbard model have been determined in [72] for bipartite lattices in $d=1$–3 dimensions, as well as for the limit $d\to \infty$. The results for $E_0$ are reproduced in Figure 7. In the case of the 1D Hubbard model, the IFE approximation in Equation (57) is almost indistinguishable from the exact Bethe-ansatz solution [84]. The relative error $\Delta E=|E_0^{\mathrm{ex}}-E_0^{\mathrm{IFE}}|/|E_0^{\mathrm{ex}}|$ is smaller than 0.1% in the whole interaction range from weak to strong correlations [72]. Remarkably, the IFE approximation yields the exact result $E_0=-4N_{a}ln(2)t^2/U$ in the strongly-correlated Heisenberg limit. One can furthermore show that this very good accuracy is not the result of a compensation of errors since both the kinetic energy T and the average number of double occupations D are very accurately obtained. The largest relative error found for the double occupations is $\Delta D=0.18\%$ while for the kinetic energy the largest discrepancy is $\Delta T=0.12\%$.

The ground-state energy $E_0$ and the average number of double occupations D obtained with the IFE approximation for the 2D square lattice are in good agreement with available QMC simulations [85,86,87]. One observes, however, that the approximation tends to underestimate the double occupations slightly for weak interactions ($U/t\lesssim 4$) whereas D is slightly overestimated if the interactions are important ($U/t\gtrsim 4$). In the strongly correlated limit $E_0$ can be inferred quite accurately from the ground-state energy ${\epsilon }_{2\mathrm{DH}}$ of the spin-$\frac{1}{2}$ Heisenberg model. By using the Schrieffer–Wolff transformation [83], one obtains $E_0=-\alpha t^2/U$ with $\alpha =2-4{\epsilon }_{2\mathrm{DH}}$. QMC simulations [88] on the spin-$\frac{1}{2}$ Heisenberg model yield ${\epsilon }_{2\mathrm{DH}}=-0.669$ which implies ${\alpha }_{\mathrm{QMC}}=4.68$. As in the 1D case, the IFE approximation reproduces correctly the linear dependence of $E_0$ on $t^2/U$ although with a somewhat larger coefficient ${\alpha }_{\mathrm{IFE}}=8ln2\approx 5.55$. Thus, the binding energy for the strongly correlated 2D Hubbard model is overestimated by 18%.

The dependence of $E_0$, T and W on d shows a rapid convergence to the limit of infinite dimensions once the NN hopping is scaled as $t_d=t/\sqrt{d}$ in order that all the local DOSs have the same second moment $w_2=2d{t}_d^2=2t^2$. In other words, most of the dependence of $E_0$, T and W on the lattice dimension is concealed in the variance of the single-particle spectrum. Another result worth mentioning is that the IFE approximation yields $E_0=-Jdln2=-4dln(2)t_d^2/U$ in the strongly correlated limit. This becomes $E_0=-4ln(2)t^2/U$ for all d after the d-dependent scaling of the NN hopping integrals is taken into account ($U/t\gg 1$). This behavior contrasts with the outcome of QMC simulations and exact diagonalizations for low d, which show no such simple scaling relation between the ground-sate energies of the 1D and 2D Heisenberg models [88,89,90]. Further applications of the present reciprocal-space approach to LDFT including the frustrated triangular lattice and spin-polarized systems may be found in [72].

5. Conclusions

The study of strong electron-correlation effects in the framework of density-functional theory remains one of the most difficult current challenges in condensed matter physics. In this paper, we review some of the recent developments in the density-matrix functional theory of lattice models. Based on the general formulation of the many-body problem in terms of the single-particle density matrix $\gamma$, we introduce the total energy functional $E\left[\gamma \right]=T\left[\gamma \right]+W\left[\gamma \right]$, which can be naturally separated into the single-particle or kinetic-energy functional $T\left[\gamma \right]$ and the interaction-energy functional $W\left[\gamma \right]$. As in any density-functional approach, the main problem is to derive physically sound approximations to $T\left[\gamma \right]$ and $W\left[\gamma \right]$, which allow us to obtain accurate predictions of the electronic properties. Since an exact explicit expression for $T\left[\gamma \right]$ is available in the density-matrix approach, all the methodological developments are focused on assessing the elusive $W\left[\gamma \right]$.

Different complementary perspectives are discussed. One of them takes advantage of the local nature of the dominant strong interactions and of the short-range character of the interatomic hybridizations. The real-space density matrix ${\gamma }_{ij}$, where i and j refer to the lattice sites, is considered as the central variable of the many-body problem and the scaling properties of $W\left[\gamma \right]$ are exploited. Taking the inhomogeneous Hubbard model as representative example, it has been possible to demonstrate that the dependence of W on the nearest-neighbor bond order ${\gamma }_{12}$ is almost independent of the system size, dimensionality of the lattice, and band filling, once W is appropriately scaled within the domain of representability of $\gamma$. In this way, a simple approximation to W could be derived by extracting the functional dependence of W from the Hubbard dimer. This two-site problem plays the role of a reference system, pretty much as the homogeneous electron gas did in the early stages of DFT. From the perspective of lattice models, the Hubbard dimer already contains the fundamental interplay between electronic delocalization, charge transfer, and strong correlations. It is therefore particularly suited as reference system since it covers the whole interaction range and the explicit analytic expression of $W\left[\gamma \right]$ is available.

The studies of the Anderson model combine a local description of a magnetic impurity, where the electrons are subject to strong correlations, and a delocalized description of the conduction band states with which the impurity couples. In this case, one exploits the universality of $W\left[\gamma \right]$ within lattice density-functional theory (LDFT) and its invariance under unitary transformations among the single-particle orbitals. A symmetry-adapted conduction state can then be identified through which the dynamic charge fluctuations between the impurity orbital and the conduction band are channeled. This symmetry-adapted conduction state and the impurity orbital are central to the interaction-energy ansatz, which takes only these two single-particle states into account upon deriving the functional dependence of W. The two-level approximation to $W\left[\gamma \right]$ is thus derived, which can be shown to be exact in two important limits: a totally degenerate conduction band and a conduction band with widely separated discrete levels.

The third and final considered approach to LDFT is formulated from a reciprocal-space perspective and therefore applies only to periodic lattices. In this case, the density matrix is diagonal in the Bloch states and can be characterized by its eigenvalues or natural-orbital occupations ${\eta }_{\mathit{k}\sigma }$. Consequently, the interaction energy can be regarded as a functional $W\left[{\eta }_{\mathit{k}\sigma }\right]$ of the occupation-number distribution ${\eta }_{\mathit{k}\sigma }$. In the case of half-band filling, a very interesting correspondence has been identified between the degree of electron correlations and the independent-fermion entropy $S\left[{\eta }_{\mathit{k}\sigma }\right]$ associated to the orbital occupations ${\eta }_{\mathit{k}\sigma }$. The non-interacting case corresponds to a zero entropy state (occupation numbers equal to 0 or 1), whereas the strongly-correlated limit corresponds to a maximum entropy state (all orbital occupations equal to $1/2$). Guided by this observation, an approximate linear relation between $W\left[{\eta }_{\mathit{k}\sigma }\right]$ and $S\left[{\eta }_{\mathit{k}\sigma }\right]$ is revealed which could then be successfully exploited to obtain a simple, explicit and broadly applicable lattice-density-functional ansatz.

The ability of LDFT to describe the physics of electron correlations has been successfully tested by taking the Anderson and Hubbard models as representative examples and by comparing its predictions with analytical solutions, numerical diagonalizations and quantum Monte Carlo simulations. Accurate results for the most important ground-state properties have been obtained in the complete range of model parameters, from weak to strong correlations. In particular, the comparison of the kinetic, interaction, and total energies, the charge distribution, the degree of charge fluctuations, and the local magnetic moments with far more involved numerical methodologies has been quite satisfactory. One concludes that LDFT with an appropriate interaction-energy functional provides a most appealing and promising theoretical perspective to the subtle problem of strong electron correlations in narrow bands.

Finally, to identify the most interesting directions of future methodological developments and applications, it is useful to point out briefly some of the main goals and limitations of density-functional approaches to many-body lattice models. From a fundamental perspective, density-functional theory is extremely appealing because of the remarkable simplification and new perspective to many-electron problems that it represents. However, some electron-correlation phenomena remain difficult to grasp in the DFT framework. For example, the separation of charge and spin degrees of freedom and the Heisenberg spin-coupling limit, which appears when atoms are pulled far apart and their hybridizations tend to vanish, is certainly difficult to grasp in terms of the electronic density $\rho (\mathit{r})$. This behavior appears quite naturally when the concepts of DFT are applied to lattice models or when a minimal valence-electron basis is chosen, as it has been clearly demonstrated in several examples in the previous sections. Besides these new perspectives and conceptual merits of LDFT, the density-matrix functional theory of lattice models provides a number of practical advantages. The first and most obvious one is the simplicity of the practical calculations. Once an explicit approximation to the interaction energy $W\left[\gamma \right]$ is available, performing the actual minimization of energy functional $E\left[\gamma \right]$ in the domain of ensemble representable $\gamma$s can be done in a rather straightforward and numerically reliable way for practically any lattice structure or system size. From this perspective, the LDFT approach should be contrasted with the complexity of implementation and high numerical demands of any of the alternatives such as the density-matrix renormalization group (DMRG) method for 1D systems [91,92], quantum Monte Carlo (QMC) methods [85,86,87], and exact diagonalization (ED) methods [14,79].

However, of course, LDFT has the unmissable downside that obtaining reliable generally applicable approximations to $W\left[\gamma \right]$ is far from obvious. However, we show in this review that very often simple effective approximations can be obtained by performing interpolations between known results in the weakly and strongly correlated limits, by using a simple reference system which captures the essential interplay between electron delocalization and Coulomb repulsion, or by exploiting statistical analogies. The simplicity of the above-discussed approximations to $W\left[\gamma \right]$ and their remarkable success might remind us of the simplicity and success of the early local density approximation, which can be justified by simple sum rules. However, as for the LDA, the thus far derived functionals in LDFT are nearly impossible to improve systematically and in a controlled way. From this perspective, LDFT cannot compete with the above-mentioned explicitly correlated methods (DMRG, QMC and ED, for example). In LDFT, we may well verify a posteriori the quality of a given approximation, when exact or highly precise results are available, but is it impossible to predict their accuracy or control the error a priori. An interesting perspective of future systematic accuracy improvements in LDFT would be to extend the set of single-particle states involved in the derivation of $W\left[\gamma \right]$, for example, by adding further conduction-band states to the two-level system considered for the Anderson model, or by performing a local cluster expansion in the context of the Hubbard model. In this way, more realistic multiband models could also be addressed, eventually leading to a link with first-principles methodologies. It is our hope that the theory, specific approximations and new physical insights discussed in this review could serve as a starting point for such future developments.