A Novel Method for Pressure Mapping between Shell Meshes of Varying Geometries and Resolutions †
Abstract
:1. Introduction
2. Set-Up
- Find the centroid of the triangle element, and in the case of an element being a quad, the triangle that forms half of the quad element surface
- –
- If a quad, then the first three node elements are used to calculate the area. Afterwards, the process is repeated with the first, second, and fourth node. Regardless of the node order, this should create two triangles that form the quad.
- –
- The centroid coordinates are found by simply averaging the X, Y, and Z locations of the three nodes that made up the surface triangle.
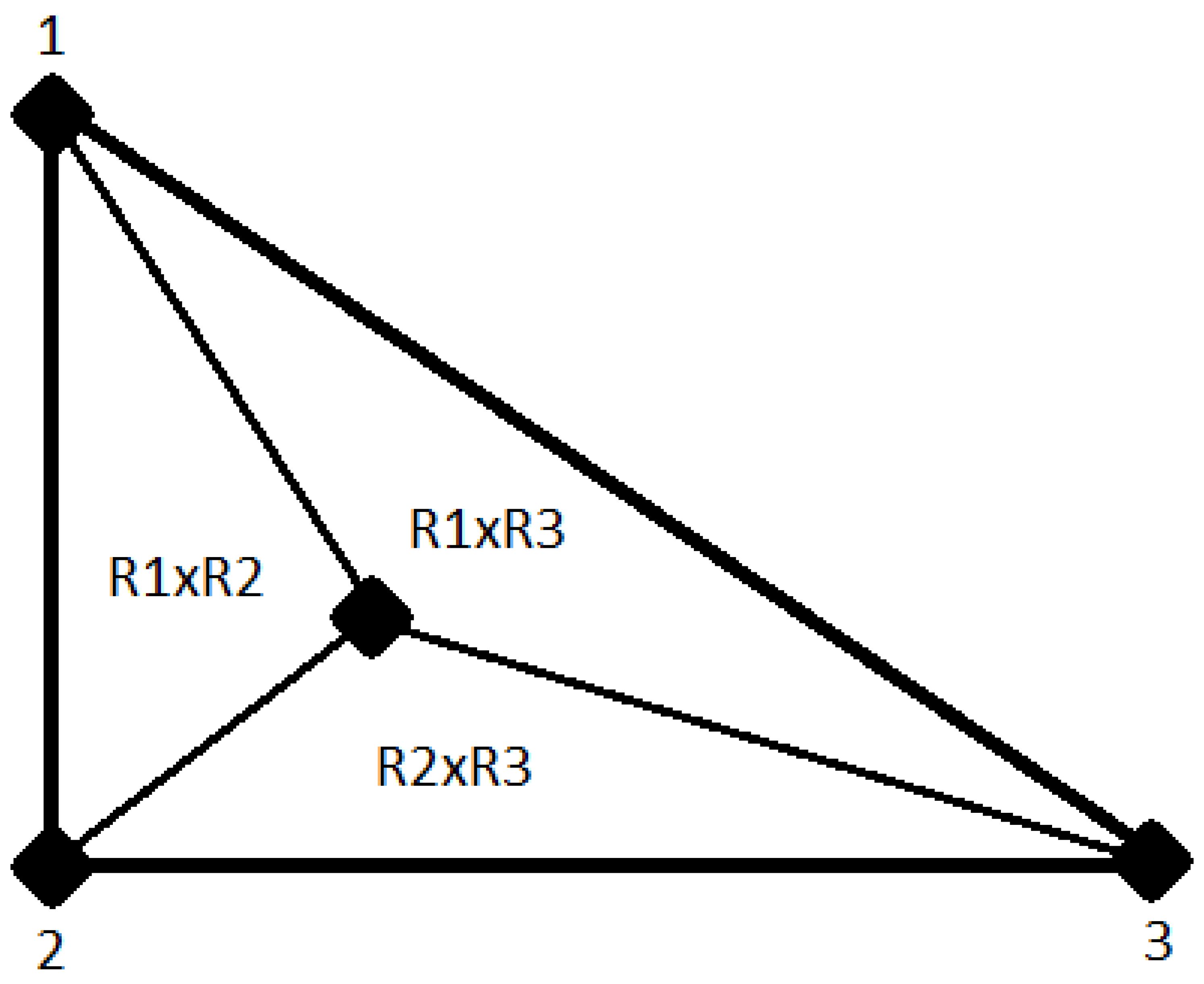
- Generate the vectors from each node to the centroid.
- Find the area formed by each of the three pairs of vectors three times.
- –
- , , and , where , , and represent the vector formed in between the centroid and node 1, 2, and 3, respectively.
- –
- The area is calculated as half of the absolute value of the cross product of the two vectors, to form each smaller trianglewhere and are vectors of components A, B, and C.
- The areas of these three small triangles is added up to determine the area of the larger triangle (Figure 1)
- If the element surface is a quad, this process is performed twice, treating the quad as two triangles
- –
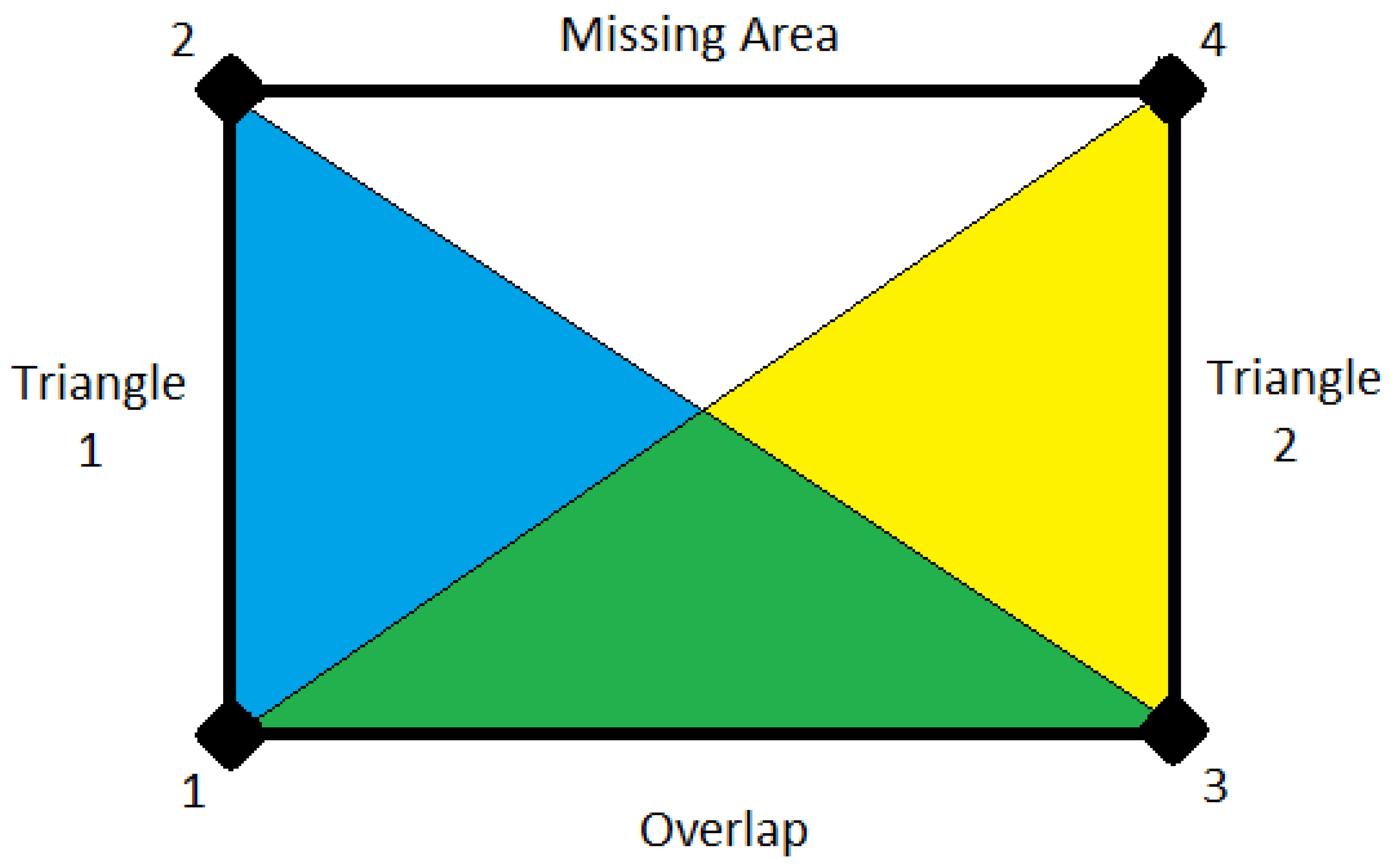
- Different software packages use different node patterns. If the wrong pattern is used, the area could be erroneously calculated (Figure 2),
- –
- It is not an option to find the node the greatest distance away, as an oddly shaped element would give an erroneous calculation (Figure 3),
- –
- The areas of all three combinations of two possible triangles are calculated (Table 1),
- –
- The maximum of these three possible areas is selected as the area of the quad of interest.
3. Algorithm
- Sorting through the array of for each source element,
- Adding to the target number found, the location in a array,
- –
- That source element, the source element number, and the pressure magnitude data .
- Incrementing the count of sources proximate to a given target
- –
- Stored in a separate integer vector (),
- –
- Used to track how many source elements are proximate to the given target element,
- –
- Can be expected to exceed provided the number of source elements is greater than the number of target elements,
- –
- Should never exceed ; if this happens, it is necessary to increase the value of to avoid memory errors,
- Save the transfer matrix.
- Number of elements
- –
- This number is saved so a future mapping algorithm knows the number of target pressures to generate,
- For times, list the specific target and the following information,
- –
- Target number, Number of Sources Proximate, and Sum of Pressure Impacts
- –
- The reason for the sum of is because each individual value of is normalized by the cumulative sum of for all proximate targets, so that the pressure of the target element is a proportional average of these proximate source elements.
- For each target, for the number of proximate source elements,
- –
- Sequential number, source element number, and pressure impact
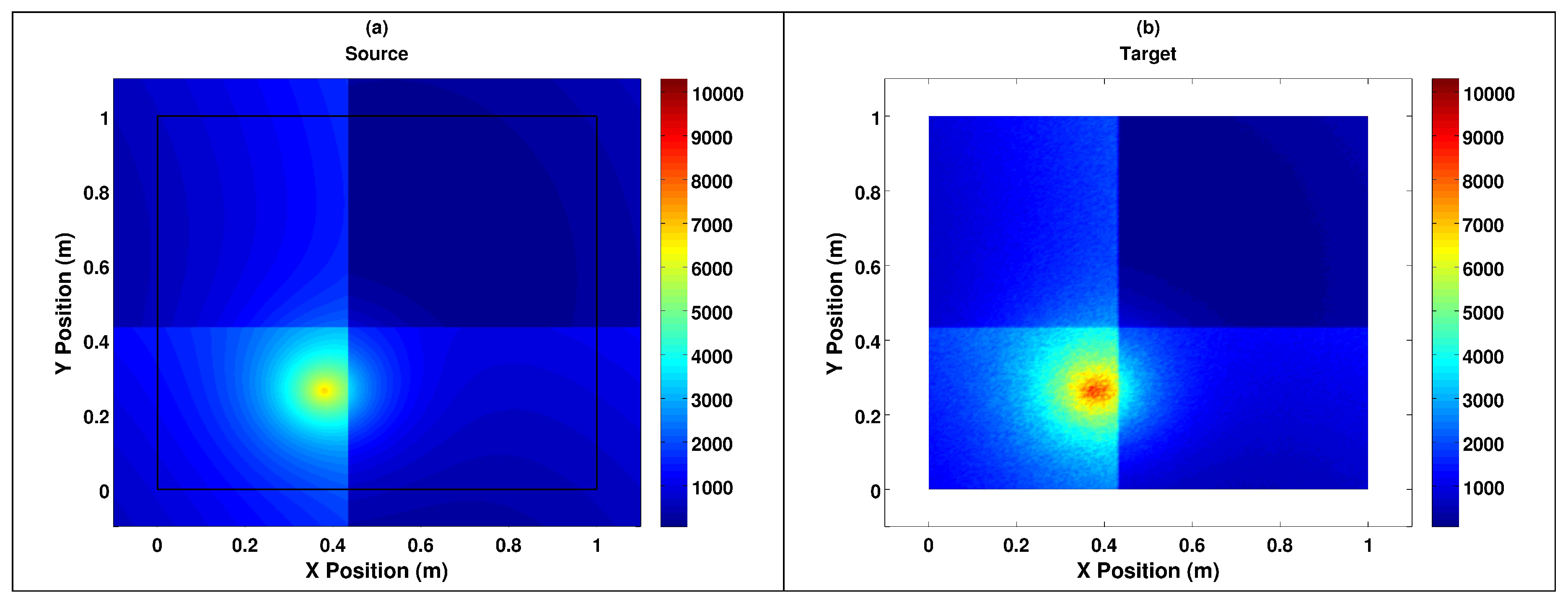
4. Test Example
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ALE | Arbitrary-Lagrangian-Eulerian |
| FSI | Fluid Solid Interactions |
| CFD | Computational Fluid Dynamics |
| CSD | Computational Solid Dynamics |
| FEA | Finite Element Analysis |
| ANSYS | Analysis Systems, Inc. |
| NAVAIR | Naval Air Systems Command |
Appendix A. Sample Code
Appendix A.1. Introduction
Appendix A.2. Generating the Input Files
Appendix A.3. Generating the Transfer Matrix
- Nx = 5: This is the maximum number of targets that can be considered proximate to a given source. Matrix arrays of will be generated, so it must be small enough that the script does not exceed the memory resources of the computer. Even if there is a lot of memory, unless the target elements are smaller than the source (definitely possible but often not the case in practice), then it should not be desirable for Nx to be greater than a few, as one would not want the source element to be mapped onto elements a significant distance away.
- Nx2 = 500: This is the maximum number of sources that can be considered proximate to a given target and used in the transfer matrix. Matrix arrays of will be generated, so it must be small enough that the script does not exceed the memory resources of the computer, but also large enough to contain every source matrix considered proximate to a given target; in practice, having a value of Nx2 that is 100 times greater than Nx was found to work well.
- MinW0 = 0.0000000001: This is the minimum value of W that is necessary for a target particle to be considered proximate to a source. This value can be set to zero, but the computational time will be dramatically increased, and there is a risk that source elements that do not in fact overlap a target can be used for the final pressure. If a minimum value is set, then target elements that do not have any proximate source elements will not be mapped, resulting in a consistent pressure of zero. Different circumstances may prefer or oppose this possibility. This value of was used in the example in the manuscript.
- hcoef = 1.0: This is a coefficient to calculate the weighting function between a source and target element centroid as a function of distance apart. The smoothing length is proportional to this arbitrary value times the square root of the average area of all of the target elements. The larger hcoef is, the more likely a source element fully separated from a target element will influence the pressure, and the less likely a target element will turn out to not be mapped.
- ct1 = 1: This value is not used in the mapping, only in the generation of the final target pressure output files. This fifth line is the number of the first of the input pressures, and should be 1 unless modified by the user.
- ct2 = 180: This value is not used in the mapping, only in the generation of the final target pressure output files. This sixth line is the number of inputs, and should be 180 to capture all 180 input pressures unless modified by the user.
Appendix A.4. Generating New Pressures
Appendix A.5. Post-Processing
References
- Haberman, R. Applied Partial Differential Equations with Fourier Series and Boundary Value Problems, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Nagel, R.K.; Saff, E.B.; Snider, A.D. Fundamentals of Differential Equations, 5th ed.; Addison Wesley: Boston, MA, USA, 1999. [Google Scholar]
- Garcia, A. Numerical Methods for Physics, 2nd ed.; Addison-Wesley: Boston, MA, USA, 1999. [Google Scholar]
- White, F. Fluid Mechanics, 5th ed.; McGraw-Hill: Boston, MA, USA, 2003. [Google Scholar]
- Cengel, Y. Heat Transfer, a Practical Approach, 2nd ed.; Mcgraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Banerjee, D.K. Software Independent Data Mapping Tool for Structural Fire Analysis. NIST Tech. Note 2014, 1828, 1–45. [Google Scholar]
- Smith, W.G.; Ebert, M.P. A Method for Unstructured Mesh-to-Mesh Interpolation; Hydromechanics Department Report; NSWCCD-50-TR-2010; Naval Surface Warfare Center Carderock Division: Bethesda, MD, USA, 2010; p. 056. [Google Scholar]
- Tang, T. Moving Mesh Methods for Computational Fluid Dynamics. Contemp. Math. 2005, 383. [Google Scholar] [CrossRef]
- Budd, C.J.; Huang, W.; Russell, R.D. Adaptivity with Moving Grids. Acta Numer. 2009, 18, 111–241. [Google Scholar] [CrossRef]
- Gao, Q.; Zhang, S. Moving Mesh Strategies of Adaptive Methods for Solving Nonlinear Partial Differential Equations. Algorithms 2016, 9, 86. [Google Scholar] [CrossRef]
- Budd, C.J.; Williams, J.F. Moving Mesh Generation Using the Parabolic Monge–Ampere Equation. SIAM J. Sci. Comput. 2009, 31, 3438–3465. [Google Scholar] [CrossRef]
- Wang, W.; Yan, Y. Strongly coupling of partitioned fluid-solid interaction solvers using reduced-order models. Appl. Math. Model. 2010, 34, 3817–3830. [Google Scholar] [CrossRef]
- Basting, S.; Quaini, A.; Canic, S.; Glowinski, R. Extended ALE Method for fluid-structure interaction problems with large structural displacements. J. Comput. Phys. 2017, 331, 312–336. [Google Scholar] [CrossRef]
- Farhat, C.; van der Zee, K.G.; Geuzaine, P. Provably second-order time-accurate loosely-coupled solution algorithms for transient nonlinear computational aeroelasticity. Comput. Methods Appl. Mech. Eng. 2006, 195, 1973–2001. [Google Scholar] [CrossRef]
- Degroote, J.; Haelterman, R.; Annerel, S.; Bruggeman, P.; Vierendeels, J. Performance of partitioned procedures in fluid-structure interaction. Comput. Struct. 2010, 88, 446–457. [Google Scholar] [CrossRef]
- Wick, T. Fluid-structure interactions using different mesh motion techniques. Comput. Struct. 2011, 89, 1456–1467. [Google Scholar] [CrossRef]
- Amsallam, D.; Farhat, C. An Online Method for Interpolating Linear Parametric Reduced–Order Models. SIAM J. Sci. Comput. 2011, 33, 2169–2198. [Google Scholar] [CrossRef]
- Amsallem, D.; Zahr, M.; Choi, Y.; Farhat, C. Design optimization using hyper-reduced-order models. Struct. Multidiscip. Optim. 2015, 51, 919–940. [Google Scholar] [CrossRef]
- Assessment of Computational Fluid Dynamics (CFD) for Nuclear Reactor Safety Problems; NEA/CSNI/R(2007)13 OECD Nuclear Energy Agency: Le Seine Saint–Germain—12, boulevard des Illesm F-92130 Issy-les-Moulineaux, France, January 2008. Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:44037880 (accessed on 11 June 2019).
- Lee, Y.; Gwak, M.C.; Cho, H.; Joo, H.S.; Shin, S.J.; Yo, J.J.; Shin, J.C. Numerical Simulation of Fluid Structure Interaction Problem Associated with Vertical Launching System. J. Spacecr. Rockets 2018, 55, 948–958. [Google Scholar] [CrossRef]
- Cirak, F.; Radovitzky, R. A Lagrangian Eulerian shell fluid coupling algorithm based on level sets. Comput. Struct. 2005, 83, 491–498. [Google Scholar] [CrossRef]
- Tremel, U.; Sorensen, K.A.; Hitzel, S.; Rieger, H.; Hassan, O.; Weatherill, N.P. Parallel remeshing of unstructured volume grids for CFD applications. Int. J. Numer. Methods Fluids 2007, 53, 1361–1379. [Google Scholar] [CrossRef]
- You, Y.H.; Na, D.; Jung, S.N. Data Transfer Schemes in Rotorcraft Fluid–Structure Interaction Predictions. Hindawi Int. J. Aerosp. Eng. 2018, 2018, 3426237. [Google Scholar] [CrossRef]
- Samareh, J.A. Discrete Data Transfer Technique for Fluid–Structure Interaction. In Proceedings of the 18th American Institute of Aeronautics and Astronautics Computational Fluids Dynamics Conference, Miami, FL, USA, 25–28 June 2007. Session: CFD–17: Fluid–Structure Interaction. [Google Scholar] [CrossRef]
- Guruswamy, G.P. A review of numerical fluids/structures interface methods for computations using high-fidelity equations. Comput. Struct. 2002, 80, 31–41. [Google Scholar] [CrossRef]


| Quad Area | Node (First Triangle) | Node (Second Triangle) |
|---|---|---|
| Area 1 | Node 1, 2, 3 | Node 1, 2, 4 |
| Area 2 | Node 1, 3, 2 | Node 1, 3, 4 |
| Area 3 | Node 1, 4, 2 | Node 1, 4, 3 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marko, M.D. A Novel Method for Pressure Mapping between Shell Meshes of Varying Geometries and Resolutions. Computation 2019, 7, 29. https://doi.org/10.3390/computation7020029
Marko MD. A Novel Method for Pressure Mapping between Shell Meshes of Varying Geometries and Resolutions. Computation. 2019; 7(2):29. https://doi.org/10.3390/computation7020029
Chicago/Turabian StyleMarko, Matthew David. 2019. "A Novel Method for Pressure Mapping between Shell Meshes of Varying Geometries and Resolutions" Computation 7, no. 2: 29. https://doi.org/10.3390/computation7020029
APA StyleMarko, M. D. (2019). A Novel Method for Pressure Mapping between Shell Meshes of Varying Geometries and Resolutions. Computation, 7(2), 29. https://doi.org/10.3390/computation7020029




