Numerical Solution of Fractional Diffusion Wave Equation and Fractional Klein–Gordon Equation via Two-Dimensional Genocchi Polynomials with a Ritz–Galerkin Method

Abstract

In this paper, two-dimensional Genocchi polynomials and the Ritz–Galerkin method were developed to investigate the Fractional Diffusion Wave Equation (FDWE) and the Fractional Klein–Gordon Equation (FKGE). A satisfier function that satisfies all the initial and boundary conditions was used. A linear system of algebraic equations was obtained for the considered equation with the help of two-dimensional Genocchi polynomials along with the Ritz–Galerkin method. The FDWE and FKGE, including the nonlinear case, were reduced to solve the linear system of the algebraic equation. Hence, the proposed method was able to greatly reduce the complexity of the problems and provide an accurate solution. The effectiveness of the proposed technique is demonstrated through several examples.

1. Introduction

This paper emphasises on solving two types of fractional partial differential equations, namely Fractional Diffusion Wave Equation (FDWE) and Fractional Klein–Gordon Equation (FKGE). The Fractional Diffusion Wave Equation (FDWE) is as follows:

$$\begin{array}{c}\frac{{\partial }^{\alpha }u(x,t)}{\partial t^{\alpha }}+\frac{\partial u(x,t)}{\partial t}=\frac{{\partial }^{2}u(x,t)}{\partial t^2}+A(x,t),\hfill \\ 0<x<L,0<t<T,\hfill \end{array}$$

(1)

with the initial conditions

$$u(x,0)=f_0\left(x\right),\frac{\partial u(x,0)}{\partial t}=f_1\left(x\right),0\le x\le L,$$

(2)

and the boundary conditions are

$$u(0,t)=g_0\left(t\right),u(L,t)=g_1\left(t\right),0\le t\le T,$$

(3)

where $T>0,L>0$ and $1<\alpha \le 2$ are the fractional order Caputo sense derivative. $f_0,f_1,g_0$ and $g_1$ are given and represent sufficiently smooth functions, whereas u is unknown and needs to be determined.

In a more general setting, FDWE can be extended to become the Fractional Klein–Gordon Equation, (FKGE) is defined as follows:

$$\begin{array}{c}\hfill {\kappa }^{\alpha -1}\frac{{\partial }^{\alpha }u(x,t)}{\partial t^{\alpha }}+\sigma \frac{\partial u(x,t)}{\partial t}+\lambda u(x,t)=\frac{{\partial }^{2}u(x,t)}{\partial t^2}+{\kappa }^{\alpha -1}B(x,t),(x,t)\in [0,L]\times [0,T],\end{array}$$

(4)

with the initial conditions

$$u(x,0)={\theta }_0\left(x\right),\frac{\partial u(x,0)}{\partial t}={\theta }_1\left(x\right),0\le x\le L,$$

(5)

and the boundary conditions are

$$u(0,t)={\vartheta }_0\left(t\right),u(L,t)={\vartheta }_1\left(t\right),0\le t\le T,$$

(6)

where $1<\alpha \le 2$ is the fractional order Caputo sense derivative. For the linear time-fractional Klein–Gordon equation, we set the Equation (4) as $\kappa =1$, $\sigma =0$, $\lambda =1$, where the FKGE is reduced to FDWE. Meanwhile, ${\theta }_0$, ${\theta }_1$, ${\vartheta }_0$ and ${\vartheta }_1$ are given and represent the sufficiently smooth functions, whereas u is unknown and needs to be determined. The FKGE in Equation (4) can also be extended to nonlinear FKGE if there are nonlinear terms such as ${\left(u(x,t)\right)}^{\beta }$ involved in the equation.

These two equations are very important and widely used in many applications. The diffusion wave equations have been extensively used in some important physical phenomena such as percolation clusters, amorphous, colloid, glassy and porous materials through fractals, dielectrics, semiconductors, polymers and biological systems [1]. Moreover, the variety of physical phenomena such as ferroelectric and ferromagnetic domain walls, dislocations and Josephson junctions and DNA dynamics can be described well by the Klein–Gordon partial differential equation [2].

In this research direction, some researchers have investigated and proposed a few methods for the solution of FDWE. Ref. [3] had proposed the spectral tau method based on the Jacobi operational matrix to solve the FDWE. Ref. [4] applied Legendre wavelets via the operational matrix of integration for the solution of the FDWE while [5] also solved the FDWE by using a meshless local radial point interpolation scheme based on Galerkin weak form. Furthermore, the spectral collocation method for the time-fractional diffusion-wave equation was developed by [6]. Moreover, second order finite difference schemes were recommended for the solution of the time-fractional diffusion wave equation in [7]. A finite difference scheme based on cubic trigonometric B splines was derived by [8] to solve the FDWE.

In contrast, in [9], fractional reduced differential transform method was applied to solve time-fractional order linear and nonlinear Klein–Gordon equations. A high-order difference scheme was used by [10] to solve fractional partial differential equations including the linear time-fractional Klein–Gordon equation. Recently, the modified trial equation method had been applied to obtain the solution for some nonlinear fractional differential equations which include FKGE [11].

On the other hand, the Ritz–Galerkin method has been receiving more and more attention by researchers in the field of numerical analysis and computational science. The Ritz–Galerkin method is used to transform a problem from a continuous state to a discrete state. Additionally, in the context of this research, a suitable satisfier function was used together with the Ritz–Galerkin method as discussed in [12,13]. In the Ritz–Galerkin method, the implementation of an appropriate satisfier function is useful to reduce computational time and to obtain a system of algebraic equations of a smaller size. Recently, Ref. [14,15] had successfully incorporated the Ritz–Galerkin method with Bernoulli polynomials and Bernoulli wavelets to solve a number of fractional calculus problems. Since the results were encouraging, we hope to apply this method to Genocchi polynomials. Some of the applications using Genocchi polynomials to solve differential equation problems are shown in [16], and also [17,18,19]. This proposed method is able to reduce the FDWE and FGKE to only solve the linear system of algebraic equations. Hence, the proposed method greatly reduces the complexity of the problems and provides accurate solutions at the same time. In short, this paper comprises the use of two-dimensional Genocchi polynomials along with the Ritz–Galerkin method and a satisfier function to provide the approximate solutions of FKGE and FDWE. We also compared our results with existing numerical methods. The comparison of the numerical examples shows that our scheme is more accurate and less computational compared to other published methods. More specifically, we show that our new scheme is able to solve nonlinear cases, whereas existing similar methods as in [14,15] are only limited to linear cases.

The outline of the present paper is given as follows. Some basic concepts for fractional calculus are mentioned in Section 2. Section 3 comprises of some definitions and properties of Genocchi polynomials and function approximation for Genocchi polynomials. Section 4 discusses the Ritz–Galerkin method in relation to two-dimensional Genocchi polynomials and the satisfier function. The error bound is given in Section 5 while several numerical experiments are included in Section 6. Section 7 provides the conclusions of the paper.

2. Basic Concept for Fractional Calculus

In this section, some necessary and basic definitions of fractional calculus are mentioned below: the fractional derivative in Caputo’s sense is defined as in [20]:

$$\begin{array}{c}\hfill D_t^{\alpha }f\left(t\right)=\left\{\begin{array}{c}\frac{1}{\Gamma (n-\alpha )}{\int }_0^t\frac{f^n\left(\tau \right)}{{(t-\tau )}^{\alpha -n+1}}d\tau ,n-1<\alpha <n,\mathbb{N},\hfill \\ \frac{d^n}{d{t}^n}f\left(t\right),n=\alpha ,\hfill \end{array}\right.\end{array}$$

(7)

where $\alpha >0$ and n is the smallest integer greater than $\alpha .$ In addition, we have the following for Caputo’s derivative

$$\begin{array}{cc}\hfill D^{\alpha }{t}^{\eta }& =\left\{\begin{array}{c}\frac{\Gamma (\eta +1)}{\Gamma (\eta +1-\alpha )}{t}^{\eta -\alpha },\eta \in {\mathbb{N}}_0,\eta \ge \lceil \alpha \rceil \hfill \\ 0,\eta \in {\mathbb{N}}_0,\eta <\lceil \alpha \rceil ,\hfill \end{array}\right.\hfill \\ \hfill D^{\alpha }c& =0,c\in \mathbb{R}.\hfill \end{array}$$

(8)

Some properties of fractional derivative in Caputo’s sense are

$$\begin{array}{cc}\hfill D^{\alpha }(\lambda f\left(t\right)+\mu g\left(t\right))& =\lambda D^{\alpha }f\left(t\right)+\mu D^{\alpha }g\left(t\right),\hfill \\ \hfill \frac{d^n}{d{t}^n}\left[\varnothing \left(t\right)f\left(t\right)\right]& =\sum _{k=0}^n{\varnothing }^k\left(t\right)f^{n-k}\left(t\right),\hfill \\ \hfill I^{\alpha }{D}_t^{\alpha }f\left(t\right)& =f\left(t\right)-\sum _{k=0}^{m-1}\frac{f^{\left(k\right)}\left(0^{+}\right)}{k!}{t}^k,t>0.\hfill \end{array}$$

(9)

3. Genocchi Polynomials and Function Approximation

3.1. Definition and Properties of Genocchi Polynomials

The exponential generating function for Genocchi numbers in the complex plane has been given as

$$\frac{2t}{e^t+1}=e^{Gt}=\sum _{r=0}^{\infty }{G}_r\frac{t^r}{r!},(\left|t\right|<\pi ).$$

(10)

The formula for Genocchi polynomials can be obtained when we multiply the left-hand side of Equation (10) by $e^{xt}$,

$$\frac{2t{e}^{xt}}{e^t+1}=\sum _{r=0}^{\infty }{G}_r\left(x\right)\frac{t^r}{r!},(\left|t\right|<\pi ),$$

(11)

where $G_r\left(x\right)$ is the Genocchi polynomial of degree r. In the special case when $x=0$, we define $G_r\left(0\right)=G_r,r\ge 0$ and $G_{2r+1}=0,r\ge 1$ are called the Genocchi numbers. We have the following expression for Genocchi polynomials:

$$G_r\left(x\right)=\sum _{i=0}^r\left(\begin{array}{c}r\\ i\end{array}\right)G_{r-i}{x}^i=2B_r\left(x\right)-2^{r+1}{B}_r\left(x\right),$$

(12)

where $G_i=2B_i-2^{i+1}{B}_i$ is the Genocchi number, $B_r$ and $B_r\left(x\right)$ are the Bernoulli numbers and Bernoulli polynomials respectively. The first few Genocchi numbers are, $G_1=1,G_2=-1,$$G_3=0,G_4=1,G_5=0.$ Some of the Genocchi polynomials are:

$$\begin{array}{cc}\hfill G_1\left(x\right)& =1,\hfill \\ \hfill G_2\left(x\right)& =2x-1,\hfill \\ \hfill G_3\left(x\right)& =3x^2-3x,\hfill \\ \hfill G_4\left(x\right)& =4x^3-6x^2+1,\hfill \\ \hfill G_5\left(x\right)& =5x^4-10x^3+5x.\hfill \end{array}$$

(13)

Some important properties of Genocchi polynomials are stated below:

$$\begin{array}{cc}\hfill {\int }_0^1{G}_r\left(x\right)G_u\left(x\right)dx& =\frac{2{(-1)}^{r}r!u!}{(u+r)!}{G}_{u+r},r,u\ge 1,\hfill \\ \hfill \frac{d}{dx}{G}_r\left(x\right)& =r{G}_{r-1}\left(x\right),r\ge 1,\hfill \\ \hfill G_r\left(1\right)+G_r\left(0\right)& =0,r>1.\hfill \end{array}$$

(14)

3.2. Function Approximation of Genocchi Polynomials

The two-dimensional Genocchi polynomials are defined as a product function of two Genocchi polynomials

$$G_{pq}(x,t)=G_p\left(t\right)G_q\left(x\right),$$

(15)

$$p=1,2,\cdots ,M,q=1,2,\cdots ,M.$$

The expansion of any function $\upsilon (x,t)$ defined over the interval $[0,1]\times [0,1]$ in terms of Genocchi polynomials, can be written as

$$u(x,t)=\sum _{p=1}^{\infty }\sum _{q=1}^{\infty }{K}_{ab}{G}_p\left(t\right)G_q\left(x\right).$$

(16)

If the infinite series in Equation (16) is truncated, then it could be written as:

$$u(x,t)\approx \sum _{p=1}^i\sum _{q=1}^i{K}_{pq}{G}_p\left(t\right)G_q\left(x\right).$$

(17)

Equation (17) can be written in vector notation as

$$u(x,t)={\mathit{G}}^T\left(t\right){\mathit{K}}_{\mathit{M}\times \mathit{M}}\mathit{G}\left(x\right).$$

(18)

The Genocchi coefficient matrix $\mathit{K}$ which consists of the unique coefficients $k_{pq}$ as follows:

$${\mathit{K}}^T={\mathit{A}\left(t\right)}^{-\mathbf{1}}{\mathcal{H}}^{\mathit{T}}{\mathit{A}\left(x\right)}^{-\mathbf{1}},$$

(19)

where

$$\begin{array}{cc}\hfill \mathcal{H}& ={\int }_{\mathbf{0}}^{\mathbf{1}}{\int }_{\mathbf{0}}^{\mathbf{1}}\upsilon (x,t)G_p\left(t\right)G_q\left(x\right)dxdt,\hfill \\ \hfill \mathit{A}\left(x\right)& ={\int }_{\mathbf{0}}^{\mathbf{1}}{G}_p\left(x\right)G_{p^{\prime }}\left(x\right)dx,\hfill \\ \hfill \mathit{A}\left(t\right)& ={\int }_{\mathbf{0}}^{\mathbf{1}}{G}_q\left(t\right)G_{q^{\prime }}\left(t\right)dt.\hfill \end{array}$$

(20)

4. Ritz–Galerkin Method with the Two-Dimensional Genocchi Polynomials Basis

4.1. Ritz–Galerkin Method

If the FDWE and FKGE as shown in Equations (1) and (4) are written as follows :

$$L\left[v\right(x,t\left)\right]+f(x,t)=0$$

(21)

over the interval $i\le x,t\le j.$

Any arbitrary weight function $\sigma (x,t)$ would be multiplied with Equation (21). We can get the following relation after integrating over the interval $[i,j]$

$${\int }_i^j{\int }_i^j\sigma (x,t)(L\left[v(x,t)\right]+f(x,t))dxdt=0.$$

(22)

Due to the arbitrary weight function, Equations (21) and (22) are equivalent.

Let the trial solution for Equation (21) be written as

$$u(x,t)={\xi }_0(x,t)+\sum _{p=1}^m\sum _{q=1}^m{K}_{pq}{\xi }_{pq}(x,t).$$

(23)

The residual equation could be written in the following form by replacing $v(x,t)$ with $u(x,t)$ on the left-hand side of Equation (21):

$$R(x,t)=L\left[u\right(x,t\left)\right]+f(x,t).$$

(24)

For some choices of weight functions, the integral of the residual will be zero to construct $u(x,t)$. It means that, in this manner, the function $u(x,t)$ satisfies Equation (22) partially as

$${\int }_i^j{\int }_i^{j}f(x,t)+\sigma (x,t)L\left[u(x,t)\right]dxdt=0.$$

(25)

4.2. Satisfier Function

In the Ritz–Galerkin method, with two-dimensional Genocchi polynomials, the approximate solution $u(x,t)$ for Equations (1) and (4) is denoted as $\tilde{u}(x,t)$. Hence, we have

$$\tilde{u}(x,t)=\sum _{p=0}^M\sum _{q=0}^M{K}_{pq}{\omega }_{pq}(x,t)+\zeta (x,t),(x,t)\in [0,L]\times [0,T],$$

(26)

where ${\omega }_{pq}(x,t)=x(x-L)t^2{G}_p\left(x\right)G_q\left(t\right)$ and the satisfier function is represented by $\zeta (x,t)$. It is worth noting that the satisfier function satisfies all the initial and boundary conditions. While using the Ritz–Galerkin method, the most important point to be noted is to find the satisfier function:

$$\begin{array}{ccc}\hfill u(x,0)& =f_0\left(t\right),\hfill & \hfill 0\le x\le L,\\ \hfill u_t(\eta ,0)& =f_1\left(x\right),\hfill & \hfill 0\le x\le L,\\ \hfill u(0,t)& =g_0\left(t\right),\hfill & \hfill 0\le t\le T,\\ \hfill u(L,t)& =g_1\left(t\right),\hfill & \hfill 0\le t\le T.\end{array}$$

(27)

We have the following compatibility conditions where the function $f_0\left(x\right),$$f_1\left(x\right),$$g_0\left(t\right),$ and $g_1\left(t\right)$ satisfies as

$$\begin{array}{ccc}\hfill f_0\left(0\right)& =g_0\left(0\right),f_0\left(L\right)\hfill & \hfill =g_1\left(0\right),\\ \hfill f_1\left(0\right)& =g_0^{{}^{\prime }}\left(0\right),f_0\left(L\right)\hfill & \hfill =g_1^{{}^{\prime }}\left(0\right).\end{array}$$

(28)

4.3. Transformation of Nonhomogeneous Initial and Boundary Conditions into Homogeneous Conditions

Let

$$u(x,t)=\varpi (x,t)+\phi (x,t),$$

(29)

where

$$\phi (x,t)=(1-\frac{x}{L})g_0\left(t\right)+\frac{x}{L}{g}_1\left(t\right).$$

(30)

The homogeneous boundary conditions for the function $\varpi (x,t)$ will be written as the following to satisfy the given problem

$$\begin{array}{cc}\varpi (x,0)=F_0\left(x\right),\hfill & \hfill 0\le x\le L,\\ {\varpi }_t(x,0)=F_1\left(x\right),\hfill & \hfill 0\le x\le L,\\ \varpi (0,t)=0,\hfill & \hfill 0\le t\le T,\\ \varpi (L,t)=0,\hfill & \hfill 0\le t\le T.\end{array}$$

(31)

We have

$$\begin{array}{c}{F}_0\left(x\right)=f_0\left(x\right)-\phi (x,0),\hfill \\ F_1\left(x\right)=f_1\left(x\right)-{\phi }_t(x,0).\hfill \end{array}$$

(32)

The following compatibility conditions can be derived from Equation (31)

$$F_0\left(0\right)=F_0\left(L\right)=F_1\left(0\right)=F_1\left(L\right)=0.$$

Hence, $R(x,t)=F_0\left(x\right)+t{F}_1\left(x\right)$ satisfies the conditions given in Equation (31) and finally, for Equation (27), we introduce the satisfier function as

$$\zeta (x,t)=R(x,t)+\phi (x,t).$$

(33)

Furthermore, the coefficients $K_{pq}$ in Equation (26) can be calculated by using the equations given as

$$<F\left(\tilde{u}\right),G_p\left(x\right)G_q\left(t\right)>=0,$$

(34)

where

$$F\left(u\right)=\frac{{\partial }^{\alpha }u(x,t)}{\partial t^{\alpha }}+\frac{\partial u(x,t)}{\partial t}-\frac{{\partial }^{2}u(x,t)}{\partial x^2}-A(x,t),$$

(35)

and

$$<F\left(\tilde{u}\right),G_p\left(x\right)G_q\left(t\right)>={\int }_0^L{\int }_0^{T}F\left(\tilde{u}\right)G_p\left(x\right)G_q\left(t\right)dtdx,$$

(36)

where $G_p$ and $G_q$ are the Genocchi polynomials. A linear system of equations can be formed by using Equation (34), which can be solved for the entries of $K_{pq}$ where $p=1,...,M,q=1,...,M.$

5. Error Bound

Theorem 1.

Let $u^m(x,t)$ be the best approximation of the enough smooth function $u(x,t)$ by the use of Genocchi polynomials. Then, the error bound can be given as

$${\parallel Eu(x,t)\parallel }_{\infty }\le \frac{1}{M!}{G}_M^2{U}_{M,M},$$

(37)

where $G_M$ and $U_{M,M}$ denote the maximum value of $G_M\left(x\right)$ and $U_{M,M}(x,t)$ in the interval $[0,1]\times [0,1],$ respectively.

Proof. 

The proof is followed through Theorem 4.2 in [17]. ☐

Lemma 1.

Supposing that $f\left(t\right)\in C^{n+1}[0,1]$ and $Y=\mathrm{span}\{G_1\left(t\right),G_2\left(t\right),...,G_N\left(t\right)\}$, if $C^{T}G\left(t\right)$ is the best approximation of $f\left(t\right)$ out of Y, then

$$\parallel f\left(t\right)-C^{T}G\left(t\right)\parallel \le \frac{h^{\frac{2n+3}{2}}R}{(n+1)!\sqrt{2n+3}},t\in [t_i,t_{i+1}],\subseteq [0,1],$$

(38)

where $R=max|f^{(n+1)}\left(t\right)|$ and $h=t_{i+1}-t_i$.

Proof. 

See Section 3.2 in [18]. ☐

Theorem 2.

Assume that $u_{M,M}(x,t)\in C^{n,n}(I\times I)$ and let $X=\mathrm{span}\{G_1\left(x\right),\cdots ,G_M\left(x\right)\}$ and $X^{\prime }=span\{G_1\left(t\right),\cdots ,G_K\left(t\right)\}$. Since X and $X^{\prime }$ are the finite dimensional subspaces of $L^2[0,1]$ , then there exists $u_{M,M}^m(x,t)=X\times X^{\prime }$ as the best unique approximation by means of Genocchi polynomials:

$$\parallel u_{M,M}(x,t)-u_{M,M}^m{(x,t)\parallel }_2\le \frac{2M_{\gamma }{(H_x+H_t)}^{(p+2)}}{(p+1)!\sqrt{(2p+3)(2p+4)}}.$$

(39)

Proof. 

We define

$$u(x^{*},t^{*})=\sum _{r=0}^{p+1}\frac{(p+1)!}{r!(p+1-r)!}\frac{{\partial }^{p+1}f}{\partial x^r\partial t^{p+1-r}}{\left(h_x\right)}^r{\left(h_t\right)}^{p+1}.$$

(40)

If all the partial derivatives of $u(x,t)$ of order $p+1$ are bounded in magnitude by $M_{\gamma }$, then, by using the Taylor’s expansion of two variables as follows,

$$\begin{array}{ll}\mid u_{M,M}(x,t)-u_{M,M}^m(x,t)\mid \hfill & \approx \mid u(x^{*},t^{*})-u_{M,M}^m(x^{*},t^{*})\mid \hfill \\ & =\frac{1}{(p+1)!}\mid u^{n+1}(x^{*},t^{*})\mid \hfill \\ & =\frac{1}{(p+1)!}\mid \sum _{r=0}^{p+1}\frac{(p+1)!}{r!(p+1-r)!}\frac{{\partial }^{p+1}f}{\partial x^r\partial t^{p+1-r}}{\left(h_x\right)}^r{\left(h_t\right)}^{p+1}\mid \hfill \\ & =\frac{M_{\gamma }}{(p+1)!}\left(\right|h_x|+|h_t{\left|\right)}^{p+1},\hfill \end{array}$$

(41)

where

$$M_{\gamma }=max\left|\frac{{\partial }^{p+1}f}{\partial x^r\partial t^{p+1-r}}\right|,h_x=x^{*},h_t=t^{*}.$$

(42)

Applying the fact that $u_{M,M}^m(x,t)\in X\times X^{{}^{\prime }}$ is the best approximation of $u_{M,M}(x,t)$ out of $X\times X^{{}^{\prime }},$ respectively, then we have

$$\begin{array}{ll}\parallel u_{M,M}(x,t)-u_{M,M}^m{(x,t)\parallel }_2^2\hfill & \le \parallel u(x^{*},t^{*})-u_{M,M}^{*}(x^{*},t^{*}){\parallel }_2^2\hfill \\ & ={\int }_0^1{\int }_0^1{|u(x^{*},t^{*})-u_{M,M}^m(x^{*},t^{*})|}^{2}dxdt\hfill \\ & \le {\int }_0^1{\int }_0^1\frac{M_{\gamma }^2}{(p+1){!}^2}\left[\right(|h_x|+|h_t{\left|\right)}^{n+1}{]}^2\hfill \\ & =\frac{M_{\gamma }^2}{(p+1){!}^2}{\int }_0^1{\int }_0^1[\left(\right|h_x|+|h_t{\left|\right)]}^{2n+2}\hfill \\ & \le \frac{4M_{\gamma }^2{(H_x+H_t)}^{(2p+4)}}{(p+1){!}^2(2p+3)(2p+4)}.\hfill \end{array}$$

(43)

By taking the square root on both sides, one can obtain

$$\begin{array}{c}\hfill \parallel u_{M,M}(x,t)-u_{M,M}^m{(x,t)\parallel }_2\le \frac{2M_{\gamma }{(H_x+H_t)}^{(p+2)}}{(p+1)!\sqrt{(2p+3)(2p+4)}}.\end{array}$$

(44)

 ☐

6. Numerical Results

Some illustrated examples are given in this section based on the technique described in the previous sections. The maximum error is calculated at the final time $t=T$ to validate the accuracy of the presented technique on the interval $[0,T]$ as

$$\begin{array}{c}{E}_{\infty }={\parallel u_{exact}-u_{M,M}\parallel }_{\infty }\hfill \\ =\underset{1\le a\le M_t}{\max }\mid u_{exact}(x_i,T)-u_{M,M}(x_i,T)\mid .\hfill \end{array}$$

(45)

In addition, the absolute errors of the proposed technique in $(x_i,t_i)\in [0,1]\times [0,1]$ are given by

$$|E(x_i,t_i)|=|\tilde{u}(x_i,t_i)-u(x_i,t_i)|.$$

(46)

Problem 1.

Consider the following benchmark problem for linear time-fractional diffusion-wave equation with damping as solved in [3,4,21,22]:

$$\begin{array}{cc}\hfill \frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}+\rho (x,t),& (x,t)\in [0,1]\times [0,1],1<\alpha \le 2,\hfill \end{array}$$

(47)

where $\rho (x,t)=3t^2{e}^x-t^3{e}^x+\frac{6t^{3-\alpha }}{\Gamma (4-\alpha )}{e}^x$ along with the following initial and boundary conditions:

$$\begin{array}{cc}\hfill u(x,0)& =0,u_t(x,0)=0,\hfill \\ \hfill u(0,t)& =t^3,u(1,t)=e{t}^3.\hfill \end{array}$$

(48)

The exact solution of the problem is given as

$$u(x,t)=e^x{t}^3.$$

(49)

By using Equation (33), we have $\zeta (x,t)=t^3(1-x+ex)$ for the present problem and then our technique for different values of M and $\alpha$ is used. In Table 1, the comparison of our method with the result in [3,21,22] for the maximum absolute error when $\alpha =1.85$ and different values of M are shown. Table 2 shows the comparison of absolute errors of our method with [4] when $M=3$ with different values of $\alpha .$ It can be observed from the tables that our method yielded better results than others.

Table 1. Comparison of the maximum absolute errors (MAEs) of Problem 1 with [3,21,22] for $\alpha =1.85$.

M	Ref. [3]	Ref. [21]	Ref. [22]	Our Method
4	5.46 $\times {10}^{-5}$	3.38 $\times {10}^{-3}$	1.09 $\times {10}^{-1}$	4.39377 $\times {10}^{-6}$
8	5.50 $\times {10}^{-6}$	9.69 $\times {10}^{-4}$	2.76 $\times {10}^{-2}$	4.39381 $\times {10}^{-6}$

Table 2. Comparison of the absolute errors with [4] of Problem 1 for different values of $\alpha$ and $M=3$.

$(\mathit{x},\mathit{t})$	$\mathit{\alpha }=1.1$		$\mathit{\alpha }=1.5$		$\mathit{\alpha }=1.9$
	Our Method	Ref. [4]	Our Method	Ref. [4]	Our Method	Ref. [4]
(0.1,0.1)	1.15559 $\times {10}^{-8}$	6.7028 $\times {10}^{-5}$	4.97870 $\times {10}^{-8}$	6.0407 $\times {10}^{-5}$	1.15539 $\times {10}^{-7}$	2.0243 $\times {10}^{-5}$
(0.2, 0.2)	5.15080 $\times {10}^{-7}$	1.8718 $\times {10}^{-4}$	3.22420 $\times {10}^{-7}$	1.5683 $\times {10}^{-4}$	1.02961 $\times {10}^{-8}$	5.9155 $\times {10}^{-5}$
(0.3, 0.3)	2.63293 $\times {10}^{-6}$	3.0913 $\times {10}^{-4}$	2.27559 $\times {10}^{-6}$	2.7985 $\times {10}^{-4}$	1.66006 $\times {10}^{-6}$	1.0947 $\times {10}^{-4}$
(0.4, 0.4)	4.60055 $\times {10}^{-6}$	4.0221 $\times {10}^{-4}$	4.25541 $\times {10}^{-6}$	3.7035 $\times {10}^{-4}$	3.66878 $\times {10}^{-6}$	1.6790 $\times {10}^{-4}$
(0.5, 0.5)	5.41170 $\times {10}^{-7}$	4.5801 $\times {10}^{-4}$	5.14200 $\times {10}^{-7}$	3.8089 $\times {10}^{-4}$	4.80654 $\times {10}^{-7}$	1.6277 $\times {10}^{-4}$
(0.6, 0.6)	1.50610 $\times {10}^{-5}$	4.5260 $\times {10}^{-4}$	1.44824 $\times {10}^{-5}$	3.6309 $\times {10}^{-4}$	1.35084 $\times {10}^{-5}$	1.9284 $\times {10}^{-4}$
(0.7, 0.7)	3.84166 $\times {10}^{-5}$	4.0597 $\times {10}^{-4}$	3.71459 $\times {10}^{-5}$	3.2603 $\times {10}^{-4}$	3.51060 $\times {10}^{-5}$	6.2825 $\times {10}^{-5}$
(0.8, 0.8)	5.05410 $\times {10}^{-5}$	3.1039 $\times {10}^{-4}$	4.88530 $\times {10}^{-5}$	6.5594 $\times {10}^{-4}$	4.63092 $\times {10}^{-5}$	1.0181 $\times {10}^{-5}$
(0.9, 0.9)	2.89942 $\times {10}^{-5}$	1.7283 $\times {10}^{-4}$	2.76030 $\times {10}^{-5}$	7.1269 $\times {10}^{-3}$	2.57007 $\times {10}^{-5}$	2.0918 $\times {10}^{-5}$

Figure 1 shows the fast reduction in maximum absolute errors, MAEs, for our proposed method when M is increasing. The calculation is done using Maple with 15 digits. Furthermore, we only need a small M to achieve very high accuracy.

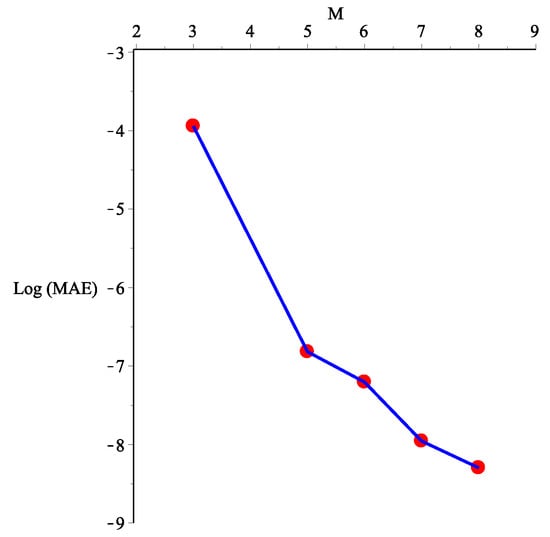
Figure 1. Graph of $lo{g}_{10}\left(MAE\right)$ at $\alpha =1.85$ for Problem 1.

Problem 2.

Consider the linear time-fractional diffusion wave equation [3]:

$$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+\frac{\partial u}{\partial t}=-\frac{{\partial }^{2}u}{\partial x^2}+\frac{2x(l-x)}{\Gamma (3-\alpha )}{t}^{2-\alpha }+2tx(l-x)+2t^2,1<\alpha \le 2,$$

(50)

$$\begin{array}{cc}\hfill u(x,0)& =0,u_t(x,0)=0,0<x<l,\hfill \\ \hfill u(0,t)& =0,u(l,t)=0,0<t<\tau .\hfill \end{array}$$

(51)

The exact solution of the Problem 2 is $u(x,t)=t^{2}x(l-x).$

We can obtain the exact solution of the given problem for different values of $\alpha$ and when $M=3$. This shows the compatibility of our present technique compared to the existing results. For instance, Ref. [3] deals with the Jacobi tau spectral method with the Jacobi operational matrix for fractional integrals. For the given problem, they presented their results in Table 5 in their paper for $t=1,L=1,\tau =1$ with $N=M=8$ for different values of $\alpha ,\beta$ and $\nu$. More precisely, Table 3 shows the comparison of our result (using $M=3$) while [3]$M=8$ was used. In addition, Ref. [4] applied Legendre wavelets for this problem by using the fractional operational matrix of integration for different values of $\alpha$ and $M=3,k=3$.

Table 3. Comparison of the maximum absolute errors (MAEs) of Problem 2 with [3] for different values of $\alpha$.

$\mathit{\alpha }$	Our Method	Ref. [3]
1.2	1.11 $\times {10}^{-16}$	5.35 $\times {10}^{-6}$
1.4	1.11 $\times {10}^{-16}$	1.01 $\times {10}^{-6}$
1.6	1.11 $\times {10}^{-16}$	8.77 $\times {10}^{-6}$
1.8	1.11 $\times {10}^{-16}$	2.27 $\times {10}^{-6}$

The errors showed in our calculation are very small. They may be caused by the rounding in floating point arithmetic instead of errors caused by our algorithm.

Problem 3.

Consider the following linear time-fractional Klein–Gordon equation as solved in [10] :

$$\begin{array}{cc}\hfill \frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+u=\frac{{\partial }^{2}u}{\partial x^2}+\rho (x,t),& (x,t)\in [0,1]\times [0,1],1<\alpha \le 2,\hfill \end{array}$$

(52)

where $\rho (x,t)=\frac{2t^{2-\alpha }}{(2-\alpha )\Gamma (2-\alpha )}(e-e^x)sin\left(x\right)+t^2(2e-e^x)sin\left(x\right)+2t^2{e}^{x}cos\left(x\right).$ along with the following initial and boundary conditions:

$$\begin{array}{cc}\hfill u(x,0)& =0,u_t(x,0)=0,\hfill \\ \hfill u(0,t)& =0,u(1,t)=0.\hfill \end{array}$$

(53)

The exact solution of the given problem is $u(x,t)=t^2(e-e^x)sin\left(x\right).$ By using Equation (33), we have $\zeta (x,t)=0$ for the present problem and then used our technique for different values of M and $\alpha$. In Table 4 and Table 5, the comparison of our method with the result in [10] for the maximum absolute error when $\alpha =1.25$ and $\alpha =1.75$ for different values of M are shown. It can be observed from the tables that our method yields better results compared to other methods.

Table 4. Comparison of the maximum absolute errors (MAEs) with [10] of Problem 3 for $\alpha =1.25$ and for different values of M.

M	$\mathit{\tau }$	Our Method	Ref. [10]
3	$\frac{1}{10}$	8.2146 $\times {10}^{-4}$	1.3189 $\times {10}^{-3}$
4	$\frac{1}{20}$	2.9523 $\times {10}^{-5}$	3.3035 $\times {10}^{-4}$
5	$\frac{1}{40}$	7.9725 $\times {10}^{-7}$	8.2925 $\times {10}^{-5}$
6	$\frac{1}{80}$	6.1421 $\times {10}^{-7}$	2.0856 $\times {10}^{-5}$
7	$\frac{1}{160}$	9.9173 $\times {10}^{-6}$	5.2649 $\times {10}^{-6}$

Table 5. Comparison of the maximum absolute errors (MAEs) with [10] of Problem 3 for $\alpha =1.75$ and for different values of M.

M	$\mathit{\tau }$	Our Method	Ref. [10]
3	$\frac{1}{10}$	8.2677 $\times {10}^{-4}$	3.7014 $\times {10}^{-3}$
4	$\frac{1}{20}$	2.9040 $\times {10}^{-5}$	1.5270 $\times {10}^{-3}$
5	$\frac{1}{40}$	2.4291 $\times {10}^{-7}$	6.2904 $\times {10}^{-4}$
6	$\frac{1}{80}$	5.6104 $\times {10}^{-7}$	2.5916 $\times {10}^{-4}$
7	$\frac{1}{160}$	7.7767 $\times {10}^{-6}$	1.0715 $\times {10}^{-4}$

Problem 4.

Consider the following nonlinear time-fractional Klein–Gordon equation as solved in [2]:

$$\begin{array}{cc}\hfill \frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=\frac{{\partial }^{2}u}{\partial x^2}-u^2+\rho (x,t),& (x,t)\in [0,1]\times [0,1],1<\alpha \le 2,\hfill \end{array}$$

(54)

where $\rho (x,t)=\frac{\Gamma \left(\frac{5}{2}\right)}{\Gamma (\frac{5}{2}-\alpha )}{(1-x)}^{\frac{5}{2}}{t}^{\frac{3}{2}-\alpha }-\frac{15}{4}{(1-x)}^{\frac{1}{2}}{t}^{\frac{3}{2}}+{(1-x)}^5{t}^3$ along with the following initial and boundary conditions:

$$\begin{array}{cc}\hfill u(x,0)& =0,u_t(x,0)=0,\hfill \\ \hfill u(0,t)& =t^{\frac{3}{2}},u(1,t)=0.\hfill \end{array}$$

(55)

The exact solution of the given problem is

$$u(x,t)={(1-x)}^{\frac{5}{2}}{t}^{\frac{3}{2}}.$$

(56)

By using Equation (33), we have $\zeta (x,t)=(1-x)t^{\frac{3}{2}}$ for the present problem and then used our technique for different values of M. We obtained the results as shown in Table 6, which clearly show that our method led to better results compared to other published works [2].

Table 6. Comparison of the maximum absolute errors (MAEs) of Problem 4 with [2] for $\alpha =1.3$ and different values of M.

M	Our Method	Ref. [2]
4	1.8485 $\times {10}^{-3}$	6.9789 $\times {10}^{-3}$
6	3.0582 $\times {10}^{-4}$	2.7048 $\times {10}^{-3}$
8	8.3497 $\times {10}^{-5}$	1.1765 $\times {10}^{-3}$
10	3.4893 $\times {10}^{-4}$	5.7402 $\times {10}^{-4}$

7. Conclusions

In this paper, we used two-dimensional Genocchi polynomials with the Ritz–Galerkin method in Caputo’s sense to solve the fractional diffusion wave equation (FDWE) and the time-fractional Klein–Gordon equation (FKGE). Our method is able to solve the equation with very high accuracy even for nonlinear cases. The use of the satisfier function makes it easy to tackle the problem with initial and boundary conditions. Comparison tables are given to show the present technique in comparison with existing work.