1. Introduction
Viruses are very small infectious agents that need to penetrate inside a cell of their host to replicate and multiply. Several viruses attack the human body, such as influenza virus, human immunodeficiency virus (HIV), hepatitis B virus (HBV), hepatitis C virus (HCV), Ebola virus, Zika virus, and so on. Viral infections caused by these viruses represent a major global health problem by causing the mortality of millions of people and the expenditure of enormous amounts of money in health care and disease control. In this study, we are interested in the viral infection caused by HIV. The World Health Organization (WHO) estimates that
million people were living with HIV at the end of 2016, and more than 1 million people died from HIV-related causes in 2016 [
1]. In Morocco, the number of people living with HIV is estimated at 28,740, and 1097 people died from AIDS in 2014, while the cumulative number of HIV/AIDS cases reported since the beginning of the epidemic is 10,017 [
2].
Many mathematical models have been developed to better understand the dynamics of HIV infection. One of the earliest of these models was presented by Perelson et al. [
3] in 1996. This model is given by the following system:
where
,
, and
are the concentrations of healthy CD4
T cells, infected cells, and free virus at time
t, respectively. Healthy cells are produced at rate
, die at rate
d, and become infected by free virus at rate
. The parameter
a is the death rate of infected cells. Free virus is produced by an infected cell at rate
k and is removed at rate
.
In the system given by Equation (
1), the cell infection is instantaneous and is caused only by contact with free virus. In reality, there are two kinds of delays: one in cell infection, and the other in virus production. In addition, HIV can spread by two fundamental modes, one by virus-to-cell infection, and the other by direct cell-to-cell transmission. For these above reasons, Lai and Zou [
4] improved the model of Perelson et al. [
3] by incorporating the two modes of transmission and infinite distributed delay in cell infection. They obtained the following model:
where
denotes the rate for a target cell to contact with an infected cell. It is assumed that the virus or infected cell contacts an uninfected target cell at time
and the cell becomes infected at time
t, where
is a random variable taken from a probability distribution
. The term
represents the probability of surviving from time
to time
t, where
is the death rate for infected but not yet virus-producing cells. The other parameters have the same biological meaning as in Equation (
1).
On the other hand, the adaptive immune responses of cytotoxic T lymphocytes (CTLs) and antibodies play an important role in the control of HIV infection. The first immune response exerted by CTL cells is called the cellular immunity. However, the second immune response mediated by antibodies is called the humoral immunity. In the literature, several authors are interested in modeling the role of these arms of immunity in viral infections. In 2016, Wang et al. [
5] improved the model given by Equation (
2) by considering the role of cellular immune response. In the same year, Elaiw et al. [
6] improved the model given by Equation (
2) by considering only the role of humoral immune response and infinite distributed delay in virus production. In 2017, Lin et al. [
7] improved the models of Wang and Zou [
8] and Murase et al. [
9] by incorporating both modes of transmission, intracellular delay and humoral immunity.
The aim of this work is to improve and generalize all the above models by proposing a new mathematical model that takes into account the role of the adaptive immune response in HIV infection and incorporates both modes of transmission. To this end, the next section deals with the presentation of our model and some properties of solutions, such as positivity and boundedness. In
Section 2, we derive the threshold parameters of our model and discuss the existence of equilibria. The global stability of equilibria is investigated in
Section 3. Some numerical simulations of our main results are presented in
Section 4. The mathematical and biological conclusions are given in
Section 5.
2. Presentation of the Model
To model the role of the adaptive immune response in HIV infection with both virus-to-cell infection and cell-to-cell transmission, we propose the following model:
where
and
are the concentrations of antibodies and CTL cells at time
t, respectively. Free HIV particles are neutralized by the antibodies at rate
. However, the infected cells are killed by CTL cells at rate
. Antibodies develop in response to free virus at rate
, and CTL cells expand in response to viral antigens derived from infected cells at rate
. The parameters
h and
b are, respectively, the death rates of antibodies and CTL cells. Further, we assume that the time necessary for the newly produced virions to become mature and infectious is a random variable with a probability distribution
. The term
denotes the probability of surviving the immature virions during the delay period, where
is the average lifetime of an immature virus. Therefore, the integral
describes the mature viral particles produced at time
t. The other variables and parameters are defined as those in the systems given by Equations (
1) and (
2).
In this section, we first investigate the nonnegativity and boundedness of solutions under the following nonnegative initial conditions:
We define the Banach space for the fading memory type as follows:
where
is a positive constant and
.
Theorem 1. For any initial condition satisfying Equation (4), the model given by Equation (3) has a unique solution on . Furthermore, this solution is nonnegative and bounded for all . Proof. By the fundamental theory of functional differential equations [
10,
11,
12], the model given by Equation (
3) with initial condition
has a unique local solution on
, where
is the maximal existence time for the solution of Equation (
3).
First, we prove that
for all
. In fact, supposing the contrary, we let
be the first time such that
and
. By the first equation of the model given by Equation (
3), we have
, which is a contradiction. Thus,
for all
. By Equation (
3), we have
which implies that
,
,
, and
are nonnegative for all
.
Next, we show the boundedness of each solution. From the first equation of the model given by Equation (
3), we have
, which implies that
Then
is bounded. Let
Because
is bounded and
, the integral in
is well defined and differentiable with respect to
t. Hence,
where
and
Thus,
, which implies that
and
are bounded. It remains to prove that
and
are bounded. To this end, we consider
then
where
. Similarly to the above, we deduce that
and
are also bounded. We have proved that all variables of Equation (
3) are bounded, which implies that
and that the solution exists globally. ☐
If in addition to Equation (
4), we suppose that
for all
; then we obtain the following remark.
Remark 1. If satisfies Equation (4) with , then each solution of Equation (3) with initial condition ϕ remains positive and bounded for all . Next, we derive threshold numbers and identify biological equilibria for the model given by Equation (
3). Clearly, Equation (
3) always has an infection-free equilibrium of the form
, where
. Therefore, the basic reproduction number of Equation (
3) can be defined as
As in [
13],
can be rewritten as
, where
is the basic reproduction number corresponding to the virus-to-cell infection mode, and
is the basic reproduction number corresponding to the cell-to-cell transmission mode.
When
, Equation (
3) has another infection equilibrium without immunity,
, where
If both humoral and cellular immune responses have not been established, we have
and
. Thus, we define the reproduction number for humoral immunity:
and the reproduction number for cellular immunity:
Hence, and are equivalent to and , respectively.
When
, Equation (
3) has an infection equilibrium with only humoral immunity,
, where
with
,
, and
.
It is not hard to see that
,
and
are positive. It remains to check that
is positive. Because
and
we easily deduce that
. If cellular immunity has not been established, we have
. For this, we define the reproduction number for cellular immunity in competition as
which implies that
is equivalent to
.
When
, Equation (
3) has an infection equilibrium with only cellular immunity,
, where
We have that
,
, and
are positive. It suffices to check that
is positive. Because
and
we deduce that
. If humoral immunity has not been established, we have
. In this case, we define the reproduction number for humoral immunity in competition as
which implies that
is equivalent to
.
When
and
, Equation (
3) has an infection equilibrium with both cellular and humoral immune responses,
, where
We have
,
,
, and
(as
). It remains to check that
. On the other hand,
is equivalent to
. By a simple computation, we have
Summarizing the above discussions, we obtain the following theorem.
Theorem 2. - (i)
If , then Equation (3) always has one infection-free equilibrium, , where . - (ii)
If , then Equation (3) has an infection equilibrium without immunity, , where - (iii)
If , then Equation (3) has an infection equilibrium with only humoral immunity, , where - (iv)
If , then Equation (3) has an infection equilibrium with only cellular immunity, , where - (v)
If and , then Equation (3) has an infection equilibrium with both cellular and humoral immune responses, , where
It is important to note that
3. Global Stability
In this section, we investigate the global stability of the five equilibria of Equation (
3) by constructing appropriate Lyapunov functionals. We first analyze the global stability of the infection-free equilibrium.
Theorem 3. The infection-free equilibrium is globally asymptotically stable when .
Proof. To study the global stability of
, we consider a Lyapunov functional defined as follows:
where
for
. It is not hard to see that
for all
. Hence, the functional
is nonnegative.
In order to simplify the presentation, we use the following notations:
and
for any
. Calculating the time derivative of
along the positive solution of Equation (
3), we obtain
If follows from
that
. It is straightforward to show that the largest invariant set in
is
. By LaSalle’s invariance principle [
14], the infection-free equilibrium
is globally asymptotically stable when
. ☐
When
, Equation (
3) has four infection steady states
,
. The following theorem characterizes the global stability of these steady states.
Theorem 4. Assume .
- (i)
The infection equilibrium without immunity is globally asymptotically stable if and .
- (ii)
The infection equilibrium with only humoral immunity is globally asymptotically stable if and .
- (iii)
The infection equilibrium with only cellular immunity is globally asymptotically stable if and .
- (iv)
The infection equilibrium with both cellular and humoral immune responses is globally asymptotically stable if and .
Proof. For
(i), consider the following Lyapunov functional:
Then
By
and
, we obtain
Thus,
Because
for
,
, and
, we have
with equality if and only if
,
,
,
, and
. It follows from LaSalle’s invariance principle that
is globally asymptotically stable.
For
(ii), consider the following Lyapunov functional:
Hence,
By
,
, and
, we obtain
Thus,
Because
and
for
, we have
with equality if and only if
,
, and
. Then
and
, which leads to
and
. Therefore, the largest compact invariant set in
is the singleton
, and the proof of
(ii) is completed.
For
(iii), consider the following Lyapunov functional:
From
,
, and
, we easily have
Consequently, with equality if and only if , , and . It follows from and that and . By LaSalle’s invariance principle, we deduce that is globally asymptotically stable.
Finally, we show
(iv) by considering the following Lyapunov functional:
By
,
, and
, we obtain
Hence,
Thus,
with equality holds if and only if
,
, and
. Let
From the second and third equations of the model given by Equation (
3), we have
which implies that
and
. Then the largest compact invariant set in
is the singleton
. Therefore,
is globally asymptotically stable. ☐
The conditions of the global stability of and those of given in (ii) and (iii) of Theorem 4 do not hold simultaneously. In fact, supposing the contrary, then and . Because and , we have . This is a contradiction with .
According to Equation (
12) and Theorem 4, we have the following important result.
Remark 2. Assume .
- (1)
If , then Equation (3) converges to without immunity. - (2)
If , two cases arise:
- (i)
When , the humoral immunity is dominant, and Equation (3) converges to if or to if . - (ii)
When , the cellular immunity is dominant, and Equation (3) converges to without humoral immunity.
From this important remark, we can define the over-domination of humoral immunity when and and the over-domination of cellular immunity when and .
4. Numerical Simulations
In this section, we present some numerical simulations in order to validate our theoretical results. For simplicity, we chose
and
with
and
to be the delays in cell infection and virus production, respectively, and
to be the Dirac function; then our model becomes
This system improves the model presented in 2017 by Lin et al. [
7], which considered only the humoral immunity and discrete delay in cell infection and ignored the time delay in virus production; that is,
. In addition, Equation (
13) includes many special cases existing in the literature. For example, when
and
, we obtain the model presented by Wodarz in [
15] and analyzed by Hattaf et al. in [
16]. When
and
, we obtain the model of Yan and Wang [
17].
The algorithm for the numerical treatment of the delay differential system given by Equation (
13) can be derived for the numerical method presented in [
18,
19]. Recently, this numerical method has been used for delayed partial differential equations [
20]; it is called the “mixed” Euler method, as it is a mixture of both forward and backward Euler methods. In addition, it is shown that this mixed Euler method preserves the qualitative properties of the corresponding continuous system, such as positivity, boundedness, and global behaviors of solutions. Hence, we discretize the continuous system given by Equation (
13) by this numerical method. Thus, we let
be a time step size and assume that there exist two integers
with
and
. The grids points are
for
. By applying the mixed Euler method and using the approximations
,
,
,
, and
, we obtain the following discrete model:
where the discrete initial conditions are
The five threshold parameters
,
,
,
, and
for Equation (
13) are given by Equations (
7)–(
11) with
and
. In order to study the impact of cell-to-cell transmission and both arms of adaptive immunity on the HIV dynamics, we chose
,
g, and
c as free parameters. The units of state variables
T,
I, and
Z were given by cells
. Further, the units of
V and
W were given by virions
and molecules
, respectively. The other parameter values for the simulation are listed in
Table 1.
For the case in which
,
, and
, we obtained
. It follows from Theorem 2 that Equation (
13) has one infection-free equilibrium
. From
Figure 1, we see that the concentration of uninfected CD4
T cells increased and tended to the value
, while the concentrations of infected cells, free HIV particles, antibodies, and CTL cells decreased and tended to zero. This means that
is globally asymptotically stable and that the virus will be cleared. This confirms the result in Theorem 3.
For the case in which
,
, and
, we obtained
,
, and
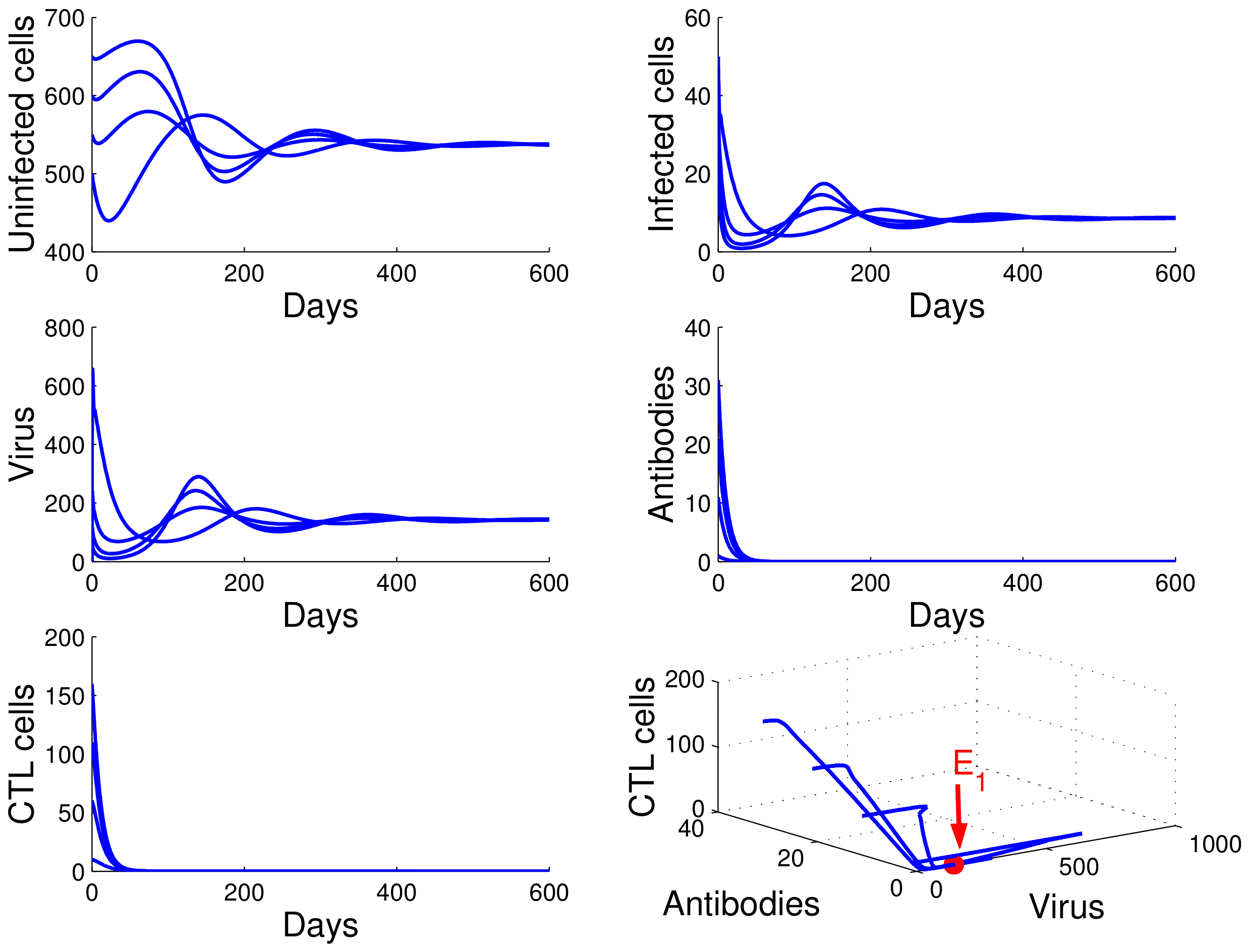
. It follows that case
of Theorem 4 occurs, and the infection equilibrium without immunity
is globally asymptotically stable (see
Figure 2).
For the case in which
,
, and
, we obtained
,
, and
. From
of Theorem 4, the infection equilibrium with only humoral immunity
is globally asymptotically stable (see
Figure 3).
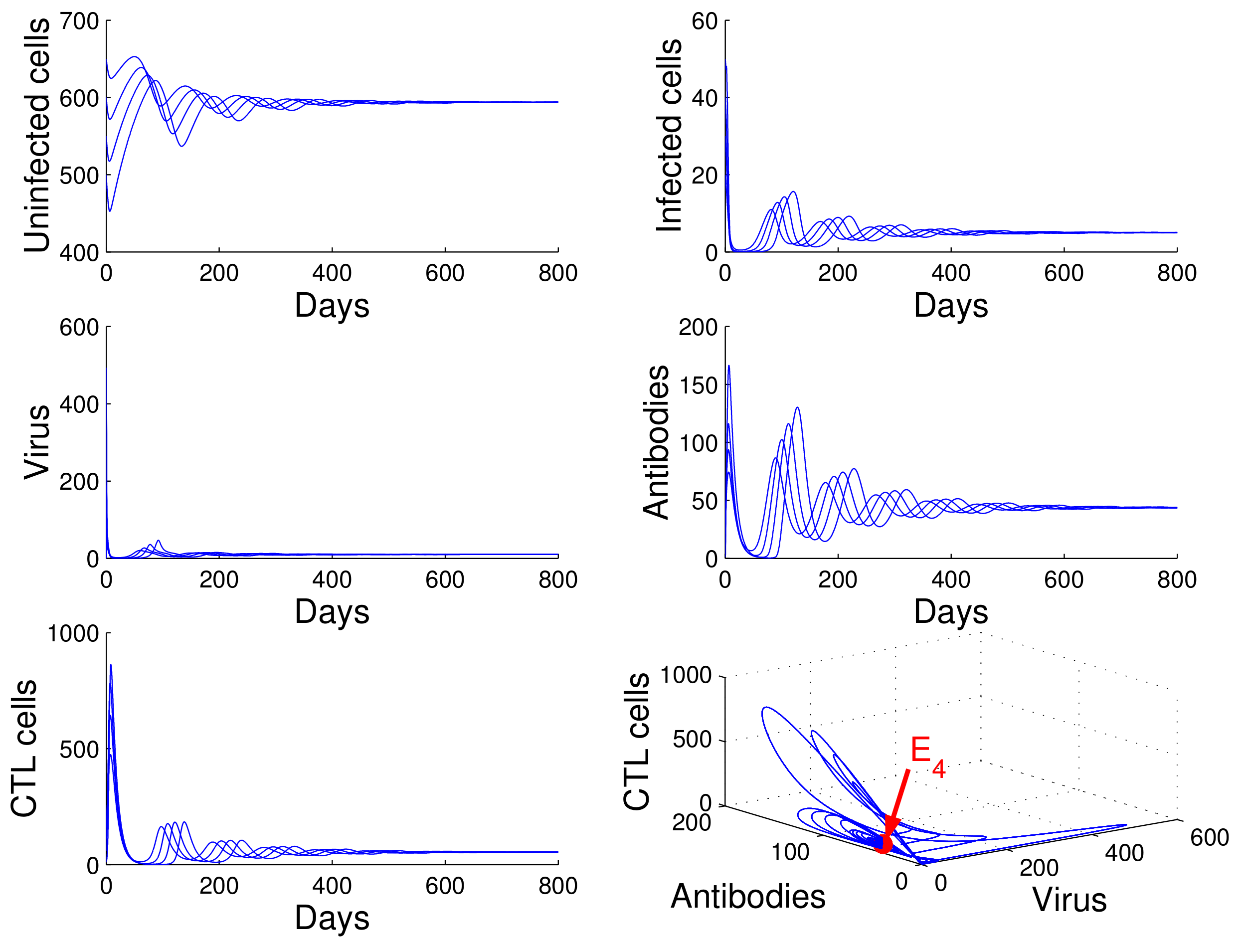
For the case in which
,
, and
, we obtained
,
, and
. By
of Theorem 4, the infection equilibrium with only cellular immunity
is globally asymptotically stable (see
Figure 4).
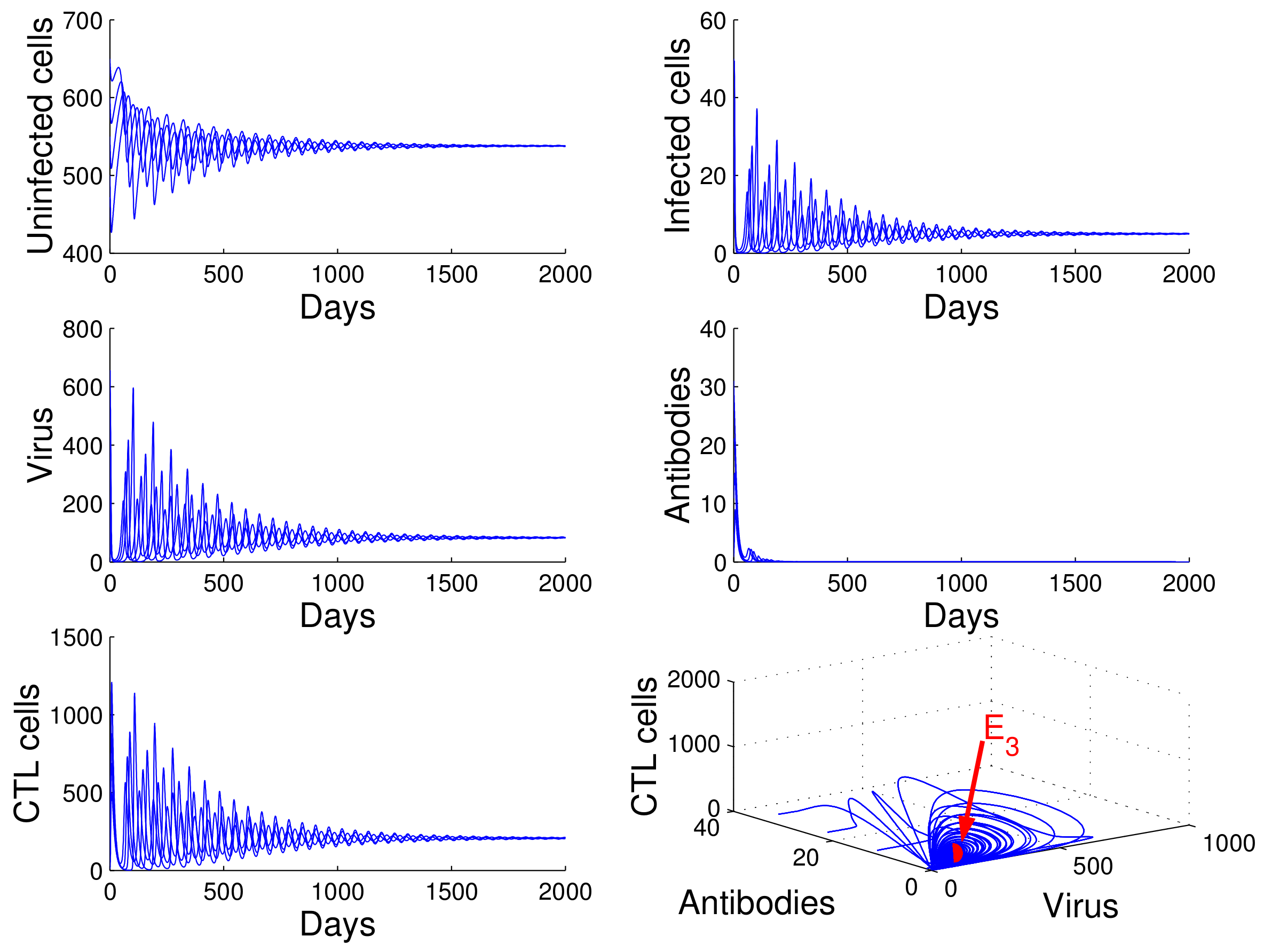
For the case in which
,
, and
, we obtained
,
, and
. Using
of Theorem 4, we deduce that the infection equilibrium with both arms of immunity
is globally asymptotically stable (see
Figure 5).
5. Conclusions
In this paper, we have modeled the role of the adaptive immunity in HIV infection by proposing a new mathematical model that takes into account the classical virus-to-cell infection, the direct cell-to-cell transmission, and the two kinds of delays during infection processes and virus production. By a rigorous mathematical analysis, we have proved that the global dynamics of the proposed model is fully determined by five threshold parameters, which are the basic reproduction number , and the reproduction numbers for humoral immunity , for cellular immunity , for cellular immunity in competition , and for humoral immunity in competition . More precisely, the infection-free equilibrium is globally asymptotically stable if , which biologically means that the HIV is cleared and the infection dies out. When , our model has four infection equilibria, which are the following: the infection equilibrium without immunity is globally asymptotically stable if and ; the infection equilibrium with only humoral immunity is globally asymptotically stable if and ; the infection equilibrium with only cellular immunity is globally asymptotically stable if and ; the infection equilibrium with both cellular and humoral immune responses is globally asymptotically stable if and . Biologically, this implies that the HIV persists and the infection becomes chronic when the basic reproduction number is greater than 1. Additionally, the activation of one or both arms of immunity is unable to eliminate the virus in the human body.
From Remark 2, we can deduce that the over-domination of cellular immunity leads to the absence of the humoral immunity, and the over-domination of the humoral immunity leads to the persistence of HIV infection with a weak response of both arms of immunity. This biological result may be an explanation for the dysfunction of the adaptive immunity in HIV-infected patients. Our model can be adapted for HBV infection, and the above result can also explain the dysfunction of the adaptive immune response in patients infected with HBV, which is still largely incomplete [
33].
Furthermore, the model and the results presented in this study improve and generalize the models and the corresponding results in more recent papers with only cellular immunity [
5], with only humoral immunity [
6,
7,
8,
9], and with both arms of immunity [
15,
17].