Shannon Entropy in Atoms: A Test for the Assessment of Density Functionals in Kohn-Sham Theory
Abstract
:1. Introduction
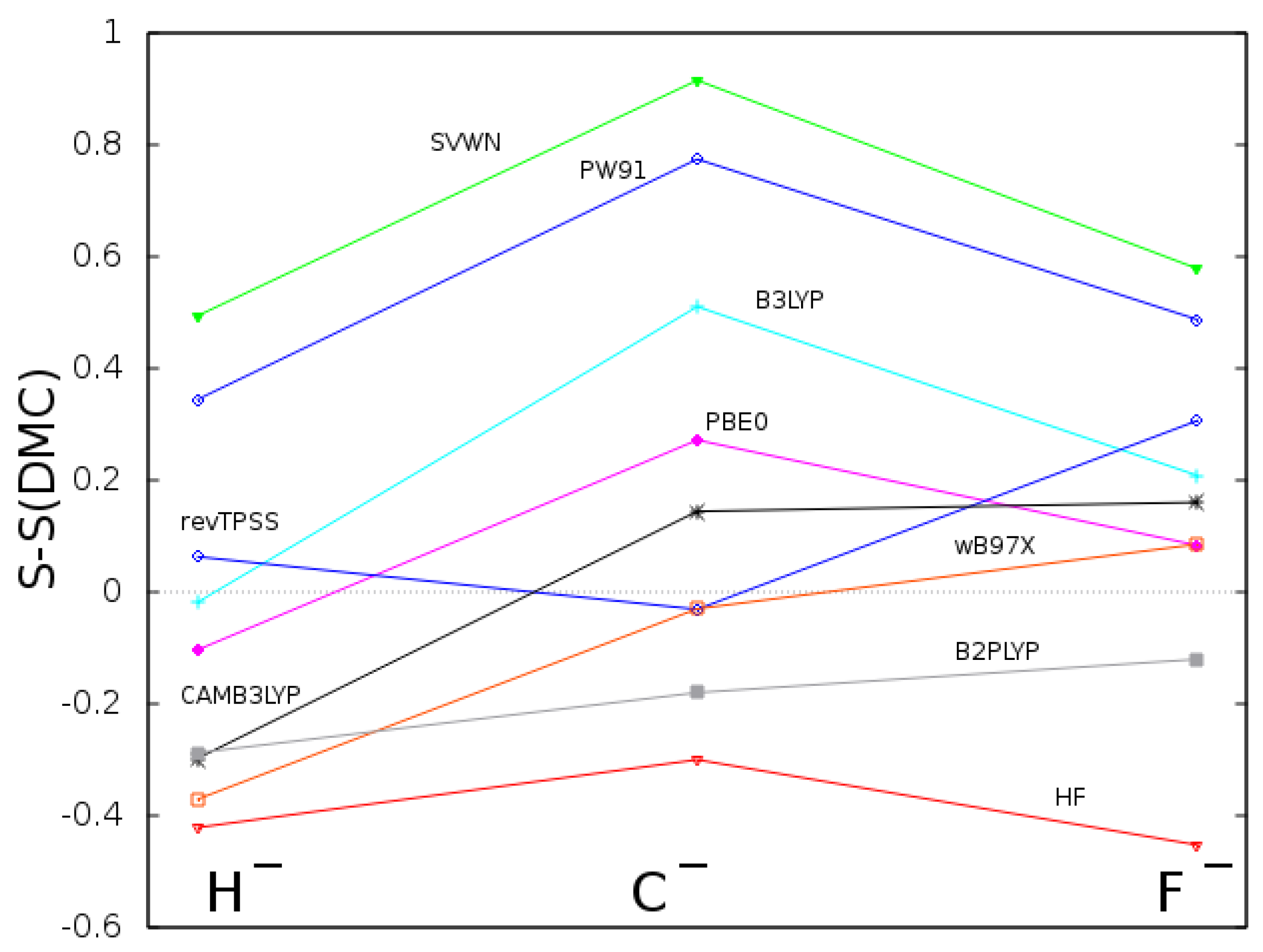
2. Calculations and Discussion of Results
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SWVN | Slater, Vosko, Wilk, and Nusair functional [25] |
| PW91 | Perdew and Wang 1991 functional [26] |
| PBE0 | Perdew–Burke–Ernzerhof with 0.25 Hartree–Fock exchange functional [27,28] |
| B3LYP | Becke, three-parameter, Lee–Yang–Parr hybrid functional [29,30] |
| revTPSS | revised Tao, Perdew, Staroverov, and Scuseria meta-GGA functional [31,32] |
| CAMB3LYP | Cambridge B3LYP functional [33] |
| B97X | long-range corrected Becke 97 hybrid functional [34] |
| B2PLYP | double hybrid BLYP functional [35] |
References and Note
- Amovilli, C.; Floris, F.M. Shannon entropy and correlation energy for electrons in atoms. In Many-Body Approaches at Different Scales; Angilella, G.G.N., Amovilli, C., Eds.; Springer International Publishing: Heidelberg, Germany, 2018; pp. 187–198. ISBN 978-3-319-72373-0. [Google Scholar]
- Janzing, D. Entropy of Entanglement. In Compendium of Quantum Physics; Greenberger, D., Hentschel, K., Weinert, F., Eds.; Springer International Publishing: Heidelberg, Germany, 2009; pp. 205–209. ISBN 978-3-540-70622-9. [Google Scholar]
- Collins, D.M. Entropy Maximizations on Electron-Density. Z. Naturforsc. A 1993, 48, 68–74. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Rodriguez, A.L.; Sagar, R.P.; Ho, M.; Smith, V.H., Jr. Physical interpretation of information entropy: Numerical evidence of the Collins conjecture. Phys. Rev. A 1996, 54, 259–265. [Google Scholar] [CrossRef] [PubMed]
- Ziesche, P. Correlation strength and information entropy. Int. J. Quantum Chem. 1995, 56, 363–369. [Google Scholar] [CrossRef]
- Nagy, A.; Romera, E. Link between generalized nonidempotency and complexity measures. J. Mol. Model. 2017, 23, 159. [Google Scholar] [CrossRef] [PubMed]
- Romera, E.; Dehesa, J.S. The Fisher-Shannon information plane, an electron correlation tool. J. Chem. Phys. 2004, 120, 8906–8912. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Hansen, A. Practicable Real-Space Measure and Visualization of Static Electron-Correlation Effects. Angew. Chem. Int. Ed. 2015, 54, 12308–12313. [Google Scholar] [CrossRef] [PubMed]
- Amovilli, C.; March, N.H. Use of ab initio methods to classify four existing energy density functionals according to their possible variational validity. Phys. Rev. A 2004, 69, 054302. [Google Scholar] [CrossRef]
- Delle Site, L. Shannon entropy and many-electron correlations: Theoretical concepts, numerical results, and Collins conjecture. Int. J. Quantum Chem. 2015, 115, 1396–1404. [Google Scholar] [CrossRef]
- Ghiringhelli, L.M.; Hamilton, I.P.; Delle Site, L. Interacting electrons, spin statistics, and information theory. J. Chem. Phys. 2010, 132, 014106. [Google Scholar] [CrossRef] [PubMed]
- Trickey, S.B.; Karasiev, V.V.; Vela, A. Positivity constraints and information-theoretical kinetic energy functionals. Phys. Rev. B 2011, 84, 075146. [Google Scholar] [CrossRef]
- Wasserman, A.; Nafziger, J.; Jiang, K.L.; Kim, M.C.; Sim, E.; Burke, K. The Importance of Being Inconsistent. Ann. Rev. Phys. Chem. 2017, 68, 555–581. [Google Scholar] [CrossRef] [PubMed]
- Amovilli, C.; March, N.H.; Bogar, F.; Gál, T. Use of ab initio methods to classify four existing energy density functionals according to their possible variational validity. Phys. Lett. A 2009, 373, 3158–3160. [Google Scholar] [CrossRef]
- Perdew, J.P.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Conf. Proc. 2001, 577, 1–20. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, N.K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Burkatzki, M.; Filippi, C.; Dolg, M. Energy-consistent pseudopotentials for quantum Monte Carlo calculations. J. Chem. Phys. 2007, 126, 234105. [Google Scholar] [CrossRef] [PubMed]
- The Cornell-Holland Ab-initio Materials Package (CHAMP) is a quantum Monte Carlo suite of programs for electronic structure calculations of atomic and molecular systems. See, for more information: http://www.utwente.nl/tnw/ccp/research/CHAMP.html (28 April 2018).
- Filippi, C.; Umrigar, C.J. Multiconfiguration wave functions for quantum Monte Carlo calculations of first row diatomic molecules. J. Chem. Phys. 1996, 105, 213–226. [Google Scholar] [CrossRef]
- Umrigar, C.J.; Toulouse, J.; Filippi, C.; Sorella, S.; Hennig, R.G. Alleviation of the Fermion-Sign Problem by Optimization of Many-Body Wave Functions. Phys. Rev. Lett. 2007, 98, 110201. [Google Scholar] [CrossRef] [PubMed]
- Casula, M. Beyond the locality approximation in the standard diffusion Monte Carlo method. Phys. Rev. B 2006, 74, 161102. [Google Scholar] [CrossRef]
- Drake, G.W.F.; Swainson, R.A. Bethe logarithms for hydrogen up to n = 20, and approximations for two-electron atoms. Phys. Rev. A 1990, 41, 1243–1246. [Google Scholar] [CrossRef] [PubMed]
- Hogreve, H. On the maximal electronic charge bound by atomic nuclei. J. Phys. B At. Mol. Phys. 1998, 31, L439–L446. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Burke, K.; Perdew, J.P.; Wang, Y. Derivation of a Generalized Gradient Approximation: The PW91 Density Functional. In Electronic Density Functional Theory; Dobson, J.F., Vignale, G., Das, M.P., Eds.; Springer: Boston, MA, USA, 1988; pp. 81–111. ISBN 978-1-4899-0316-7. [Google Scholar]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. TPSS: Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Marsman, M.; Csonka, G.; Ruzsinszky, A.; Hao, P.; Kim, Y.-S.; Kresse, G.; Perdew, J.P. Self-consistent meta-generalized gradient approximation within the projector-augmented-wave method. Phys. Rev. B 2011, 84, 035117. [Google Scholar] [CrossRef]
- Yanaia, T.; Handy, D.N. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Da Chaia, J.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Schwabe, T.; Grimme, S. Double-hybrid density functionals with long-range dispersion corrections: Higher accuracy and extended applicability. Phys. Chem. Chem. Phys. 2007, 9, 3397–3406. [Google Scholar] [CrossRef] [PubMed]
| Method | Total Energy | Kinetic Energy | Entropy | Total Energy | Kinetic Energy | Entropy | Total Energy | Kinetic Energy | Entropy |
|---|---|---|---|---|---|---|---|---|---|
| H− | He | Li+ | |||||||
| RHF | −0.48793 | 0.48793 | 9.8889 | −2.86163 | 2.86148 | 4.0100 | −7.23599 | 7.23474 | 1.1203 |
| SVWN | −0.51425 | 0.48054 | 10.8040 | −2.83479 | 2.76771 | 4.2066 | −7.14240 | 7.05513 | 1.2467 |
| PW91 | −0.53052 | 0.50957 | 10.6541 | −2.89995 | 2.86266 | 4.1155 | −7.26720 | 7.22341 | 1.1834 |
| PBE0 | −0.52450 | 0.50023 | 10.2064 | −2.89513 | 2.85773 | 4.0816 | −7.26205 | 7.21907 | 1.1659 |
| B3LYP | −0.53065 | 0.51090 | 10.2912 | −2.90806 | 2.86808 | 4.0927 | −7.27821 | 7.22723 | 1.1733 |
| revTPSS | −0.53325 | 0.50611 | 10.3734 | −2.91200 | 2.87003 | 4.0424 | −7.28824 | 7.24107 | 1.1396 |
| CAMB3LYP | −0.53100 | 0.50802 | 10.0120 | −2.90138 | 2.85372 | 4.1173 | −7.26518 | 7.21801 | 1.1816 |
| B97X | −0.52898 | 0.50860 | 9.9390 | −2.90437 | 2.87235 | 4.0709 | −7.28655 | 7.27475 | 1.1302 |
| B2PLYP | −0.52488 | 0.50280 | 10.0224 | −2.90463 | 2.86924 | 4.0547 | −7.26813 | 7.23682 | 1.1480 |
| VMC | −0.52755(4) | 0.5248(6) | 10.3775 | −2.90359(7) | 2.912(4) | 4.0106 | −7.27991(4) | 7.292(6) | 1.1204 |
| DMC | −0.52779(2) | 0.5237(9) | 10.3119 | −2.90386(7) | 2.908(3) | 4.0256 | −7.27997(4) | 7.298(6) | 1.1143 |
| Method | Total Energy | Kinetic Energy | Entropy | Total Energy | Kinetic Energy | Entropy | Total Energy | Kinetic Energy | Entropy |
|---|---|---|---|---|---|---|---|---|---|
| C− | N | O+ | |||||||
| UHF | −5.35111 | 3.59151 | 16.5669 | −9.67304 | 6.80209 | 11.2305 | −15.27536 | 10.78233 | 7.5464 |
| USVWN | −5.44029 | 3.52699 | 17.7825 | −9.72520 | 6.75214 | 11.5299 | −15.29526 | 10.73464 | 7.7365 |
| UPW91 | −5.48765 | 3.58086 | 17.6413 | −9.79981 | 6.83133 | 11.4282 | −15.39928 | 10.84028 | 7.6524 |
| UPBE0 | −5.47450 | 3.58184 | 17.1388 | −9.79225 | 6.81302 | 11.3493 | −15.39264 | 10.81020 | 7.6112 |
| UB3LYP | −5.46483 | 3.59524 | 17.3775 | −9.78493 | 6.83758 | 11.3852 | −15.38900 | 10.83889 | 7.6330 |
| UrevTPSS | −5.49420 | 3.61922 | 16.8359 | −9.81463 | 6.82378 | 11.3659 | −15.41653 | 10.82372 | 7.6172 |
| UCAMB3LYP | −5.46771 | 3.62211 | 17.0112 | −9.78632 | 6.83303 | 11.4052 | −15.38512 | 10.82775 | 7.6555 |
| UB97X | −5.46535 | 3.66699 | 16.8368 | −9.78760 | 6.86984 | 11.3268 | −15.39130 | 10.87310 | 7.5819 |
| UB2PLYP | −5.43696 | 3.61515 | 16.6868 | −9.74356 | 6.79620 | 11.3129 | −15.38589 | 10.81562 | 7.5928 |
| VMC | −5.46486(4) | 3.6547(5) | 16.8599 | −9.78662(5) | 6.8672(9) | 11.2796 | −15.39153(8) | 10.855(2) | 7.5655 |
| DMC | −5.47112(2) | 3.6689(3) | 16.8686 | −9.79314(2) | 6.9054(5) | 11.2699 | −15.39865(2) | 10.9094(6) | 7.5608 |
| Method | Total Energy | Kinetic Energy | Entropy | Total Energy | Kinetic Energy | Entropy |
|---|---|---|---|---|---|---|
| F− | Ne | |||||
| RHF | −23.98621 | 18.82316 | 10.994 | −34.70905 | 27.73954 | 5.272 |
| SVWN | −24.21194 | 19.00417 | 12.025 | −34.87089 | 27.72792 | 5.722 |
| PW91 | −24.35071 | 18.97835 | 11.934 | −35.05853 | 27.97595 | 5.601 |
| PBE0 | −24.30801 | 18.93859 | 11.530 | −35.02224 | 27.90528 | 5.481 |
| B3LYP | −24.32192 | 18.96881 | 11.655 | −35.03774 | 27.94395 | 5.545 |
| revTPSS | −24.34359 | 18.95492 | 11.753 | −35.05088 | 27.93728 | 5.553 |
| CAMB3LYP | −24.32105 | 18.97777 | 11.607 | −35.03248 | 27.93379 | 5.571 |
| B97X | −24.32782 | 19.00417 | 11.532 | −35.04599 | 27.98958 | 5.475 |
| B2PLYP | −24.20896 | 18.92158 | 11.326 | −34.93208 | 27.87075 | 5.422 |
| VMC | −24.3011(1) | 19.075(3) | 11.4523 | −35.01487(8) | 27.998(3) | 5.441 |
| DMC | −24.31239(3) | 19.201(1) | 11.4481 | −35.02504(3) | 28.166(1) | 5.440 |
| Method | MARE |
|---|---|
| RHF | 0.0329 |
| SVWN | 0.0508 |
| PW91 | 0.0405 |
| PBE0 | 0.0111 |
| B3LYP | 0.0167 |
| revTPSS | 0.0115 |
| CAMB3LYP | 0.0171 |
| B97X | 0.0151 |
| B2PLYP | 0.0165 |
| VMC | 0.0024 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amovilli, C.; Floris, F.M. Shannon Entropy in Atoms: A Test for the Assessment of Density Functionals in Kohn-Sham Theory. Computation 2018, 6, 36. https://doi.org/10.3390/computation6020036
Amovilli C, Floris FM. Shannon Entropy in Atoms: A Test for the Assessment of Density Functionals in Kohn-Sham Theory. Computation. 2018; 6(2):36. https://doi.org/10.3390/computation6020036
Chicago/Turabian StyleAmovilli, Claudio, and Franca Maria Floris. 2018. "Shannon Entropy in Atoms: A Test for the Assessment of Density Functionals in Kohn-Sham Theory" Computation 6, no. 2: 36. https://doi.org/10.3390/computation6020036
APA StyleAmovilli, C., & Floris, F. M. (2018). Shannon Entropy in Atoms: A Test for the Assessment of Density Functionals in Kohn-Sham Theory. Computation, 6(2), 36. https://doi.org/10.3390/computation6020036




