3D FEM Analysis of a Pile-Supported Riverine Platform under Environmental Loads Incorporating Soil-Pile Interaction
Abstract
:1. Introduction
2. Model Description
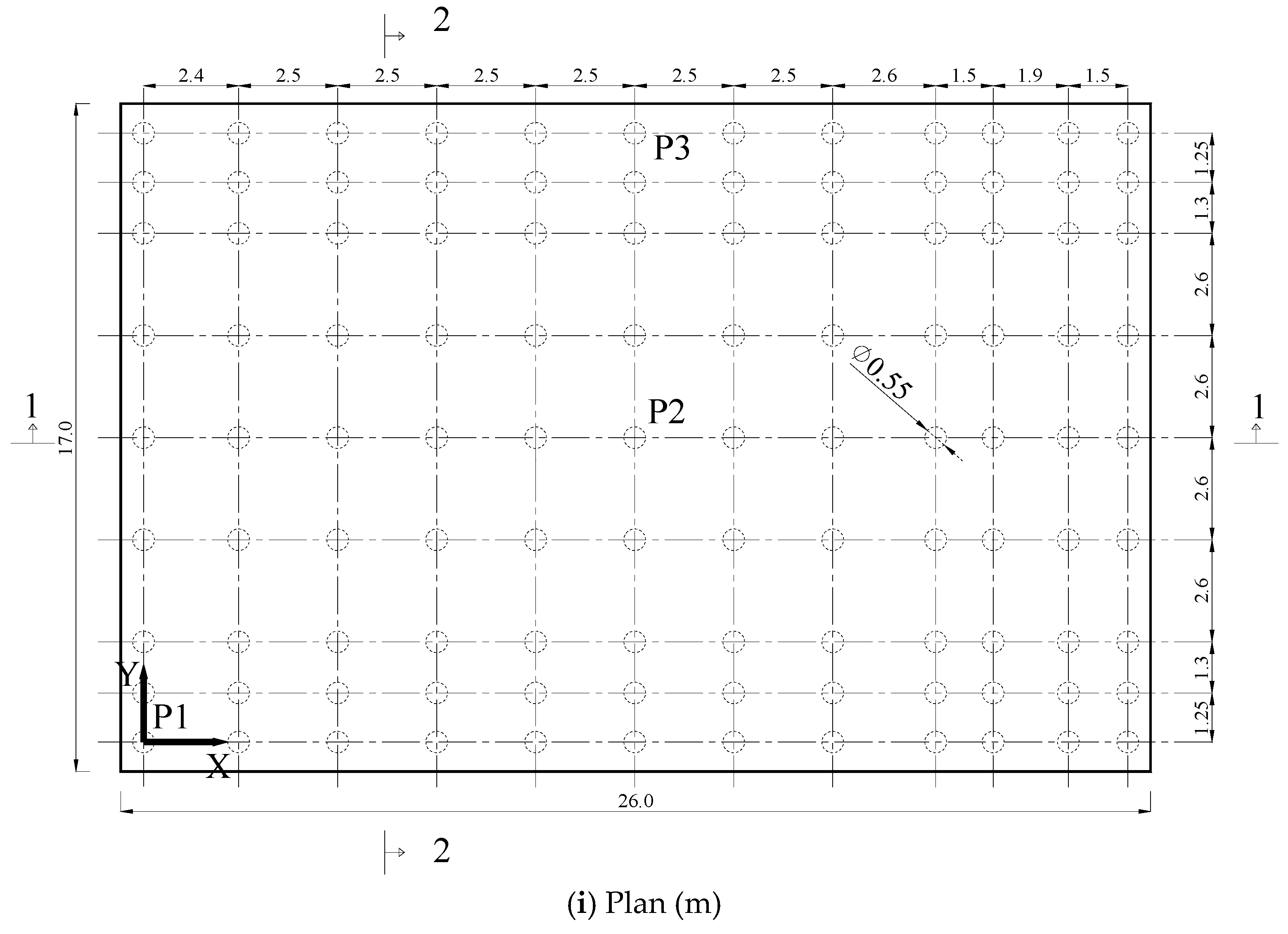
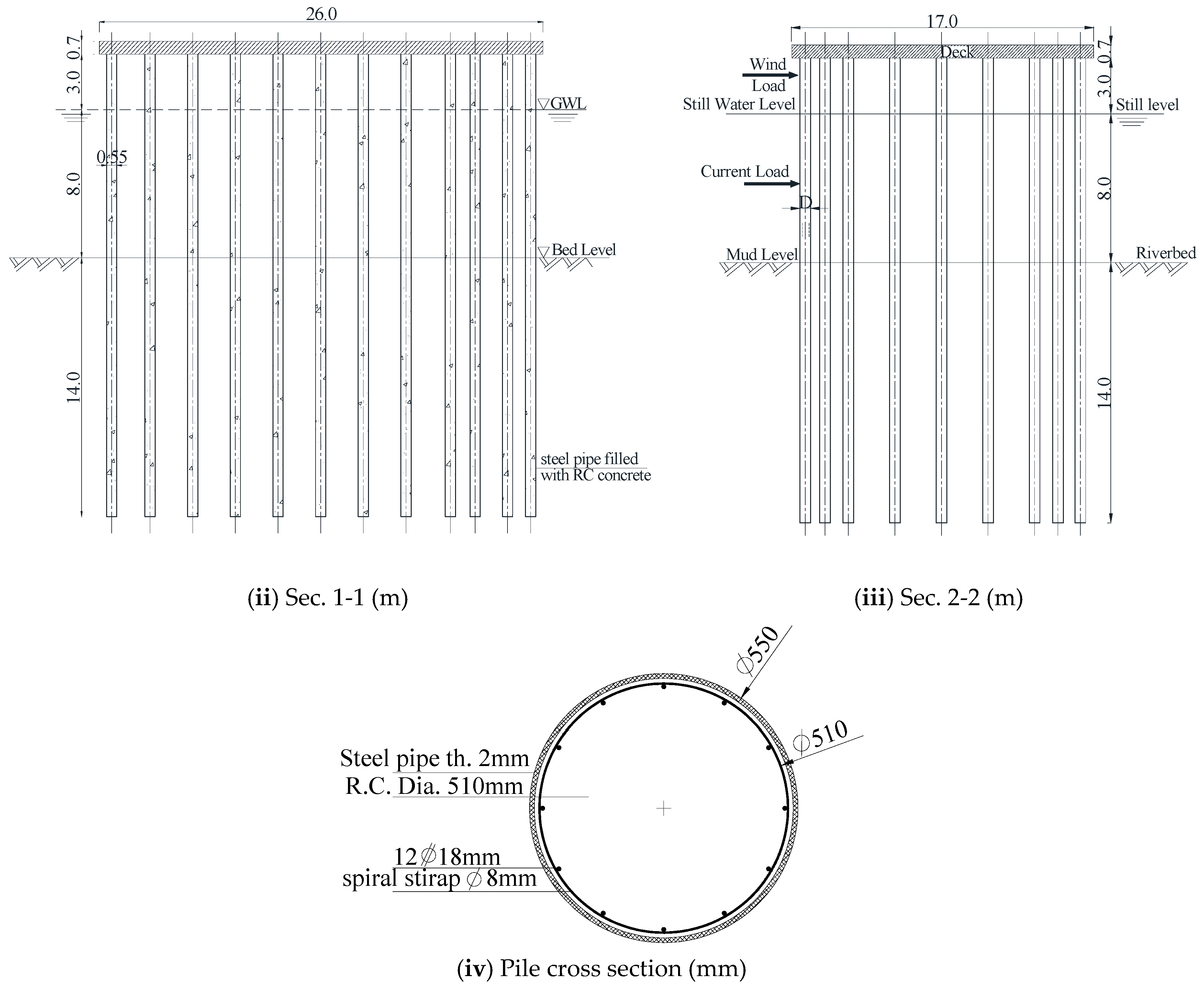
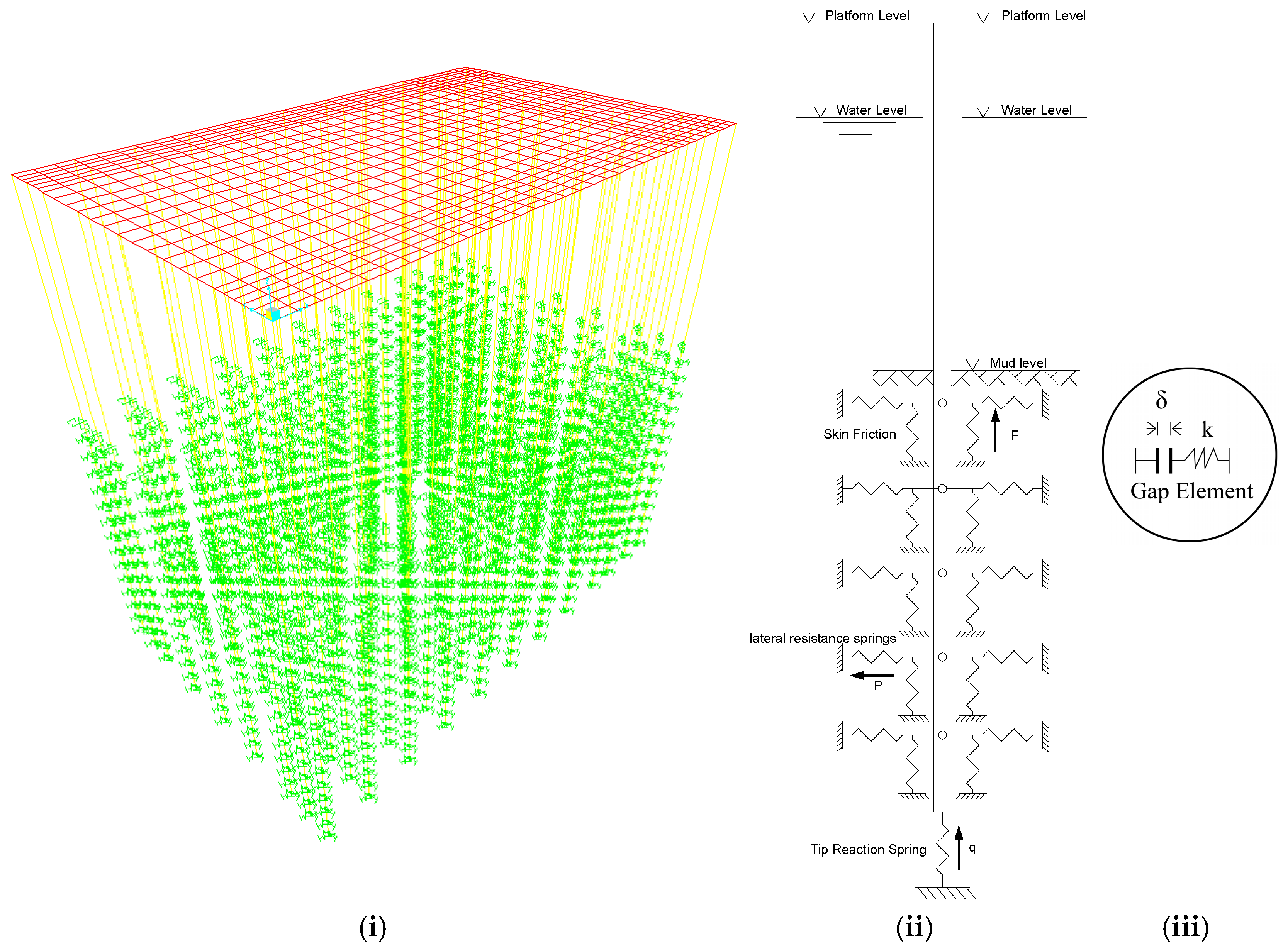
2.1. Computer Modeling of Platform
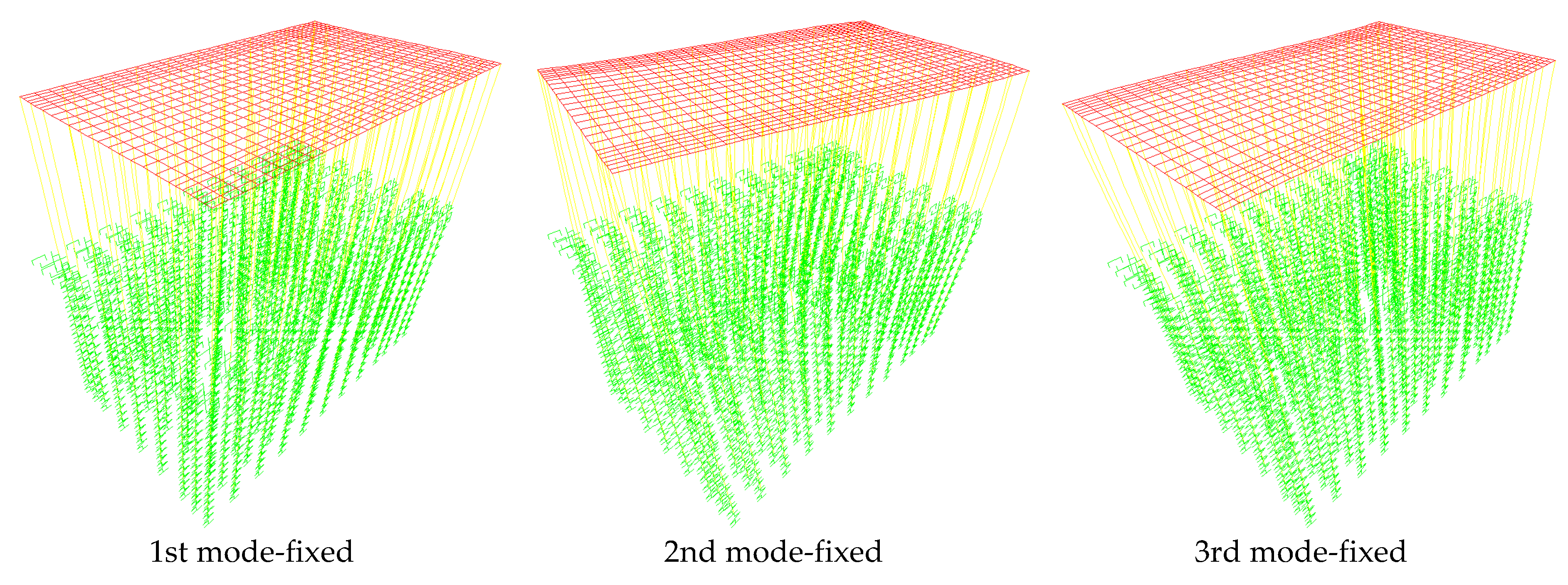
2.2. Natural Vibration Analysis
2.3. Environmental Loads
2.3.1. Current Force
2.3.2. Wave Force
2.3.3. Wind Force
2.4. Design of Piles for Skin Friction and Tip Resistance
2.5. Soil Layers of River Bed
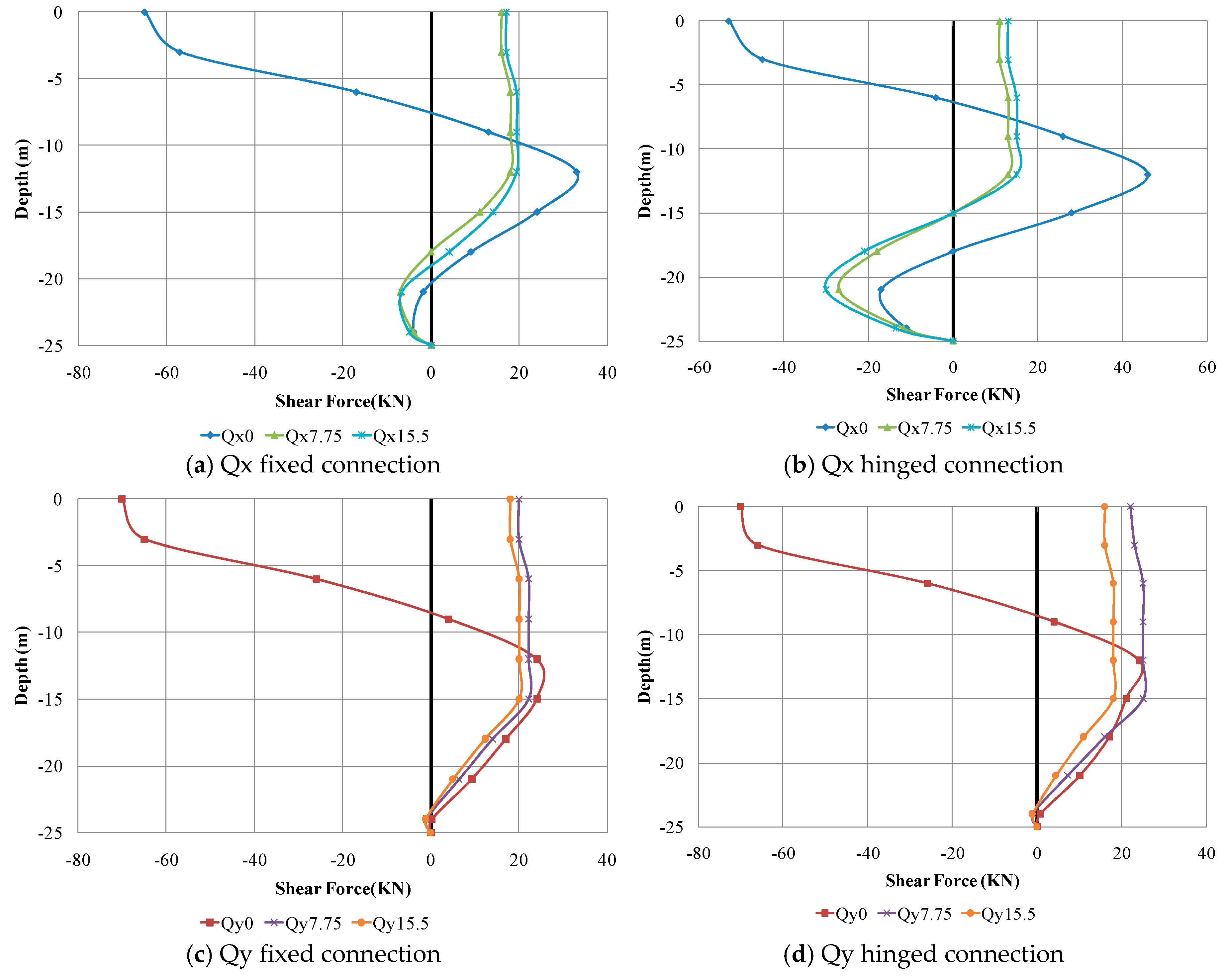
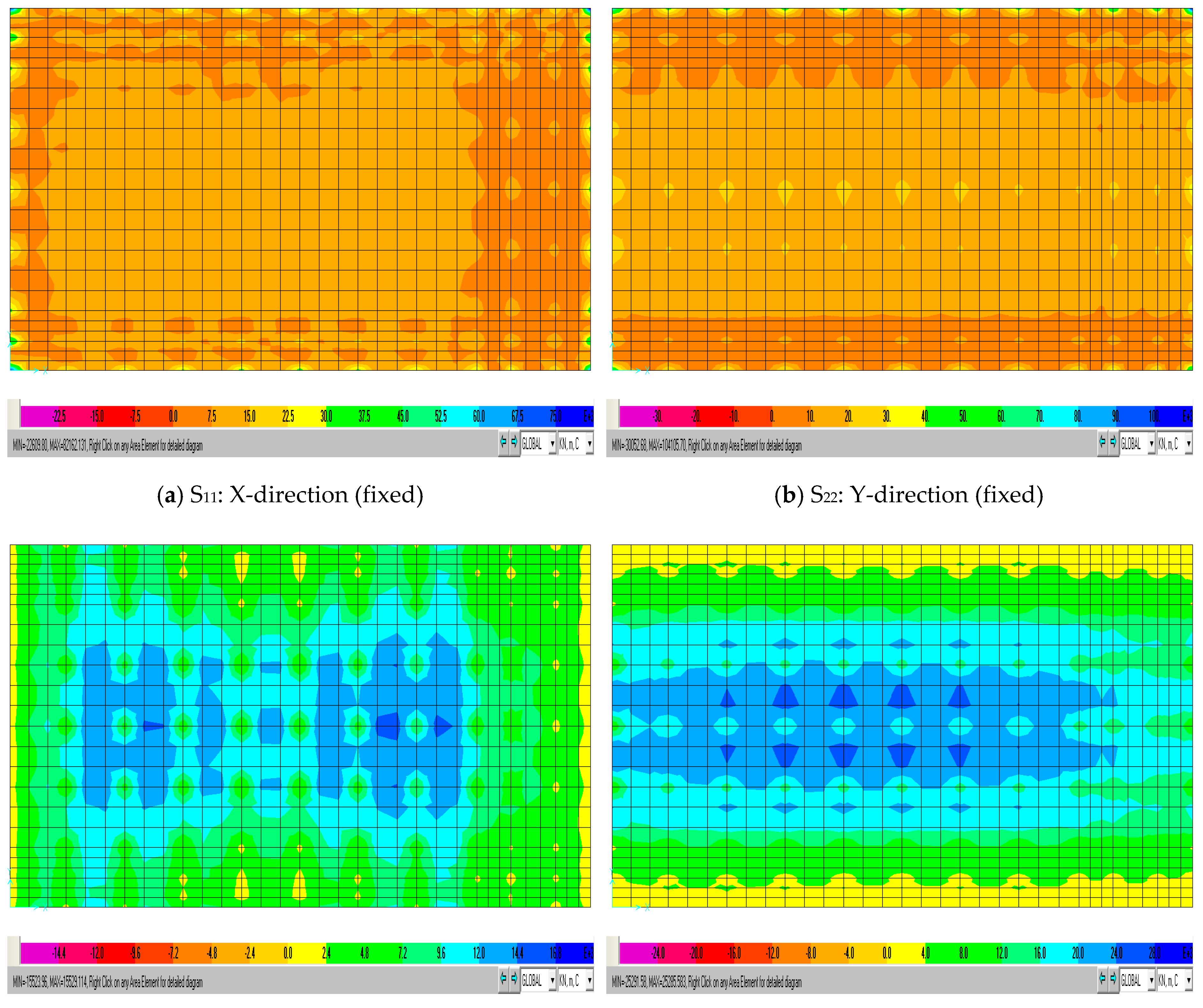
3. Results and Discussion
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Lysmer, J.; Kuhlemeyer, R.L. Finite Dynamic Model for Infinite Media. J. Eng. Mech. Div. (ASCE) 1969, 95, 859–878. [Google Scholar]
- Tallavó, F.; Martinez, M.E.; Ewins, D.J. Experimental evaluation of vibrations in an operating offshore platform. In Proceedings of the 13th International Modal Analysis Conference (IMAC XIII), Nashville, TN, USA, 13–16 February 1995; Society for Experimental Mechanics Inc.: Bethel, CT, USA, 1995; pp. 1847–1852. [Google Scholar]
- Razavi, S.A.; Fakher, A.; Mirghaderi, S.R. An Insight into the Bad Reputation of Batter Piles in Seismic Performance of Wharves. In Proceedings of the 4th International Conference on Earthquake Geotechnical Engineering, Thessaloniki, Greece, 25–28 June 2007; Pitilakis, K.D., Ed.; Springer: Dordrecht, Germany, 2007; pp. 1–10. ISBN 978-1-4020-5893-6. Available online: http://extras.springer.com/2007/978-1-4020-5893-6/paperpdf/1423_raz.pdf (accessed on 2 January 2017).
- Chau, K.T.; Shen, C.Y.; Guo, X. Nonlinear seismic soil–pile–structure interactions: Shaking table tests and FEM analyses. Soil Dyn. Earthq. Eng. 2009, 29, 300–310. [Google Scholar] [CrossRef]
- Hussien, M.N.; Tobita, T.; Iai, S. Experimental and FE analysis of seismic soil-pile-superstructure interaction in sand. Ann. Disaster Prev. Res. Inst. B 2010, 53, 299–306. Available online: http://www.dpri.kyoto-u.ac.jp/nenpo/no53/ronbunB/a53b0p34.pdf (accessed on 2 January 2017).
- Abu Seif, E.-S.S.; El-Shater, A.A. Engineering aspects and associated problems of flood plain deposits in Sohag Governorate, Upper Egypt. J. Am. Sci. 2010, 6, 1614–1623. [Google Scholar] [CrossRef]
- Mandal, B.; Roy, R.; Dutta, S.C. Lateral capacity of piles in layered soil: A simple approach. Struct. Eng. Mech. 2012, 44, 571–584. [Google Scholar] [CrossRef]
- Chore, H.S.; Ingle, R.K.; Sawant, V.A. Building frame–pile foundation–soil interaction analysis: A parametric study. Interact. Multiscale Mech. 2010, 3, 55–79. [Google Scholar] [CrossRef]
- Ravi Kumar Reddy, C.; Gunneswara Rao, T.D. Experimental study of a modeled building frame supported by pile groups embedded in cohesionless soil. Interact. Multiscale Mech. 2011, 4, 321–336. [Google Scholar] [CrossRef]
- Kaynia, A.M. Dynamic response of pile foundations with flexible slabs. Earthq. Struct. 2012, 3, 495–506. [Google Scholar] [CrossRef]
- Asgarian, B.; Shokrgozar, H.R.; Shahcheraghi, D.; Ghasemzadeh, H. Effect of soil pile structure interaction on dynamic characteristics of jacket type offshore platforms. Coupled Syst. Mech. 2012, 1, 381–395. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, X.-I. Reliability analysis of steel cable-stayed bridges including soil-pile interaction. Steel Compos. Struct. 2012, 13, 109–122. [Google Scholar] [CrossRef]
- Hamilton, M. Pile-Soil Interaction in Unsaturated Soil Conditions; Senior Honors Thesis in Partial Fulfillment of the Requirements for Honors in Civil Engineering; University of New Hampshire: Durham, NH, USA, 2014; Available online: http://scholars.unh.edu/cgi/viewcontent.cgi?article=1181&context=honors (accessed on 2 January 2017).
- Dode, P.A.; Chore, H.S.; Agrawal, D.K. Interaction analysis of a building frame supported on pile groups. Coupled Syst. Mech. 2014, 3, 305–318. [Google Scholar] [CrossRef]
- Mehndiratta, S.; Sawant, V.A.; Samadhiya, N.K. Nonlinear dynamic analysis of laterally loaded pile. Struct. Eng. Mech. 2014, 49, 479–489. [Google Scholar] [CrossRef]
- Abdel-Mohti, A.; Khodair, Y. Analytical investigation of pile–soil interaction in sand under axial and lateral loads. Int. J. Adv. Struct. Eng. 2014, 6, 1–16. [Google Scholar] [CrossRef]
- Kaynia, A.M.; Andersen, K.H. Development of nonlinear foundation springs for dynamic analysis of platforms. In Proceedings of the Frontiers in Offshore Geotechnics III–3rd International Symposium on Frontiers in Offshore Geotechnics (ISFOG 2015), Oslo, Norway, 10–12 June 2015; Meyer, V., Ed.; CRCPress/Balkema–Taylor & Francis Group: Leiden, The Netherlands, 2015; Volume 1, pp. 1067–1072. [Google Scholar]
- Kaynia, A.M.; Norén-Cosgriff, K.; Andersen, K.H.; Tuen, K.A. Nonlinear foundation spring and calibration using measured dynamic response of structure. In Proceedings of the 34th International Conference on Ocean, Offshore and Arctic Engineering, OMAE2015, St. John’s, NL, Canada, 31 May–5 June 2015; ASME: New York, NY, USA, 2015; Volume 1. [Google Scholar] [CrossRef]
- Kim, S.B.; Yoon, G.L.; Yi, J.H.; Lee, J.H. Reliability analysis of laterally loaded piles for an offshore wind turbine support structure using response surface methodology. Wind Struct. 2015, 21, 597–607. [Google Scholar] [CrossRef]
- Yi, J.-H.; Kim, S.-B.; Yoon, G.-L.; Andersen, L.V. Natural frequency of bottom-fixed offshore wind turbines considering pile-soil-interaction with material uncertainties and scouring depth. Wind Struct. 2015, 21, 625–639. [Google Scholar] [CrossRef]
- Durante, M.G.; Di Sarno, L.; Mylonakis, G.; Taylor, C.A.; Simonelli, A.L. Soil–pile–structure interaction: Experimental outcomes from shaking table tests. Earthq. Eng. Struct. Dyn. 2015, 45, 1041–1061. [Google Scholar] [CrossRef]
- Chatterjee, K.; Choudhury, D.; Poulos, H.G. Seismic analysis of laterally loaded pile under influence of vertical loading using finite element method. Comput. Geotech. 2015, 67, 172–186. [Google Scholar] [CrossRef]
- Ukritchon, B.; Faustino, J.C.; Keawsawasvong, S. Numerical investigations of pile load distribution in pile group foundation subjected to vertical load and large moment. Geomech. Eng. 2016, 10, 577–598. [Google Scholar] [CrossRef]
- Elnashai, A.S.; Di Sarno, L. Fundamentals of Earthquake Engineering: From Source to Fragility, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2015; ISBN 978-1118678923. [Google Scholar]
- SAP2000® Version 17. Integrated Software for Structural Analysis and Design, Computers and Structures, Inc.: Walnut Creek, CA, USA; New York, NY, USA, 2015.
- Chore, H.S.; Ingle, R.K. Interaction Analysis of Building Frame Supported on Pile Group. Indian Geotech. J. 2008, 38, 483–501. [Google Scholar]
- American Concrete Institute (ACI). Building Code Requirements for Structural Concrete (ACI318-08) and Commentary (ACI318R-08); ACI: Farmington Hills, MI, USA, 2008; ISBN 978-0-87031-264-9. [Google Scholar]
- Egyptian Code of Practice for loading (ECP-201). Egyptian Code for Calculating Loads and Forces in Structural Work and Masonry; (ECP-201); Housing and Building National Research Center, Ministry of Housing, Utilities and Urban Planning: Cairo, Egypt, 2008.
- American Petroleum Institute (API). API Recommended Practice 2A-WSD (RP 2A-WSD), Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms–Working Stress Design, 21st ed.; American Petroleum Institute (API): Washington, DC, USA, 2000. [Google Scholar]
- Chandrasekaran, S. Dynamic Analysis and Design of Offshore Structures, 1st ed.; Springer India: New Delhi, India, 2015; ISBN 978-81-322-2277-4 (eBook); 978-81-322-2276-7 (Hardcover); 978-81-322-3433-3 (Softcover). [Google Scholar] [CrossRef]
- Sutcliffe, J.V.; Parks, Y.P. The Hydrology of the Nile; Institute of Hydrology, International Association of Hydrological Sciences (IAHS) Special Publication No. 5; IAHS Press: Wallingford, UK, 1999; Available online: www.hydrosciences.fr/sierem/produits/biblio/hydrology%20of%20the%20Nile.pdf (accessed on 2 January 2017).
- Mosher, R.L.; Dawkins, W.P. Theoretical Manual for Pile Foundations, Report ERDC/ITL TR-00-5. U.S. Army Corps of Engineers, Engineer Research and Development Center: Washington, DC, USA, 2000. Available online: https://erdc-library.erdc.dren.mil/xmlui/bitstream/handle/11681/10873/9451.pdf?sequence=1&isAllowed=y (accessed on 2 January 2017).
- Naval Facilities Engineering Command (NAVFAC). Foundations and Earth Structures–Naval Facilities Engineering Command Design Manual 7.02 (NAVFAC DM 7.02); Naval Facilities Engineering Command (NAVFAC): Alexandria, VA, USA, 1986; Available online: http://web.mst.edu/~rogersda/umrcourses/ge441/dm7_02.pdf (accessed on 2 January 2017).
- Warner, J.W.; Gates, T.K.; Fahim, W.; Ibrahim, M.; Awad, M.; Ley, T.W. Hydraulic Conductivity and Vertical Leakage in the Clay Silt Layer of the Nile Alluvium in Egypt; Technical Report No. 60; Egypt Water Use and Management Project, Water Distribution Research Institute, Water Research Center, Ministry of Irrigation, Government of Egypt: Cairo, Egypt, 1984. Available online: http://pdf.usaid.gov/pdf_docs/PNAAR143.pdf (accessed on 2 January 2017).
- Newmark, N.M.; Rosenblueth, E. Fundamentals of Earthquake Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971; ISBN 013336206X. [Google Scholar]

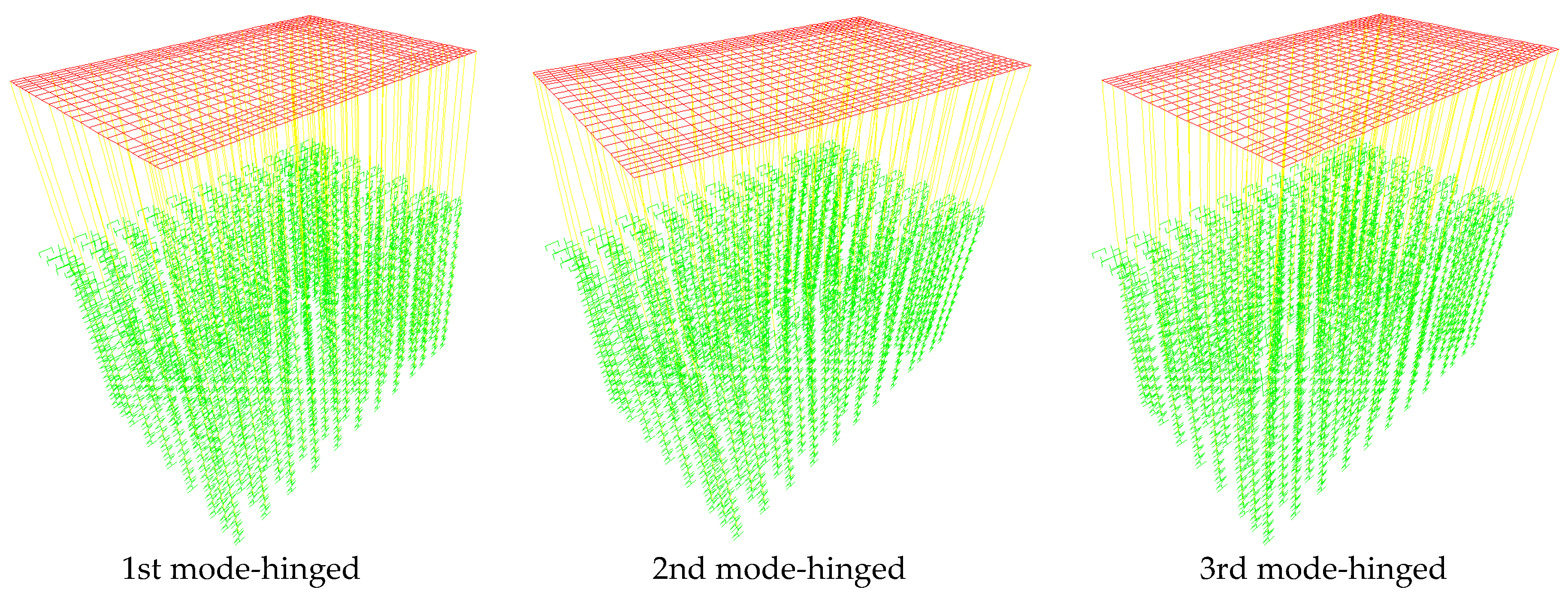
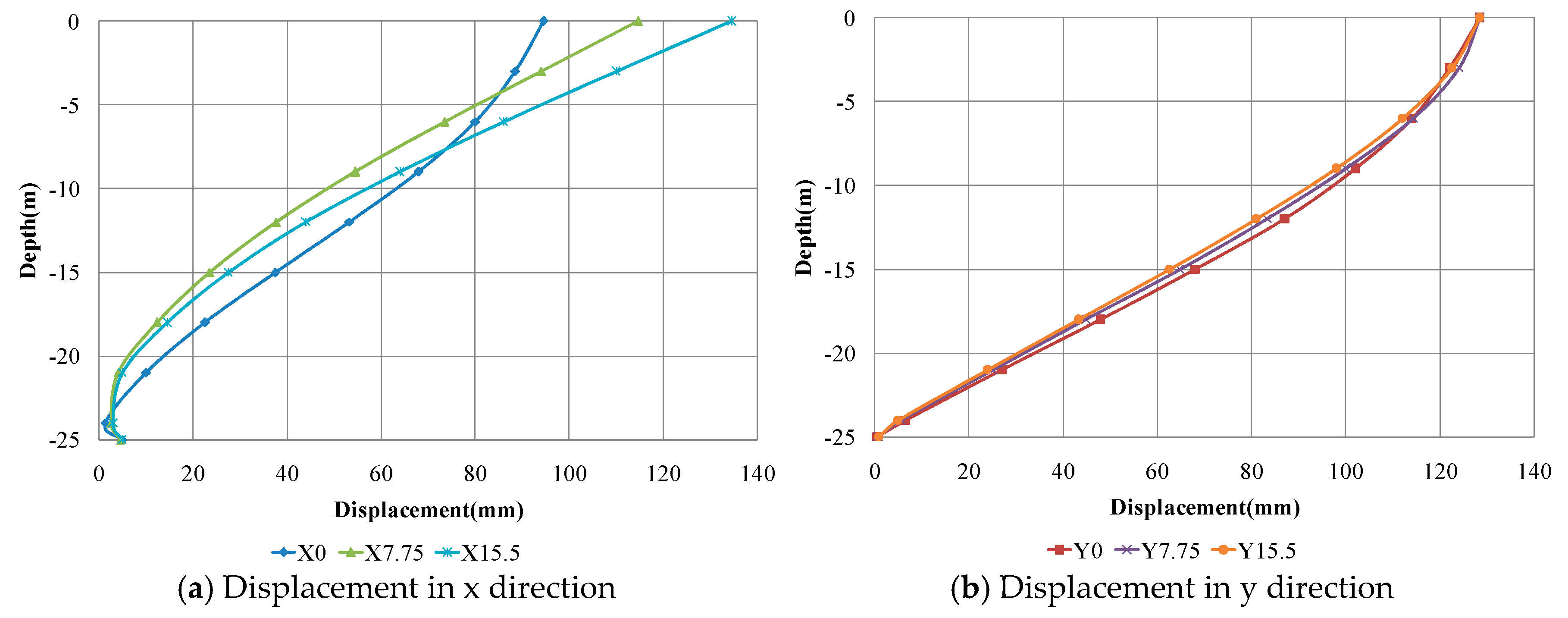
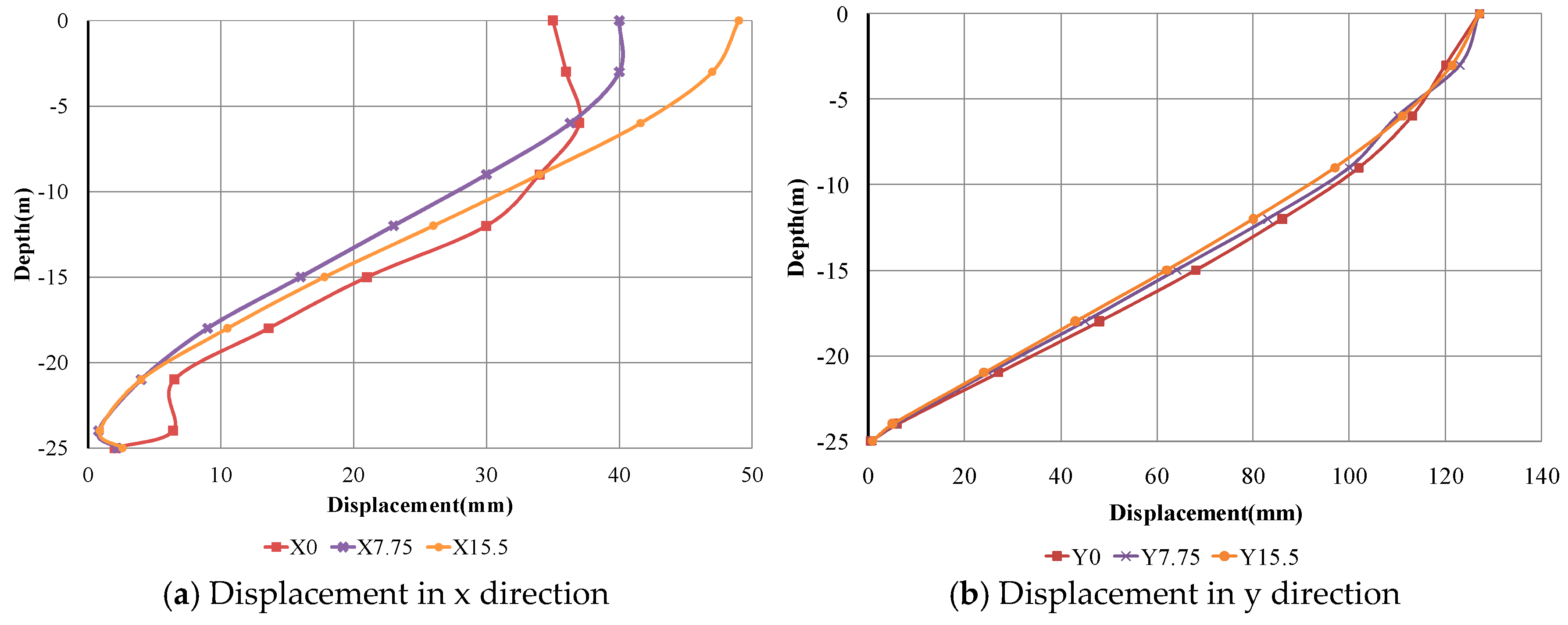

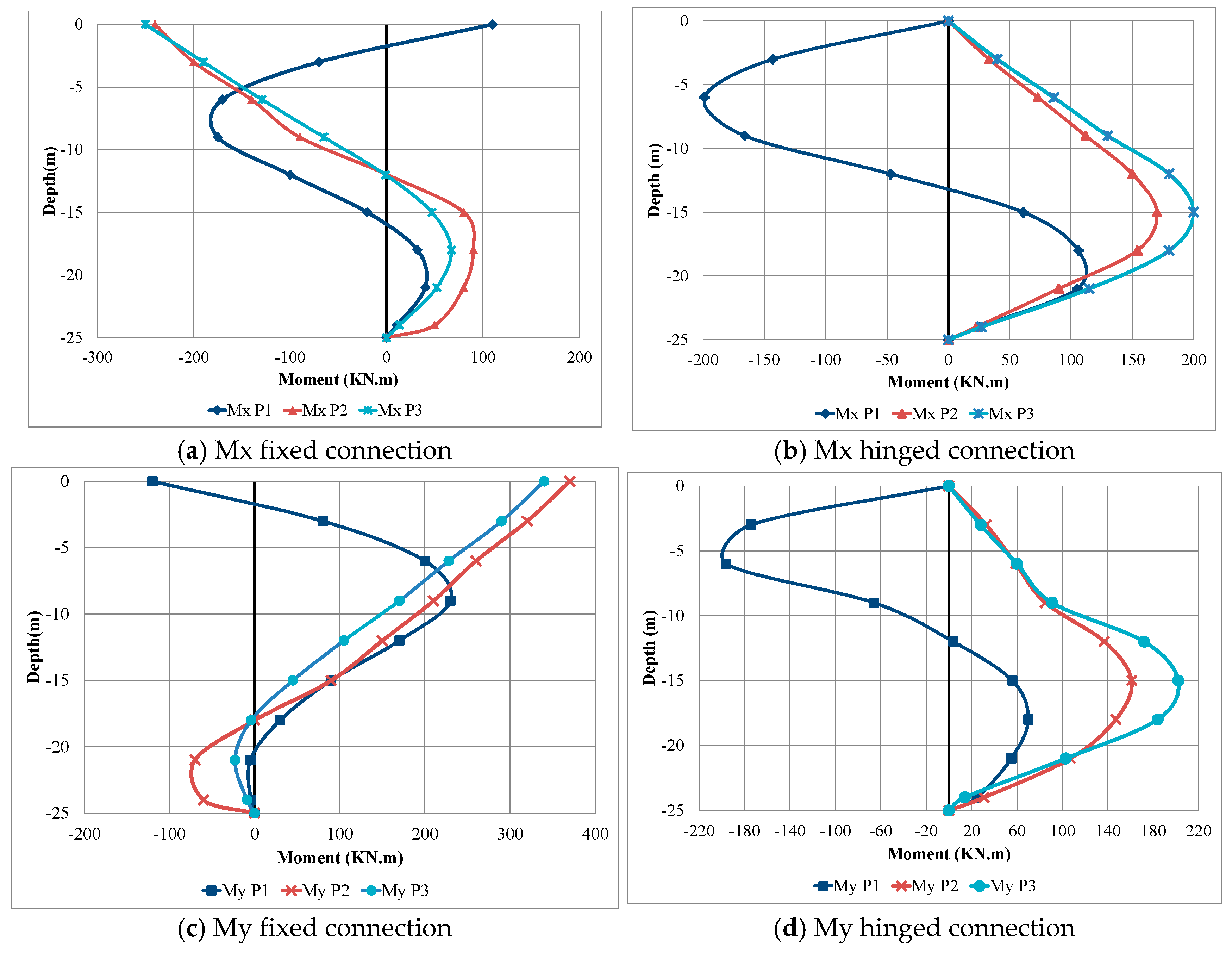
| Properties | Corresponding Values |
|---|---|
| Pile diameter (D) | 550 mm |
| Length of pile (L) | 25 m |
| Thickness of pile cap | 800 mm |
| Grade of concrete used for pile cap | Characteristic compressive strength: 40 MPa |
| Young’s modulus of elasticity (EC) | 0.3605 × 108 kPa |
| Poisson’s ratio for concrete (μC) | 0.15 |
| Mode | Fixed | Hinged | ||
|---|---|---|---|---|
| ω2 (rad/s)2 | T (s) | ω2 (rad/s)2 | T (s) | |
| 1 | 7.47 | 2.30 | 2.12 | 4.31 |
| 2 | 13.8 | 1.68 | 4.86 | 2.85 |
| 3 | 22.6 | 1.32 | 9.39 | 2.05 |
| 4 | 195 | 0.45 | 150 | 0.51 |
| 5 | 202.6 | 0.44 | 150 | 0.51 |
| 6 | 221.7 | 0.42 | 150 | 0.51 |
| Layer | Depth (m) | Description | Cu (kN/m2) | γ (kN/m3) | φ(ο) | ν | Es (kN/m2) | Stiffness (kN/m) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Kx | Ky | Kz | ||||||||
| Layer (1) | −2:−4 | Medium | 50 | 18 | 30 | 0.45 | 3200 | 25 | 25 | 72 |
| Layer (2) | −4:−8 | Stiff | 100 | 19 | 35 | 0.35 | 5625 | 66 | 66 | 122 |
| Layer (3) | −8:−14 | Very stiff | 200 | 22 | 37 | 0.30 | 11,250 | 100 | 100 | 201 |
| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| X 0 | Displacement in x-direction for pile P1 (at zero distance from platform) | Mx 0, Mx P1 | Bending moment in x-direction in pile P1 (at zero distance from platform) |
| X 7.75 | Displacement in x-direction for pile P2 (at 7.75 m distance from platform) | Mx 7.75, Mx P2 | Bending moment in x-direction in pile P2 (at 7.75 m distance from platform) |
| X 15.5 | Displacement in x-direction for pile P3 (at 15.5 m distance from platform) | Mx 15.5, Mx P3 | Bending moment in x-direction in pile P3 (at 15.5 m distance from platform) |
| Y 0 | Displacement in y-direction for pile P1 (at zero distance from platform) | My 0, My P1 | Bending moment in y-direction in pile P1 (at zero distance from platform) |
| Y 7.75 | Displacement in y-direction for pile P2 (at 7.75 m distance from platform) | My 7.75, My P2 | Bending moment in y-direction in pile P2 (at 7.75 m distance from platform) |
| Y 15.5 | Displacement in y-direction for pile P3 (at 15.5 m distance from platform) | My 15.5, My P3 | Bending moment in y-direction in pile P3 (at 15.5 m distance from platform) |
| Nf 0 | Normal force in pile P1 (at zero distance from platform) with fixed end condition | Qx 0 | Shear force in x-direction in pile P1 (at zero distance from platform) |
| Nf 7.75 | Normal force in pile P2 (at 7.75 m distance from platform) with fixed end condition | Qx 7.75 | Shear force in x-direction in pile P2 (at 7.75 m distance from platform) |
| Nf 15.5 | Normal force in pile P3 (at 15.5 m distance from platform) with fixed end condition | Qx 15.5 | Shear force in x-direction in pile P3 (at 15.5 m distance from platform) |
| Nh 0 | Normal force in pile P1 (at zero distance from platform) with hinged end condition | Qy 0 | Shear force in y-direction in pile P1 (at zero distance from platform) |
| Nh 7.75 | Normal force in pile P2 (at 7.75 m distance from platform) with hinged end condition | Qy 7.75 | Shear force in y-direction in pile P2 (at 7.75 m distance from platform) |
| Nh 15.5 | Normal force in pile P3 (at 15.5 m distance from platform) with hinged end condition | Qy 15.5 | Shear force in y-direction in pile P3 (at 15.5 m distance from platform) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontoni, D.-P.N.; Farghaly, A.A. 3D FEM Analysis of a Pile-Supported Riverine Platform under Environmental Loads Incorporating Soil-Pile Interaction. Computation 2018, 6, 8. https://doi.org/10.3390/computation6010008
Kontoni D-PN, Farghaly AA. 3D FEM Analysis of a Pile-Supported Riverine Platform under Environmental Loads Incorporating Soil-Pile Interaction. Computation. 2018; 6(1):8. https://doi.org/10.3390/computation6010008
Chicago/Turabian StyleKontoni, Denise-Penelope N., and Ahmed Abdelraheem Farghaly. 2018. "3D FEM Analysis of a Pile-Supported Riverine Platform under Environmental Loads Incorporating Soil-Pile Interaction" Computation 6, no. 1: 8. https://doi.org/10.3390/computation6010008
APA StyleKontoni, D.-P. N., & Farghaly, A. A. (2018). 3D FEM Analysis of a Pile-Supported Riverine Platform under Environmental Loads Incorporating Soil-Pile Interaction. Computation, 6(1), 8. https://doi.org/10.3390/computation6010008






