1. Introduction
The Pascal approximation was first introduced in [
1]. However, this approximation lacked one basic attribute all polynomial approximations used in filter design should share, namely the value of 1 at Ω = 1. Furthermore, a new modified Pascal function with the above feature was introduced in [
2], where a filter-appropriate modified symmetric Pascal function was acquired after some manipulation of the Pascal function. This later form of Pascal function is exploited further here.
The Pascal approximation [
1,
2,
3,
4], like other similar approximations used in filter design, uses a polynomial as the approximating function in the filter gain response
where N is the order of the filter, λ is the ripple factor, corresponding to the ε ripple factor of Chebyshev approximation,
is the maximum permitted passband gain and
is the modified Pascal polynomials of degree N from [
3,
4]
The frequency
is the frequency where the shifted and scaled symmetric Pascal function takes the value
, where
is the higher local maximum in the interval (−1, 1). Both variables are independent of Ω and they depend solely on the order of the filter (N). Their values for range of filter orders N is tabulated in [
3].
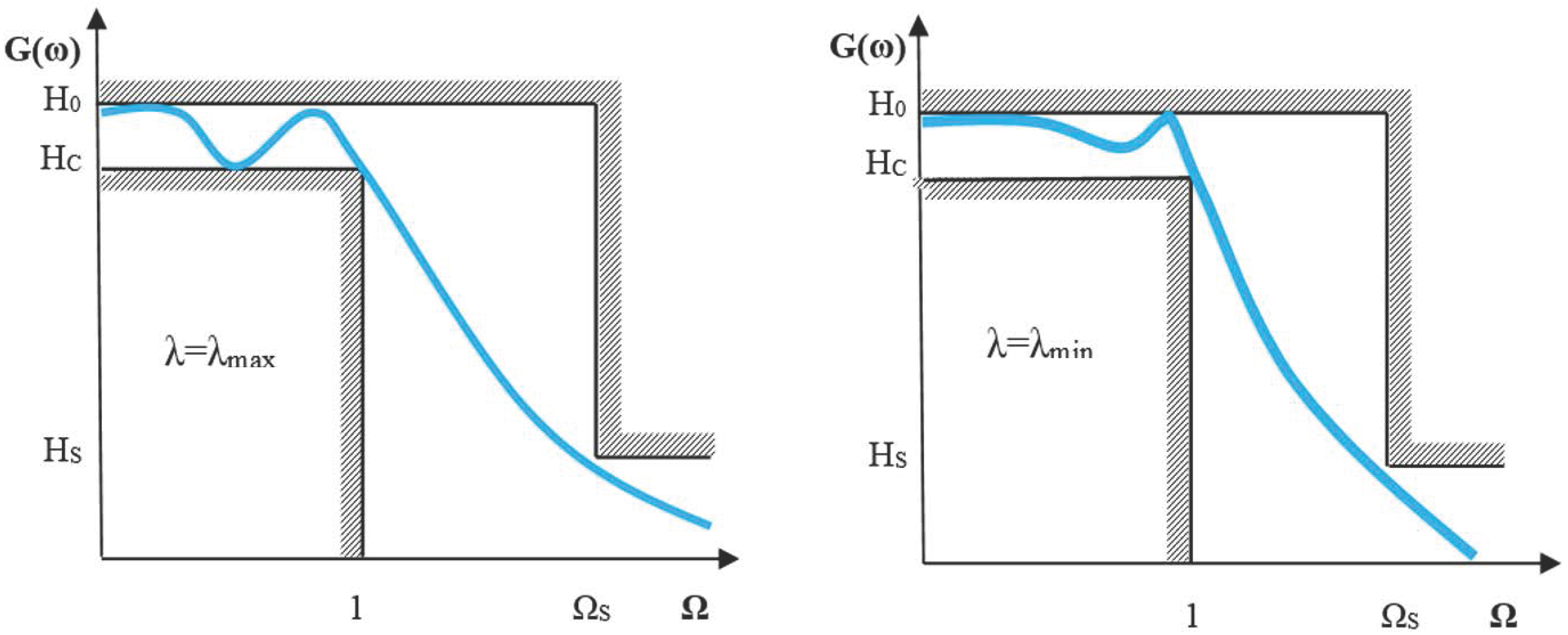
The ripple factor λ is bounded between
and
as presented in
Figure 1. The two bounds can be expressed either in linear form, as functions of the gains (
,
,
) or in the logarithmic form of logarithmic, as functions of the attenuation bounds
and
both bounds are positive
For the calculation of the filter order N, as (4) cannot be solved analytically for N, can be determined either from the nomograph in [
3] or from the inequality
In the above inequality, the only unknown is N therefore, order N can be calculated using a numerical software tool (e.g., Mathcad, MATLAB, etc.). As it has been shown in [
3], under the best case scenario, the order of the Pascal polynomial is the same with the order of the Chebyshev one (especially for low order filters) while under the worst case scenario it will be
.
The transfer function of the filter can be derived from the squared magnitude response
Since Equation (5) is a polynomial approximation, the filter transfer function is expected to be all-pole, given that the numerator will not have any finite zeros. The poles of the transfer function cannot be calculated analytically and again a numerical software tool should be used; the poles of the filter, however, must be selected as the roots lying on the left half s-plane (Hurwitz polynomial). The transfer function of the Pascal approximation can be expressed in the form
where
is the leading coefficient of the polynomial
and can be calculated from the Equation (3)
A more detailed version of this paper is presented in [
5], where the tables that have been created, are depicting the normalized values of passive elements for N = 2–9 for a variety of values of A
max.
2. Calculations of the Pascal Function Coefficients
In contrast to the most popular approximations used in the design of electric filters, the Pascal polynomials are not orthogonal. This feature results in some difficulties in the calculation of the coefficients of the polynomial. As a result of non-orthogonality, a recursive method (Christoffel–Darboux formula) cannot be used to calculate the coefficients of the polynomials. In this paper, a novel method is proposed to calculate all the coefficients of the Pascal polynomial.
The leading coefficient can be calculated directly from Equation (7). The key step for the calculation of the rest of them is to calculate the basic terms, as in the equation
The coefficients can then be calculated from the unique combinations of the basic terms, while the unique combinations will be expressed as
(see
Appendix A for the calculation of the coefficients for N = 8). The equation below yields the remaining coefficients of the Pascal function
The lowest order coefficient can be calculated three alternative ways. The first alternative uses Equation (9) with k = (Ν − h)/2, while the second is derived from [
3]
The third alternative is based on Equation (10). Instead of using a product the lowest coefficient can be calculated using the Gamma function
The number of terms of every coefficient can be calculated from the Pascal triangle. Indeed, a Pascal triangle is formed by the either the even or the odd columns in
Table 1. Alternatively, the number of terms can be obtained by the binomial coefficient as expressed below [
5]
Table 1 tabulates the number of terms of every coefficient for N = 2 to 9; it must be noted that the leading coefficient and the lowest order coefficient (A
k) will always have only one term.
The sum of the terms of every coefficient is equal to
. It must be mentioned that the ratio of the modified Pascal polynomial (P
D) over P
D(N, 1) = P
Dmax for N = 2 to 3, yields the C
Ν(Ω) of Chebyshev [
5].
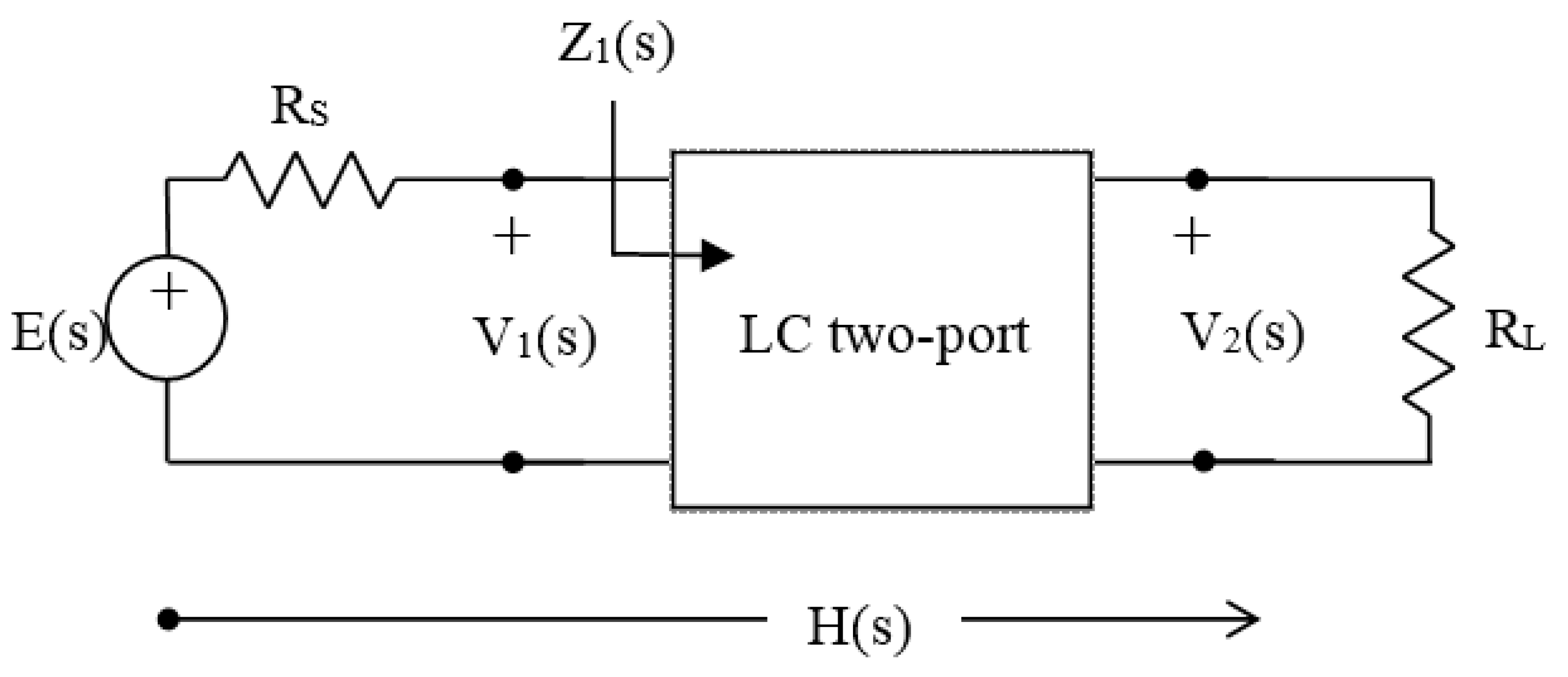
3. Passive Filter Design through the Pascal Approximation
The passive filter design has the form of the doubly resistively terminated two-port LC circuit, as shown in
Figure 2.
The passive filters have two more specifications than the active filters, namely R
S and R
L. Specifications are typically given in the form of effective attenuation A(Ω)
where P
max is the maximum power the source can deliver and P
2(Ω) is the average power of the load (R
L). Effective attenuation A(Ω) is assumed to have only positive values; it becomes zero at the frequencies of maximum power transfer.
The attenuation at dc (Ω = 0) is given by
The above equation is zero only when R
s = R
L and assumes only positives values for the other cases. The attenuation function Α (Ω) for all approximations must have Α (0) = Α
0 for the design of the passive doubly resistively terminated LC low-pass filter. The Pascal attenuation is given from [
4]
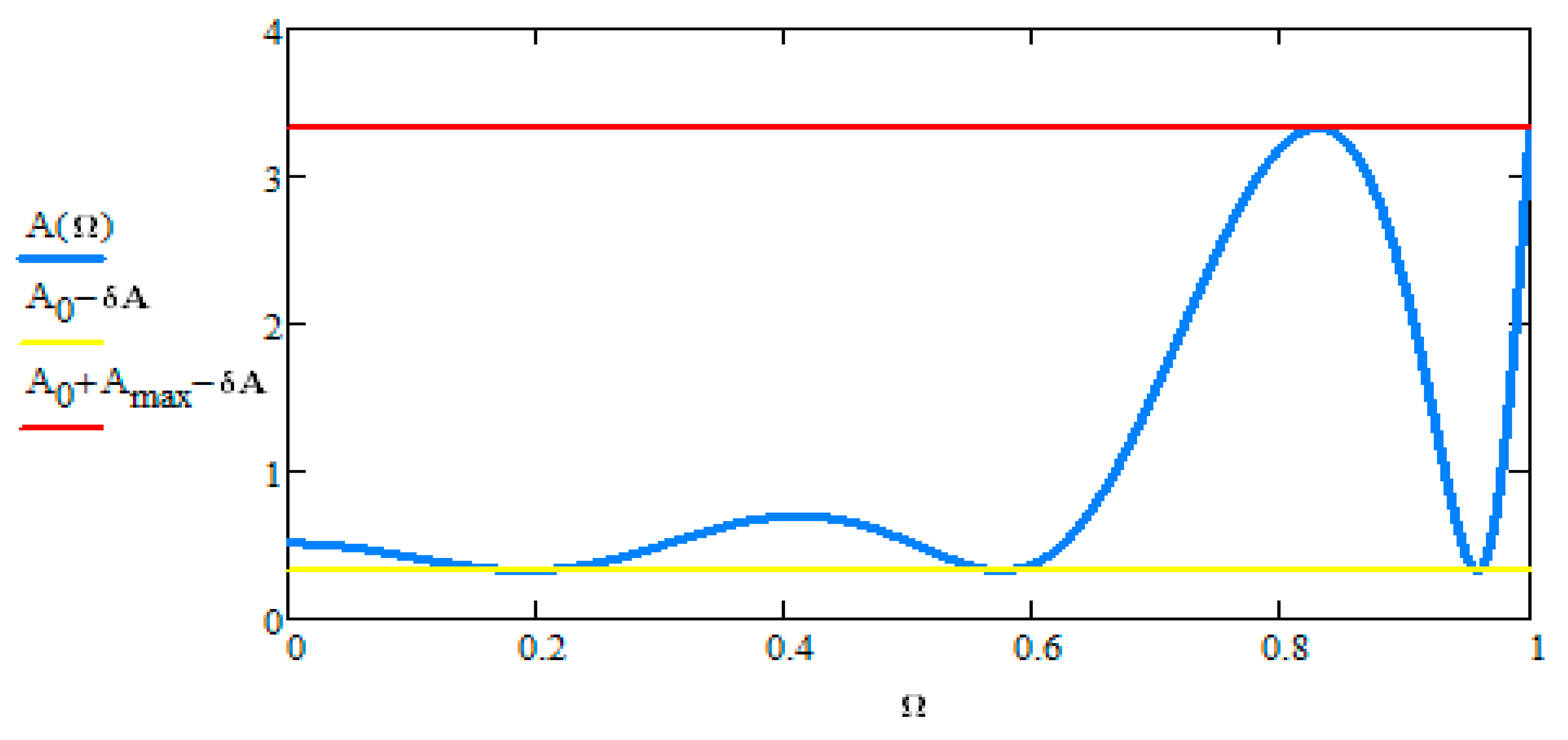
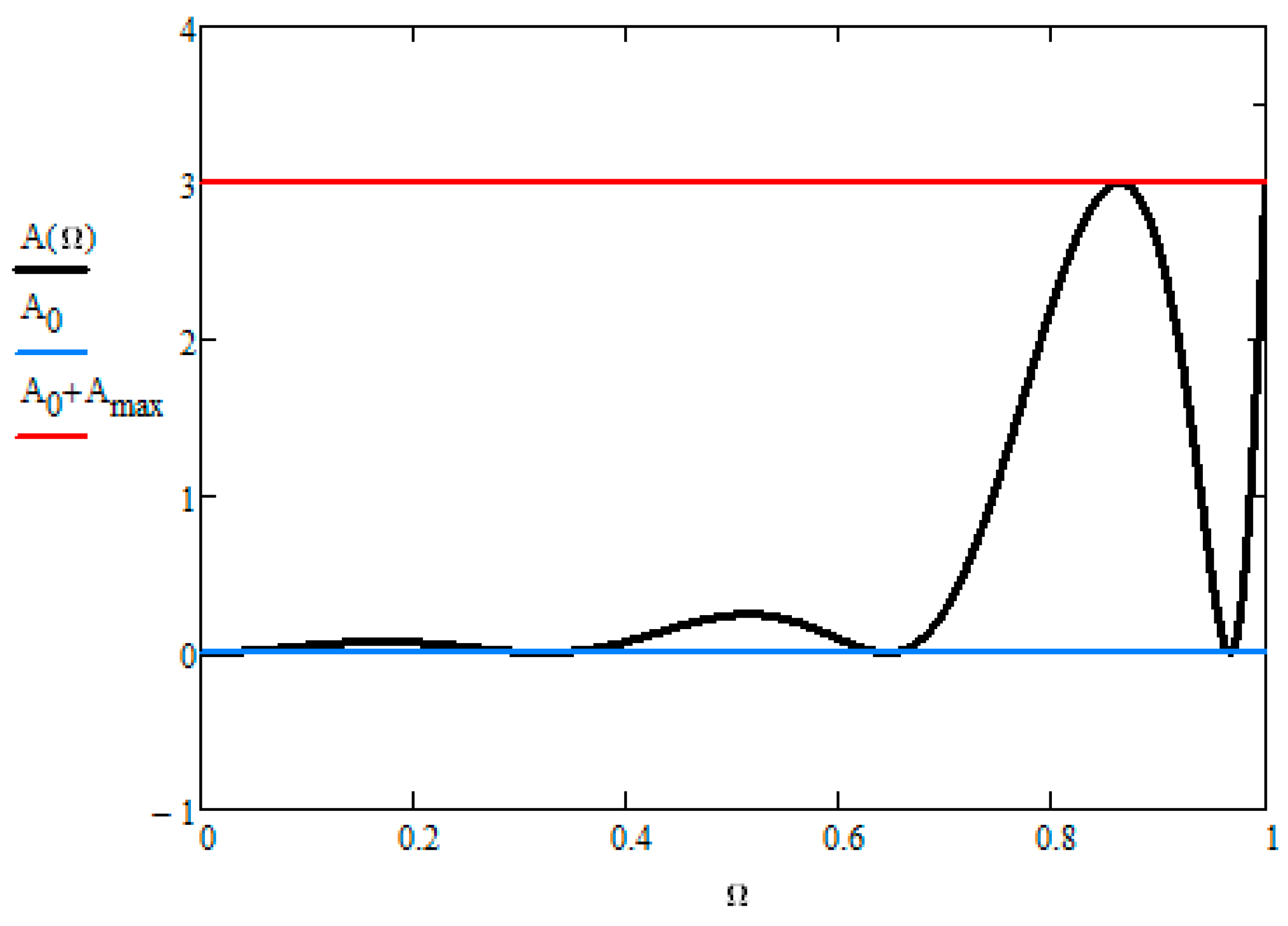
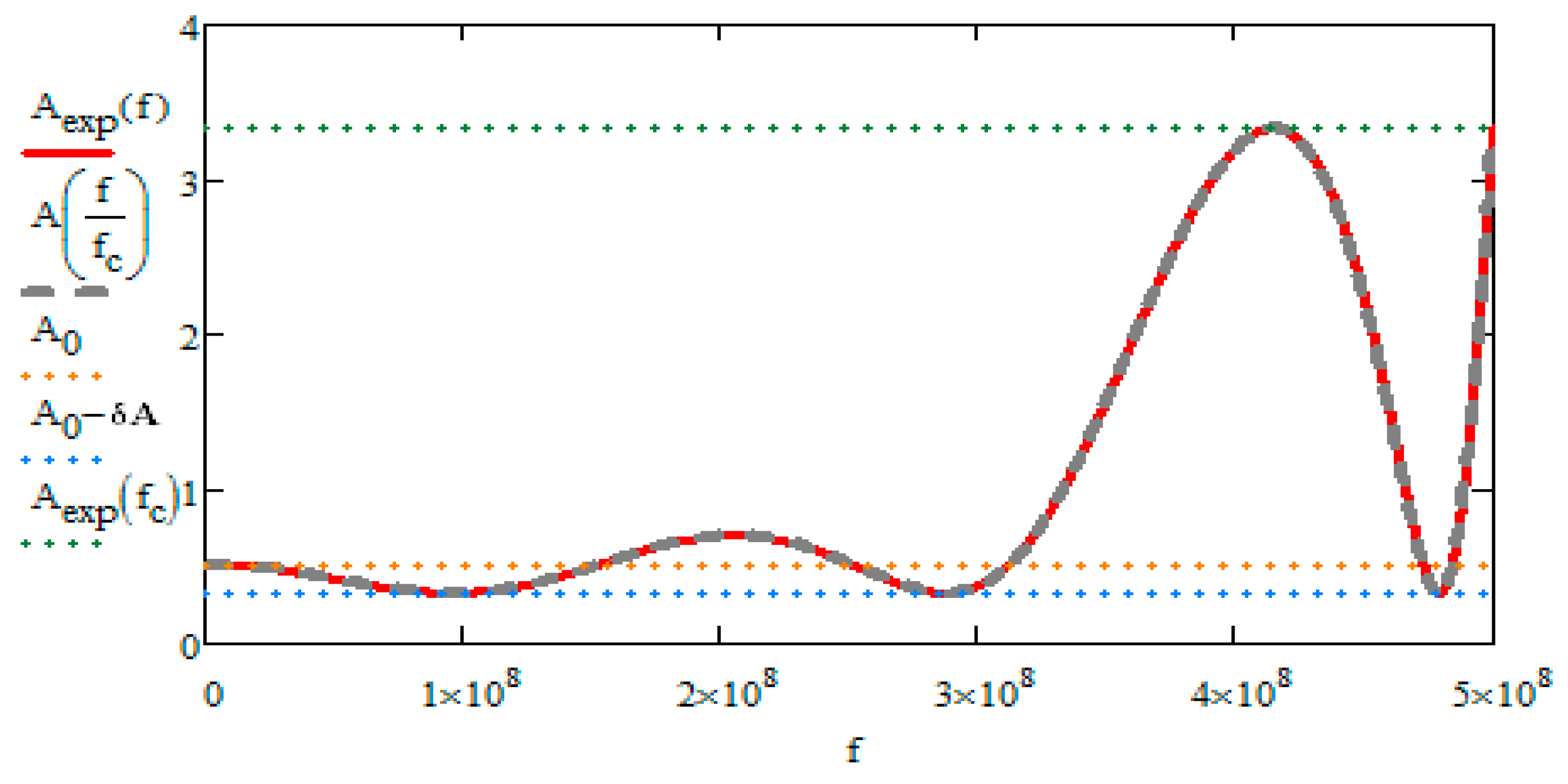
Figure 3 and
Figure 4 depict the passband region of a Pascal filter for order N = 6 and 7 respectively. From Equation (15) we can make some assumptions on the minimum and maximum passband attenuation.
The attenuation function from Equation (1) must be made equal to A
Pascal (Ω). If we modify the squared magnitude response
The reflection coefficient function ρ(s) can be determined from Feldkeller’s equation, [
6,
7]
The reflection coefficient function obeys two major rules:
The poles of ρ(s) must be a Hurwitz polynomial, i.e., the poles must lie on the left half plane of s and ρ(−s) must have the other poles
There are no restrictions on the location of the zeros to be implemented to Zin(s).
After having obtained ρ(s) by Feldkeller equation, the input impedance, Zin(s), can be expressed as [
2,
6,
7,
8]
After the calculation of Zin(s), the synthesis of the passive filter ladder can begin by removing the poles at infinity. The procedure of removing poles at infinity requires a positive real function (Zin(s)), which the degree of numerator is greater by one from the order of denominator. The passive normalized element is exported from the division between the coefficients of highest order of numerator and denominator. This process is recursively repeated for all next elements, up to the filter order N [
6,
7,
8].
4. Even Order Pascal Filters
For even order filter design through the Pascal approximation, the same restriction as in the Chebyshev approximation case holds, namely, R
s = R
L. Indeed, if, R
s = R
L then A
0 is zero and the attenuation for some frequencies is below 0 (the Attenuation by definition takes on only non-negative values). To overcome this problem, the order of the filter must be increased by one. In this paper, the term ‘direct design’, inherited from [
4], will be used to imply that no order increase will be made and the filter can be synthesized in the usual manner.
Another problem arises when δΑ > Α
0 i.e., when R
S1 < R
s < R
s2. In that case, the filter cannot be directly designed. The design of the filter is then achieved with lower ripple at passband area. To find the range for which the filter cannot be designed directly, the roots must be calculated from the equation [
4]
If the R
s obtained by the specifications lies in the forbidden range, the maximum ripple (A
max0) that can be realized for even order passive Pascal filter, and provided that the specification A
min is lower than the maximum stopband specification A
min0, can be determined from [
4]
Conversely to the Chebyshev approximation case, the Pascal approximation offers the advantage that the forbidden range depends on the two constants (Amax, N).
In order to give a summary of the passive filter design with Pascal Approximation, the following steps are listed:
For N odd:
For N even:
If by specs, then
If (), then
If & then, design the passive filter with new attenuation specifications, & ,
If then,
If & then,
For or , design directly the passive filter.
5. Design Examples
5.1. Example 1
The first example designs a low-pass filter, given the normalized specifications
. The Pascal order N is calculated from Equation (4) which yields N
Pascal = 6, the order of the Chebyshev approximation is the same as that of the Pascal approximation and δA is 0.183 (A
0 > δΑ). The ripple factor λ
max is 42.5 as calculated from Equation (3). In order to design the passive filter with λ
max at Ω
S, the attenuation is greater than A
0 + A
Min − δΑ and Α
0 is 0.512. The forbidden range of R
S for the Chebyshev approximation can be calculated from Equation (7)
which yields R
s1 = 0.1721 and R
s2 = 5.8089. For the Pascal approximation as in Equation (19) also produces the order of the filter, it yields R
s1 Pascal = 0.6711 and R
s2 Pascal = 1.5012. For the specified R
S the filter can be directly designed by the Pascal approximation. On the other hand, through the Chebyshev approximation, the filter has to be designed with reduced ripple in passband. From the tables given in [
5] with passband ripple A
max = 3 dB, the normalized values of passive elements of the Pascal approximation can be obtained as in first and third lines of the
Table 2. The next step is to de-normalize the passive elements with F
c = 500 MHz, R
0 = 50 Ohm (second and fifth lines in
Table 2) and then to simulate the passive filter which is presented in
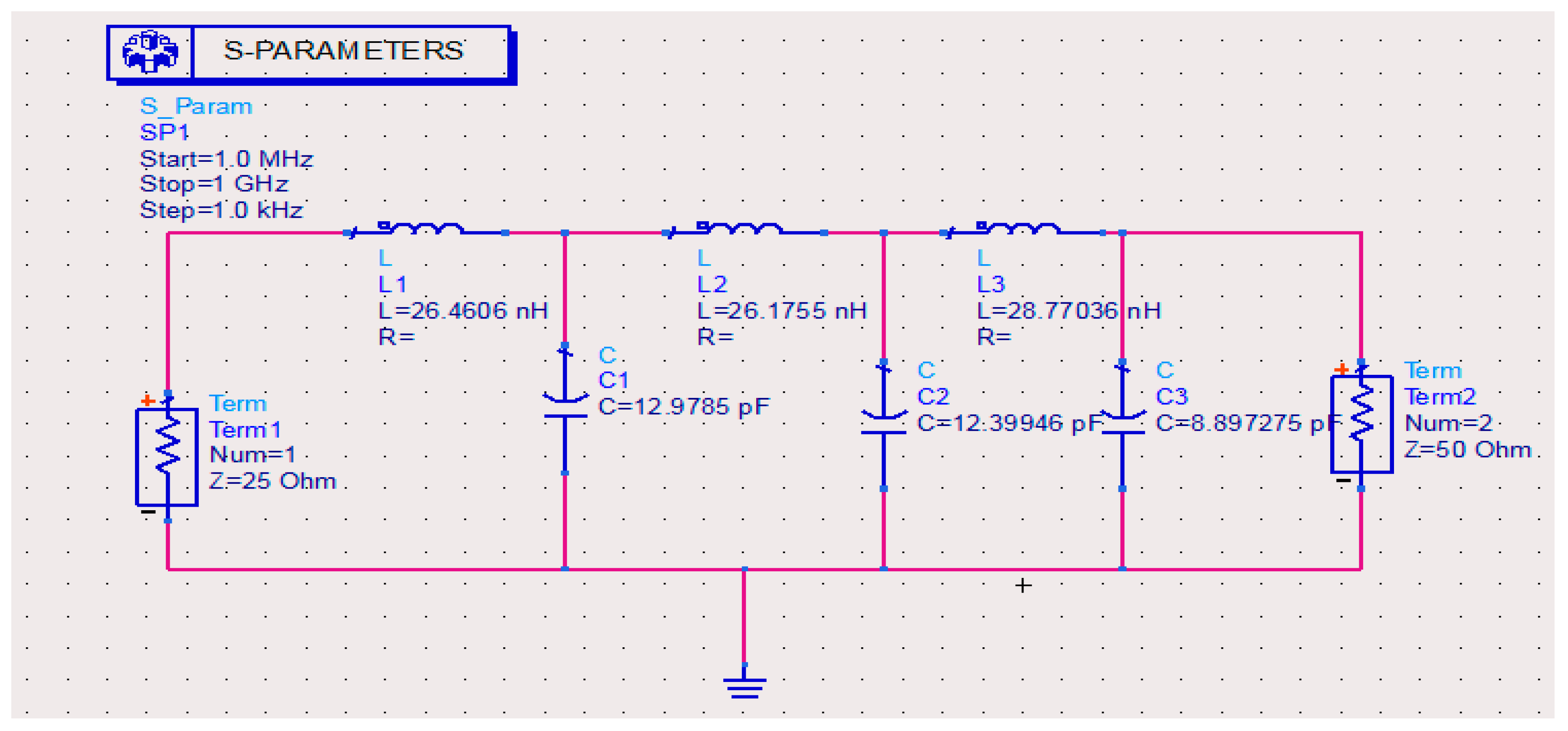
Figure 5 with the use of an appropriate software tool, e.g., ADS 2011.
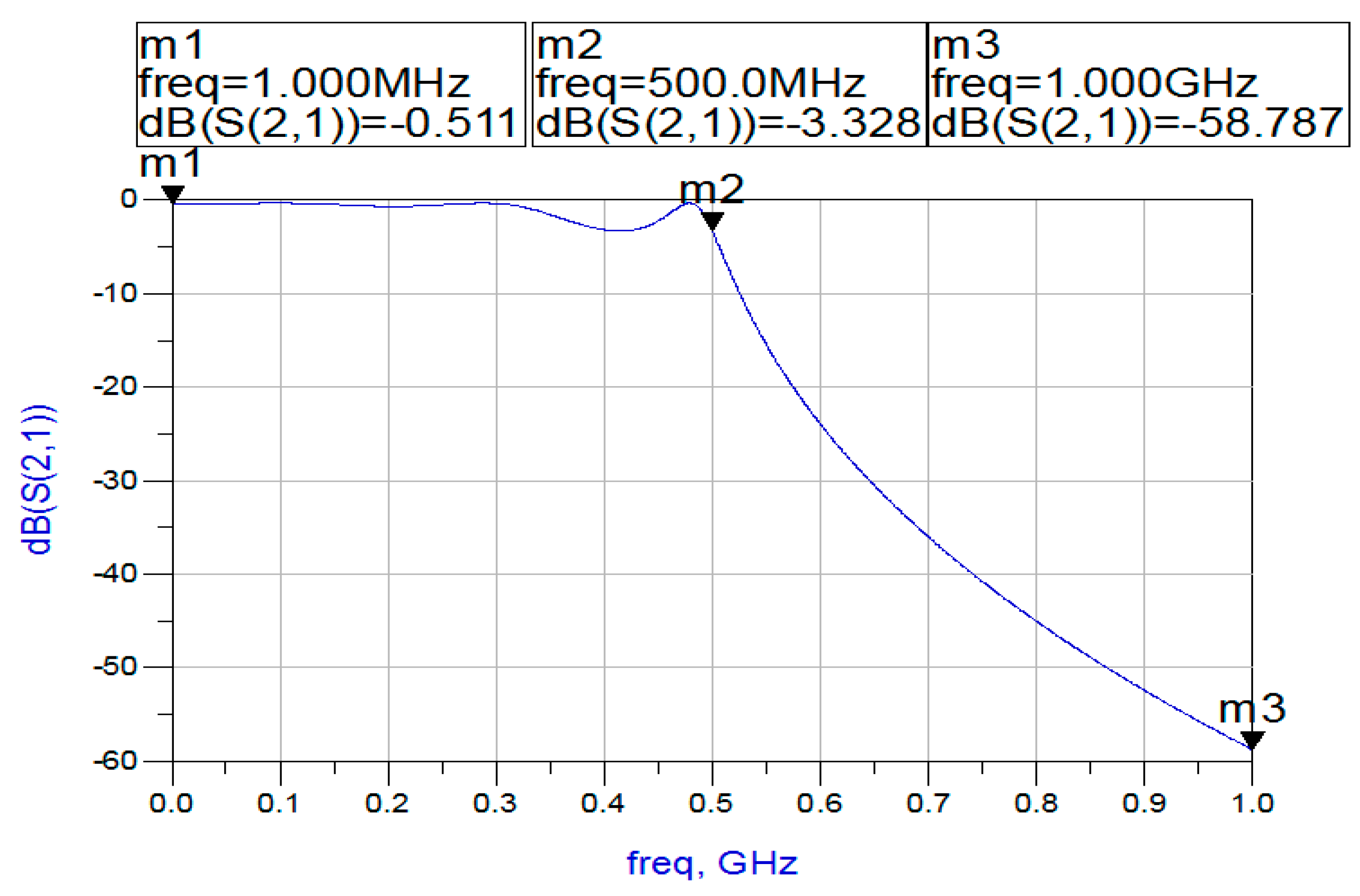
Figure 6 verifies that the experimental one (red continuous line) coincides with high accuracy to the theoretical ones (grey dotted color), thus the procedure of removing the poles at infinity from Equation (8) has been successfully completed and the next step is to simulate the passive filter.
The proximity between the experimental model, obtained through simulation and the theoretical model. In theory, the attenuation at 500 MHz must be equal to
The value obtained by simulation is −3.328 (it must be highlighted that these values are of opposite signs, because ADS simulate Gain rather than Attenuation, so it holds A(Ω) = −G(Ω) [
2]). The other parameter that should be checked is the attenuation at the edge of the stopband Ω
sxF
c. Both the model value and the simulated value (as presented in
Figure 7) for the gain are −58.787 and from the mathematical program is exactly the same. As the design has opted for maximum ripple factor λ
max, the gain is expected to be less than A
0 + A
min − δΑ = 55.328.
5.2. Example 2
The second design example assumes that the normalized specifications given are:
. The order N of Pascal approximation is calculated from Equation (4) yields N
Pascal = 7, while the order of the Chebyshev approximation is same. The ripple factor λ
max is 18.369 as calculated from Equation (3). For this example it has been selected to design the passive filter with λ
max at Ω
s; the gain is therefore less than A
0 − A
min. The tables of [
5] provide the normalized values of passive elements for the Pascal approximation, while those for the Chebyshev approximation can be obtained from [
6].
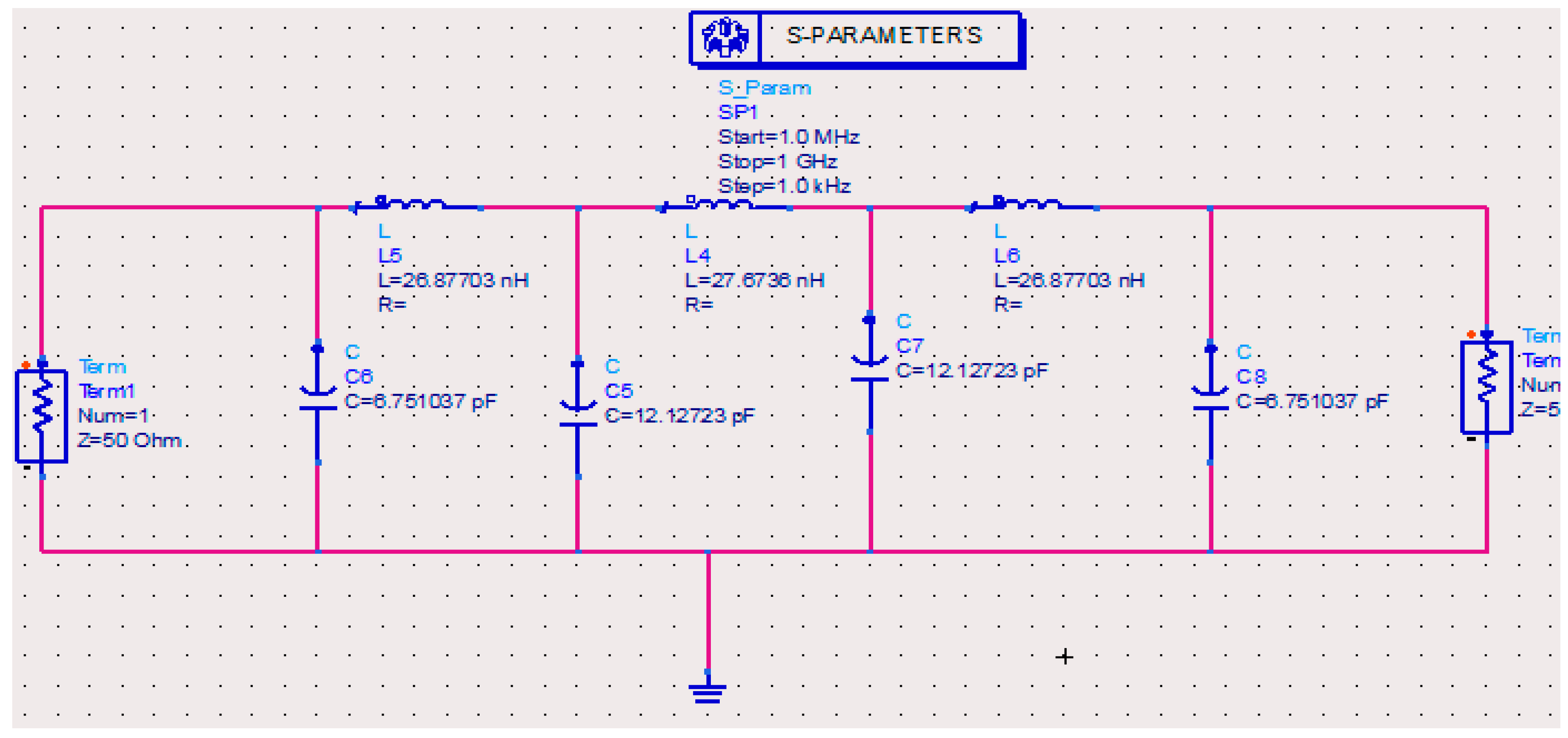
Table 3 presents the normalized values of passive elements of Pascal approximation for order N = 7, in first and third lines. A minimum-inductance ladder is selected here, thus implementation will be less bulky and less expensive than constructing it with the method of minimum capacitance [
7]. The next step is to de-normalize the passive elements with F
c = 500 MHz, R
0 = 50 Ohm as
Table 3 presents in the second and fourth lines for 7th order Pascal filter. The last step is the filter design using the ADS 2011 software as presented in
Figure 8.
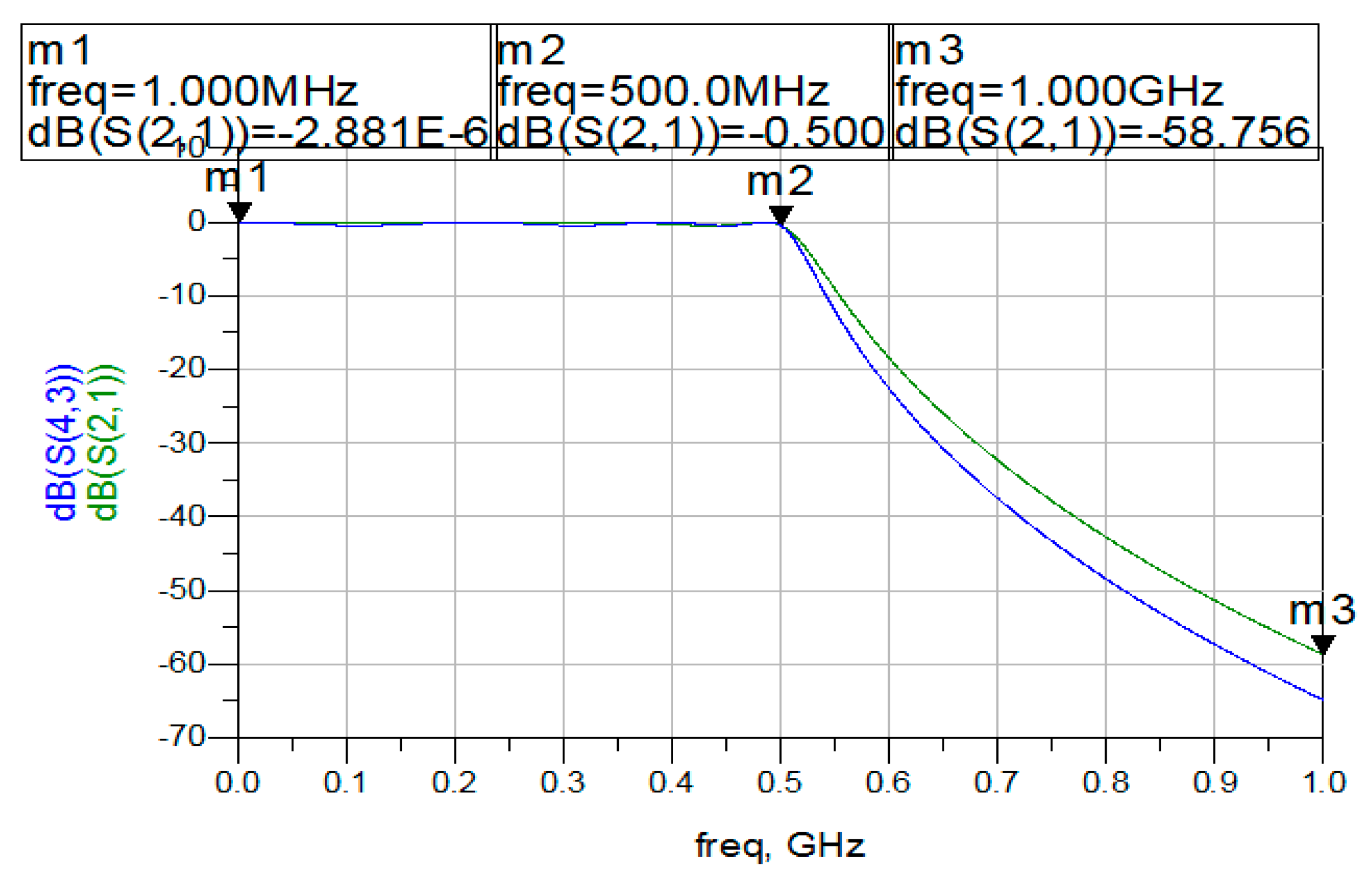
Figure 9 verifies that the theoretical model (blue dotted line) coincides with the experimental (red continuous line). The grey dotted line shows the passband attenuation of Chebyshev approximation. The normalized values of the passive elements are founded by removing the poles at infinity from Equation (18).
Once again, the experimental results coincide with the theoretical ones with high accuracy. In theory, the attenuation at 500 MHz must be equal to
The value obtained by simulation is −0.5 as presented in
Figure 10 (m
2 point), which is the precise theoretically obtained value. The other parameter to be checked is the attenuation at the edge of the stopband Ω
s*F
c. Both the model value and the simulated value for the attenuation are −58.756. As this design has opted for maximum ripple factor λ
max, the gain is expected to be less than A
0 + A
min = 55 dB.
6. Conclusions
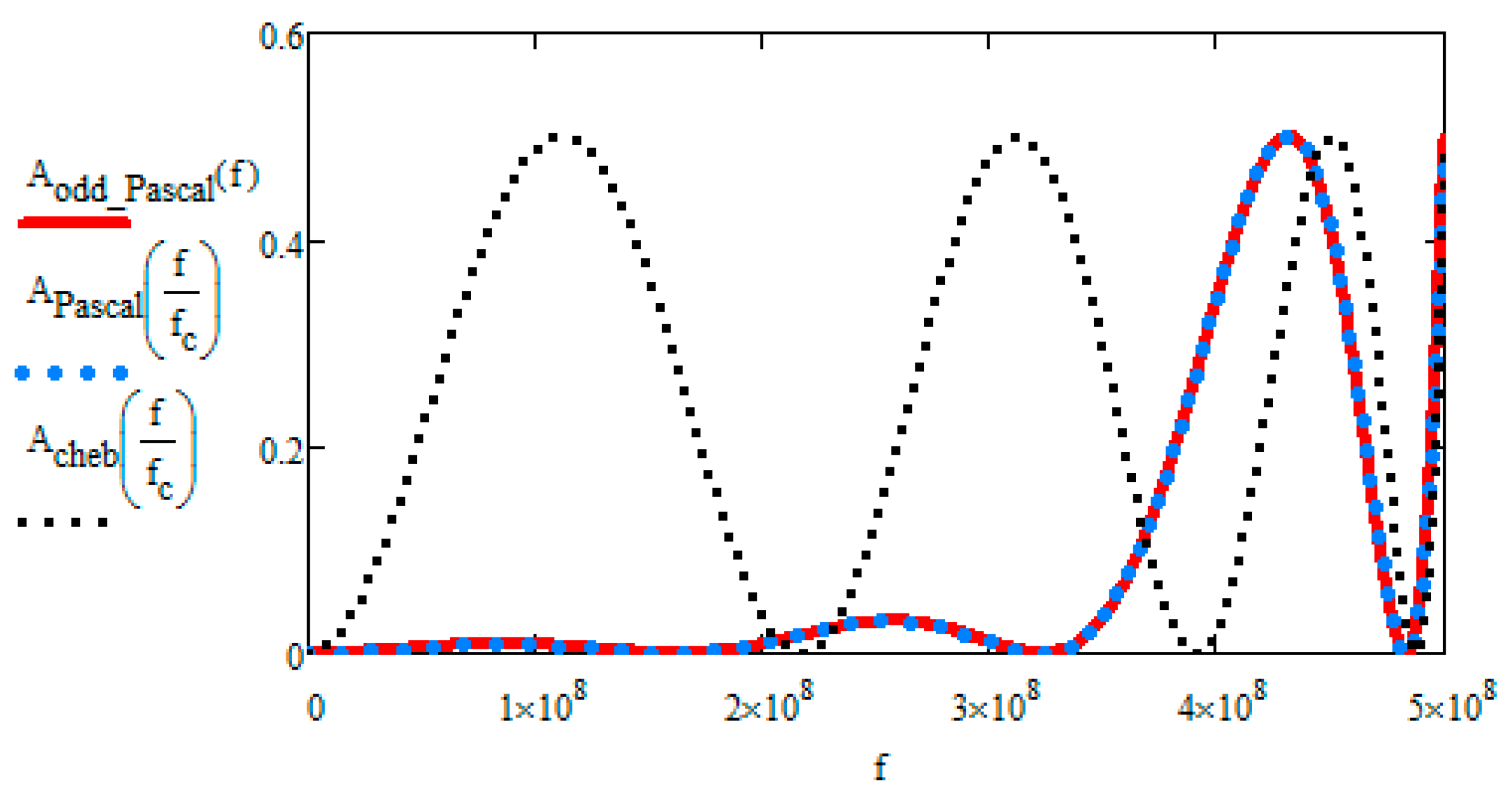
The Pascal all-pole approximation exhibits a non equiripple attenuation in the passband. On the other hand, the Chebyshev approximation has equiripple magnitude passband. In this work, it has been proven and presented that the ratio of the modified Pascal polynomial PD over PDmax yields the Cn of Chebyshev, for orders N = 2 to 3.
The Pascal approximation has two drawbacks, the calculation of the order (N) has to be done with the assistance of a numerical program and the location of the poles cannot be derived analytically. The filter order and the poles of for a N > 3 had to be calculated by numerical methods (software).
A novel method to calculate all the coefficients of the Pascal approximation polynomial has been proposed and tested through simulation in this paper, the results between the theoretical and the simulated values not only converge on given specifications, but they are the results are identical, with a high accuracy (of nine decimals, as tested). So, an analytical pattern has been established to derive the coefficients of the Pascal function. For all other cases, a numerical software tool is necessary in order to find the roots of the filter, which must lie on the left half of the complex plane.
The passive design in general, has similar difficulties in the design of odd or even-order passive filters. The superiority of the Pascal approximation, however, is that the forbidden range for Rs is much narrower than the Chebyshev approximation for even-order passive filters design. This is owing to the fact that Equation (20) depends not only from the passband ripple, but from the order of the filter as well. In contrary, on the Chebyshev design the forbidden range depends solely from the passband ripple; which results in the forbidden range being wider than the Pascal.
Indirectly, through the examples presented in this paper, the values of the normalized elements have been acquired from created tables for a given order and a given Amax. The same tables have been created by Zverev but not for the Pascal approximation. The roll-off of the Chebyshev is steeper than the Pascal approximation.