1. Introduction
Molecular dynamics (MD) simulations are nowadays a fundamental tool used to complement experimental investigations in biomolecular modeling [
1]. Although the accessible processes are usually limited to the microsecond timescale for classical MD with empirical force fields, with the help of enhanced sampling methods [
2,
3,
4] it is possible to effectively sample events that would require a much longer time in order to spontaneously happen. However, the quality of the results is still limited by the accuracy of the employed force fields, making experimental validations a necessary step. The usual procedure consists in performing a simulation and computing some observable for which an experimental value has been already measured. If the calculated and experimental values are compatible, the simulation can be trusted and other observables can be estimated in order to make genuine predictions. If the discrepancy between calculated and experimental values is significant, one is forced to make a step back and perform a new simulation with a refined force field. For instance, current force fields still exhibit visible limitations in the study of protein-protein interactions [
5], in the structural characterization of protein unfolded states [
6], in the simulation of the conformational dynamics of unstructured RNAs [
7,
8,
9], and in the blind prediction of RNA structural motifs [
9,
10,
11]. However, improving force fields is a far-from-trivial task because many correlated parameters should be adjusted. Furthermore, the employed functional forms might have an intrinsically limited capability to describe the real energy function of the system. Largely due to these reasons, it is becoming more and more common to restrain the simulations in order to enforce agreement with experimental data. Whereas this approach might appear not satisfactory, one should keep in mind that often experimental knowledge is anyway implicitly encoded in the simulation of complex systems (e.g., if the initial structure of a short simulation is taken from experiment, then the simulation will be biased toward it). In addition, one should consider that validation can still be made against independent experiments or against some of the data suitably removed from the set of restraints. From another point of view, the pragmatic approach of combining experiments with imperfect potential energy models allows one to extract the maximum amount of information from sparse experimental data. Particular care should be taken when interpreting bulk experiments that measure averages over a large number of copies of the same molecule. These experiments are valuable in the characterization of dynamical molecules, where heterogeneous structures might be mixed and contribute with different weights to the experimental observation. If properly combined with MD simulations, these experiments can be used to construct a high resolution picture of molecular structure and dynamics [
12,
13,
14,
15].
In this review we discuss some recent methodological developments related to the application of the maximum entropy principle to combine MD simulations with ensemble averages obtained from experiments (see, e.g., Refs. [
16,
17] for an introduction on this topic). We briefly review the maximum entropy principle and show how it can be cast into a minimization problem. We then discuss the equivalent formulation based on averaging between multiple simultaneous simulations. Special explanations are dedicated to the incorporation of experimental errors in the maximum entropy principle and to the protocols that can be used to enforce the experimental constraints. Simple model systems are used to illustrate the typical difficulties encountered in real applications. Source code for the model systems is available at
https://github.com/bussilab/review-maxent.
2. The Maximum Entropy Principle
The maximum entropy principle dates back to 1957 when Jaynes [
18,
19] proposed it as a link between thermodynamic entropy and information-theory entropy. Previously, the definition of entropy was considered as an arrival point in the construction of new theories, and only used as a validation against laws of thermodynamics [
18]. In Jaynes formulation, maximum entropy was for the first time seen as the starting point to be used in building new theories. In particular, distributions that maximize the entropy subject to some physical constraints were postulated to be useful in order to make inference on the system under study. In its original formulation, the maximum entropy principle states that, given a system described by a number of states, the best probability distribution for these states compatible with a set of observed data is the one maximizing the associated Shannon’s entropy. This principle has been later extended to a maximum relative entropy principle [
20] which has the advantage of being invariant with respect to changes of coordinates and coarse-graining [
21] and has been shown to play an important role in multiscale problems [
22]. The entropy is computed here relative to a given prior distribution
and, for a system described by a set of continuous variables
, is defined as
This quantity should be maximized subject to constraints in order to be compatible with observations:
Here M experimental observations constrain the ensemble average of M observables computed over the distribution to be equal to , and an additional constraint ensures that the distribution is normalized. encodes the knowledge available before the experimental measurement and is thus called probability distribution. instead represents the best estimate for the probability distribution after the experimental constraints have been enforced and is thus called posterior probability distribution. Here, the subscript denotes the fact that this is the distribution that maximizes the entropy.
Since the relative entropy
is the negative of the Kullback-Leibler divergence
[
23], the procedure described above can be interpreted as a search for the posterior distribution that is as close as possible to the prior knowledge and agrees with the given experimental observations. In terms of information theory, the Kullback-Leibler divergence measures how much information is gained when prior knowledge
is replaced with
.
The solution of the maximization problem in Equation (
2) can be obtained using the method of Lagrangian multipliers, namely searching for the stationary points of the Lagrange function
where
and
are suitable Lagrangian multipliers. The functional derivative of
with respect to
is
By setting
and neglecting the normalization factor, the posterior reads
Here the value of the Lagrangian multipliers
should be found by enforcing the agreement with the experimental data. In the following, in order to have a more compact notation, we will drop the subscript from the Lagrangian multipliers and write them as a vector whenever possible. Equation (
5) could thus be equivalently written as
Notice that the vectors and have dimensionality M, whereas the vector has dimensionality equal to the number of degrees of freedom of the analyzed system.
In short, the maximum relative entropy principle gives a recipe to obtain the posterior distribution that is as close as possible to the prior distribution and agrees with some experimental observation. In the following, we will drop the word “relative” and we will refer to this principle as the maximum entropy principle.
2.1. Combining Maximum Entropy Principle and Molecular Dynamics
When combining the maximum entropy principle with MD simulations the prior knowledge is represented by the probability distribution resulting from the employed potential energy, that is typically an empirical force field in classical MD. In particular, given a potential energy
, the associated probability distribution
at thermal equilibrium is the Boltzmann distribution
, where
,
T is the system temperature, and
is the Boltzmann constant. According to Equation (
5), the posterior will be
The posterior distribution can thus be generated by a modified potential energy in the form
In other words, the effect of the constraint on the ensemble average is that of adding a term to the energy that is linear in the function
with prefactors chosen in order to enforce the correct averages. Such a linear term should be compared with constrained MD simulations, where the value of some function of the coordinates is fixed at every step (e.g., using the SHAKE algorithm [
24]), or harmonic restraints, where a quadratic function of the observable is added to the potential energy function. Notice that the words constraint and restraint are usually employed when a quantity is exactly or softly enforced, respectively. Strictly speaking, in the maximum entropy context, ensemble averages
are constrained whereas the corresponding functions
are (linearly) restrained.
If one considers the free energy as a function of the experimental observables (also known as potential of mean force), which is defined as
the effect of the corrective potential in Equation (
7) is just to tilt the free-energy landscape
where
C is an arbitrary constant. A schematic representation of this tilting is reported in
Figure 1.
Any experimental data that is the result of an ensemble measurement can be used as a constraint. Typical examples for biomolecular systems are nuclear-magnetic-resonance (NMR) experiments such as measures of chemical shifts [
25], scalar couplings [
26], or residual dipolar couplings [
27], and other techniques such as small-angle X-ray scattering (SAXS) [
28], double electron-electron resonance (DEER) [
29], and Förster resonance energy transfer [
30]. The only requirement is the availability of a so-called
forward model for such experiments. The forward model is a function mapping the atomic coordinates of the system to the measured quantity and thus allows the experimental data to be back-calculated from the simulated structures. For instance, in the case of 3J scalar couplings, the forward model is given by the so-called Karplus relations [
26], that are trigonometric functions of the dihedral angles. It must be noted that the formulas used in standard forward models are often parameterized empirically, and one should take into account errors in these parameters on par with experimental errors (see
Section 3). Without entering in the complexity of the methods mentioned above, we will only consider cases where experimental data can be trusted to be ensemble averages.
In short, the maximum entropy principle can be used to derive corrective potentials for MD simulations that constrain the value of some ensemble average. The choice to generate an ensemble that is as close as possible to the prior knowledge implies that the correcting potential has a specific functional form, namely that it is linear in the observables that have been measured.
2.2. A Minimization Problem
In order to chose the values of
that satisfy Equation (
2), it is possible to recast the problem into a minimization problem. In particular, consider the function [
16,
31]
Notice that the first term is the logarithm of the ratio between the two partition functions associated to the potential energy functions
and
, that is proportional to the free-energy difference between these two potentials. The gradient of
is
and is thus equal to zero when the average in the posterior distribution is identical to the enforced experimental value. This means that the constraints in Equation (
2) can be enforced by searching for a stationary point
of
(see
Figure 1). The Hessian of
is
and is thus equal to the covariance matrix of the forward models in the posterior distribution. Unless the enforced observables are dependent on each other, the Hessian will be positive definite [
16]. The solution of Equation (
2) will thus correspond to a minimum of
that can be searched for instance by a steepest descent procedure. However there are cases where such minimum might not exist. In particular, one should pay attention to the following cases:
When data are incompatible with the prior distribution.
When data are mutually incompatible. As an extreme case, one can imagine two different experiments that measure the same observable and report different values.
In both cases
will have no stationary point. Clearly, there is a continuum of possible intermediate situations where data are almost incompatible. In
Section 4 we will see what happens when the maximum entropy principle is applied to model systems designed in order to highlight these difficult situations.
2.3. Connection with Maximum Likelihood Principle
The function
allows to easily highlight a connection between maximum entropy and maximum likelihood principles. Given an arbitrary set of
molecular structures
chosen such that
, it is possible to rewrite
as
The last term is the ratio between the probability of drawing the structures
from the posterior distribution and that of drawing the same structures from the prior distribution. Since the minimum of
corresponds to the maximum of
, the distribution that maximizes the entropy under experimental constraints is identical to the one that, among an exponential family of distributions, maximizes the likelihood of a set of structures with average value of the observables
equal to the experimental value [
32,
33]. This equivalence can be considered as an added justification for the maximum entropy principle [
32]: if the notion of selecting a posterior
that maximizes the entropy is not compelling enough, one can consider that this same posterior is, among the distributions with the exponential form of Equation (
5), the one that maximizes the likelihood of being compatible with the experimental sample.
Equation (
13) can also be rearranged to
and, after proper manipulation, it can be shown that
where
is an arbitrary distribution with averages equal to the experimental ones. Thus, minimizing
is equivalent to choosing the distribution with the exponential form of Equation (
5) that is as close as possible to the experimental one. Since at its minimum, by construction,
, it follows that
. In other words, the maximum entropy restraint is guaranteed to make the posterior distribution closer to the experimental one than the prior distribution [
34].
2.4. Enforcing Distributions
We so far considered the possibility of enforcing ensemble averages. However, one might be interested in enforcing the full distribution of an observable. This can be done by noticing that the marginal probability distribution
of a quantity
can be computed as the expectation value of a Dirac-delta function:
An example of experimental technique that can report distance distributions is the already mentioned DEER [
29]. If the form of
has been measured experimentally, the maximum entropy principle can be used to enforce it in a MD simulation. Notice that this corresponds to constraining an infinite number of data points (that is, the occupation of each bin in the observable
). In this case,
will be a function of
and Equation (
5) will take the following form
Thus, the correction to the potential should be a function of the observable
chosen in order to enforce the experimental distribution
. Different approaches can be used to construct the function
with such property. For instance, one might take advantage of iterative Boltzmann inversion procedures originally developed to derive coarse-grained models from atomistic simulations [
35]. As an alternative, one might use a time-dependent adaptive potential. In target metadynamics [
36,
37] such potential is constructed as a sum of Gaussians centered on the previously visited values of
. It can be shown that by properly choosing the prefactors of those Gaussians an arbitrary target distribution can be enforced.
Alternatively, it is possible to directly minimize the function
as mentioned in
Section 2.2. In this context,
would be a functional of
with the form
Interestingly, this functional is identical to the one introduced in the variationally enhanced sampling (VES) method of Ref. [
38]. In its original formulation, VES was used to enforce a flat distribution in order to sample rare events. However, the method can also be used to enforce an arbitrary a priori chosen distribution [
39,
40]. The analogy with maximum entropy methods, together with the relationship in Equation (
14), was already noticed in Ref. [
40] and is interesting for a twofold reason: (a) It provides a maximum-entropy interpretation of VES, and (b) the numerical techniques used for VES might be used to enforce experimental averages in a maximum-entropy context. We will further comment about this second point in
Section 5.4.
2.5. Equivalence to the Replica Approach
A well established method to enforce ensemble averages in molecular simulations is represented by restrained ensembles [
41,
42,
43]. The rationale behind this method is to mimic an ensemble of structures by simulating in parallel
multiple identical copies (replicas) of the system each of which having its own atomic coordinates. The agreement with the
M experimental data is then enforced by adding a harmonic restraint for each observable, centered on the experimental reference and acting on the average over all the simulated replicas. This results in a restraining potential with the following form:
where
k is a suitably chosen force constant. It has been shown [
16,
44,
45] that this method produces the same ensemble as the maximum entropy approach in the limit of large number of replicas
. Indeed, the potential in Equation (
18) results in the same force
applied to the observable
in each replica. As the number of replicas grows, the fluctuations of the average decrease and the applied force becomes constant in time, so that the explored distribution will have the same form as Equation (
5) with
. If
k is chosen large enough, the average between the replicas will be forced to be equal to the experimental one. It is possible to show that, in order to enforce the desired average,
k should grow faster than
[
45]. In practical implementations,
k should be finite in order to avoid infinite forces. A direct calculation of the entropy-loss due to the choice of a finite
has been proposed to be an useful tool in the search for the correct number of replicas [
46]. An approach based on a posteriori reweighting (
Section 5.1) of replica-based simulations and named Bayesian inference of ensembles has been also proposed in order to eliminate the effect of choosing a finite number of replicas [
47].
3. Modelling Experimental Errors
The maximum entropy method can be modified in order to account for uncertainties in experimental data. This step is fundamental in order to reduce over-fitting. In this section we will briefly consider how the error can be modeled according to Ref. [
48]. Here errors are modeled modifying the experimental constraints introduced in Equation (
2) by introducing an auxiliary variables
for each data point representing the discrepancy or residual between the experimental and the simulated value. The new constraints are hence defined as follows:
The auxiliary variable
is a vector with dimensionality equal to the number of constraints and models all the possible sources of error, including inaccuracies of the forward models (
Section 2.1) as well as experimental uncertainties. Errors can be modeled by choosing a proper prior distribution function for the variable
. A common choice is represented by a Gaussian prior with a fixed standard deviation
for the
ith observable
The value of
corresponds to the level of confidence in the
ith data point, where
implies to completely discard the data in the optimization process while
means having complete confidence in the data, that will be fitted as best as possible. Notice that, for additive errors,
and
are independent variables and Equation (
19) can be written as:
where
is computed in the posterior distribution
. Incorporating the experimental error in the maximum entropy approach is then as easy as enforcing a different experimental value, corresponding to the one in Equation (
21). Notice that the value of
only depends on its prior distribution
and on
. For a Gaussian prior with standard deviation
Equation (
20) we have:
Thus, as grows in magnitude, a larger discrepancy between simulation and experiment will be accepted. In addition, it can be seen that applying the same constraint twice is exactly equivalent to applying a constraint with a reduced by a factor two. This is consistent with the fact that the confidence in the repeated data point is increased.
Other priors are also possible in order to better account for outliers and to deal with cases where the standard deviation of the residual is not known a priori. One might consider the variance of the
ith residual
as a variable sampled from a given prior distribution
:
A flexible functional form for
can be obtained using the following Gamma distribution
In the above equation
is the mean parameter of the Gamma function and must be interpreted as the typical expected variance of the error on the
ith data point.
, which must satisfy
, is the shape parameter of the Gamma distribution and expresses how much the distribution is peaked around
. In practice, it controls how much the optimization is tolerant to large discrepancies between the experimental data and the enforced average. Notice that in Ref. [
48] a different convention was used with a parameter
. By setting
a Gaussian prior on
will be recovered. Smaller values of
will lead to a prior distribution on
with “fatter” tails and thus able to accommodate larger differences between experiment and simulation. For instance, the case
leads to a Laplace prior
. After proper manipulation, the resulting expectation value
can be shown to be
In this case, it can be seen that applying the same constraint twice is exactly equivalent to applying a constraint with a reduced by a factor two and a multiplied by a factor two.
In terms of the minimization problem of
Section 2.2, modeling experimental errors as discussed here is equivalent to adding a contribution
to Equation (
10):
For a Gaussian noise with preassigned variance (Equation (
20)) the additional term is
For a prior on the error in the form of Equations (
23) and (
24) one obtains
In the limit of large
, Equation (
28) is equivalent to Equation (
27). If the data points are expected to all have the same error
, unknown but with a typical value
(see Ref. [
48]), Equation (
28) should be modified to
.
Equation (
28) shows that by construction the Lagrangian multiplier
will be limited in the range
. The effect of using a prior with
is thus that of restricting the range of allowed
in order to avoid too large modifications of the prior distribution. In practice, values of
chosen outside these boundaries would lead to a posterior distribution
that cannot be normalized.
Except for trivial cases (e.g., for Gaussian noise with ), the contribution originating from error modeling has positive definite Hessian and as such it makes a strongly convex function. Thus, a suitable error treatment can make the minimization process numerically easier.
It is worth mentioning that a very similar formalism can be used to include not only errors but more generally any quantity that influences the experimental measurement but cannot be directly obtained from the simulated structures. For instance, in the case of residual dipolar couplings [
27], the orientation of the considered molecule with the respect to the external field is often unknown. The orientation of the field can then be used as an additional vector variable to be sampled with a Monte Carlo procedure, and suitable Lagrangian multipliers can be obtained in order to enforce the agreement with experiments [
49]. Notice that in this case the orientation contributes to the ensemble average in a non-additive manner so that Equation (
21) cannot be used. Interestingly, thanks to the equivalence between multi-replica simulations and maximum entropy restraints (
Section 2.5), equivalent results can be obtained using the tensor-free method of Ref. [
50].
Finally, we note that several works introduced error treatment using a Bayesian framework [
47,
51,
52,
53]. Interestingly, Bayesian ensemble refinement [
47] introduces an additional parameter (
) that takes into account the confidence in the prior distribution. In case of Gaussian error, this parameter enters as a global scaling factor in the errors
for each data point. Thus, the errors
discussed above can be used to modulate both our confidence in experimental data and our confidence in the original force field. The equivalence between the error treatment of Ref. [
47] and the one reported here is further discussed in Ref. [
48], in particular for what concerns non-Gaussian error priors.
4. Exact Results on Model Systems
In this section we illustrate the effects of adding restraints using the maximum entropy principle on simple model systems. In order to do so we first derive some simple relationship valid when the prior has a particular functional form, namely a sum of
Gaussians with center
and covariance matrix
, where
:
The coefficients
provide the weights of each Gaussian and are normalized (
). We assume here that the restraints are applied on the variable
. For a general system, one should first perform a dimensional reduction in order to obtain the marginal prior probability
. By constraining the ensemble averages of the variable
to an experimental value
the posterior becomes:
With proper algebra it is possible to compute explicitly the normalization factor
. The function
to be minimized is thus equal to:
and the average value of
in the posterior is
We could not find a close formula for
given
and
. However, the solution can be found numerically with the gradient descent procedure discussed in
Section 5 (see Equation (
33)).
4.1. Consistency between Prior Distribution and Experimental Data
We consider a one dimensional model with a prior expressed as a sum of two Gaussians, one centered in
with standard deviation
and one centered in
with standard deviation
. The weights of the two Gaussians are
and
, respectively. The prior distribution is thus
, has an average value
, and is represented in
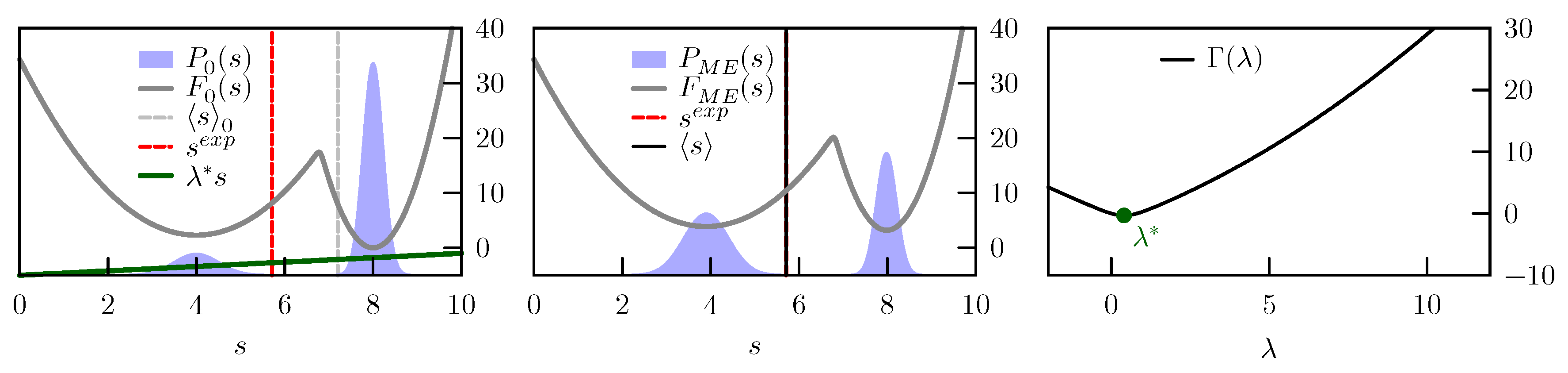
Figure 2, left column top panel.
We first enforce a value
, which is compatible with the prior probability. If we are absolutely sure about our experimental value and set
, the
which minimizes
is
(
Figure 2 right column, bottom panel). In case values of
are used, the
function becomes more convex and the optimal value
is decreased. As a result, the average
s in the posterior distribution is approaching its value in the prior. The evolution of the ensemble average
with
values between zero and ten, with respect to the initial
and the experimental
, is shown in
Figure 2, right column top panel. In all these cases the posterior distributions remain bimodal and the main effect of the restraint is to change the relative population of the two peaks (
Figure 2, left and middle columns).
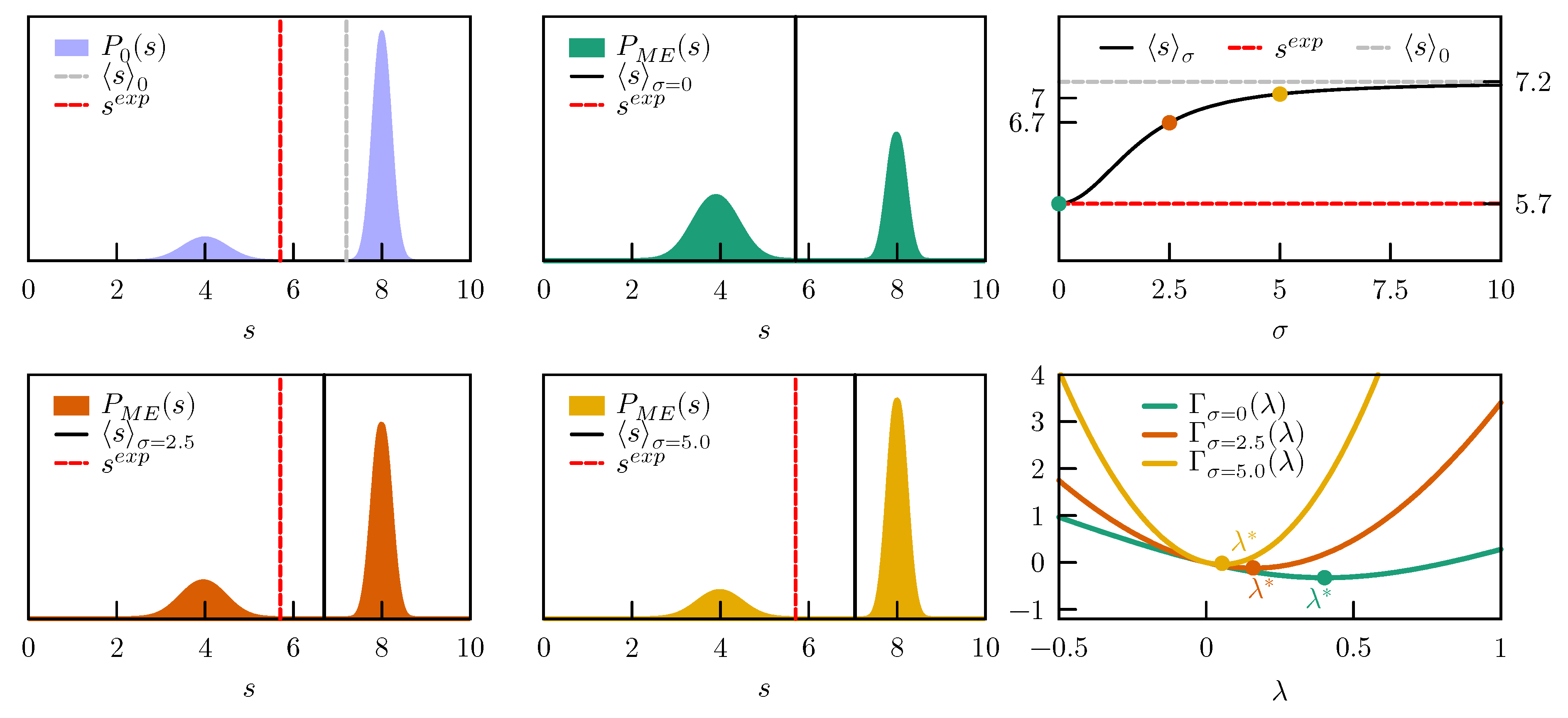
We then enforce an average value
, which is far outside the original probability distribution (see
Figure 3). If we are absolutely sure about our experimental value and set
, the
which minimizes
is very large,
(
Figure 3 right column, bottom panel). Assuming zero error on the experimental value is equivalent to having poor confidence in the probability distribution sampled by the force field, and leads in fact to a
completely different from
. The two peaks in
are replaced by a single peak centered around the experimental value, which is exactly met by the ensemble average (
;
Figure 3 middle column top panel). Note that this is possible only because the experimental value is not entirely incompatible with the prior distribution, i.e., it has a small, non-zero probability also in the prior. If the probability had been zero,
would have had no minimum and no optimal
would have been found. If we have more confidence in the distribution sampled by the force field, assume that there might be an error in our experimental value, and set
,
is more than one order of magnitude lower (
). The two peaks in
are only slightly shifted towards lower
s, while their relative populations are shifted in favor of the peak centered around 4 (
Figure 3, left column bottom panel). According to our estimate of the probability distribution of the error, the ensemble average
is more probably the true value than the experimentally measured one. In case we have very high confidence in the force field and very low confidence in the experimental value and set
, the correction becomes very small (
) and the new ensemble average
, very close to the initial
(
Figure 3, middle column bottom panel). The evolution of the ensemble average
with
values between zero and ten, with respect to the initial
and the experimental
, is shown in
Figure 3, right column top panel.
In conclusion, when data that are not consistent with the prior distribution are enforced, the posterior distribution could be severely distorted. Clearly, this could happen either because the prior is completely wrong or because the experimental values are affected by errors. By including a suitable error model in the maximum entropy procedure it is possible to easily interpolate between the two extremes in which we completely trust the force field or the experimental data.
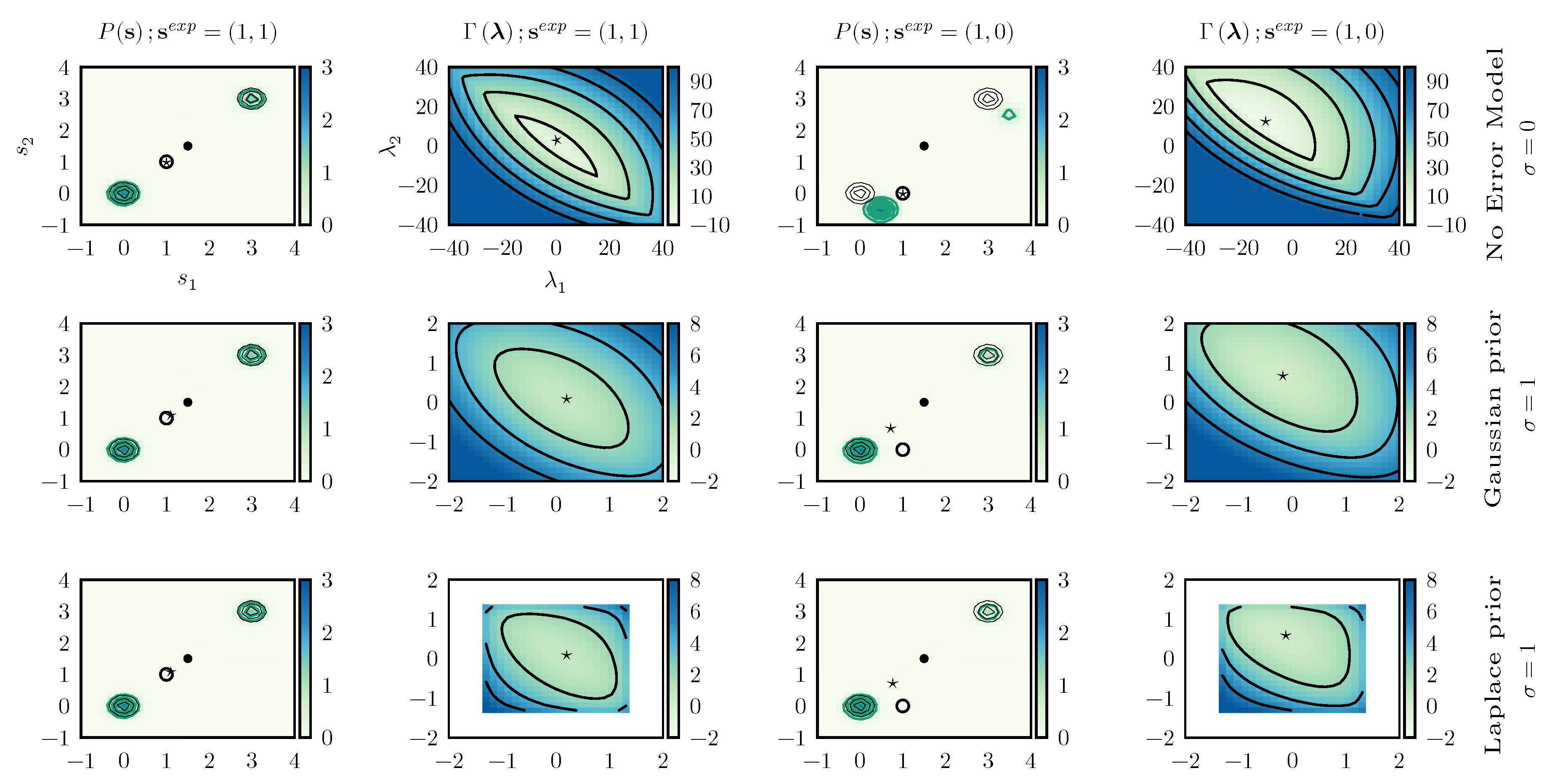
4.2. Consistency between Data Points
We then consider a two dimensional model with a prior expressed as a sum of two Gaussians centered in
and
with identical standard deviations
and weights
. The prior distribution is represented in
Figure 4.
This model is particularly instructive since, by construction, the two components of
are highly correlated and is hence possible to see what happens when inconsistent data are enforced. To this aim we study the two scenarios (i.e., consistent and inconsistent data) using different error models (no error model, Gaussian prior with
, and Laplace prior with
), for a total of six combinations. In the
consistent case we enforce
, whereas in the
inconsistent one we enforce
.
Figure 4 reports the posterior distributions obtained in all these cases.
When consistent data are enforced the posterior distribution is very similar to the prior distribution, the only difference being a modulation in the weights of the two peaks. The optimal value
, marked with a ★ in
Figure 4, does not depend significantly on the adopted error model. The main difference between including or not including error models can be seen in the form of the
function. When errors are not included,
is almost flat in a given direction, indicating that one of the eigenvalues of its Hessian is very small. On the contrary, when error modeling is included, the
function becomes clearly convex in all directions. In practical applications, the numerical minimization of
would be more efficient.
When enforcing inconsistent data without taking into account experimental error, the behavior is significantly different. Indeed, the only manner to enforce data where the value of the two components of are different is to significantly displace the two peaks. On the contrary, the distortion is significantly alleviated when taking into account experimental errors. Obviously, in this case the experimental value is not exactly enforced and, with both Gaussian and Laplace prior, we obtain .
By observing it can be seen that the main effect of using a Laplace prior instead of a Gaussian prior for the error is that the range of suitable values for is limited. This allows one to decrease the effect of particularly wrong data points on the posterior distribution.
In conclusion, when data that are not consistent among themselves are enforced, the posterior distribution could be severely distorted. Inconsistency between data could either be explicit (as in the case where constraints with different reference values are enforced on the same observable) or more subtle. In the reported example, the only way to know that the two components of should have similar values is to observe their distribution according to the original force field. In the case of complex molecular systems and of observables that depend non-linearly on the atomic coordinates, it is very difficult to detect inconsistencies between data points a priori. By properly modeling experimental error it is possible to greatly alleviate the effect of these inconsistencies on the resulting posterior. Clearly, if the quality of the prior is very poor, correct data points might artificially appear as inconsistent.
5. Strategies for the Optimization of Lagrangian Multipliers
In order to find the optimal values of the Lagrangian multipliers, one has to minimize the function
. The simplest possible strategy is gradient descent (GD), that is an iterative algorithm in which function arguments are adjusted by following the opposite direction of the function gradient. By using the gradient in Equation (
11) the value of
at the iteration
can be obtained from the value of
at the iteration
k as:
where
represents the step size at each iteration and might be different for different observables. Here we explicitly indicated that the average
should be computed using the Lagrangian multipliers at the
kth iteration
. In order to compute this average it is in principle necessary to sum over all the possible values of
. This is possible for the simple model systems discussed in
Section 4, where integrals can be done analytically. However, for a real molecular system, summing over all the conformations would be virtually impossible. Below we discuss some possible alternatives.
Notice that this whole review is centered on constraints in the form of Equation (
2). The methods discussed here can be applied to inequality restraints as well, as discussed in Ref. [
48].
5.1. Ensemble Reweighting
If a trajectory has been already produced using the prior force field
, samples from this trajectory might be used to compute the function
. In particular, the integral in Equation (
10) can be replaced by an average over
snapshots
sampled from
:
A gradient descent on
results in a procedure equivalent to Equation (
33) where the ensemble average
is computed as a weighted average on the available frames:
It is also possible to use conjugated gradient or more advanced minimization methods. Once the multipliers have been found one can compute any other expectation value by just assigning a normalized weight to the snapshot .
A reweighting procedure related to this one is at the core of the ensemble-reweighting-of-SAXS method [
54], that has been used to construct structural ensembles of proteins compatible with SAXS data [
54,
55]. Similar reweighting procedures were used to enforce average data on a variety of systems [
47,
51,
53,
56,
57,
58,
59,
60]. These procedures are very practical since they allow incorporating experimental constraints a posteriori without the need to repeat the MD simulation. For instance, in Ref. [
59] it was possible to test different combinations of experimental restraints in order to evaluate their consistency. However, reweighting approaches must be used with care since they are effective only when the posterior and the prior distributions are similar enough [
61]. In case this is not true, the reweighted ensembles will be dominated by a few snapshots with very high weight, leading to a large statistical error. The effective number of snapshots with a significant weight can be estimated using the Kish’s effective sample size [
62], defined as
where
are the normalized weights, or similar measures [
63], and is related to the increase of the statistical error of the averages upon reweighting.
5.2. Iterative Simulations
In order to decrease the statistical error, it is convenient to use the modified potential
to run a new simulation, in an iterative manner. For instance, in the iterative Boltzmann method, pairwise potentials are modified and new simulations are performed until the radial distribution function of the simulated particles does match the desired one [
35].
It is also possible to make a full optimization of
using a reweighting procedure like the one illustrated in
Section 5.1 at each iteration. One would first perform a simulation using the original force field and, based on samples taken from that simulation, find the optimal
with a gradient descent procedure. Only at that point a new simulation would be required using a modified potential that includes the extra
contribution. This whole procedure should be then repeated until the value of
stops changing. This approach was used in Ref. [
64] in order to adjust a force field to reproduce ensembles of disordered proteins. The same scheme was later used in a maximum entropy context to enforce average contact maps in the simulation of chromosomes [
65,
66]. A similar iterative approach was used in Refs. [
67,
68].
In principle, iterative procedures are supposed to converge to the correct values of . However, this happens only if the simulations used at each iteration are statistically converged. For systems that exhibit multiple metastable states and are thus difficult to sample it might be difficult to tune the length of each iteration so as to obtain good estimators of the gradients.
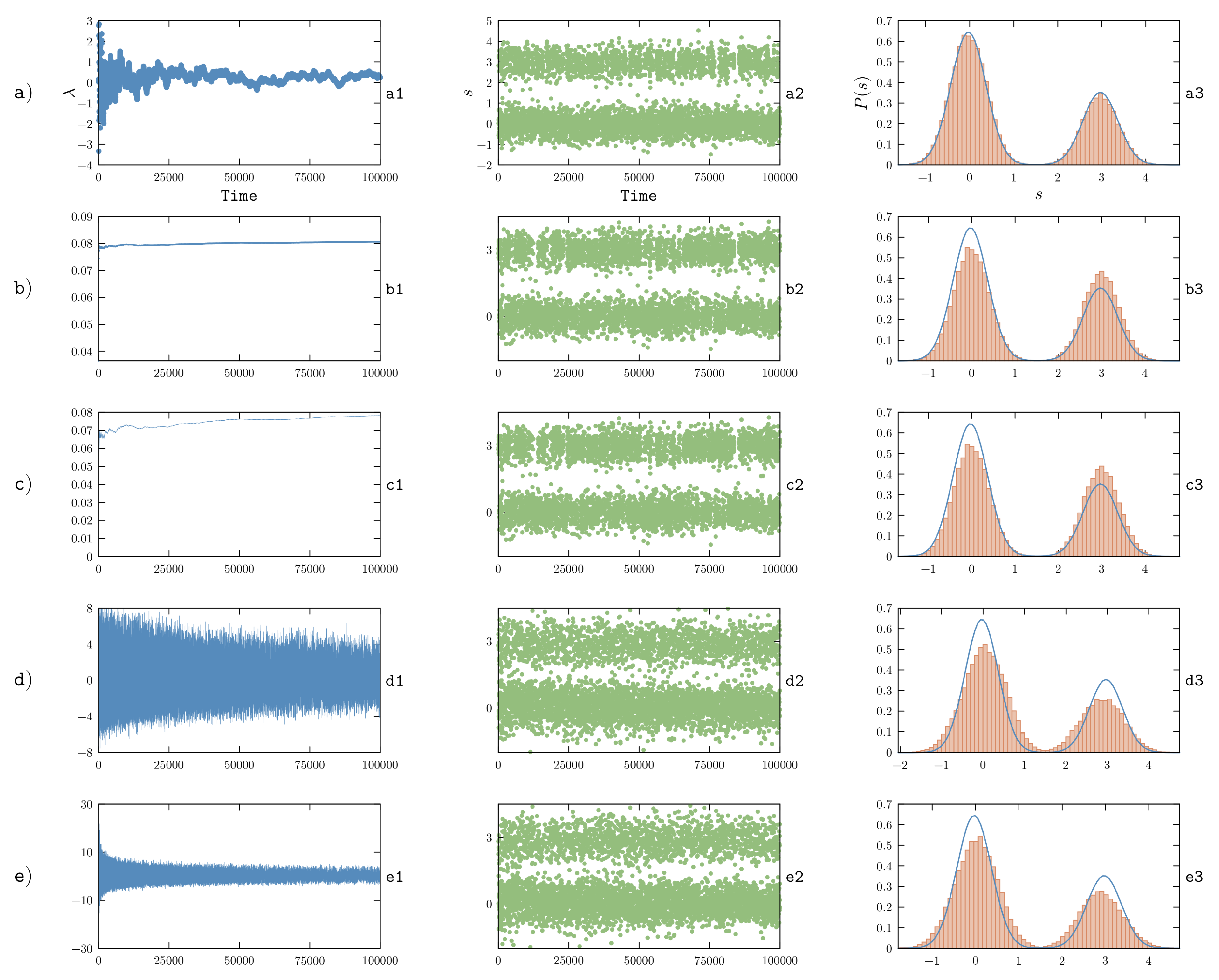
5.3. On-the-Fly Optimization with Stochastic Gradient Descent
Instead of trying to converge the calculation of the gradient at each individual iteration and, only at that point, modify the potential in order to run a new simulation, one might try to change the potential on-the-fly so as to force the system to sample the posterior distribution:
An earlier approach aimed at enforcing time-averaged constraints was reported in Ref. [
69]. However, here we will focus on methods based on the maximum-entropy formalism.
The simplest choice in order to minimize the
function is to use a stochastic gradient descent (SGD) procedure, where an unbiased estimator of the gradient is used to update
. In particular, the instantaneous value of the forward model computed at time
t, that is
, can be used to this aim. The update rule for
can thus be rewritten as a differential equation:
with initial condition
.
Notice that now
plays the role of a
learning rate and depends on the simulation time
t. This choice is motivated by the fact that approximating the true gradient with its unbiased estimator introduces a noise into its estimate. In order to decrease the effect of such noise, a common choice when using SGD is to reduce the learning rate as the minimization (learning) process progresses with a typical schedule
for large times. In our previous work [
48] we adopted a learning rate from the class
search then converge [
70], which prescribes to choose
. Here
represents the initial learning rate and
represents its damping time. In this manner, the learning rate is large at the beginning of the simulation and decreases proportionally to
for large simulation times. The parameters
and
are application specific and must be tuned by a trial and error procedure. In particular, a very small value of
will cause the learning rate to decrease very fast, increasing the probability to get stuck in a suboptimal minimum. On the other hand, a very large value of
will prevent step-size shrinking and thus will hinder convergence. Analogous reasoning also applies to
k (see
Section 6.1 for numerical examples). Also notice that the
’s are measured in units of the inverse of the observable squared multiplied by an inverse time and could thus in principle be assigned to different values in case of heterogeneous observables. It appears reasonable to choose them inversely proportional to the observable variance in the prior, in order to make the result invariant with respect to a linear transformation of the observables. On the other hand, the
parameter should probably be independent of
i in order to avoid different
’s to converge on different timescales.
Once Lagrangian multipliers are converged or, at least, stably fluctuating around a given value, the optimal value
can be estimated by taking a time average of
over a suitable time window. At that point, a new simulation could be performed using a static potential
, either from a different molecular structure or starting from the structure obtained at the end of the learning phase. Such a simulation done with a static potential can be used to rigorously validate the obtained
. Notice that, if errors have been included in the model, such validation should be made by checking that
. Even if the resulting
are suboptimal, it is plausible that such a simulation could be further reweighted (
Section 5.1) more easily than the one performed with the original force field. When modeling errors, if an already restrained trajectory is reweighted one should be aware that restraints will be overcounted resulting in an effectively decreased experimental error (see
Section 3).
As an alternative, one can directly analyze the learning simulation. Whereas strictly speaking this simulation is performed out of equilibrium, this approach has the advantage that it allows the learning phase to be prolonged until the agreement with experiment is satisfactory.
The optimization procedure discussed in this Section was used in order to enforce NMR data on RNA nucleosides and dinucleotides in Ref. [
48], where it was further extended in order to simultaneously constrain multiple systems by keeping their force fields chemically consistent. This framework represents a promising avenue for the improvement of force fields, although it is intrinsically limited by the fact that the functional form of the correcting potential is by construction related to the type of available experimental data. However, the method in its basic formulation described here can be readily used in order to enforce system-specific experimental constraints.
Finally, notice that Equation (
37) is closely related to the on-the-fly procedure proposed in the appendix of Ref. [
47], where a term called “generalized force” and proportional to
is calculated from an integral over the trajectory. Using the notation of this review, considering a Gaussian prior for the error (
Section 3), and setting the confidence in the force field
, the time-evolution of
proposed in Ref. [
47] could be rewritten in differential form as Equation (
37) with
, however with a different initial condition
.
5.4. Other On-the-Fly Optimization Strategies
Other optimization strategies have been proposed in the literature. The already mentioned target metadynamics (
Section 2.4) provides a framework to enforce experimental data, and was applied to enforce reference distributions obtained from more accurate simulation methods [
36], from DEER experiments [
37], or from conformations collected over structural databases [
71]. It is however not clear if it can be extended to enforce individual averages.
Also the VES method [
38] (
Section 2.4) is designed to enforce full distributions. However, in its practical implementation, the correcting potential is expanded on a basis set and the average values of the basis functions are actually constrained, resulting thus numerically equivalent to the other methods discussed here. In VES, a function equivalent to
is optimized using the algorithm by Bach and Moulines [
72] that is optimally suitable for non-strongly-convex functions. This algorithm requires to estimate not only the gradient but also the Hessian of the function
. We recall that
can be made strongly convex by suitable treatment of experimental errors (see
Section 3). However, there might be situations where the Bach-Moulines algorithm outperforms the SGD.
The experiment-directed simulation (EDS) approach [
73] instead does not take advantage of the function
but rather minimizes with a gradient-based method [
74] the square deviation between the experimental values and the time-average of the simulated ones. A later paper tested a number of related minimization strategies [
75]. In order to compute the gradient of the ensemble averages
with respect to
it is necessary to compute the variance of the observables
in addition to their average. Average and variance are computed on short simulation segments. It is worth observing that obtaining an unbiased estimator for the variance is not trivial if the simulation segment is too short. Errors in the estimate of the variance would anyway only affect the effective learning rate of the Lagrangian multipliers. In the applications performed so far, a few tens of MD time steps were shown to be sufficient to this aim, but the estimates might be system dependent. A comparison of the approaches used in Refs. [
73,
75] with the SGD proposed in Ref. [
48] in practical applications would be useful to better understand the pros and the cons of the two algorithms. EDS was used to enforce the gyration radius of a 16-bead polymer to match the one of a reference system [
73]. Interestingly, the restrained polymer was reported to have not only the average gyration radius in agreement with the reference one, but also its distribution. This is a clear case where a maximum entropy (linear) restraint and a harmonic restraint give completely different results. The EDS algorithm was recently applied to a variety of systems (see, e.g., Refs. [
34,
75,
76]).
7. Discussion and Conclusions
In this work, we reviewed a number of recently introduced techniques that are based on the maximum entropy principle and that allow experimental observations to be incorporated in MD simulations preserving the heterogeneity of the ensemble. We discuss here some general features of the reviewed methods.
First, one must keep in mind that, by design, the maximum entropy principle provides a distribution that, among those satisfying the experimental constraints, is as close as possible to the prior distribution. If the prior distribution is reasonable, a minimal correction is expected to be a good choice. However, for systems where the performance of classical force fields is very poor, the maximum entropy principle should be used with care and, if possible, should be based on a large number of experimental data so as to diminish the impact of force-field deficiencies on the final result. As a related issue, different priors are in principle expected to lead to different posteriors, and thus different ensemble averages for non-restrained quantities. There are indications that current force fields restrained by a sufficient number of experimental data points lead to equivalent posterior distributions at least for trialanine [
51] and for larger disordered peptides [
86,
89]. It would be valuable to perform similar tests on other systems where force fields are known to be poorly predictive, such as unstructured RNAs or difficult-to-predict RNA structural motifs.
We here discussed both the possibility of reweighting a posteriori a trajectory and that of performing a simulation where the restraint is iteratively modified. Techniques where the elements of a previously generated ensemble are reweighted have the disadvantage that if the initial ensemble averages are far from the experimental values the weights will be distributed very inhomogeneously (i.e., very large will be needed), which means that singular conformations with observables close to the experimental values can be heavily overweighted to obtain the correct ensemble average. In the extreme case, it might not even be possible to find weights that satisfy the desired ensemble average, since important conformations are simply missing in the ensemble. On the other hand, reweighting techniques have the advantage that they can be readily applied to new or different experimental data, without performing new simulations. Additionally, they can be used to reweight a non-converged simulation performed with an on-the-fly optimization.
When simulating systems that exhibit multiple metastable states, it might be crucial to combine the experimental constraints with enhanced sampling methods. This is particularly important if multiple metastable states contribute to the experimental average. As usual in enhanced sampling simulations, one should observe as many as possible transitions between the relevant metastable states. When using replica-based methods (either to enhance sampling or to compute averages), transitions should be observed in the continuous trajectories.
Several methods are based on the idea of simulating a number of replicas of the system with a restraint on the instantaneous average among the replicas and have been extended to treat experimental errors. These methods are expected to reproduce the maximum entropy distribution in the limit of a large number of replicas. However, if the number of replicas is too low, the deviation from the maximum entropy distribution might be significant. Indeed, the number of replicas should be large enough for all the relevant states to be represented with the correct populations. The easiest way to check if the number of replicas is sufficient is to compare simulations done using a different number of replicas. Methods based on Lagrangian multipliers reproduce the experimental averages by means of an average over time rather than an average over replicas. Thus, they can be affected by a similar problem if the simulation is not long enough. This sort of effect is expected to decrease when the simulation length increases and when using enhanced sampling techniques.
The on-the-fly refinement of Lagrangian multipliers typically requires ad hoc parameters for the learning phase that should be chosen in a system-dependent manner. Properly choosing these parameters is not trivial. Several different algorithms have been proposed in the last years and a systematic comparison on realistic applications would be very useful. It might also be beneficial to consider other stochastic optimization algorithms that have been proposed in the machine-learning community. Interestingly, all the methods discussed in this review for on-the-fly optimization (target metadynamics, maximum entropy with SGD, VES, and EDS) are available in the latest release of the software PLUMED [
90] (version 2.4), which also implements replica-based methods, forward models to calculate experimental observables [
91], and enhanced sampling methods.
Finally, we notice that there are cases where results might be easier to interpret if only a small number of different conformations were contributing to the experimental average. In order to obtain small sets of conformations that represent the ensemble and provide a clearer picture about the different states, several
maximum parsimony approaches have been developed. Naturally, the selection of a suitable set of structures is done on an existing ensemble and not on-the-fly during a simulation. While some approaches use genetic algorithms to select the structures of a fixed-size set [
28,
92,
93], others use matching pursuit [
94] or Bayes-based reweighting techniques to obtain correct ensemble averages [
95,
96,
97,
98] while minimizing the number of non-zero weights, i.e., structures, in the set. These approaches are not central to this review and so were not discussed in detail.
In conclusion, the maximum (relative) entropy principle provides a consistent framework to combine molecular dynamics simulations and experimental data. On one hand, it allows improving not-satisfactory results sometime obtained when simulating complex systems with classical force fields. On the other hand, it allows the maximum amount of structural information to be extracted from experimental data, especially in cases where heterogeneous structures contribute to a given experimental signal. Moreover, if experimental errors are properly modeled, this framework allows to detect experimental data that are either mutually inconsistent or incompatible with the employed force field. For all these reasons, we expect this class of methods to be increasingly applied for the characterization of the structural dynamics of biomolecular systems in the coming future.