A Microwave Reflectometry Technique for Profiling the Dielectric-Conductivity Properties of the Hagia Sophia Globe

Abstract

A microwave free space reflectometry technique with swept frequency measurements for the profiling of wall structures and the detection of hidden (covered) layers has been applied to the Hagia Sophia byzantine monument. Experimental measurement results are presented and compared with three-dimensional (3D) simulated results, exhibiting fair agreement in some (though not all) aspects. Based on the experimental results, the possibility of clear discrimination between regions with and without covered mosaic layers, and hence the detection of such layers, is demonstrated.

1. Introduction

The in-depth characterization of wall structures is of considerable interest for monument conservation and restoration [1]. More particularly, the detection of successive layers of different materials may reveal hidden architectural or decorative elements of historical and/or artistic significance. To this end, the identification of the geometry and electric properties (complex dielectric permittivities) of stratified media is desirable, since the walls of many monuments may be modeled as multilayered planar (or nearly planar) structures. Various methods exist for the measurement of complex dielectric permittivities; among them, microwave techniques appear particularly well suited to the dimensions of the layered structures of interest, as well as their limited transparency at optical frequencies. Further on, in the area of monument conservation, a strong motivation obviously exists for the use of nondestructive and contactless techniques rather than destructive ones such as e.g., waveguide, coaxial, or cavity fixtures. Thus, free space methods [2] appear as a reasonable choice. The relevant literature is quite large; a good portion of earlier publications is reviewed in References [2,3,4], while a comprehensive selection of more recent pertinent work may be found in References [5,6]. Such methods are based on reflection or reflection-transmission measurements, with the materials under test being usually in stratified geometries. Transmission measurements have been extensively applied, as in Reference [5], where typical construction materials are studied and dielectric parameters are estimated for a variety of frequencies; in another recent study [6], an interesting comparison is carried out between measurements inside and outside an anechoic chamber. However, application of the technique for in situ measurements presents considerable difficulties [5]. Thus, for application to wall structures, reflectometry is an attractive choice in terms of simplicity and practicability. Reflectometry (or interferometry) techniques are widely used in microwave frequencies (see e.g., Reference [3], where the measurement of the S₁₁ reflection coefficient by use of a metal-backed stratified configuration was proposed, to be followed by a considerable number of studies). Such techniques are also (or even more) popular in optical frequencies (see e.g., Reference [7] and references therein), with applications in the measurement of the thickness or complex permittivity of layered materials. A problem is posed by the fact that, for wall structures, neither of these parameters is a priori known with sufficient accuracy to allow the accurate determination of the other one via some fitting procedure. However, in the present case, the actual goal is the detection of hidden elements rather than the accurate measurement of the corresponding parameters. For the same reason, another limitation of free space methods, namely poor performance for small loss tangents (which is the case for the building materials of interest), may be considered insignificant here.

In this paper, the use of a microwave reflectometry technique to detect hidden layers in the walls of the Hagia Sophia temple is investigated and corresponding measurements for X band microwave frequencies are presented, along with preliminary simulation results for comparison.

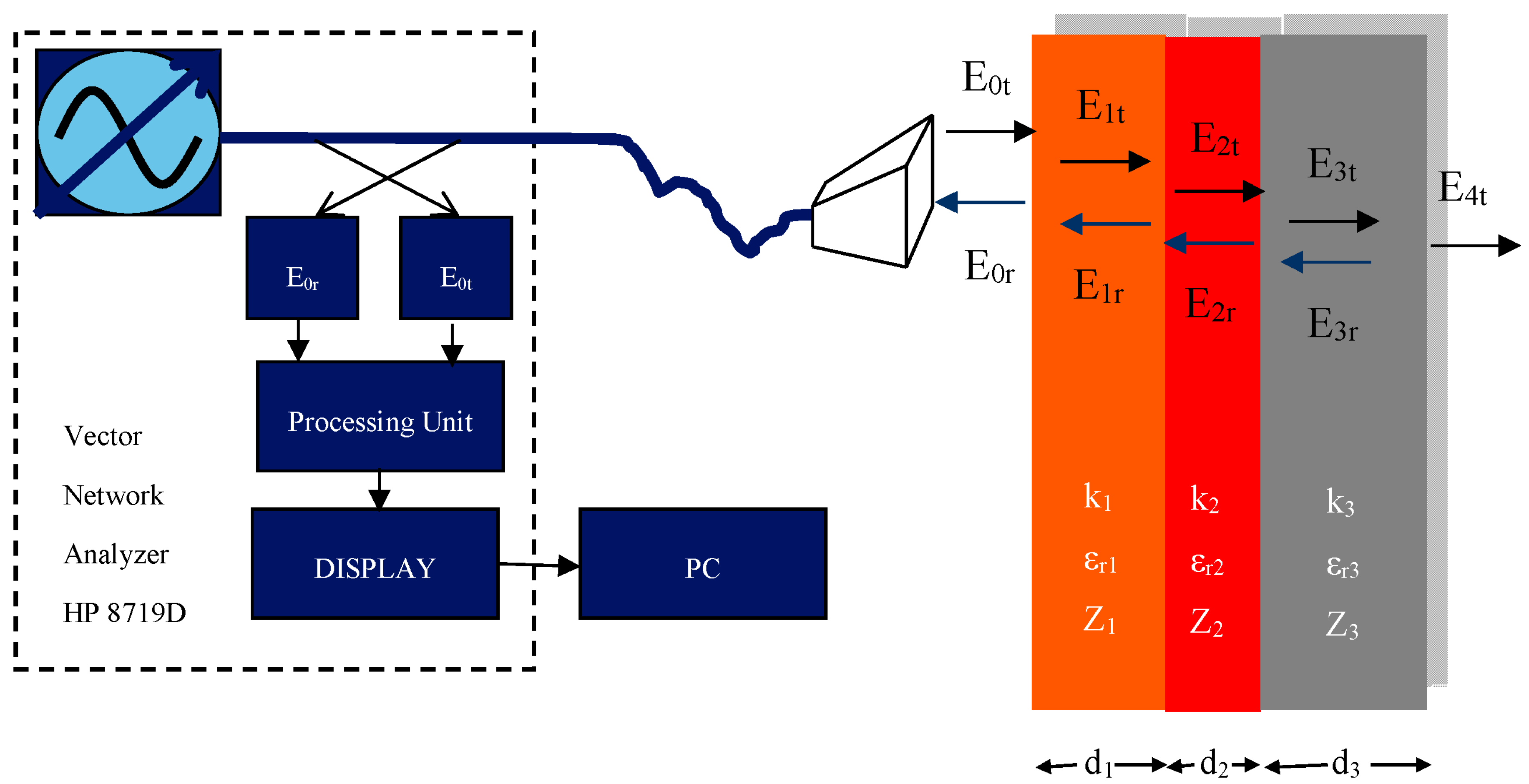
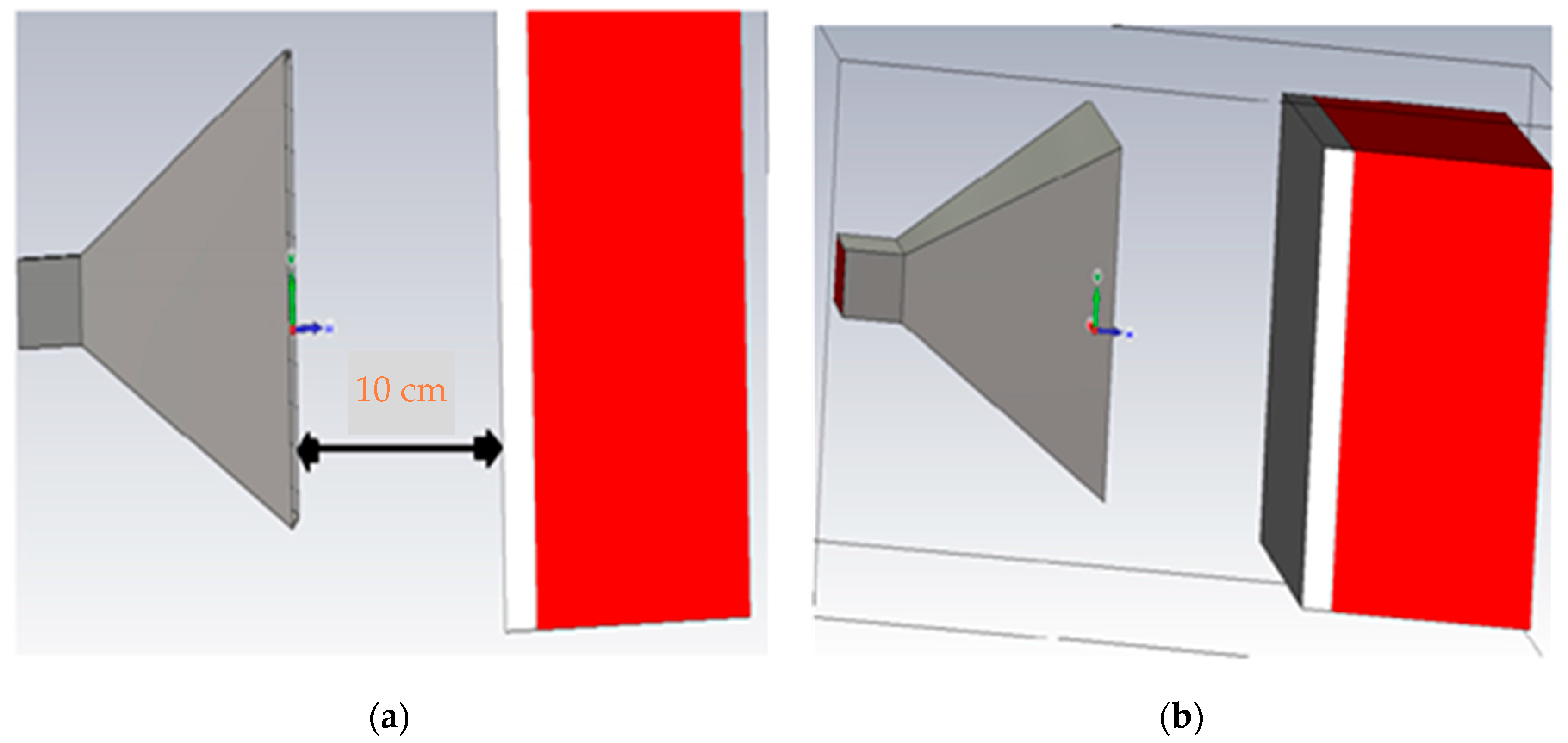
2. Materials and Methods

Measurement of the reflected wave impinging from the wall surface was carried out at the Hagia Sophia dome, along the 19th and 20th rib, which are known to contain various layers, including regions of covered mosaics of various periods, as well as regions without mosaics [8]. The existence of regions without mosaics is quite helpful, providing the reference measurements usually required for the application of such methods. The operating principle of the microwave reflectometry method applied is shown in Figure 1.

A signal from a sweep generator is emitted towards the wall via a microwave horn antenna, which also receives the reflected wave. A directional coupler is used to connect to a microwave vector network analyzer (VNA) that measures (and outputs for recording) the reflection coefficient between the two coupler ports. Amplitude measurements for the reflection coefficient are presented and discussed in the following. At the present stage, no attempt was made to exploit phase measurements, mainly due to a lack of precise knowledge of the thickness values for all layers, as well as significant uncertainties in the value of the distance (gap) between the antenna and the wall surface due to the curved surface of the dome, but also due to the difficulty of precise mounting near the dome. An additional reason is the proximity of the antenna to the dome surface, implying near field measurements. Moreover, by relying on amplitude measurements, the procedure can be carried out by the use of a scalar network analyzer (SNA) instead of a costlier vector one. A spectrum analyzer equipped with a tracking generator (as is now the case for various relatively inexpensive devices) would be sufficient; the development of the USB devices market allows us to expect further price drops in such instruments in the near future. Further on, based on the wide availability of cheap and reliable integrated microwave frequency synthesizers with sweeping and phase locking capabilities for impressively large frequency regions, building an even lower cost, tailor-made experimental system appears quite feasible. Hence, detection is based on the reflection loss values versus frequency observed. Investigation of the possible utilization of phase observations is of interest for future study.

Measurements were carried out in the 8–12 GHz (X band) frequency range, using an HP 8719D microwave network analyzer and a waveguide (WR-90) horn antenna for transmission and reception, with dimensions W × H × L = 43 × 41 × 46 mm and a nominal 10-dB gain. Aspects of the measurement setup are shown in Figure 2, including the overall internal layout of the temple, a picture of the dome surface, and the VNA used. The antenna was placed at an approximate distance of several cm from the dome surface and connected to the analyzer through a 2-m coaxial cable and a directional coupler. A set of measurements in the 4–8 GHz (C band) frequency range were also taken, which is expected to be the object of future study.

To compare with experimental results, for purposes of verification, qualitative assessment, and exploration of the potential for a more precise parameter fitting, two sets of numerical computations were carried out. The first is a very simple calculation of plane wave reflection and transmission coefficients, while the second is a three-dimensional (3D) numerical simulation using the state-of-the-art tools of the CST MICROWAVE STUDIO^® simulation software. In the first computation, a canonical planar stratified configuration (infinite planar layers) and linearly polarized plane wave normal incidence is assumed. The second computation assumes a rectangular patch of the layered medium combined with a transmitting/receiving horn antenna of the dimensions actually used, as depicted in Figure 3. A test configuration was adopted, with thickness values of d₁ = 0.2 cm (lime), d₂ = 0.5 cm (glass), and d₃ = 5 cm (red brick) for each layer. To save computation time, a 15 × 15 cm surface patch and a d = 10 cm antenna-surface distance (gap) was assumed for the 3D simulations. The rationale for performing a plane wave calculation, besides more accurate 3D simulations, was based on the advantage of simplicity and speed, providing an independent benchmark to check as well as a possible application with a parameter fitting procedure to obtain quantitative estimates of the thickness or the electric parameters of the wall layers, which is expected to be impractical with the intensely time-consuming 3D simulations.

Both approaches require the electric (permittivity and conductivity) parameters of the materials constituting the layered medium under consideration. As is known [9], three layers of different building materials were used for the Hagia Sophia walls in the measured region (dome), namely lime (on the wall surface), mosaic (glass with traces of gold or solely glass), and red brick (the wall body). The second layer (mosaic) may or may not be present in any specific part of the dome, and its detection is one of the main goals of this study. However, precise values of the electric parameters for the specific materials of the monument walls studied are not available (and their direct measurement would most probably require some kind of destructive testing which of course would be impossible/undesirable to arrange during the specific measurement campaign). Instead, typical values of such materials from the literature have been used as a starting point for the simulations, as presented in

Table 1. Typical electric properties of building materials.

Material	Relative Permittivity εr	Conductivity σ (S/m)	Source
Lime (CaO)	7.4	${\mathsf{\sigma }}_{wet}$ = 4.76 × 10−6	[10]
		${\mathsf{\sigma }}_{\mathrm{dry}}$ = 4.35 × 10−8
Glass	5–10	$\mathsf{\sigma }$ = 7 × 10−3	[11,12]
Red Brick	≅6 1	$\mathsf{\sigma }$ ≅ 0.034 2	[13]

¹ Estimated value from Reference [13] corresponding to a frequency of 5.25 GHz; beyond this, no estimate is given, but from measurements up to 7 GHz presented therein, a trend increasing with frequency is implied, so we may expect a larger ε_r value in the X band. ² Based on the estimated value of loss tangent at 5.25 GHz from Reference [13].

(where a whole range of typical values is given, the mean value was adopted for preliminary simulations).

The plane wave coefficient calculation is based on solution of an 8 × 8 system of linear equations, derived by the standard boundary condition matching procedure, written in matrix form as follows:

$$\mathrm{A}\cdot \mathrm{X}=\mathrm{B}$$

(1)

where

$$\mathrm{A}=\left[\begin{array}{cccccccc}1& -1& -1& 0& 0& 0& 0& 0\\ -1/{\mathrm{Z}}_0& -1/{\mathrm{Z}}_1& 1/{\mathrm{Z}}_1& 0& 0& 0& 0& 0\\ 0& {\mathrm{e}}^{-\mathrm{j}\cdot {\mathrm{k}}_1{\mathrm{d}}_1}& {\mathrm{e}}^{\mathrm{j}\cdot {\mathrm{k}}_1{\mathrm{d}}_1}& -1& -1& 0& 0& 0\\ 0& \frac{{\mathrm{e}}^{-\mathrm{j}\cdot {\mathrm{k}}_1{\mathrm{d}}_1}}{{\mathrm{Z}}_1}& -\frac{{\mathrm{e}}^{\mathrm{j}\cdot {\mathrm{k}}_1{\mathrm{d}}_1}}{{\mathrm{Z}}_1}& -1/{\mathrm{Z}}_2& 1/{\mathrm{Z}}_2& 0& 0& 0\\ 0& 0& 0& {\mathrm{e}}^{-\mathrm{j}\cdot {\mathrm{k}}_2{\mathrm{d}}_2}& {\mathrm{e}}^{\mathrm{j}\cdot {\mathrm{k}}_2{\mathrm{d}}_2}& -1& -1& 0\\ 0& 0& 0& \frac{{\mathrm{e}}^{-\mathrm{j}\cdot {\mathrm{k}}_2{\mathrm{d}}_2}}{{\mathrm{Z}}_2}& -\frac{{\mathrm{e}}^{\mathrm{j}\cdot {\mathrm{k}}_2{\mathrm{d}}_2}}{{\mathrm{Z}}_2}& -1/{\mathrm{Z}}_3& 1/{\mathrm{Z}}_3& 0\\ 0& 0& 0& 0& 0& {\mathrm{e}}^{-\mathrm{j}\cdot {\mathrm{k}}_3{\mathrm{d}}_3}& {\mathrm{e}}^{\mathrm{j}\cdot {\mathrm{k}}_3{\mathrm{d}}_3}& -1\\ 0& 0& 0& 0& 0& \frac{{\mathrm{e}}^{-\mathrm{j}\cdot {\mathrm{k}}_3{\mathrm{d}}_3}}{{\mathrm{Z}}_3}& -\frac{{\mathrm{e}}^{\mathrm{j}\cdot {\mathrm{k}}_3{\mathrm{d}}_3}}{{\mathrm{Z}}_3}& -1/{\mathrm{Z}}_0\end{array}\right]$$

(2)

$$\mathrm{X}=\left[\begin{array}{c}{\mathrm{E}}_{0\mathrm{r}}\\ {\mathrm{E}}_{1\mathrm{t}}\\ {\mathrm{E}}_{1\mathrm{r}}\\ {\mathrm{E}}_{2\mathrm{t}}\\ {\mathrm{E}}_{2\mathrm{r}}\\ {\mathrm{E}}_{3\mathrm{t}}\\ {\mathrm{E}}_{3\mathrm{r}}\\ {\mathrm{E}}_{4\mathrm{t}}\end{array}\right]\mathrm{B}=\left[\begin{array}{c}-1\\ -1/{\mathrm{Z}}_0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]$$

(3)

Z_i (i = 1,2,3) is the wave impedance and k_i is the wavenumber for each layer (see e.g., [12,14]), with ε₀, μ₀ the free space permittivity and permeability, respectively, and

Z₀ = 120π ≅ 377 Ω

(4)

$${\mathrm{Z}}_{\mathrm{i}}={\mathrm{Z}}_0/\sqrt{{\mathsf{\epsilon }}_{\mathrm{r},\mathrm{i}}-\mathrm{j}\frac{{\mathsf{\sigma }}_{\mathrm{i}}}{\mathsf{\omega }{\mathsf{\epsilon }}_0}}$$

(5)

$${\mathrm{k}}_0=2\mathsf{\pi }/\mathsf{\lambda }$$

(6)

$${\mathrm{k}}_{\mathrm{i}}={\mathrm{k}}_0\sqrt{{\mathsf{\epsilon }}_{\mathrm{r},\mathrm{i}}-\mathrm{j}\frac{{\mathsf{\sigma }}_{\mathrm{i}}}{\mathsf{\omega }{\mathsf{\epsilon }}_0}}$$

(7)

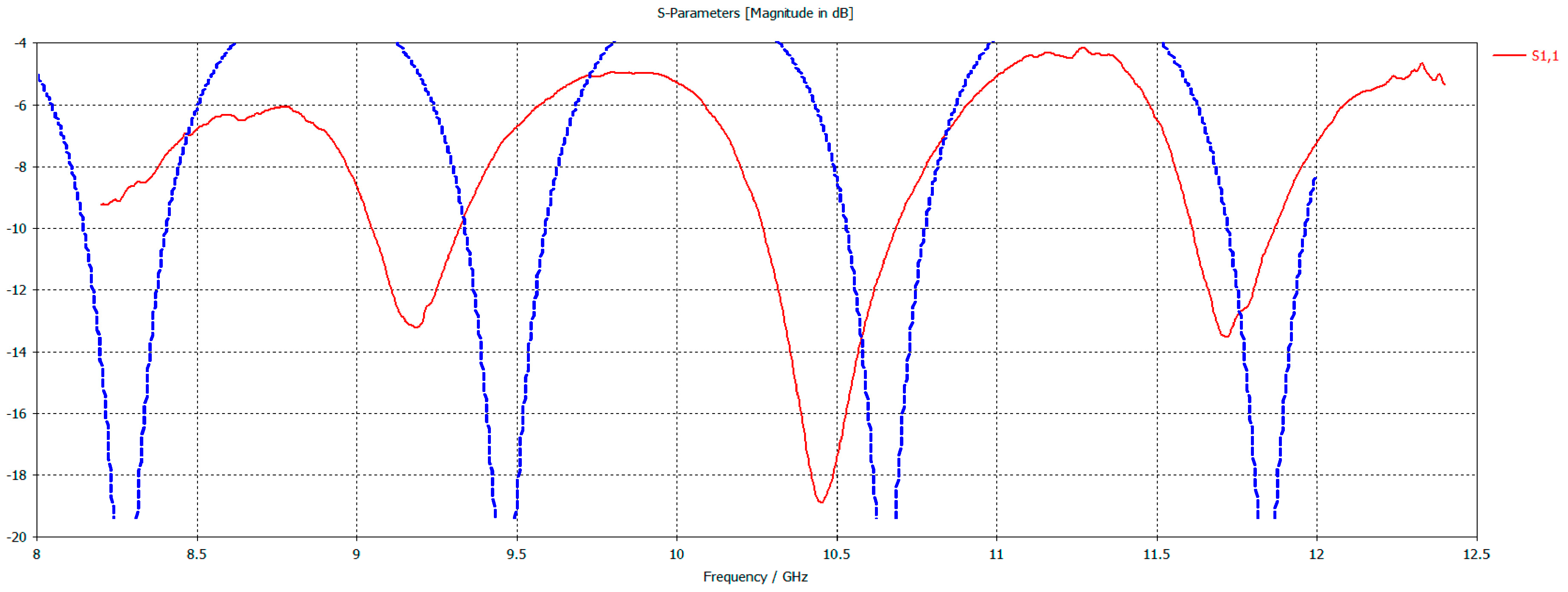
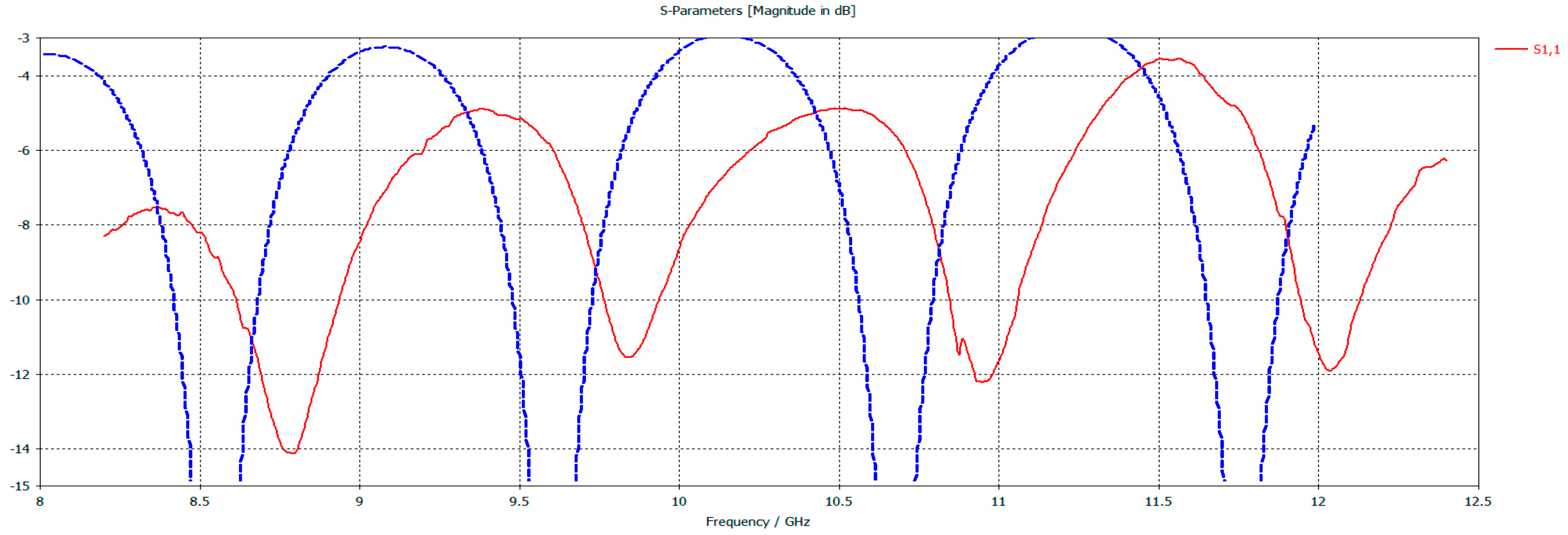
3. Results

For benchmark testing of the simulation results, the test configuration described above was adopted, along with the permittivity values given in Table 1 combined with very small conductivity values (around 10⁻⁸, 10⁻¹¹, and 10⁻⁷ for the three layers) to check for cases of relatively large reflection. Varying the frequency between 8–12 GHz, results for the reflection coefficient amplitude were first obtained for a reference two-layer configuration (no hidden mosaic), setting d₂ = 0 (i.e., removing the intermediate glass layer), as plotted in Figure 4, by 3D and plane wave simulation. Observing the two waveforms, it was confirmed that at nearly the same frequencies (9.2, 10.4, and 11.7 GHz), the reflection coefficient S₁₁ falls below −10 dB.

The corresponding 3D and plane wave results for the corresponding test configuration with mosaic (d₂ = 0.5 cm) are presented in Figure 5. We note that both methods have roughly the same response in terms of input reflection coefficient. In the plane wave approach the S₁₁ response has slipped slightly to the left, while the frequency differences where the reflection coefficient is lower than −10 dB (at 8.8, 9.8, 10.9, 12.1 GHz for the 3D approach and at 8.6, 9.7, 10.6, 11.8 GHz for the plane wave approach) are almost identical (every 1.1 GHz).

Upon comparison of the results of the two approaches (3D and plane wave simulation), a remarkably close agreement was observed, implying a good approximation given by the plane wave simulation. Based on this, the plane wave simulation was further used for comparison with the experimental results. Actual values of conductivity from Table 1 were adopted as a starting point for the simulations (for the front layer of lime, where a whole range of values is given, the mean value between extremes was used), and were subsequently varied along with the thickness parameters of the layers by trial and error in order to approach the experimental plots. Indicative results of this procedure follow.

The experimental (measured) results for a dome surface part where no mosaic exists and the corresponding results for a part where mosaic is known to exist are depicted in Figure 6 and Figure 7, respectively.

By a series of trial and error tests, it was found that:

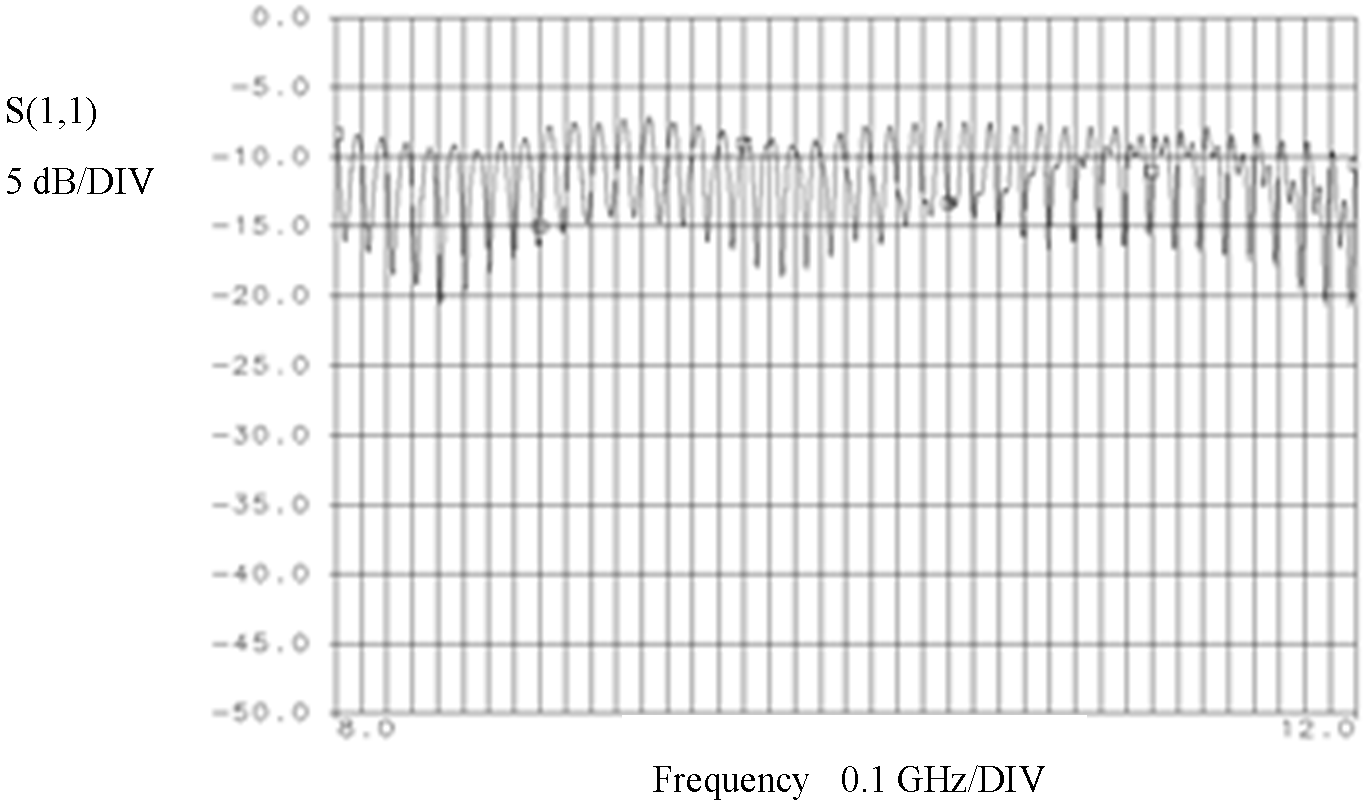
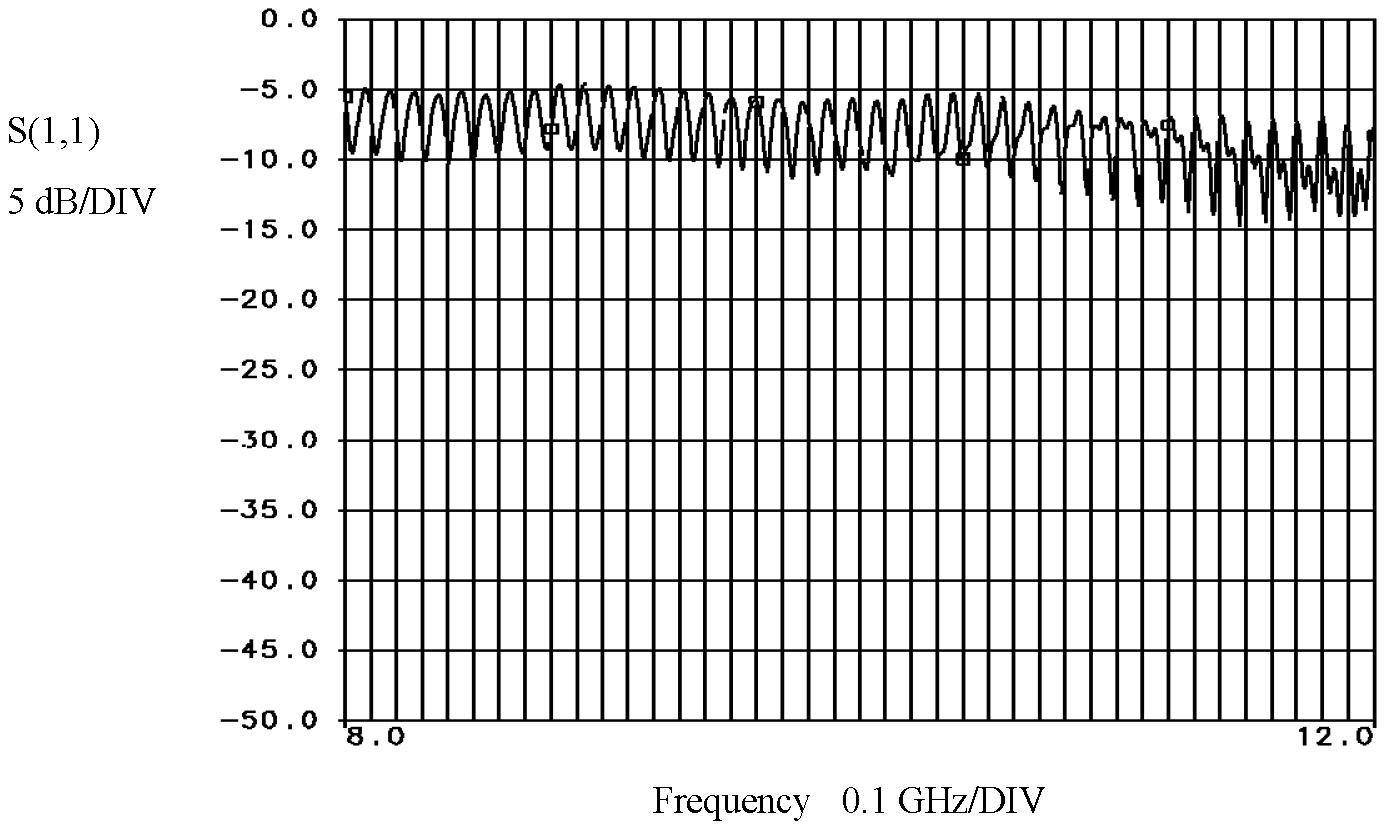
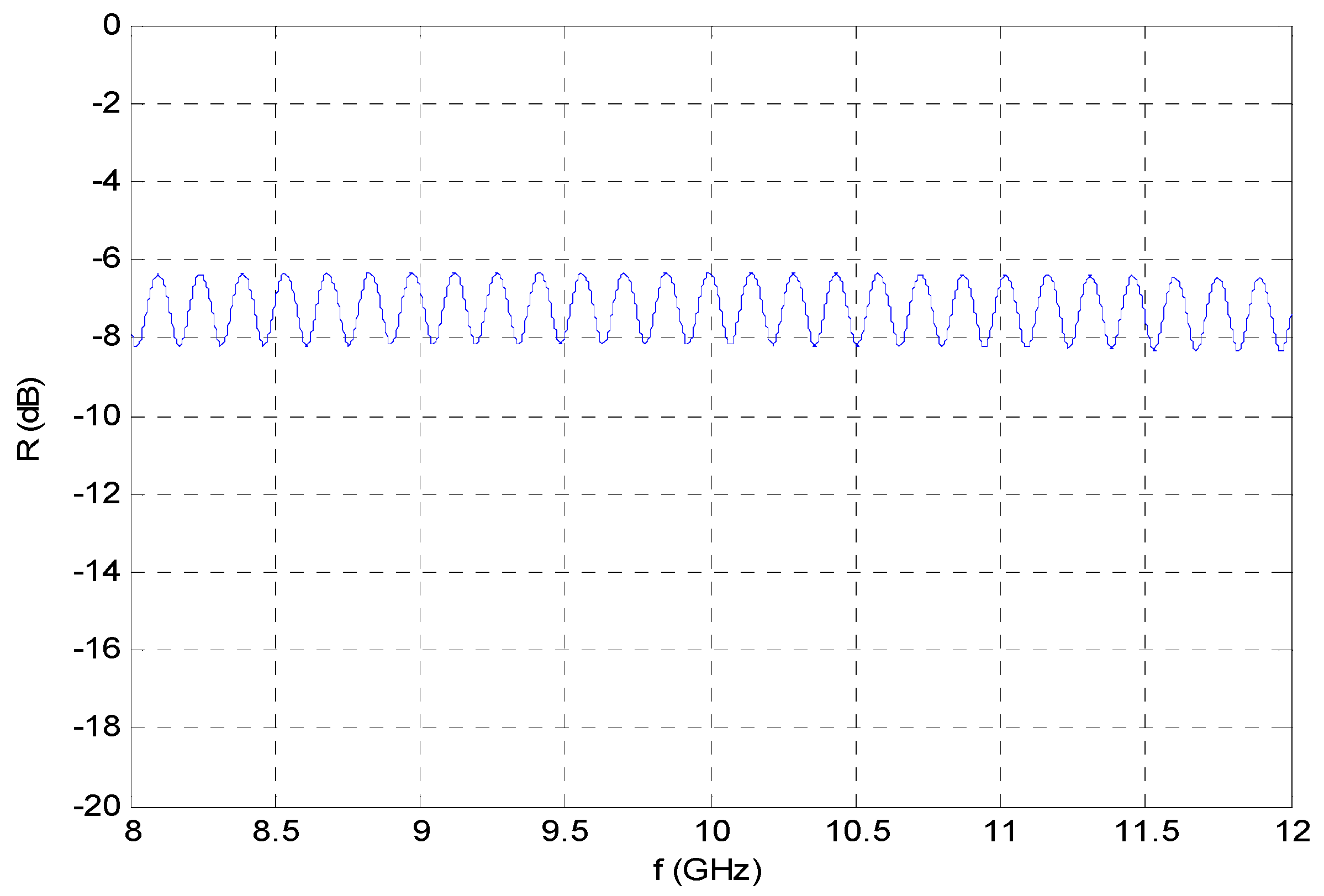
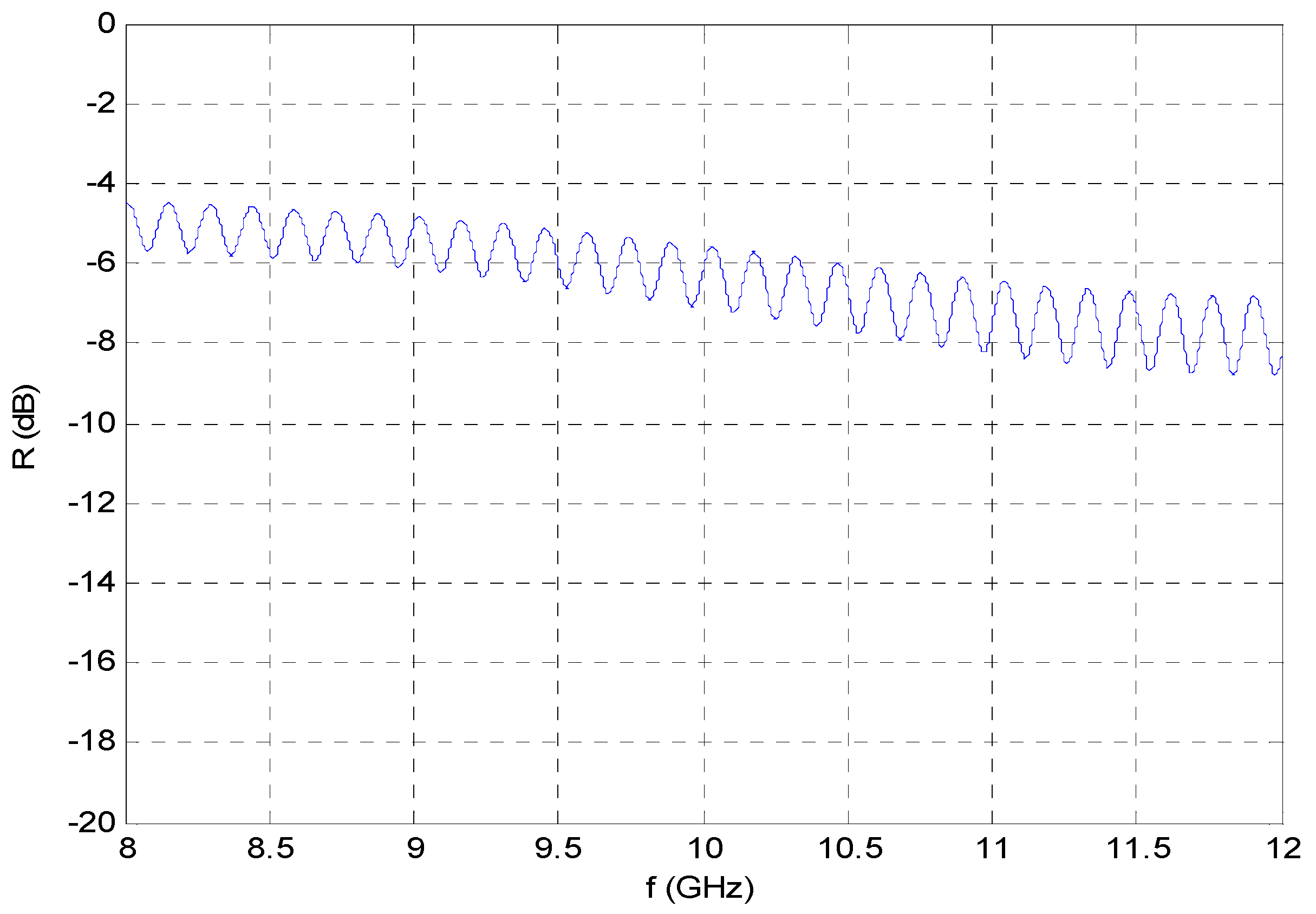
• the simulated data (and, of course, the measured ones) exhibit the fluctuating behavior expected for the stratified structure under consideration
• the density of the fluctuations seems to depend mainly on the thickness of the third layer (red brick), which was significantly increased accordingly
• the depth of the fluctuations seems to depend mainly on the difference between the dielectric parameters of the second (glass) and third (red brick) layer; a slight decrease of the glass permittivity and an increase of the brick permittivity beyond the values reported in the literature (which in any event refer to materials and frequency ranges not identical to the ones actually measured in the Hagia Sophia) result in better matching of the experimental results
• matching of the overall form of the fluctuations is improved with a slight increase in the depth of the first (lime) and second (glass) layer (as compared with the initial benchmark values adopted).

In view of the above remarks, Figure 8 and Figure 9 depict the simulation results for the reflection coefficient with and without the glass layer for ε_1,r = 7.4, ε_2,r = 4.5, ε_3,r = 6.5, σ₁ = 2.4 × 10⁻⁶ (the mean value between the two extreme literature values), σ₂ = 7 × 10⁻³, σ₃ = 0.034 (the literature value), and d₁ = 0.3 cm (lime), d₂ = 0.55 cm (glass), d₃ = 40 cm (red brick).

4. Discussion

Interestingly (and somewhat surprisingly), the results of the plane wave simulations agree quite well with those of the more realistic (and significantly more time-consuming) 3D simulations. The form of the fluctuations observed is almost identical, while the plane wave results exhibit slightly larger peak values and considerably smaller minimum values, i.e., sharper variations in the “trough” regions of the plots, which nevertheless are quite narrow. Both effects can be attributed to the finite directivity of the horn antenna, combined with the limited scattering surface considered for the 3D simulations; this seems to be confirmed by the increase of the reflection coefficient given by the 3D simulation in the upper frequency region, which corresponds to larger scattering surface in terms of wavelength. A somewhat surprising aspect of the good agreement observed is the implication that the plane wave model (usually applicable in the far field region) appears to offer a fairly good approximation of the antenna reflection losses even in the near field region. A possible explanation for this might be based on a simple transmission line analogy, where the wave impedance “seen” by the antenna in the immediate vicinity of its aperture (i.e., near field), which for a layered planar medium is given by the plane wave model at all points, corresponds to the terminal impedance, and the wave impedance on the aperture of the antenna in the absence of the layered medium, which is just the free space impedance, corresponds to the characteristic impedance near termination; the antenna reflection coefficient may be approximated by the line reflection coefficient at termination due to the difference (mismatch) between the two impedances.

Regarding the experimental results, upon comparison of the measured values with and without the glass layer (mosaic), a clear distinction between the two cases is experimentally evident. More specifically, measurement results with and without mosaic differ by a significant margin of about 2–3 dB across the whole swept frequency range. We consider this a very encouraging result, demonstrating the capability to detect hidden layers by the use of the microwave reflectometry technique based on clear and simple criteria. Since the physical reason for the measured differences is wave propagation through the intermediate glass layer, an interesting question arises about the possibility of improving the sensitivity of the method (i.e., the difference between results with and without glass) by means of bistatic measurements using two separate transmitting and receiving antennas and oblique incidence; the rationale for such a modification is based on the observation that oblique incidence implies a longer propagation path of the signal inside each layer, as if layer thicknesses were extended. Such an approach, however, would significantly increase the complexity of the experimental setup, with serious difficulties in accurate antenna positioning and orientation. Additional errors would possibly be introduced by the antenna beam width, and larger attenuation of the reflected signal might decrease sensitivity at the detector. Thus, such an extension of the methodology may be regarded as a distinct topic for future study.

Upon comparison of the experimental and simulated plots, fairly good approaching of the measured values of reflection coefficient is achieved. Due to the trial and error approach in the selection of the layer parameters, these results have an indicative character; a more thorough investigation of parameter matching is of interest for future study, which might reduce some discrepancies observed between the measured and simulated plots, mainly with respect to the depth of the fluctuations. Some discrepancies are also seen in the absolute values of the reflection coefficient. More specifically, the experimental results exhibit somewhat larger reflection losses, which seem reasonable due to various losses inherent in the experimental setup, including the finite antenna gain. Another possible source of reflection losses in the actual physical configuration is the lime surface roughness, though its effect is not expected to be very pronounced within the range of wavelengths used. Finally, the curved surface of the dome is also a possible source of discrepancies.

5. Conclusions

A microwave reflectometry technique has been applied to detect hidden layers in the walls of the Hagia Sophia temple, demonstrating the potential of nondestructive contactless microwave techniques for use in the area of monument conservation and restoration. The Hagia Sophia, a very renowned byzantine monument, has been a longtime object of great interest in many relevant fields (dynamic behavior and earthquake response, protection of mosaics, etc.). The method applied is based on free space reflection coefficient measurements by a network analyzer. Experimental results for the X band frequency region are presented, exhibiting a clear difference in the amplitude of the reflection coefficient between wall regions with or without hidden glass (mosaic) layers, which allows the unambiguous detection of such layers by inspection. Thus, an experimental demonstration of the detection capabilities of the method for such structures has been accomplished, and may be expected to hold for monuments of similar construction. The simulation results for comparison were calculated with state-of-the-art 3D numerical tools, as well as a simple and very fast plane wave approach, and were found to well approach most features of the experimental results. Some discrepancies were observed, which may be attributed to inaccuracies of the simulation process, as well as a lack of precise knowledge of the layer thicknesses and the electric parameters of the building materials involved, and so on. Of considerable interest for future study is the application of some parameter fitting procedure to extract more precise quantitative information for the wall structure profile. Extension to frequency regions beyond the X band for various layered structures (making use of the HP 8510C VNA for frequencies up to 40 GHz available by the NTUA Microwave Laboratory) is also envisaged.