A Holistic Scalable Implementation Approach of the Lattice Boltzmann Method for CPU/GPU Heterogeneous Clusters
Abstract
:1. Introduction
2. Related Work
3. The Lattice Boltzmann Method
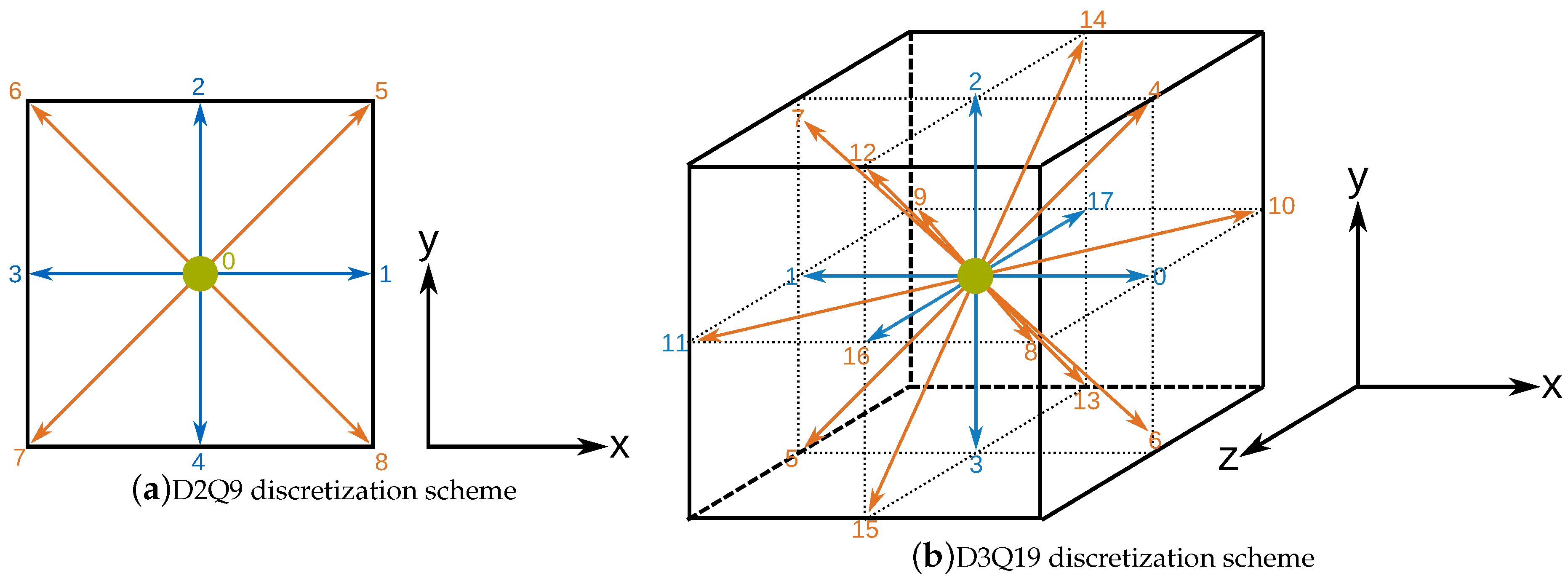
3.1. Discretization Schemes
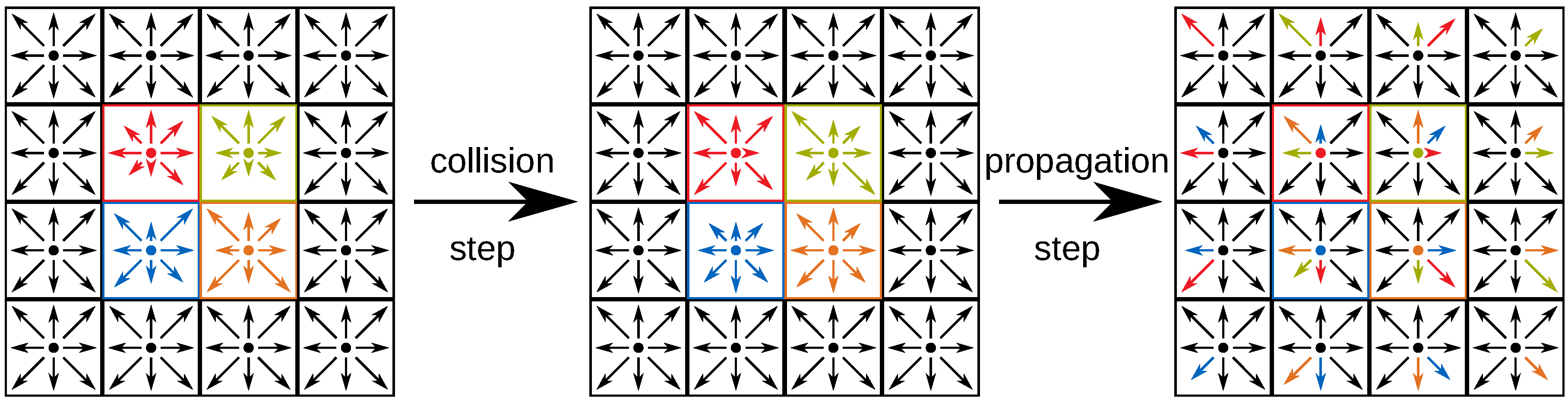
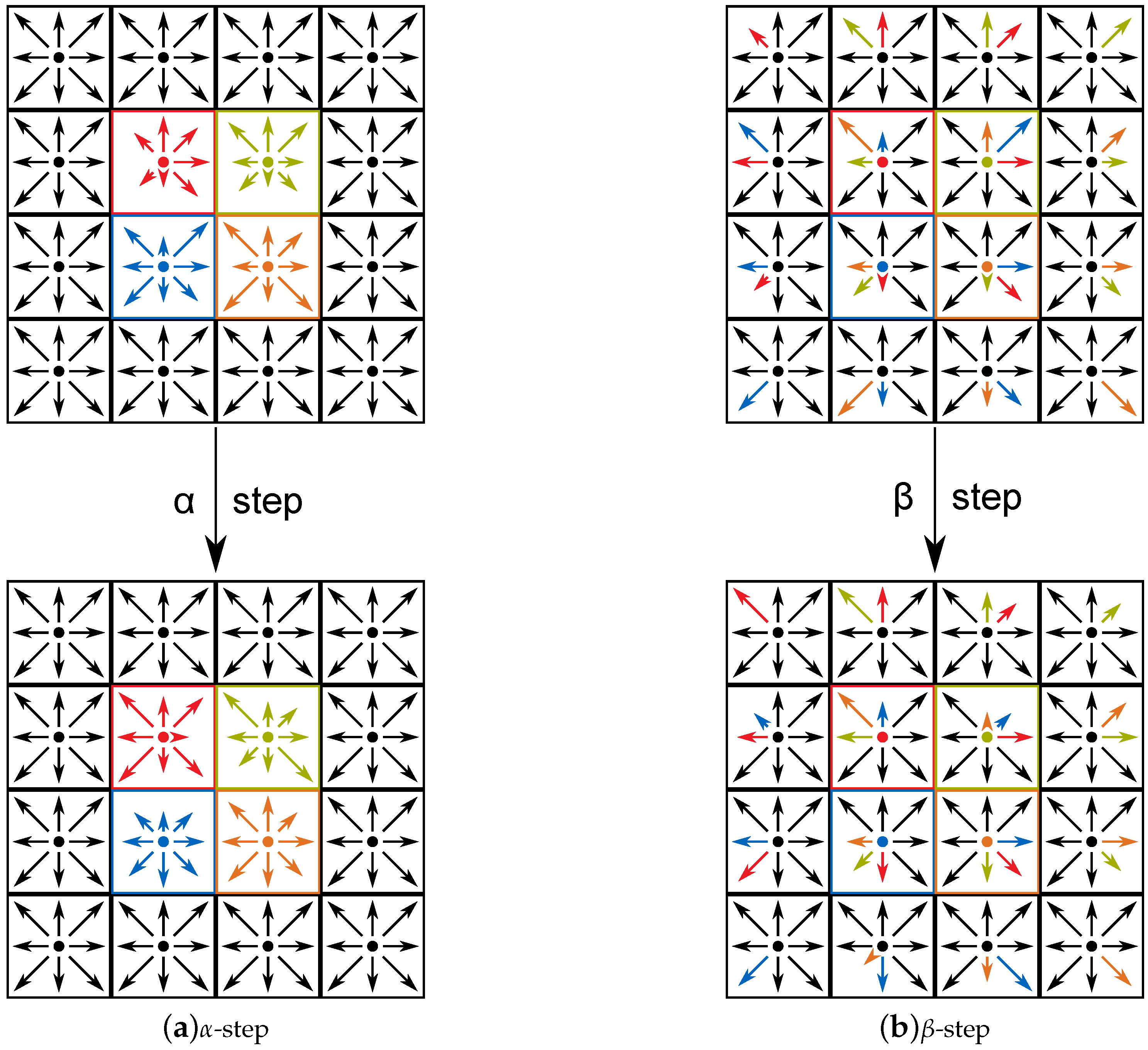
3.2. Collision and Propagation
4. Implementation of the Lattice Boltzmann Method
4.1. Optimization and Parallelization on Computing Device Level
4.1.1. Memory Layout Pattern
4.1.2. Lattice Boltzmann Method Kernels for the CPU
4.1.3. Lattice Boltzmann Method Kernels for the GPU
4.2. Domain Decomposition and Resource Assignment
- (a)
- One MPI process for each GPU and one MPI process for each CPU (or all CPU cores of one node)
- (b)
- One MPI process for each GPU and one MPI process for each CPU core
- (c)
- One MPI process for every node
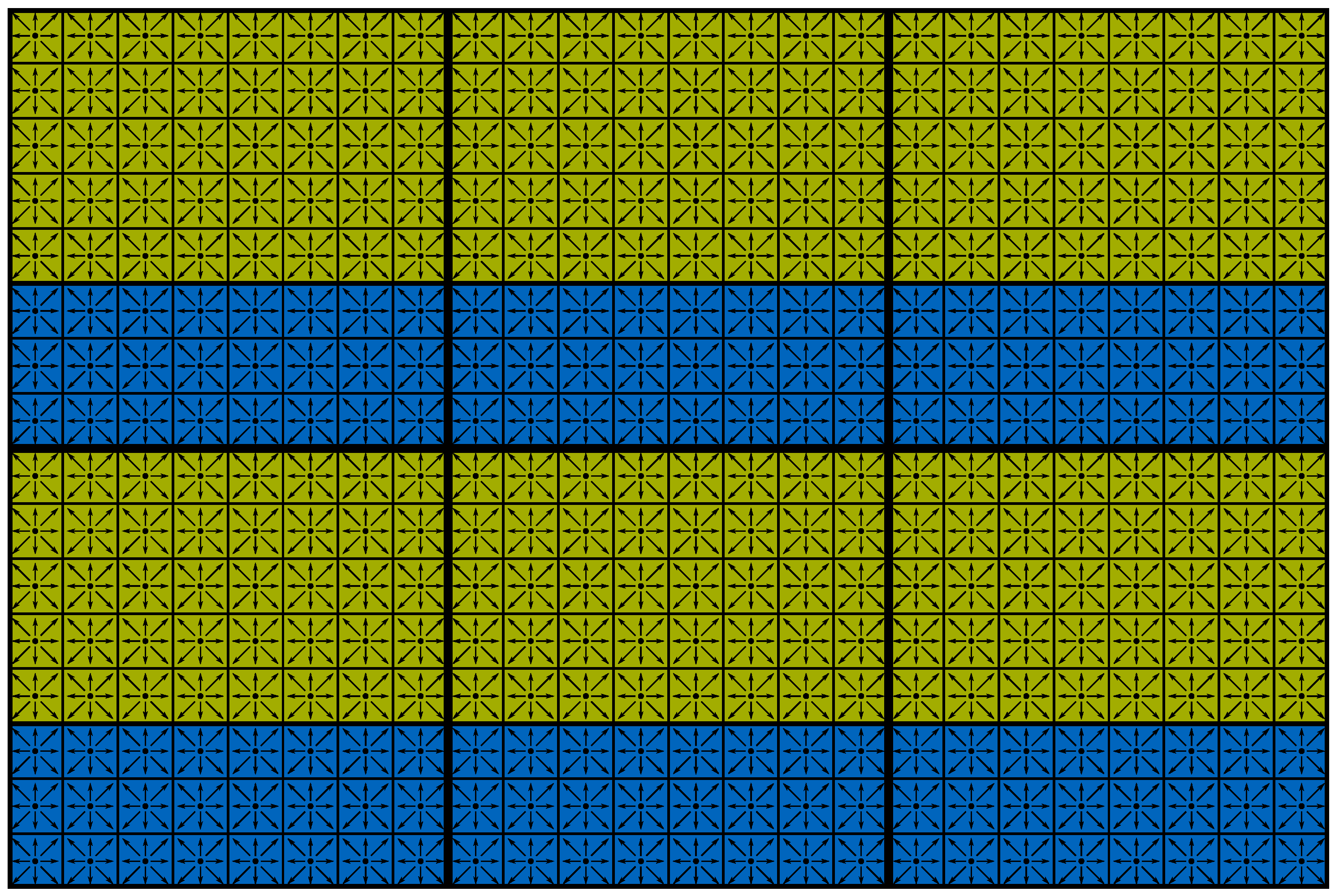
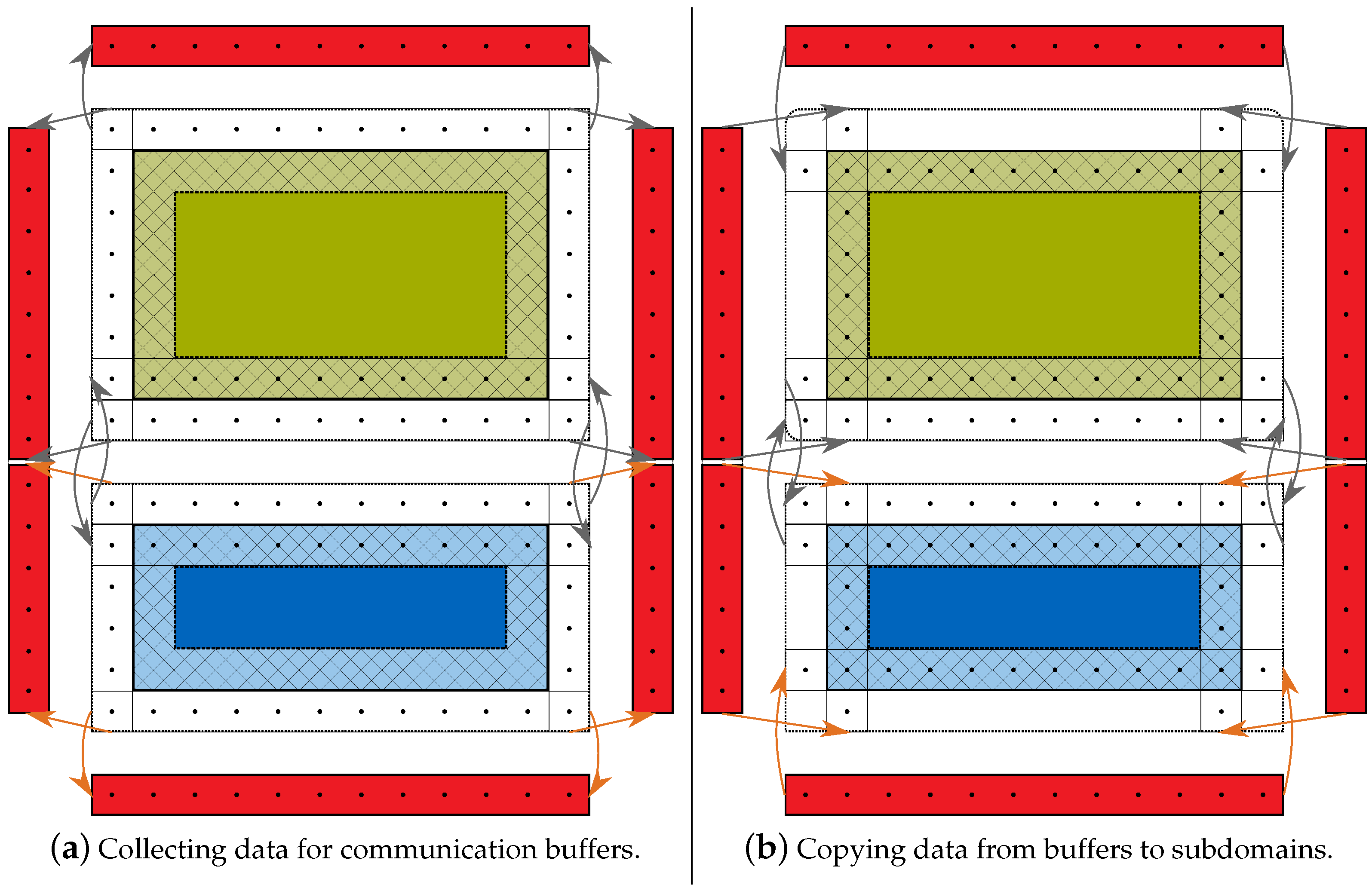
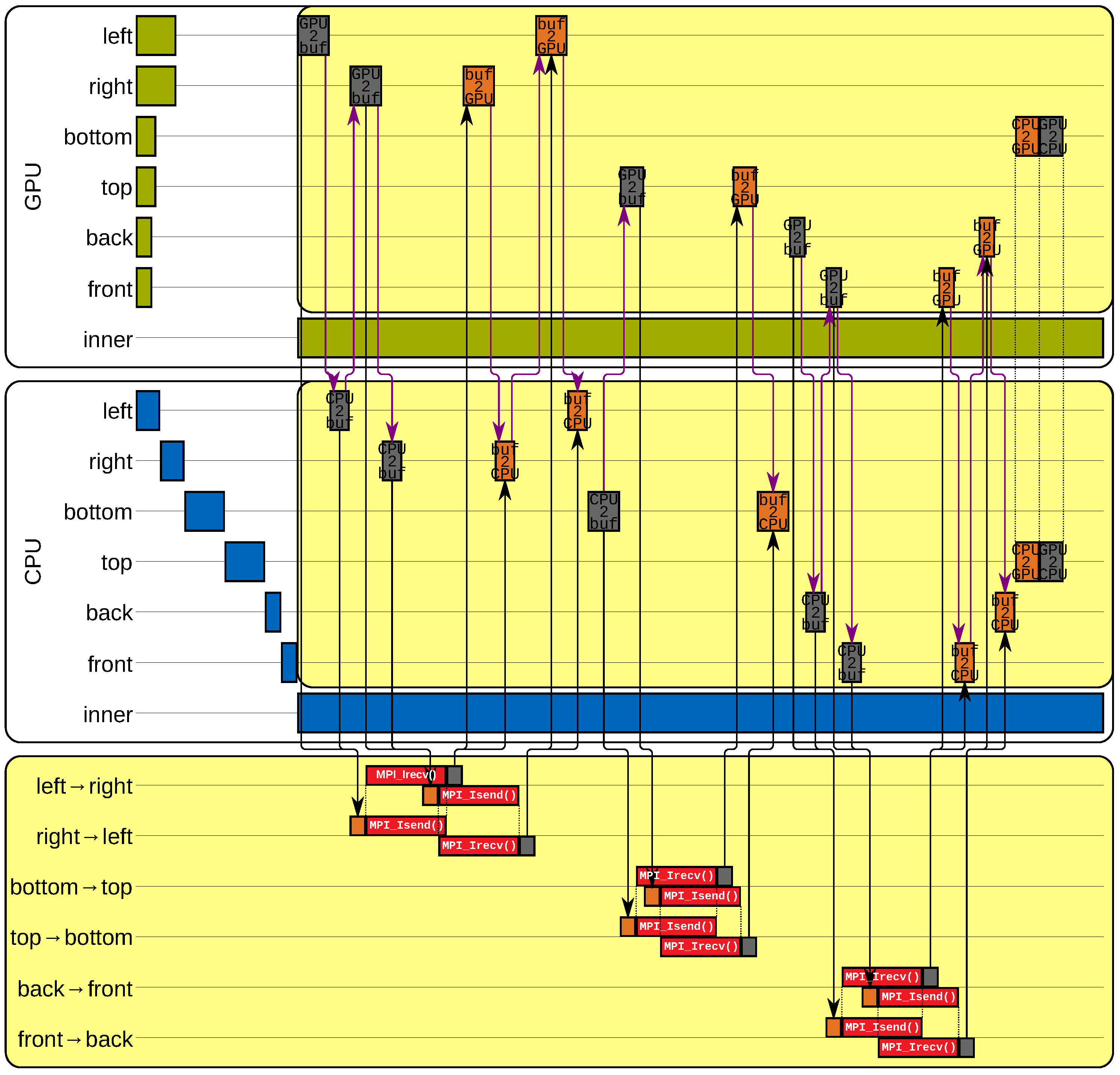
4.3. Communication Scheme
- (a)
- The boundary cells are updated, i.e., the - or -step is applied. No copy operations or communication takes place.
- (b)
- The inner cells are updated. In the meantime, the data updated in phase (a) is communicated to the corresponding proximate computing device.
| Algorithm 1 Pseudocode of an MPI process to update its subdomain and to exchange boundary cells during an - or -step according to Figure 7. sendBfrs and recvBfrs are arrays containing pointers to the communication buffers for sending and receiving data conforming to the red colored memory in Figure 5 and Figure 6, thus, with storage for data from the CPU and the GPU. The array reqs contains elements of type MPI_Request, streams is an array with elements of type cudaStream_t. -/-kernelCPU(a) and -/-kernelGPU(a) apply an - or -step to a on the CPU and the GPU, respectively. The simplified signature of MPI_Isend(a, b) reads “send data from memory a to MPI process b” and MPI_Irecv(a, b, c) reads “receive data from MPI process b and store it to memory a using request handle c”. MPI_Wait(a) blocks depending on request handle a and cudaMemcpy3DAsync(a, b) copies data within the MPI process from memory b to a. |
|
5. Results
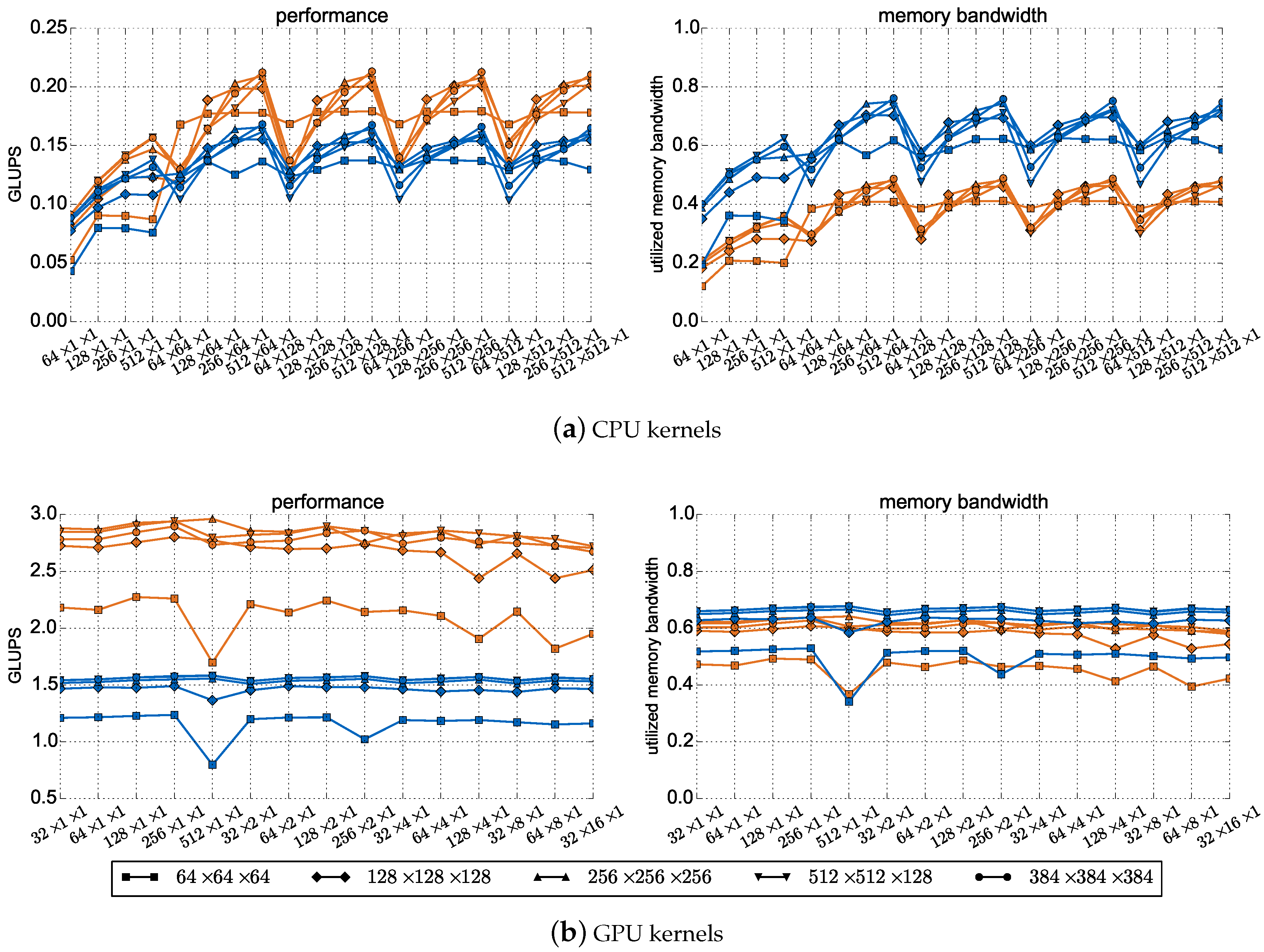
5.1. Performance of the CPU and GPU Kernels
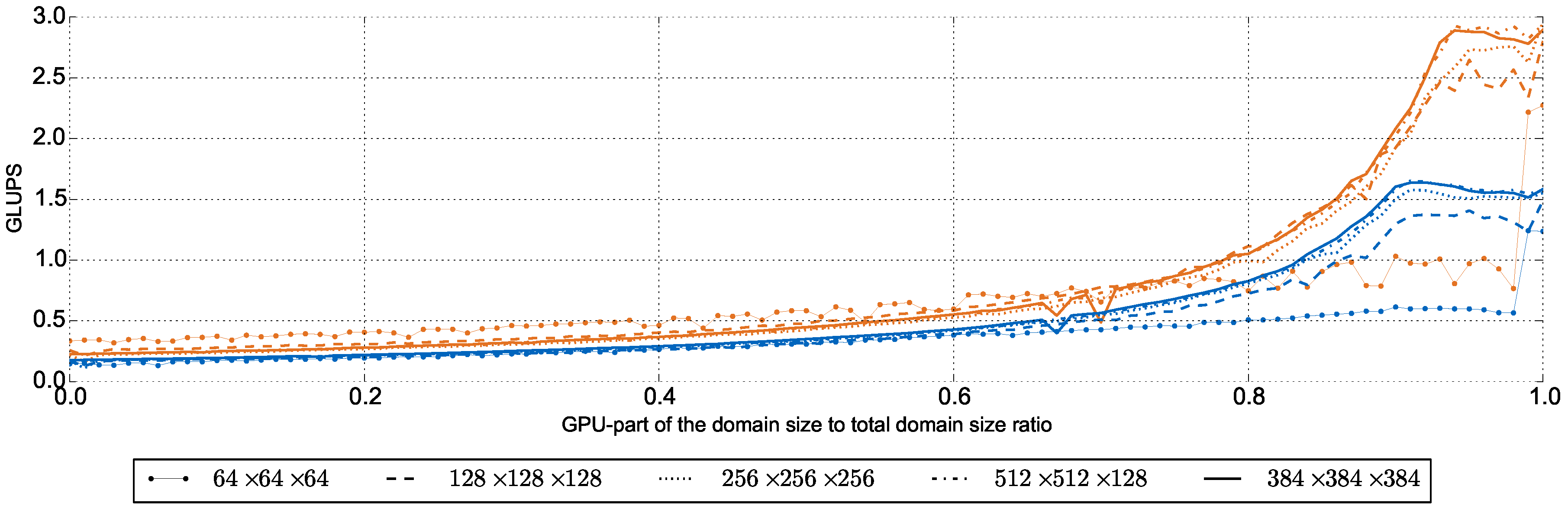
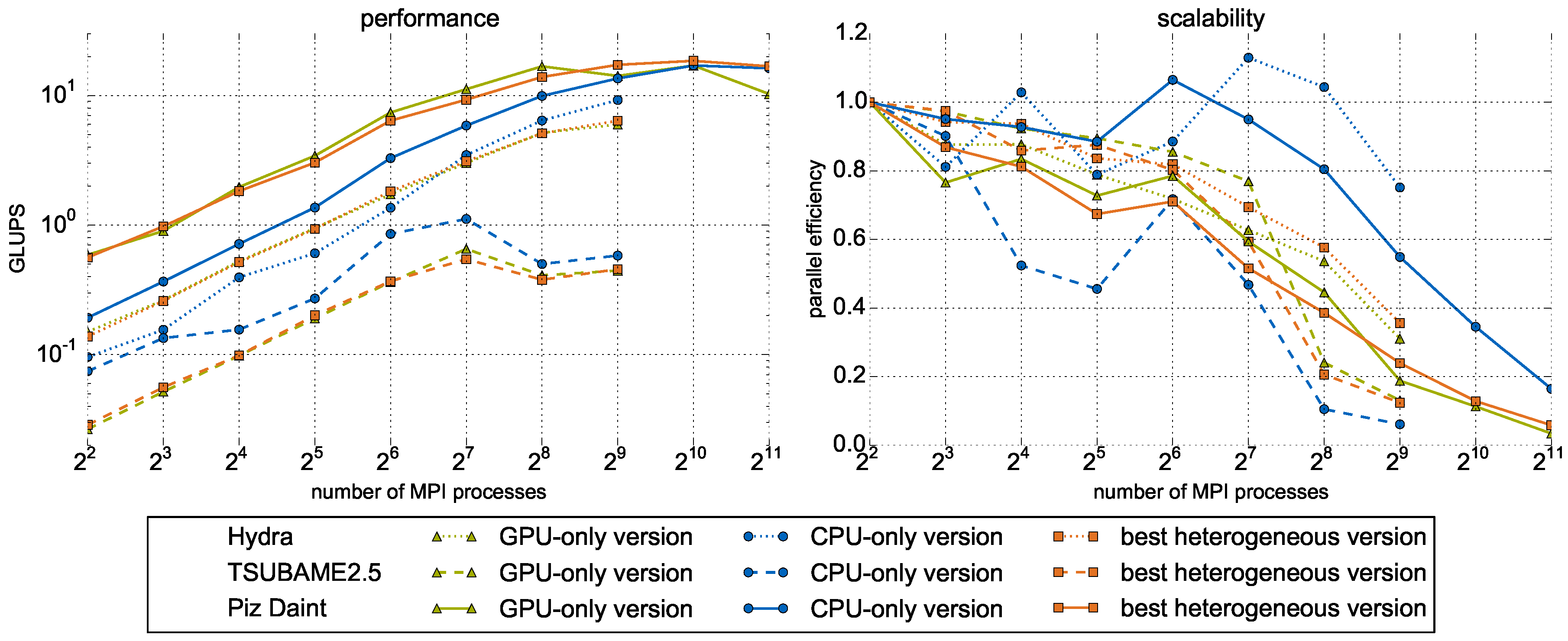
5.2. Single Subdomain Results on Heterogeneous Systems
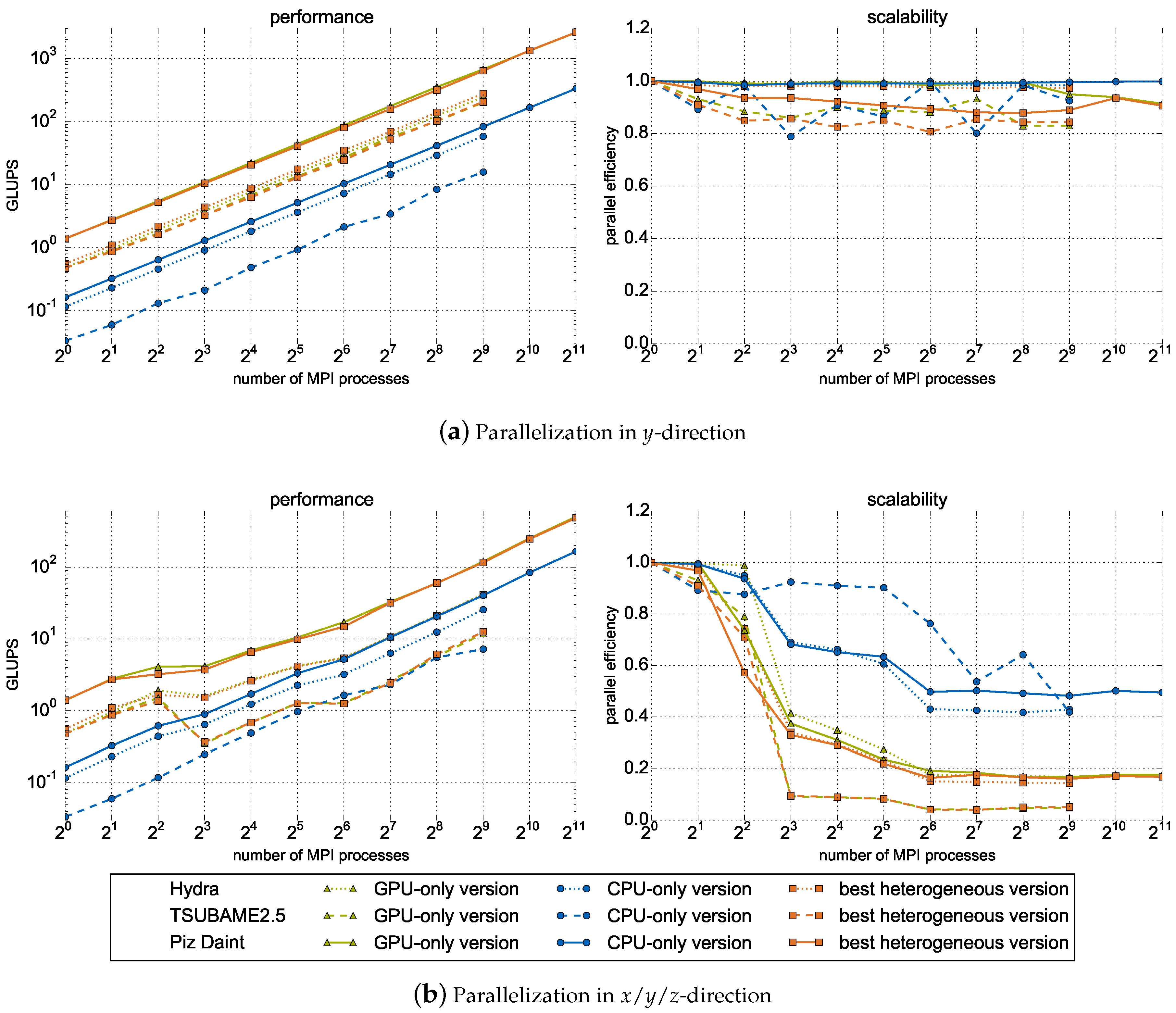
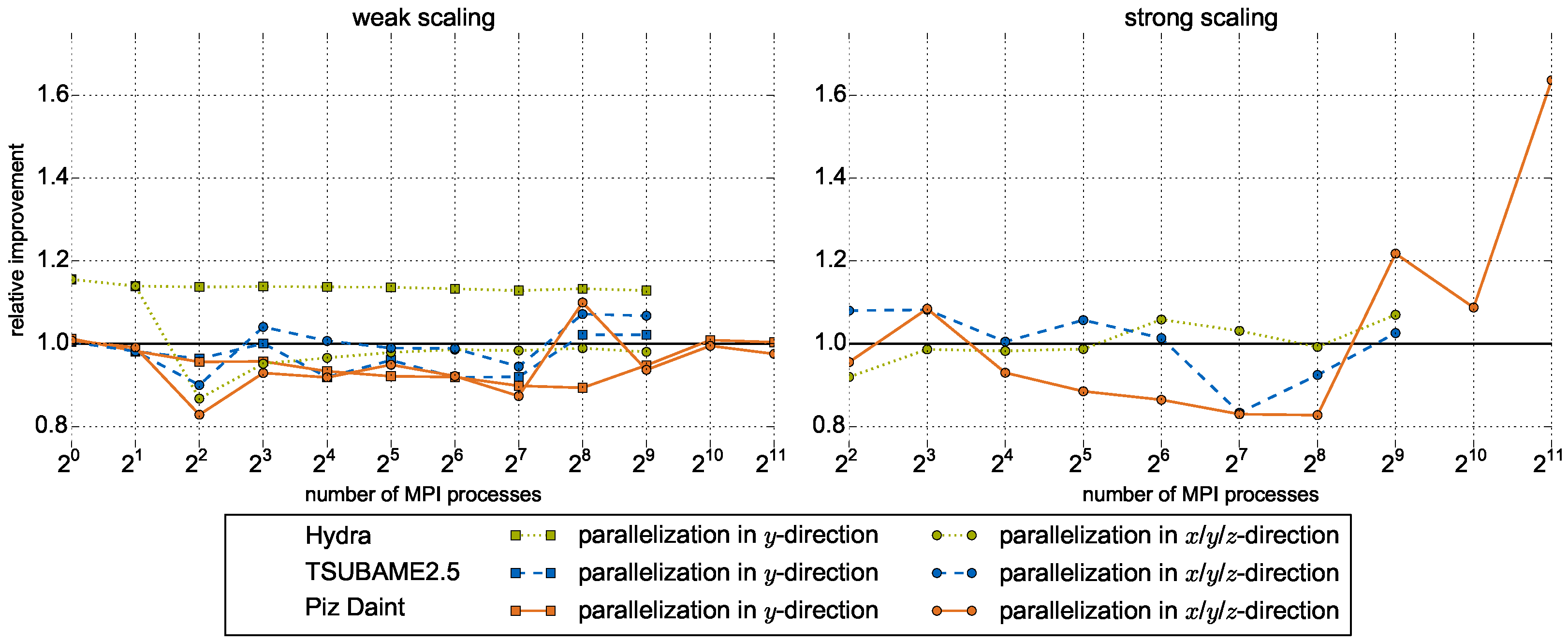
5.3. Large-Scale Results on Heterogeneous Systems
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AMR | Adaptive mesh refinement |
| AoS | Array of structures |
| BGK | Bhatnagar-Gross-Krook |
| CFD | Computational fluid dynamics |
| CFL | Courant-Friedrichs-Lewy |
| CPU | Central processing unit |
| ECC | Error-correcting code |
| ELBE | Efficient lattice boltzmann environment |
| FLOPS | Floating point operations per second |
| FPGA | Field programmable gate array |
| FSI | Fluid-structure interaction |
| GLUPS | Giga lattice updates per second |
| GPU | Graphics processing unit |
| HPC | High performance computing |
| LBM | Lattice Boltzmann method |
| MPI | Message passing interface |
| MRT | Multiple-relaxation-time |
| NUMA | Non-uniform memory access |
| PGAS | Partitioned global address space |
| SIMD | Single instruction multiple data |
| SoA | Structure of arrays |
| SRT | Single-relaxation-time |
| TPU | Tensor processing unit |
References
- PEZY Computing. Available online: http://pezy.jp/ (accessed on 16 October 2017).
- TOP500.org. Top500 List—November 2017. Available online: https://www.top500.org/list/2017/11/ (accessed on 16 October 2017).
- Riesinger, C.; Bakhtiari, A.; Schreiber, M. Available online: https://gitlab.com/christoph.riesinger/lbm/ (accessed on 16 October 2017).
- Wellein, G.; Zeiser, T.; Hager, G.; Donath, S. On the single processor performance of simple lattice Boltzmann kernels. Comput. Fluids 2006, 35, 910–919. [Google Scholar] [CrossRef]
- Tölke, J.; Krafczyk, M. TeraFLOP computing on a desktop PC with GPUs for 3D CFD. Int. J. Comput. Fluid Dyn. 2008, 22, 443–456. [Google Scholar] [CrossRef]
- Bailey, P.; Myre, J.; Walsh, S.D.C.; Lilja, D.J.; Saar, M.O. Accelerating lattice boltzmann fluid flow simulations using graphics processors. In Proceedings of the International Conference on Parallel Processing, Vienna, Austria, 22–25 September 2009; pp. 550–557. [Google Scholar]
- Kuznik, F.; Obrecht, C.; Rusaouen, G.; Roux, J.J. LBM based flow simulation using GPU computing processor. Comput. Math. Appl. 2010, 59, 2380–2392. [Google Scholar] [CrossRef]
- Obrecht, C.; Kuznik, F.; Tourancheau, B.; Roux, J.J. A new approach to the lattice Boltzmann method for graphics processing units. Comput. Math. Appl. 2011, 61, 3628–3638. [Google Scholar] [CrossRef]
- Rinaldi, P.R.; Dari, E.A.; Vénere, M.J.; Clausse, A. A Lattice-Boltzmann solver for 3D fluid simulation on GPU. Simul. Model. Pract. Theory 2012, 25, 163–171. [Google Scholar] [CrossRef]
- Habich, J.; Feichtinger, C.; Köstler, H.; Hager, G.; Wellein, G. Performance engineering for the lattice Boltzmann method on GPGPUs: Architectural requirements and performance results. Comput. Fluids 2013, 80, 276–282. [Google Scholar] [CrossRef]
- Obrecht, C.; Kuznik, F.; Tourancheau, B.; Roux, J.J. Multi-GPU implementation of the lattice Boltzmann method. Comput. Math. Appl. 2013, 65, 252–261. [Google Scholar] [CrossRef]
- Wang, X.; Aoki, T. Multi-GPU performance of incompressible flow computation by lattice Boltzmann method on GPU cluster. Parallel Comput. 2011, 37, 521–535. [Google Scholar]
- Calore, E.; Marchi, D.; Schifano, S.F.; Tripiccione, R. Optimizing communications in multi-GPU Lattice Boltzmann simulations. In Proceedings of the 2015 International Conference on High Performance Computing & Simulation (HPCS), Amsterdam, The Netherlands, 20–24 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 55–62. [Google Scholar]
- Feichtinger, C.; Habich, J.; Köstler, H.; Hager, G.; Rüde, U.; Wellein, G. A flexible Patch-based lattice Boltzmann parallelization approach for heterogeneous GPU-CPU clusters. Parallel Comput. 2011, 37, 536–549. [Google Scholar] [CrossRef]
- Ye, Y.; Li, K.; Wang, Y.; Deng, T. Parallel computation of Entropic Lattice Boltzmann method on hybrid CPU–GPU accelerated system. Comput. Fluids 2015, 110, 114–121. [Google Scholar] [CrossRef]
- Shimokawabe, T.; Aoki, T.; Takaki, T.; Yamanaka, A.; Nukada, A.; Endo, T.; Maruyama, N.; Matsuoka, S. Peta-scale Phase-Field Simulation for Dendritic Solidification on the TSUBAME 2.0 Supercomputer. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis—SC ’11, Seatle, WA, USA, 12–18 November 2011; pp. 1–11. [Google Scholar]
- Xiong, Q.; Li, B.; Xu, J.; Fang, X.; Wang, X.; Wang, L.; He, X.; Ge, W. Efficient parallel implementation of the lattice Boltzmann method on large clusters of graphic processing units. Chin. Sci. Bull. 2012, 57, 707–715. [Google Scholar] [CrossRef]
- Calore, E.; Gabbana, A.; Kraus, J.; Pellegrini, E.; Schifano, S.F.; Tripiccione, R. Massively parallel lattice–Boltzmann codes on large GPU clusters. Parallel Comput. 2016, 58, 1–24. [Google Scholar] [CrossRef]
- Riesinger, C. Scalable Scientific Computing Applications for GPU-Accelerated Heterogeneous Systems. Ph.D. Thesis, Technische Universität München, München, Germany, May 2017. [Google Scholar]
- Schreiber, M.; Neumann, P.; Zimmer, S.; Bungartz, H.J. Free-Surface Lattice-Boltzmann Simulation on Many-Core Architectures. Procedia Comput. Sci. 2011, 4, 984–993. [Google Scholar] [CrossRef]
- Li, W.; Wei, X.; Kaufman, A. Implementing lattice Boltzmann computation on graphics hardware. Vis. Comput. 2003, 19, 444–456. [Google Scholar] [CrossRef]
- Zhe, F.; Feng, Q.; Kaufman, A.; Yoakum-Stover, S. GPU Cluster for High Performance Computing. In Proceedings of the ACM/IEEE SC2004 Conference, New Orleans, LA, USA, 31 August–4 September 2009; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Janßen, C.; Mierke, D.; Überrück, M.; Gralher, S.; Rung, T. Validation of the GPU-Accelerated CFD Solver ELBE for Free Surface Flow Problems in Civil and Environmental Engineering. Computation 2015, 3, 354–385. [Google Scholar] [CrossRef]
- Debudaj-Grabysz, A.; Rabenseifner, R. Nesting OpenMP in MPI to Implement a Hybrid Communication Method of Parallel Simulated Annealing on a Cluster of SMP Nodes. In Proceedings of the Recent Advances in Parallel Virtual Machine and Message Passing Interface, 12th European PVM/MPI Users’ Group Meeting, Sorrento, Italy, 18–21 September 2005; Di Martino, B., Kranzlmüller, D., Dongarra, J.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 18–27. [Google Scholar]
- Rabenseifner, R.; Hager, G.; Jost, G. Hybrid MPI/OpenMP Parallel Programming on Clusters of Multi-Core SMP Nodes. In Proceedings of the 2009 17th Euromicro International Conference on Parallel, Distributed and Network-based, Weimar, Germany, 18–20 February 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 427–436. [Google Scholar]
- Linxweiler, J. Ein Integrierter Softwareansatz zur Interaktiven Exploration und Steuerung von Strömungssimulationen auf Many-Core-Architekturen. Ph.D. Thesis, Technische Universität Braunschweig, Braunschweig, Germany, June 2011. [Google Scholar]
- Valero-Lara, P.; Jansson, J. LBM-HPC - An Open-Source Tool for Fluid Simulations. Case Study: Unified Parallel C (UPC-PGAS). In Proceedings of the 2015 IEEE International Conference on Cluster Computing, Chicago, IL, USA, 8–11 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 318–321. [Google Scholar]
- Calore, E.; Gabbana, A.; Schifano, S.F.; Tripiccione, R. Optimization of lattice Boltzmann simulations on heterogeneous computers. Int. J. High Perform. Comput. Appl. 2017. [Google Scholar] [CrossRef]
- Valero-Lara, P.; Igual, F.D.; Prieto-Matías, M.; Pinelli, A.; Favier, J. Accelerating fluid–solid simulations (Lattice-Boltzmann & Immersed-Boundary) on heterogeneous architectures. J. Comput. Sci. 2015, 10, 249–261. [Google Scholar] [Green Version]
- Valero-Lara, P.; Jansson, J. Heterogeneous CPU+GPU approaches for mesh refinement over Lattice-Boltzmann simulations. Concurr. Comput. Pract. Exp. 2017, 29, e3919. [Google Scholar] [CrossRef]
- Shimokawabe, T.; Endo, T.; Onodera, N.; Aoki, T. A Stencil Framework to Realize Large-Scale Computations Beyond Device Memory Capacity on GPU Supercomputers. In Proceedings of the 2017 IEEE International Conference on Cluster Computing (CLUSTER), Honolulu, HI, USA, 5–8 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 525–529. [Google Scholar]
- He, X.; Luo, L.S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Wolf-Gladrow, D.A. Lattice-Gas Cellular Automata and Lattice Boltzmann Models—An Introduction; Springer: Berlin, Germany, 2000. [Google Scholar]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann Method for Complex Flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation: for Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method: Principles and Practice; Graduate Texts in Physics; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- He, X.; Luo, L.S. Lattice Boltzmann Model for the Incompressible Navier–Stokes Equation. J. Stat. Phys. 1997, 88, 927–944. [Google Scholar] [CrossRef]
- Ansumali, S.; Karlin, I.V.; Öttinger, H.C. Minimal entropic kinetic models for hydrodynamics. Europhys. Lett. 2003, 63, 798–804. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- D’Humières, D.; Ginzburg, I.; Krafczyk, M.; Lallemand, P.; Luo, L.S. Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef] [PubMed]
- Boghosian, B.M.; Yepez, J.; Coveney, P.V.; Wager, A. Entropic lattice Boltzmann methods. Proc. R. Soc. A Math. Phys. Eng. Sci. 2001, 457, 717–766. [Google Scholar] [CrossRef]
- Geier, M.; Greiner, A.; Korvink, J.G. Cascaded digital lattice Boltzmann automata for high Reynolds number flow. Phys. Rev. E 2006, 73, 066705. [Google Scholar] [CrossRef] [PubMed]
- Wolfe, M. OpenACC for Multicore CPUs; PGI, NVIDIA Corporation: Beaverton, OR, USA, 2015; p. 6. [Google Scholar]
- Bailey, D.H. Twelve ways to fool the masses when giving performance results on parallel computers. In Supercomputing Review; MIT Press: Cambridge, MA, USA, 1991; pp. 54–55. [Google Scholar]
- Höfler, T.; Belli, R. Scientific benchmarking of parallel computing systems. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis—SC ’15, Austin, TX, USA, 15–20 November 2015; ACM Press: New York, NY, USA, 2015; pp. 1–12. [Google Scholar]
- Valero-Lara, P. Reducing memory requirements for large size LBM simulations on GPUs. Concurr. Comput. Pract. Exp. 2017, 29, e4221. [Google Scholar] [CrossRef]
- Wittmann, M.; Zeiser, T.; Hager, G.; Wellein, G. Comparison of different propagation steps for lattice Boltzmann methods. Comput. Math. Appl. 2013, 65, 924–935. [Google Scholar] [CrossRef]
- Neumann, P.; Bungartz, H.J.; Mehl, M.; Neckel, T.; Weinzierl, T. A Coupled Approach for Fluid Dynamic Problems Using the PDE Framework Peano. Commun. Comput. Phys. 2012, 12, 65–84. [Google Scholar] [CrossRef]
- Geier, M.; Schönherr, M. Esoteric Twist: An Efficient in-Place Streaming Algorithmus for the Lattice Boltzmann Method on Massively Parallel Hardware. Computation 2017, 5. [Google Scholar] [CrossRef]
- Lam, M.D.; Rothberg, E.E.; Wolf, M.E. The cache performance and optimizations of blocked algorithms. In Proceedings of the Fourth International Conference on Architectural Support for Programming Languages and Operating Systems—ASPLOS-IV, Santa Clara, CA, USA, 8–11 April 1991; ACM Press: New York, NY, USA, 1991; pp. 63–74. [Google Scholar]
- Ayguadé, E.; Copty, N.; Duran, A.; Hoeflinger, J.; Lin, Y.; Massaioli, F.; Su, E.; Unnikrishnan, P.; Zhang, G. A Proposal for Task Parallelism in OpenMP. In A Practical Programming Model for the Multi-Core Era; Chapman, B., Zheng, W., Gao, G.R., Sato, M., Ayguadé, E., Wang, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–12. [Google Scholar]
- Schreiber, M. GPU Based Simulation and Visualization of Fluids with Free Surfaces. Diploma Thesis, Technische Universität München, München, Germany, June 2010. [Google Scholar]
- NVIDIA Corporation. Tuning CUDA Applications for Kepler. Available online: http://docs.nvidia.com/cuda/kepler-tuning-guide/ (accessed on 16 October 2017).
- NVIDIA Corporation. Achieved Occupancy. Available online: https://docs.nvidia.com/gameworks/content/developertools/desktop/analysis/report/cudaexperiments/kernellevel/achievedoccupancy.htm (accessed on 16 October 2017).
- Bakhtiari, A. MPI Parallelization of GPU-Based Lattice Boltzmann Simulations. Master’s Thesis, Technische Universität München, München, Germany, October 2013. [Google Scholar]
- Bozeman, J.D.; Dalton, C. Numerical study of viscous flow in a cavity. J. Comput. Phys. 1973, 12, 348–363. [Google Scholar] [CrossRef]
- Ghia, U.; Ghia, K.N.; Shin, C.T. High-Re solutions for incompressible flow using the Navier–Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Intel Corporation. Intel Xeon Processor E5-2690v3. Available online: https://ark.intel.com/products/81713/ (accessed on 16 October 2017).
- Global Scientific Information and Computing Center. TSUBAME2.5 Hardware Software Specifications; Technical Report; Tokyo Institute of Technology: Tokyo, Japan, 2013. [Google Scholar]

| System | Hydra | TSUBAME2.5 | Piz Daint | |
|---|---|---|---|---|
| devices | CPU | Xeon E5-2680v2 | Xeon X5670 | Xeon E5-2690v3 |
| #cores/CPU | 10 | 6 | 12 | |
| GPU | Tesla K20x | Tesla P100 | ||
| cluster | #CPUs/node | 2 | 1 | |
| #GPUs/node | 2 | 3 | ||
| #nodes | 338 | 1442 | 5320 | |
| interconnect | FDR IB | QDR IB | Aries ASIC | |
| software | C++ compiler | ICPC 16.0 | ICPC 15.0.2 | ICPC 17.0.0 |
| CUDA compiler | NVCC 7.5 | NVCC 8 | ||
| MPI | Intel MPI 5.1.3 | Open MPI 1.8.2 | Cray MPICH 7.5.0 | |
| Model | Tesla K20x | Tesla P100 | |
|---|---|---|---|
| GPU architecture | Kepler | Pascal | |
| chip | GK110 | GP100 | |
| compute capability | |||
| #processing elements | single precision | ||
| double precision | |||
| shared memory (KByte) | 16–48 | 64 | |
| L1 cache (KByte) | 24 | ||
| base block rate (MHz) | 732 | 1328 | |
| peak performance | single precision | ||
| (TFLOPS) | double precision | ||
| peak memory bandwidth (GByte/s) | |||
| ratio | single precision | ||
| double precision | |||
| Cluster | GPU | CPU | Ratio | Imp. GPU | Theoretical imp. GPU | Imp. CPU |
|---|---|---|---|---|---|---|
| Hydra | K20x | E5-2680v2 | ||||
| TSUBAME2.5 | X5670 | |||||
| Piz Daint | P100 | E5-2690v3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riesinger, C.; Bakhtiari, A.; Schreiber, M.; Neumann, P.; Bungartz, H.-J. A Holistic Scalable Implementation Approach of the Lattice Boltzmann Method for CPU/GPU Heterogeneous Clusters. Computation 2017, 5, 48. https://doi.org/10.3390/computation5040048
Riesinger C, Bakhtiari A, Schreiber M, Neumann P, Bungartz H-J. A Holistic Scalable Implementation Approach of the Lattice Boltzmann Method for CPU/GPU Heterogeneous Clusters. Computation. 2017; 5(4):48. https://doi.org/10.3390/computation5040048
Chicago/Turabian StyleRiesinger, Christoph, Arash Bakhtiari, Martin Schreiber, Philipp Neumann, and Hans-Joachim Bungartz. 2017. "A Holistic Scalable Implementation Approach of the Lattice Boltzmann Method for CPU/GPU Heterogeneous Clusters" Computation 5, no. 4: 48. https://doi.org/10.3390/computation5040048
APA StyleRiesinger, C., Bakhtiari, A., Schreiber, M., Neumann, P., & Bungartz, H.-J. (2017). A Holistic Scalable Implementation Approach of the Lattice Boltzmann Method for CPU/GPU Heterogeneous Clusters. Computation, 5(4), 48. https://doi.org/10.3390/computation5040048




