Abstract
Heterogeneous clusters are a widely utilized class of supercomputers assembled from different types of computing devices, for instance CPUs and GPUs, providing a huge computational potential. Programming them in a scalable way exploiting the maximal performance introduces numerous challenges such as optimizations for different computing devices, dealing with multiple levels of parallelism, the application of different programming models, work distribution, and hiding of communication with computation. We utilize the lattice Boltzmann method for fluid flow as a representative of a scientific computing application and develop a holistic implementation for large-scale CPU/GPU heterogeneous clusters. We review and combine a set of best practices and techniques ranging from optimizations for the particular computing devices to the orchestration of tens of thousands of CPU cores and thousands of GPUs. Eventually, we come up with an implementation using all the available computational resources for the lattice Boltzmann method operators. Our approach shows excellent scalability behavior making it future-proof for heterogeneous clusters of the upcoming architectures on the exaFLOPS scale. Parallel efficiencies of more than are achieved leading to GLUPS utilizing 24,576 CPU cores and 2048 GPUs of the CPU/GPU heterogeneous cluster Piz Daint and computing more than lattice cells.
1. Introduction
Computational fluid dynamics (CFD) allows for the virtual exploration and investigation of fluid flow avoiding costly or impossible lab experiments. However, performing state-of-the-art numerical fluid simulations requires high computational performance. This holds particularly for 3D simulations due to steadily rising demands in spatial and hence, temporal resolution, larger and more complex domains, and the tracking of fine-scale phenomena such as turbulence. Besides continuum models such as the Euler and the Navier-Stokes equations, the lattice Boltzmann method (LBM) has evolved as an alternative model to describe the nature of fluids at both the continuum and the mesoscale. Due to its algorithmic simplicity and the spatial locality of its stencil-like advection and diffusion operators, LBM can be parallelized in an efficient way. This makes the LBM especially suitable for large-scale high performance computing (HPC) systems providing reasonable computational performance for CFD.
Today’s large-scale HPC systems are based on various architectures. One example of such an architecture is given by heterogeneous clusters assembled from different types of computing devices (CPU, GPU, field programmable gate array (FPGA), Intel (Santa Clara, CA, USA) Xeon Phi, accelerators such as the PEZY accelerator [1] or Google’s tensor processing unit (TPU), etc.), node sizes (thin nodes, fat nodes), or network topologies (torus, fat tree, dragonfly, etc.). We focus on CPU/GPU heterogeneous clusters, in the following just denoted as CPU/GPU clusters, where the clusters’ nodes are uniformly equipped with at least one CPU and one GPU computing device. However, all discussed concepts are generalizable to heterogeneous systems consisting of alternative computing devices, too. Large-scale CPU/GPU clusters provide huge computational performance, but successfully exploiting this computational potential introduces several challenges. Currently, there are two representatives of such systems in the top five of the fastest supercomputers [2] and more systems of that kind are expected to evolve in the next years for energy and efficiency reasons. Multiple levels of hardware parallelism are introduced by CPU/GPU clusters. On a lower level, that is at the level of the particular computing devices, CPUs contain multiple cores, each usually augmented with a SIMD unit, and a GPU is composed of multiprocessors each containing several processing elements. On a higher level, multiple CPUs and GPUs, potentially located in different nodes of the cluster, have to be orchestrated to cooperatively perform the computational tasks. Facing this complexity, programming all these levels of parallelism in a scalable way is a non-trivial task. For the application of the LBM, it requires tailored implementations of the LBM operators for CPUs and GPUs, a domain decomposition to evenly distribute work among different computing devices, and a communication scheme to exchange data of subdomain boundaries hiding communication times behind computation.
In the following, a comprehensive set of best practices and techniques targeting the challenges when programming CPU/GPU clusters to achieve scalability of the LBM is presented, eventually leading to a hybrid reference implementation [3]. There are already numerous successful attempts to implement the LBM on single multi- [4] and many-core processors [5,6,7,8,9,10], on small- [11] and large-scale clusters [12,13], and on heterogeneous systems consisting of single [14,15] and multiple nodes [16,17,18]. Many existing attempts for large-scale heterogeneous systems assign communication tasks [17,18] or minor workloads to the CPUs [16] underusing their computational performance. In contrast, we aim at fully exploiting all available computing devices of a large-scale CPU/GPU cluster at all times. Hence, an approach in which all different kinds of computing devices perform the same actions, namely the operations of the LBM, is pursued. We show that CPUs can contribute a considerable amount of performance in a heterogeneous scenario and that parallel efficiencies of more than are achievable by simultaneously running on 2048 GPUs and 24,576 CPU cores on the heterogeneous supercomputer Piz Daint, thus, with a number of resources on the petaFLOPS scale.
The holistic scalable implementation approach of the LBM for CPU/GPU heterogeneous clusters was first proposed by Riesinger in [19]. This paper builds on Riesinger’s work providing a compact representation and focusing on the essential topics. Initial work on the hybrid reference code was done by Schreiber et al. [20] and we use these GPU kernels. Our work significantly extends this implementation by porting and parallelizing them for the CPU, then, utilizing multiple CPUs and GPU concurrently. For a performance efficient and scalable implementation, this requires simultaneous data copies, non-blocking communication, and communication hiding.
The remainder of this paper is structured as follows: In Section 2, related work on LBM in the context of HPC is discussed and put into context with our holistic CPU/GPU approach. A brief introduction to the basic implementation concepts of the LBM is provided in Section 3. Section 4 lists the implementation techniques for the LBM leading to a scalable code to fully exploit CPU/GPU heterogeneous clusters including optimization and parallelization of the CPU and GPU kernels, a domain decomposition and resource assignment, and an efficient communication scheme. The performance of the particular LBM kernels, the advantage of a heterogeneous over a homogeneous approach, and the scalability of our implementation are evaluated in Section 5, followed by Section 6 giving a brief conclusion and summary.
2. Related Work
Besides multi-core CPUs [4], GPUs have been a target platform of the LBM for more than a decade, dating back to the pre-CUDA era [21,22]. For single-GPU setups, Tölke et al. [5] provide a first attempt using the D3Q13 discretization scheme. By applying the D3Q19 discretization scheme, Bailey et al. [6] experimentally validate that a GPU implementation can deliver superior performance to an optimized CPU implementation. Due to this fact, GPU-only frameworks coping with complex applications from engineering and science have also evolved throughout the last years; one example is given by the efficient lattice boltzmann environment (ELBE) [23].
The LBM is memory-bound, so many implementations aim for memory optimizations [10]. Obrecht et al. [8] achieve up to of the theoretical peak memory bandwidth of a GPU with a tailored memory access pattern and Rinaldi et al. [9] can even excel this performance value by performing all LBM operations in shared memory making kernel fusion indispensable.
Classical examples for hybrid programming incorporating more than one programming model are given by Debudaj-Grabysz et al. [24] and Rabenseifner et al. [25]. They use OpenMP for the shared memory and MPI for the distributed memory parallelization for arbitrary applications detached from the LBM but limited to homogeneous CPU clusters. These hybrid programming techniques can also be utilized for the LBM as shown by Linxweiler in [26]. A comparison of the efficiency of OpenMP in combination with MPI with Unified Parallel C, a partitioned global address space (PGAS) language, for the LBM is provided in [27].
Moving on to homogeneous GPU clusters, an implementation of the LBM is reported by Obrecht et al. [11] for small-scale and by Wang et al. [12] for large-scale clusters. In the latter work, the authors overlap communication with computations as we do in this work, too. Communication becomes more complex if multi-layered boundaries are exchanged between multiple GPUs as occurring when using larger stencils such as the D2Q37 discretization scheme. Nonetheless, Calore et al. [13] testify that such tasks can be efficiently handled by homogeneous GPU clusters. Since we restrict considerations to the D3Q19 discretization scheme, we do not have to deal with multi-layered boundary exchange.
Proceeding to heterogeneous systems, Ye et al. [15] present an approach to assign work to the CPUs and to the GPU of one node using OpenMP and CUDA. Calore et al. [28] do not only deal with CPU/GPU heterogeneous nodes but with CPU/Intel Xeon Phi heterogeneous installations. A more flexible, patch-based idea is proposed by Feichtinger et al. [14] implicitly introducing an adjustable load balancing mechanism. This mechanism requires management information besides the actual simulation data making it more flexible but introducing information which has to be managed in a global manner. Hence, we refrain from global management information. Such implementations for single node or small-scale heterogeneous systems are not exclusively limited to the LBM but can be extended to scenarios in which the LBM is incorporated as the fluid solver in a fluid-structure interaction (FSI) application [29]; similar to our implementation, both computing devices execute the same functionality and the heterogeneous setup performs better than a homogeneous setup. Heterogeneous systems can even speed-up the LBM using adaptive mesh refinement (AMR) as demonstrated by Valero-Lara et al. [30].
A massively parallel implementation of the LBM for large-scale CPU/GPU heterogeneous clusters is presented by Calore et al. [18] to carry out studies of convective turbulence. Yet, Calore et al. degrade the CPUs to communication devices omitting their computational performance. A more comprehensive solution is chosen by Shimokawabe et al. [16] who assign the boundary cells of a subdomain to the CPU and the inner cells to the GPU. This leads to a full utilization of the GPUs but just to a minor utilization of the CPUs. We follow Shimokawabe’s parallelization strategy which does not evenly partition the domain along the three spatial dimensions but favors certain directions and applies static resource assignment. Furthermore, our approach is able to assign an arbitrary amount of work to the CPUs and is not limited to boundary cells. While Shimokawabe’s solution relys on non-blocking MPI communication and CUDA streams, Xiong et al. [17] are the first who also incorporate OpenMP to deal with multiple GPUs managed by one MPI process. Hence, the shared memory parallelization does not target the CPU for LBM computations but for work distribution among the GPUs on the node level. In another publication, Shimokawabe et al. [31] present a framework for large-scale stencil computations on CPU/GPU heterogeneous clusters incorporating the host memory but not the computational resources of the CPU. Instead, all computations are carried out on the GPUs.
All these works deal with particular aspects also included by our holistic hybrid implementation of the LBM discussed in more detail in Section 4. However, none of them provides the full level of complexity necessary to fully utilize all computational resources of the target architecture in a scalable way. A smart combination of these techniques allows the full utilization of the entire computational potential of large-scale CPU/GPU heterogeneous clusters. Our approach is capable to deal with nodes equipped with an arbitrary number of CPU cores and GPUs as well as with different ratios of CPU and GPU performance.
3. The Lattice Boltzmann Method
In the following, we briefly introduce the LBM [32]. See [33,34,35,36,37] for further details on algorithmic, physical and mathematical backgrounds.
3.1. Discretization Schemes
The LBM discretizes space by a simple Cartesian grid using square- (2D) or cube-shaped (3D) (lattice) cells. Fluid flow is predicted by using probability densities (also called density distribution functions). The scalar-valued probability densities are assigned to the center of every lattice cell. They model the probability that a virtual particle moves along the direction of lattice velocity within a small region around at time t. To guarantee that the virtual particles traverse exactly one lattice cell per timestep , the lattice velocities have to be chosen accordingly. The number of utilized dimensions d and probability densities q per lattice cell determine the actual discretization scheme, noted by . Two examples of such discretization schemes are D2Q9 and D3Q19. They are depicted in Figure 1. We apply the D3Q19 scheme for the implementation, but throughout the remainder of this paper, the D2Q9 scheme is used for simplicity and illustration.
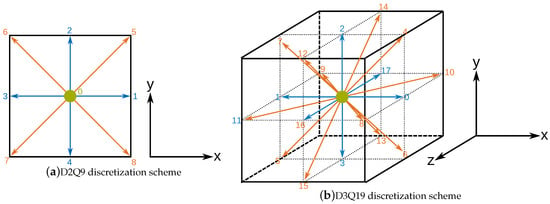
Figure 1.
Discretization schemes for the LBM using probability densities in 2D (a) and probability densities in 3D (b), respectively [19]. Blue arrows represent probability densities with lattice speed , red arrows with lattice speed , and green dots with lattice speed . The orientation of the corresponding coordinate systems is indicated in the right parts of the subfigures.
Probability densities do not have a direct physical interpretation, but the macroscopic quantities fluid density and flow velocity can be obtained via
and
with a position in space and a point in time t. For the sake of simplicity and to conform with standard dimensionality procedures in the LBM context, the spatial mesh size and the timestep are scaled to unity throughout the following and all LBM quantities are dimensionless.
3.2. Collision and Propagation
The LBM applies alternating collision (also called relaxation) and propagation (also called streaming) steps to evolve the system. Both operators originate from the lattice Boltzmann equation
in which collisions model local diffusion,
and propagations evolve due to convection,
with denoting the discretized equilibrium functions. A depiction of affected probability densities is given in Figure 2 for one collision and one propagation step. On the one hand, the collision operator expresses the interaction of the virtual particles which requires computations of these interactions. On the other hand, propagation steps describe the movement of the particles which requires memory copy operations from and to other cells.
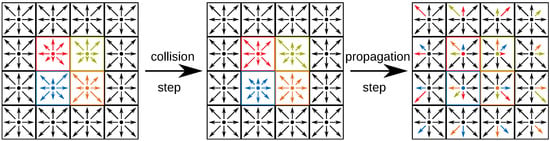
Figure 2.
Probability densities of four processed cells (colored in red, green, blue, and orange) affected by collision and propagation steps [19]. Different lengths of same-color arrows in the same direction represent an update of the probability densities due to a collision step.
We stick to the standard polynomial form for the discretized equilibrium functions
with speed of sound and lattice weights . Several alternative formulations for can be found amongst others in [38,39]. Furthermore, there are various collision models for , e.g., the Bhatnagar-Gross-Krook (BGK) scheme [40], also called single-relaxation-time (SRT) scheme:
Alternatively, the multiple-relaxation-time (MRT) [41], entropic [42] or cascaded [43] schemes are other examples. All of them share the property of local updates only involving local and directly neighboring cells. The relaxation time is directly related to the kinematic viscosity of the fluid. Derived from this relation, has to satisfy to ensure a positive viscosity. Due to stability and accuracy, is usually further chosen to satisfy which is a necessary but not a sufficient boundary.
So far, the default operators are introduced neglecting the treatment of any boundary conditions. However, boundary conditions have an influence on the structure of collision and propagation steps and they have to be adapted accordingly. Since we focus on optimization and parallelization on large-scale CPU/GPU heterogeneous clusters, we omit a discussion on operators for different boundary conditions and refer to [37]. Yet, our implementation supports no-slip and moving wall boundary conditions based on half-way bounce back.
4. Implementation of the Lattice Boltzmann Method
Due to the different types of computing devices in a heterogeneous system, hybrid programming is required. This also implies the application of multiple programming models. C++ is used for the CPU code utilizing OpenMP for the multi-core parallelization. The GPU kernels are written in CUDA. The usage of OpenCL would be obvious because CPU and GPU kernels implement the same functionality, but CUDA is favored due to its better availability in large-scale CPU/GPU clusters, its superior support by NVIDIA (Santa Clara, CA, USA), hence, improved performance, and its convenient built-in functions for 3D memory copies. Furthermore, OpenACC is a noticeable candidate when it comes to the development of portable code for multi-core CPUs and GPUs. Nonetheless, current OpenACC compilers do not support the generation of a unified binary with machine code for both architectures stemming from the same kernels yet [44] which is essential to simultaneously engage CPUs and GPUs with the LBM operators. Hence, we do not apply OpenACC in this work but consider it for future work. However, none of the discussed concepts is limited to this list of technologies and tools but can also be realized with different technologies. For the distributed memory parallelization, two-sided MPI communication is sufficient.
For more intuitive explanations, the terms “left”,“right”/“bottom”,“top”/“back”,“front” are used for neighboring index relations along x/y/z-axis.
4.1. Optimization and Parallelization on Computing Device Level
Before discussing techniques to parallelize the LBM among multiple computing devices, we focus on optimizations for single computing devices which is as important to actually reach high performance as scalability itself [45,46].
4.1.1. Memory Layout Pattern
It is crucial how the probability densities are stored in memory to achieve high performance and low memory consumption. Both computing devices utilize the same memory layout pattern and little-endian storage, thus, no conversion is necessary if data is copied from the GPU to the CPU for processing and vice versa.
Intuitively, would be stored cell-wise. Hence, the data of one lattice cell is kept continuously in memory, resembling the array of structures (AoS) pattern. Though, this strategy avoids efficient caching on the CPU and coalesced memory access on the GPU because probability densities of the same lattice velocity of neighboring lattice cells grasped in parallel are located far away from each other in memory. Storing the probability densities of one particular direction continuously in memory, which is known as structure of arrays (SoA) pattern, enables efficient memory access and thus, is applied by us.
Probability densities of the 3D lattice are interpreted as a three-dimensional array and linearly stored in memory using an -ordering, with the first of the indices addressing consecutive memory locations and the last of the indices describing entire blocks of probability densities in the same direction [4].
There is no implicit synchronization if the collision and propagation operator are executed in parallel. Depending on the assignment of lattice cells to threads (cf. Section 4.1.2 and Section 4.1.3), it is possible that a thread reads a probability density that has already been updated by another thread in the same step. The straight-forward solution to avoid such race conditions manages two dedicated instances of all probability densities in memory. Data is read from one instance, the collision operator is applied, and according to the propagation operator, updated values are written to the other instance. In the next step, source and destination sets are swapped. Since two copies of the data are kept, this solution is called A-B memory layout pattern. It resolves the race conditions at the cost of doubled memory consumption.
We apply a more efficient approach which uses only one data instance in memory and is known as the A-A memory layout pattern [6,47], cf. Figure 3. It rearranges the collisions and propagations of two consecutive (first an odd, then an even) steps of the LBM into an - and a -step. -steps are just the collision of the odd regular LBM steps while -steps combine the propagations of the odd regular LBM steps and the collisions and propagations of the even regular LBM steps. In each step, data that is required to process a lattice cell is read from and written to the same memory locations. Thus, when executed in parallel, no threads interfere with each other, making explicit synchronization on computing device level and an additional buffer obsolete. If an -step is executed on a particular lattice cell, only probability densities assigned to this lattice cell are altered. In contrast, a -step just manipulates data of adjacent cells (except the probability densities with lattice speed 0). After performing a -step, the simulation is in a consistent state, that is a state which corresponds to an even step when using the A-B memory layout pattern. Further details concerning the A-A memory layout pattern are provided in [19,48]. The latter source also lists additional memory layout patterns for the LBM. An even more sophisticated alternative is the Esoteric twist (EsoTwist) [49,50] which offers higher geometric flexibility, however, this is not the focus of this work.
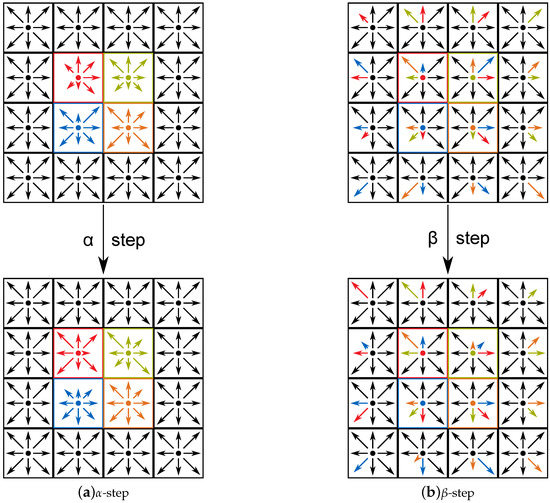
Figure 3.
Probability densities of four processed cells (colored in red, green, blue, and orange) affected by memory accesses using the A-A memory layout pattern [19]. Different lengths of same-color arrows in the same direction represent an update of the probability densities due to a collision step. (a) Illustrates the -step consisting of one collision step, (b) depicts the -step consisting of two propagation steps and one collision step.
4.1.2. Lattice Boltzmann Method Kernels for the CPU
The computational workload of our LBM simulation stems from the - and -steps. Both steps are implemented in dedicated kernels named - and -kernel. Since both steps perform a collision operation, - and -kernel just differ in the read-from- and write-to-memory locations but not in their computational operations.
Three nested loops iterate over the lattice cells of the domain. To fit the alignment of data in memory, the innermost loop iterates in x-direction, the outermost loop iterates in z-direction. Blocking [51] is applied to increase the cache efficiency of the CPU code. Since the LBM is memory-bound, cache efficiency is of high relevance. Cache lines are a contiguous chunk of linear data. Hence, large block sizes in x-direction and small block sizes in z-direction result in better cache efficiency because data in x-direction is linearly stored in memory. Accordingly, if such blocks are not possible, e.g., when processing a plane-shaped domain in -direction with only a few or even only one lattice cell in x-direction, performance significantly degrades.
OpenMP is utilized to parallelize the CPU kernels. The straight-forward approach would be the application of OpenMP parallel-for to the outermost loop. But this construct leads to a loss of program control until the parallel section is finished by all threads. This renders the approach useless for our case because GPU kernels, memory copy operations, and communication have to be issued during the execution of the CPU kernels for concurrent execution (cf. Section 4.3). Instead, we take advantage of OpenMP tasks [52], originally introduced to deal with asymmetric work in OpenMP programs. When spawning a new OpenMP task, the task is assigned to a thread and program control is immediately returned. As for multi-threaded programming in general, the number of OpenMP tasks should be as small as possible (but large enough to utilize all available CPU cores) and the load per task should be maximized to reduce overheads. Instead of creating new OpenMP tasks for iterations of loops, we initiate one OpenMP task for every block that is used to increase the cache efficiency.
4.1.3. Lattice Boltzmann Method Kernels for the GPU
Analogously to the CPU kernels, there are also an - and a -kernel for the GPU which implement the same functionality and which are based on [20,53]. In contrast to [12,16] in which a thread deals with an entire row of lattice cells, we assign one thread to each lattice cell [9,18]. This invokes a large amount of threads at runtime enabling memory latency hiding. Mapping consecutive threads to continuous lattice cells makes coalesced memory access possible which is crucial for memory-bound problems such as the LBM.
- and -steps are strictly executed in an alternating manner, i.e., they are not overlapped or fused in any way. During the execution of one kernel, data is thus read and written only once. Therefore, data is directly loaded to and stored from registers neglecting shared memory which could be exploited to increase the size of the L2 cache Kepler GPU architecture [54] (see Table 2). However, this approach induces high register consumption because a dedicated register is used for every probability density of a lattice cell. Hence, there are two limiting factors for high occupancy. On the one hand, large thread block sizes limit occupancy due to a high per-thread register usage. On the other hand, small thread block sizes result in an insufficient number of active threads because the product of the maximum number of blocks that can be simultaneously active and threads per block is too low. A detailed discussion on this issue can be found in [55].
Similar to the CPU kernels, the performance on the GPU strongly depends on the shape of the processed domain. Preference is given to enough lattice cells in x-direction to utilize all the linear threads of a warp (warps are groups of 32 threads executed in parallel created, managed, and scheduled by a multiprocessor), leading to coalesced memory access and high performance with respect to the bandwidth. If the domain extends rather along y/z-direction, performance is severely limited; providing an alternative implementation applying the A-A pattern along, e.g., y-axis could cure this issue. x/z- and x/y-planes do not suffer from this effect.
4.2. Domain Decomposition and Resource Assignment
We use a data-parallel approach to parallelize the LBM among multiple computing devices. Different sets of lattice cells and their probability densities are assigned to different processing elements. On a higher level, the entire domain is subdivided into equally-sized cuboid-shaped subdomains. There is no overlap of the subdomains and every lattice cell belongs to exactly one subdomain. Each subdomain is assigned to one MPI process. On a lower level, each of the subdomains is further subdivided by a plane in -direction. The resulting bottom cuboid is assigned to at least one CPU core, the top cuboid to one GPU. Accordingly, they are called GPU- and CPU-part of the subdomain. Figure 4 illustrates the partitioning in a 2D setting.

Figure 4.
Decomposition of a 2D domain consisting of lattice cells in subdomains [19]. Each subdomain is subdivided in a upper part assigned to a GPU (green) and a lower part assigned to a CPU (blue).
The ratio of CPU- to GPU-part can be arbitrarily set and is equal for all subdomains. So, an adaption of the simulation to computing devices with any ratio of computational performance is possible. A CPU- or GPU-part size of 0 in y-direction is also supported resulting in a GPU-only or CPU-only scenario, respectively. Since one subdomain is assigned to one MPI process and the GPU-part of a subdomain is managed by one GPU, the number of MPI processes assigned to one node corresponds to the number of GPUs per node and the total number of launched MPI processes corresponds to the total number of available GPUs. Each OpenMP thread is pinned to a dedicated CPU core and no hyperthreading and no oversubscription are applied. The CPU cores and threads, respectively, are uniformly distributed among the MPI processes. Hence, every subdomain is handled by the same amount of processing elements. Non-uniform memory access (NUMA) effects originating from nodes equipped with more than one CPU are coped with by ensuring NUMA locality with pinning.
On the one side, this assignment of data to MPI processes and computing devices is special in terms of rigid rules. On the other side, it offers best performance. Alternatively, one of the following three assignment policies could be applied:
- (a)
- One MPI process for each GPU and one MPI process for each CPU (or all CPU cores of one node)
- (b)
- One MPI process for each GPU and one MPI process for each CPU core
- (c)
- One MPI process for every node
Option (a) increases flexibility because every computing device is encapsulated in a dedicated MPI process, but communication between computing devices would only be possible via MPI messages making direct memory copy operations impossible. Furthermore, it is much harder to evenly distribute work among GPUs and CPUs depending on their computational performance. All disadvantages of option (a) are inherited to option (b). Even worse, communication between different CPU cores cannot be accomplished in a shared memory way where different cores have direct access to the memory with data of another core anymore. Instead, access is implemented via node-internal MPI messages. Nonetheless, options (a) and (b) benefit from implicit synchronization by exploiting MPI mechanisms keeping the complexity of the implementation low. Suchlike synchronization has to be entirely realized by the application developer when selecting option (c) leading to a high degree of code complexity, but enabling full control for node-level optimizations.
4.3. Communication Scheme
Executing the LBM operators requires access to neighboring lattice cells. If they reside in the memory of other computing devices, the probability densities of the affected lattice cells have to be copied to the local device. In the following, we present a scalable strategy to perform this communication, hidden behind LBM computation.
We distinguish boundary cells, the outermost layer of lattice cells of the CPU- or GPU-part of a subdomain, and inner cells, the remaining non-boundary cells. Furthermore, a layer of ghost cells is added and surrounds each CPU- or GPU-part of a subdomain in the memory of a computing device to store data from neighboring subdomains. Additionally, for every neighbor, a communication buffer is installed in host memory. Figure 5 and Figure 6 illustrate the different kinds of cells and communication buffers.
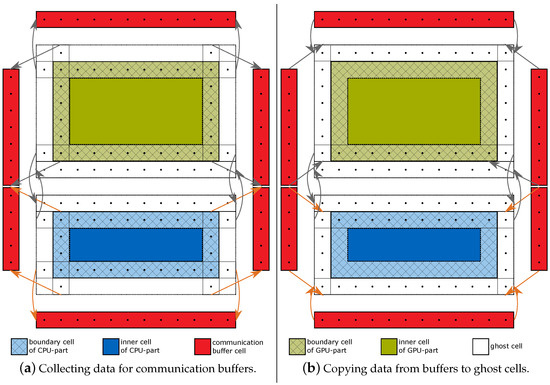
Figure 5.
-step collection (a) and distribution (b) of data. The behavior of one MPI process with four communication partners is illustrated in 2D. GPU- and CPU-part of the subdomain are colored in green and blue. Boundary cells are hatched and colored in light-green and light-blue, ghost cells are colored in white. Memory for the communication buffers is colored in red. Gray arrows indicate copy direction between and location of host and device. Analogously, orange arrows express in-host memory copy operations. Lattice cells affected by read/write operations are marked with a dot.
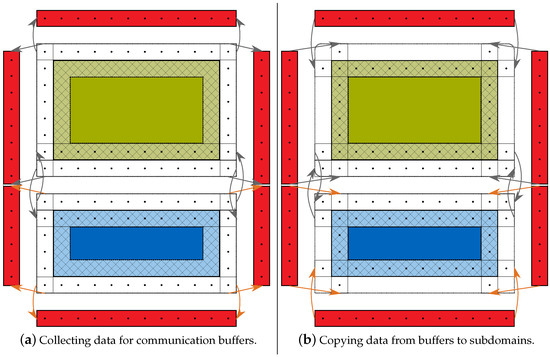
Figure 6.
-step collection (a) and distribution (b) of data. The behavior of one MPI process with four communication partners is illustrated in 2D. For color coding and meaning of data transfer arrows, see Figure 5. Lattice cells affected by read/write operations are marked with a dot.
At runtime, - and -steps are each run in two phases:
- (a)
- The boundary cells are updated, i.e., the - or -step is applied. No copy operations or communication takes place.
- (b)
- The inner cells are updated. In the meantime, the data updated in phase (a) is communicated to the corresponding proximate computing device.
For both phases (a) and (b), the same kernels are carried out with the same functionality but on different parts of the simulation domain at different times. This strategy enables us to hide communication behind computation of the inner cells during phase (b).
Phase (b) requires in-host memory copy operations, data transfers between the host and device (and vice versa), and MPI communication between different processes. For the first two types of memory copy operations, the CUDA function cudaMemcpy3DAsync() is applied. It copies data of any cuboid-shaped region of a subdomain; source and target can either be the device or the host. In our case, these cuboid-shaped regions correspond to the data of lattice cells to be transferred and always have a thickness of one cell. For the MPI communication, the point-to-point communication functions MPI_Isend() and MPI_Irecv() are utilized. All three functions (cudaMemcpy3DAsync(), MPI_Isend(), and MPI_Irecv()) are non-blocking and immediately return the program control to the application developer. Thus, computations can be issued while memory copy operations and communication take place.
Figure 5a and Figure 6a illustrate the collection of data to be transferred within an MPI process during phase (b) of an - and -step, respectively. Probability densities are either copied from the computing device to the communication buffer or are directly exchanged between the CPU- or GPU-part of subdomain at the corresponding interface (top face of CPU- and bottom face of GPU-part). In x-direction, data is copied from the CPU- and GPU-part; in y-direction, data is copied either from the CPU- or GPU-part. Once the data for the neighboring subdomains is collected, it is sent via MPI to the destination processes. Received data is copied to the communication buffers. Special care is taken to avoid overwriting of communication buffer data by dedicated buffers for sending and receiving. Figure 5b and Figure 6b depict the distribution of data from the communication buffers to the computing device memories after reception. Communicating data of a lattice cell to an adjacent subdomain does not imply a transfer of all probability densities of this cell but only of those which are required by the LBM operators within the target subdomain. This leads to a significant reduction in memory copy and communication effort as discussed in more detail in [19,56]. Since only neighboring processes exchange data and no global information has to be exchanged, no collective MPI operations are necessary. Hence, the amount of inter-process communication only depends on the surface size of a subdomain but not on the number of subdomains.
The discretization scheme determines the number of communication partners for every MPI process. They correspond to the directions of the lattice velocities. For the D3Q19 discretization scheme, there are six communication partners along the faces (called face neighbors) of the cuboid and twelve along the edges (called edge neighbors). A particular ordering of the communication can reduce the number of communication partners to the six face neighbors: Instead of executing all transfers simultaneously, they are grouped in spatial directions. First, data is exchanged between neighbors in x-direction (left and right), afterwards in y-direction (bottom and top), and finally in z-direction (back and front). Thereby, for example, data designated to the left back edge neighbor is first transferred to the left neighbor in x-direction and later from there to the back neighbor in z-direction. This concept leads to a serialization of inter-process communication in three distinct phases but substantially reduces the number of communication partners and hence, MPI communication.
Similar to the CPU and GPU kernels, the performance of cudaMemcpy3DAsync() strongly depends on the shape of the cuboid of data to be copied. This CUDA function delegates copy transactions to successive calls of memcpy() or cudaMemcpy(), each processing a linear chunk of data contiguously stored in memory. Assuming a subdomain of size , copying one face of boundary cells in y-direction leads to O function calls of memcpy() or cudaMemcpy(), respectively, each transferring M elements at a time. Analogously, copying one face in z-direction leads to N function calls, each transferring M elements at a time, too. This is much more efficient than copying in x-direction where calls are issued, each transferring only one element.
Figure 7 illustrates a timeline of one MPI process during an - and -step. Copy operations between the communication buffers managed by the application developer and the MPI buffers maintained by MPI are also depicted by orange (before MPI_Isend()) and gray bars (after MPI_Irecv()). Data dependencies have to be obeyed, e.g., probability densities cannot be sent via MPI before they are copied from the computing devices to the communication buffers and cannot be copied to the computing devices before received via MPI. Accordingly, dependencies due to shared resources also have to be considered, for example either data from the CPU- or the GPU-part of the subdomain is written to the communication buffers at a time. There are associated operations occurring simultaneously in two blocks connected with dotted lines in Figure 7 such as direct copy operations between CPU and GPU. Communication (yellow areas) and computation (white areas) periods are carried out concurrently. Phase (b) starts with the communication period on the computing devices. Different lengths in runtimes due to various sizes of the cuboid to process or effects such as coalesced memory access or caching are expressed by non-proportional varying lengths of the bars. The finishing time of an - or -step depends on the communication time and the time to update the inner cells.
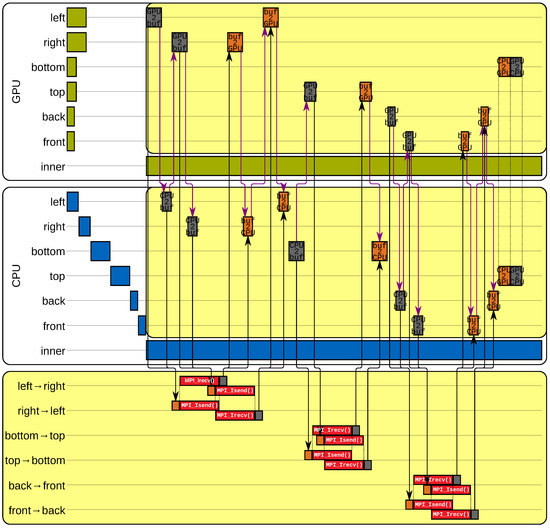
Figure 7.
Timeline of one MPI process during an - or -step [19]. Operations are grouped in GPU (top), CPU (middle), and MPI (bottom) activities. Within each computing device’s group, operations affecting the six faces and the inner cells are illustrated. Communication and copy actions are highlighted by yellow background, computations by white background. Green and blue bars indicate computations on the GPU and CPU. Red bars symbolize MPI communication distinguished between sending (MPI_Isend()) and receiving (MPI_Irecv()). Communication directions are denoted by “from …neighbor → …boundary layer”. Grey and orange bars represent memory transfers to and from the communication buffers stored on the host, respectively. Bars marked with “GPU2buf” perform a copy operation from the GPU to the communication buffers and those with “CPU2buf” from the CPU to the communication buffers. The copy operations from the communication buffers to the computing devices are marked with “buf2GPU” and “buf2CPU”. Copy operations along the interface between CPU- and GPU-part of the subdomain are called “CPU2GPU” and “GPU2CPU”. Black arrows indicate data dependencies, purple arrows illustrate dependencies due to shared resources.
Turning the operations represented in Figure 7 to code leads to Algorithm 1 summarizing our implementation in a C-like pseudocode with simplified functions -/-kernelGPU(), cudaMemcpy3DAsync(), MPI_Isend(), MPI_Irecv(), and MPI_Wait(). The pseudocode assumes a subdomain with neighbors in all six directions (similar to Figure 7). Adequate treatment of subdomains at the edge of the domain has to be considered during implementation. While lines 5–18 represent the phase (a) of an - or -step, the phase (b) is expressed by lines 2–4 and 19–61. Updates of the lattice cells are issued in lines 6, 14, 19, and 25. The OpenMP tasking construct for processing the boundary cells is given in lines 8, 9, and 13, for the inner cells it is expressed by lines 20, 21, and 24. All commands except those ones in lines 17, 18, 61, 62, and the calls of MPI_Wait() are non-blocking. Communication in x-direction is represented by lines 27–38, in z-direction by lines 47–58, and in y-direction by lines 39–46, 59, and 60.
| Algorithm 1 Pseudocode of an MPI process to update its subdomain and to exchange boundary cells during an - or -step according to Figure 7. sendBfrs and recvBfrs are arrays containing pointers to the communication buffers for sending and receiving data conforming to the red colored memory in Figure 5 and Figure 6, thus, with storage for data from the CPU and the GPU. The array reqs contains elements of type MPI_Request, streams is an array with elements of type cudaStream_t. -/-kernelCPU(a) and -/-kernelGPU(a) apply an - or -step to a on the CPU and the GPU, respectively. The simplified signature of MPI_Isend(a, b) reads “send data from memory a to MPI process b” and MPI_Irecv(a, b, c) reads “receive data from MPI process b and store it to memory a using request handle c”. MPI_Wait(a) blocks depending on request handle a and cudaMemcpy3DAsync(a, b) copies data within the MPI process from memory b to a. |
|
5. Results
Experiments were carried out on three CPU/GPU heterogeneous clusters: Hydra, TSUBAME2.5, and Piz Daint. Their details are summarized in Table 1. The clusters differ in the number of CPUs and GPUs per node, cores per CPU, GPU architecture (cf. Table 2), and software such as CUDA version and MPI implementation. Hence, they represent a broad variety of examples of our target architecture. Performance is measured in giga lattice updates per second (GLUPS). Error-correcting code (ECC) is deactivated on all clusters for the host and the device memory. To improve the readability, the term “CPU/GPU ratio” is used to express the ratio of the CPU- and the GPU-part of a subdomain within an MPI process.

Table 1.
Properties of the CPU/GPU heterogeneous clusters used to benchmark performance throughout this work. All CPUs are Intel CPUs. Only 338 of the total 4000 nodes of Hydra are equipped with GPUs. Besides the 5320 nodes equipped with GPUs, Piz Daint has 2862 CPU-only homogeneous nodes. We limit our benchmarks to the GPU-equipped nodes.

Table 2.
Properties of the GPUs utilized to benchmark performance throughout this work. All GPUs are NVIDIA GPUs.
We validate our hybrid reference implementation of the LBM with the 3D lid-driven cavity benchmark scenario [57,58]. Simple in its design, the scenario is yet representative for a large class of problems regarding performance considerations for LBM simulations on regular Cartesian grids. It is further used as a benchmark in a variety of LBM performance evaluations and comparisons [7,9,10,14]. A relaxation time is applied and all test runs take 1024 timesteps, thus, 512 - and -steps are executed. Since - and -kernel perform the same amount of computations and memory accesses and benefit from caching and coalesced memory access, they do not differ in performance.
5.1. Performance of the CPU and GPU Kernels
To evaluate the performance of the CPU and GPU kernels without any copy operations and communication, we run benchmarks on one node of Piz Daint. All twelve cores of the CPU are occupied. Results are plotted in Figure 8. Performance values for the CPU depend on the block size used to increase cache efficiency denoted by “number of cells in x-direction” × “number of cells in y-direction” × “number of cells in z-direction”. The parallel setup for the GPU is denoted by “threads per block in x-direction” × “threads per block in y-direction” × “threads per block in z-direction” and assigned to the abscissas of the GPU plots. Five different problem sizes are evaluated and depicted by different lines: Cube-shaped scenarios range from to lattice cells and one cuboid-shaped domain of size is tested. For the Intel Xeon E5-2690v3, the theoretical peak memory bandwidth is 68GByte/s [59], the according value for the NVIDIA Tesla P100 is GByte/s (cf. Table 2).
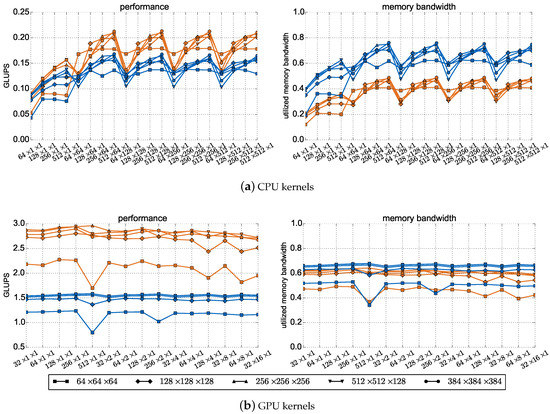
Figure 8.
Performance in GLUPS (left) and share of utilized memory bandwidth in peak memory bandwidth (right). (a) Shows results for the CPU kernels, (b) for the GPU kernels. Values for the CPU depend on the block size used to increase cache efficiency and for the GPU on the parallel setup, each assigned to the abscissas. Different lines depict different problem sizes. Single precision (float) performance is colored in orange, double precision (double) performance in blue.
On the CPU, a significant drop in performance can be observed for small block sizes in x-direction. The larger the block size in x-direction, the better the performance because caching takes effect. This behavior also holds for block sizes in y-direction, but it is less significant. Since probability densities are only used once per - or -step, the only performance improvement due to caching stems from data already moved to the cache as part of a cache line previously loaded. A definite statement to the influence of the domain size on performance is not possible, but larger domain sizes tend to enable higher performance. The double precision version exploits more of the available memory bandwidth ( memory bandwidth efficiency, domain size , block size ) than the single precision version ( memory bandwidth efficiency, domain size , block size ) resulting in best performance on the CPU of GLUPS and GLUPS, respectively. In general, the difference between single and double precision performance ranges from (domain size , block size ) to (domain size , block size ). Block sizes in z-direction have no impact on performance due to the chosen memory layout pattern, thus, they are not depicted in Figure 8a.
On the GPU, the parallel setup only has a minor effect on performance. Just for large thread numbers per block in x-direction in combination with small domain sizes, there is a drop in performance. Apart from that, GLUPS numbers are almost constant. Hence, also the memory bandwidth utilization is very robust to the size of the blocks. Larger domains generally lead to more GLUPS, but performance grows only slowly for domains bigger than . In contrast to the CPU kernels, the choice of single or double precision has a very significant influence on the performance. Comparing the same problem size, the single precision version shows between ( GLUPS vs. GLUPS, domain size , parallel setup ) and ( GLUPS vs. GLUPS, domain size , parallel setup ) higher performance than the double precision version. Best performance on the GPU is GLUPS in single precision ( memory bandwidth efficiency, domain size , parallel setup ) and GLUPS in double precision ( memory bandwidth efficiency, domain size , parallel setup ). Even if such memory bandwidth efficiency appears low on a first view, it is expectable and satisfying due to the complexity of the kernels for - and -step and integer overheads for index computations, especially to check the boundary conditions. Boundary conditions are checked for all cells, including inner cells, and therefore, results also hold for more complex domains.
Comparing CPU and GPU performance in terms of GLUPS, the NVIDIA Tesla P100 delivers (single precision)/ (double precision) more GLUPS than one single Intel Xeon E5-2690v3 in our approach. This is in agreement with the ratio of peak memory bandwidth of both devices which differs by a factor of .
The best performing block size for the CPU kernels when running a lattice cells domain is . Accordingly, the best performing block size for the GPU kernels for the same domain size is threads per block. Both configurations hold for double precision. These values are used throughout the remainder of this section for collecting results on heterogeneous systems.
5.2. Single Subdomain Results on Heterogeneous Systems
To investigate the benefit of using heterogeneous systems instead of homogeneous ones, a detailed analysis on one entire node of Piz Daint is plotted in Figure 9. Hence, a single subdomain is considered without any communication to neighbors. Performance in GLUPS is assigned to the abscissa, the ordinate shows the share of the GPU-part in the total subdomain. Just as in the previous section, the same five problem sizes are used depicted by different lines.
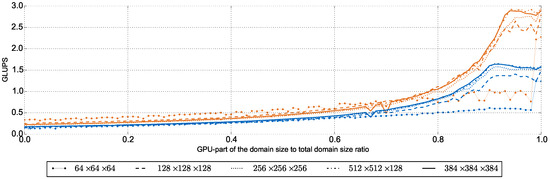
Figure 9.
Performance in GLUPS of a heterogeneous system in dependence of the size of the GPU-part of the domain. Size is given as share of the GPU-part in the total subdomain ranging from 0 ( CPU/GPU ratio) to 1 ( ratio). The CPU-part is processed by a Intel Xeon E5-2690v3, the GPU-part by a NVIDIA Tesla P100. Different lines depict different domain sizes. Single and double precision are colored in orange and blue, respectively.
For single precision, no heterogeneous version is able to excel the homogeneous GPU-only version. Only the larger domains consisting of and lattice cells achieve at least similar performance to the GPU-only version ( and , respectively) with a CPU/GPU ratio of . Overheads such as copy operations between the CPU- and GPU-part of the subdomain counterbalance the additional computational potential of the CPU. Since it takes more time to execute double precision than single precision operations, constant communication overheads such as copy invocation times have a smaller influence in double precision scenarios. Hence, for double precision, an improvement of , , and can be realized for the , , and domain, respectively, when applying the optimal CPU/GPU ratio of . Theoretically, an acceleration of is possible corresponding to the improvement of the accumulated peak memory bandwidth of CPU and GPU in comparison to the GPU’s peak memory bandwidth. Once again, communication overheads consume the theoretical maximum improvement but an acceleration is clearly observable. Small domains do not benefit from the heterogeneous version at all because they require less runtime to be processed and thus, constant communication overheads become even more dominant.
Besides the fine grained analysis of Figure 9, Table 3 lists additional values of improvement when utilizing one entire CPU and one GPU of the heterogeneous clusters Hydra and TSUBAME2.5. The evaluation is limited to the domain, and double precision is used. On Hydra, heterogeneous computing is clearly superior to the homogeneous approach: incorporating one CPU of Hydra enhances performance by compared to the homogeneous GPU-only version. In contrast, the negligible acceleration by heterogeneous computing on TSUBAME2.5 can be explained by its complex PCIexpress bus [60] due to its node setup containing three GPUs and two CPUs.

Table 3.
Performance improvement by using a heterogeneous system instead of a homogeneous one. Experiments are carried out for a domain using double precision. Column “ratio” lists the best performing CPU/GPU ratio. All CPUs are Intel Xeons, all GPUs NVIDIA Teslas. Imp. stands for improvement. Values in the columns “imp. GPU” and “imp. CPU” list the measured relative performance improvement of the heterogeneous version compared to the particular computing devices in percent (%) or whole factors (×) where appropriate. The theoretical improvement in comparison to the GPU-only configuration is given in the corresponding column.
5.3. Large-Scale Results on Heterogeneous Systems
To evaluate scalability of our hybrid reference implementation of the LBM, weak (see Figure 10) and strong scaling (see Figure 11) experiments are performed using different parallelization strategies. Adding subdomains in y-direction in such a way that communication is performed between bottom and top faces is denoted as parallelization in y-direction. Analogously, there is parallelization in z-direction. If subdomains have neighbors in all spatial directions, it is called parallelization in x/y/z-direction. Values of interest are the absolute performance in GLUPS (cf. left plots) and scalability expressed by parallel efficiency (cf. right plots). For the weak scaling benchmarks, every subdomain consists of lattice cells. Such a subdomain has different communication times in all directions to represent the non-isotropic communication behavior of our implementation. For the strong scaling benchmarks, a domain with lattice cells is used initially, subdivided into subdomains. Orange lines represent the results for the best performing heterogeneous version. The CPU/GPU ratio of this version varies for different parallelization strategies and clusters. Tests are run in double precision on the three CPU/GPU heterogeneous clusters listed in Table 1. On TSUBAME2.5, only two of the three available GPUs per node are utilized because this configuration led to better overall performance in our experiments. Sharing the CPU memory bandwidth among three MPI processes and the complex PCIexpress bus of a TSUBAME2.5 node [60] limited performance.
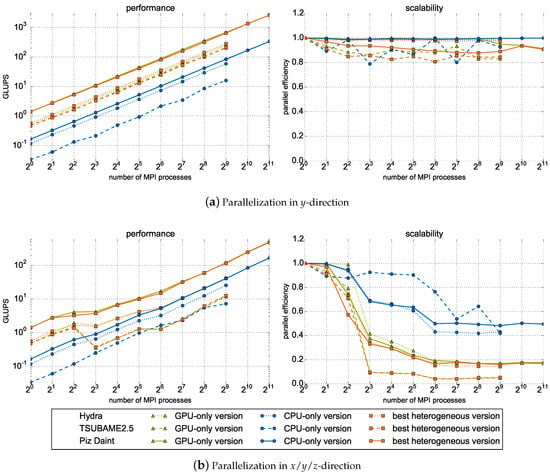
Figure 10.
Weak scaling performance in GLUPS (left) and scalability expressed by parallel efficiency (right) for two different parallelization strategies. (a) Depicts results for parallelization in y-direction, (b) for parallelization in x/y/z-direction. Degree of parallelism expressed by number of subdomains is assigned to the ordinates. Different line markers denote different CPU/GPU heterogeneous clusters. The CPU-only homogeneous version is colored in blue, the GPU-only homogeneous version in green, and the best performing heterogeneous version in orange.
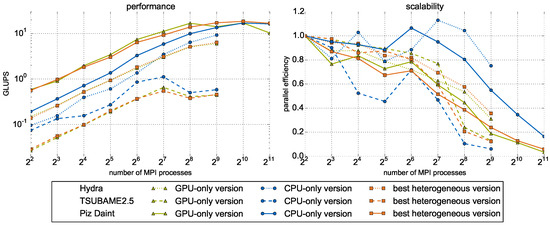
Figure 11.
Strong scaling performance in GLUPS (left) and scalability expressed by parallel efficiency (right) for parallelization in x/y/z-direction. Axes assignments, line markers, and color coding are equal to Figure 10.
Almost perfect weak scalability is obtained when parallelizing in y-direction as depicted in Figure 10a. Parallel efficiencies of on Hydra (512 MPI processes, CPU/GPU ratio), on TSUBAME2.5 (512 MPI processes, CPU/GPU ratio), and on Piz Daint (2048 MPI processes, CPU/GPU ratio, are achieved. Largest runs on Hydra and TSUBAME2.5 manage lattice cells, the largest run on Piz Daint consists of cells. This demonstrates that our approach to communication hiding is indeed very efficient. The run on Piz Daint results in the highest measured performance of GLUPS utilizing 2048 GPUs and 24,576 CPU cores. Results for parallelization in x/y/z-direction plotted in Figure 10b reveal the influence of the parallelization strategy. As mentioned in Section 4.1, communication performance in x-direction is much worse than in other directions limiting performance when parallelizing in x-direction. Every time additional communication is introduced along x-direction (, , and MPI processes), the increase in performance is not in line with the increase in computational resources. This can be especially observed on TSUBAME2.5.
Depending on the heterogeneous cluster and the considered problem size, performance saturates at a certain point in strong scaling scenarios as shown in Figure 11. On TSUBAME2.5, performance stagnates or even drops when applying more than 128 MPI processes; on Piz Daint, this point is reached for 512 MPI processes. The performance limit on Hydra would occur for approximately 1024 MPI processes but since there are only 676 GPUs available in this cluster, no saturation is observable in the plot. At this point, communication efforts become dominant because they are not reduced in the same order (the face area of only one direction is halved if the number of MPI processes is doubled) as the computational effort (indirect proportional to number of MPI processes) with increasing degree of parallelism. Besides, subdomains become very small, e.g., for 2048 processes, a subdomain consists of only lattice cells. However, good strong scalability can be achieved in even such challenging scenarios. For example on Hydra, parallel efficiencies of (GPU-only), ( CPU/GPU ratio), and (CPU-only) with 512 subdomains were measured. Especially for large subdomain numbers where communication efforts become dominant, the CPU-only version outperforms the GPU-only and heterogeneous version; on TSUBAME2.5, this effect appears already for low degrees of parallelism. Such a behavior stems from the factor that communication to the GPU is needlessly in the CPU-only version saving data copy efforts.
In addition to good scalability, large-scale experiments benefit from heterogeneous systems in many cases as depicted by Figure 12. It shows the factors of improvement () and degradation (), respectively, of the best performing heterogeneous version over the homogeneous GPU-only version. Considering the largest runs (512 MPI processes on Hydra and TSUBAME2.5, 2048 MPI processes on Piz Daint), all heterogeneous versions applying parallelization in y-direction for weak scaling ( GLUPS ( CPU/GPU ratio) vs. GLUPS on Hydra, GLUPS ( CPU/GPU ratio) vs. GLUPS on TSUBAME2.5, and GLUPS ( CPU/GPU ratio) vs. GLUPS on Piz Daint) and parallelization in x/y/z-direction for strong scaling ( GLUPS ( CPU/GPU ratio) vs. GLUPS on Hydra, GLUPS ( CPU/GPU ratio) vs. GLUPS on TSUBAME2.5, and GLUPS ( CPU/GPU ratio) vs. GLUPS on Piz Daint) outperform the GPU-only versions.
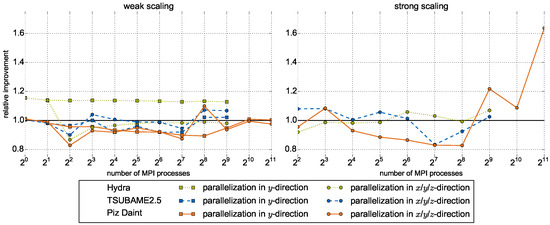
Figure 12.
Factor of improvement (ordinates) of the heterogeneous version with the optimal CPU/GPU ratio in comparison to the heterogeneous GPU-only version in dependence of the degree of parallelism (abscissas). Weak scaling results (see Figure 10) are plotted on the left, strong scaling results (see Figure 11) on the right. Results for the three different CPU/GPU heterogeneous clusters are tinted in different colors, parallelization in different directions is distinguished by different line markers.
6. Conclusions
In this work, we present a holistic scalable implementation approach of the LBM for CPU/GPU heterogeneous clusters generalizable to arbitrary heterogeneous systems. For the first time, all computational resources of such a system are exploited for the LBM. It comprises optimization and parallelization of the LBM for the particular computing devices, decomposing the simulation domain and assigning work to the computing devices according to their computational potential, and a runtime schedule continuously occupying the computing devices with computations while memory copy operations and communication is carried out in the background. Broadening the view, all findings of this article are applicable to grid based methods in a generic way with the LBM being just one example of such a method.
We use an A-A pattern LBM version which focuses on a memory efficient implementation. On a CPU (Intel Xeon E5-2690v3), up to of the peak memory bandwidth could be reached for a lattice cells domain using double precision resulting in GLUPS. Accordingly, on a GPU (NVIDIA Tesla P100), the highest achieved peak memory bandwidth utilization is leading to GLUPS for a lattice cells domain using double precision. Considering a heterogeneous system consisting of one CPU and one GPU, we are able to show a performance improvement in comparison to a GPU-only version of up to on Hydra (domain size , CPU/GPU ratio /). That is of the theoretically achievable improvement. Hence, the usage of heterogeneous systems is reasonable, especially in the context of already provisioned CPUs in the system which do not have to be acquired separately. Excellent weak scalability in large-scale heterogeneous scenarios with parallel efficiencies of on Hydra (512 MPI processes, CPU/GPU ratio), on TSUBAME2.5 (512 MPI processes, CPU/GPU ratio), and on Piz Daint (2048 MPI processes, CPU/GPU ratio) is achieved. The latter test on Piz Daint realizes GLUPS and runs on a partition in the petascale region, i.e., provides theoretically more than one peta () FLOPS. Restricting to large-scale homogeneous scenarios, parallel efficiencies of for the CPU- and (both on Hydra with 512 subdomains) for the GPU-only version are reached. Regarding strong scalability, ( CPU/GPU ratio) and (CPU-only) parallel efficiency, respectively, are measured processing 512 subdomains on Hydra.
Programming heterogeneous clusters requires a look on different programming models and technologies introducing a high level of complexity. We could not only show that the application of heterogeneous systems is beneficial in terms of performance enhancement but also that this is possible in a scalable way on large-scale CPU/GPU heterogeneous clusters. In an ideal case, the performance values of resources sum up in a heterogeneous case. So for compute-bound problems, FLOPS rates accumulate and in a memory-bound setting, peak memory bandwidth adds up. For the memory-bound LBM, communication latencies and management overheads reduce this theoretical gain but a significant portion of it is reachable with a proper implementation.
Supplementary Materials
The source code of our implementation is available under Apache License Version 2.0 at https://gitlab.com/christoph.riesinger/lbm/.
Acknowledgments
This work was supported by the German Research Foundation (DFG) as part of the Transregional Collaborative Research Centre “Invasive Computing” (SFB/TR 89). In addition, this work was supported by a grant from the Swiss National Supercomputing Centre (CSCS) under project ID d68. We further thank the Max Planck Computing & Data Facility (MPCDF) and the Global Scientific Information and Computing Center (GSIC) for providing computational resources.
Author Contributions
Christoph Riesinger developed and implemented the communication scheme for heterogeneous clusters and realized the CPU kernels. Furthermore, he wrote major parts of this paper. Arash Bakhtiari came up with the software design and included the distributed memory parallelization using MPI. Martin Schreiber established and optimized the GPU kernels and thus, laid the foundation of the hybrid reference implementation. Philipp Neumann advised this project, especially the LBM-specific aspects. In addition, he significantly improved the structure and wording of this manuscript. Hans-Joachim Bungartz supervised the work, coordinated investigations and contributed to the arrangement of this article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AMR | Adaptive mesh refinement |
| AoS | Array of structures |
| BGK | Bhatnagar-Gross-Krook |
| CFD | Computational fluid dynamics |
| CFL | Courant-Friedrichs-Lewy |
| CPU | Central processing unit |
| ECC | Error-correcting code |
| ELBE | Efficient lattice boltzmann environment |
| FLOPS | Floating point operations per second |
| FPGA | Field programmable gate array |
| FSI | Fluid-structure interaction |
| GLUPS | Giga lattice updates per second |
| GPU | Graphics processing unit |
| HPC | High performance computing |
| LBM | Lattice Boltzmann method |
| MPI | Message passing interface |
| MRT | Multiple-relaxation-time |
| NUMA | Non-uniform memory access |
| PGAS | Partitioned global address space |
| SIMD | Single instruction multiple data |
| SoA | Structure of arrays |
| SRT | Single-relaxation-time |
| TPU | Tensor processing unit |
References
- PEZY Computing. Available online: http://pezy.jp/ (accessed on 16 October 2017).
- TOP500.org. Top500 List—November 2017. Available online: https://www.top500.org/list/2017/11/ (accessed on 16 October 2017).
- Riesinger, C.; Bakhtiari, A.; Schreiber, M. Available online: https://gitlab.com/christoph.riesinger/lbm/ (accessed on 16 October 2017).
- Wellein, G.; Zeiser, T.; Hager, G.; Donath, S. On the single processor performance of simple lattice Boltzmann kernels. Comput. Fluids 2006, 35, 910–919. [Google Scholar] [CrossRef]
- Tölke, J.; Krafczyk, M. TeraFLOP computing on a desktop PC with GPUs for 3D CFD. Int. J. Comput. Fluid Dyn. 2008, 22, 443–456. [Google Scholar] [CrossRef]
- Bailey, P.; Myre, J.; Walsh, S.D.C.; Lilja, D.J.; Saar, M.O. Accelerating lattice boltzmann fluid flow simulations using graphics processors. In Proceedings of the International Conference on Parallel Processing, Vienna, Austria, 22–25 September 2009; pp. 550–557. [Google Scholar]
- Kuznik, F.; Obrecht, C.; Rusaouen, G.; Roux, J.J. LBM based flow simulation using GPU computing processor. Comput. Math. Appl. 2010, 59, 2380–2392. [Google Scholar] [CrossRef]
- Obrecht, C.; Kuznik, F.; Tourancheau, B.; Roux, J.J. A new approach to the lattice Boltzmann method for graphics processing units. Comput. Math. Appl. 2011, 61, 3628–3638. [Google Scholar] [CrossRef]
- Rinaldi, P.R.; Dari, E.A.; Vénere, M.J.; Clausse, A. A Lattice-Boltzmann solver for 3D fluid simulation on GPU. Simul. Model. Pract. Theory 2012, 25, 163–171. [Google Scholar] [CrossRef]
- Habich, J.; Feichtinger, C.; Köstler, H.; Hager, G.; Wellein, G. Performance engineering for the lattice Boltzmann method on GPGPUs: Architectural requirements and performance results. Comput. Fluids 2013, 80, 276–282. [Google Scholar] [CrossRef]
- Obrecht, C.; Kuznik, F.; Tourancheau, B.; Roux, J.J. Multi-GPU implementation of the lattice Boltzmann method. Comput. Math. Appl. 2013, 65, 252–261. [Google Scholar] [CrossRef]
- Wang, X.; Aoki, T. Multi-GPU performance of incompressible flow computation by lattice Boltzmann method on GPU cluster. Parallel Comput. 2011, 37, 521–535. [Google Scholar]
- Calore, E.; Marchi, D.; Schifano, S.F.; Tripiccione, R. Optimizing communications in multi-GPU Lattice Boltzmann simulations. In Proceedings of the 2015 International Conference on High Performance Computing & Simulation (HPCS), Amsterdam, The Netherlands, 20–24 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 55–62. [Google Scholar]
- Feichtinger, C.; Habich, J.; Köstler, H.; Hager, G.; Rüde, U.; Wellein, G. A flexible Patch-based lattice Boltzmann parallelization approach for heterogeneous GPU-CPU clusters. Parallel Comput. 2011, 37, 536–549. [Google Scholar] [CrossRef]
- Ye, Y.; Li, K.; Wang, Y.; Deng, T. Parallel computation of Entropic Lattice Boltzmann method on hybrid CPU–GPU accelerated system. Comput. Fluids 2015, 110, 114–121. [Google Scholar] [CrossRef]
- Shimokawabe, T.; Aoki, T.; Takaki, T.; Yamanaka, A.; Nukada, A.; Endo, T.; Maruyama, N.; Matsuoka, S. Peta-scale Phase-Field Simulation for Dendritic Solidification on the TSUBAME 2.0 Supercomputer. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis—SC ’11, Seatle, WA, USA, 12–18 November 2011; pp. 1–11. [Google Scholar]
- Xiong, Q.; Li, B.; Xu, J.; Fang, X.; Wang, X.; Wang, L.; He, X.; Ge, W. Efficient parallel implementation of the lattice Boltzmann method on large clusters of graphic processing units. Chin. Sci. Bull. 2012, 57, 707–715. [Google Scholar] [CrossRef]
- Calore, E.; Gabbana, A.; Kraus, J.; Pellegrini, E.; Schifano, S.F.; Tripiccione, R. Massively parallel lattice–Boltzmann codes on large GPU clusters. Parallel Comput. 2016, 58, 1–24. [Google Scholar] [CrossRef]
- Riesinger, C. Scalable Scientific Computing Applications for GPU-Accelerated Heterogeneous Systems. Ph.D. Thesis, Technische Universität München, München, Germany, May 2017. [Google Scholar]
- Schreiber, M.; Neumann, P.; Zimmer, S.; Bungartz, H.J. Free-Surface Lattice-Boltzmann Simulation on Many-Core Architectures. Procedia Comput. Sci. 2011, 4, 984–993. [Google Scholar] [CrossRef]
- Li, W.; Wei, X.; Kaufman, A. Implementing lattice Boltzmann computation on graphics hardware. Vis. Comput. 2003, 19, 444–456. [Google Scholar] [CrossRef]
- Zhe, F.; Feng, Q.; Kaufman, A.; Yoakum-Stover, S. GPU Cluster for High Performance Computing. In Proceedings of the ACM/IEEE SC2004 Conference, New Orleans, LA, USA, 31 August–4 September 2009; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Janßen, C.; Mierke, D.; Überrück, M.; Gralher, S.; Rung, T. Validation of the GPU-Accelerated CFD Solver ELBE for Free Surface Flow Problems in Civil and Environmental Engineering. Computation 2015, 3, 354–385. [Google Scholar] [CrossRef]
- Debudaj-Grabysz, A.; Rabenseifner, R. Nesting OpenMP in MPI to Implement a Hybrid Communication Method of Parallel Simulated Annealing on a Cluster of SMP Nodes. In Proceedings of the Recent Advances in Parallel Virtual Machine and Message Passing Interface, 12th European PVM/MPI Users’ Group Meeting, Sorrento, Italy, 18–21 September 2005; Di Martino, B., Kranzlmüller, D., Dongarra, J.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 18–27. [Google Scholar]
- Rabenseifner, R.; Hager, G.; Jost, G. Hybrid MPI/OpenMP Parallel Programming on Clusters of Multi-Core SMP Nodes. In Proceedings of the 2009 17th Euromicro International Conference on Parallel, Distributed and Network-based, Weimar, Germany, 18–20 February 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 427–436. [Google Scholar]
- Linxweiler, J. Ein Integrierter Softwareansatz zur Interaktiven Exploration und Steuerung von Strömungssimulationen auf Many-Core-Architekturen. Ph.D. Thesis, Technische Universität Braunschweig, Braunschweig, Germany, June 2011. [Google Scholar]
- Valero-Lara, P.; Jansson, J. LBM-HPC - An Open-Source Tool for Fluid Simulations. Case Study: Unified Parallel C (UPC-PGAS). In Proceedings of the 2015 IEEE International Conference on Cluster Computing, Chicago, IL, USA, 8–11 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 318–321. [Google Scholar]
- Calore, E.; Gabbana, A.; Schifano, S.F.; Tripiccione, R. Optimization of lattice Boltzmann simulations on heterogeneous computers. Int. J. High Perform. Comput. Appl. 2017. [Google Scholar] [CrossRef]
- Valero-Lara, P.; Igual, F.D.; Prieto-Matías, M.; Pinelli, A.; Favier, J. Accelerating fluid–solid simulations (Lattice-Boltzmann & Immersed-Boundary) on heterogeneous architectures. J. Comput. Sci. 2015, 10, 249–261. [Google Scholar]
- Valero-Lara, P.; Jansson, J. Heterogeneous CPU+GPU approaches for mesh refinement over Lattice-Boltzmann simulations. Concurr. Comput. Pract. Exp. 2017, 29, e3919. [Google Scholar] [CrossRef]
- Shimokawabe, T.; Endo, T.; Onodera, N.; Aoki, T. A Stencil Framework to Realize Large-Scale Computations Beyond Device Memory Capacity on GPU Supercomputers. In Proceedings of the 2017 IEEE International Conference on Cluster Computing (CLUSTER), Honolulu, HI, USA, 5–8 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 525–529. [Google Scholar]
- He, X.; Luo, L.S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Wolf-Gladrow, D.A. Lattice-Gas Cellular Automata and Lattice Boltzmann Models—An Introduction; Springer: Berlin, Germany, 2000. [Google Scholar]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann Method for Complex Flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation: for Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method: Principles and Practice; Graduate Texts in Physics; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- He, X.; Luo, L.S. Lattice Boltzmann Model for the Incompressible Navier–Stokes Equation. J. Stat. Phys. 1997, 88, 927–944. [Google Scholar] [CrossRef]
- Ansumali, S.; Karlin, I.V.; Öttinger, H.C. Minimal entropic kinetic models for hydrodynamics. Europhys. Lett. 2003, 63, 798–804. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- D’Humières, D.; Ginzburg, I.; Krafczyk, M.; Lallemand, P.; Luo, L.S. Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef] [PubMed]
- Boghosian, B.M.; Yepez, J.; Coveney, P.V.; Wager, A. Entropic lattice Boltzmann methods. Proc. R. Soc. A Math. Phys. Eng. Sci. 2001, 457, 717–766. [Google Scholar] [CrossRef]
- Geier, M.; Greiner, A.; Korvink, J.G. Cascaded digital lattice Boltzmann automata for high Reynolds number flow. Phys. Rev. E 2006, 73, 066705. [Google Scholar] [CrossRef] [PubMed]
- Wolfe, M. OpenACC for Multicore CPUs; PGI, NVIDIA Corporation: Beaverton, OR, USA, 2015; p. 6. [Google Scholar]
- Bailey, D.H. Twelve ways to fool the masses when giving performance results on parallel computers. In Supercomputing Review; MIT Press: Cambridge, MA, USA, 1991; pp. 54–55. [Google Scholar]
- Höfler, T.; Belli, R. Scientific benchmarking of parallel computing systems. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis—SC ’15, Austin, TX, USA, 15–20 November 2015; ACM Press: New York, NY, USA, 2015; pp. 1–12. [Google Scholar]
- Valero-Lara, P. Reducing memory requirements for large size LBM simulations on GPUs. Concurr. Comput. Pract. Exp. 2017, 29, e4221. [Google Scholar] [CrossRef]
- Wittmann, M.; Zeiser, T.; Hager, G.; Wellein, G. Comparison of different propagation steps for lattice Boltzmann methods. Comput. Math. Appl. 2013, 65, 924–935. [Google Scholar] [CrossRef]
- Neumann, P.; Bungartz, H.J.; Mehl, M.; Neckel, T.; Weinzierl, T. A Coupled Approach for Fluid Dynamic Problems Using the PDE Framework Peano. Commun. Comput. Phys. 2012, 12, 65–84. [Google Scholar] [CrossRef]
- Geier, M.; Schönherr, M. Esoteric Twist: An Efficient in-Place Streaming Algorithmus for the Lattice Boltzmann Method on Massively Parallel Hardware. Computation 2017, 5. [Google Scholar] [CrossRef]
- Lam, M.D.; Rothberg, E.E.; Wolf, M.E. The cache performance and optimizations of blocked algorithms. In Proceedings of the Fourth International Conference on Architectural Support for Programming Languages and Operating Systems—ASPLOS-IV, Santa Clara, CA, USA, 8–11 April 1991; ACM Press: New York, NY, USA, 1991; pp. 63–74. [Google Scholar]
- Ayguadé, E.; Copty, N.; Duran, A.; Hoeflinger, J.; Lin, Y.; Massaioli, F.; Su, E.; Unnikrishnan, P.; Zhang, G. A Proposal for Task Parallelism in OpenMP. In A Practical Programming Model for the Multi-Core Era; Chapman, B., Zheng, W., Gao, G.R., Sato, M., Ayguadé, E., Wang, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–12. [Google Scholar]
- Schreiber, M. GPU Based Simulation and Visualization of Fluids with Free Surfaces. Diploma Thesis, Technische Universität München, München, Germany, June 2010. [Google Scholar]
- NVIDIA Corporation. Tuning CUDA Applications for Kepler. Available online: http://docs.nvidia.com/cuda/kepler-tuning-guide/ (accessed on 16 October 2017).
- NVIDIA Corporation. Achieved Occupancy. Available online: https://docs.nvidia.com/gameworks/content/developertools/desktop/analysis/report/cudaexperiments/kernellevel/achievedoccupancy.htm (accessed on 16 October 2017).
- Bakhtiari, A. MPI Parallelization of GPU-Based Lattice Boltzmann Simulations. Master’s Thesis, Technische Universität München, München, Germany, October 2013. [Google Scholar]
- Bozeman, J.D.; Dalton, C. Numerical study of viscous flow in a cavity. J. Comput. Phys. 1973, 12, 348–363. [Google Scholar] [CrossRef]
- Ghia, U.; Ghia, K.N.; Shin, C.T. High-Re solutions for incompressible flow using the Navier–Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Intel Corporation. Intel Xeon Processor E5-2690v3. Available online: https://ark.intel.com/products/81713/ (accessed on 16 October 2017).
- Global Scientific Information and Computing Center. TSUBAME2.5 Hardware Software Specifications; Technical Report; Tokyo Institute of Technology: Tokyo, Japan, 2013. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).