Multiresolution Modeling of Semidilute Polymer Solutions: Coarse-Graining Using Wavelet-Accelerated Monte Carlo
Abstract
:1. Introduction
2. Methods
2.1. The WAMC Method
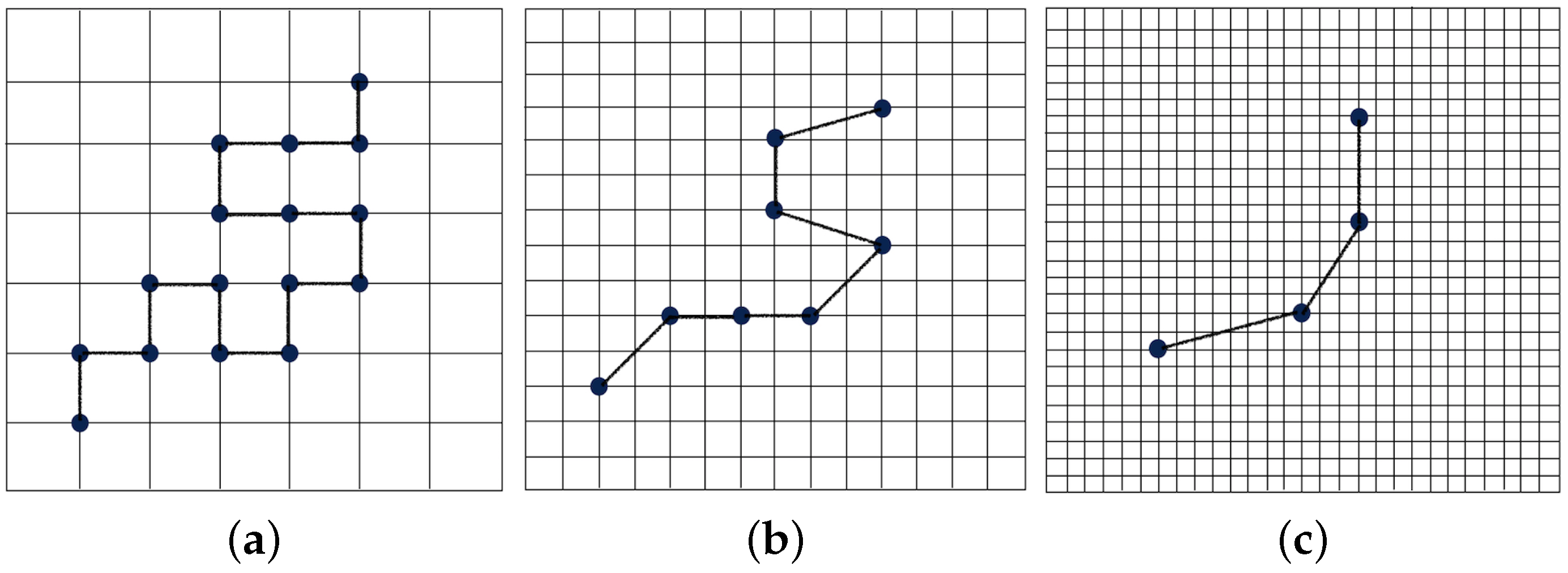
2.1.1. Wavelet Transform Representation of a Polymer Chain
2.1.2. Wavelet-Accelerated Monte Carlo Algorithm
- The WAMC algorithm starts with a full-atomistic simulation of a smaller segment of the initial chain with beads. A simulation of a much shorter segment of the fully-atomistic chain helps cut down on the computational cost. Thus, each bead still has an effective size , where the subscript ”1” indicates the simulation stage.
- The subsystem is sampled using the pivot algorithm [28].
- The wavelet transform is applied times to obtain the positions of each coarse-grained bead at regular intervals of steps. The effective size of the coarse-grained bead corresponds to beads in the fully-atomistic representation. The distribution representing interactions between these “virtual” coarse-grained beads, which are also referred to as “superatoms”, is calculated.
- The probability distributions obtained from the the first stage are then used in the second stage of the (real) simulation that consists of a chain of length beads (). The effective size of the coarse-grained bead is , and the total effective chain length is .
- If desired, further coarse-graining of the system occurs by transferring the probability distributions obtained from the current stage to the next stage of resolution as discussed above.
2.1.3. Translate-Jiggle Algorithm
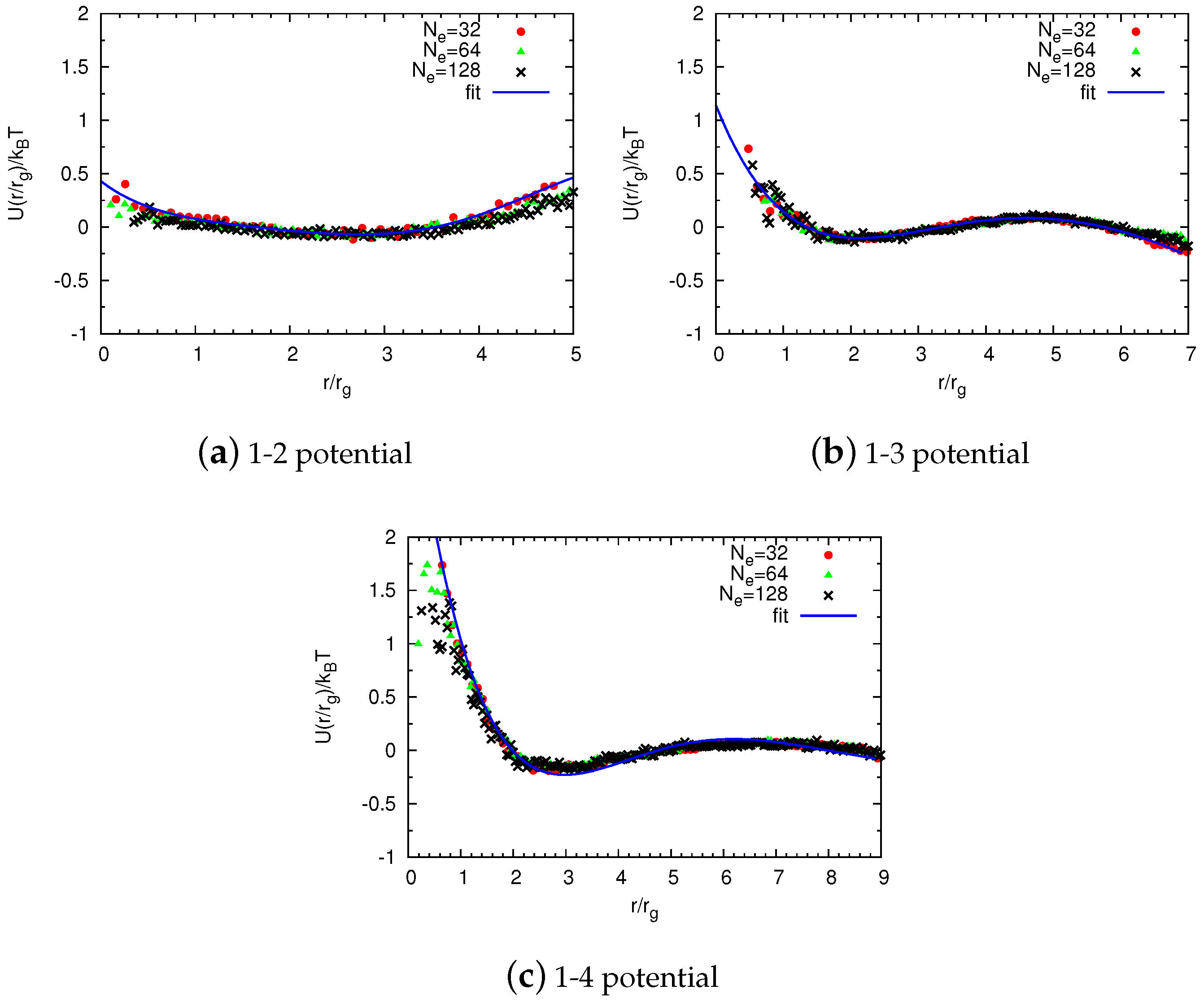
2.2. Potentials in a Coarse-Grained System
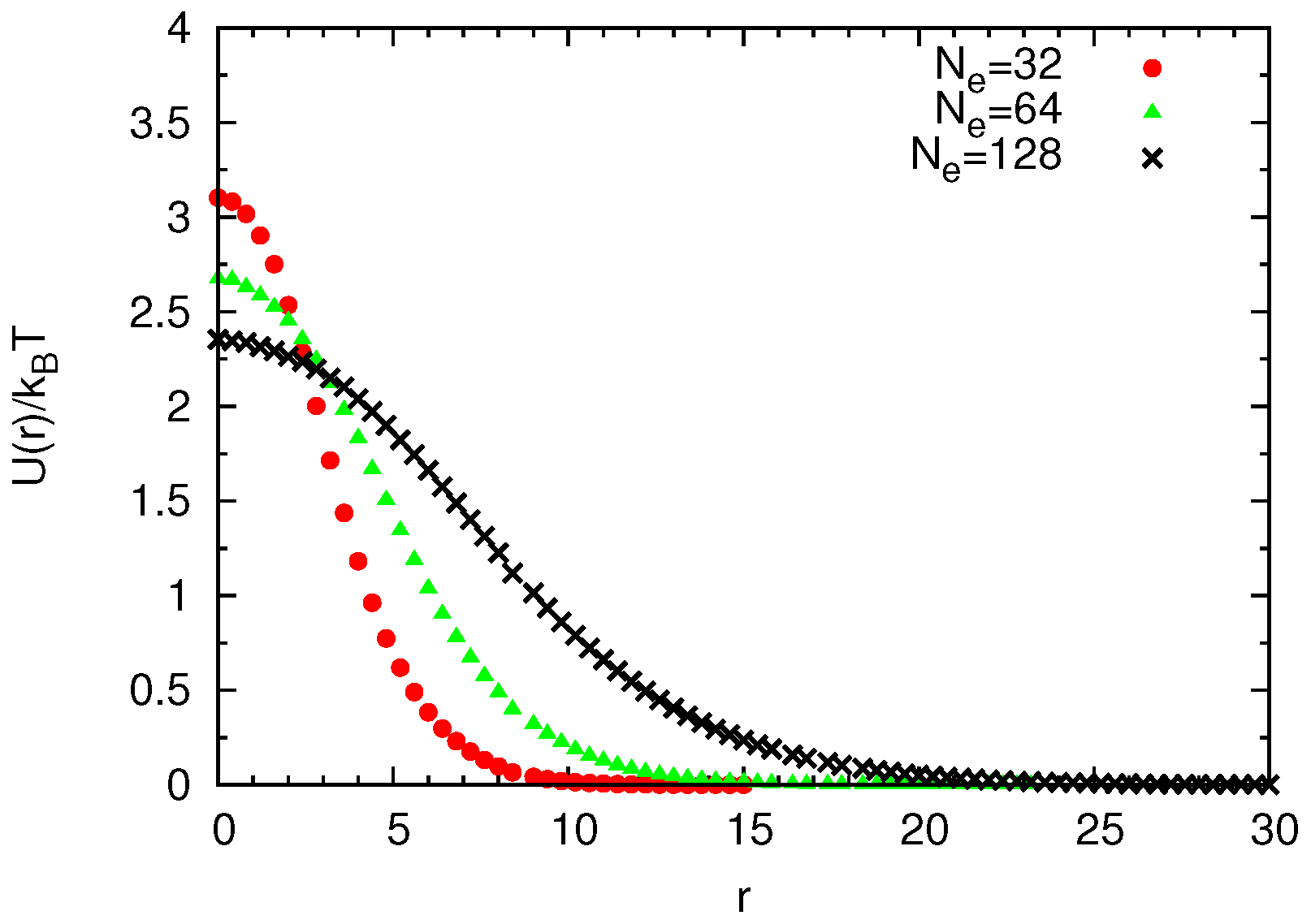
2.2.1. Non-Bonded Potentials
Construction of Coarse-Grained Force Fields
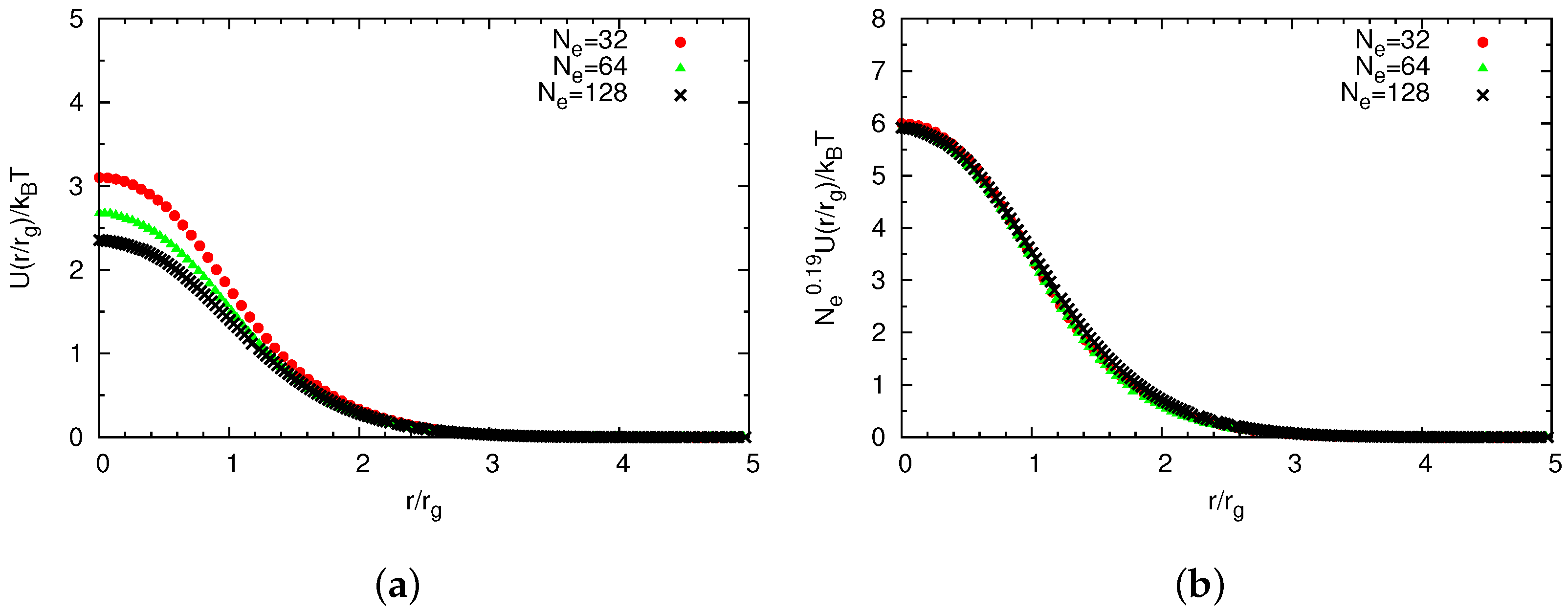
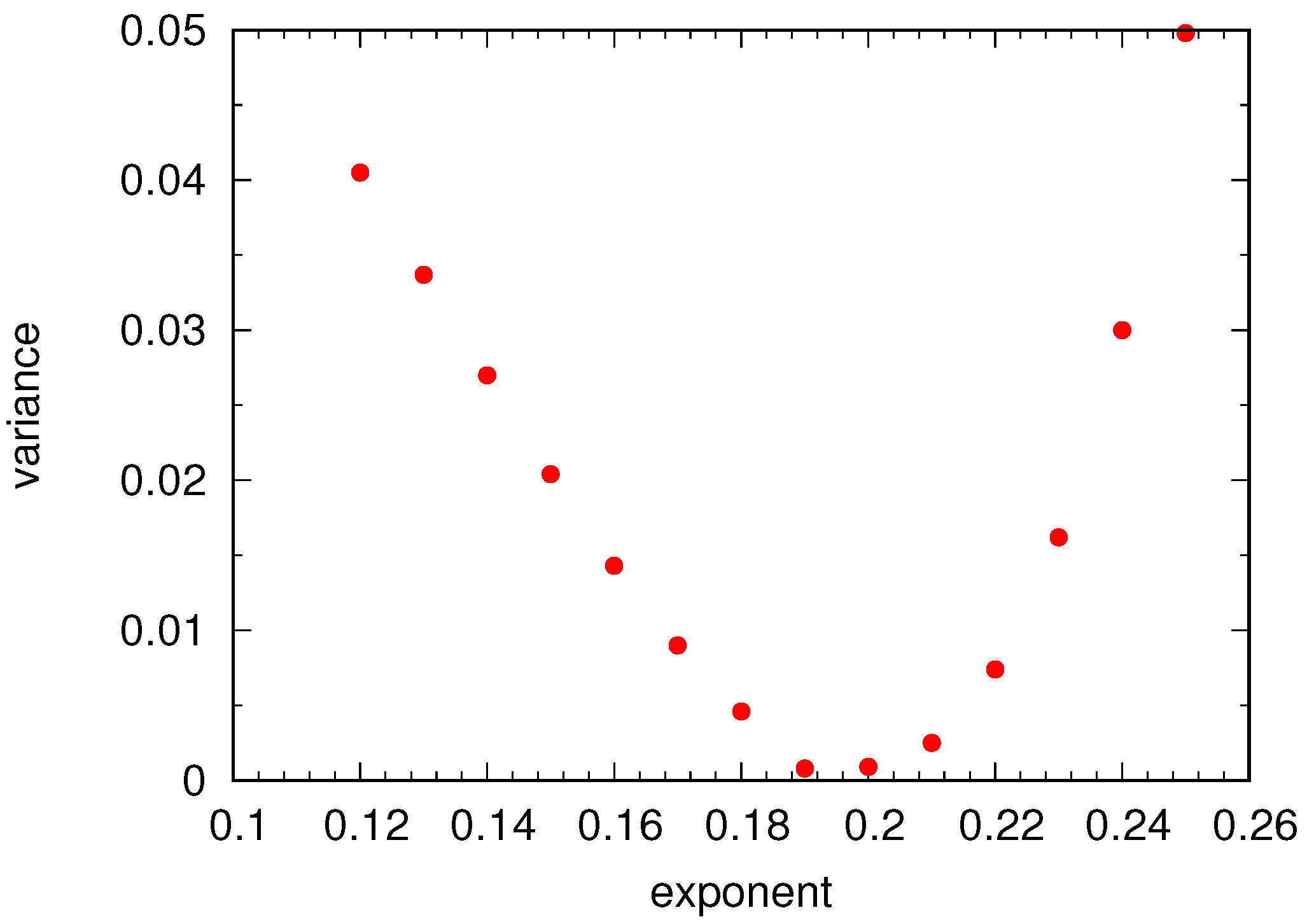
Universal Scaling
2.2.2. Bonded Potentials
Reverse Monte Carlo Simulations
Universal Scaling
3. Extension to Semidilute Systems
3.1. Semidilute Solutions
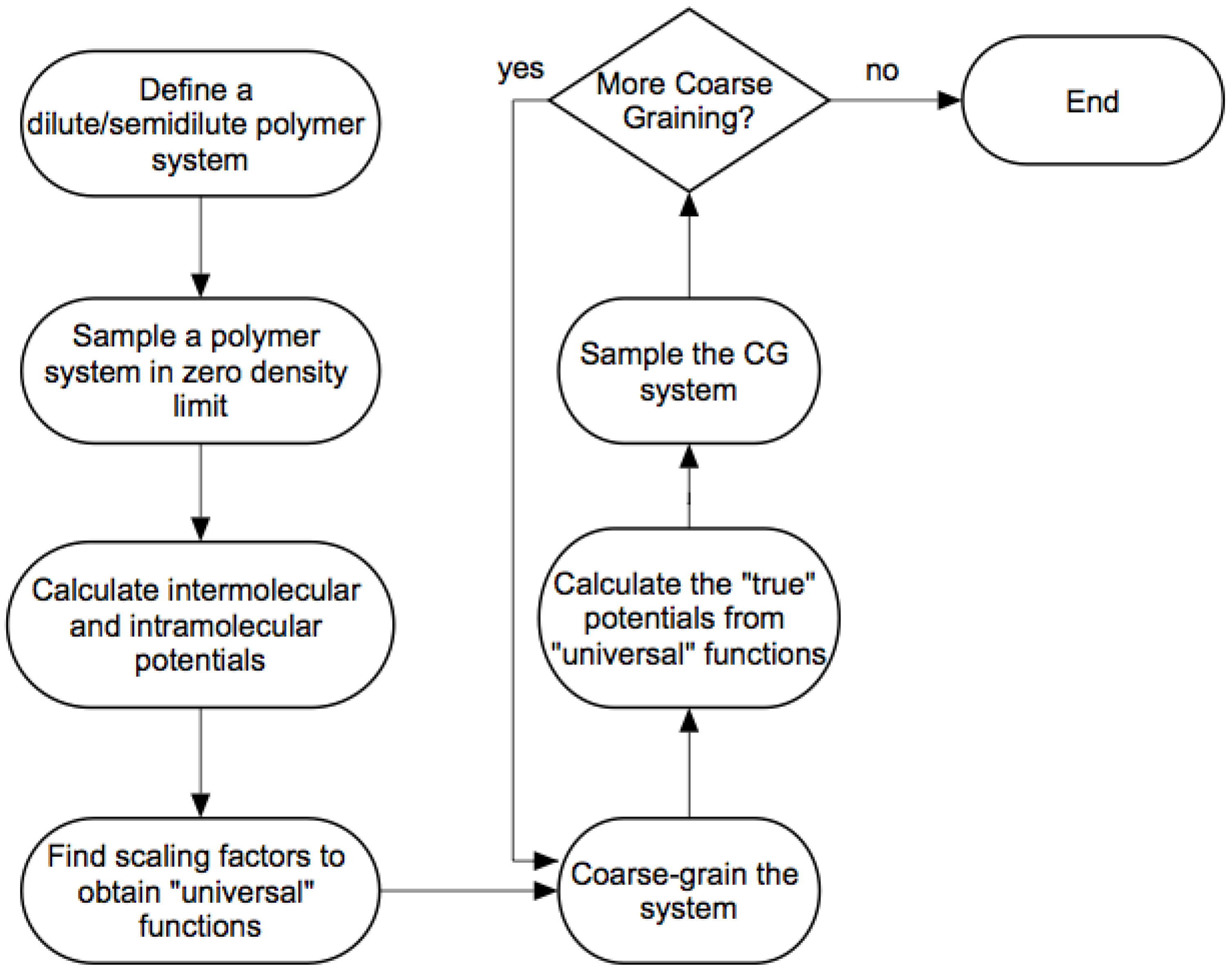
3.2. Modified WAMC Algorithm for Semidilute Solutions
- We define a dilute/semi-dilute polymer system containing M polymer chains, where each polymer chain consists of N beads.
- The first stage is an atomistic simulation in the limit of zero density to calculate intermolecular and intramolecular potentials discussed in the previous sections. The number of atomistic beads represented by a coarse-grained bead is in the first stage, by definition.
- If the level of coarse-graining is sufficient, then we can stop after this coarse-grained simulation. Otherwise, we apply the wavelet transform (Equation (2)) again times to obtain coarse-grained beads with an effective size of .
4. Results and Discussion
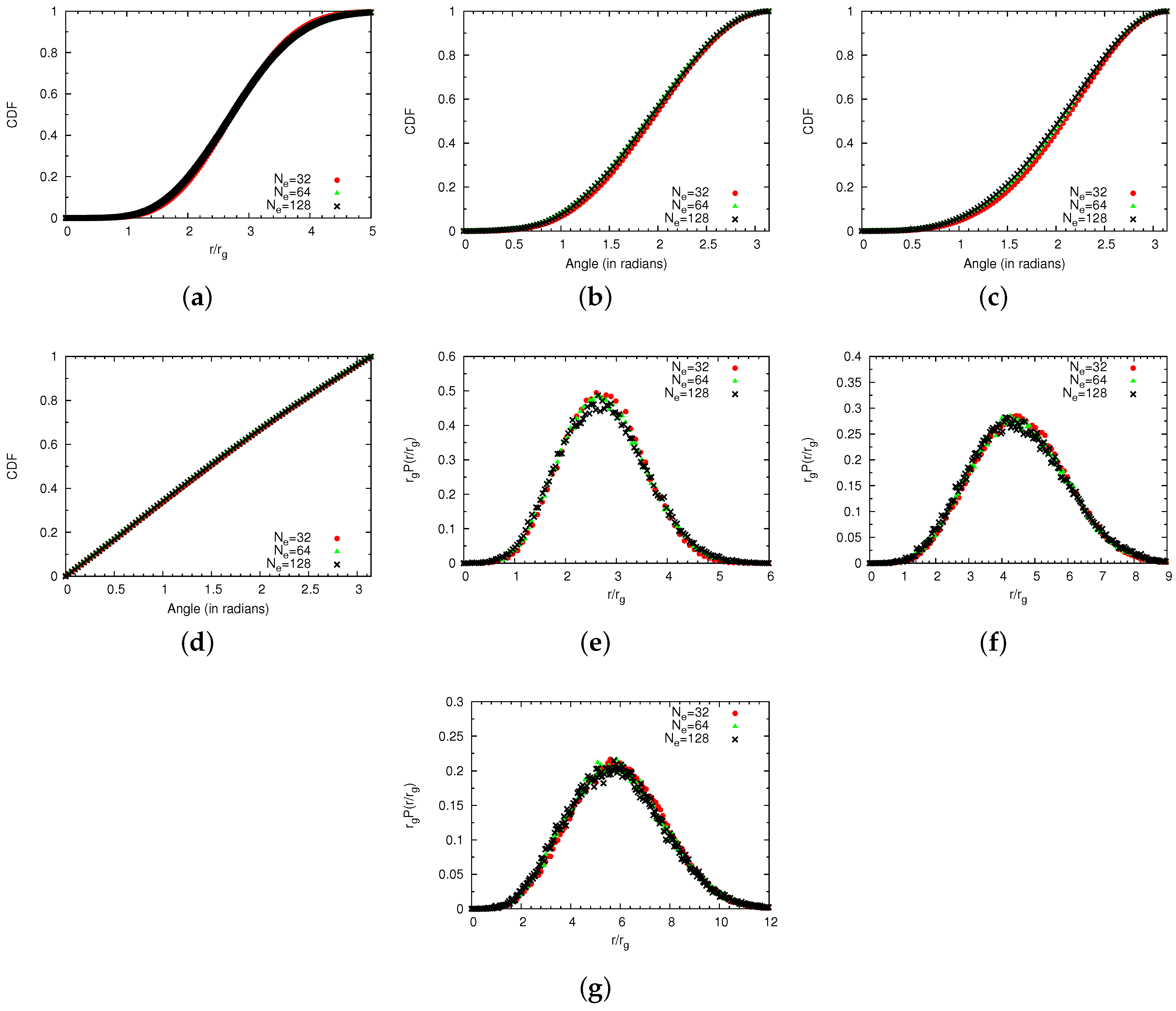
4.1. Single Chains
4.1.1. Technical Details
4.1.2. Comparison of Coarse-Grained and Atomistic Results
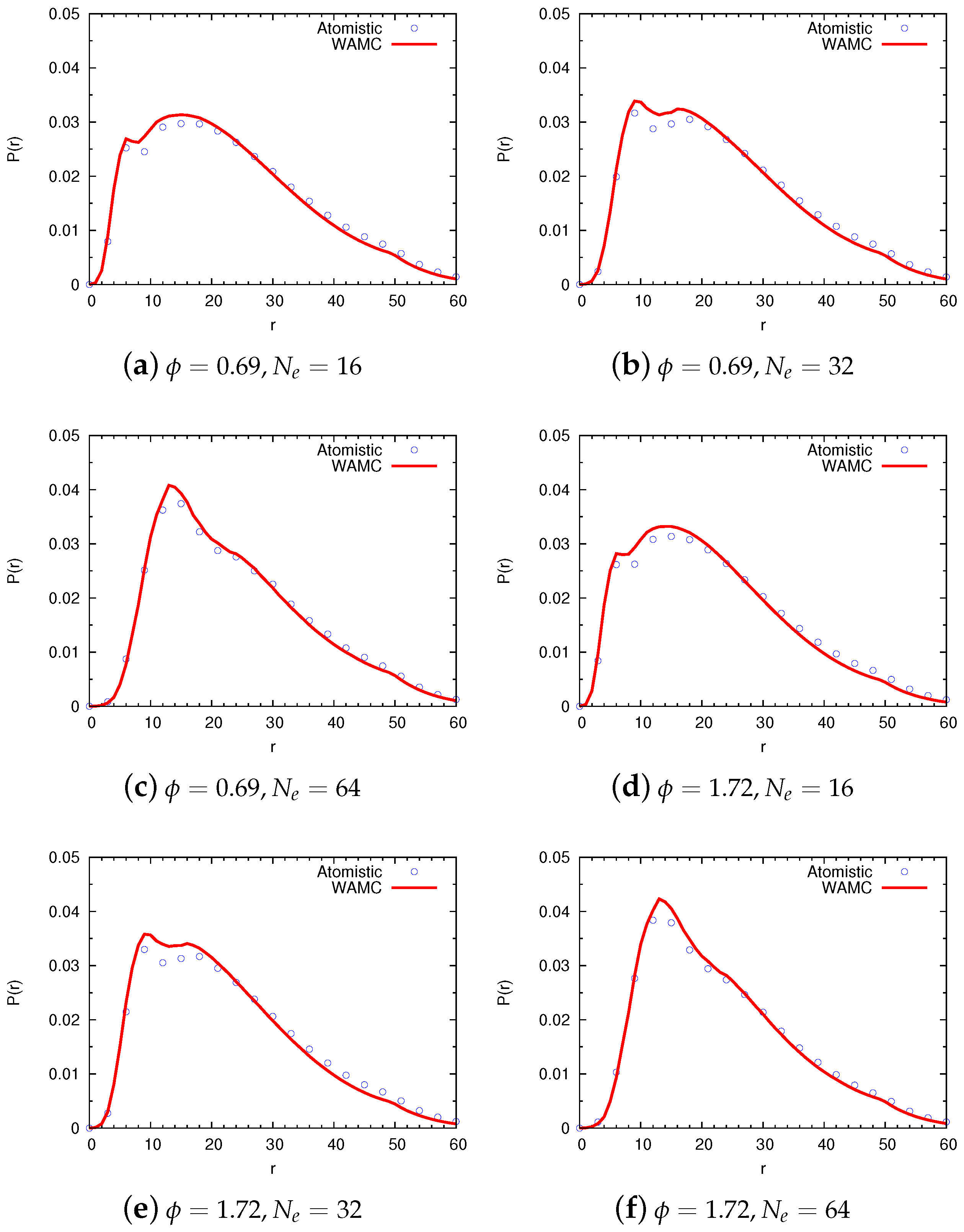
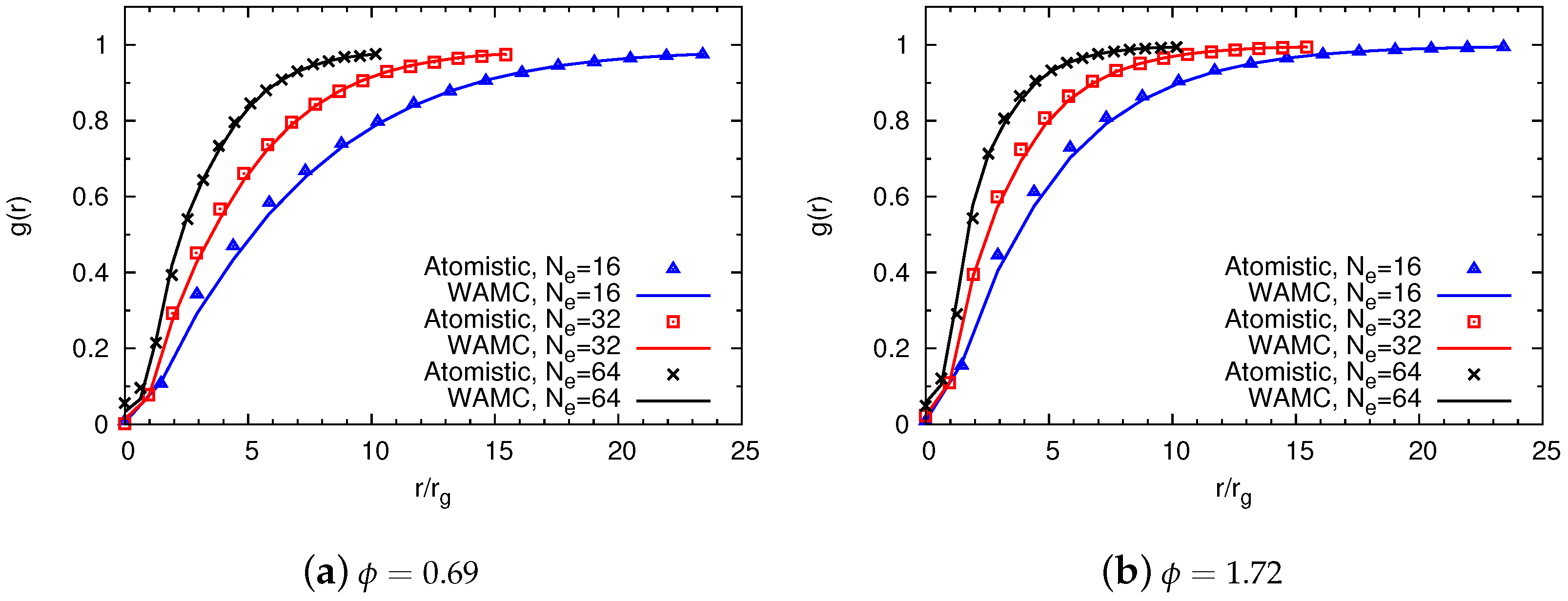
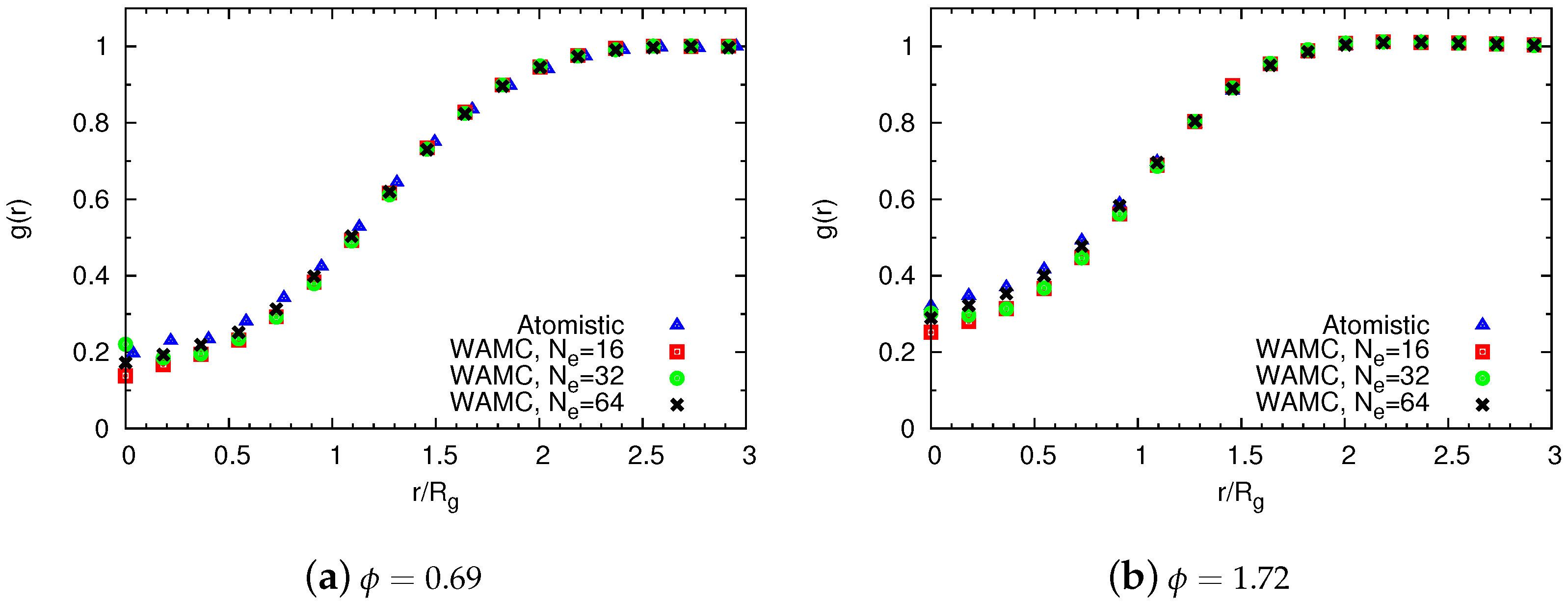
4.2. Semidilute Solutions
4.2.1. Technical Details
4.2.2. Comparison of Coarse-Grained and Atomistic Models
5. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Validity of Using Zero-Density Potentials for the Intermolecular Potential
References
- Akkermans, R.; Briels, W. Coarse-grained interactions in polymer melts: A variational approach. J. Chem. Phys. 2001, 115, 6210–6219. [Google Scholar] [CrossRef]
- Baschnagel, J.; Binder, K.; Doruker, P.; Gusev, A.; Hahn, O.; Kremer, K.; Mallice, W.; Muller-Plathe, F.; Murat, M.; Paul, W.; et al. Bridging the gap between atomistic and coarse-grained models of polymers: Status and perspectives. Adv. Polym. Sci. 2000, 152, 41–156. [Google Scholar]
- Lyubarstev, A.; Karttunen, M.; Vattulainen, I.; Laaksonen, A. On coarse-graining by the inverse Monte Carlo method: Dissipative particle dynamics simulations made to a precise tool in soft matter modeling. Soft Matter 2003, 1, 121–137. [Google Scholar]
- Tan, R.; Petrov, A.; Harvey, S. YUP: A molecular simulation program for coarse-grained and multi-scaled models. J. Chem. Theory Comput. 2006, 2, 529–540. [Google Scholar] [CrossRef] [PubMed]
- Clementi, C. Coarse-grained models of protein folding: Toy models or predictive tools? Curr. Opin. Struct. Biol. 2008, 18, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Ashbaugh, H.; Patel, H.; Kumar, S.; Garde, S. Mesoscale model of polymer melt structure: Selt consistent mapping of molecule correlations to coarse-grained potentials. J. Chem. Phys. 2005, 122. [Google Scholar] [CrossRef] [PubMed]
- Fukunaga, H.; Takimoto, J.; Doi, M. A coarse-graining procedure for flexible polymer chains with bonded and nonbonded interactions. J. Chem. Phys. 2002, 116, 8183–8190. [Google Scholar] [CrossRef]
- Harmandaris, V.; Adhikari, N.; Van der Vegt, N.; Kremer, K. Heirarchical modeling of polystyrene: From atomistic to coarse-grained simualtions. Macromolecules 2006, 39, 6708–6719. [Google Scholar] [CrossRef]
- Kamio, K.; Moorthi, K.; Theodorou, D. Coarse grained end bridging Monte Carlo simulations of poly(ethylene terephthalate) melt. Macromolecules 2007, 49, 710–722. [Google Scholar] [CrossRef]
- Pandiyan, S.; Parandekar, P.V.; Prakash, O.; Tsotsis, T.K.; Basu, S. Systematic coarse graining of a high-performance polyimide. Macromol. Theory Simul. 2015, 24, 513–520. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Naome, A.; Vercauteren, D.P.; Laaksonen, A. Systematic hierarchical coarse-graining with the inverse Monte Carlo method. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Wang, Q. Systematic and simulation-free coarse graining of homopolymer melts: A relative-entropy-based study. Soft Matter 2015, 11, 7109–7118. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Wang, Q. Systematic and simulation-free coarse graining of homopolymer melts: A structure-based study. J. Chem. Phys. 2015, 142. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Moreira, L.A.; Stuehn, T.; Daoulas, K.C.; Kremer, K. Equilibration of high molecular weight polymer melts: A hierarchical strategy. ACS Macro Lett. 2014, 3, 198–203. [Google Scholar] [CrossRef]
- Ismail, A.E.; Rutledge, G.C.; Stephanopoulos, G. Topological coarse-graining of polymer chains using wavelet-accelerated Monte Carlo. I. Freely jointed chains. J. Chem. Phys. 2005, 122. [Google Scholar] [CrossRef] [PubMed]
- Ismail, A.E.; Rutledge, G.C.; Stephanopoulos, G. Topological coarse-graining of polymer chains using wavelet-accelerated Monte Carlo. II. Self-avoiding chains. J. Chem. Phys. 2005, 122. [Google Scholar] [CrossRef] [PubMed]
- Ismail, A.E.; Rutledge, G.C.; Stephanopoulos, G. Multiresolution analysis in statistical mechanics. I. Using wavelets to calculate thermodynamic properties. J. Chem. Phys. 2003, 118. [Google Scholar] [CrossRef]
- Ismail, A.E.; Stephanopoulos, G.; Rutledge, G.C. Multiresolution analysis in statistical mechanics. II. The wavelet transform as a basis for Monte Carlo simulations on lattices. J. Chem. Phys. 2003, 118. [Google Scholar] [CrossRef]
- Rinderspacher, B.; Bardhan, J.; Ismail, A. Theory of wavelet-based coarse-graining hierarchies for molecular dynamics. Phys. Rev. E 2017, 96. [Google Scholar] [CrossRef]
- Chen, J.; Teng, H.; Nakano, A. Wavelet-based multi-scale coarse graining approach for DNA molecules. Finite Elem. Anal. Des. 2007, 43, 346–360. [Google Scholar] [CrossRef]
- Maiolo, M.; Vancheri, A.; Krause, R.; Danani, A. Wavelets as basis functions to represent the coarse-graining potential in multiscale coarse graining approach. J. Comput. Phys. 2015, 300, 592–604. [Google Scholar] [CrossRef]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Adaptive resolution molecular-dynamics simulation: Changing the degrees of freedom on the fly. J. Chem. Phys. 2005, 123. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Hartmann, C.; Schütte, C.; Delle Site, L. Grand-canonical-like molecular-dynamics simulations by using an adaptive-resolution technique. Phys. Rev. X 2013, 3. [Google Scholar] [CrossRef]
- Daubechies, I. Ten lectures on wavelets. In CBMS-NSF Regional Conference Series in Applied Mathematics: Ten Lectures on Wavelets No. 61 by Ingrid Daubechies; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Strang, G.; Nguyen, T. Wavelets and Filter Banks; Wellesley-Cambridge Press: Wellesley, MA, USA, 1996. [Google Scholar]
- Haar, A. Zur Theorie der orthogonalen Funktionensysteme, (Erste Mitteilung). Math. Ann. 1910, 69, 331–369. [Google Scholar] [CrossRef]
- Muller-Plathe, F. Coarse-graining in polymer simulation: From the atomistic to the mesoscopic scale and back. Chem. Phys. Chem. 2002, 3, 754–769. [Google Scholar] [CrossRef]
- Lal, M. ‘Monte Carlo’ computer simulations of chain molecules. Mol. Phys. 1969, 17, 57–64. [Google Scholar] [CrossRef]
- Dickman, R.; Hall, C. Equation of state for chain molecules: Continuous space analog of Flory theory. J. Chem. Phys. 1986, 85. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Peter, C.; Kremer, K. Multiscale simulation of soft matter systems-from the atomistic to the coarse-grained level and back. Soft Matter 2009, 5, 4357–4366. [Google Scholar] [CrossRef]
- Bolhuis, P.; Louis, A.; Hansen, J.; Meijer, E. Accurate effective pair potentials for polymer solutions. J. Chem. Phys. 2001, 114, 4296–4311. [Google Scholar] [CrossRef]
- Bolhuis, P.; Louis, A.; Hansen, J. Many-body interactions and correlations in coarse-grained descriptions of polymer solutions. Phys. Rev. E 2001, 64. [Google Scholar] [CrossRef] [PubMed]
- Dautenhahn, J.; Hall, C. Monte Carlo simulation of off-lattice polymer chains: Effective pair potentials in dilute solution. Macromolecules 1994, 27, 5399–5412. [Google Scholar] [CrossRef]
- Kremer, K.; Binder, K. Monte Carlo simulation of lattice models for macromolecules. Comput. Phys. Rep. 1988, 7, 259–310. [Google Scholar] [CrossRef]
- Lyubartsev, A.; Laaksonen, A. Calculation of effective interaction potentials from radial distribution functions: A reverse Monte Carlo approach. Phys. Rev. E 1995, 52, 3730–3737. [Google Scholar] [CrossRef]
- D’Adamo, G.; Pelissetto, A.; Pierleoni, C. Coarse-grained strategies in polymer solutions. Soft Matter 2012, 8, 5151–5167. [Google Scholar] [CrossRef]
- D’Adamo, G.; Pelissetto, A.; Pierleoni, C. Consistent and transferable coarse-grained model for semidilute polymer solutions in good solvent. J. Chem. Phys. 2012, 137. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Vacatello, M.; Yoon, D. Offlattice Monte Carlo simulations of polymer melts confined between two plates. J. Chem. Phys. 1988, 89. [Google Scholar] [CrossRef]
- Moore, T.; Iacovella, C.; McCabe, C. Derivation of coarse-grained potentials via multistate iterative Boltzmann inversion. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef] [PubMed]
- Hsu, D.; Xia, W.; Arturo, S.; Keten, S. Systematic method for thermomechanically consistent coarse-graining: A universal model for methacrylate-based polymers. J. Chem. Theory Comput. 2014, 10, 2514–2527. [Google Scholar] [CrossRef] [PubMed]
- Hsu, D.; Xia, W.; Arturo, S.; Keten, S. Thermomechanically consistent and temperature transferable coarse-graining of atactic polystyrene. Macromolecules 2015, 48, 3057–3068. [Google Scholar] [CrossRef]

| N | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 256 | 177 | 184 | 165 | 143 | 142 | 139 | 133 | 132 | 125 |
| 512 | 410 | 422 | 378 | 322 | 325 | 316 | 298 | 299 | 283 |
| 1024 | 957 | 990 | 916 | 755 | 759 | 716 | 659 | 697 | 641 |
| 2048 | 2198 | 2283 | 2130 | 1732 | 1737 | 1657 | 1493 | 1591 | 1481 |
| 4096 | 5052 | 5151 | 4895 | 3973 | 3932 | 3772 | 3583 | 3618 | 3373 |
| 8192 | 11,767 | 11,858 | 11,243 | 9006 | 8935 | 8548 | 7864 | 8070 | 7613 |
| 16,384 | 27,184 | 27,240 | 26,190 | 20,662 | 20,468 | 19,500 | 17,818 | 18,282 | 17,249 |
| 32,768 | 62,799 | 62,582 | 61,009 | 47,404 | 46,893 | 44,490 | 40,370 | 41,424 | 39,083 |
| Atomistic | CG, | CG, | |
|---|---|---|---|
| 0.0 | 0.604 | 0.601 | 0.610 |
| −0.10 | 0.599 | 0.598 | 0.595 |
| −0.15 | 0.590 | 0.595 | 0.593 |
| N | L | M | |
|---|---|---|---|
| 0.69 | 512 | 100 | 20 |
| 1.72 | 512 | 100 | 50 |
| Model | ||||
|---|---|---|---|---|
| 2–5 | Atomistic | CG, | CG, | CG, |
| 0.0 | 20.23 | 20.08 | 19.87 | 19.57 |
| 0.69 | 17.12 | 16.98 | 16.75 | 16.59 |
| 1.72 | 16.61 | 16.24 | 16.04 | 15.98 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agarwal, A.; Rabideau, B.D.; Ismail, A.E. Multiresolution Modeling of Semidilute Polymer Solutions: Coarse-Graining Using Wavelet-Accelerated Monte Carlo. Computation 2017, 5, 44. https://doi.org/10.3390/computation5040044
Agarwal A, Rabideau BD, Ismail AE. Multiresolution Modeling of Semidilute Polymer Solutions: Coarse-Graining Using Wavelet-Accelerated Monte Carlo. Computation. 2017; 5(4):44. https://doi.org/10.3390/computation5040044
Chicago/Turabian StyleAgarwal, Animesh, Brooks D. Rabideau, and Ahmed E. Ismail. 2017. "Multiresolution Modeling of Semidilute Polymer Solutions: Coarse-Graining Using Wavelet-Accelerated Monte Carlo" Computation 5, no. 4: 44. https://doi.org/10.3390/computation5040044
APA StyleAgarwal, A., Rabideau, B. D., & Ismail, A. E. (2017). Multiresolution Modeling of Semidilute Polymer Solutions: Coarse-Graining Using Wavelet-Accelerated Monte Carlo. Computation, 5(4), 44. https://doi.org/10.3390/computation5040044





