A Diagonally Updated Limited-Memory Quasi-Newton Method for the Weighted Density Approximation
Abstract
:1. Introduction
2. Methods
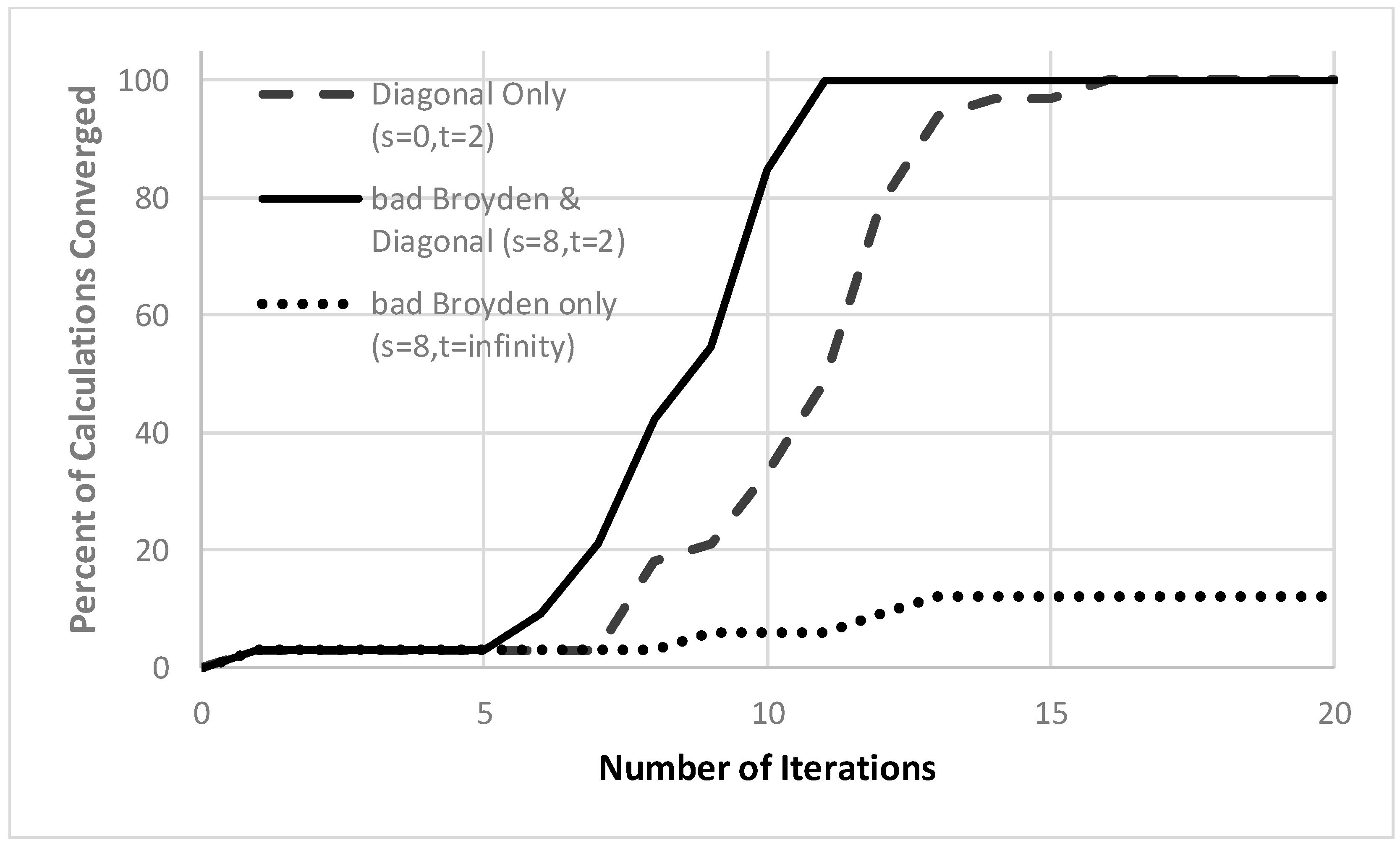
3. Results
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cohen, A.J.; Mori-Sanchez, P.; Yang, W.T. Challenges for density functional theory. Chem. Rev. 2012, 112, 289–320. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Tao, J.M.; Staroverov, V.N.; Scuseria, G.E.; Csonka, G.I. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. J. Chem. Phys. 2005, 123, 062201. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.J.; Mori-Sanchez, P.; Yang, W.T. Insights into current limitations of density functional theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford UP: New York, NY, USA, 1989. [Google Scholar]
- Savin, A. On degeneracy, near-degeneracy, and density functional theory. In Recent Developments and Applications of Modern Density Functional Theory; Seminario, J.M., Ed.; Elsevier: New York, NY, USA, 1996; p. 327. [Google Scholar]
- Gori-Giorgi, P.; Savin, A. Degeneracy and size consistency in electronic density functional theory. In Ab Initio Simulation of Crystalline Solids: History and Prospects—Contributions in Honor of Cesare Pisani; Dovesi, R., Orlando, R., Roetti, C., Eds.; IOP: Bristol, UK, 2008; Volume 117, p. 12017. [Google Scholar]
- Savin, A. Is size-consistency possible with density functional approximations? Chem. Phys. 2009, 356, 91–97. [Google Scholar] [CrossRef]
- Ayers, P.W.; Levy, M. Tight constraints on the exchange-correlation potentials of degenerate states. J. Chem. Phys. 2014, 140, 18a537. [Google Scholar] [CrossRef] [PubMed]
- Levy, M.; Anderson, J.S.M.; Heidar-Zadeh, F.H.; Ayers, P.W. Kinetic and electron-electron energies for convex sums of ground state densities with degeneracies and fractional electron number. J. Chem. Phys. 2014, 140, 18a538. [Google Scholar] [CrossRef] [PubMed]
- Merkle, R.; Savin, A.; Preuss, H. Singly ionized 1st-row dimers and hydrides calculated with the fully numerical density-functional program numol. J. Chem. Phys. 1992, 97, 9216–9221. [Google Scholar] [CrossRef]
- Cuevas-Saavedra, R.; Chakraborty, D.; Rabi, S.; Cardenas, C.; Ayers, P.W. Symmetric non local weighted density approximations from the exchange-correlation hole of the uniform electron gas. J. Chem. Theory Comp. 2012, 8, 4081–4093. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P. What do the kohn-sham orbital energies mean? How do atoms dissociate? NATO ASI Ser. 1985, 123, 265–308. [Google Scholar]
- Mori-Sanchez, P.; Cohen, A.J.; Yang, W.T. Discontinuous nature of the exchange-correlation functional in strongly correlated systems. Phys. Rev. Lett. 2009, 102, 066403. [Google Scholar] [CrossRef] [PubMed]
- Chacon, E.; Tarazona, P. Self-consistent weighted-density approximation for the electron-gas 1. Bulk properties. Phys. Rev. B 1988, 37, 4013–4019. [Google Scholar] [CrossRef]
- Alonso, J.A.; Girifalco, L.A. Nonlocal approximation to exchange energy of non-homogenous electron-gas. Solid State Commun. 1977, 24, 135–138. [Google Scholar] [CrossRef]
- Alonso, J.A.; Girifalco, L.A. Nonlocal approximation to exchange potential and kinetic-energy of an inhomogeneous electron-gas. Phys. Rev. B 1978, 17, 3735–3743. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Jonson, M.; Lundqvist, B.I. Exchange and correlation in inhomogeneous electron-systems. Solid State Commun. 1977, 24, 765–768. [Google Scholar] [CrossRef]
- Cuevas-Saavedra, R.; Chakraborty, D.; Ayers, P.W. Symmetric two-point weighted density approximation for exchange energies. Phys. Rev. A 2012, 85. [Google Scholar] [CrossRef]
- Cuevas-Saavedra, R.; Thompson, D.C.; Ayers, P.W. Alternative ornstein-zernike models from the homogeneous electron liquid for density functional theory calculations. Int. J. Quantum Chem. 2016, 116, 852–861. [Google Scholar] [CrossRef]
- Cuevas-Saavedra, R.; Ayers, P.W. Using the spin-resolved electronic direct correlation function to estimate the correlation energy of the spin-polarized uniform electron gas. J. Phys. Chem. Solids 2012, 73, 670–673. [Google Scholar] [CrossRef]
- Ayers, P.W.; Cuevas-Saavedra, R.; Chakraborty, D. A variational principle for the electron density using the exchange hole & its implications for n-representability. Phys. Lett. A 2012, 376, 839–844. [Google Scholar]
- Cuevas-Saavedra, R.; Ayers, P.W. Addressing the coulomb potential singularity in exchange-correlation energy integrals with one-electron and two-electron basis sets. Chem. Phys. Lett. 2012, 539, 163–167. [Google Scholar] [CrossRef]
- Antaya, H.; Zhou, Y.X.; Ernzerhof, M. Approximating the exchange energy through the nonempirical exchange-factor approach. Phys. Rev. A 2014, 90, 032513. [Google Scholar] [CrossRef]
- Patrick, C.E.; Thygesen, K.S. Adiabatic-connection fluctuation-dissipation dft for the structural properties of solids-the renormalized alda and electron gas kernels. J. Chem. Phys. 2015, 143, 102802. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.X.; Bahmann, H.; Ernzerhof, M. Construction of exchange-correlation functionals through interpolation between the non-interacting and the strong-correlation limit. J. Chem. Phys. 2015, 143, 124103. [Google Scholar] [CrossRef] [PubMed]
- Precechtelova, J.P.; Bahmann, H.; Kaupp, M.; Ernzerhof, M. Design of exchange-correlation functionals through the correlation factor approach. J. Chem. Phys. 2015, 143, 144102. [Google Scholar]
- GarciaGonzalez, P.; Alvarellos, J.E.; Chacon, E. Kinetic-energy density functional: Atoms and shell structure. Phys. Rev. A 1996, 54, 1897–1905. [Google Scholar] [CrossRef]
- Garcia-Aldea, D.; Alvarellos, J.E. Kinetic-energy density functionals with nonlocal terms with the structure of the thomas-fermi functional. Phys. Rev. A 2007, 76, 052504. [Google Scholar] [CrossRef]
- Garcia-Aldea, D.; Alvarellos, J.E. Approach to kinetic energy density functionals: Nonlocal terms with the structure of the von weizsacker functional. Phys. Rev. A 2008, 77, 022502. [Google Scholar] [CrossRef]
- Garcia-Aldea, D.; Alvarellos, J.E. Fully nonlocal kinetic energy density functionals: A proposal and general assessment for atomic systems. J. Chem. Phys. 2008, 129, 074103. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Gonzalez, P.; Alvarellos, J.E.; Chacon, E. Kinetic-energy density functionals based on the homogeneous response function applied to one-dimensional fermion systems. Phys. Rev. A 1998, 57, 4192–4200. [Google Scholar] [CrossRef]
- Wang, Y.A.; Govind, N.; Carter, E.A. Orbital-free kinetic-energy density functionals with a density-dependent kernel. Phys. Rev. B 1999, 60, 16350–16358. [Google Scholar] [CrossRef]
- Wang, Y.A.; Carter, E.A.; Schwartz, S.D. Orbital-free kinetic-energy density functional theory. In Theoretical Methods in Condensed Phase Chemistry; Kluwer: Dordrecht, The Netherlands, 2000; pp. 117–184. [Google Scholar]
- Zhou, B.J.; Ligneres, V.L.; Carter, E.A. Improving the orbital-free density functional theory description of covalent materials. J. Chem. Phys. 2005, 122, 044103. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Gonzalez, P.; Alvarellos, J.E.; Chacon, E. Nonlocal symmetrized kinetic-energy density functional: Application to simple surfaces. Phys. Rev. B 1998, 57, 4857–4862. [Google Scholar] [CrossRef]
- Rushton, P.P.; Tozer, D.J.; Clark, S.J. Nonlocal density-functional description of exchange and correlation in silicon. Phys. Rev. B 2002, 65, 235203. [Google Scholar] [CrossRef]
- Gori-Giorgi, P.; Angyan, J.G.; Savin, A. Charge density reconstitution from approximate exchange-correlation holes. Can. J. Chem. 2009, 87, 1444–1450. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Jones, R.O. Self-interaction corrections in the density functional formalism. Solid State Commun. 1981, 37, 249–252. [Google Scholar] [CrossRef]
- Perdew, J.P. Orbital functional for exchange and correlation—Self-interaction correction to the local density approximation. Chem. Phys. Lett. 1979, 64, 127–130. [Google Scholar] [CrossRef]
- Almbladh, C.O.; Von Barth, U. Exact results for the charge and spin-densities, exchange- correlation potentials, and density-functional eigenvalues. Phys. Rev. B 1985, 31, 3231–3244. [Google Scholar] [CrossRef]
- Levy, M.; Perdew, J.P.; Sahni, V. Exact differential-equation for the density and ionization- energy of a many-particle system. Phys. Rev. A 1984, 30, 2745–2748. [Google Scholar] [CrossRef]
- Qian, Z.X.; Sahni, V. Analytical asymptotic structure of the pauli, coulomb, and correlation-kinetic components of the kohn-sham theory exchange-correlation potential in atoms. Int. J. Quantum Chem. 1998, 70, 671–680. [Google Scholar] [CrossRef]
- Qian, Z.X.; Sahni, V. Analytical properties of the kohn-sham theory exchange and correlation energy and potential via quantal density functional theory. Int. J. Quantum Chem. 2000, 80, 555–566. [Google Scholar] [CrossRef]
- Ayers, P.W.; Levy, M. Sum rules for exchange and correlation potentials. J. Chem. Phys. 2001, 115, 4438–4443. [Google Scholar] [CrossRef]
- Tozer, D.J.; Handy, N.C. Improving virtual kohn-sham orbitals and eigenvalues: Application to excitation energies and static polarizabilities. J. Chem. Phys. 1998, 109, 10180–10189. [Google Scholar] [CrossRef]
- Tozer, D.J. Relationship between long-range charge-transfer excitation energy error and integer discontinuity in kohn-sham theory. J. Chem. Phys. 2003, 119, 12697–12699. [Google Scholar] [CrossRef]
- Wu, Q.; Ayers, P.W.; Yang, W.T. Density-functional theory calculations with correct long-range potentials. J. Chem. Phys. 2003, 119, 2978–2990. [Google Scholar] [CrossRef]
- Dreuw, A.; Weisman, J.L.; Head-Gordon, M. Long-range charge-transfer excited states in time-dependent density functional theory require non-local exchange. J. Chem. Phys. 2003, 119, 2943–2946. [Google Scholar] [CrossRef]
- Andrade, X.; Aspuru-Guzik, A. Prediction of the derivative discontinuity in density functional theory from an electrostatic description of the exchange and correlation potential. Phys. Rev. Lett. 2011, 107, 183002. [Google Scholar] [CrossRef] [PubMed]
- Ayers, P.W.; Morrison, R.C.; Parr, R.G. Fermi-amaldi model for exchange-correlation: Atomic excitation energies from orbital energy differences. Mol. Phys. 2005, 103, 2061–2072. [Google Scholar] [CrossRef]
- Savin, A.; Umrigar, C.J.; Gonze, X. Relationship of kohn-sham eigenvalues to excitation energies. Chem. Phys. Lett. 1998, 288, 391–395. [Google Scholar] [CrossRef]
- Balbas, L.C.; Alonso, J.A.; Rubio, A. One-electron energy eigenvalues in the weighted-density approximation to exchange and correlation. Europhys. Lett. 1991, 14, 323–329. [Google Scholar] [CrossRef]
- Robertson, J.; Xiong, K.; Clark, S.J. Band structure of functional oxides by screened exchange and the weighted density approximation. Phys. Status Solidi B 2006, 243, 2054–2070. [Google Scholar] [CrossRef]
- Wu, Z.G.; Singh, D.J.; Cohen, R.E. Electronic structure of calcium hexaboride within the weighted density approximation. Phys. Rev. B 2004, 69, 193105. [Google Scholar] [CrossRef]
- Wu, Z.G.; Cohen, R.E.; Singh, D.J.; Gupta, R.; Gupta, M. Weighted-density-approximation description of rare-earth trihydrides. Phys. Rev. B 2004, 69, 085104. [Google Scholar] [CrossRef]
- Zheng, G.; Clark, S.J.; Brand, S.; Abram, R.A. Non-local density functional description of poly-para-phenylene vinylene. Chin. Phys. Lett. 2007, 24, 807–810. [Google Scholar]
- Cuevas-Saavedra, R.; Ayers, P.W. Exchange-correlation functionals from the identical-particle ornstein-zernike equation: Basic formulation and numerical algorithms. In Condensed Matter Theory; Ludena, E.V., Bishop, R.F., Iza, P., Eds.; World Scientific: Singapore, 2011; Volume 25. [Google Scholar]
- Becker, M.S. Integrodifferential equation for the ground state of an electron gas. Phys. Rev. 1969, 185, 168–171. [Google Scholar] [CrossRef]
- March, N.H. Boson and fermion many-body assemblies: Fingerprints of excitations in the ground-state wave functions, with examples of superfluid He-4 and the homogeneous correlated electron liquid. Phys. Chem. Liq. 2008, 46, 465–480. [Google Scholar] [CrossRef]
- Amovilli, C.; March, N.H. Ornstein-zernike function and coulombic correlation in the homogeneous electron liquid. Phys. Rev. B 2007, 76, 195104. [Google Scholar] [CrossRef]
- Cuevas-Saavedra, R.; Ayers, P.W. Exchange-correlation functionals from the identical-particle ornstein-zernike equation: Basic formulation and numerical algorithms. Int. J. Mod. Phys. B 2010, 24, 5115–5127. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, P.; Alvarellos, J.E.; Chacon, E.; Tarazona, P. Image potential and the exchange-correlation weighted density approximation functional. Phys. Rev. B 2000, 62, 16063–16068. [Google Scholar] [CrossRef]
- Becke, A.D. A multicenter numerical-integration scheme for polyatomic molecules. J. Chem. Phys. 1988, 88, 2547–2553. [Google Scholar] [CrossRef]
- Lee, C.; Parr, R.G. Gaussian and other approximations to the first-order density matrix of electronic systems, and the derivation of various local-density-functional theories. Phys. Rev. A 1987, 35, 2377–2383. [Google Scholar] [CrossRef]
- Broyden, C.G. On the discovery of the "good broyden" method. Math. Program. 2000, 87, 209–213. [Google Scholar] [CrossRef]
- Broyden, C.G. A class of methods for solving nonlinear simultaneous equations. Math. Comput. 1965, 19, 577–593. [Google Scholar] [CrossRef]
- Anglada, J.M.; Bofill, J.M. How good is a broyden-fletcher-goldfarb-shanno-like update hessian formula to locate transition structures? Specific reformulation of broyden-fletcher-goldfarb-shanno for optimizing saddle points. J. Comput. Chem. 1998, 19, 349–362. [Google Scholar] [CrossRef]
- Kvaalen, E. A faster broyden method. BIT 1991, 31, 369–372. [Google Scholar] [CrossRef]
- Griewank, A. Broyden updating, the good and the bad! Doc. Math. 2012, ISMP, 301–315. [Google Scholar]
- Brune, P.R.; Knepley, M.G.; Smith, B.F.; Tu, X. Composing scalable nonlinear algebraic solvers. Siam Rev. 2015, 57, 535–565. [Google Scholar] [CrossRef]
- Al-Baali, M.; Spedicato, E.; Maggioni, F. Broyden‘s quasi-newton methods for a nonlinear system of equations and unconstrained optimization: A review and open problems. Optim. Methods Softw. 2014, 29, 937–954. [Google Scholar] [CrossRef]
- Gori-Giorgi, P.; Perdew, J.P. Pair distribution function of the spin-polarized electron gas: A first-principles analytic model for all uniform densities. Phys. Rev. B 2002, 66, 165118. [Google Scholar] [CrossRef]
- Burger, S.K.; Ayers, P.W. Quasi-newton parallel geometry optimization methods. J. Chem. Phys. 2010, 133, 034116. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, M.; Cuevas-Saavedra, R.; Chakraborty, D.; Ayers, P.W. A Diagonally Updated Limited-Memory Quasi-Newton Method for the Weighted Density Approximation. Computation 2017, 5, 42. https://doi.org/10.3390/computation5040042
Chan M, Cuevas-Saavedra R, Chakraborty D, Ayers PW. A Diagonally Updated Limited-Memory Quasi-Newton Method for the Weighted Density Approximation. Computation. 2017; 5(4):42. https://doi.org/10.3390/computation5040042
Chicago/Turabian StyleChan, Matthew, Rogelio Cuevas-Saavedra, Debajit Chakraborty, and Paul W. Ayers. 2017. "A Diagonally Updated Limited-Memory Quasi-Newton Method for the Weighted Density Approximation" Computation 5, no. 4: 42. https://doi.org/10.3390/computation5040042
APA StyleChan, M., Cuevas-Saavedra, R., Chakraborty, D., & Ayers, P. W. (2017). A Diagonally Updated Limited-Memory Quasi-Newton Method for the Weighted Density Approximation. Computation, 5(4), 42. https://doi.org/10.3390/computation5040042




