Time-Dependent Density-Functional Theory and Excitons in Bulk and Two-Dimensional Semiconductors
Abstract
:1. Introduction
2. Charge Susceptibility, Absorption Spectrum and Excitons
2.1. Many-Body Susceptibility
2.2. TDDFT Susceptibility
2.3. Susceptibility: Finite vs. Extended (Periodic) Systems
2.4. Absorption Spectrum
3. Many-Body Approaches for Excitons
3.1. Semiconductor Bloch Equations and the Wannier Equation
3.2. Bethe-Salpeter Equation
4. TDDFT and Excitons: the Density-Matrix Approach
- (1)
- to calculate the dielectric function with a given fxc, as described in Section 2. Then, the excitonic binding energies will be identified as peaks in the absorption spectrum.
- (2)
- to propagate in time the KS equation, with consequent frequency transformation of the polarization matrix element which also defines the absorption spectrum that might include excitonic peaks.
- (3)
- to solve the linearized Equation (69) for the excitonic binding energies.
5. XC Kernels
5.1. BSE Kernel: General Definition and the Nanoquanta Approximation
5.2. Adiabatic Local XC Kernels
5.3. Adiabatic LR XC Kernels
5.4. Exact-Exchange (Frequency-Dependent) Kernels
5.5. Semi-Local Approximation: Tao-Mo Kernel
5.6. Bootstrap Kernel
5.7. RPA Bootstrap (RBO) Kernel
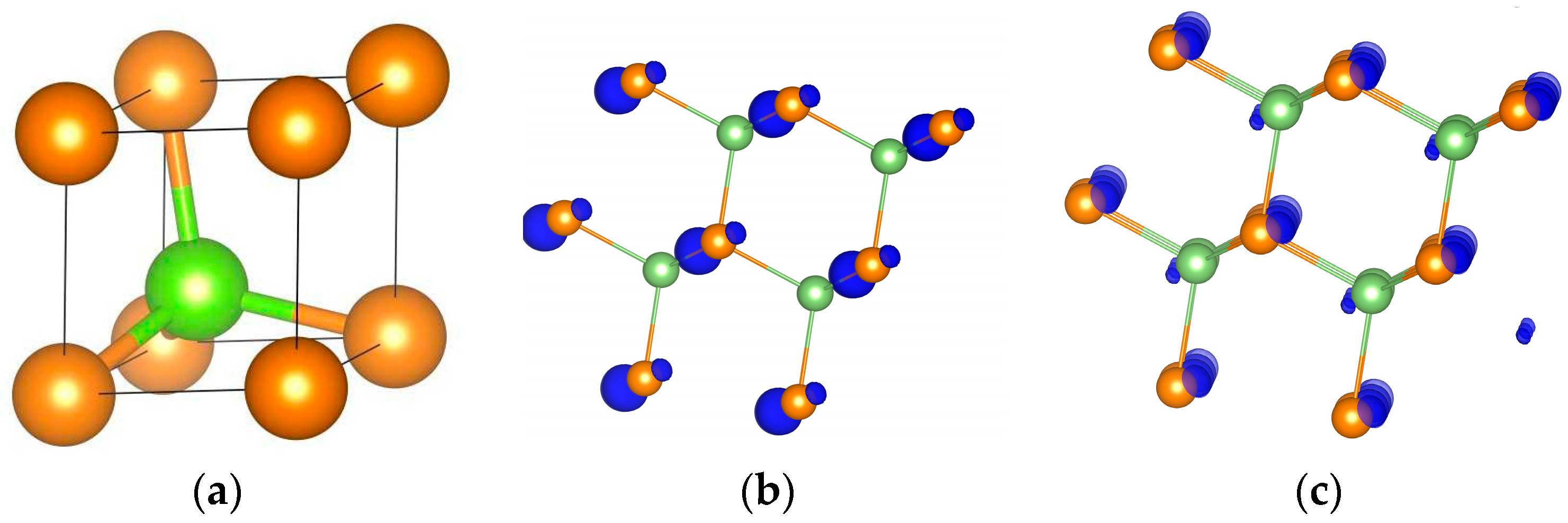
6. Applications: Bulk GaAs and Monolayer MoS2
6.1. GaAs
6.2. MoS2
7. Discussion
- (1)
- Construction of kernels that can reproduce accurately exciton (not-necessarily) Rydberg series. For this, frequency-dependence of the kernel might be crucial.
- (2)
- Description of excitons with different spins (dark and bright excitons, etc.). In this case spin TDDFT must be considered, together with possible spin-dependent kernels (matrices).
- (3)
- Accurate description of the excitonic time-resolved emission spectra, in which phonon effects must be taken into account. In this sense, for practical purposes it would be desirable to construct a non-adiabatic kernel that incorporates memory effects related to electron-phonon interaction.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Kohn-Sham Response Function
References
- Onida, G.; Reining, L.; Rubio, A. Electronic excitations: Density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997. [Google Scholar] [CrossRef]
- Botti, S.; Schindlmayr, A.; Del Sole, R.; Reining, L. Time-dependent density-functional theory for extended systems. Rep. Prog. Phys. 2007, 70, 357. [Google Scholar] [CrossRef]
- Turkowski, V.; Ullrich, C.A. Time-dependent density-functional theory for ultrafast interband excitations. Phys. Rev. B 2008, 77, 075204. [Google Scholar] [CrossRef]
- Turkowski, V.; Leonardo, A.; Ullrich, C.A. Time-dependent density-functional theory approach for exciton binding energies. Phys. Rev. B 2009, 79, 233201. [Google Scholar] [CrossRef]
- Hanke, W.; Sham, L.J. Many-particle effects in the optical spectrum of a semiconductor. Phys. Rev. B 1980, 21, 4656. [Google Scholar] [CrossRef]
- Albrecht, S.; Reining, L.; Del Sole, R.; Onida, G. Ab Initio Calculation of Excitonic Effects in the Optical Spectra of Semiconductors. Phys. Rev. Lett. 1998, 80, 4510. [Google Scholar] [CrossRef]
- Rohlfing, M.; Louie, S.G. Electron-Hole Excitations in Semiconductors and Insulators. Phys. Rev. Lett. 1998, 81, 2312. [Google Scholar] [CrossRef]
- Von Barth, U.; Dahlen, N.E.; van Leeuwen, R.; Stefanucci, G. Conserving approximations in time-dependent density functional theory. Phys. Rev. B 2005, 72, 235109. [Google Scholar] [CrossRef]
- Sottile, F.; Olevano, V.; Reining, L. Parameter-Free Calculation of Response Functions in Time-Dependent Density-Functional Theory. Phys. Rev. Lett. 2003, 91, 056402. [Google Scholar] [CrossRef] [PubMed]
- Marini, A.; Del Sole, R.; Rubio, A. Bound Excitons in Time-Dependent Density-Functional Theory: Optical and Energy-Loss Spectra. Phys. Rev. Lett. 2003, 91, 256402. [Google Scholar] [CrossRef]
- Reining, L.; Olevano, V.; Rubio, A.; Onida, G. Excitonic Effects in Solids Described by Time-Dependent Density-Functional Theory. Phys. Rev. Lett. 2002, 88, 066404. [Google Scholar] [CrossRef] [PubMed]
- Botti, S.; Sottile, F.; Vast, N.; Olevano, V.; Reining, L.; Weissker, H.-C.; Rubio, A.; Onida, G.; Del Sole, R.; Godby, R.W. Long-range contribution to the exchange-correlation kernel of time-dependent density functional theory. Phys. Rev. B 2004, 69, 155112. [Google Scholar] [CrossRef]
- Botti, S.; Fourreau, A.; Nguyen, F.; Renault, Y.-O.; Sottile, F.; Reining, L. Energy dependence of the exchange-correlation kernel of time-dependent density functional theory: A simple model for solids. Phys. Rev. B 2005, 72, 125203. [Google Scholar] [CrossRef]
- Sottile, F.; Karlsson, K.; Reining, L.; Aryasetiawan, F. Macroscopic and microscopic components of exchange-correlation interactions. Phys. Rev. B 2003, 68, 205112. [Google Scholar] [CrossRef]
- Wełnic, W.; Botti, S.; Reining, L.; Wuttig, M. Origin of the Optical Contrast in Phase-Change Materials. Phys. Rev. Lett. 2007, 98, 236403. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.-X.; Tkatchenko, A.; Paier, J.; Appel, H.; Scheffler, M. Van der Waals Interactions in Ionic and Semiconductor Solids. Phys. Rev. Lett. 2011, 107, 245501. [Google Scholar] [CrossRef] [PubMed]
- Hübener, H.; Luppi, E.; Véniard, V. Ab initio calculation of many-body effects on the second-harmonic generation spectra of hexagonal SiC polytypes. Phys. Rev. B 2011, 83, 115205. [Google Scholar] [CrossRef]
- Ramirez-Torres, A.; Turkowski, V.; Rahman, T.S. Time-Dependent density-matrix functional theory for trion excitations: Application to monolayer MoS2 and other transition-metal dichalcogenides. Phys. Rev. B 2014, 90, 085419. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Gustavo, E.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Mo, Y. Accurate Semi-Local Density Functional for Condensed-Matter Physics and Quantum Chemistry. Phys. Rev. Lett. 2016, 117, 073001. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Görling, A. Excitonic Optical Spectrum of Semiconductors Obtained by Time-Dependent Density-Functional Theory with the Exact-Exchange Kernel. Phys. Rev. Lett. 2002, 89, 096402. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.-H.; Görling, A. Exact Kohn-Sham exchange kernel for insulators and its long-wavelength behavior. Phys. Rev. B 2002, 66, 035114. [Google Scholar] [CrossRef]
- Bruneval, F.; Sottile, F.; Olevano, V.; Reining, L. Beyond time-dependent exact exchange: The need for long-range correlation. J. Chem. Phys. 2006, 124, 144113. [Google Scholar] [CrossRef] [PubMed]
- Ullrich, C.A. Time-Dependent Density-Functional Theory: Concepts and Applications, 1st ed.; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Krieger, J.B.; Li, Y.; Iafrate, G.J. Construction and application of an accurate local spin-polarized Kohn-Sham potential with integer discontinuity: Exchange-only theory. Phys. Rev. A 1992, 45, 101. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Dewhurst, J.K.; Sanna, A.; Gross, E.K.U. Bootstrap Approximation for the Exchange-Correlation Kernel of Time-Dependent Density-Functional Theory. Phys. Rev. Lett. 2011, 107, 186401. [Google Scholar] [CrossRef]
- Sharma, A.; Dewhurst, J.K.; Sanna, A.; Rubio, A.; Gross, E.K.I. Enhanced excitonic effects in the energy loss spectra of LiF and Ar at large momentum transfer. New J. Phys. 2012, 14, 053052. [Google Scholar] [CrossRef]
- Yang, Z.-H.; Li, Y.; Ullrich, C.A. A minimal model for excitons within time-dependent density-functional theory. J. Chem. Phys. 2012, 137, 014513. [Google Scholar] [CrossRef] [PubMed]
- Rigamonti, S.; Botti, S.; Veniard, V.; Draxl, C.; Reining, L.; Sottile, F. Estimating Excitonic Effects in the Absorption Spectra of Solids: Problems and Insight from a Guided Iteration Scheme. Phys. Rev. Lett. 2015, 114, 146402. [Google Scholar] [CrossRef] [PubMed]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Qu, F.; MacDonald, A.H. Exciton band structure of monolayer MoS2. Phys. Rev. B 2015, 91, 075310. [Google Scholar] [CrossRef]
- Del Sole, R.; Fiorino, E. Macroscopic dielectric tensor at crystal surfaces. Phys. Rev. B 1984, 29, 4631. [Google Scholar] [CrossRef]
- Haug, H.; Koch, S.W. Quantum Theory of the Optical and Electronic Properties of Semiconductors; World Scientific Publishing Co., Inc.: Singapore, 2009. [Google Scholar]
- Wannier, G.H. The Structure of Electronic Excitation Levels in Insulating Crystals. Phys. Rev. 1937, 52, 191. [Google Scholar] [CrossRef]
- Stefanucci, G.; van Leeuwen, R. Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction, 1st ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Talman, J.D.; Shadwick, W.F. Optimized effective atomic central potential. Phys. Rev. A 1976, 14, 36. [Google Scholar] [CrossRef]
- Norman, M.R.; Koelling, D.D. Towards a Kohn-Sham potential via the optimized effective-potential method. Phys. Rev. B 1984, 30, 5530. [Google Scholar] [CrossRef]
- Yang, Z.-H.; Ullrich, C.A. Direct calculations of exciton binding energy with time-dependent density-functional theory. Phys. Rev. B 2013, 87, 195204. [Google Scholar] [CrossRef]
- Sharma, A.; Dewhurst, J.K.; Sanna, A.; Gross, E.K.U. Comment on “Estimating Excitonic Effects in the Absorption Spectra of Solids: Problems and Insight from a Guided Iteration Scheme”. Phys. Rev. Lett. 2016, 117, 159701. [Google Scholar] [CrossRef]
- Rigamonti, S.; Botti, S.; Veniard, V.; Draxl, C.; Reining, L.; Sottile, F. Reply. Phys. Rev. Lett. 2016, 117, 159702. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum espresso: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Parenteau, M.; Carlone, C. Damage coefficient associated with free exciton lifetime in GaAs irradiated with neutrons and electrons. J. Appl. Phys. 1992, 71, 3747. [Google Scholar] [CrossRef]
- Adachi, S. Physical Properties of III–V Semiconductor Compounds; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Ullrich, C.A.; Yang, Z.-H. Excitons in time-dependent density-functional theory. In Density-Functional Methods for Excited States; Topics in Current Chemistry; Ferre, N., Filatov, M., Huix-Rotllant, M., Eds.; Springer: Berlin, Germany, 2015; Volume 368, pp. 185–217. [Google Scholar]
- Yang, Z.-H.; Sottile, F.; Ullrich, C.A. Simple screened exact-exchange approach for excitonic properties in solids. Phys. Rev. B 2015, 92, 035202. [Google Scholar] [CrossRef]
- Byun, Y.-M.; Ullrich, C.A. Assessment of long-range-corrected exchange-correlation kernels for solids: Accurate exciton binding energies via an empirically scaled bootstrap kernel. Phys. Rev. B 2017, 95, 205136. [Google Scholar] [CrossRef]



| XC Kernel | (hh1) | (hh2) | (lh) |
|---|---|---|---|
| contact | −2.000 | −2.284 | −1.437 |
| Slater | −1.332 | −1.833 | −1.293 |
| LR | −0.492 | −0.511 | −0.442 |
| GEA | −0.183 | −0.221 | −0.224 |
| LDA | −0.216 | −0.270 | −0.308 |
| PBE | −0.250 | −0.323 | −0.447 |
| PW91 | −0.222 | −0.282 | −0.295 |
| PW corr | −0.0004 | −0.00067 | −0.001488 |
| XC Kernel | Binding Energy, eV |
|---|---|
| local | −2.661 |
| local | −0.300 |
| Slater | −1.067 |
| LR | −0.106 |
| LR | −0.300 |
| GEA | −0.007 |
| LDA | −0.0096 |
| PBE | −0.0118 |
| PW91 | −0.0097 |
| PW corr. | −0.00001 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turkowski, V.; Din, N.U.; Rahman, T.S. Time-Dependent Density-Functional Theory and Excitons in Bulk and Two-Dimensional Semiconductors. Computation 2017, 5, 39. https://doi.org/10.3390/computation5030039
Turkowski V, Din NU, Rahman TS. Time-Dependent Density-Functional Theory and Excitons in Bulk and Two-Dimensional Semiconductors. Computation. 2017; 5(3):39. https://doi.org/10.3390/computation5030039
Chicago/Turabian StyleTurkowski, Volodymyr, Naseem Ud Din, and Talat S. Rahman. 2017. "Time-Dependent Density-Functional Theory and Excitons in Bulk and Two-Dimensional Semiconductors" Computation 5, no. 3: 39. https://doi.org/10.3390/computation5030039
APA StyleTurkowski, V., Din, N. U., & Rahman, T. S. (2017). Time-Dependent Density-Functional Theory and Excitons in Bulk and Two-Dimensional Semiconductors. Computation, 5(3), 39. https://doi.org/10.3390/computation5030039




