CFD-PBM Approach with Different Inlet Locations for the Gas-Liquid Flow in a Laboratory-Scale Bubble Column with Activated Sludge/Water
Abstract
:1. Introduction
2. Mathematical Models
2.1. Euler-Euler Two-Fluid Model
2.2. Turbulence Modeling
2.3. Non-Newtonian Fluid Rheological Model
2.4. Population Balance Model
3. Model Setup and Calculation Algorithm
3.1. Model and Mesh
3.1.1. Physical Model
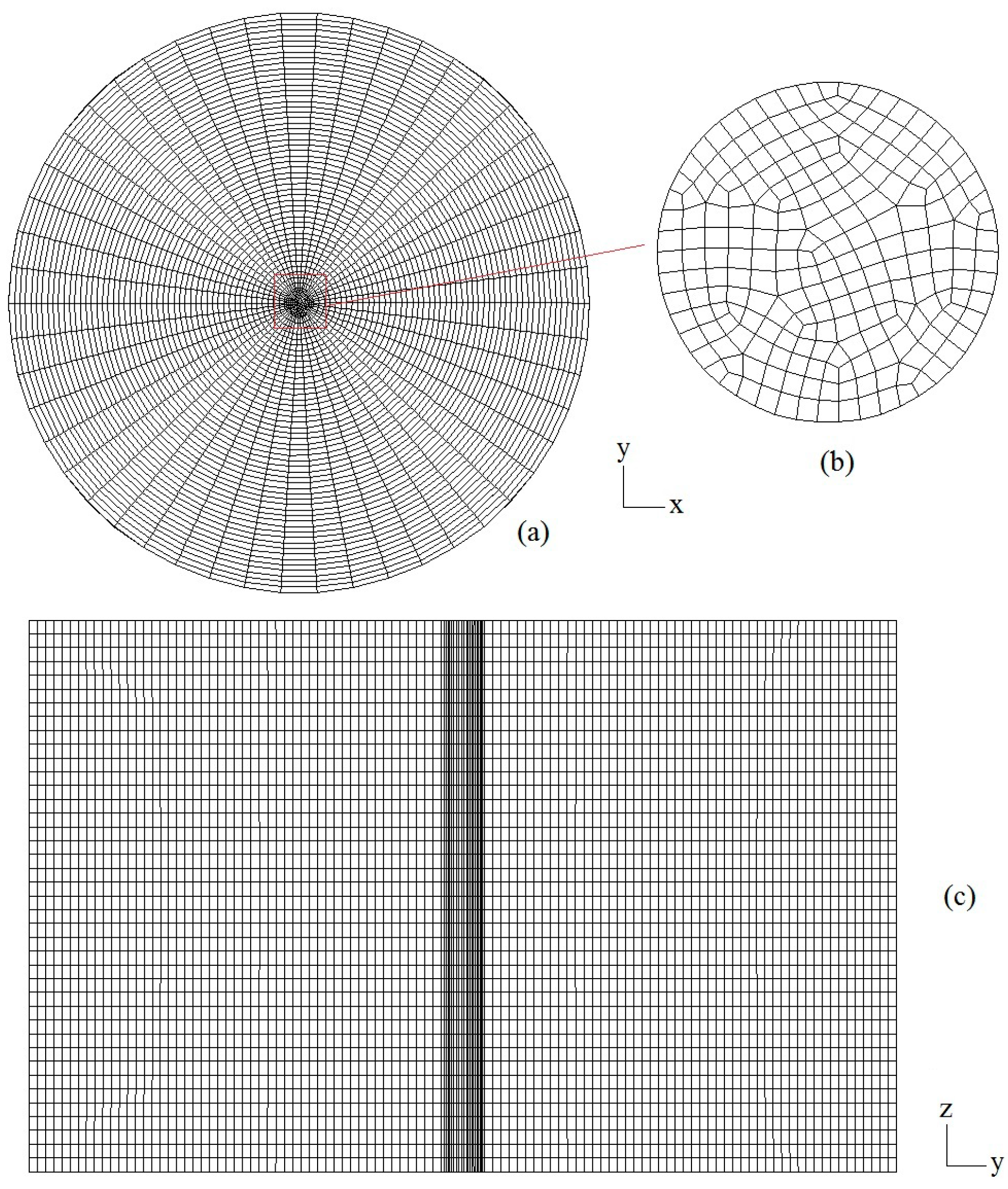
3.1.2. Mesh
3.2. Calculation Methods
4. Validation
4.1. Mesh Validation
4.2. Flow Visualization: Experimental versus Simulated Results
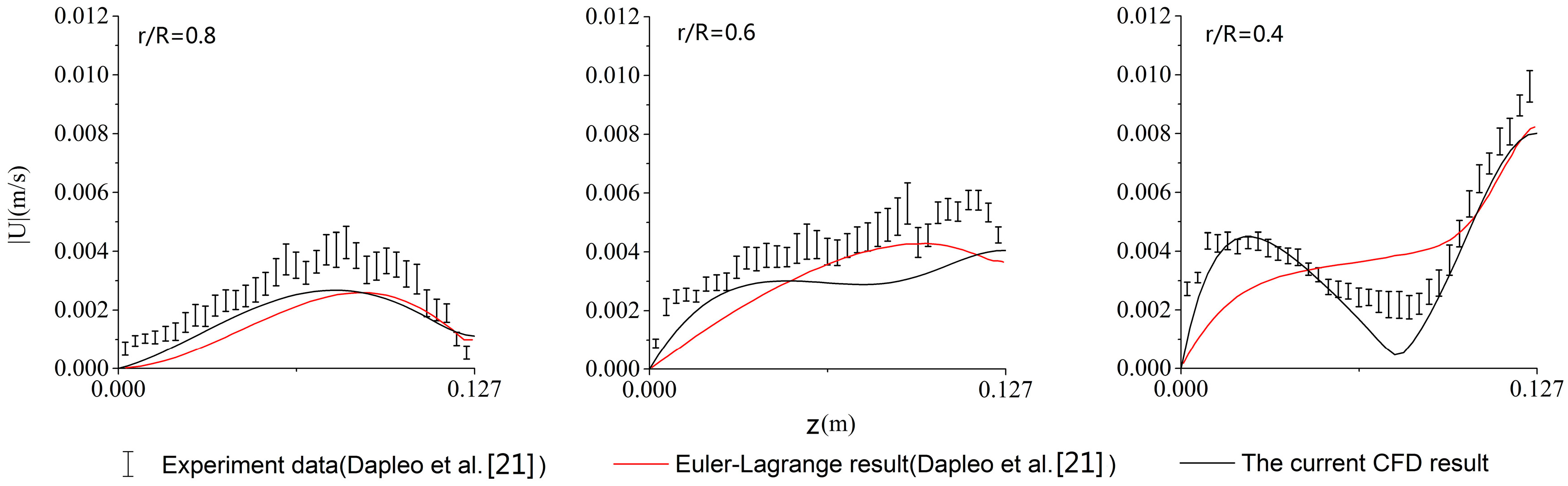
4.3. Non-Newtonian Velocity Field Verification
5. Results and Discussion
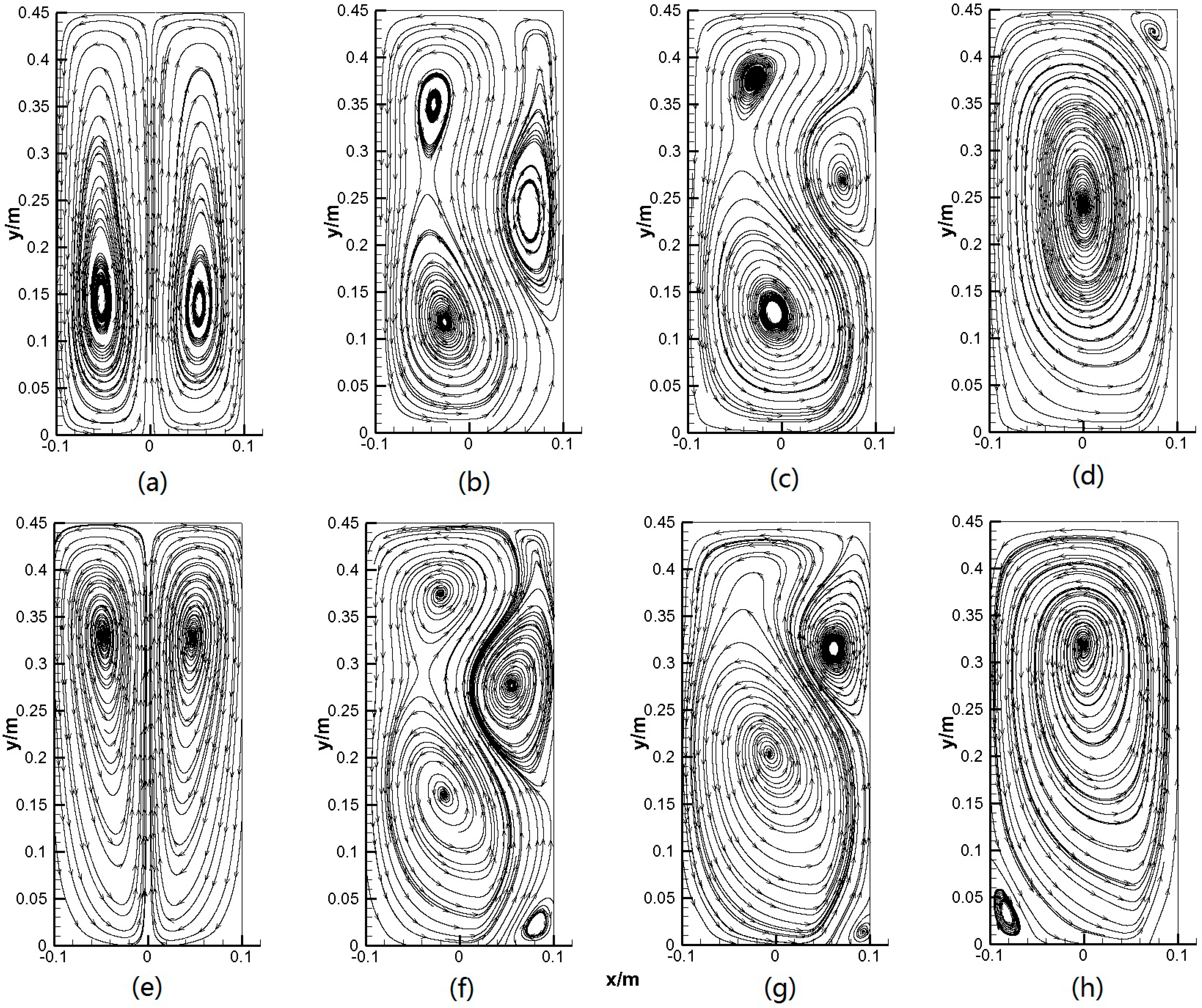
5.1. Flow Field
5.2. Velocity
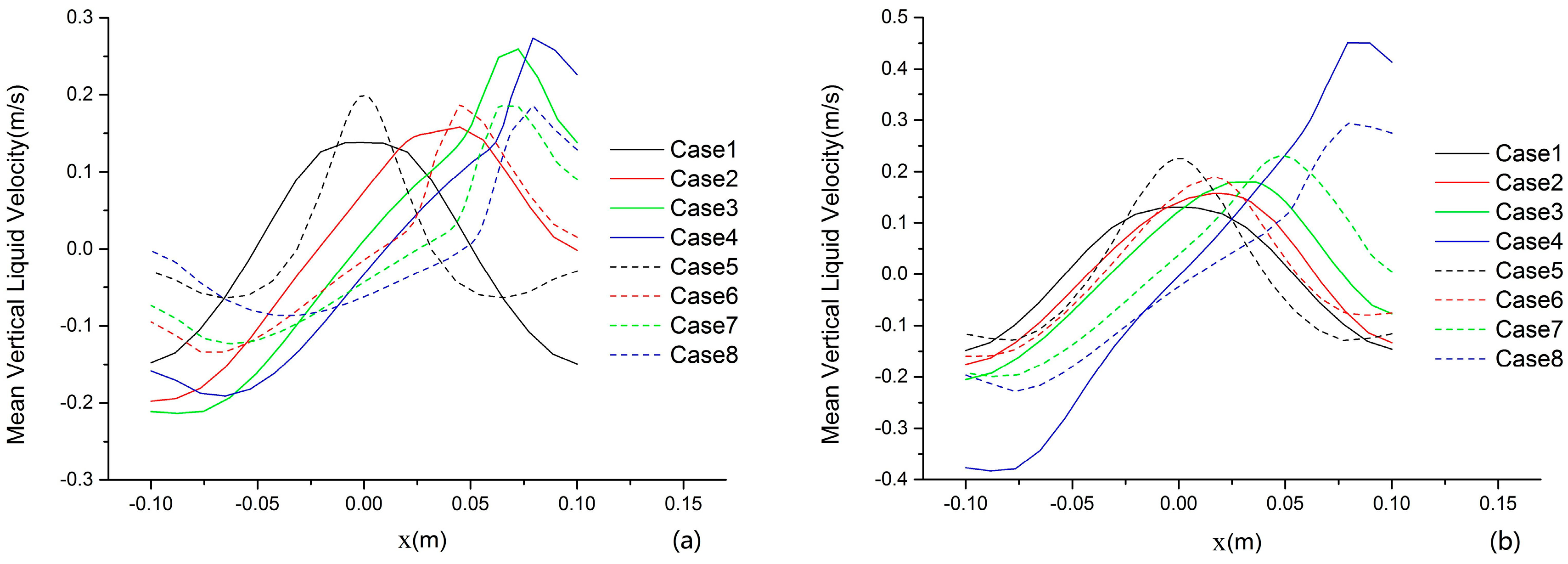
5.2.1. Liquid-Phase Velocity in the y-Direction
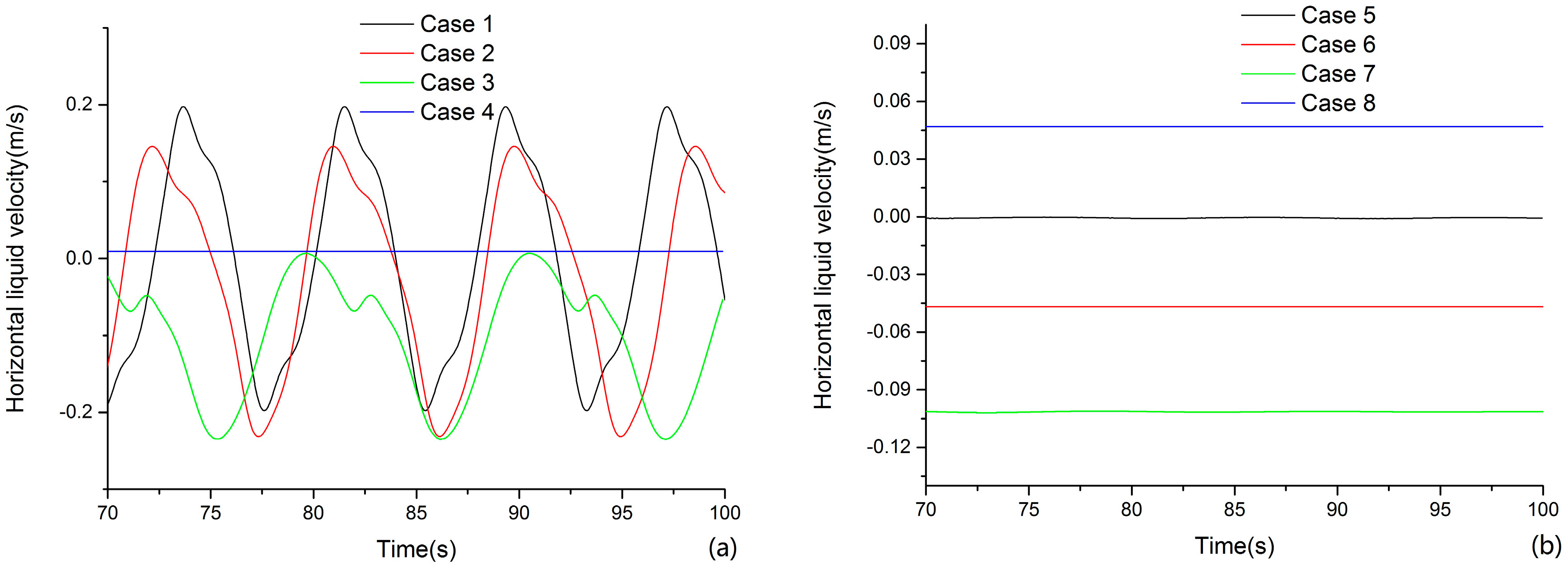
5.2.2. Liquid-Phase Velocities at Different Monitoring Points
5.3. Gas Hold-Up
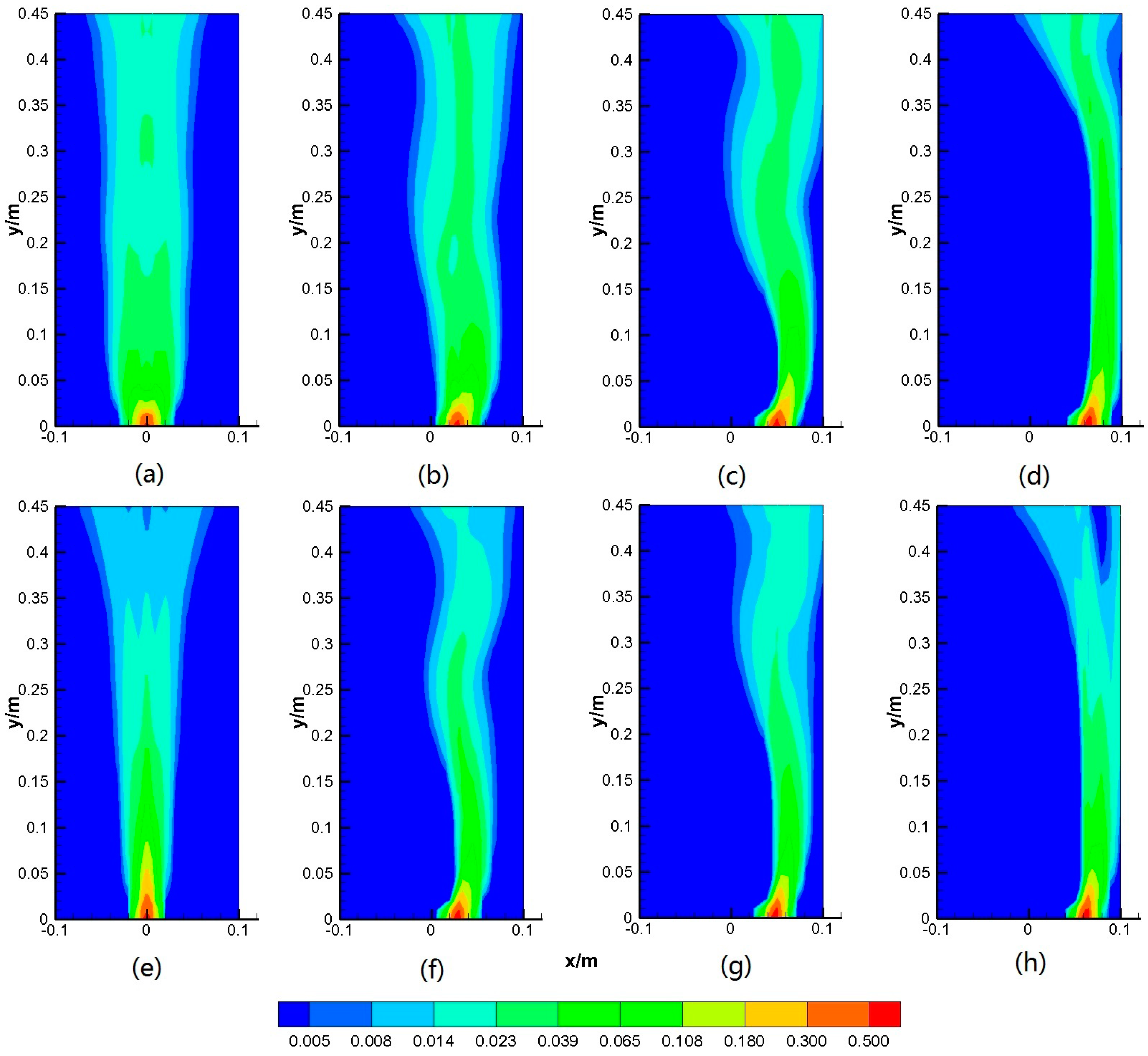
5.3.1. Gas Hold-Up Distribution
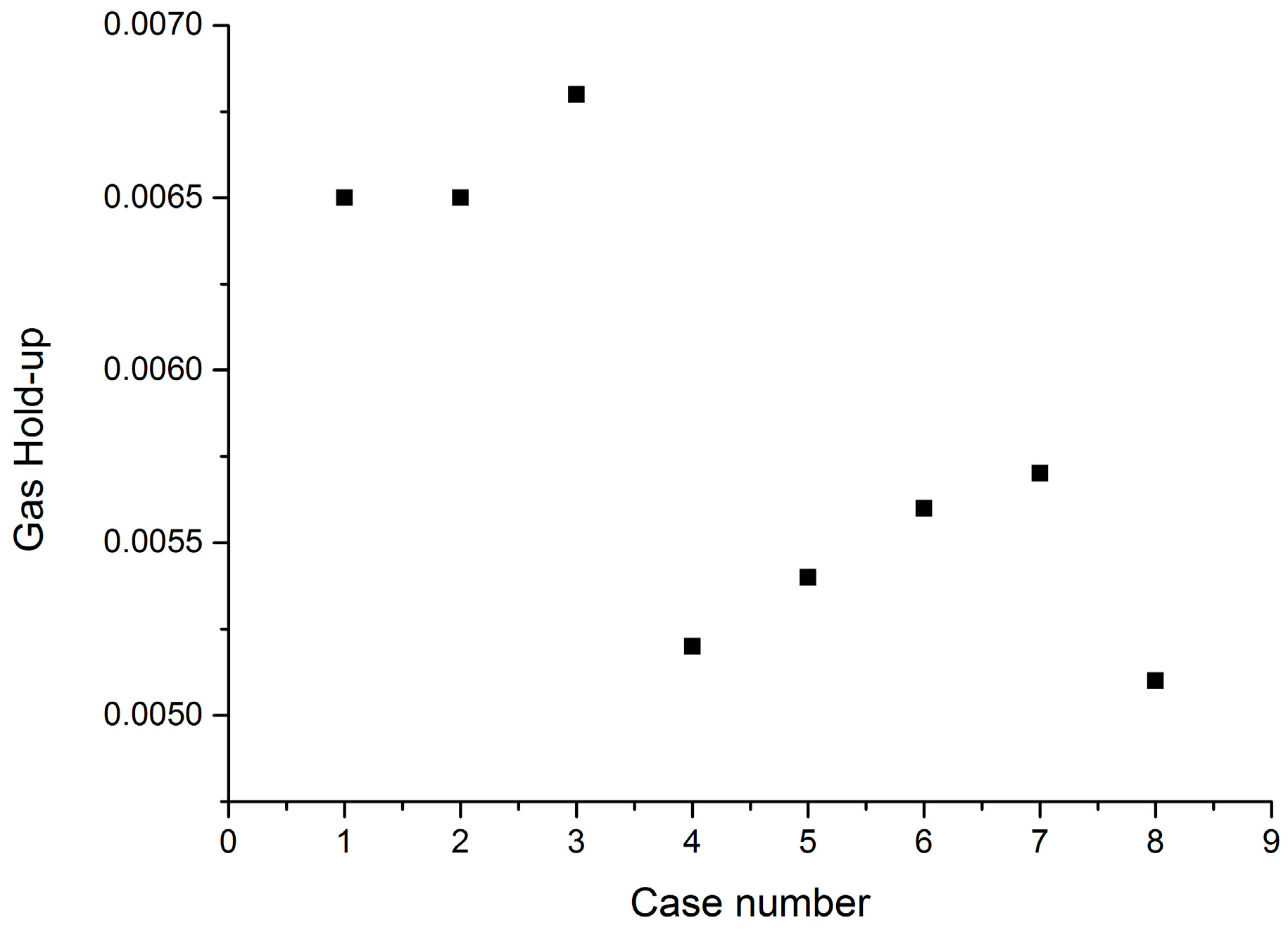
5.3.2. Global Gas Hold-Up
5.4. Non-Newtonian Liquid Dynamic Viscosity
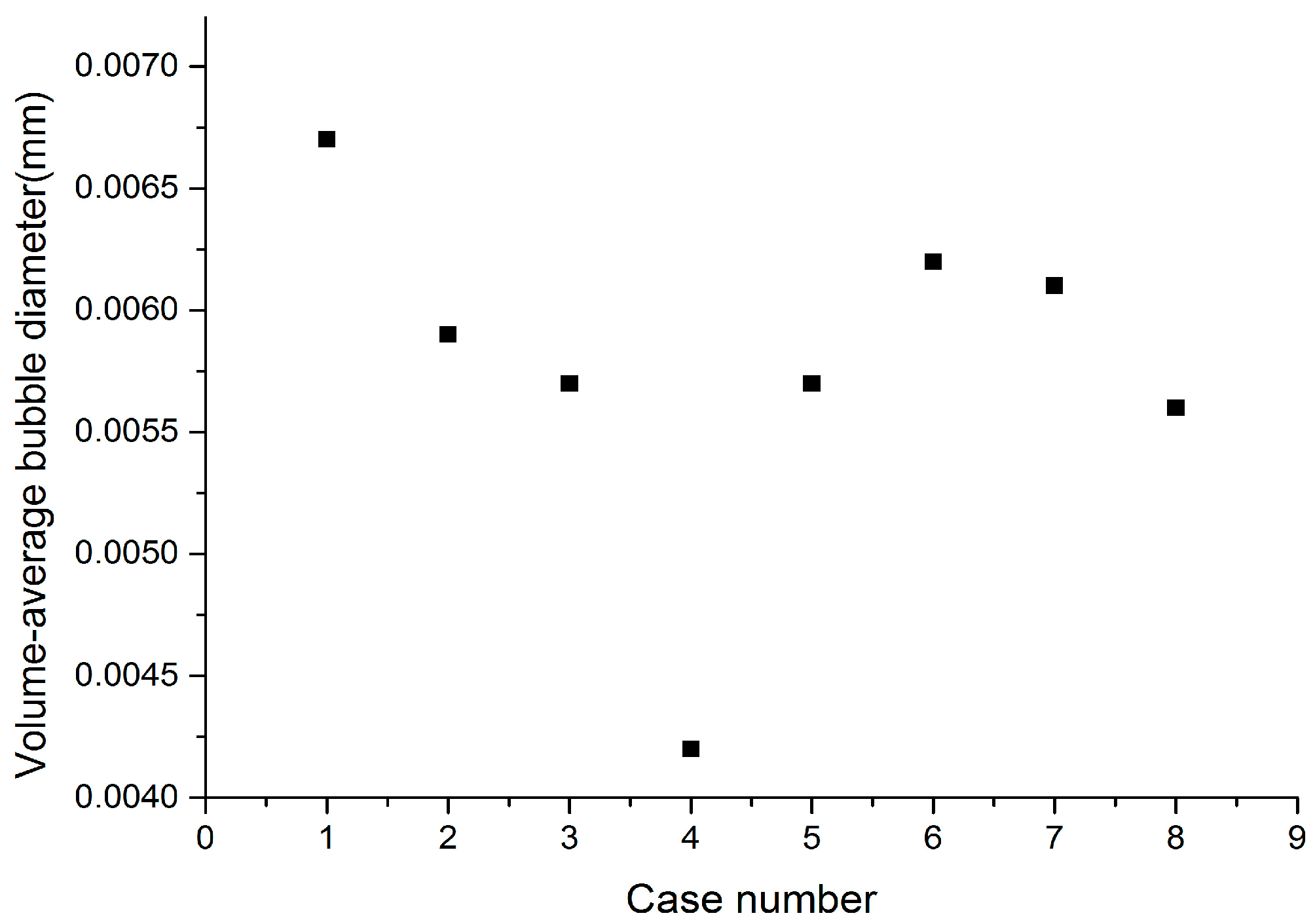
5.5. Volume-Average Bubble Diameter
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Ali, B.A.; Kumar, C.S.; Pushpavanam, S. Analysis of liquid circulation in a rectangular tank with a gas source at a corner. Chem. Eng. J. 2008, 144, 442–452. [Google Scholar] [CrossRef]
- Sun, H.; Mao, Z.S.; Yu, G. Experimental and numerical study of gas hold-up in surface aerated stirred tanks. Chem. Eng. Sci. 2006, 61, 4098–4110. [Google Scholar] [CrossRef]
- Díaz, M.E.; Montes, F.J.; Galán, M.A. Experimental study of the transition between unsteady flow regimes in a partially aerated two-dimensional bubble column. Chem. Eng. Process. 2008, 47, 1867–1876. [Google Scholar] [CrossRef]
- Ali, B.A.; Pushpavanam, S. Analysis of unsteady gas-liquid flows in a rectangular tank: Comparison of Euler-Eulerian and Euler-Lagrangian simulations. Int. J. Multiph. Flow 2011, 37, 268–277. [Google Scholar] [CrossRef]
- Pfleger, D.; Becker, S. Modelling and simulation of the dynamic flow behaviour in a bubble column. Chem. Eng. Sci. 2001, 56, 1737–1747. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J. Numerical simulations of gas-liquid mass transfer in bubble columns with a CFD-PBM coupled model. Chem. Eng. Sci. 2007, 62, 7107–7118. [Google Scholar] [CrossRef]
- Gupta, A.; Roy, S. Euler-Euler simulation of bubbly flow in a rectangular bubble column: Experimental validation with radioactive particle tracking. Chem. Eng. J. 2013, 225, 818–836. [Google Scholar] [CrossRef]
- Liang, X.F.; Pan, H.; Su, Y.H.; Luo, Z.H. CFD-PBM approach with modified drag model for the gas-liquid flow in a bubble column. Chem. Eng. Res. Des. 2016, 112, 88–102. [Google Scholar] [CrossRef]
- Xing, C.; Wang, T.; Wang, J. Experimental study and numerical simulation with a coupled CFD-PBM model of the effect of liquid viscosity in a bubble column. Chem. Eng. Sci. 2013, 95, 313–322. [Google Scholar] [CrossRef]
- Hounslow, M.J.; Ryall, R.L.; Marshall, V.R. A discretized population balance for nucleation, growth, and aggregation. AIChE J. 1988, 34, 1821–1832. [Google Scholar] [CrossRef]
- Tomiyama, A.; Shimada, N. (N+2)-field modeling for bubbly flow simulation. Comput. Fluid Dyn. J. 2001, 9, 418–426. [Google Scholar]
- McGraw, R. Description of aerosol dynamics by the quadrature method of moments. Aerosol Sci. Technol. 1997, 27, 255–265. [Google Scholar] [CrossRef]
- Marchisio, D.L.; Fox, R.O. Solution of population balance equations using the direct quadrature method of moments. J. Aerosol Sci. 2005, 36, 43–73. [Google Scholar] [CrossRef]
- Tabib, M.V.; Roy, S.A.; Joshi, J.B. CFD simulation of bubble column—An analysis of interphase forces and turbulence models. Chem. Eng. J. 2008, 139, 589–614. [Google Scholar] [CrossRef]
- Laborde-Boutet, C.; Larachi, F.; Dromard, N.; Delsart, O.; Schweich, D. CFD simulation of bubble column flows: Investigations on turbulence models in RANS approach. Chem. Eng. Sci. 2009, 64, 4399–4413. [Google Scholar] [CrossRef]
- Liu, Y.; Hinrichsen, O. Study on CFD-PBM turbulence closures based on k–ε and Reynolds stress models for heterogeneous bubble column flows. Comput. Fluids 2014, 105, 91–100. [Google Scholar] [CrossRef]
- Durán, C.; Fayolle, Y.; Pechaud, Y.; Cockx, A.; Gillot, S. Impact of suspended solids on the activated sludge non-Newtonian behaviour and on oxygen transfer in a bubble column. Chem. Eng. Sci. 2016, 141, 154–165. [Google Scholar] [CrossRef]
- Esmaeili, A.; Guy, C.; Chaouki, J. Local hydrodynamic parameters of bubble column reactors operating with non-Newtonian liquids: Experiments and models development. AIChE J. 2016, 62, 1382–1396. [Google Scholar] [CrossRef]
- Godbole, S.P.; Schumpe, A.; Shah, Y.T.; Carr, N.L. Hydrodynamics and mass transfer in non-Newtonian solutions in a bubble column. AIChE J. 1984, 30, 213–220. [Google Scholar] [CrossRef]
- Passos, A.D.; Voulgaropoulos, V.P.; Paras, S.V.; Mouza, A.A. The effect of surfactant addition on the performance of a bubble column containing a non-Newtonian liquid. Chem. Eng. Res. Des. 2015, 95, 93–104. [Google Scholar] [CrossRef]
- Dapelo, D.; Alberini, F.; Bridgeman, J. Euler-Lagrange CFD modelling of unconfined gas mixing in anaerobic digestion. Water Res. 2015, 85, 497–511. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, T.K.; Das, S.K. Non-Newtonian and gas-non-Newtonian liquid flow through elbows-CFD analysis. J. Appl. Fluid Mech. 2013, 6, 131–141. [Google Scholar]
- Wu, B. CFD simulation of gas and non-Newtonian fluid two-phase flow in anaerobic digesters. Water Res. 2010, 44, 3861–3874. [Google Scholar] [CrossRef] [PubMed]
- Dewsbury, K.; Karamanev, D.; Margaritis, A. Hydrodynamic characteristics of free rise of light solid particles and gas bubbles in non-Newtonian liquids. Chem. Eng. Sci. 1999, 54, 4825–4830. [Google Scholar] [CrossRef]
- Hasar, H.; Kinaci, C.; Ünlü, A.; Toǧrul, H.; Ipek, U. Rheological properties of activated sludge in a sMBR. Biochem. Eng. J. 2004, 20, 1–6. [Google Scholar] [CrossRef]
- Mohapatra, D.P.; Brar, S.K.; Tyagi, R.D.; Picard, P.; Surampalli, R.Y. Ferro-sonication and partial ozonation pre-treatment and biotransformation of wastewater sludge for degradation of bisphenol a: Rheology studies. Chem. Eng. Sci. 2012, 81, 20–27. [Google Scholar] [CrossRef]
- Gresch, M.; Armbruster, M.; Braun, D.; Gujer, W. Effects of aeration patterns on the flow field in wastewater aeration tanks. Water Res. 2011, 45, 810–818. [Google Scholar] [CrossRef] [PubMed]
- Sato, Y.; Sadatomi, M.; Sekoguchi, K. Momentum and heat transfer in two-phase bubble flow-I. Theory. Int. J. Multiph. Flow 1981, 7, 167–177. [Google Scholar] [CrossRef]
- Pourtousi, M.; Sahu, J.; Ganesan, P. Effect of interfacial forces and turbulence models on predicting flow pattern inside the bubble column. Chem. Eng. Process. 2014, 75, 38–47. [Google Scholar] [CrossRef]
- Li, G.; Yang, X.; Dai, G. CFD simulation of effects of the configuration of gas distributors on gas-liquid flow and mixing in a bubble column. Chem. Eng. Sci. 2009, 64, 5104–5116. [Google Scholar] [CrossRef]
- Silva, M.K.; d’Ávila, M.A.; Mori, M. Study of the interfacial forces and turbulence models in a bubble column. Comput. Chem. Eng. 2012, 44, 34–44. [Google Scholar] [CrossRef]
- Zhang, D.; Deen, N.G.; Kuipers, J.A.M. Numerical simulation of the dynamic flow behavior in a bubble column: A study of closures for turbulence and interface forces. Chem. Eng. Sci. 2006, 61, 7593–7608. [Google Scholar] [CrossRef]
- Wu, B.X.; Chen, S.L. CFD simulation of non-Newtonian fluid flow in anaerobic digesters. Biotechnol. Bioeng. 2008, 99, 700–711. [Google Scholar] [CrossRef] [PubMed]
- Lali, A.M.; Khare, A.S.; Joshi, J.B.; Nigam, K.D.P. Behaviour of solid particles in viscous non-Newtonian solutions: Settling velocity, wall effects and bed expansion in solid-liquid fluidized beds. Powder Technol. 1989, 57, 39–50. [Google Scholar] [CrossRef]
- Grace, J.R.; Wairegi, T.; Nguyen, T.H. Shapes and velocities of single drops and bubbles moving freely through immiscible liquids. Trans. Inst. Chem. Eng. 1976, 54, 167–173. [Google Scholar]
- Ranade, V.V.; Tayalia, Y. Modelling of fluid dynamics and mixing in shallow bubble column reactors: Influence of sparger design. Chem. Eng. Sci. 2001, 56, 1667–1675. [Google Scholar] [CrossRef]
- Pourtousi, M.; Ganesan, P.; Sahu, J.N. Effect of bubble diameter size on prediction of flow pattern in Euler-Euler simulation of homogeneous bubble column regime. Measurement 2015, 76, 255–270. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems in Engineering; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Luo, H.; Svendsen, H.F. Theoretical model for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci. 1996, 66, 766–776. [Google Scholar] [CrossRef]
- Luo, H. Coalescence, Breakup and Liquid Circulation in Bubble Column Reactors; Norwegian Institute of Technology: Trondheim, Norway, 1993. [Google Scholar]
- Masood, R.M.A.; Khalid, Y.; Delgado, A. Scale adaptive simulation of bubble column flows. Chem. Eng. J. 2015, 262, 1126–1136. [Google Scholar] [CrossRef]
- Buwa, V.V.; Ranade, V.V. Dynamics of gas-liquid flow in a rectangular bubble column: Experiments and single/multi-group CFD simulations. Chem. Eng. Sci. 2002, 57, 4715–4736. [Google Scholar] [CrossRef]
- Böhm, L.; Kurita, T.; Kimura, K.; Kraume, M. Rising behaviour of single bubbles in narrow rectangular channels in Newtonian and non-Newtonian liquids. Int. J. Multiph. Flow 2014, 65, 11–23. [Google Scholar] [CrossRef]
- Mineta, R.; Salehi, Z.; Yoshikawa, H.; Kawase, Y. Oxygen transfer during aerobic biodegradation of pollutants in a dense activated sludge slurry bubble column: Actual volumetric oxygen transfer coefficient and oxygen uptake rate in p-nitrophenol degradation by acclimated waste activated sludge. Biochem. Eng. J. 2011, 53, 266–274. [Google Scholar] [CrossRef]
- Fransolet, E.; Crine, M.; Marchot, P.; Toye, D. Analysis of gas holdup in bubble columns with non-Newtonian fluid using electrical resistance tomography and dynamic gas disengagement technique. Chem. Eng. Sci. 2005, 60, 6118–6123. [Google Scholar] [CrossRef]
- Fabiyi, M.E.; Novak, R. Evaluation of the factors that impact successful membrane biological reactor operations at high solids concentration. Proc. Water Environ. Fed. 2007, 503–512. [Google Scholar] [CrossRef]
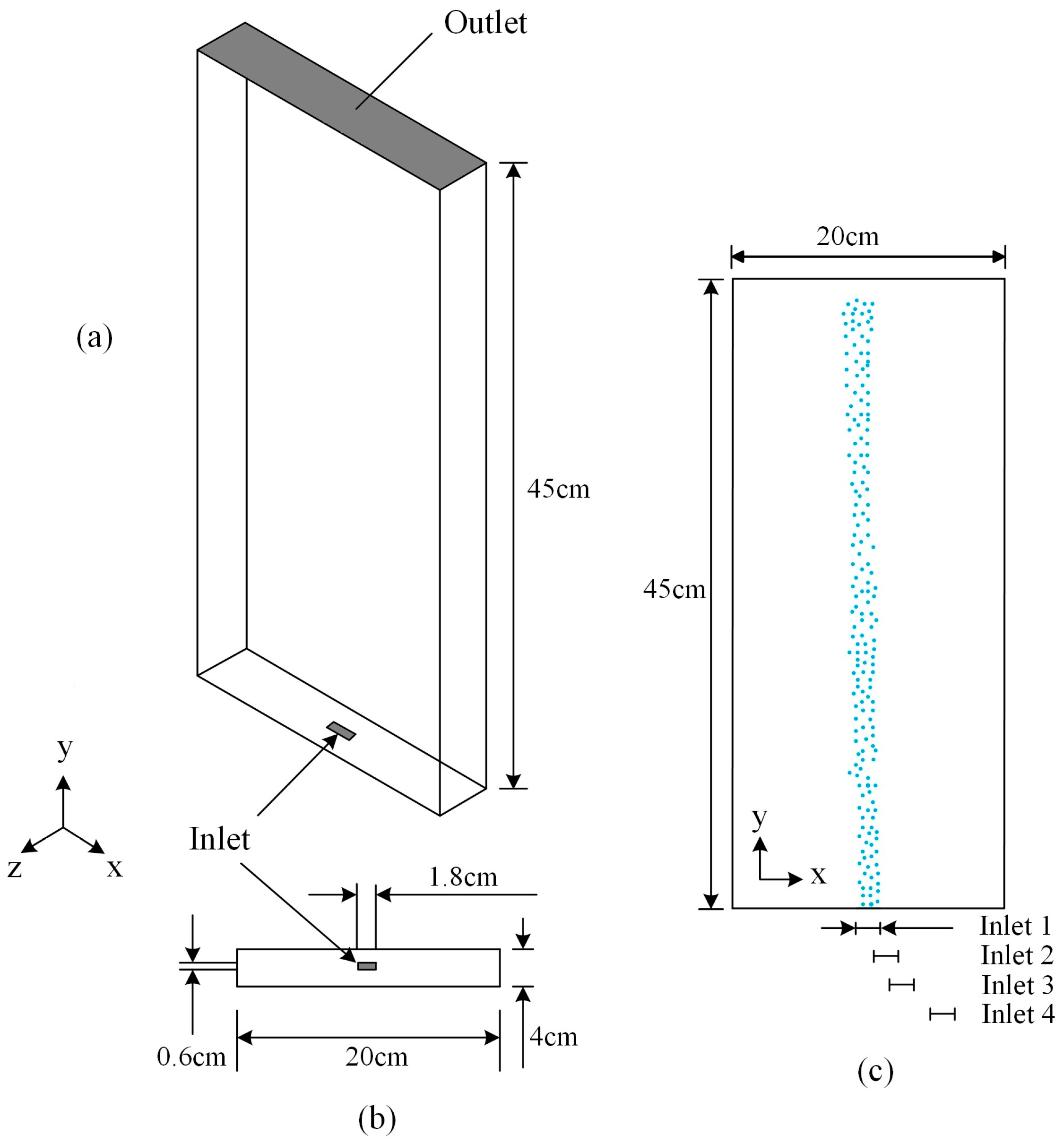



| No. of Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Distance from inlet center to bubble column’s bottom center (m) | 0 | 0.025 | 0.045 | 0.06 | 0 | 0.025 | 0.045 | 0.06 |
| Liquid property | Newtonian | Non-Newtonian | ||||||
| Elements Number | Time Step Size (s) | Max Iterations | Gas Hold-Up * |
|---|---|---|---|
| 1872 | 0.01 | 30 | 0.0058 |
| 3360 | 0.01 | 30 | 0.0060 |
| 10,395 | 0.01 | 30 | 0.0065 |
| 22,185 | 0.01 | 30 | 0.0057 |
| 10,395 | 0.01 | 10 | 0.0064 |
| 10,395 | 0.01 | 50 | 0.0065 |
| 10,395 | 0.02 | 30 | 0.0064 |
| 10,395 | 0.005 | 30 | 0.0065 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Pan, Q.; Chen, J.; Yang, S. CFD-PBM Approach with Different Inlet Locations for the Gas-Liquid Flow in a Laboratory-Scale Bubble Column with Activated Sludge/Water. Computation 2017, 5, 38. https://doi.org/10.3390/computation5030038
Wang L, Pan Q, Chen J, Yang S. CFD-PBM Approach with Different Inlet Locations for the Gas-Liquid Flow in a Laboratory-Scale Bubble Column with Activated Sludge/Water. Computation. 2017; 5(3):38. https://doi.org/10.3390/computation5030038
Chicago/Turabian StyleWang, Le, Qiang Pan, Jie Chen, and Shunsheng Yang. 2017. "CFD-PBM Approach with Different Inlet Locations for the Gas-Liquid Flow in a Laboratory-Scale Bubble Column with Activated Sludge/Water" Computation 5, no. 3: 38. https://doi.org/10.3390/computation5030038
APA StyleWang, L., Pan, Q., Chen, J., & Yang, S. (2017). CFD-PBM Approach with Different Inlet Locations for the Gas-Liquid Flow in a Laboratory-Scale Bubble Column with Activated Sludge/Water. Computation, 5(3), 38. https://doi.org/10.3390/computation5030038




