Abstract
The accurate first-principles prediction of the energetic properties of molecules and clusters from efficient semilocal density functionals is of broad interest. Here we study the performance of a non-empirical Tao-Mo (TM) density functional on binding energies and excitation energies of titanium dioxide and water clusters, as well as reaction barrier heights. To make a comparison, a combination of the TM exchange part with the TPSS (Tao–Perdew–Staroverov–Scuseria) correlation functional—called TMTPSS—is also included in this study. Our calculations show that the best binding energies of titanium dioxide are predicted by PBE0 (Perdew–Burke–Ernzerhof hybrid functional), TM, and TMTPSS with nearly the same accuracy, while B3LYP (Beck’s three-parameter exchange part with Lee-Yang-Parr correlation), TPSS, and PBE (Perdew–Burke–Ernzerhof) yield larger mean absolute errors. For excitation energies of titanium and water clusters, PBE0 and B3LYP are the most accurate functionals, outperforming the performance of semilocal functionals due to the nonlocality problem suffered by the latter. Nevertheless, TMTPSS and TM functionals are still good accurate semilocal methods, improving upon the commonly-used TPSS and PBE functionals. We also find that the best reaction barrier heights are predicted by PBE0 and B3LYP, thanks to the nonlocality incorporated into these two hybrid functionals, but TMTPSS and TM are obviously more accurate than SCAN (Strongly Constrained and Appropriately Normed), TPSS, and PBE, suggesting the good performance of TM and TMTPSS for physically different systems and properties.
1. Introduction
Kohn–Sham density functional theory (DFT) [1,2] is the most popular electronic structure theory, and has achieved practical success in the first-principles prediction of the electronic structure of matter. In this theory, only the exchange-correlation energy component—which accounts for all many-body effects—remains unknown and has to be approximated as a functional of the electron density. As such, the predictive power of DFT largely depends on the density functional approximation to the exchange-correlation energy. Therefore, the development of exchange-correlation density functionals with better accuracy and wider applicability has been the central topic of the field [3,4,5,6,7,8]. More importantly, achieving high accuracy for wide-ranging properties and diverse systems will greatly enhance the computer design of new materials and devices.
The exchange-correlation energy is defined by
where is the electron density and is the exchange-correlation hole at around the electron at (spin index has been suppressed and atomic units () are used). Density functionals can be developed by imposing the exact constraints on the exchange-correlation energy , or on the exchange-correlation hole , or on both. The constraints on the exchange-correlation energy are global, while the constraints on the exchange-correlation hole are local and thus are more difficult to impose. Most density functionals have been proposed from the energy constraints. While the functional form is rather restricted for the local spin-density approximation (LSDA) [3,4], the GGA (Generalized Gradient Approximation) [5] is more flexible and can incorporate more constraints. A meta-GGA [6,7,8] is even more flexible and can incorporate more local ingredients or inputs than LSDA and GGA. The simplest construction is the LSDA [3,4], in which the exchange part (i.e., Slater exchange) is calculated from the noninteracting plane wave, while the correlation part is calculated numerically with the quantum Monte Carlo (QMC) method. The LSDA is uniquely defined, although different parameterizations of the QMC data have been proposed. Since the typical valence electron density in solids is nearly uniform, the LSDA has been widely used in solid-state calculations. However, the LSDA tends to overestimate the short-range interaction arising from the orbital overlap of valence electrons in a molecule or solid and thus displays strong overbinding tendency. This tendency becomes more serious when the electron density becomes more inhomogeneous. For example, the LSDA yields moderately too-high cohesive energies of solids, but it significantly overestimates the atomization energies of molecules, in which the electron density is not slowly varying, leading to too-short bond lengths and lattice constants.
GGA [5] is designed to correct the overbinding tendency of the LSDA. It was shown that GGA can significantly reduce the error of the LSDA in molecular atomization energy by a factor of about 10. However, this correction leads GGA to produce too-long bond lengths and lattice constants, and worsens the good performance of the LSDA for molecular solids, physisorption, and layered materials, in which the long-range van der Waals (vdW) interaction is important. A fundamental reason for this is that the excess short-range interaction of the LSDA effectively compensates for the absent long-range part of the vdW interaction. GGA removes the excess short-range interaction of the LSDA, but it is unable to provide the nonlocal long-range vdW interaction, because it is semilocal after all. This leads GGA to yield too-long bond lengths and lattice constants. In other words, GGA approaches experiments from the opposite side of the LSDA. To cure the shortcoming of GGA, meta-GGA functionals have been developed by including the orbital kinetic energy densities as an additional input [6,7,8] beyond those of GGA. Using the kinetic energy density as another local ingredient makes the functional form of meta-GGA very flexible. This flexibility enables a meta-GGA to recover the correct slowly varying gradient expansion of the exchange-correlation energy up to fourth order in density gradient, and at the same time can reduce the self-interaction error of GGA. As a result, meta-GGA can extend the short-range part of the vdW interaction to a wider range. The former can improve the GGA description of usual bulk solids and molecules, while the latter can greatly improve GGA functionals for systems in which the long-range vdW interaction is important (e.g., molecular complexes and solids). There are two ways to achieve this goal. One is to include many parameters fitted to many sets of properties such as M06L (Minnesota 06 Local functional) meta-GGA [6], and the other is to incorporate many known constraints on , such as TPSS (Tao–Perdew–Staroverov–Scuseria) [7] and SCAN meta-GGAs [8].
A more appealing approach for developing meta-GGA functionals is to incorporate exact constraints not only via , but also via the hole . This will allow one to build more exact constraints into a meta-GGA than a meta-GGA constructed by only the constraints on the energy , and thus has a better chance of achieving high accuracy. The starting point of this method is to approximate the hole directly, rather than approximating the hole with the reverse engineering approach [9], as is done in most density functionals. From the hole, one can calculate the underlying functional via Equation (1). Then, one can establish a desirable one-to-one relationship between a density functional and the associated hole. This is a natural method. The difficulty is that the conventionally defined exchange hole is nonlocal in nature. It was shown that this difficulty can be largely reduced with a general coordinate transformation [10], because the conventional exchange hole becomes localized under the general coordinate transformation. This offers a way to approximate the exchange hole with a semilocal functional. We have recently illustrated this approach by developing a nonempirical Tao-Mo (TM) meta-GGA functional [11]. Numerical tests show that this functional can achieve remarkable accuracy for wide-ranging properties of molecules and solids [12,13].
Here we apply the TM meta-GGA to study the excitation and binding energies of titanium dioxide and water clusters, as well as reaction barrier heights. To have a better understanding of the performance of the TM functional, a combination of the TM exchange part with the original TPSS correlation (i.e., TMTPSS) is also included in this study. The selection of these systems is based on two considerations. First, these systems are formed with different bonding types (e.g., ionic bonds, covalent bonds, and hydrogen-bonds), and are thus physically different systems. Second, these clusters by themselves are of great interest, due to their remarkable properties and applications. All of these properties (i.e., excitation energies of clusters and reaction barrier heights) are closely related to electronic nonlocality. They represent a stringent test for semilocal DFT methods. Our calculations show that in all the cases, the TM and TMTPSS functionals consistently show better accuracy, improving upon commonly-used semilocal functionals. It is competitive with computationally more expensive hybrid functionals, pushing cost-effective first-principles prediction to higher accuracy.
2. Results
2.1. Binding Energies and Excitation Energy of Titanium Dioxide Cluster
Titanium dioxide () has attracted great attention in the past few decades [14,15,16,17], due to its low cost, environmental compatibility, and experimentally proven potential for photocatalytic and photovoltaic applications [14,15]. In particular, the use of as heterogeneous catalysts for photochemical splitting of water to produce renewable hydrogen and dye-sensitized solar cells has been the subject of intense research [14,15,16,17].
To understand the microscopic structure of , the binding energies of with n = 2–4 clusters in the gas phase are investigated. Figure 1 shows the chemical structure of , while Table 1 displays the binding energies of clusters from density functional calculations. From Table 1, we observe that the binding energies between molecules are in the range of a normal chemical bond. However, due to the large practicabilities of the ion and transition-metal ions, there exist strong vdW interactions in these ionic solid clusters. Because the long-range vdW interaction is missing in standard density functionals, this effect leads to large mean absolute errors (MAE) of all conventional DFT methods studied for this kind of cluster. Nevertheless, the TM and TMTPSS functionals give good improvement upon other semilocal DFT methods studied, such as PBE (Perdew–Burke–Ernzerhof) and TPSS. They are comparable to the more expensive hybrid PBE0 or even more accurate than B3LYP, as shown in Table 1. This performance is consistent with other recent studies [18,19].
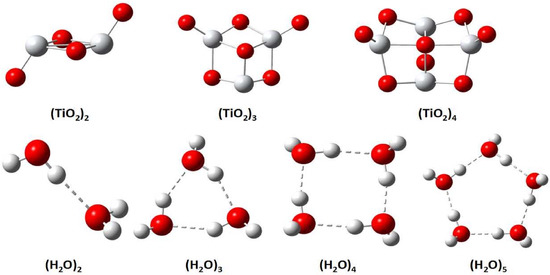
Figure 1.
Equilibrium structure of and clusters.

Table 1.
Binding energy per molecule (kcal/mol) of (n = 2–4) clusters evaluated with different methods using the 6-311++G(3df,3pd) basis set. B3LYP: a hybrid functional with Beck’s three-parameter exchange part and Lee-Yang-Parr correlation; PBE: Perdew–Burke–Ernzerhof functional; PBE0: Perdew–Burke–Ernzerhof hybrid functional; TM: Tao-Mo density functional; TPSS: Tao–Perdew–Staroverov–Scuseria correlation functional; TMTPSS: combination of the TM exchange part with the original TPSS correlation; MP2: Mller-Plesset expansion truncated at second-order. ME: Mean Error; MAE: mean absolute error; ME = Theory-MP2.
Table 1 also shows that the binding energy per molecule () increases with cluster size, as predicted by all DFT methods. This trend qualitatively agrees with MP2 prediction. For all methods including MP2, the increasing rate becomes smaller and should be gradually saturated to the cohesive energy of the bulk titanium dioxide when n > 7 [20].
Next, we study the lowest singlet excitation energies of titanium dioxide clusters with time-dependent DFT (TDDFT) within the adiabatic approximations. These excitation energies correspond to the HOMO–LUMO energy gaps of the cluster. In the large-size (n > 7) or bulk limit, they should converge to the band gap of bulk titanium dioxide [20,21]. Figure 2 shows the lowest excitation energies of the (n = 1–4) clusters calculated from PBE, TPSS, TM, TMTPSS, B3LYP, and PBE0 within the adiabatic TDDFT. As shown in Figure 2, for small clusters with n = 1–4, all these excitation energies show strong odd–even oscillation in accordance with previous DFT results [20], and the predicted values are still far above the experimental results [20,21]. All of these clusters show a large energy gap consistent with the previous calculations [20]. However, the calculations overestimated the gaps considerably, probably because relaxation effects were not included [21,22].
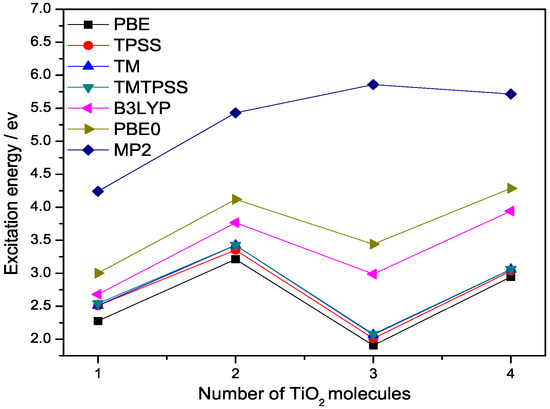
Figure 2.
Lowest singlet excitation energies (eV) of (n = 1–4) calculated with different methods at 6-311++G(3df,3pd) basis set.
From Figure 2 we can see that all these DFT methods exhibit a similar trend for the lowest excitation energies of the (n = 2–4) clusters. All DFT lines show a drop of the excitation energy from 2 to 3 molecules, but MP2 shows an increase. There is a noticeable excitation energy shift between semilocal and hybrid functionals, leading to the excitation energies of hybrid functionals being closer to the accurate MP2 values. This shift clearly arises from the Hatree–Fock (HF) exchange built in these two hybrid functionals. The magnitude of the shift is dependent upon the amount of the HF exchange included in a hybrid functional. For example, PBE0 contains 1/4 HF exchange, while B3LYP contains 1/5 HF exchange. The HF exchange not only provides electronic nonlocality, which is necessary for some properties discussed above, but also improves the density tail behaviour of the exchange potential and reduces self-interaction error. As a result, hybrid functionals are more accurate than semilocal DFT for excitation energies, as argued by Becke and demonstrated in the literature [23]. However, this does not mean that the more HF exchange contained in a hybrid functional, the more accuracy we can achieve, because one needs to consider the balance between the exchange and correlation parts or error cancellation.
Figure 2 also shows that the deviation of semilocal functionals from hybrid functionals becomes slightly larger as cluster size increases. Similar to hybrid functionals, the lowest singlet excitation energies of all the semilocal functionals will eventually saturate to the band gap of the bulk titanium dioxide. We observe that among the semilocal functionals, TM and TMTPSS are more accurate than others. In contrast, PBE gives the lowest excitation energies. While PBE0 does correct the exchange description relative to PBE, there is no correction whatsoever in PBE0 when it comes to dispersive interactions—a nonlocal correlation effect.
2.2. Binding Energies and Excitation Energy of Water Cluster
Water is the most abundant matter that covers about four-fifths of the Earth’s surface. It has a complicated structure and anomalous properties that have not been well understood [24]. Despite considerable efforts, many of the properties of water remain puzzling [25]. Study shows that liquid water is not homogeneous at the nanoscopic level [26]. To understand the detail of the structure, a fundamental understanding of water clusters is important [27,28]. A feature of water clusters is their intermolecular interaction consisting of hydrogen bonds and a smaller part of the vdW interaction. Accurate description of these weak interactions presents a great challenge to DFT [29]. Figure 1 shows the optimized structures of various water clusters, while Table 2 shows the comparison of the binding energies of water clusters (n = 2–5) between DFT methods and MP2. From Table 2, we can observe that TM can achieve high accuracy, substantially improving upon other DFT methods. From Table 2, one can find that PBE0 performs worst. This is because PBE0 corrects the exchange description relative to PBE, but there is no correction whatsoever in PBE0 when it comes to dispersive interactions—a nonlocal correlation effect.

Table 2.
Binding energies (kcal/mol) of (n = 2–5) clusters from various DFT methods at the 6-311++G(3df,3pd) basis set. MP2 values of water clusters are taken from Reference [26]. ME = Theory-MP2. D3BJ: Grimme’s third generation dispersion with Becke-Johnson rational damping.
Dispersion plays a vital role in the energetics of water systems. Table 2 also shows the results of PBE-D3BJ and TPSS-D3BJ developed by Grimme [30,31] for comparison. It is shown that the addition of dispersion (DFT-D3) to a semi-local functional always increases binding energy , as expected [29,32], but is not correctly described by the semi-local functionals. The same results are obtained by others [29,32]. The addition of dispersion to a semi-local functional can bring large changes in the structure and equilibrium density of the liquid, so that errors are large [29].
To have a better understanding of water clusters, we calculate the lowest vertical excitation energies of a few small water clusters, in which the accurate ab initio values are available for comparison. The results are displayed in Figure 3. From Figure 3, we observe that the lowest vertical excitation energy of a water cluster quickly saturates to the band gaps of ice, which are smaller than experiment ( eV) [33,34,35,36,37,38,39,40], but with PBE0 being the closest one, followed by B3LYP and semilocal DFT methods for the same reason discussed above. We also observe that TM and TMTPSS give good match results with MP2 value among semilocal DFT methods, although the discrepancy is still too large due to the nonlocality issue. This indicates the robustness of the TM exchange. From Figure 3, we can also observe that all the calculated excitation energies tend to be red-shifted with respect to the MP2 values, as expected.
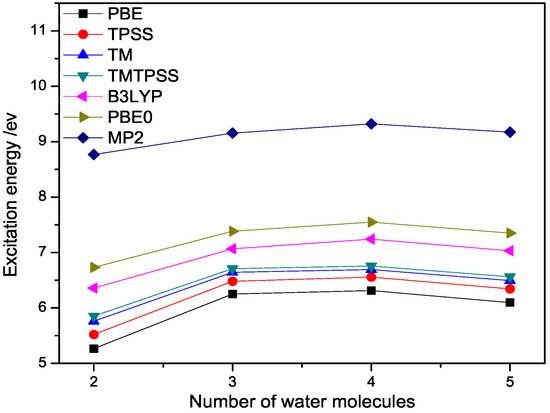
Figure 3.
The lowest excitation energy (eV) of (n = 2–5) calculated with different methods at 6-311++G(3df,3pd) basis set.
2.3. BH76 Barrier Heights
Prediction of reaction barrier heights presents a great challenge to semilocal DFT, due to the presence of stretched bonds in a transition state, which is closely related to electronic nonlocality. The BH76 (76 Barrier Heights) test set consists of 38 hydrogen transfer barrier heights and 38 non-hydrogen transfer barrier heights. It is a standard test set that has been widely used to benchmark the theoretical methods [41,42]. Table 3 shows the statistical errors of the reaction barrier heights evaluated with the TM and TMTPSS functionals, compared with other density functionals.

Table 3.
Summary of deviations of the calculated reaction barrier heights from best values [41] for the BH76 test set. Results are taken from Reference [42] for M06L, Reference [8] for SCAN, and Reference [41] for local spin-density approximation (LSDA), PBE, TPSS, B3LYP, and PBE0. All values are in kcal/mol. ME = theory − best values from Reference [41].
From Table 3, we can see that like other semilocal functionals, the TM and TMTPSS functionals tend to underestimate reaction barrier heights. The order of MAE for the BH76 set with different methods is PBE0 < M06L < B3LYP < TMTPSS < TM < SCAN < TPSS < PBE < LSDA. Reaction barrier heights are generally predicted more accurately with nonlocal density functionals, because such functionals exhibit a small delocalization error [43] for species with stretched bonds (i.e., transition states). From Table 3, we can also see a large reduction of errors in reaction barrier heights from non-hybrid to hybrid functionals (e.g., from PBE to PBE0). Since BH76 was used to parameterize the M06L meta-GGA functional, we have not included it for comparison, but list it in Table 3 for reference.
3. Materials and Methods
All calculations of clusters were carried out using the modified Gaussian 09 [44] with 6-311++G(3df,3pd) basis set. The ground-state geometries of molecules and clusters were performed self-consistently with respective density functionals. Based on the optimized geometries, we evaluated the lowest vertical excitation energies of clusters with TDDFT within the adiabatic approximation. The binding energies of clusters were calculated as energy difference between cluster and constituent molecules. Since our calculations involve the treatment of both the ground state (optimization of molecular geometry) and excited states, for consistency, the same basis was used in all calculations. The ultrafine grid (Grid = Ultrafine) in numerical integration and the tight self-consistent field convergence criterion (SCF = Tight) were used. To make comparison consistent, we performed the calculations with all density functionals, rather than taking the data directly from the literature for and clusters. Since reaction barrier height calculations are highly sensitive to the basis set, in this work, TM and TMTPSS methods were used to perform the geometries optimization and frequency analysis of the reactants, transition states, and products with MG3 (Multi-coefficient Gaussian-3) basis set by using their QCISD(Quadratic configuration interaction single and double excitation methods)/MG3 structure [41]. Throughout the paper, ME and MAE are mean error (deviation) and absolute mean error (deviation) respectively.
4. Conclusions
We have studied the binding energies and excitation energies of clusters, as well as the BH76 barrier heights, which cover all bonding types, with recently proposed semilocal functionals. In this study, commonly-used semilocal and hybrid density functionals have also been included for comparison. Our calculations show that the TM and TMTPSS functionals can achieve good performance for these properties and systems, improving upon commonly-used semilocal DFT methods. We find that in some cases, they are competitive to the most popular hybrid functionals, but with lower computational cost.
A striking feature of the TM functional is that it incorporates many exact constraints through the underlying exchange hole, such as uniform coordinate scaling [45], negativity, correct uniform-gas limit, and spin scaling relationship [46]. The high accuracy of the TM functional may greatly benefit from its exchange enhancement factor, which has the same small oscillatory behavior as M06L [47]. Therefore, the TM functional can capture or extend the short-range part of the van der Waals interaction due to the de-enhancement (relative to the LSDA) in some regions, leading to an improvement for most properties. The TM correlation functional was developed separately from the exchange part, which respects all the exact conditions that the TPSS correlation satisfies, and improvement over TPSS in the low-density (strong-interaction) limit. Therefore, it is not surprising that the TMTPSS (TMx+TPSSc) functional can give the best results of energy calculation in many systems studied.
Acknowledgments
G.T. was supported by National Natural Science Foundation of China under Grant No. 51264021, the China Scholarship Council and by Back-up Personnel Foundation of Academic and Technology Leaders of Yunnan Province under Grant No. 2011HR013. J.T. and Y.M. acknowledge support from the NSF under Grant No. CHE-1640584. J.T. also acknowledges support from Temple start-up via John Perdew. Partial computational support was provided by Temple University.
Author Contributions
G.T. conceived and designed the experiments; G.T. performed the experiments; G.T. and J.T. analyzed the data; G.T. wrote the paper; G.T., Y.M. and J.T. contributed the discussions and revisions of the manuscript.
Conflicts of Interest
The authors declare no conflict of interests.
References
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1136. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Vosko, H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1201. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Constantin, L.A.; Perdew, J.P.; Tao, J. Meta-generalized gradient approximation for the exchange-correlation hole with an application to the jellium surface energy. Phys. Rev. B 2006, 73, 205104. [Google Scholar] [CrossRef]
- Tao, J.; Springborg, M.; Perdew, J.P. Properties of the exchange hole under an appropriate coordinate transformation. J. Chem. Phys. 2003, 119, 6457–6502. [Google Scholar] [CrossRef]
- Tao, J.; Mo, Y. Accurate semilocal density functional for condensed-matter physics and quantum chemistry. Phys. Rev. Lett. 2016, 117, 073001. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.; Tian, G.; Car, R.; Staroverov, V.N.; Scuseria, G.E.; Tao, J. Performance of a nonempirical density functional on molecules and hydrogen-bonded complexes. J. Chem. Phys. 2016, 145, 234306. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.; Car, R.; Staroverov, V.N.; Scuseria, G.E.; Tao, J. Assessment of a nonempirical semilocal density functional on solids and surfaces. Phys. Rev. B. 2017, 95, 035118. [Google Scholar] [CrossRef]
- Gratzel, M. Photoelectrochemical cells. Nature 2001, 414, 338–344. [Google Scholar] [CrossRef] [PubMed]
- Tyo, E.C.; Vajda, S. Catalysis by clusters with precise numbers of atoms. Nature Nanotech. 2015, 10, 577–588. [Google Scholar] [CrossRef] [PubMed]
- Cernuto, G.; Masciocchi, N.; Cervellino, A.; Colonna, G.M.; Guagliardi, A. Size and shape dependence of the photocatalytic activity of TiO2 nanocrystals: A total scattering Debye function study. J. Am. Chem. Soc. 2011, 133, 3114–3119. [Google Scholar] [CrossRef] [PubMed]
- Cho, D.; Ko, K.C.; Lamiel-Garcia, O. Effect of size and structure on the ground-state and excited-state electronic structure of TiO2 Nanoparticles. J. Chem. Theory Comput. 2016, 12, 3751–3763. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.; Tian, G.; Tao, J. Performance of a nonempirical exchange functional from the density matrix expansion: Comparative study with different correlation. Phys. Chem. 2017. resubmitted. [Google Scholar]
- Tian, G.; Mo, Y.; Tao, J. Performance of a nonempirical semilocal density-functional on noncovalent interactions. J. Chem. Phys. 2017. resubmitted. [Google Scholar]
- Qu, Z.; Kroes, G.J. Theoretical study of the electronic structure and stability of titanium dioxide clusters (TiO2)n with n = 1–9. J. Phys. Chem. B 2006, 110, 8998–9007. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wang, L.S. Electronic structure of titanium oxide clusters: TiOy (y = 1–3) and (TiO2)n (n = 1–4). J. Chem. Phys. 1997, 107, 8221–8228. [Google Scholar] [CrossRef]
- Zhai, H.J.; Wang, L.S. Probing the Electronic Structure and Band Gap Evolution of Titanium Oxide Clusters (n = 1–10) Using Photoelectron Spectroscopy. J. Am. Chem. Soc. 2007, 129, 3022–3026. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Armstrong, G. Supercooled water: Ice maybe. Nat. Chem. 2010, 2, 256. [Google Scholar] [CrossRef]
- Moore, E.B.; Molinero, V. Structural transformation in supercooled water controls the crystallization rate of ice. Nature 2011, 479, 506–508. [Google Scholar] [CrossRef] [PubMed]
- Xantheas, S.S.; Burnham, C.J.; Harrison, R.J. Development of transferable interaction models for water. II. Accurate energetics of the first few water clusters from first principles. J. Chem. Phys. 2002, 116, 1493–1499. [Google Scholar] [CrossRef]
- Liu, K.; Cruzan, J.D.; Saykally, R.J. Water clusters. Science 1996, 271, 929–931. [Google Scholar] [CrossRef]
- Pradzynski, C.C.; Forck, R.M.; Zeuch, T.; Slavíček, P.; Buck, U. A fully size-resolved perspective on the crystallization of water clusters. Science 2012, 337, 1529–1532. [Google Scholar] [CrossRef] [PubMed]
- Gillan, M.J.; Alfé, D.; Michaelides, A. Perspective: How good is DFT for water? J. Chem. Phys. 2016, 144, 130901. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Santra, B.; Michaelides, A.; Fuchs, M.; Tkatchenko, A.; Filippi, C.; Scheffler, M. On the accuracy of density-functional theory exchange-correlation functionals for H bonds in small water clusters. II. The water hexamer and van der Waals interactions. J. Chem. Phys. 2008, 129, 194111. [Google Scholar] [CrossRef] [PubMed]
- Hahn, P.H.; Schmidt, W.G.; Seino, K.; Preuss, M.; Bechstedt, F.; Bernholc, J. Optical absorption of water: Coulomb effects versus hydrogen bonding. Phys. Rev. Lett. 2005, 94, 037404. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Li, W.-F.; Koster, R.S.; Klime, J.; van Blaaderen, A.; van Huis, M.A. The accurate calculation of the band gap of liquid water by means of GW corrections applied to plane-wave density functional theory molecular dynamics simulations. Phys. Chem. Chem. Phys. 2015, 17, 365–375. [Google Scholar] [CrossRef] [PubMed]
- Warren, S.G. Optical constants of ice from the ultraviolet to the microwave. Appl. Opt. 1984, 23, 1206–1225. [Google Scholar] [CrossRef] [PubMed]
- Minton, A.P. Far-ultraviolet spectrum of ice. J. Phys. Chem. 1971, 75, 1162–1164. [Google Scholar] [CrossRef]
- Painter, L.R.; Birkhoff, R.D.; Arakawa, E.T. Collective oscillation in liquid water. J. Chem. Phys. 1969, 51, 243. [Google Scholar] [CrossRef]
- Seki, M.; Kobayashi, K.; Nakahara, J. Optical spectra of hexagonal ice. J. Phys. Soc. Jpn. 1981, 50, 2643–2648. [Google Scholar] [CrossRef]
- Shibaguchi, T.; Onuki, H.; Onaka, R. Electronic structures of water and ice. J. Phys. Soc. Jpn. 1977, 42, 152–154. [Google Scholar] [CrossRef]
- Engel, E.A.; Monserrat, B.; Needs, R.J. Vibrational renormalisation of the electronic band gap in hexagonal and cubic ice. J. Chem. Phys. 2015, 143, 244708. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Gonzlez-Garca, N.; Truhlar, D.G. Benchmark Database of barrier heights for heavy atom transfer, nucleophilic substitution, association, and unimolecular reactions and its use to test theoretical methods. J. Phys. Chem. A 2005, 109, 2012–2018. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Haunschild, R.; Xiao, B.; Bulik, I.W.; Scuseria, G.E.; Perdew, J.P. Semilocal and hybrid meta-generalized gradient approximations based on the understanding of the kinetic-energy-density dependence. J. Chem. Phys. 2013, 138, 044113. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.J.; Mori-Snchez, P.; Yang, W. Challenges for Density Functional Theory. Chem. Rev. 2012, 112, 289. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Levy, M.; Perdew, J.P. Hellmann-Feynman, virial, and scaling requisites for the exact universal density functionals. Shape of the correlation potential and diamagnetic susceptibility for atoms. Phys. Rev. A 1985, 32, 2010. [Google Scholar] [CrossRef]
- Oliver, G.L.; Perdew, J.P. Spin-density gradient expansion for the kinetic energy. Phys. Rev. A 1979, 20, 397. [Google Scholar] [CrossRef]
- Johnson, E.R.; Becke, A.D.; Sherrill, C.D.; DiLabio, G.A. Oscillations in meta-generalized-gradient approximation potential energy surfaces for dispersion-bound complexes. J. Chem. Phys. 2009, 131, 034111. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).