An Incompressible, Depth-Averaged Lattice Boltzmann Method for Liquid Flow in Microfluidic Devices with Variable Aperture
Abstract
:1. Introduction
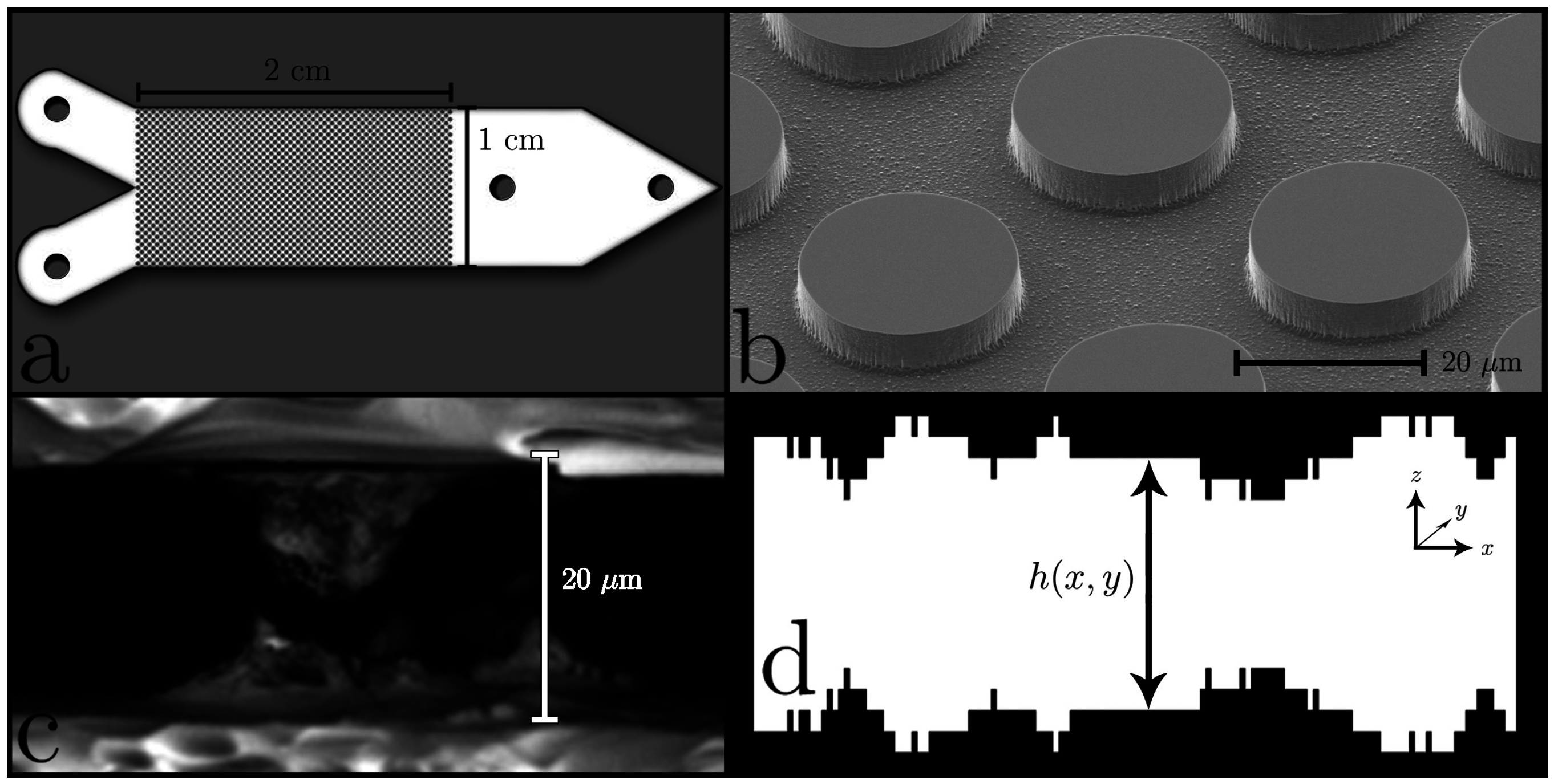
2. Methods
2.1. Governing Equations
2.2. The Lattice Boltzmann Method: A Brief Overview
2.3. Solving for and : Determining the True Velocity Field
2.4. Solving for and : Approximating the True Velocity Field
2.5. Comparing and to
2.6. Computing Permeability
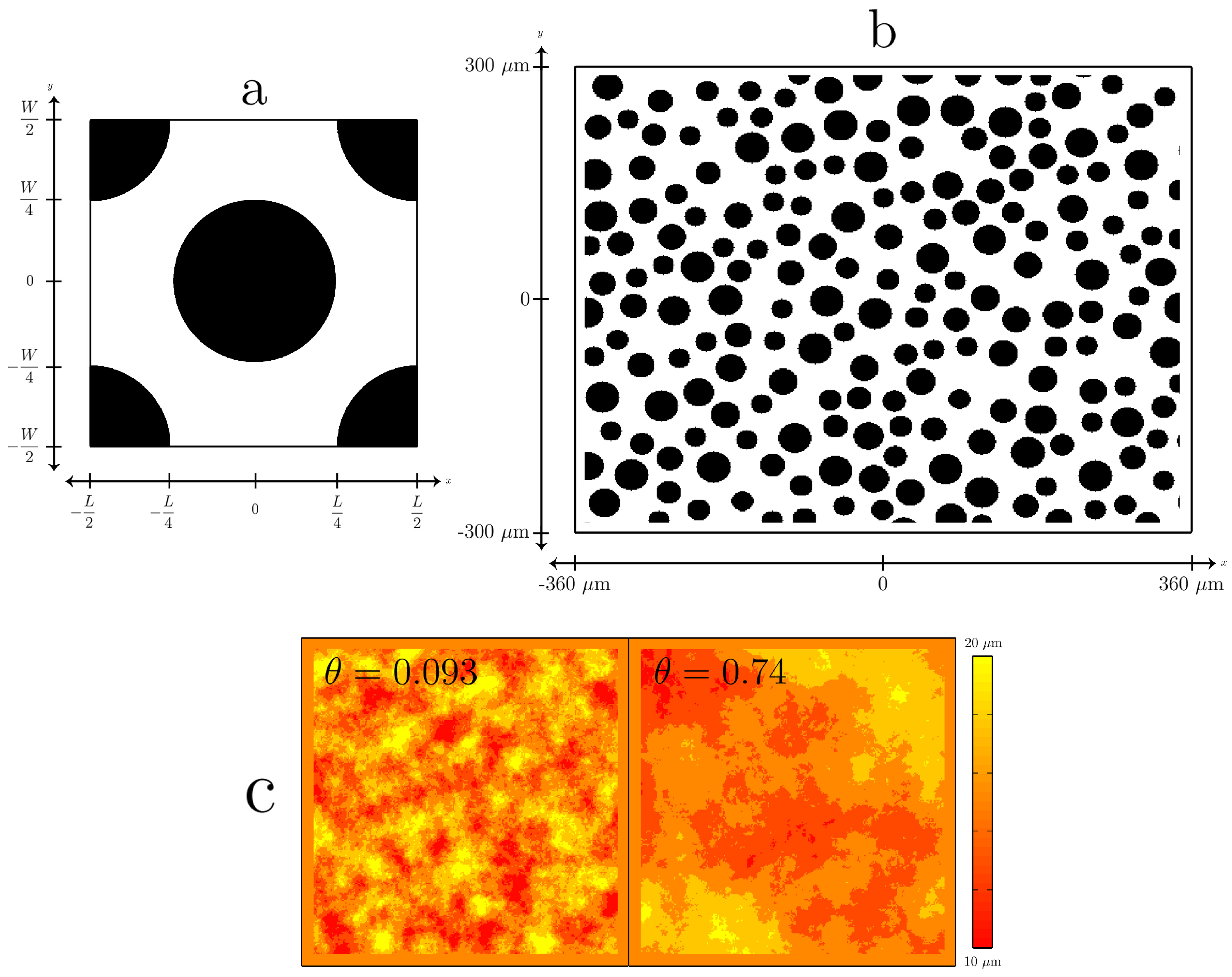
3. Test Cases
4. Results
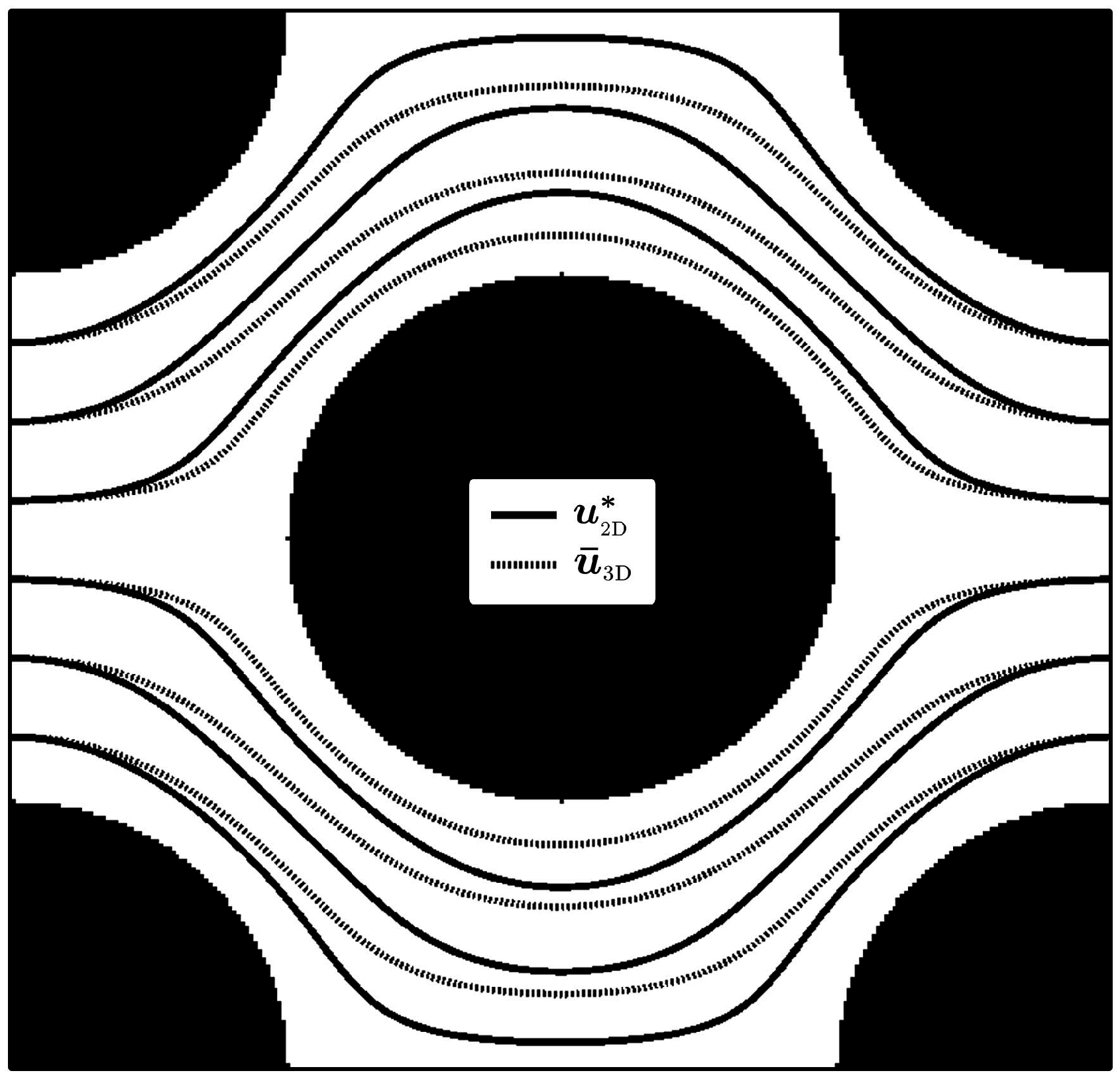
4.1. Unit Cell with Uniform Aperture
| Normalized RMSE | ||||||
|---|---|---|---|---|---|---|
| Test Case | Error in k | Speedup | ||||
| unit cell (uniform aperture) | 0.0090 | 0.0045 | 0.18 | 0.088 | 0.8% | 49.6 |
| unit cell (variable aperture) | 0.020 | 0.026 | 0.19 | 0.19 | 8.3 ± 2.7 % | 41.1 ± 3.5 |
| heterogeneous pore geometry | 0.0094 | 0.0069 | 0.086 | 0.054 | 11% | 40.5 |
4.2. Unit Cell with Spatially-Variable Aperture
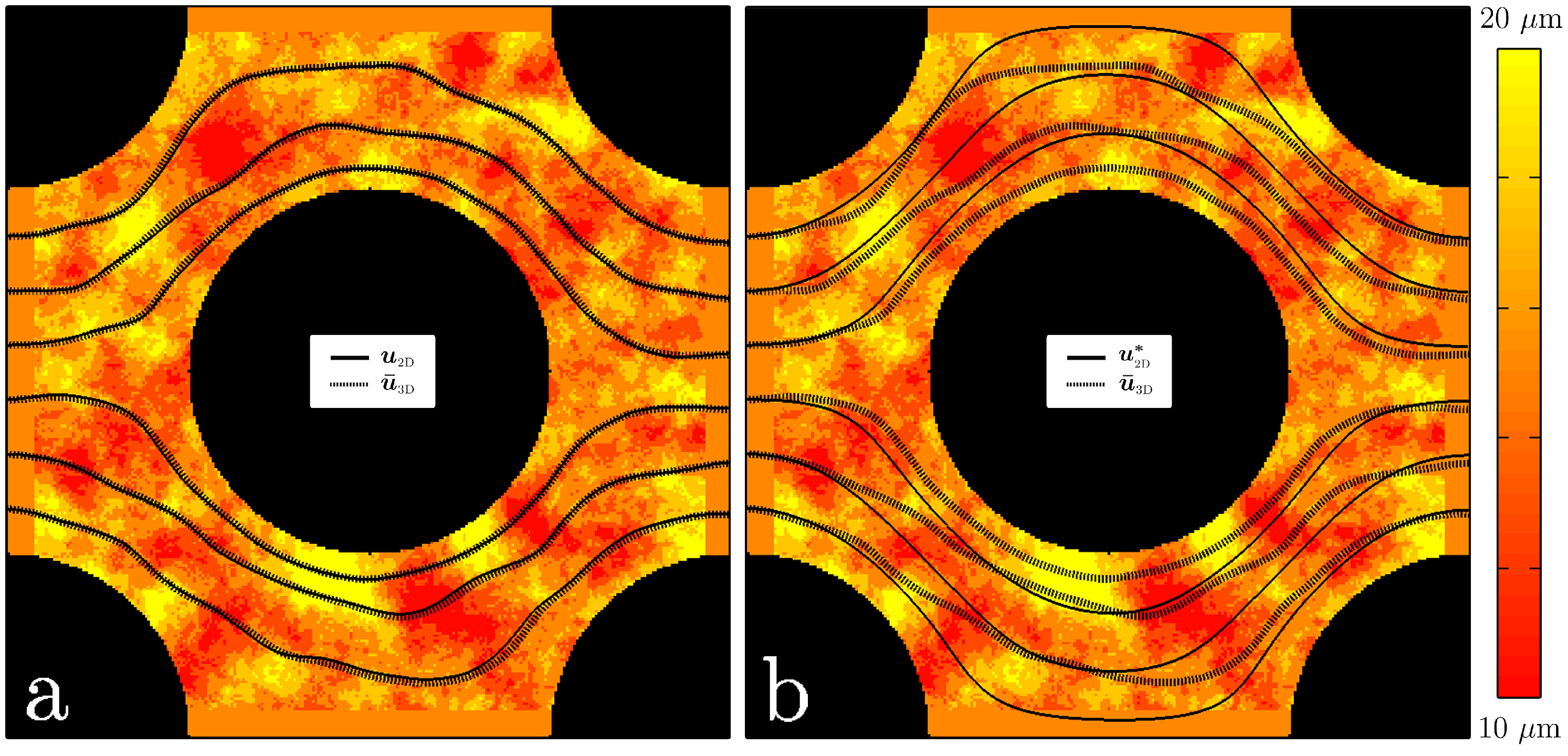
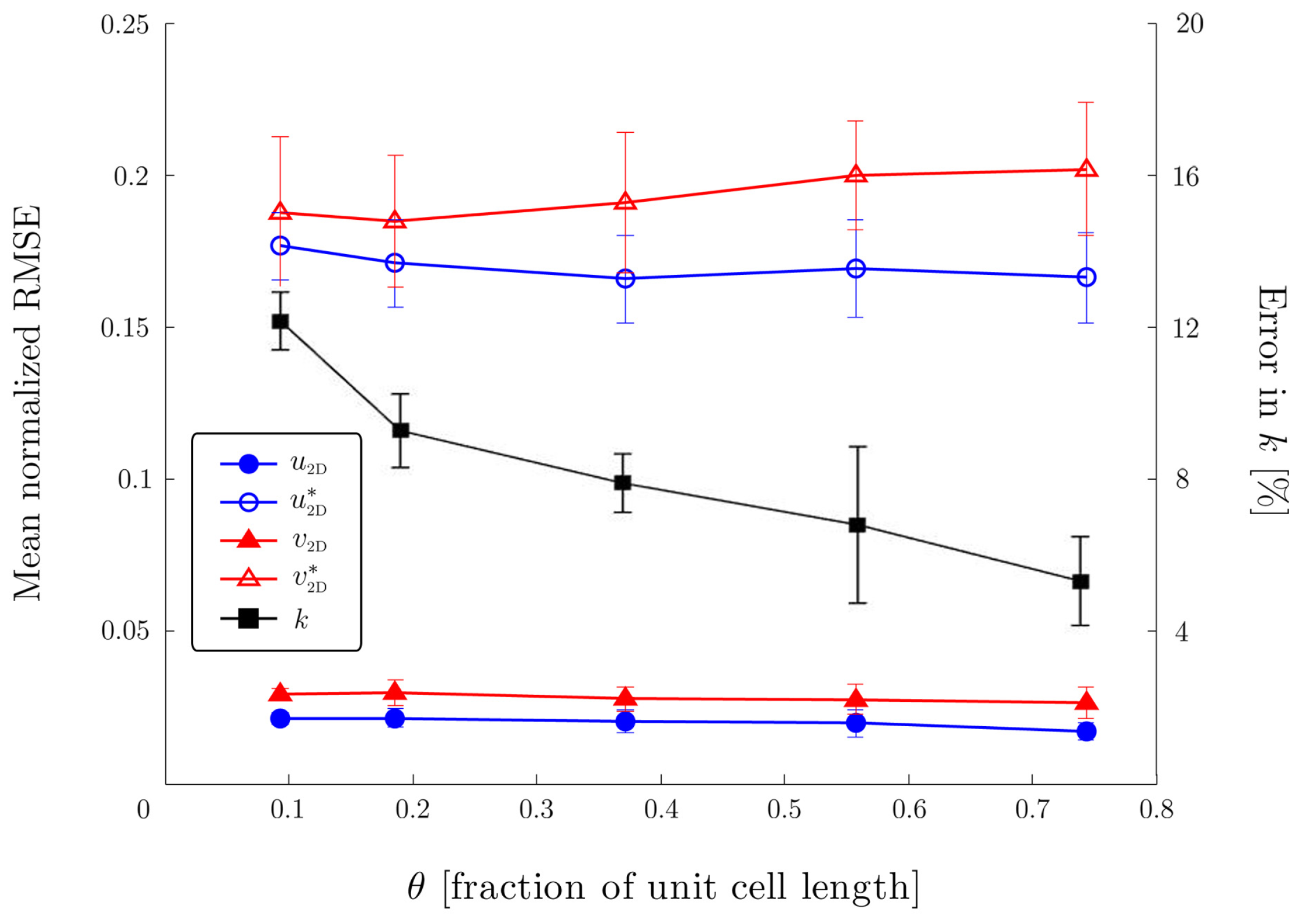
4.3. Heterogeneous Pore Geometry

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Boyd, V.; Yoon, H.; Zhang, C.; Oostrom, M.; Hess, N.; Fouke, B.; Valocchi, A.J.; Werth, C.J. Influence of Mg2+ on CaCO3 precipitation during subsurface reactive transport in a homogeneous silicon-etched pore network. Geochim. Cosmochim. Acta 2014, 135, 321–335. [Google Scholar] [CrossRef]
- Zhang, C.; Dehoff, K.; Hess, N.; Oostrom, M.; Wietsma, T.W.; Valocchi, A.J.; Fouke, B.W.; Werth, C.J. Pore-Scale Study of Transverse Mixing Induced CaCO3 Precipitation and Permeability Reduction in a Model Subsurface Sedimentary System. Environ. Sci. Technol. 2010, 44, 7833–7838. [Google Scholar] [CrossRef] [PubMed]
- Willingham, T.W.; Werth, C.J.; Valocchi, A.J. Evaluation of the Effects of Porous Media Structure on Mixing-Controlled Reactions Using Pore-Scale Modeling and Micromodel Experiments. Environ. Sci. Technol. 2008, 42, 3185–3193. [Google Scholar] [CrossRef] [PubMed]
- Yoon, H.; Valocchi, A.J.; Werth, C.J.; Dewers, T. Pore-scale simulation of mixing-induced calcium carbonate precipitation and dissolution in a microfluidic pore network. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Knutson, C.E.; Werth, C.J.; Valocchi, A.J. Pore-scale simulation of biomass growth along the transverse mixing zone of a model two-dimensional porous medium. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Tang, Y.; Valocchi, A.J.; Werth, C.J.; Liu, H. An improved pore-scale biofilm model and comparison with a microfluidic flow cell experiment. Water Resour. Res. 2013, 49, 8370–8382. [Google Scholar] [CrossRef]
- Willingham, T.; Zhang, C.; Werth, C.J.; Valocchi, A.J.; Oostrom, M.; Wietsma, T.W. Using dispersivity values to quantify the effects of pore-scale flow focusing on enhanced reaction along a transverse mixing zone. Adv. Water Resour. 2010, 33, 525–535. [Google Scholar] [CrossRef]
- Venturoli, M.; Boek, E.S. Two-dimensional lattice-Boltzmann simulations of single phase flow in a pseudo two-dimensional micromodel. Phys. A Stat. Mech. Appl. 2006, 362, 23–29. [Google Scholar] [CrossRef]
- Boek, E.S.; Venturoli, M. Lattice-Boltzmann Studies of Fluid Flow in Porous Media with Realistic Rock Geometries. Comput. Math. Appl. 2010, 59, 2305–2314. [Google Scholar] [CrossRef]
- Stewart, M.; Ward, A.; Rector, D. A study of pore geometry effects on anisotropy in hydraulic permeability using the lattice-Boltzmann method. Adv. Water Resour. 2006, 29, 1328–1340. [Google Scholar] [CrossRef]
- Harting, J.; Kunert, C.; Hyvaluoma, J. Lattice Boltzmann simulations in microfluidics: Probing the no-slip boundary condition in hydrophobic, rough, and surface nanobubble laden microchannels. Microfluid. Nanofluid. 2010, 8, 1–10. [Google Scholar] [CrossRef]
- Karlin, I.; Bosch, F.; Chikatamarla, S. Gibbs’ principle for the lattice-kinetic theory of fluid dynamics. Phys. Rev. E 2014, 90, 031302. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Luo, L.S.; Miller, C.T. An evaluation of lattice Boltzmann schemes for porous medium flow simulation. Comput. Fluid. 2006, 35, 898–909. [Google Scholar] [CrossRef]
- Talon, L.; Bauer, D.; Gland, N.; Youssef, S.; Auradou, H.; Ginzburg, I. Assessment of the two relaxation time Lattice-Boltzmann scheme to simulate Stokes flow in porous media. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Oron, A.; Davis, S.H.; Bankoff, S.G. Long-scale evolution of thin liquid films. Rev. Mod. Phys. 1997, 69, 931–980. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Brush, D.J.; Thomson, N.R. Fluid Flow in Synthetic Rough-Walled Fractures: Navier-Stokes, Stokes, and Local Cubic Law Simulations. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Flekkøy, E.G.; Oxaal, U.; Feder, J.; Jøssang, T. Hydrodynamic dispersion at stagnation points: Simulations and experiments. Phys. Rev. E 1995, 52, 4952–4962. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific Publishing Co.: Singapore, 2013. [Google Scholar]
- d’Humieres, D.; Ginzburg, I.; Krafczyk, M.; Lallemand, P.; Luo, L.S. Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef] [PubMed]
- McCracken, M.E.; Abraham, J. Multiple-relaxation-time lattice-Boltzmann model for multiphase flow. Phys. Rev. E 2005, 71, 036701. [Google Scholar] [CrossRef] [PubMed]
- Zou, Q.; Hou, S.; Chen, S.; Doolen, G. An improved incompressible lattice Boltzmann model for time-independent flows. J. Stat. Phys. 1995, 81, 35–48. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef] [PubMed]
- Hou, S.; Zou, Q.; Chen, S.; Doolen, G.; Cogley, A.C. Simulation of Cavity Flow by the Lattice Boltzmann Method. J. Comput. Phys. 1995, 118, 329–347. [Google Scholar] [CrossRef]
- Kozintsev, B. Computations with Gaussian Random Fields. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 1999. [Google Scholar]
- Neuville, A.; Flekkøy, E.; Toussaint, R. Influence of asperities on fluid and thermal flow in a fracture: A coupled lattice Boltzmann study. J. Geophys. Res. Solid Earth 2013, 118, 3394–3407. [Google Scholar] [CrossRef]
- Clipped Gaussian Random Fields. Available online: http://math4411.math.umd.edu/cgi-bin/bak/generate.cgi/ (acccessed on 23 November 2015).
- Bouzidi, M.; d’Humieres, D.; Lallemand, P.; Luo, L.S. Lattice Boltzmann Equation on a Two-Dimensional Rectangular Grid. J. Comput. Phys. 2001, 172, 704–717. [Google Scholar] [CrossRef]
- Sukop, M.C.; Thorne, D.T. Lattice Boltzmann Modeling: An Introduction for Geoscientists and Engineers, 1st ed.; Springer Publishing Company: Berlin, Germany, 2010. [Google Scholar]
- Kundu, P.K.; Cohen, I.M. Fluid Mechanics, 4th ed.; Elsevier: Burlington, VT, USA, 2008. [Google Scholar]
- Hiorth, A.; Jettestuen, E.; Cathles, L.; Madland, M. Precipitation, dissolution, and ion exchange processes coupled with a lattice Boltzmann advection diffusion solver. Geochim. Cosmochim. Acta 2013, 104, 99–110. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laleian, A.; Valocchi, A.J.; Werth, C.J. An Incompressible, Depth-Averaged Lattice Boltzmann Method for Liquid Flow in Microfluidic Devices with Variable Aperture. Computation 2015, 3, 600-615. https://doi.org/10.3390/computation3040600
Laleian A, Valocchi AJ, Werth CJ. An Incompressible, Depth-Averaged Lattice Boltzmann Method for Liquid Flow in Microfluidic Devices with Variable Aperture. Computation. 2015; 3(4):600-615. https://doi.org/10.3390/computation3040600
Chicago/Turabian StyleLaleian, Artin, Albert J. Valocchi, and Charles J. Werth. 2015. "An Incompressible, Depth-Averaged Lattice Boltzmann Method for Liquid Flow in Microfluidic Devices with Variable Aperture" Computation 3, no. 4: 600-615. https://doi.org/10.3390/computation3040600
APA StyleLaleian, A., Valocchi, A. J., & Werth, C. J. (2015). An Incompressible, Depth-Averaged Lattice Boltzmann Method for Liquid Flow in Microfluidic Devices with Variable Aperture. Computation, 3(4), 600-615. https://doi.org/10.3390/computation3040600






