A Scale Invariant Distribution of the Prime Numbers

Abstract

The irregular distribution of prime numbers amongst the integers has found multiple uses, from engineering applications of cryptography to quantum theory. The degree to which this distribution can be predicted thus has become a subject of current interest. Here, we present a computational analysis of the deviations between the actual positions of the prime numbers and their predicted positions from Riemann’s counting formula, focused on the variance function of these deviations from sequential enumerative bins. We show empirically that these deviations can be described by a class of probabilistic models known as the Tweedie exponential dispersion models that are characterized by a power law relationship between the variance and the mean, known by biologists as Taylor’s power law and by engineers as fluctuation scaling. This power law behavior of the prime number deviations is remarkable in that the same behavior has been found within the distribution of genes and single nucleotide polymorphisms (SNPs) within the human genome, the distribution of animals and plants within their habitats, as well as within many other biological and physical processes. We explain the common features of this behavior through a statistical convergence effect related to the central limit theorem that also generates 1/f noise.

1. Introduction

Prediction of the positions of the prime numbers within the sequence of integers has been a goal that has long interested mathematicians, engineers, and physicists [1]. The prime counting function π(x) gives the actual number of prime numbers up to the positive real value x and takes the form of a step function that increases by the value of 1 with each new prime number. In 1808, Legendre empirically showed that π(x) could be approximated by the formula x/[log(x) − B]; B being a numerical constant [2]. A further improvement in the estimation of π(x) was provided by Gauss, who used the logarithmic integral, defined on the positive real numbers x ≠ 1 for this purpose [3]:

$$\text{li}(x)={\displaystyle {\int }_0^{x}dt/\ln (t)}$$

(1)

These approximations lead to the prime number theorem:

$$\pi (x)\text{ ~ }x/\ln (x)$$

(2)

with initial proofs delivered by Hadamard [4] and de la Vallée Poussin [5] in 1896. A more detailed formula for the general trend in the position of prime numbers has been attributed to Bernhard Riemann [6]:

$$R(x)={\displaystyle \sum _{n=1}^{\infty }}\frac{\mathrm{\mu }(n)}{n}\text{li}(x^{1/n})$$

(3)

expressed in terms of the Möbius function on the integer values n:

$$\mathrm{\mu }(n)=\{\begin{array}{cc}1& \text{if }n=1\hfill \\ 0& \text{if }n\text{ has one or more repeated prime factors }\hfill \\ {(-1)}^k& \text{if }n\text{ is a product of }k\text{ distinct primes}\hfill \end{array}$$

(4)

The present report focuses on the local behavior of the deviations between π(x) and R(x) that have been conjectured to obey the equation [7]:

$$D(x)=R(x)-\pi (x)~{\displaystyle \sum _{\mathrm{\rho }}}R(x^{\mathrm{\rho }})$$

(5)

The summation here is specified over the nontrivial (complex) zeros ρ of the Riemann zeta function, providing a link to Riemann’s hypothesis that the nontrivial zeros of the Riemann zeta function should have as their real component the value of ½ [6]. An equivalent form of this (yet unproven) hypothesis can be stated using the summatory Mertens function [8]:

$$M(n)={\displaystyle \sum _{i=1}^n\mathrm{\mu }(i)}$$

(6)

namely that:

$$M(n)=O(n^{1/2+\mathrm{\epsilon }})$$

(7)

for every positive ε [9].

The deviations D(x) empirically reveal chaotic features, as well as long range correlations [10], that would seem to indicate an underlying structure. Indeed, the positional irregularities of prime numbers have the characteristics of 1/f noise [11], and can be related to the eigenvalues of random matrices from the Gaussian unitary ensemble that are employed in quantum chaos [12]. It remains unclear, though, why the distribution of prime numbers should exhibit such features. Here these deviations are empirically shown to correspond to a probabilistic model characterized by a power law relationship between the variance and the mean. This model belongs to the class of scale invariant, or Tweedie, exponential dispersion models [13] which appear as weak limits for other models under a certain central limit-like effect [14]. This convergence effect, we will argue, leads to a wide manifestation of these models within complex natural and physical systems, analogous to what is seen with the Gaussian distribution within more restricted systems governed by the central limit theorem itself. Moreover, this Tweedie convergence effect can explain the genesis of 1/f noise in such sequences that has implications regarding self-organized criticality [15].

2. Experimental Section

The Riemann prime counting function Equation (3) was estimated here using the Gram series [16]. The absolute values of the prime number deviations |D(x)| were estimated for sequential equal-sized enumerative bins that span the integers. The values of |D(x)| from within each bin were summed and the means and variances of these sums estimated over the region of interest. This process was repeated for successively larger bin sizes so that a log-log plot could be constructed of the sampled variances versus the sampled means with different sized bins. A straight line relationship in such a plot would imply a power law relationship between the variance and the mean, variously referred to in the literature as Taylor’s ecological power law as well as fluctuation scaling.

Empirical cumulative distribution functions (CDFs) were also constructed from the primary sequences of |D(x)| and then compared to the theoretical CDF from the Tweedie compound Poisson-gamma distribution [13], a distribution which inherently expresses a variance to mean power law with its power law exponent constrained to range between 1 and 2.

3. Results and Discussion

3.1. The Variance Function of the Prime Number Deviations

We empirically reviewed the absolute values of the deviations |D(x)| for the first 50,000 integers (Figure 1), focusing on their variance function [13]: The mean and variance of the sequence |D(x)| were estimated and, to extend the range of values for the mean, the sequence |D(x)| was divided into non-overlapping and adjacent counting bins, 10 integers long. The values within each bin were summed and the mean and variance of these sums were estimated over all the bins. This process was repeated for successively larger and larger bin sizes. Figure 2a demonstrates the log-log plot of the empirical variances versus their respective means. A linear relationship was evident on the log-log plot, indicative of a power law relationship ${\mathrm{\sigma }}^2=a\cdot {\overline{m}}^p$ between the variance σ2 and the mean $\overline{m}$ with exponent p = 1.83.

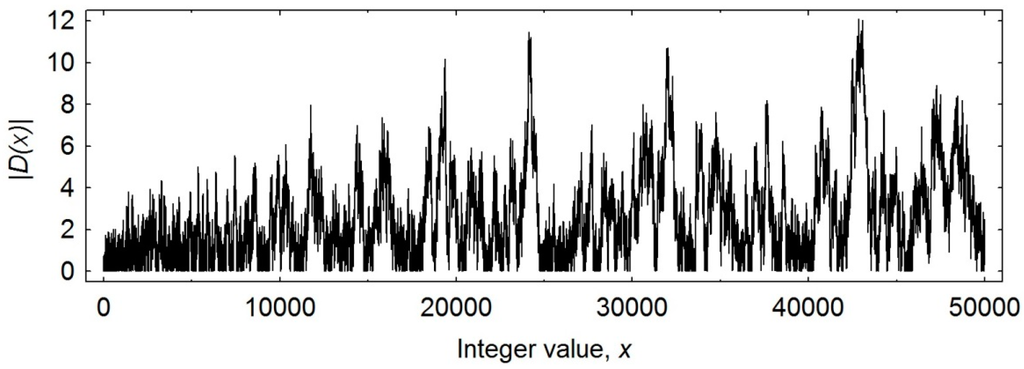
Figure 1. The absolute value |D(x)| of the discrepancy between the prime counting function π(x) and Riemann’s formula R(x) for the first 50,000 integers.

Figure 1. The absolute value |D(x)| of the discrepancy between the prime counting function π(x) and Riemann’s formula R(x) for the first 50,000 integers.

Figure 2. (a) The variance function for the deviations of the prime numbers. A power law relationship was obtained with exponent p = 1.83 and constant a = 1.37; (b) Probability-probability plot. A frequency histogram was constructed for the values |D(x)|. The empirical CDF obeyed a Tweedie compound Poisson-gamma distribution with θ = −0.837, λ = 0.934, α = −0.586 and p = 1.63.

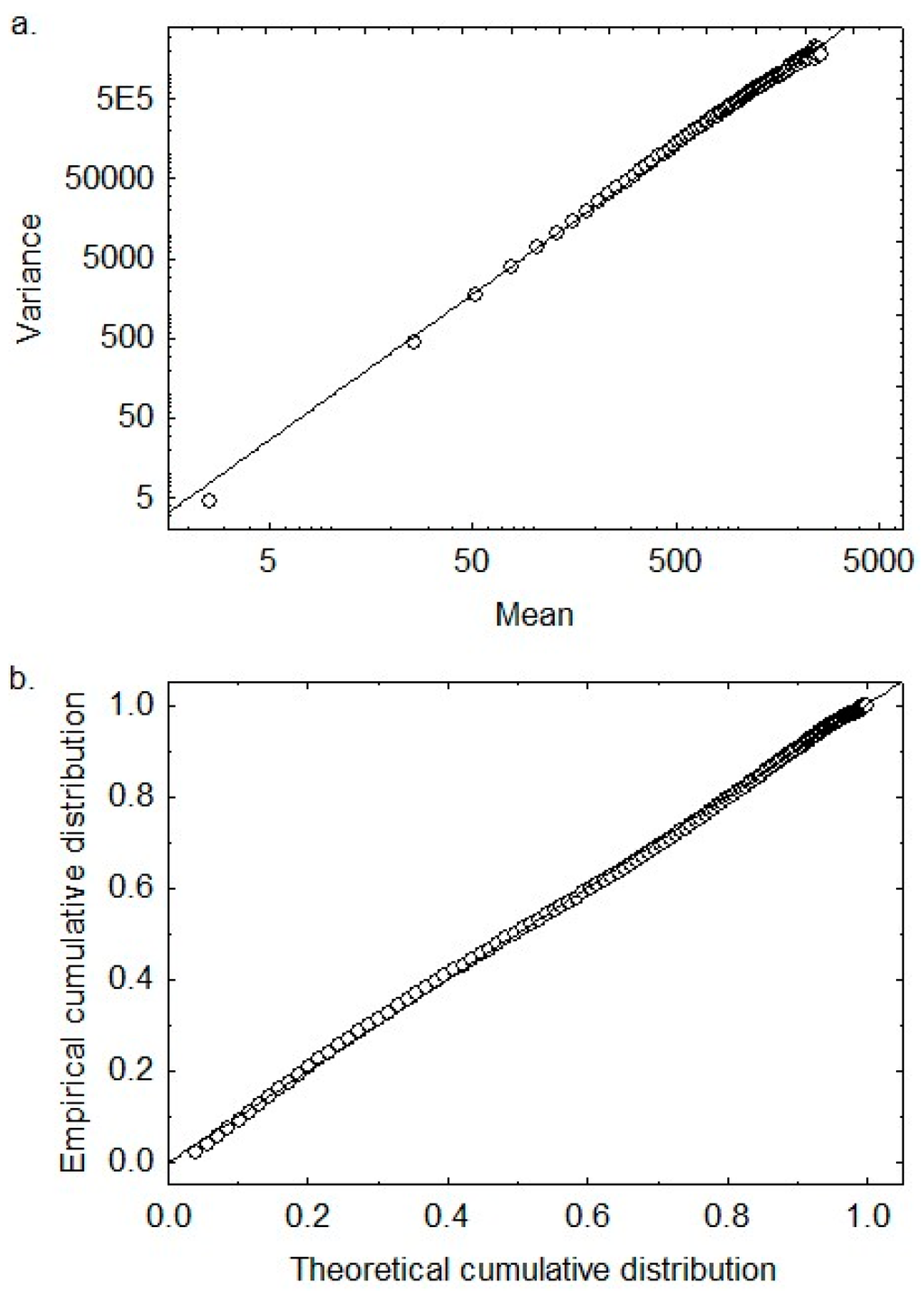
Figure 2. (a) The variance function for the deviations of the prime numbers. A power law relationship was obtained with exponent p = 1.83 and constant a = 1.37; (b) Probability-probability plot. A frequency histogram was constructed for the values |D(x)|. The empirical CDF obeyed a Tweedie compound Poisson-gamma distribution with θ = −0.837, λ = 0.934, α = −0.586 and p = 1.63.

We sought to determine the behavior of the power law for the deviations |D(x)| beyond the first 50,000 integers in order to make sure that this behavior was not simply a loco-regional artifact. Figure 3a provides this function determined from the integers x = 10⁶…10⁷, in steps of 10³. The variance to mean power law fitted this sequence well with p = 1.66. In Figure 3c,e this process was repeated for the integer sequences x = 10⁸…10⁹ in steps of 10⁵ and x = 10¹¹…10¹² in steps of 10⁸, to reveal that variance to mean power law was evident for over 12 orders of magnitude.

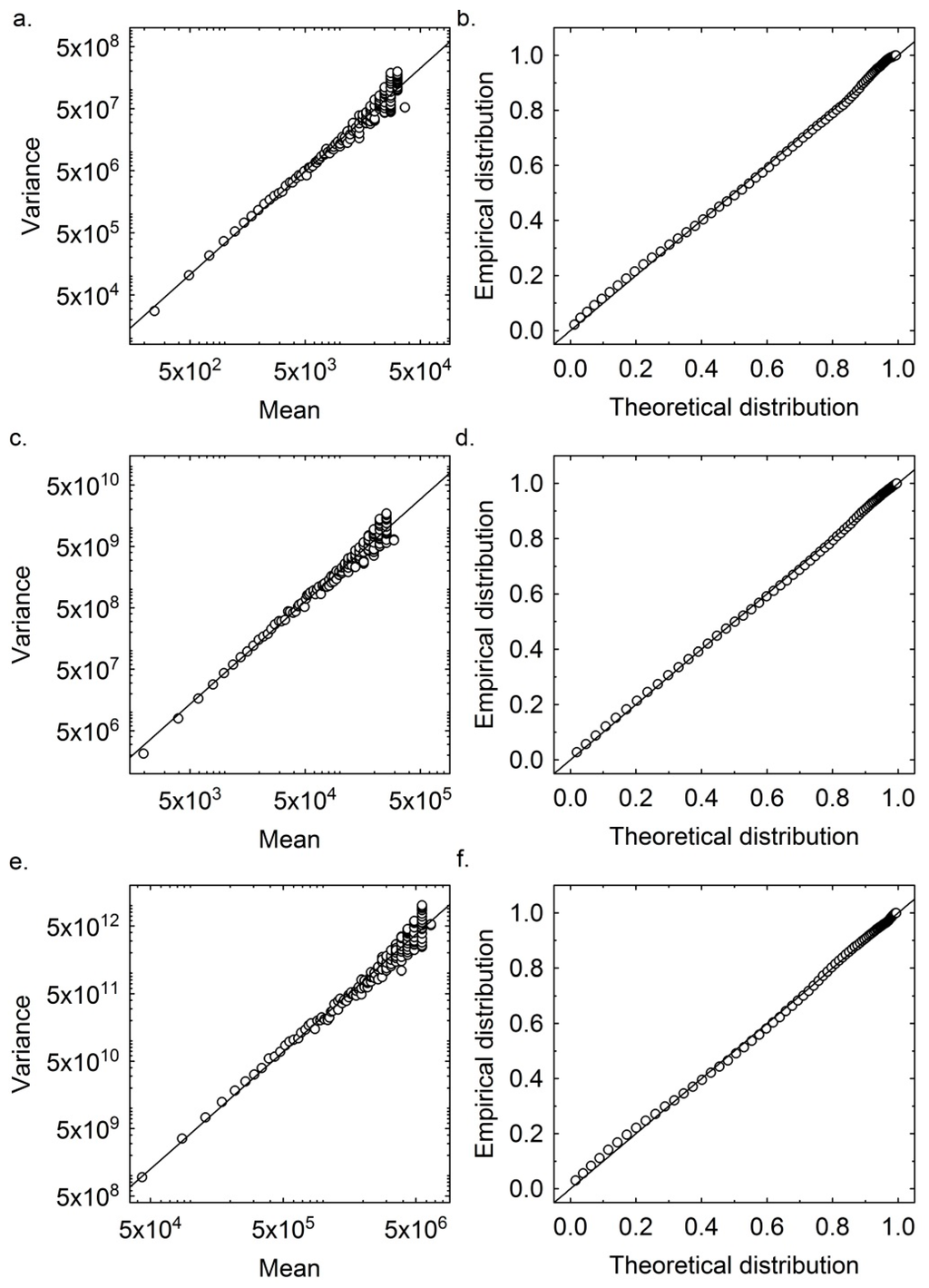
Figure 3. (a) Variance function of |D(x)| for x = 10⁶…10⁷ in steps of 10³. Linear regression gave p = 1.66 and a = 3.53; (b) CDF with x = 10⁶…10⁷ in steps of 10³. Here θ = −0.096, λ = 0.62, α = −0.38 and p = 1.73; (c) Variance function of |D(x)| for x = 10⁸…10⁹ in steps of 10⁵. Here p = 1.67 and a = 9.28; (d) CDF with x = 10⁸…10⁹ in steps of 10⁵. Here θ = −9.94 × 10⁻³, λ = 0.34, α = −0.30 and p = 1.77; (e) Variance function of |D(x)| for x = 10¹¹…10¹² in steps of 10⁸. Here p = 1.74 and a = 8.57; (f) CDF with x = 10¹¹…10¹² in steps of 10⁸. Here θ = −5.37 × 10⁻⁴, λ = 0.067, α = −0.41 and p = 1.71.

Figure 3. (a) Variance function of |D(x)| for x = 10⁶…10⁷ in steps of 10³. Linear regression gave p = 1.66 and a = 3.53; (b) CDF with x = 10⁶…10⁷ in steps of 10³. Here θ = −0.096, λ = 0.62, α = −0.38 and p = 1.73; (c) Variance function of |D(x)| for x = 10⁸…10⁹ in steps of 10⁵. Here p = 1.67 and a = 9.28; (d) CDF with x = 10⁸…10⁹ in steps of 10⁵. Here θ = −9.94 × 10⁻³, λ = 0.34, α = −0.30 and p = 1.77; (e) Variance function of |D(x)| for x = 10¹¹…10¹² in steps of 10⁸. Here p = 1.74 and a = 8.57; (f) CDF with x = 10¹¹…10¹² in steps of 10⁸. Here θ = −5.37 × 10⁻⁴, λ = 0.067, α = −0.41 and p = 1.71.

3.2. Prime Number Deviations as a Self-Similar Process

In our analysis we examined the sequence of prime number deviations Y = (Y_i = |D(i)|: i = 1, 2,…, N) using expanding enumerative bins. Let the mean and variance of this initial sequence be represented by the constants $\widehat{\mathrm{\mu }}=E[Y]$ and ${\widehat{\mathrm{\sigma }}}^2=\mathrm{var}[Y]$, respectively. One can construct a sequence of equal-sized and non-overlapping enumerative bins of integer size m to yield a new set of sequences Y^(m) with the reproductive property:

$$Y_i^{(m)}=\frac{1}{m}\text{(}{Y}_{im-m+1}+\dots +Y_{im}),i>1$$

(8)

The values of m were chosen here so that N/m was an integer. We then have $E[Y^{(m)}]=E[Y]=\widehat{\mathrm{\mu }}$, which is a constant provided that the initial sequence remains unaltered.

Alternatively, the enumerative bins can be used to construct a set of additive sequences Z^(m) so that:

$$Z_i^{(m)}=(Y_{im-m+1}+\dots +Y_{im})$$

(9)

as was done with the prime number deviations |D(x)|. These additive and reproductive sequences are related to each other by the equation $Z_i^{(m)}=m{Y}_i^{(m)}$. We have for their means and variances, $E[Z^{(m)}]=mE[Y^{(m)}]$ and $\mathrm{var}[Z^{(m)}]=m^2\mathrm{var}[Y^{(m)}]$.

The variance to mean power law, demonstrated with the prime number deviations, implies the existence of long range correlations within the initial sequence of deviations. Long range correlations have been studied by Leland [17] in the context of self-similar processes, where the general form for the correlation function r(k) takes the form,

$$r(k)=k^{-\mathrm{\beta }}L(k),k\to \infty$$

(10)

Here, k is the autocorrelation shift, β is a real valued constant such that 0 < β < 1, and L(k) is a slowly varying function for large values of k. For large values of k, this correlation approximates a power law with r(k) ~ k^−β.

Consider the case where the reproductive sequences Y^(m) obey the property:

$$\mathrm{var}[Y^{(m)}]={\widehat{\mathrm{\sigma }}}^2{m}^{-\mathrm{\beta }}$$

(11)

Tsybakov and Georganis [18] have shown that Equation (11) holds if and only if the autocorrelation for the sequence Y is:

$$r(k)=\frac{1}{2}[{(k+1)}^{2-\mathrm{\beta }}-2k^{2-\mathrm{\beta }}+{(k-1)}^{2-\mathrm{\beta }}]$$

(12)

In the limit this formula takes the form [18]:

$$\underset{k\to \infty }{\lim }\frac{r(k)}{k^{-\mathrm{\beta }}}=\frac{1}{2}(2-\mathrm{\beta })(1-\mathrm{\beta }))$$

(13)

where the constant β is related to the Hurst exponent H, β = 2 (1− H) For additive sequences the variance takes the form:

$$\mathrm{var}[Z_i^{(m)}]=m^2\mathrm{var}[Y^{(m)}]=({\widehat{\mathrm{\sigma }}}^2/{\widehat{\mathrm{\mu }}}^{2-\mathrm{\beta }})E{[Z_i^{(m)}]}^{2-\mathrm{\beta }}$$

(14)

Since $\widehat{\mathrm{\mu }}$ and ${\widehat{\mathrm{\sigma }}}^2$ are constant, this represents a variance to mean power law with exponent p = 2 – β = 2H. The power law found from the prime number deviations revealed that p = 1.83, and so the Hurst exponent was H = 0.92.

3.3. 1/f Noise from the Prime Number Deviations

Autocorrelations of the form r(k) ~ k−β imply, by virtue of the Wiener-Khintchine theorem [19], that the corresponding power spectral density will approximate S(f) ~ fβ−1, where f is the frequency. In the case of the prime number deviations |D(x)|, this would imply S(f) ~ f−0.83, where the frequency is determined from the spacing of the consecutive values of the data sequence. Power spectra like this, with $S(f)\propto 1/f^{\mathrm{\gamma }}$ and 0 < γ < 2, are the hallmark of 1/f noise.

3.4. Prime Number Deviations Described by a Tweedie Exponential Dispersion Model

In addition to 1/f noise, the variance-to-mean power law is associated with a class of probability distributions, known as the Tweedie exponential dispersion models, named after the man who first described them [20]. There are several types of Tweedie models, each distinguished by the values of their power law exponent p, including the Gaussian (p = 0), Poisson (p = 1), compound Poisson-gamma (PG) (1 < p < 2), gamma (p = 2) and inverse Gaussian (p = 3) distributions [13]. We employ here the class of PG distributions, characterized by gamma distributed jumps over the domain of the positive real numbers plus zero, to model the deviations |D(x)|. The additive form for the cumulant generating function for this PG distribution can be written as:

$$K^{*}(s)=\mathrm{\lambda }\mathrm{\kappa }(\mathrm{\theta })[{(1+\frac{s}{\mathrm{\theta }})}^{\mathrm{\alpha }}-1]$$

(15)

Here, s is the variable of the generating function, θ is the canonical parameter, λ is the index statistic, and the constant α and the cumulant function k(θ) are given by:

$$\mathrm{\alpha }=(p-2)/(p-1)\text{ and}$$

(16)

$$\mathrm{\kappa }(\mathrm{\theta })=\frac{\mathrm{\alpha }-1}{\mathrm{\alpha }}{\left(\frac{\mathrm{\theta }}{\mathrm{\alpha }-1}\right)}^{\mathrm{\alpha }}$$

(17)

The PG distribution is thus specified by 3 independent adjustable parameters α, λ and θ. The parameter α relates to Taylor’s power law exponent p, whereas λ and θ relate to the notions of shape and scale parameter employed in the conventional description of distributions.

The probability density function on the variable z, p*(z, θ, λ, α), that corresponds to this distribution does not exist in closed form. However, it can be expressed as an infinite series [13]:

$$p^{*}(z;\mathrm{\theta },\mathrm{\lambda },\mathrm{\alpha })=c^{*}(z;\mathrm{\lambda })\exp [\mathrm{\theta }·z-\mathrm{\lambda }\mathrm{\kappa }(\mathrm{\theta }\left)\right],\text{ with}$$

(18)

$$c^{*}(z;\mathrm{\lambda })=\{\begin{array}{cc}\frac{1}{z}{\displaystyle \sum _{n=1}^{\infty }}{\mathrm{\lambda }}^n{\mathrm{\kappa }}^n(-1/z)/\Gamma (-\mathrm{\alpha }·n)n!& \text{for }z>\text{0}\hfill \\ 1& \text{for }z=0\hfill \end{array}$$

(19)

Figure 2b provides a probability-probability plot of the respective CDF fitted to data derived from the sequence of |D(x)| from the first 50,000 integers. The empirical and theoretical CDFs agreed well. Similarly Figure 3b provides the probability-probability plot corresponding to |D(x)| derived from the integers x = 10⁶…10⁷, in steps of 10³. The Tweedie PG CDF agreed closely with the empirical CDF. Figure 3d,f provides the probability-probability plots corresponding to the Tweedie PG distribution fitted from the prime number deviations corresponding to the integer sequences x = 10⁸…10⁹ in steps of 10⁵ and x = 10¹¹…10¹² in steps of 10⁸. The Tweedie PG distribution thus appeared to remain valid for over 12 orders of magnitude of data.

3.5. The Tweedie Convergence Theorem

For exponential dispersion models ED(μ, σ²) with unit variance functions of the form $V(\mathrm{\mu })\propto {\mathrm{\mu }}^p$ Jørgensen et al. have shown that as $\mathrm{\mu }\to 0$ or $\mathrm{\mu }\to \infty$ then, within the constant factor c, c − 1 ED(cμ, σ² c^2−p) will converge to the form of a Tweedie model as either c → 0 or $c\to \infty$ [14]. Since the variance functions for many probability distributions approximate the form $V(\mathrm{\mu })\propto {\mathrm{\mu }}^p$, for small or large values of μ, the Tweedie distributions will act as the foci of convergence for a wide variety of data [14]. This convergence property appears related to stable generalizations of the CLT [13], suggesting that the Tweedie models have a role analogous to that of the Gaussian distribution in statistical theory. As will be shown below, this theorem has implications with respect to the distribution of prime numbers. Parenthetically, it should also be mentioned that the mean and variance of an additive random variable Z are given by the equations E(Z) = λμ and var(Z) = λV(μ).

3.6. The Theoretical Behavior of the Prime Number Deviations

We have described the empirical behavior of the statistic |D(x)| = |R(x) – π(x). The Tweedie convergence theorem requires for complex statistical systems with variance functions, which approximate $V(\mathrm{\mu })\propto {\mathrm{\mu }}^p$, that these systems be mathematically required to converge towards a Tweedie exponential dispersion model. The empirical demonstrations from the prime number deviations established that their variance function had this approximate behavior and the convergence requirements appeared justified.

3.7. Other Examples of Variance to Mean Power Laws and 1/f Noise

Similar variance to mean power laws have been extensively reported with nonlinear phenomena in connection with the clustering of species within their habitats (where it is known as Taylor’s power law) [21], human sexual contacts in AIDS [22], pediatric leukemia cases [23] and murine experimental metastases [24]. As well, this relationship is evident with spatial and temporal data associated with long range correlations, such as temporal changes in measles incidence [25], regional blood flow heterogeneity (Bassingthwaighte’s fractal scaling relation) [26], the genomic distributions of SNPs [27] and genes [28], auditory nerve spike trains [29], fluctuations in foreign exchange quotations [30], and with internet traffic [18] (where it has been called fluctuation scaling). With such diverse manifestations of this power law, the question would arise as to whether a more fundamental process could be implicated. We explain the wide manifestation of this power law by an asymptotic convergence of systems towards the Tweedie distributions [14].

The Gaussian and other stable distributions have their elementary role in probability theory consequent to the (generalized) central limit theorem, where they appear as the limiting forms for standardized sums of independent random variables with the Gaussian distribution appearing when the components have finite variances. The Tweedie convergence theorem [13] implies that a wide range of exponential dispersion models can be approximated by the Tweedie models according to a central limit-like effect. For this reason many types of non-Gaussian data will exhibit a power law relationship between the variance and the mean.

Recently, Taylor’s power law and its implicit fluctuation scaling have been explained in terms of physical processes. Eisler et al. have provided a mean field framework that employs the summation of random variables to show that Taylor’s law can be considered a consequence of a limiting theorem they relate to impact inhomogeneity [31]. Fronczak and Fronczak provided an alternative explanation that employed fluctuation dissipation in equilibrium and non-equilibrium systems to argue that Taylor’s law is a consequence of the second law of thermodynamics and the action of a putative external field [32]. In the case of the prime number deviations, an explanation based on thermodynamic principles would not seem applicable.

The Tweedie convergence theorem has a more general scope than the limit theorem offered by Eisler et al. Indeed, the Tweedie models act as limiting distributions for a wide range of statistical models through a convergence effect that generalizes upon the central limit theorem [13,14,33,34]. Distributions within the domain of attraction of positive or extreme stable distributions can thus converge to manifest the variance to mean power law. One can hypothesize physical principles, or specific biological mechanisms, to explain the manifestation of Taylor’s law, but it would seem that this mathematically demonstrable convergence property would provide a more robust and general explanation.

Sequences like the Riemann deviations D(x), that express a variance to mean power law and that also obey the Tweedie PG distribution have similarly been generated from random matrices of the Gaussian unitary and orthogonal ensembles [35], the Mertens function (Equation (6)) [36], Chebyshev’s function [37], as well as within the genomic distribution of SNPs along chromosome 1 of the horse [36]. Fronczak and Fronczak’s derivation of the variance to mean power law, mentioned above, [32] can be shown to exactly yield the Tweedie distributions (Equations (15)–(17)) [36], and Eisler et al. have shown their model for impact inhomogeneity to yield equations similar to Tweedie’s [31]. The Tweedie convergence effect, which has as its focus these equations, can be further extended by theorem to multiplicative statistical models which, in turn, allow for a mechanistic explanation for the genesis of multifractality [38].

1/f noise is another empirical phenomenon that has been widely observed in physical and biological systems [39,40]. There is no generally accepted explanation for the appearance of 1/f noise, though it notably has been explained in terms of the self-organized criticality of evolutionary behavior in extended dissipative systems [41]. As noted above, 1/f noise is directly related to long-range correlations and, in turn, to a variance to mean power law [18]. In this latter context, certain types of 1/f noise can thus be viewed as consequences of the statistical convergence behavior associated with the Tweedie PG model. In fact, Taylor’s law and 1/f noise have been demonstrated to occur together within the genomic distribution of genes and SNPs along human chromosome 1 [42].

4. Conclusions

The variance to mean power law implies a statistical self-similarity that can underlie certain fractal patterns. Related fractal patterns have been demonstrated within the distributions of the prime numbers [43] and the Riemann zeta zeros [44]. Holdom showed that the deviations b(i) of the offset logarithmic integral of the ith prime number p_i, $b(i)\equiv Li(p_i)-i$, exhibited scale invariant correlations that were related to the Riemann hypothesis [45]. Indeed, it is possible to express the Riemann hypothesis in terms of the behavior of a random walk on a fractal lattice [46]. In this context it should not seem surprising that Taylor’s scale invariant law would manifest with the deviations |D(x)|.

It is the long range correlations in the distribution of the prime numbers that have been interpreted to indicate a fractal pattern [43]. The variance to mean power law is a manifestation of a fractal pattern where the power law exponent directly relates to the fractal dimension $D=H-2$ through the equation, $p=4-2D$. The assessments from Figure 2a and Figure 3, though, yielded values for p that ranged between 1 and 2. Some of this variation might reflect numerical artifact, but a component might also be attributable to the distribution of the prime numbers, itself. Indeed p can be shown to vary between 1 to 2 over different regions of the natural numbers and with different sample sizes (data not provided). When regions of a data sequence are found to have different fractal properties, as implied by the regional differences in p within the sequence of prime number deviations, that sequence would be said to be multifractal [47]. Multifractality of this nature has been described from the sequential deviations of ordered eigenvalues from the Gaussian unitary and orthogonal ensembles [38]. A current area of investigation deals with the apparent multifractality of the Riemann deviations |D(x)|.

The Riemann deviations D(x) are intimately related to the positions of the prime numbers. Our examinations have revealed their absolute values to behave asymptotically as Tweedie probability distributions, perhaps due to a central limit-like effect, much like Erdös and Kac’s demonstration of the asymptotic Gaussianity of the number of prime divisors of the integers [48]. Thus far, our evidence for a power variance to mean relationship with each of these functions is empirical, but it extends over many orders of magnitude and it adds to the growing evidence of a unifying description for disparate mathematical, physical and biological phenomena obtainable through the Tweedie exponential dispersion models. Additionally, any statistical model for sequential data designed to produce Taylor’s law is mathematically required to converge towards a Tweedie model, and to yield 1/f noise [35].

Self-organized criticality was mentioned earlier in the introduction. This is a widely-held hypothesis used to explain the genesis of 1/f noise and other power law scaling behaviors [41]. Sandpile model simulations have generally been used to demonstrate 1/f noise and, thus, to support this hypothesis [41], yet the fluctuations evident to sandpile simulations also manifest a variance to mean power law and conform to the Tweedie compound Poisson-gamma distribution, raising the possibility that phenomena attributed to self-organized criticality can alternatively be attributed to the convergence behavior associated with the Tweedie models [15]. The irregular distribution of prime numbers thus appears to be one of many examples of Taylor’s law and fluctuation scaling that are similarly implicated with this mathematical convergence behavior.

Self-organized criticality is postulated to occur within dynamical systems that naturally progress to borderline unstable and organized states, without any outside manipulation of the dynamical parameters. However, with the Riemann deviations examined here the manifestation of 1/f noise (the hallmark of self-organized criticality) would appear here to be possibly attributable to a mathematical convergence effect related to the central limit theorem of statistics. Further investigation into this matter could lead to a paradigm change in our understanding of processes that have conventionally been attributed to self-organized criticality.